2012高考专题训练五.空间几何体
2012吉林高考数学二轮复习—空间几何体

2012吉林高考数学二轮复习-空间几何体I 卷一、选择题1.一个空间几何体的正视图、侧视图均是长为2、高为3的矩形,俯视图是直径为2的圆(如下图),则这个几何体的表面积为( )A .12π+B .7πC . π8D .π20【答案】C2.设长方体的长、宽、高分别为a 2、a 、a ,其顶点都在一个球面上,则该球的表面积为( )A .23a πB .26a πC .212a πD .224a π【答案】B3. 如图是某四棱锥的三视图,则该几何体的表面积等于 ( )A .3465+B .66543+C .663413+D .175+【答案】A4. 一个二面角的两个面分别垂直于另一个二面角的两个面,那么这两个二面角( )A .相等B .互补C .相等或互补D .不能确定【答案】D5.若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积...等于 ( )A .6B .2C .23D 3【答案】A6. 一几何体的三视图如下图所示,则该几何体的体积是( )A . 2B . 43C .312+ D .316+【答案】B7.下列四个几何体中,各几何体的三视图有且仅有两个视图相同的是( )A .①②B .②③C .②④D .①③【答案】C解析:①的三个视图都相同;②的主视图与左视图相同,与俯视图不同;③的三个视图互不相同;④的主视图与左视图相同,而与俯视图不同。
8.某几何体的三视图如图所示,则它的体积是( )A .283π-B .8-3πC .82π-D .23π【答案】A9.如图是某一几何体的三视图,则这个几何体的体积为()A. 4 B. 8 C. 16 D. 20【答案】C10.在正三棱锥S-ABC中,M、N分别是SC、BC的中点,且AMMN⊥,若侧菱SA=32,则正三棱 S-ABC外接球的表面积为()A.12πB.32πC.36πD.48π【答案】C11.已知六棱锥P ABCDEF-的底面是正六边形,PA⊥平面ABC.则下列结论不正确...的是()A.//CD平面PAFB.DF⊥平面PAFC.//CF平面PABD.CF⊥平面PAD【答案】D12.已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是()A .38000cm 3B .34000cm 3C .20003D .40003【答案】A13.如图是一个几何体的三视图,根据图中数据,可得该几何体的体积是( )A .3πB .43πC .133πD .683π【答案】C14.某几何体的三视图如图所示,则该几何体的体积为 ( )A .21 B .31 C .41 D .61【答案】A15.某几何体的三视图如图所示,则该几何体的体积为( )A .21 B .31 C .41 D .61【答案】A16.已知α、β是两上不同的平面,m ,n 是两条不同的直线,给出下列命题: ①若,,m m αβαβ⊥⊂⊥则;②若,,//,//m n m n ααββ⊂⊂,则//αβ③如果,,,m n m n αα⊂⊄是异面直线,那么n 与α相交; ④若,//,,,m n m n n αβαβ=⊄⊄且则////n n αβ且。
高中数学高考专题(5)立体几何的高考解答题型及求解策略

高中数学高考专题(5)立体几何的高考解答题型及求解策略立体几何的解答题型主要采用“论证与计算”相结合的模式,即首先是利用定义、定理、公理等证明空间的线线、线面、面面平行或垂直,再计算几何体的体积.试题背景有折叠问题、探索性问题等,考查空间想象能力、逻辑思维能力及转化与化归思想的应用能力.题型一线面位置关系的证明题型概览:空间中线面的平行与垂直的证明有两种思路:一是利用相应的判定定理和性质定理去解决;二是利用空间向量法来论证,应用向量证明线、面的位置关系的关键是把空间线面位置关系的判定定理和性质定理与空间向量建立对应关系,把空间位置关系的证明转化为空间向量的运算,通过运算解决证明问题.这里以传统方法为例建立审题程序与答题模板,向量方法参照本专题题型二.如图,四边形ABCD是菱形,四边形MADN是矩形,平面MADN⊥平面ABCD,E、F分别为MA、DC的中点,求证:(1)EF∥平面MNCB;(2)平面MAC⊥平面BND.[审题程序]第一步:利用中位线、平行四边形的性质在四边形MNCB内确定与EF平行的直线;第二步:在平面MAC和平面BND中寻找与另一平面垂直的直线;第三步:应用面面垂直、菱形的性质,由线线垂直解决.[规范解答](1)如图,取NC的中点G,连接FG,MG.因为ME∥ND且ME=12ND,F、G分别为DC、NC的中点,FG∥ND且FG=12ND,所以FG与ME平行且相等,所以四边形MEFG是平行四边形,所以EF∥MG,又MG⊂平面MNCB,EF⊄平面MNCB,所以EF∥平面MNCB.(2)如图,连接BD、MC.因为四边形MADN是矩形,所以ND⊥AD.因为平面MADN⊥平面ABCD,平面ABCD∩平面MADN=AD,DN⊂平面MADN,所以ND⊥平面ABCD,所以ND⊥AC.因为四边形ABCD是菱形,所以AC⊥BD.因为BD∩ND=D,所以AC⊥平面BDN.又AC⊂平面MAC,所以平面MAC⊥平面BDN.[答题模板]解决这类问题的答题模板如下:1.(2016·北京西城区高三期末)如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G,H分别是CE,CF的中点.(1)求证:AC⊥平面BDEF;(2)求证:平面BDGH∥平面AEF;(3)求多面体ABCDEF的体积.[解](1)证明:因为四边形ABCD是正方形,所以AC⊥BD.又平面BDEF⊥平面ABCD,平面BDEF∩平面ABCD=BD,且AC⊂平面ABCD,所以AC⊥平面BDEF.(2)证明:在△CEF中,因为G,H分别是CE,CF的中点,所以GH∥EF.又GH⊄平面AEF,EF⊂平面AEF,所以GH∥平面AEF.设AC∩BD=O,连接OH.在△ACF中,因为OA=OC,CH=HF,所以OH∥AF.因为OH⊄平面AEF,AF⊂平面AEF,所以OH∥平面AEF.因为OH∩GH=H,OH,GH⊂平面BDGH,所以平面BDGH∥平面AEF.(3)由(1)得AC⊥平面BDEF.因为AO=2,四边形BDEF的面积S▱BDEF=3×22=62,=4.所以四棱锥A-BDEF的体积V1=13×AO×S▱BDEF同理,四棱锥C-BDEF的体积V2=4.所以多面体ABCDEF的体积V=V1+V2=8.题型二求空间几何体的体积题型概览:计算几何体的体积,关键是根据条件找出相应的底面和高,应注意充分利用多面体的截面和旋转体的轴截面,将空间问题转化为平面问题.(1)直接法:对于规则几何体,直接利用公式计算即可.(2)割补法:当一个几何体的形状不规则时,常通过分割或者补形的手段将此几何体变为一个或几个规则的、体积易求的几何体,然后再计算.经常考虑将三棱锥还原为三棱柱或长方体,将三棱柱还原为平行六面体,将台体还原为锥体.(3)等体积法:一般利用三棱锥的“等积性”求三棱锥体积,可以把任何一个面作为三棱锥的底面.注意两点:一是求体积时,可选择“容易计算”的方式来计算;二是利用“等积性”可求“点到面的距离”,关键是在面中选取三个点,与已知点构成三棱锥.(2016·全国卷Ⅲ)如图,四棱锥P-ABCD中,P A⊥底面ABCD,AD∥BC,AB=AD=AC=3,P A=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(1)证明:MN∥平面P AB;(2)求四面体N-BCM的体积.[审题程序]第一步:由线线平行或面面平行证明(1);第二步:由N 为PC 中点,推证四面体N -BCM 的高与P A 的关系; 第三步:利用直接法求四面体的体积.[规范解答] (1)由已知得AM =23AD =2.取BP 的中点T ,连接AT ,TN ,由N 为PC 中点知TN ∥BC ,TN =12BC =2.又AD ∥BC ,故TN 綊AM ,四边形AMNT 为平行四边形, 于是MN ∥AT .因为AT ⊂平面P AB ,MN ⊄平面P AB , 所以MN ∥平面P AB .(2)因为P A ⊥平面ABCD ,N 为PC 的中点,所以N 到平面ABCD 的距离为12P A .取BC 的中点E ,连接AE .由AB =AC =3得AE ⊥BC ,AE =AB 2-BE 2= 5.由AM ∥BC 得M 到BC 的距离为5, 故S △BCM =12×4×5=2 5.所以四面体N -BCM 的体积V N -BCM =13×S △BCM ×P A 2=453. [答题模板] 解决这类问题的答题模板如下:2.(2016·深圳一模)如图所示,在四棱锥S-ABCD中,底面ABCD是平行四边形,侧面SBC是正三角形,E是SB的中点,且AE⊥平面SBC.(1)证明:SD∥平面ACE;(2)若AB⊥AS,BC=2,求点S到平面ABC的距离.[解](1)证明:连接BD,交AC于点F,连接EF.∵四边形ABCD是平行四边形,∴F是BD的中点,又∵E是SB的中点,∴EF∥SD.∵SD⊄平面ACE,EF⊂平面ACE,∴SD∥平面ACE.(2)∵AB⊥AS,BC=BS=2,且E是SB的中点,∴AE=1.∵AE⊥平面SBC,BS、CE⊂平面SBC,∴AE⊥BS,AE⊥CE.∴AB=AE2+BE2= 2.又侧面SBC 是正三角形,∴CE =3, ∴AC =AE 2+CE 2=2,∴△ABC 是底边长为2,腰长为2的等腰三角形, ∴S △ABC =12×2×4-12=72.设点S 到平面ABC 的距离为h .由V 三棱锥S -ABC =V 三棱锥A -SBC ,得13h ·S △ABC =13AE ·S △SBC ,∴h =AE ·S △SBC S △ABC =237=2217.题型三 立体几何中的探索性问题题型概览:如果知道的是试题的结论,而要求的却是试题的某一个存在性条件(如存在某个定点、定直线、定值等),这种试题称为存在探索型试题.解题策略一般是先假设结论成立,然后以该结论作为一个已知条件,再结合题目中的其他已知条件,逆推(即从后往前推),一步一步推出所要求的特殊条件,即要求的存在性条件.若能求出,则存在;若不能求出,则不存在.(2016·石家庄调研)如图,在三棱柱ABC -A 1B 1C 1中,A 1A ⊥平面ABC ,AC ⊥BC ,E 在线段B 1C 1上,B 1E =3EC 1,AC =BC =CC 1=4.(1)求证:BC ⊥AC 1;(2)试探究:在AC 上是否存在点F ,满足EF ∥平面A 1ABB 1?若存在,请指出点F 的位置,并给出证明;若不存在,请说明理由.[审题程序]第一步:由B 1E =3EC 1及EF ∥平面A 1ABB 1猜想点F 的位置;第二步:在平面A 1ABB 1内探求与EF 平行的直线或寻找经过EF 与平面A 1ABB 1平行的平面; 第三步:由线线平行或面面平行推理论证.[规范解答] (1)证明:∵AA 1⊥平面ABC ,BC ⊂平面ABC ,∴BC ⊥AA 1. 又∵BC ⊥AC ,AA 1∩AC =A ,∴BC ⊥平面AA 1C 1C . 又AC 1⊂平面AA 1C 1C ,∴BC ⊥AC 1.(2)解法一:当AF=3FC时,EF∥平面A1ABB1.证明如下:如图1,在平面A1B1C1内过点E作EG∥A1C1交A1B1于点G,连接AG.∵B1E=3EC1,∴EG=34A1C1.又AF∥A1C1且AF=3,4A1C1∴AF∥EG且AF=EG,∴四边形AFEG为平行四边形,∴EF∥AG.又EF⊄平面A1ABB1,AG⊂平面A1ABB1,∴EF∥平面A1ABB1.解法二:当AF=3FC时,EF∥平面A1ABB1.证明如下:如图2,在平面BCC1B1内过点E作EG∥BB1交BC于点G,连接FG. ∵EG∥BB1,EG⊄平面A1ABB1,BB1⊂平面A1ABB1,∴EG∥平面A1ABB1.∵B1E=3EC1,∴BG=3GC,∴FG∥AB.又AB⊂平面A1ABB1,FG⊄平面A1ABB1,∴FG∥平面A1ABB1.又EG⊂平面EFG,FG⊂平面EFG,EG∩FG=G,∴平面EFG∥平面A1ABB1.∵EF⊂平面EFG,∴EF∥平面A1ABB1.[答题模板]解决这类问题的答题模板如下:3.如图,三棱柱ABC-A1B1C1的底面是边长为4的正三角形,侧棱AA1⊥底面ABC,M为A1B1的中点.(1)证明:MC⊥AB;(2)若AA1=26,侧棱CC1上是否存在点P,使得MC⊥平面ABP?若存在,求PC的长;若不存在,请说明理由.[解](1)证明:取AB的中点N,连接MN,CN,则MN⊥底面ABC,MN⊥AB.因为△ABC是正三角形,所以NC⊥AB.因为MN∩NC=N,MN⊂平面MNC,NC⊂平面MNC,所以AB⊥平面MNC,所以AB⊥MC.(2)由(1)知MC⊥AB,若存在点P使得MC⊥平面ABP,则必有MC⊥BP.过M作MQ⊥B1C1,垂足为Q,连接QC,则QC是MC在平面BCC1B1内的射影,只需QC⊥BP即可,此时Rt△QC1C与Rt△PCB相似,QC1C1C =PCCB,所以PC=QC1·CBC1C=3×426=6,点P恰好是CC1的中点.。
高考数学复习空间几何体的表面积与体积专题训练(含答案)

高考数学复习空间几何体的表面积与体积专题训练(含答案)答案 C4.已知三棱锥S-ABC的所有顶点都在球O的球面上,ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此棱锥的体积为().A. B. C. D.解析在直角三角形ASC中,AC=1,SAC=90,SC=2,SA==;同理SB=.过A点作SC的垂线交SC于D点,连接DB,因SAC≌△SBC,故BDSC,故SC平面ABD,且平面ABD为等腰三角形,因ASC=30,故AD=SA=,则ABD的面积为1=,则三棱锥的体积为2=.答案 A.某品牌香水瓶的三视图如下(单位:cm),则该几何体的表面积为().A.cm2B.cm2C.cm2D.cm2解析该几何体的上下为长方体,中间为圆柱.S表面积=S下长方体+S上长方体+S圆柱侧-2S圆柱底=244+442+233+431+21-22=94+.答案 C.已知球的直径SC=4,A,B是该球球面上的两点,AB=,ASC=BSC=30,则棱锥SABC的体积为().A.3B.2C.D.1解析由题可知AB一定在与直径SC垂直的小圆面上,作过AB的小圆交直径SC于D,设SD=x,则DC=4-x,此时所求棱锥即分割成两个棱锥SABD和CABD,在SAD和SBD中,由已知条件可得AD=BD=x,又因为SC为直径,所以SBC=SAC=90,所以DCB=DCA=60,在BDC中,BD=(4-x),所以x=(4-x),所以x=3,AD=BD=,所以三角形ABD为正三角形,所以V=SABD4=.答案 C二、填空题.已知S、A、B、C是球O表面上的点,SA平面ABC,ABBC,SA=AB=1,BC=,则球O的表面积等于________.解析将三棱锥S-ABC补形成以SA、AB、BC为棱的长方体,其对角线SC为球O的直径,所以2R=SC=2,R=1,表面积为4.答案 4.如图所示,已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成,则该多面体的体积是________.解析由题知该多面体为正四棱锥,底面边长为1,侧棱长为1,斜高为,连接顶点和底面中心即为高,可求得高为,所以体积V=11=.答案9.已知某几何体的直观图及三视图如图所示,三视图的轮廓均为正方形,则该几何体的表面积为________.解析借助常见的正方体模型解决.由三视图知,该几何体由正方体沿面AB1D1与面CB1D1截去两个角所得,其表面由两个等边三角形、四个直角三角形和一个正方形组成.计算得其表面积为12+4.答案 12+4.如图所示,正方体ABCD-A1B1C1D1的棱长为6,则以正方体ABCD-A1B1C1D1的中心为顶点,以平面AB1D1截正方体外接球所得的圆为底面的圆锥的全面积为________.解析设O为正方体外接球的球心,则O也是正方体的中心,O到平面AB1D1的距离是体对角线长的,即为.又球的半径是正方体对角线长的一半,即为3,由勾股定理可知,截面圆的半径为=2,圆锥底面面积为S1=(2)2=24,圆锥的母线即为球的半径3,圆锥的侧面积为S2=23=18.因此圆锥的全面积为S=S2+S1=18=(18+24).答案 (18+24)三、解答题.一个几何体的三视图如图所示.已知主视图是底边长为1的平行四边形,左视图是一个长为,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.(1)求该几何体的体积V;(2)求该几何体的表面积S.解 (1)由三视图可知,该几何体是一个平行六面体(如图),其底面是边长为1的正方形,高为,所以V=11=.(2)由三视图可知,该平行六面体中,A1D平面ABCD,CD平面BCC1B1,所以AA1=2,侧面ABB1A1,CDD1C1均为矩形,S=2(11+1+12)=6+2..在直三棱柱ABC-A1B1C1中,底面为直角三角形,ACB=90,AC=6,BC=CC1=,P是BC1上一动点,如图所示,求CP+PA1的最小值.解 PA1在平面A1BC1内,PC在平面BCC1内,将其铺平后转化为平面上的问题解决.铺平平面A1BC1、平面BCC1,如图所示.计算A1B=AB1=,BC1=2,又A1C1=6,故A1BC1是A1C1B=90的直角三角形.CP+PA1A1C.在AC1C中,由余弦定理,得A1C===5,故(CP+PA1)min=5..某高速公路收费站入口处的安全标识墩如图1所示,墩的上半部分是正四棱锥PEFGH,下半部分是长方体ABCDEFGH.图2、图3分别是该标识墩的主视图和俯视图.(1)请画出该安全标识墩的左视图;(2)求该安全标识墩的体积.(1)左视图同主视图,如图所示:(2)该安全标识墩的体积为V=VPEFGH+VABCDEFGH=40260+40220=64 000(cm3)..如图(a),在直角梯形ABCD中,ADC=90,CDAB,AB=4,AD=CD=2,将ADC沿AC折起,使平面ADC平面ABC,得到几何体D-ABC,如图(b)所示.(1)求证:BC平面ACD;(2)求几何体D-ABC的体积.(1)证明在图中,可得AC=BC=2,从而AC2+BC2=AB2,故ACBC,又平面ADC平面ABC,平面ADC平面ABC=AC,BC平面ABC,BC平面ACD.(2)解由(1)可知,BC为三棱锥B-ACD的高,BC=2,SACD=2,VB-ACD=SACDBC=22=,由等体积性可知,几何体D-ABC的体积为.空间几何体的表面积与体积专题训练及答案的全部内容就是这些,查字典数学网预祝考生可以取得优异的成绩。
22012年高考数学立体几何专题练习及答案

绝密★启用前2012届高三数学二轮精品专题卷:专题9 立体几何考试范围:立体几何一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个符合题目要求的)1.若直线l 与平面α垂直,则下列结论正确的是 ( )A .直线l 与平面α内所有直线都相交B .在平面α内存在直线m 与l 平行C .在平面α内存在直线m 与l 不垂直D .若直线m 与平面α平行,则直线l ⊥m 2.某个几何体的三视图如图所示,根据图中标出的长度,那么这个几何体的体积是 ( ) A .3 B .33C .332D .3 3.(理)如下图所示是一个半径等于2的半球,现过半球底面的中心作一个与底面成80°角的截面,则截面的面积为( )A .2πB .πC .π2D . 80sin π(文)如上图所示是一个半径等于2的半球,则这个半球的表面积为 ( ) A .π4 B .π8 C .π12 D .π16 4.(理)如下图,三棱锥P -ABC 中,三条侧棱两两垂直,且长度相等,点E 为BC 中点,则直线AE 与平面PBC 所成角的余弦值为 ( )A .33B .36C .31D .32(文)如上图,三棱锥P -ABC 中,三条侧棱两两垂直,且长度都为1,点E 为BC 上一点,则截面P AE 面积的最小值为 ( ) A .33 B .36 C .42 D .325.设a ,b ,c 表示三条直线,βα,表示两个平面,则下列命题中逆命题不成立的是 ( )A .α⊥c ,若β⊥c ,则βα∥B .α⊂b ,α⊄c ,若α∥c ,则c b ∥C .β⊂b ,若α⊥b ,则αβ⊥D .α⊂b a ,,P b a =⋂,b c a c ⊥⊥,,若βα⊥,则β⊂c6.一个圆锥的母线长为2,且侧面积为π2,则该圆锥的主视图面积为 ( ) A .1B .3C .2D .67.已知长方体ABCD D C B A -1111的外接球的体积为332π,则该长方体的表面积的最大值为 ( )A .16B .32C .36D .488.一个几何体是由若干个边长为1的正方体组成的,其主视图和左视图如图所示,若把这个几何体放到一个底面半径为π13的盛若干水的圆柱形容器,没入水中,则水面上升的高度(不溢出)最大为 ( )(1)121B .131C .π12D .π139.如图,四棱锥P -ABCD 的底面是边长为3的正方形,侧棱P A ⊥平面ABCD ,点E 在侧棱PC 上,且BE ⊥PC ,若6=BE ,则四棱锥P -ABCD 的体积为 ( )A .6B .9C .18D .2710.如图,四棱锥S -ABCD 的底面是边长为2的正方形,且6====SD SC SB SA ,E 是边BC 的中点,动点P 在表面上运动,并且总保持PE ⊥AC ,则动点P 的轨迹所围成的图形的面积为 ( )A .22B .1C .3D .6一、填空题(本大题共5小题,每小题5分,共25分.把正确答案填在题中横线上)11.已知一个空间几何体的三视图及其尺寸如图所示,则该空间几何体的体积是 .12.(理)平面P 与平面Q 所成的二面角是锐角α,直线AB ⊂平面P 且与二面角的棱成的角为锐角β,又AB 和平面Q 成的角为θ,则α,β,θ之间的某一三角函数关系为 . (文)我们知道,正三角形的内切圆和外接圆的圆心重合,且外接圆和内切圆的半径之比为2:1,类比这一结论,若一个三棱锥的所有棱长都相等,则其外接球与内切球的球心重合,则外接球与内切球半径之比为 .13.已知圆锥的母线和底面半径的夹角为60°,则其全面积与侧面积之比为 . 14.由曲线22x y =,2||=x 围成的图形绕y 轴旋转一周所得的旋转体的体积为1V ;满足422≤+y x ,1)1(22≥-+y x ,1)1(22≥++y x 的点组成的图形绕y 轴旋转一周所得的旋转体的体积为2V ,则1V :2V = .15.设圆锥的母线长为l ,底面半径为r ,满足条件“它的一个内接圆柱的侧面积等于圆锥侧面积的41”的情况有且只有一种,则=lr .三、解答题(本大题共6小题,满分75分.解答时应写出文字说明、证明过程或演算步骤) 16.(本题满分10分)如图,四棱锥P -ABCD 中,底面ABCD 是一个边长为2的正方形,P A ⊥平面ABCD ,且24=PC .M 是PC 的中点,在DM 上有点G ,过G 和AP 作平面交平面BDM 于GH .(1)求四棱锥P -ABCD 的体积; (2)求证:AP ∥GH .17.(本题满分12分)如图,已知三棱柱'''C B A ABC -的所有棱长都是2,且60''=∠=∠AC A AB A .(1)求证:点'A 在底面ABC 内的射影在∠BAC 的平分线上; (2)求棱柱'''C B A ABC -的体积.18.(本题满分13分)如图,多面体ABCD —EFG 中,底面ABCD 为正方形,GD //FC //AE ,AE ⊥平面ABCD ,其正视图、俯视图及相关数据如图:(1)求证:平面AEFC ⊥平面BDG ; (2)求该几何体的体积;(3)求点C 到平面BDG 的距离.19.(本题满分13分)如图一简单几何体的一个面ABC 内接于圆O ,G ,H 分别是AE ,BC 的中点,AB 是圆O 的直径,四边形DCBE 为平行四边形,且DC ⊥平面ABC . (1)求证:GH //平面ACD ;(2)证明:平面ACD ⊥平面ADE ; (3)若AB =2,BC =1,23tan =∠EAB ,试求该几何体的体积V .20.(本题满分13分)边长为2的正方体1111D C B A A B C D -中,P 是棱CC 1上任一点,)20(<<m m CP =(1)是否存在满足条件的实数m ,使平面⊥1BPD 面11B BDD ?若存在,求出m 的值;否则,请说明理由. (2)(理)试确定直线AP 与平面D 1BP 所成的角正弦值关于m 的函数)(m f ,并求)1(f 的值.(文)是否存在实数m ,使得三棱锥PAC B -和四棱锥1111D C B A P -的体积相等?若存在,求出m 的值;否则,请说明理由.21.(本题满分14分)如图,直角梯形ABCD 中, 90=∠=∠BAD ABC ,AB =BC 且△ABC 的面积等于△ADC 面积的21.梯形ABCD 所在平面外有一点P ,满足P A ⊥平面ABCD ,PB PA =.(1)求证:平面PCD ⊥平面PAC ;(2)侧棱PA 上是否存在点E ,使得//BE 平面PCD ?若存在,指出点E 的位置并证明;若不存在,请说明理由. (3)(理)求二面角C PD A --的余弦值.2012届专题卷数学专题九答案与解析1.【命题立意】本题考查直线与平面垂直的定义及直线与平面平行的简单性质. 【思路点拨】首先根据直线与平面垂直的定义判断出直线与平面内所有直线的位置关系,再根据直线与平面的平行性质分析直线之间的关系即可.【答案】D 【解析】根据直线和平面垂直的定义可知,直线l 与平面α内的直线都垂直,可能是异面也可能相交,故A 、B 、C 都是错误的;对于D ,在平面α内一定存在直线n 与m 平行,且l ⊥n ,故l ⊥m ,所以D 是正确的. 2.【命题立意】本题借助三视图考查三棱锥体积的求解.【思路点拨】把三视图对应的几何体还原成三棱锥,根据棱锥的体积计算公式即可求解. 【答案】B 【解析】根据三视图可知,原几何体是一个三棱锥,且底面是边长为2的正三角形,高为1,故体积为331331=⨯⨯=V .3.(理)【命题立意】本题主要考查球的结构及截面特征.【思路点拨】先根据条件分析出截面的特点,再利用相应面积公式计算即可. 【答案】C 【解析】所作截面是一个半大圆,面积为ππ2421=⨯.(文)【命题立意】本题主要考查球的面积计算.【思路点拨】此半球的表面积是一个半球面的面积加上一个大圆的面积. 【答案】C 【解析】图中半球的面积为πππ1284=+. 4.(理)【命题立意】本题借助特殊的三棱锥考查线面垂直的判定、直线和平面所成角的求解.【思路点拨】根据条件易知,P A ⊥平面PBC ,故直线AE 与平面PBC 所成的角即为∠APE ,再在Rt △P AE 中利用三角函数的定义即可求解. 【答案】A 【解析】因为P A ⊥PB ,P A ⊥PC ,所以P A ⊥平面PBC ,所以,直线AE 与平面PBC 所成的角即为∠APE ,设P A =PB =PC =1,则2===BC AC AB ,因为E 为BC 中点,所以26=AE ,故33cos 22=-==∠AE PA AE AEPEAPE .(文)【命题立意】本题借助特殊的三棱锥考查线面垂直的判定、截面面积的求解.【思路点拨】先判断三角形的形状,再根据面积的表达式求最小值.【答案】C 【解析】因为三条侧棱两两垂直且长度为1,所以AP ⊥平面PBC ,∴AP ⊥PE ,PE PE AP S PAE 2121=⋅=∆,故只需PE 的长度最小,所以PE ⊥BC 时,22=PE ,面积取得最小值42.5.【命题立意】本题借助命题真假的判定考查直线与平面、平面与平面之间的平行与垂直关系.【思路点拨】先写出每个命题的逆命题,再逐个判断即可.要注意每个命题逆命题的形式. 【答案】C 【解析】选项C 的逆命题是β⊂b ,若αβ⊥,则a b ⊥显然不成立. 6.【命题立意】本题以圆锥为载体考查圆锥的侧面积计算及三视图的特征.【思路点拨】先根据圆锥的侧面积公式计算出圆锥底面圆的半径,进而可知主视图三角形各边的长即可求出面积.【答案】B 【解析】设圆锥底面半径为r ,则侧面积为ππ22==r S ,故1=r ,314=-=h ,而主视图是一个等腰三角形,面积为3=hr .7.【命题立意】本题以长方体为载体考查长方体与球的组合体的关系及简单的不等式性质应用.【思路点拨】先根据球的体积求出其半径,再根据长方体边长与球半径的关系建立方程,进而利用不等式性质求出表面积的最大值. 【答案】B 【解析】设球的半径为R ,则343323R ππ=,故R =2,设长方体三边长分别为a ,b ,c ,则16)2(2222==++R c b a ,表面积为2222222()32ab bc ca a b c ++≤++=.即长方体表面积的最大值为32. 8.【命题立意】本题借助三视图考查组合体的特征及圆柱体积的计算.【思路点拨】先根据三视图计算出组合体的体积最大值,再结合圆柱的体积公式,利用体积相等即可计算出水面上升的高度.【答案】B 【解析】由题知,底部这一层最多摆放9个正方体,上面一层最多摆放4个正方体.故组合体的体积最大值为13,设水面上升的高度为h ,则h21313)(ππ=,则131=h .9.【命题立意】本题考查直线与平面垂直、性质的应用及空间几何体体积的计算问题.【思路点拨】把直线与平面垂直的条件转化为直角三角形,再利用三角形内的关系计算出高P A 即可.【答案】B 【解析】因为P A ⊥平面ABCD ,所以BC ⊥P A ,又ABCD 是正方形,所以BC ⊥P A ,故BC ⊥平面P AB ,所以BC ⊥PB .322=-=BE BC CE ,在Rt △PBC 中,易得CP CE BC ⋅=2,故33392===CE BC CP ,在Rt △P AC 中,322=-=AC CP PA ,故四棱锥P -ABCD 的体积为933312=⨯⨯.10.【命题立意】本题以三棱锥为载体考查直线与平面垂直的判定与性质的应用.【思路点拨】先分析出轨迹图形的形状,再根据所给数据进行计算即可.【答案】A 【解析】由6====SD SC SB SA 可知S 在底面ABCD 内的射影是底面的中心,即AC 与BD 交点O .要使得PE 保持与AC 垂直,只需使得P 在AC 的垂面上运动,如图中的△EFG 即为P 的轨迹,且2621===SD FG EG ,221==BD EF ,△EFG 的面积22)21(2122=-⋅=EF FG EF S .11.【命题立意】本题考查三视图的识别及棱台体积的求解.【思路点拨】根据所给三视图分析出对应几何体的特征,再利用相关公式即可求出体积. 【答案】314【解析】这个空间几何体是一个一条侧棱垂直于底面的四棱台,这个四棱台的高是2,上底面是边长为1的正方形、下底面是边长为2的正方形,故其体积V =13×(12+12×22+22)×2=143.12.(理)【命题立意】本题考查二面角、直线与平面所成角之间的关系及空间想象能力. 【思路点拨】先找出二面角、直线与平面所成角对应的平面角,把题中的三个角转化到直角三角形内,进而可以找出他们的关系.【答案】βαθsin sin sin =【解析】如图,过A 作AO ⊥平面Q 垂足为O ,过O 作OC ⊥交线l 于点C ,连结AC ,易证AC ⊥l ,∴ACO ∠为二面角P -l-Q 的平面角,即α=∠ACO ,β=∠ABC ,因为AO ⊥平面Q ,所以ABO ∠为A 和平面Q 所成的角,所以θ=∠ABO .分别在Rt △AOB 、Rt △AOC 、Rt △ACB 中,有ABAO =θsin ,ACAO =αsin ,ABAC =βsin ,故βαθsin sin sin =.(文)【命题立意】本题考查类比推理及与球有关的组合体的计算问题,对空间想象能力要求较高.【思路点拨】根据组合体的主视图进行分析,分别计算出外接球和内切球半径即可. 【答案】3:1【解析】设该三棱锥的边长为a ,计算可得高为a 36,设外接球半径为R ,则根据球和三棱锥的对称性可知,球心在高所在的线段上,由勾股定理可得222)33()36(R a R a =+-,则a R 46=,故内切球半径为a a a r 1264636=-=,故外接球与内切球半径之比为3:1.13.【命题立意】本题考查圆锥侧面积与全面积的计算方法.【思路点拨】根据条件求出底面半径与母线的关系,再表示出全面积与侧面积即可.【答案】23【解析】设圆锥的底面半径为r ,母线长为l ,则由条件可得。
专题05 三种空间几何体解题方法(原卷版)

专题05 三种空间几何体解题方法题型一:几何体体积的求法 题型二:几何体表面积的求法题型三:几何体“内切”、“外接”球问题题型一:几何体体积的求法 一、单选题1.(2022·陕西商洛·高一期末)《九章算术》中记载了公元前344年商鞅督造的一种标准量器——商鞅铜方升,其外形由圆柱和长方体组合而成.已知某组合体由圆柱和长方体组成,如图所示,圆柱的底面直径为1寸,长方体的长、宽、高分别为3.8寸,3寸,1寸,该组合体的体积约为12.6立方寸,若π取3.14,则圆柱的母线长约为( )A .0.38寸B .1.15寸C .1.53寸D .4.59寸2.(2020·新疆·乌鲁木齐市第三十一中学高一期末)一个球的体积为36π,则这个球的表面积为( ) A .9πB .18πC .36πD .72π3.(2021·北京市延庆区教育科学研究中心高一期末)如图,正方体1111ABCD A B C D -的棱长为a ,那么三棱锥1D ABC -的体积是( )A .312aB .313aC .314aD .316a4.(2021·广东惠州·高一期末)已知圆锥轴截面为正三角形,母线长为2,则该圆锥的体积等于( )A B C .2π3D .2π二、填空题5.(2021·广东广州·高一期末)卢浮宫玻璃金字塔是著名美籍华裔建筑设计师贝聿铭的重要作品之一,主玻璃金字塔是一个底边长为35m ,高为21m 的正四棱锥,则该主玻璃金字塔所占空间的大小是______m 3.6.(2021·江苏连云港·高一期末)已知圆台下底面的半径为4cm ,高为4cm ,母线长为,则圆台的体积为______3cm .7.(2021·北京通州·高一期末)已知半径为R 的球,其表面积为S ,体积为V ,若S =V ,则R =________. 三、解答题8.(2022·陕西咸阳·高一期末)已知正方体ABCD -1111D C B A 的棱长为2.(1)求三棱锥1A C BD -的体积; (2)证明:1AC BD ⊥.题型二:几何体表面积的求法 一、单选题1.(2020·新疆·乌鲁木齐市第三十一中学高一期末)一个球的体积为36π,则这个球的表面积为( )A .9πB .18πC .36πD .72π2.(2021·北京师大附中高一期末)圆锥的母线长为5cm ,底面半径为2cm ,则圆锥的侧面积为( ) A .220cm π B .210cm π C .228cm π D .214cm π二、双空题3.(2021·北京师大附中高一期末)如图,这个组合体是小张同学自己设计的一个小奖杯,计划送给小刘同学,以鼓励其认真努力的学习数学,已知该奖杯中的四棱柱的高为10cm ,底面是长和宽分别为3cm 、2cm 的矩形,则该四棱柱的体积是__________3cm :奖杯顶部两个球的半径分别为5cm 和2cm ,则这两个球的表面积之和为__________2cm .三、填空题4.(2021·重庆·高一期末)已知一个圆锥的轴截面(过圆锥轴的一个截面)是一个等腰直角三角形,且圆锥的底面半径为1,则该圆锥的侧面积为__________.5.(2021·北京顺义·高一期末)以边长为1的正方形的一边所在的直线为旋转轴,其余三边旋转一周得到一个圆柱,则该圆柱的表面积是 _____.6.(2021·福建福州·高一期末)已知一个正六棱柱的所有顶点都在球面上,若正六棱柱的底面边长与侧棱长均为2,则这个球的表面积为_____.7.(2021·北京西城·高一期末)已知半径为r 的球的表面积为236cm π,那么半径为2r 的球的表面积为___________2cm .题型三:几何体“内切”、“外接”球问题 一、单选题1.(2021·黑龙江·)A .92πB .94π C .9π D .3π二、多选题2.(2021·辽宁·铁岭市清河高级中学高一期末)已知正四面体PABC 的棱长为2,M N 、分别为PA PB 、的中点.下列说法正确的有( ) A .MN PC ⊥B .异面直线BM 与PCCD 三、填空题3.(2020·天津市红桥区教师发展中心高一期末)将棱长为1的正方体木块切削成一个体积最大的球,则该球的体积为______.4.(2021·福建福州·高一期末)已知一个正六棱柱的所有顶点都在球面上,若正六棱柱的底面边长与侧棱长均为2,则这个球的表面积为_____.5.(2021·浙江·高一期末)若长方体的长,宽,高分别为3,5,4,且它的顶点都在同一个球面上,则这个球的表面积是_______.6.(2019·湖南衡阳·高一期末)已知一个正方形的所有顶点在一个球面上,若这个正方体的表面积为24,则这个球的表面积为_____.一、单选题1.(2021·吉林·长春外国语学校高一期末)已知正方体1111ABCD A B C D -中,以下结论错误的有( )A .点P 在直线1BC 上运动时,三棱锥1A D PC -的体积不变B .点P 在直线1BC 上运动时,直线AP 与平面1AD C 所成角的大小不变 C .点P 在直线1BC 上运动时,二面角1P AD C --的大小不变D .M 是平面1111D C B A 上到点D 和1C 距离相等的点,则点M 的轨迹是过点1D 的直线2.(2021·浙江湖州·高一期末)已知球面被互相垂直的两个平面所截,得到的两个圆公共弦长为若两个圆的半径分别为4,则该球的体积是( )A .36πB C .125π D .5003π3.(2021·四川成都·高一期末(理))已知A ,B 是球O 的球面上两点,23AOB π∠=,P 为该球面上动点,若三棱锥O PAB -,则球O 的表面积为( ) A .12πB .16πC .24πD .36π4.(2021·福建泉州·高一期末)《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为矩形的棱台称为刍童.如图所示的某刍童1111ABCD A B C D -中,1O ,O 为上、下底面的中心,1O O ⊥平面ABCD ,11112A B A D ==,4AB AD ==,侧棱1A A 所在直线与直线1O O 所成的角为45°,则该刍童1111ABCD A B C D -的体积为( )A .BC .563D 5.(2021·黑龙江·哈尔滨市第六中学校高一期末)设,,,A B C D 是同一个半径为2的球的球面上四点,ABC 是以为BC 120BAC ∠=︒,则三棱锥D ABC -体积的最大值为( )A B .C D 6.(2021·黑龙江·铁人中学高一期末)给出下列四个命题: (1)一个圆柱的底面半径为1,高为2,则该圆柱的体积为2π; (2)若样本数据1x ,2x ,,10x 标准差为2,则数据121x -,221x -,,1021x -的方差为16.(3)若ABC 中,π3A =,2AB =,若满足上述条件的三角形有两个,则BC 边的范围是)2.(4)设a ,e 均为单位向量,当a ,e 的夹角为23π时,a 在e 方向上的投影向量为12e 其中你认为正确的个数是( ) A .1B .2C .3D .47.(2021·福建省福州第一中学高一期末)我国南北朝名著《张邱建算经》中记载:“今有方亭,下方三丈,上方一丈,高二丈五尺,预接筑为方锥,问:接筑高几何?”大致意思是:有一个正四棱台的上、下底面边长分别为一丈、三丈,高为二丈五尺,现从上面补上一段,使之成为正四棱锥,则所补的小四棱锥的高是多少?那么,此高和原四棱台的体积分别是(注:1丈等于10尺)( ) A .12.5尺、10833立方尺 B .12.5尺、32500立方尺 C .3.125尺、10833立方尺D .3.125尺、32500立方尺8.(2022·陕西渭南·高一期末)古希腊数学家阿基米德最为满意的一个数学发现是“圆柱容球”,即在球的直径与圆柱底面的直径和圆柱的高相等时,球的体积是圆柱体积的23,且球的表面积也是圆柱表面积的23.已知体积为的圆柱的轴截面为正方形.则该圆柱内切球的表面积为( )A .12πB .C .6πD .二、多选题9.(2021·湖南·常德市第二中学高一期末)希罗平均数(Heronian mean )是两个非负实数的一种平均,设,a b是两个非负实数,则它们的希罗平均数H .关于希罗平均数有如下说法,其中正确的有( ) A .若0,0a b >>,则,a b 的希罗平均数2abH a b≤+; B .三棱台111A B C ABC -的体积V 恰好是以此三棱台的上、下底面为底面且与此三棱台等高的两个三棱柱的体积12,V V 的希罗平均数;C .在直角ABC 中,π2C =,则sin ,sin A B 的希罗平均数的取值范围为13⎛ ⎝⎦; D .已知正四棱锥P ABCD -的底面ABCD 的内切圆O 的半径为r (点O 为内切圆圆心),记PO h =.若2h r ≤,则正四棱锥P ABCD -的外接球的半径R 不小于,r h 的希罗平均数.10.(2021·浙江省桐庐中学高一期末)在边长为2的等边三角形ABC 中,点D ,E 分别是边AC ,AB 上的点,满足//DE BC 且AD ACλ=,()()0,1λ∈,将ADE 沿直线DE 折到'A DE 的位置,在翻折过程中,下列结论不成立的是( )A .在边A E '上存在点F ,使得在翻折过程中,满足//BF 平面ACD 'B .存在102λ∈⎛⎫⎪⎝⎭,,使得在翻折过程中的某个位置,满足平面A BC '⊥平面BCDEC .若12λ=,当二面角A DE B '--为直二面角时,A B '=D .在翻折过程中,四棱锥A BCDE '-体积的最大值记为()f λ,()f λ11.(2021·江苏宿迁·高一期末)已知边长为a 的菱形ABCD 中,π3ADC ∠=,将ADC 沿AC 翻折,下列说法正确的是( )A .在翻折的过程中,直线AD ,BC 所成角的范围是0,2π⎛⎫⎪⎝⎭B .在翻折的过程中,三棱锥D ABC -体积最大值为38aC .在翻折过程中,三棱锥D ABC -表面积最大时,其内切球表面积为2(14a π-D .在翻折的过程中,点D 在面ABC 上的投影为D ,E 为棱CD 上的一个动点,ED ' 三、双空题12.(2021·湖北·高一期末)在《九章算术》中,将四个面都为直角三角形的三棱锥称之为鳖臑(biē nào ).已知在鳖臑M ABC -中,面⊥MA ABC ,2MA AB BC ===,则该鳖臑的表面积为__________,它的内切球的半径为__________. 四、填空题13.(2021·陕西·西安市远东一中高一期末)如图,在四棱锥P ABCD -中,平面PAD ⊥平面ABCD ,PAD △是边长为4的等边三角形,四边形ABCD 是等腰梯形,12AB AD BC ==,则四棱锥P ABCD -外接球的表面积是____________.14.(2022·陕西商洛·高一期末)在棱长为2的正方体ABCD -1111D C B A 中,E ,F ,G ,H 分别为棱11A D ,11A B ,11B C ,11C D 的中点,将该正方体挖去两个大小完全相同 的四分之一圆锥,得到如图所示的几何体,现有下列四个结论:①CG //平面ADE ; ②该几何体的上底面的周长为42π+; ③该几何体的的体积为83π-; ④三棱锥F -ABC 的外接球的表面积为414π. 其中所有正确结论的序号是____________.15.(2021·湖南·常德市第二中学高一期末)如图,在水平面上放置两个边长为1的正三角形ABC 与DEF ,将DEF 沿垂直于水平面的方向向上平移至D E F '''△,得到多面体ABC D E F '''-,已知各侧面(D BC ',D E C ''△,E AC ',EF A ''△,F BA '△及F D B ''△)均为正三角形,则多面体ABC D E F '''-的外接球的体积为__________.16.(2021·陕西·西安市第三中学高一期末)A ,B ,C ,D 为球面上四点,M ,N 分别是AB ,CD 的中点,以MN 为直径的球称为AB ,CD 的“伴随球”,若三棱锥A BCD -的四个顶点在表面积为64π的球面上,它的两条边AB ,CD 的长度分别为AB ,CD 的伴随球的体积的取值范围是________.17.(2020·福建漳州·高一期末)正四面体P BDE -和边长为1的正方体1111ABCD A B C D -有公共顶点B ,D ,则该正四面体P BDE -的外接球的体积为______,线段AP 长度的取值范围为_______.五、解答题18.(2021·浙江宁波·高一期末)在棱长均为2的正三棱柱111ABC A B C -中,E 为11B C 的中点.过AE 的截面与棱1BB ,11A C 分别交于点F ,G .(1)若F 为1BB 的中点,求三棱柱被截面AGEF 分成上下两部分的体积比12V V ; (2)若四棱雉1A AGEF -AGEF 与底面ABC 所成二面角的正弦值; (3)设截面AFEG 的面积为0S ,AEG ∆面积为1S ,AEF 面积为2S ,当点F 在棱1BB 上变动时,求2012S S S 的取值范围.19.(2021·湖北黄冈·高一期末)如图,已知在四棱锥P ABCD -中,底面ABCD 是梯形,//BC AD 且 =2BC AD ,平面 PAC ⊥平面ABCD , =?PA PC ,PA AB ⊥.(1)证明:AB PC ⊥;(2)若PA PC ⊥,=2=PB PC 4,求四棱锥 P ABCD -的体积.20.(2021·安徽蚌埠·高一期末)如图,四边形ABCD 是边长为4的菱形,60C ∠=,PA ⊥平面ABCD ,将菱形ABCD 沿对角线BD 折起,使得点C 到达点Q 的位置,且平面QBD ⊥平面ABD .(1)求证://PA 平面QBD ;(2)若点,,,,A B D P Q 在同一个球面上,求三棱锥P ABD -与三棱锥Q ABD -的公共部分的体积.21.(2021·广东中山·高一期末)如图所示,在正方体1111ABCD A B C D -中,点G 在棱11D C 上,且11114D G D C =,点E 、F 、M 分别是棱1AA 、AB 、BC 的中点,P 为线段1B D 上一点,4AB =.(1)若平面EFP 交平面11DCC D 于直线l ,求证:1//l A B ;(2)若直线1B D ⊥平面EFP ,试作出平面EGM 与正方体1111ABCD A B C D -各个面的交线,并写出作图步骤,保留作图痕迹;设平面EGM 与棱11A D 交于点Q ,求三棱锥Q EFP -的体积.22.(2021·重庆·的正四面体的体积,某同学设计如下解法.解:构造一个棱长为1的正方体,如图1:则四面体11ACB D 的正四面体,且有11111111111133B ACB A AB DC B CD D ACD ACB D V V V V V V V ----=----==四面体正方体正方体.(1)类似此解法,如图2面体的体积;(2)对棱分别相等的四面体ABCD 中,AB CD =,AC BD =,AD BC =.求证:这个四面体的四个面都是锐角三角形;(3)有4条长为2的线段和2条长为m 的线段,用这6条线段作为棱且长度为m 的线段不相邻,构成一个三棱锥,问m 为何值时,构成三棱锥体积最大,最大值为多少?[(),,03a b c a b c ++>及变形()3,,03a b c abc a b c ++⎛⎫≤> ⎪⎝⎭,当且仅当a b c ==时取得等号]23.(2022·广西·昭平中学高一期末)如图,在圆柱12O O 中,AB ,CD 分别是上、下底面圆的直径,且AB CD ∥,EF ,GH 分别是圆柱轴截面上的母线.(1)若CE DE ==.(2)证明:平面ABH ∥平面ECD .24.(2021·浙江温州·高一期末)已知矩形ABCD 中,3AB =,1AD =,E 为线段CD 上一点(不在端点),沿线段AE 将ADE 折成AD E ',使得平面AD C '⊥平面ABC .(1)证明:平面ABD'与平面BCD'不可能垂直;'--大小为60°,(2)若二面角D AE B(ⅰ)求直线AD'与BC所成角的余弦值;'-的外接球的体积.(ⅰ)求三棱锥D ABC。
2012年高考数学试题分类考点33 空间几何体的结构及其三视图和直观图、空间几何体的表面积与体积
考点33 空间几何体的结构及其三视图和直观图、空间几何体的表面积与体积一、选择题1.(2012·江西高考文科·T7)若一个几何体的三视图如图所示,则此几何体的体积为()(A)112 (B)5 (C)92(D)4【解题指南】由三视图想象出几何体的直观图,由直观图求得体积.【解析】选D.由三视图可判断该几何体为直六棱柱,其底面积为4,高为1,所以体积为4.2.(2012·新课标全国高考文科·T7)与(2012·新课标全国高考理科·T7)相同如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为()(A)6 (B)9 (C)12 (D)18【解题指南】由三视图想象出几何体的直观图,由直观图求得体积.【解析】选B.由题意知,此几何体是三棱锥,其高h=3,相应底面面积为111=63=9,==93=9233S V Sh ⨯⨯∴⨯⨯.3.(2012·新课标全国高考理科·T11)已知三棱锥S-ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形,SC 为球O 的直径,且SC=2,则此棱锥的体积为( )6A (B) 6 (C)3 (D)2【解题指南】思路一:取AB 的中点为D ,将棱锥分割为两部分,利用B CDS A CDS V V V --=+求体积;思路二:设点O 到面ABC 的距离为d,利用123ABC V S d ∆=⨯求体积;思路三:利用排除法求解.【解析】选A.方法一:SC 是球O 的直径,90CAS CBS ∴∠=∠=︒.1BA BC AC ===,2SC =,AS BS ∴==AB 的中点为D ,显然AB CD ⊥,AB CS⊥SD ,AB ∴⊥平面CDS.在CDS ∆中,CD ,2DS =,2SC =,利用余弦定理可得cos CDS ∠=故sin CDS ∠=12CDS S ∆∴==,13B CDS A CDS CDS V V V S BD --∆∴=+=⨯⨯+111133326CDS CDS S AD S BA ∆∆⨯=⨯=⨯=.方法二:ABC ∆的外接圆的半径3r =,点O 到平面ABC 的距离3d ==,SC 为球O 的直径⇒点S 到平面ABC 的距离为262d =, 此棱锥的体积为113262233436ABC V S d ∆=⨯=⨯⨯=. 方法三:13236ABC V S R ∆<⨯=,排除,,B C D . 4.(2012·新课标全国高考文科·T8)平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为( )(A )6π (B )43π (C )46π (D )63π【解题指南】利用球心到截面的距离、截面圆的半径、球的半径之间满足勾股定理求得球的半径,然后利用公式求得球的体积.【解析】选B.设球O 的半径为R ,则22R 1(2)3=+=,故34433V R ππ==球.5.(2012·陕西高考文科·T8)将正方体(如图1所示)截去两个三棱锥,得到图2所示的几何体,则该几何体的左视图为( )【解题指南】结合原正方体,确定两个关键点1B ,1D 和两条重要线段1AD 和1B C 的投影.【解析】选B.图2所示的几何体的左视图由点A ,D ,1B ,1D 确定外形为正方形,判断的关键是两条对角线1AD 和1B C 是一实一虚,其中要把1AD 和1B C 区别开来,故选B.6.(2012·浙江高考文科·T3)已知某三棱锥的三视图(单位:cm )如图所示,则该三棱锥的体积是( )(A)1 cm 3 (B)2 cm 3 (C)3 cm 3 (D)6 cm 3【解题指南】由三视图可知,几何体是底面为两直角边分别是1和2的直角三角形,高为3的棱锥.【解析】选A.三棱锥的体积为11123132⨯⨯⨯⨯=(cm 3).7.(2012·北京高考文科·T7)与(2012·北京高考理科·T7)相同 某三棱锥的三视图如图所示,该三棱锥的表面积是( )(A )28+5(B )30+65(C )56+5(D )60+125【解题指南】由三视图还原直观图,再求表面积.【解析】选B.直观图如图所示,423 4侧(左)视图 俯视图底面是边长AC=5,BC=4的直角三角形,且过顶点P向底面作垂线PH,垂足在AC上,AH=2,HC=3,PH=4.145102ABCS∆=⨯⨯=,154102PACS∆=⨯⨯=.因为PH⊥面平H ABC⊥面,所以PH BC⊥.又因为所以BC PC⊥,所以145102PBCS∆=⨯⨯=.在PAB∆中,25,41PA PB AB===,取PA中点E,连结BE,则6BE=,所以1256652PABS∆=⨯⨯=.因此三棱锥的表面积为101010653065+++=+.8.(2012·湖南高考理科·T3)某几何体的正视图和侧视图均如图所示,则该几何体的俯视图不可能是( )【解题指南】从俯视图观察可知,正视图和侧视图不同的是D,正视图应有虚线. 【解析】选D.由“正视图俯视图等长,侧视图俯视图等宽”,知该几何体正视图与侧视图相同,而D项中正视图与侧视图不同,可知选D.PBA CE9.(2012·湖南高考文科·T4)某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是( )【解题指南】找出正视图和侧视图不相同的俯视图.【解析】选C.“正视图俯视图等长,侧视图俯视图等宽”,本题正视图与侧视图相同,可知选C.10.(2012·福建高考文科·T4)与(2012·福建高考理科·T4)相同一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是()(A)球 (B)三棱锥 (C)正方体 (D)圆柱【解题指南】通过了解基本空间几何体的各个视图分别是什么就能直接解题. 【解析】选D.圆柱的三视图,分别是矩形、矩形、圆,不可能三个视图都一样,而球的三视图可以都是圆,三棱锥的三视图可以都是三角形,正方体的三视图可以都是正方形.11.(2012·广东高考理科·T6)某几何体的三视图如图所示,它的体积为( )(A)12π (B)45π (C)57π (D)81π【解题指南】根据三视图准确判断出此几何体的形状,是解决本题的关键.本题显然是一个由同底的圆柱和圆锥组成的组合体.【解析】选C.此几何体是一个组合体,上方为一个圆锥,下方为一个同底的圆柱,所以其体积为2213534573V πππ=⨯⨯+⨯⨯⨯=.12.(2012·广东高考文科·T7)某几何的三视图如图所示,它的体积为(A)72π (B)48π (C)30π (D)24π【解题指南】根据三视图准确判断出此几何体的形状是解决本题的关键.显然图中几何体是一个由半球和倒立的圆锥组成的组合体.【解析】选C.由三视图可知该几何体是由半球和倒立的圆锥组成的组合体.2311434330323V πππ=⨯⨯+⨯⨯=2253-2311434330323V πππ=⨯+⨯⨯=. 13.(2012·湖北高考理科·T4)已知某几何体的三视图如图所示,则该几何体的体积为( ) (A)83π (B)3π (C)103π (D)6π【解题指南】本题考查三视图与组合体的体积的求法,解答本题的关键是正确地想象出直观图,再补体代入体积公式求解.【解析】选B.解答本题可采取补上一个与它完全相同的几何体的方法,∴V 21163.2v ππ∴=⨯⨯= 二、填空题14.(2012·湖北高考文科·T15)已知某几何体的三视图如图所示,则该几何体的体积为 .【解题指南】本题考查三视图与组合体的体积求法,解答本题的关键是正确地想象出直观图,再代入体积公式求解.【解析】由本题的三视图可知,该几何体是由三个圆柱组合而成,其中左右两个圆柱等体积.V=π×22×1×2+π×12×4=12π.【答案】12π15.(2012·江苏高考·T7)如图,在长方体1111ABCD A B C D -中,13,2AB AD cm AA cm ===,则四棱锥11A BB D D -的体积为 3cm .【解题指南】关键是求出四棱锥的高,即点A 到平面11BB D D 的距离.再利用公式进行求解.【解析】由题意知,四边形ABCD 为正方形,连接AC,交BD 于O ,则AC ⊥BD.由面面垂直的性质定理,可证AO ⊥平面11BB D D .四棱锥底面11BB D D 的面积为32262⨯=,从而1111163-=⨯⨯=A BB D D BB D D V OA S 长方形11163-=⨯⨯=A BB D D BB D D V OA S . 【答案】616.(2012·浙江高考理科·T11)已知某三棱锥的三视图(单位:cm )如图所示,则该三棱锥的体积等于________3cm .【解题指南】由锥体体积公式可得.【解析】三棱锥的体积为: 1132132⨯⨯⨯=(cm 3).【答案】117.(2012·天津高考理科·T10)一个几何体的三视图如图所示(单位:m ),则该几何体的体积为__________3m .【解题指南】由三视图正确判断出组合体的形状是关键.【解析】组合体的上面是一个长、宽、高分别为6,3,1的长方体,下面是两个球半径为32的相切的球体,所以所求的体积是:【答案】18.(2012·天津高考文科·T10)一个几何体的三视图如图所示(单位:m),则该几何体的体积为__________3m.【解题指南】由三视图正确判断出组合体的形状是关键.【解析】组合体的底座是一个棱长分别为4,3,2的长方体,上面是一个高为4的四棱柱,底面的面积S=/3 2S S,所以所求的体积是=6+24=30.【答案】3019. (2012·山东高考理科·T14)如图,正方体1111ABCD A B C D -的棱长为1,,E F 分别为线段11,AA B C 上的点,则三棱锥1D EDF -的体积为____________.【解题指南】本题考查利用换顶点法来求三棱锥的体积,只需知道C B 1上的任意一点到面1DED 的距离相等.【解析】1DED ∆的面积为正方形面积的一半,三棱锥的高即为正方体的棱长,所以612131311111=⨯⨯⨯=⋅==∆--AB AD DD h S V V DED DED F EDF D . 【答案】6120.(2012·山东高考文科·T13)如图,正方体1111ABCD A B C D -的棱长为1,E 为线段1B C 上的一点,则三棱锥1A DED -的体积为_____.【解题指南】本题考查利用换顶点法来求三棱锥的体积,只需知道C B 1上的任意一点到面1DAD 的距离相等.【解析】以△1ADD为底面,则易知三棱锥的高为1,故【答案】6121.(2012·安徽高考理科·T12)某几何体的三视图如图所示,该几何体的表面积是 .【解题指南】根据“长对正、宽相等、高平齐”的原则作出几何体的直观图. 【解析】该几何体是底面是直角梯形,高为4的直四棱柱,几何体的表面积是2212(25)4(2544(52))492 2S=⨯⨯+⨯++++-⨯=.【答案】9222.(2012·安徽高考文科·T12)某几何体的三视图如图所示,则该几何体的体积等于_____.【解题指南】根据“长对正、宽相等、高平齐”的原则得出几何体的直观图,进而求得体积.【解析】该几何体是底面是直角梯形,高为4的直四棱柱,则该几何体的体积是1(25)44562V =⨯+⨯⨯=.【答案】5623.(2012·辽宁高考理科·T13)一个几何体的三视图如图所示,则该几何体的表面积为______________.【解题指南】读懂三视图,它是长方体(挖去一个底面直径为2 cm 的圆柱),分别求表面积,注意减去圆柱的两个底面积.【解析】长方体的长宽高分别为4,3,1,表面积为43231241238⨯⨯+⨯⨯+⨯⨯=; 圆柱的底面圆直径为2,母线长为1,侧面积为2112ππ⨯⨯=;圆柱的两个底面积2212ππ⨯⨯=.故该几何体的表面积为382238ππ+-=.【答案】3824. (2012·辽宁高考文科·T13)一个几何体的三视图如图所示,则该几何体的体积为_______________.【解题指南】读懂三视图,它是圆柱和长方体的组合,分别求体积即可. 【解析】该组合体上边是一个圆柱,底面圆直径为2,母线长为1;体积111V sh ππ==⨯⨯=S2111V sh ππ==⨯⨯=,下面是一个长方体,长、宽、高分别为4,3,1,体积243112V =⨯⨯=.故组合体体积1212V V π+=+. 【答案】12π+25.(2012·辽宁高考文科·T16)已知点P ,A ,B ,C ,D 是球O 表面上的点,PA ⊥平面ABCD ,四边形ABCD 是边长为3.若6,则△OAB 的面积为______________.【解题指南】注意到已知条件中的垂直关系,将点P,A,B,C,D 看作长方体的顶点来考虑.【解析】由题意,PA ⊥平面ABCD ,则点P,A,B,C,D,可以视为球O 的内接长方体的顶点,球O 位于该长方体的对角线的交点处,那么△OAB 的面积为长方体对角面的四分之一.123,266=236=334AB PA PB OABD ==∴=∴∆⨯⨯,,面积的123,266=236=334AB PA PB OABD ==∴=∴∆⨯,面积.【答案】33三、解答题26.(2012·新课标全国高考文科·T19)如图,在三棱柱ABC-A 1B 1C 1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA 1,D 是棱AA 1的中点.(I)证明:平面BDC 1⊥平面BDC ;(Ⅱ)平面BDC 1分此棱柱为两部分,求这两部分体积的比.【解题指南】(1)证两个平面垂直,可转化为在其中一个平面内找到一条直线与另一个平面垂直,要证平面BDC 1⊥平面BDC ,可证1DC ⊥平面BDC ; (2)平面BDC 1分棱柱下面部分1B DACC -为四棱锥,可直接求体积,上面部分可用间接法求得体积,从而确定两部分体积之比.【解析】(I)由题设可知11,,BC CC BC AC CC AC C ⊥⊥=,所以BC ⊥平面11ACC A . 又1DC ⊂平面11ACC A ,所以1DC BC ⊥.由题设知1145A DC ADC ∠=∠=︒,所以190CDC ∠=︒,即1DC DC ⊥.又,DC BC C = 所以1DC ⊥平面BDC .又1DC ⊂平面1BDC ,故平面1BDC ⊥平面.BDC (II)设棱锥1B DACC -的体积为1V ,1AC =.由题意得1112111322V +=⨯⨯⨯=. 又三棱柱111ABC A B C -的体积=1V ,所以()11-:=1:1V V V . 故平面1BDC 分此棱柱所得两部分体积的比为1:1.27.(2012·江西高考文科·T19)如图,在梯形ABCD 中,AB ∥CD ,E ,F 是线段AB 上的两点,且DE ⊥AB ,CF ⊥AB ,AB=12,AD=5,BC=42,DE=4.现将△ADE ,△CFB 分别沿DE ,CF 折起,使A ,B 两点重合于点G ,得到多面体CDEFG.(1) 求证:平面DEG ⊥平面CFG ; (2) 求多面体CDEFG 的体积.【解题指南】(1)证两个平面垂直,可转化为在其中一个平面内找到一条直线与另一个平面垂直,要证平面DEG ⊥平面CFG ,可证EG ⊥平面CFG ;(2)多面体CDEFG 为四棱锥,由平面DEG ⊥平面CFG 得到四棱锥的高,利用体积公式求体积.【解析】(1)由已知可得AE=3,BF=4,则折叠完后EG=3,GF=4,又因为EF=5,所以可得EG GF ⊥.又因为CF EGF ⊥底面,可得CF EG ⊥,即EG ⊥平面CFG,所以平面DEG ⊥平面CFG. (2)过点G 作GO 垂直于EF,GO 即为四棱锥G -EFCD 的高,所以所求体积为13S 长方形DEFC ·GO=13×4×5×125=16.。
空间几何体知识点

空间几何体知识点一、知识概述《空间几何体知识点》①基本定义:空间几何体呢,说白了就是在空间里由一些面啊或者线啊啥的围成的形状。
像我们常见的正方体、球体、圆柱体之类的都是空间几何体。
正方体有六个正方形的面,每个顶点都连接着三条棱;球体就像个超级圆的球,表面上每一点到球心的距离都相等;圆柱体有两个底面是一样大的圆,侧面是个长方形卷起来的样子。
②重要程度:在几何这个学科里,空间几何体可是基础中的基础。
往后学的好多几何知识都是建立在对空间几何体的认识和理解之上的。
就好比建房子,空间几何体就是那些一块块的砖头,要是砖头都不认识,房子可就没法好好建了。
③前置知识:那在学空间几何体之前呢,得先对平面图形有点基础了解,像长方形、三角形、圆这些。
你想啊,如果连平面的图形都搞不清楚,又怎么能明白由这些平面图形组合或者变形变成的空间几何体呢。
④应用价值:实际应用可不少呢。
在建筑领域,很多建筑的设计形状都是空间几何体的变形或者组合。
像鸟巢体育场,就有点像个扭曲的正方体;还有水立方,有点像个很规则的长方体和一些特殊几何体的组合。
在工业制造上,一些容器的设计也和空间几何体有关,比如装油的圆柱罐子。
二、知识体系①知识图谱:空间几何体在几何学科里就像树根一样,其他很多知识像解析几何、立体几何计算之类的都是从这儿长出去的枝叶。
它往上能和立体几何证明、计算联系起来,往下与平面几何的一些知识也有千丝万缕的关系。
②关联知识:它和角度的知识有关系啊。
比如说正方体的各个面之间的夹角,还有棱之间的夹角等。
跟面积体积计算也联系紧密,要计算空间几何体的体积和表面积就得知道它的形状特点。
和投影知识也有关,从不同方向投影一个空间几何体就会得到不同的平面图形。
③重难点分析:- 掌握难度:说实话,空间想象能力是个难点。
很多同学刚学的时候,在脑海里很难构造出那些几何体的样子。
像那种斜着切正方体得到的截面形状,就很难想象。
- 关键点:得抓住各个几何体的特征,就是那些区别于其他几何体的地方。
2012高考数学(理)专题练习:五 空间几何体
高考专题训练五空间几何体班级________姓名________时间:45分钟分值:75分总得分________一、选择题:本大题共6小题,每小题5分,共30分.在每小题给出的四个选项中,选出符合题目要求的一项填在答题卡上.1.(2011·浙江)若某几何体的三视图如图所示,则这个几何体的直观图可以是()解析:由三视图可知,该几何体的直观图为B.答案:B2.(2011·辽宁)一个正三棱柱的侧棱长和底面边长相等,体积为23,它的三视图中的俯视图如图所示,侧(左)视图是一个矩形,则这个矩形的面积是( )A .4B .2 3C .2D. 3解析:设该正三棱柱侧棱长和底面边长为a , 则34a 2·a =23, ∴a 3=8,∴a =2,由俯视图知,该正三棱柱如图ABC -A 1B 1C 1, 其侧(左)视图即为矩形CDD 1C 1, 其面积为3×2=2 3. 答案:B3.(2011·山师大附中高三模拟)已知某一几何体的正(主)视图与侧(左)视图如图所示,则下列图形中,可以是该几何体的俯视图的图形有()A.①②③⑤B.②③④⑤C.①②④⑤D.①②③④解析:根据给出的正(主)视图和侧(左)视图可知,该组合体由上、中、下三个几何体组合而成,由于正(主)视图和侧(左)视图中三层均为矩形,所以这些几何体可能是一些长方体、底面为直角三角形的直三棱柱以及圆柱组合而成的.而第⑤个俯视图中,有两处与已知不符,一是上层几何体的俯视图不正确,由于上层几何体的正(主)视图与侧(左)视图为两个相同的矩形,所以其俯视图中矩形的两边长应该相等;二是下层几何体的俯视图不正确,如果下层几何体的底面为俯视图所示的三角形,则在正(主)视图中底层的矩形应有一条中位线,这与已知不符合,所以⑤不可能,故选D.[来源:学科网]答案:D4.(2011·湖北)设球的体积为V1,它的内接正方体的体积为V2,下列说法中最合适的是()A.V1比V2大约多一半B.V1比V2大约多两倍半C.V1比V2大约多一倍D.V1比V2大约多一倍半解析:设球的内接正方体的边长为a , 球的半径为R ,∴2R =3a ,∴R =32a .∴V 1=43πR 3=43π·338a 3=32πa 3,V 2=a 3,∴V 1=32πV 2≈2.5V 2,∴V 1-V 2≈1.5V 2.[来源:学科网] 答案:D5.(2011·北京卷)某四棱锥的三视图如图所示,该四棱锥的表面积是( )A .32B .16+16 2C .48D .16+32 2解析:由三视图可知,该四棱锥为正四棱锥 S 底=4×4=16,S 侧=4×12×4×22=16 2∴S 表面积=S 底+S 侧=16+16 2.6.(2011·辽宁)已知球的直径SC =4,A ,B 是该球球面上的两点,AB =2,∠ASC =∠BSC =45°,则棱锥S -ABC 的体积为( )[来源:学科网ZXXK]A.33B.233C.433D.533解析:如图所示.∠ASC =∠BSC =45° 且OS =OB =OA =OC =2,∴△SOB ,△SOA 为全等的等腰直角三角形, 且SC ⊥OB ,SC ⊥OA ,又OA ∩OB =O ,∴SC ⊥平面AOB 又∵AB =OB =OA =2, ∴△AOB 为等边三角形∴V S -ABC =V S -AOB +V C -AOB =13·S △AOB ·SC =13×3×4=433.二、填空题:本大题共4小题,每小题5分,共20分,把答案填在题中横线上.[来源:学科网]7.(2011·全国新课标版)已知两个圆锥有公共底面,且两圆锥的顶点和底面的圆周都在同一个球面上.若圆锥底面面积是这个球面面积的316,则这两个圆锥中,体积较小者的高与体积较大者的高的比值为________.解析:令球心为O ,圆锥底面圆圆心为O ′,球半径为R ,圆锥底面圆半径为r ,则316·4πR 2=πr 2,∴r =32R ,在Rt △AOO ′中, OO ′=AO 2-AO ′2=R 2.故h H =R -R 2R +R 2=13. 答案:138.(2011·洛阳市高三模拟)图2中的实线围成的部分是长方体(图1)的平面展开图,其中四边形ABCD 是边长为1的正方形.若向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展形图内的概率是14,则此长方体的体积是________.解析:设长方体的高为h ,则图2中虚线围成的矩形长为2+2h ,宽为1+2h ,面积为(2+2h )(1+2h ),展开图的面积为2+4h ;由几何概型的概率公式知2+4h (2+2h )(1+2h )=14,得h =3,所以长方体的体积是V =1×3=3.答案:39.(2011·北京市海淀区高三第二学期练习)如图,在正方体ABCD -A 1B 1C 1D 1中,点P 是上底面A 1B 1C 1D 1内一动点,则三棱锥P -ABC 的正(主)视图与侧(左)视图的面积的比值为________.[来源:]解析:依题意得三棱锥P-ABC的正(主)视图与侧(左)视图分别是一个三角形,且这两个三角形的底边长都等于正方体的棱长,底边上的高也都相等,因此三棱锥P-ABC的正视图与侧视图的面积之比等于1.答案:110.一个几何体的三视图如图所示,已知正(主)视图是底边长为1的平行四边形,侧(左)视图是一个长为3,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形,则该几何体的体积V是________.是边长为1的正方形,高为 3.所以V=1×1×3= 3.答案: 3三、解答题:本大题共2小题,共25分.解答应写出文字说明、证明过程或演算步骤.[来源:学*科*网Z*X*X*K]所示(其中M,N分别是AF,BC的中点).(1)求证:MN ∥平面CDEF ; (2)求二面角A -CF -B 的余弦值; (3)求多面体A -CDEF 的体积. 解:由三视图知,该多面体是底面为直角三角形的直三棱柱ADE -BCF ,且AB =BC =BF =4,DE =CF =42,∠CBF =π2.(1)证明:连接BE ,易知BE 通过点M ,连接CE .则EM =BM ,CN =BN ,∴MN ∥CE ,又CE ⊂平面CDEF ,MN⊄平面CDEF ,∴MN ∥平面CDEF .(2)作BQ ⊥CF 于Q ,连接AQ ,∵平面BFC ⊥平面ABFE ,平面ABFE ∩平面BCF =BF ,AB ⊂平面ABFE ,AB ⊥BF ,∴AB ⊥平面BCF ,又CF ⊂平面BCF ,∴AB ⊥CF ,又BQ ⊥CF ,AB ∩BQ =B ,∴CF ⊥平面ABQ ,∵AQ ⊂平面ABQ ,∴AQ ⊥CF ,故∠AQB 为所求二面角的平面角.在Rt △ABQ 中,tan ∠AQB =AB BQ =422=2,则 cos ∠AQB =33,故所求二面角的余弦值为33.[来源:学|科|网Z|X|X|K](3)多面体A -CDEF 的体积V =2×V A -CEF =2×V C -ABF =2×13S △ABF ·BC =643.12.(13分)(广东卷)某高速公路收费站入口处的安全标识墩如下图(1)所示.墩的上半部分是正四棱锥P -EFGH ,下半部分是长方体ABCD -EFGH .图(2)、(3)分别是该标识墩的正视图和俯视图.(1)请画出该安全标识墩的侧视图;(2)求该安全标识墩的体积;(3)证明:直线BD⊥平面PEG.分析:(1)根据正(主)视图和俯视图可以知道其侧(左)视图和正(主)视图是完全相同的;(2)根据两个视图给出的标记,这个安全墩的下半部分是一个底面边长为40 cm、高为20 cm的长方体,上半部分四棱锥的高为60 cm,根据公式计算即可;(3)根据正四棱锥的性质进行证明.解:(1)该安全标识墩侧(左)视图如右图所示.[来源:学科网](2)该安全标识墩的体积V =V P -EFGH +V ABCD -EFGH=13402×60+402×20=32000+32000=64000(cm 3). (3)证明:如右图所示,连接HF 、EG .由题设知四边形ABCD 和四边形EFGH 均为正方形,∴FH ⊥EG ,又∵ABCD -EFGH 为长方体,∴BD ∥FH .设点O 是EFGH 的对称中心,连接PO .∵P -EFGH 是正四棱锥,[来源:学&科&网Z&X&X&K]∴PO ⊥平面EFGH ,而FH ⊂平面EFGH ,∴PO ⊥FH .∵FH ⊥PO ,FH ⊥EG ,PO ∩EG =O ,PO ⊂平面PEG ,EG ⊂平面PEG ,∴FH ⊥平面PEG .而BD ∥FH ,故BD ⊥平面PEG .[来源:学科网ZXXK]点评:解这类给出了直观图和三视图中的两个图形的题目,只要根据直观图得出另一个视图的形状,再根据给出的两个视图上标注的几何量,在第三个视图上标注上几何量即可..精品资料。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考专题训练五空间几何体
班级_______姓名_______时间:45分钟分值:75分总得分________
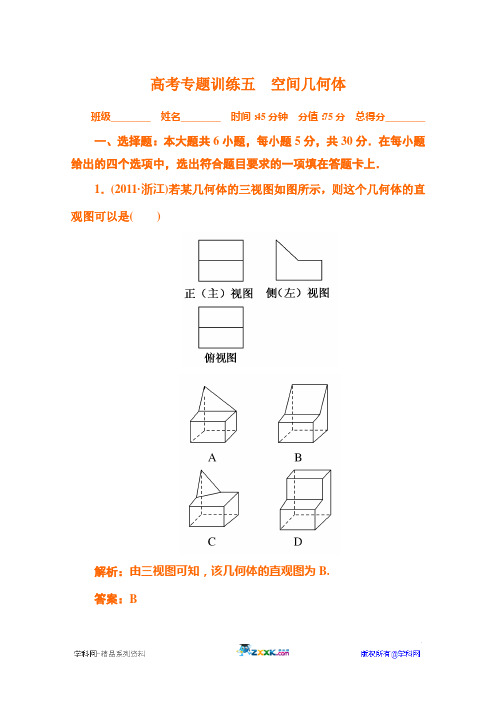
一、选择题:本大题共6小题,每小题5分,共30分.在每小题给出的四个选项中,选出符合题目要求的一项填在答题卡上.1.(2011·浙江)若某几何体的三视图如图所示,则这个几何体的直观图可以是()
解析:由三视图可知,该几何体的直观图为B.
答案:B
2.(2011·辽宁)一个正三棱柱的侧棱长和底面边长相等,体积为23,它的三视图中的俯视图如图所示,侧(左)视图是一个矩形,则
这个矩形的面积是()
A.4B.2 3
C.2 D. 3
解析:设该正三棱柱侧棱长和底面边长为a,
则
3
4a
2·a=23,
∴a3=8,∴a=2,
由俯视图知,该正三棱柱如图ABC-A1B1C1,
其侧(左)视图即为矩形CDD1C1,
其面积为3×2=2 3.
答案:B
3.(2011·山师大附中高三模拟)已知某一几何体的正视图与侧视图如图所示,则下列图形中,可以是该几何体的俯视图的图形有()
A.①②③⑤B.②③④⑤
C.①②④⑤D.①②③④
解析:根据给出的正(主)视图和侧(左)视图可知,该组合体由上、中、下三个几何体组合而成,由于正(主)视图和侧(左)视图中三层均为矩形,所以这些几何体可能是一些长方体、底面为直角三角形的直三棱柱以及圆柱组合而成的.而第⑤个俯视图中,有两处与已知不符,一是上层几何体的俯视图不正确,由于上层几何体的正(主)视图与侧(左)视图为两个相同的矩形,所以其俯视图中矩形的两边长应该相等;二是下层几何体的俯视图不正确,如果下层几何体的底面为俯视图所示的三角形,则在正(主)视图中底层的矩形应有一条中位线,这与已知不符合,所以⑤不可能,故选D.
答案:D
4.(2011·湖北)设球的体积为V1,它的内接正方体的体积为V2,下列说法中最合适的是()
A.V1比V2大约多一半B.V1比V2大约多两倍半
C.V1比V2大约多一倍D.V1比V2大约多一倍半
解析:设球的内接正方体的边长为a,
球的半径为R,∴2R=3a,∴R=
3 2a.
∴V1=4
3
πR3=
4
3
π·
33
8a
3=
3
2
πa3,
V2=a3,∴V1=
3
2
πV2≈2.5V2,∴V1-V2≈1.5V2.
答案:D
5.(2011·北京卷)某四棱锥的三视图如图所示,该四棱锥的表面积是()
A.32 B.16+16 2
C.48 D.16+32 2
解析:由三视图可知,该四棱锥为正四棱锥
S底=4×4=16,S侧=4×1
2×4×22=16 2
∴S表面积=S底+S侧=16+16 2.
答案:B
6.(2011·辽宁)已知球的直径SC=4,A,B是该球球面上的两点,AB=2,∠ASC=∠BSC=45°,则棱锥S-ABC的体积为()
A.
3
3 B.
23
3
C.433
D.533
解析:如图所示.
∠ASC =∠BSC =45° 且OS =OB =OA =OC =2,
∴△SOB ,△SOA 为全等的等腰直角三角形, 且SC ⊥OB ,SC ⊥OA ,
又OA ∩OB =O ,∴SC ⊥平面AOB 又∵AB =OB =OA =2, ∴△AOB 为等边三角形
∴V S -ABC =V S -AOB +V C -AOB =13·S △AOB ·SC =13×3×4=43 3.
答案:C
二、填空题:本大题共4小题,每小题5分,共20分,把答案填在题中横线上.
7.(2011·全国新课标版)已知两个圆锥有公共底面,且两圆锥的顶点和底面的圆周都在同一个球面上.若圆锥底面面积是这个球面面积的
3
16
,则这两个圆锥中,体积较小者的高与体积较大者的高的比值为________.
解析:令球心为O,圆锥底面圆圆心为O′,球半径为R,圆锥
底面圆半径为r,则3
16
·4πR2=πr2,
∴r=
3
2R,在Rt△AOO′中,OO′=AO
2-AO′2=
R
2.
故h
H=
R-
R
2
R+
R
2
=
1
3.
答案:1 3
8.(2011·洛阳市高三模拟)图2中的实线围成的部分是长方体(图1)的平面展开图,其中四边形ABCD是边长为1的正方形.若向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展形图内的概率是
1
4,则此长方体的体积是________.
解析:设长方体的高为h,则图2中虚线围成的矩形长为2+2h,宽为1+2h,面积为(2+2h)(1+2h),展开图的面积为2+4h;由几
何概型的概率公式知
2+4h
(2+2h)(1+2h)
=
1
4,得h=3,所以长方体的体
积是V=1×3=3.
答案:3
9.(2011·北京市海淀区高三第二学期练习)如图,在正方体ABCD -A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC 的正视图与侧视图的面积的比值为________.
解析:依题意得三棱锥P-ABC的正(主)视图与侧(左)视图分别是一个三角形,且这两个三角形的底边长都等于正方体的棱长,底边上的高也都相等,因此三棱锥P-ABC的正视图与侧视图的面积之比等于1.
答案:1
10.一个几何体的三视图如图所示,已知正(主)视图是底边长为1的平行四边形,侧(左)视图是一个长为3,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形,则该几何体的体积V是________.
解析:由三视图可知,该几何体是一个平行六面体(如图),其底面是边长为1的正方形,高为 3.
所以V=1×1×3= 3.
答案: 3
三、解答题:本大题共2小题,共25分.解答应写出文字说明、证明过程或演算步骤.
11.(12分)(2011·浙江省宁波市)一个多面体的直观图及三视图如图所示(其中M、N分别是AF、BC的中点).
(1)求证:MN∥平面CDEF;
(2)求二面角A-CF-B的余弦值;
(3)求多面体A-CDEF的体积.
解:由三视图知,该多面体是底面为直角三角形的直三棱柱ADE -BCF,且AB=BC=BF=4,
DE =CF =42,∠CBF =π
2
.
(1)证明:连接BE ,易知BE 通过点M ,连接CE .
则EM =BM ,CN =BN ,∴MN ∥CE ,又CE ⊂平面CDEF ,MN ⊄平面CDEF ,∴MN ∥平面CDEF .
(2)作BQ ⊥CF 于Q ,连接AQ ,
∵平面BFC ⊥平面ABFE ,平面ABFE ∩平面BCF =BF ,AB ⊂平面ABFE ,AB ⊥BF ,∴AB ⊥平面BCF ,
又CF ⊂平面BCF ,∴AB ⊥CF ,又BQ ⊥CF ,AB ∩BQ =B ,∴CF ⊥平面ABQ ,∵AQ ⊂平面ABQ ,∴AQ ⊥CF ,故∠AQB 为所求二面角的平面角.
在Rt △ABQ 中,tan ∠AQB =AB
BQ =422=2,则
cos ∠AQB =33,故所求二面角的余弦值为3
3
.
(3)多面体A -CDEF 的体积V =2×V A -CEF =2×V C -ABF =2×1
3S △
ABF ·BC =643
. 12.(13分)(广东卷)某高速公路收费站入口处的安全标识墩如下图(1)所示.墩的上半部分是正四棱锥P -EFGH ,下半部分是长方体ABCD -EFGH .图(2)、(3)分别是该标识墩的正视图和俯视图.
(1)请画出该安全标识墩的侧视图;
(2)求该安全标识墩的体积;
(3)证明:直线BD⊥平面PEG.
分析:(1)根据正(主)视图和俯视图可以知道其侧视图和正视图是完全相同的;(2)根据两个视图给出的标记,这个安全墩的下半部分是一个底面边长为40 cm、高为20 cm的长方体,上半部分四棱锥的高为60 cm,根据公式计算即可;(3)根据正四棱锥的性质进行证明.解:(1)该安全标识墩侧(左)视图如下图所示.
(2)该安全标识墩的体积
V=V P-EFGH+V ABCD-EFGH
=1
3×40
2×60+402×20=32000+32000=64000(cm3).
(3)证明:如下图所示,连接HF、EG.由题设知四边形ABCD和四边形EFGH均为正方形,
∴FH⊥EG,
又∵ABCD-EFGH为长方体,
∴BD∥FH.
设点O是EFGH的对称中心,连接PO.
∵P-EFGH是正四棱锥,
∴PO⊥平面EFGH,而FH⊂平面EFGH,
∴PO⊥FH.
∵FH⊥PO,FH⊥EG,PO∩EG=O,
PO⊂平面PEG,EG⊂平面PEG,
∴FH⊥平面PEG.
而BD∥FH,故BD⊥平面PEG.
点评:解这类给出了直观图和三视图中的两个图形的题目,只要根据直观图得出另一个视图的形状,再根据给出的两个视图上标注的几何量,在第三个视图上标注上几何量即可.。
