立体几何综合训练
立体几何与解析几何综合题训练

A C D E BM立体解析综合题练习11.如图,正方形ADEF 与梯形ABCD 所在平面互相垂直, 已知//,AB CD AD CD ⊥,12AB AD CD ==.(Ⅰ)求证:BF //平面CDE ;(Ⅱ)求平面BDF 与平面CDE 所成锐二面角的余弦值; (Ⅲ)线段EC 上是否存在点M ,使得平面BDM ⊥平面BDF 若存在,求出EM EC的值;若不存在,说明理由.2.已知1(2,0)F -,2(2,0)F 两点,曲线C 上的动点P 满足12123||||||2PF PF F F +=. (Ⅰ)求曲线C 的方程;(Ⅱ)若直线l 经过点(0,3)M ,交曲线C 于A ,B 两点,且12MA MB =,求直线l 的方程.立体解析综合题练习21. 在如图所示的多面体中,EA ⊥平面ABC ,DB ⊥平面ABC ,BC AC ⊥,且22====AE BD BC AC ,M 是AB 的中点. (Ⅰ)求证:CM ⊥EM ;(Ⅱ)求平面EMC 与平面BCD 所成的锐二面角的余弦值; (Ⅲ)在棱DC 上是否存在一点N ,使得直线MN 与平面EMC所成的角为60︒.若存在,指出点N 的位置;若不存在,请说明理由.2.椭圆C:22221(0)x y a b a b +=>>的两个焦点为F 1,F 2,点P 在椭圆C 上,且11212414,||,||.33PF F F PF PF ⊥==(Ⅰ)求椭圆C 的方程;(Ⅱ)若直线l 过圆M: x 2+y 2+4x-2y=0的圆心,交椭圆C 于,A B 两点,且A 、B 关于点M 对称,求直线l 的方程.立体解析综合题练习31.在如图所示的几何体中,四边形ABCD 为正方形,PA ⊥平面ABCD ,PA //BE ,AB =PA =4,BE =2. (Ⅰ)求证:CE //平面PAD ;(Ⅱ)求PD 与平面PCE 所成角的正弦值; (Ⅲ)在棱AB 上是否存在一点F ,使得平面DEF ⊥平面PCE ?如果存在,求AFAB的值; 如果不存在,说明理由.2.已知抛物线C :22y px =(0p >)的焦点F (1,0),O 为坐标原点,A ,B 是抛物线C 上异于O 的两点.(Ⅰ)求抛物线C 的方程;(Ⅱ)若直线OA ,OB 的斜率之积为12-,求证:直线AB 过x 轴上一定点.ABFED C立体解析综合题练习41.如图,在四棱锥P ABCD -中,底面ABCD 为直角梯形,AD //BC ,AD DC ⊥,平面PAD ⊥底面ABCD ,Q 为AD 的中点,M 是棱PC 的中点,12,1, 3.2PA PD BC AD CD ===== (I )求证:PQ AB ⊥;(II )求直线PB 与平面PCD 所成角的正弦值; (III )求二面角P QB M --的余弦值.2.已知椭圆,其短轴的一个端点到右焦点的距离为,且点在椭圆上. 直线的斜率为,且与椭圆交于、两点.(Ⅰ)求椭圆的方程; (Ⅱ)求面积的最大值.立体解析综合题练习51.如图,棱柱ABCD —1111A B C D 的所有棱长都为2, AC BD O =,侧棱1AA 与底面ABCD 的所成角为60°,1A O ⊥平面ABCD ,F 为1DC 的中点. (Ⅰ)证明:BD ⊥1AA ;(Ⅱ)证明://OF 平面11BCC B ; (Ⅲ)求二面角D -1AA -C 的余弦值.2.已知椭圆C 两焦点坐标分别为1(2,0)F -,2(2,0)F ,一个顶点为(0,1)A -. (Ⅰ)求椭圆C 的标准方程;(Ⅱ)是否存在斜率为(0)k k ≠的直线l ,使直线l 与椭圆C 交于不同的两点,M N ,满足AM AN =. 若存在,求出k 的取值范围;若不存在,说明理由.立体解析综合题练习61.如图, ABCD 是边长为3的正方形,DE ⊥平面ABCD ,DE AF //,AF DE 3=,BE 与平面ABCD 所成角为060.(Ⅰ)求证:AC ⊥平面BDE ; (Ⅱ)求二面角D BE F --的余弦值;(Ⅲ)设点M 是线段BD 上一个动点,试确定点M 的位置,使得//AM 平面BEF ,并证明你的结论.2.已知椭圆C :22221x y a b +=(0a b >>)过点(20),,且椭圆C 的离心率为12.(Ⅰ)求椭圆C 的方程;(Ⅱ)若动点P 在直线1x =-上,过P 作直线交椭圆C 于M N ,两点,且P 为线段MN 中点,再过P 作直线l MN ⊥.证明:直线l 恒过定点,并求出该定点的坐标.:M 22221(0)x y a b a b+=>>2A (2,1)M l 22M B C M ABC ∆ABC1B 1C 1A DF1D OA BCDFE立体解析综合题练习71.如图,在四棱锥P ABCD -中,底面ABCD 为直角梯形,且//AD BC ,90ABC PAD ∠=∠=︒,侧面PAD ⊥底面ABCD . 若12PA AB BC AD ===. (Ⅰ)求证:CD ⊥平面PAC ;(Ⅱ)侧棱PA 上是否存在点E ,使得//BE 平面PCD ?若存在,指出点E 的位置并证明,若不存在,请说明理由;(Ⅲ)求二面角A PD C --的余弦值.2.已知直线022=+-y x 经过椭圆)0(1:2222>>=+b a by a x C 的左顶点A 和上顶点D ,椭圆C 的右顶点为B ,点S 是椭圆上位于x轴上方的动点,直线AS ,BS 与直线4=x l :分别 交于N M ,两点.(Ⅰ) 求椭圆C 的方程;(Ⅱ)(ⅰ) 设直线AS ,BS 的斜率分别为21,k k ,求证21k k ⋅为定值; (ⅱ)求线段MN 的长度的最小值.立体解析综合题练习81.在如图的多面体中,EF ⊥平面AEB ,AE EB ⊥,//AD EF ,//EF BC ,24BC AD ==,3EF =,2AE BE ==, G 是BC 的中点.(Ⅰ) 求证://AB 平面DEG ; (Ⅱ) 求证:BD EG ⊥;(Ⅲ) 求二面角C DF E --的余弦2.已知椭圆()的长轴长是,且过点. (Ⅰ)求椭圆的标准方程;(Ⅱ)设直线与椭圆交于两点,为椭圆的右焦点,直线与关于轴对称.求证:直线过定点,并求出该定点的坐标.立体解析综合题练习91.在长方形11AA B B 中,124AB AA ==,C ,1C 分别是AB ,11A B 的中点(如图1). 将此长方形沿1CC 对折,使二面角11A CC B --为直二面角,D ,E 分别是11A B ,1CC 的中点(如图2). (Ⅰ)求证:1C D ∥平面1A BE ; (Ⅱ)求证:平面1A BE ⊥平面11AA B B ; (Ⅲ)求直线1BC 与平面1A BE 所成角的正弦值.2.已知直线与椭圆相交于两点,与轴相交于点,且当时,. (Ⅰ)求椭圆的方程;(Ⅱ)设点的坐标为,直线,与直线分别交于,两点. 试判断以为直径的圆是否经过点?并请说明理由.1:2222=+by a x C 0>>b a 22)221( ,C )0(≠+=k m kx y l :C N M 、F MF NF x l :1()l x my m =+∈R ()22:109x y C t t+=>,E F x B 0m =83EF =C A (3,0)-AE AF 3x =M N MN B 图(1)图(2)C 1BCAA 1B 1BCADEA 1B 1C 1MY SDN BxAOA BP CDA DFEB G C立体解析综合题练习101.如图,在直三棱柱111ABC A B C -中,5AB AC ==,D ,E 分别为BC ,1BB 的中点,四边形11B BCC 是边长为6的正方形. (Ⅰ)求证:1A B ∥平面1AC D ; (Ⅱ)求证:CE ⊥平面1AC D ; (Ⅲ)求二面角1C AC D --的余弦值. 2.如图,已知椭圆E:22221(0)x y a b a b 的离心率为32,过左焦点(3,0)F -且斜率为k 的直线交椭圆E 于A,B 两点,线段AB 的中点为M,直线l :40x ky +=交椭圆E 于C,D 两点. (Ⅰ)求椭圆E 的方程; (Ⅱ)求证:点M 在直线l 上;(Ⅲ)是否存在实数k ,使得四边形AOBC 为平行四边形?若存在求出k 的值,若不存在说明理由.。
立体几何综合训练 学生版拔尖

课题:立体几何综合训练个性化教学辅导教案学生姓名年级学科数学上课时间教师姓名课题立体几何综合训练教学过程教师活动1.若三个平面两两相交,有三条交线,则下列命题正确的是()A.三条交线为异面直线B.三条交线两两平行C.三条交线交于一点D.三条交线两两平行或交于一点2.回顾下直线,平面的平行判断与性质。
3.回顾下直线,平面垂直的性质和判定方法。
4.求线面所成角与二面角的一般步骤是什么?5.若已知条件中,已知三角形中两线段相等,你会想到什么?遇到中点呢?立体几何综合训练例1 如图,直三棱柱111ABC A B C - 中,90BAC ∠=,2AB AC ==,11AA =,点,M N 分别为1A B 和11B C 的中点.(1)证明:MN ∥平面11A ACC ; (2)求三棱锥1A MNC -的体积例2 如图,已知111ABC A B C -是正三棱柱,棱长均为5,E 、F 分别是AC 、11A C 的中点. (1)求证:平面1AB F ∥平面1BEC ; (2)求点A 到平面1BEC 的距离.例3 如图,在直角梯形SABC 中,∠B=∠C=π2,D 为边SC 上的点,且AD ⊥SC ,现将△SAD 沿AD 折起到达PAD 的位置(折起后点S 记为P ),并使得PA ⊥AB . (1)求证:PD ⊥平面ABCD ;(2)已知PD=AD ,PD +AD +DC=6,G 是AD 的中点,当线段PB 取得最小值时,则在平面PBC 上是否存在点F ,使得FG ⊥平面PBC ?若存在,确定点F 的位置,若不存在,请说明理由.立体几何综合训练教学过程: 突破1: 1.线面平行:①定义:直线与平面无公共点.②判定定理:(线线平行线面平行)③性质定理:(线面平行线线平行)④判定或证明线面平行的依据:(i )定义法(反证):(用于判断);////a b a a b ααα⎫⎪⊄⇒⎬⎪⊂⎭⇒////a a a b b αβαβ⎫⎪⊂⇒⎬⎪=⎭⇒//l l αα=∅⇒(ii )判定定理:“线线平行面面平行”(用于证明);(iii )“面面平行线面平行”(用于证明); (4)(用于判断);3.面面平行: ①定义:;②判定定理:如果一个平面内的两条相交直线都平行于另一个平面,那么两个平面互相平行; 符号表述: 【如下图①】图① 图②推论:一个平面内的两条相交直线分别平行于另一个平面的两条直线,那么这两个平面互相平行 符号表述:【如上图②】判定2:垂直于同一条直线的两个平面互相平行. 符号表述:.【如右图】③判定与证明面面平行的依据:(1)定义法;(2)判定定理及推论(常用)(3)判定2 ④面面平行的性质: (1)(面面平行线面平行); (2);(面面平行线线平行)(3)夹在两个平行平面间的平行线段相等。
立体几何综合测试题(卷).docx

立体几何一、选择、填空题I 、如下图是一个几何体的三视图,那么这个几何体外接球的表 面积为A. 87 勿B. 16勿C. 32〃D. 64勿 2、如图,在正四棱柱ABCD — A|B|CQ|中,AB = 1,AA|=2,点P是平面A|B|G0内的一个动点,那么三棱锥P-ABC 的正视图与俯视图的 面积之比的最大值为05、四棱锥P-ABCI )的三视图如下图,那么四棱锥P-ABCI )的高为A. 2B. 3C. V5D. V66、某儿何体的三视图如下图,那么该儿何体的体积为(A )8-2)3(B )8—一万 4 A. IB.2 C. 12 D. 14 帽视图第2题3、假设某儿何体的三视图(单位: A.I2JIB.24 兀C. 15 兀+12俯觇图 ITMMN cm )如右上图所示,那么此儿何体的外表积是()cm2D.127C+124、某几何体的三视图如下图,其中俯视图是正三角形,那么该几何体的体积为(A危(B)2 右 (C”(D)4A /3 主筏圈 左祝用 H 图28一一〃3- 冗8~-2 7、正四棱锥的顶点都在同一球面上,且该棱锥的高为4,底面边长为2次,那么该球的外表积为.8、假设/〃、〃是两条不同的直线,a、0、y是三个不同的平面,那么以下命题中为真命题的是人.假设m u <, a L 0 ,那么mVaB. a Q / = 7/7, Q/ = n, m // n ,那么a // /3 C.假设aJ_x,a_L”, 那么p H yD. in V p■, m H a那么a V p9、一个儿何体的三视图如下图,那么这个儿何体的体积为.10、假设/、〃1、〃是互不一样的空间三条直线,”是不重合的两个平面,以下结论正确的选项是〔)A、a/7p, /ua, nu|3nl〃n; B、/_La, /〃Bna_LBC、/±n, m_Lnn/〃m;a±p, / ca=> / ±p;11、甲几何体(上)与乙几何体〔下)的组合体的三视图如以下图所示,甲、乙几何体的体积分别为K、岭,那么V,:V2等于012、某几何体的三视图的侧视图是一个正三角形,如下图.那么该几何体的外表积等于A. 60 + 4>/3 + 2>/21B. 60 + 2占+ 2屈C. 60 + 2右 + 4他D. 60 + 4右+ 4屈13、设是两条不同的直线,”是两个不同的平面,以下命题中正确的选项是A.假设a!Ib y alla,那么 Z?//a B,假设a ± p,a!!a,那么a ±C.假设aVp.akp,那么aliaD.假设Q_L/?,Q_L Q,_L0,那么a L ft15、)一个儿何体的三视图如右上图所示,其中正视图为等腰直角三角形,侧视图与俯视图均为正方形,那么,该几何体的外接球的外表积为D、D、A. 1:4A. 1:4B. 1:3C. 2:3D. 1:7114、右图是一个空间几何体的三视图,那么该几何体的外表积为▲.二、解答题四棱台ABCD- AiB.C.D,的上下底面分别是边R为2和4的正方形,AA,=4且AAi_L底面ABCD,点P为DDi的中点.⑴求证:AB11面PBC;(II)在BC边上找一点Q,使PQ〃面AiABBi,并求三棱锥Q-PBBi的体积。
高三数学立体几何专项练习题及答案

高三数学立体几何专项练习题及答案一、选择题1. 下列哪个几何体的所有面都是三角形?A. 正方体B. 圆柱体C. 正六面体D. 球体答案:C2. 一个有8个面的多面体,其中6个面是正方形,另外2个面是等边三角形,它的名字是?A. 正八面体B. 正十二面体C. 正二十面体D. 正二十四面体答案:C3. 空间中任意一点到四个角落连线的垂直距离相等的四棱锥称为?A. 正四棱锥B. 圆锥台C. 四棱锥D. 无法确定答案:C4. 任意多面体的面数与顶点数、棱数的关系是?A. 面数 + 顶点数 = 棱数 + 2B. 面数 + 棱数 = 顶点数 + 2C. 顶点数 + 棱数 = 面数 + 2D. 顶点数 + 面数 = 棱数 + 2答案:A5. 求下列多面体的棱数:(1)正六面体(2)正八面体(3)正十二面体答案:(1)正六面体的棱数为 12(2)正八面体的棱数为 24(3)正十二面体的棱数为 30二、填空题1. 下列说法正确的是:一棱锥没有底面时,它的底面是一个______。
答案:点2. 铅垂线是指从一个多面体的一个顶点到与它相对的棱上所作的垂线,它与该棱垂足的连线相交于该多面体的______上。
答案:中点3. 对正八面体,下列说法不正确的是:_____条对角线与_____两两垂直。
答案:六,相邻面三、计算题1. 一个棱锥的底面是一个边长为6cm的正三角形,其高为8cm。
求棱锥体积。
解答:底面积 S = (1/2) ×底边长 ×高 = (1/2) × 6 × 8 = 24 cm²棱锥体积 V = (1/3) × S ×高 = (1/3) × 24 × 8 = 64 cm³所以,棱锥的体积为64 cm³。
2. 一个正四棱锥的底面是一个边长为10cm的正方形,其高为12cm。
求四棱锥的体积。
解答:底面积 S = 边长² = 10² = 100 cm²四棱锥体积 V = (1/3) × S ×高 = (1/3) × 100 × 12 = 400 cm³所以,四棱锥的体积为400 cm³。
第一章空间向量与立体几何-章节综合训练

章节综合训练[文档副标题][日期]世纪金榜[公司地址]单元质量评估(120分钟 150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知向量a=(1,,2),b=(2,-1,k),且a与b互相垂直,则k的值是( )A.-1B.C.1D.-2.若a,b,c是空间任意三个向量,λ∈R,下列关系中,不成立的是( )A.a+b=b+aB.λ(a+b)=λa+λbC.(a+b)+c=a+(b+c)D.b=λa3如图,空间四边形ABCD中,E,F分别是BC,CD的中点,则++等于( )A. B. C. D.4.若A(1,-2,1),B(4,2,3),C(6,-1,4),则△ABC的形状是( )A.不等边锐角三角形B.直角三角形C.钝角三角形D.等边三角形5.已知平面α的一个法向量为n1=(-1,-2,-1),平面β的一个法向量n2=(2,4,2),则不重合的平面α与平面β( )A.平行B.垂直C.相交但不垂直D.不确定6.若a=e1+e2+e3,b=e1+e2-e3,c=e1-e2+e3,d=e1+2e2+3e3,d=αa+βb+γc,则α,β,γ分别为( )A.,-1,-B.,1,C.-,1,-D.,1,-7.(2013·吉安高二检测)已知直线l1的方向向量a=(2,4,x),直线l2的方向向量b=(2,y,2),若|a|=6,且a⊥b,则x+y的值是( )A.1或-3B.-1或3C.-3D.18.已知A(1,-1,2),B(2,3,-1),C(-1,0,0),则△ABC的面积是( )A. B. C. D.9.下列命题正确的是( )A.若=+,则P,A,B三点共线B.若{a,b,c}是空间的一个基底,则{a+b,b+c,a+c}构成空间的另一个基底C.(a·b)·c=|a|·|b|·|c|D.△ABC为直角三角形的充要条件是·=010.如图所示,四边形ABCD为矩形,AB=3,BC=1,EF∥BC且AE=2EB,G为BC的中点,K 为△ADF的外心.沿EF将矩形折成一个120°的二面角A-EF-B,则此时KG的长是( )A.1B.3C.D.11.如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别为棱AA1,BB1的中点,G为棱A1B1上的一点,且A1G=λ(0≤λ≤1),则点G到平面D1EF的距离为( )A. B. C. D.12.如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则BC1与平面BB1D1D所成角的正弦值为( )A. B. C. D.二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)13.已知向量a=(λ+1,0,2λ),b=(6,2μ-1,2),若a∥b,则λ与μ的值分别是、.14.若A(0,2,),B(1,-1,),C(-2,1,)是平面α内的三点,设平面α的法向量为n=(x,y,z),则x∶y∶z= .15.平面α,β,γ两两相互垂直,且它们相交于一点O,P点到三个面的距离分别是1cm,2 cm,3cm,则PO的长为cm.16.如图,平面PAD⊥平面ABCD,四边形ABCD为正方形,∠PAD=90°,且PA=AD=2,E,F分别是线段PA,CD的中点,则异面直线EF与BD所成角的余弦值为.三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5),(1)求以向量,为一组邻边的平行四边形的面积S.(2)若向量a分别与向量,垂直,且|a|=,求向量a的坐标.18.(12分)如图所示,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB= 90°,侧棱AA1=2,CA=2,D是CC1的中点,试问在线段A1B上是否存在一点E(不与端点重合)使得点A1到平面AED的距离为?19.(12分)在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为CD的中点.(1)求证:B1E⊥AD1.(2)在棱AA1上是否存在一点P,使得DP∥平面B1AE?若存在,求AP的长;若不存在,说明理由.20.(12分)如图所示,在棱长为1的正方体ABCD-A'B'C'D'中,E,F分别是D'D,DB的中点,G在棱CD上,CG=CD,H为C'G的中点.(1)求证:EF⊥B'C.(2)求EF,C'G所成角的余弦值.(3)求FH的长.21.(12分)如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=PA.点O,D分别是AC,PC的中点,OP⊥底面ABC.(1)求证:OD∥平面PAB.(2)求直线OD与平面PBC所成角的正弦值.22.(12分)(能力挑战题)已知四棱锥P-ABCD中,PA⊥平面ABCD,且PA=4PQ=4,底面为直角梯形,∠CDA=∠BAD=90°,AB=2,CD=1,AD=,M,N分别是PD,PB的中点.(1)求证:MQ∥平面PCB.(2)求截面MCN与底面ABCD所成二面角的大小.(3)求点A到平面MCN的距离.答案解析1.【解析】选D.a·b=2-+2k=0,∴k=-.2.【解析】选D.由向量的运算律知,A,B,C均正确,对于D,当a=0,b≠0时,不成立.3.【解析】选C.++=++=.4.【解析】选A.=(3,4,2),=(5,1,3),=(2,-3,1).由·>0,得A为锐角;由·>0,得C为锐角;由·>0,得B为锐角,且||≠||≠||,所以△ABC为不等边锐角三角形.5.【解析】选A.∵n2=-2n1,∴n2∥n1,故α∥β.6.【解析】选A.由d=αa+βb+γc=α(e1+e2+e3)+β(e1+e2-e3)+γ(e1-e2+e3)=(α+β+γ)e1+(α+β-γ)e2+(α-β+γ)e3=e1+2e2+3e3.∴解得α=,β=-1,γ=-.7.【解析】选A.根据|a|=6,可得x=±4,当x=4时,y=-3,当x=-4时,y=1,所以x+y=1或-3.8.【解析】选C.易知=(1,4,-3),=(-2,1,-2),∴||=,||=3,cos<,>==,∴sin<,>==,∴S△ABC=||·||sin<,>=.9.【解析】选B.P,A,B三点共面不一定共线,故A错误;由数量积公式知C错误;△ABC为直角三角形时可能·=0,也可能·=0,或·=0,故D错误.10.【解析】选D.由题意知K为AF的中点,取EF的中点H,连接KH,GH易证明∠KHG即为二面角A-EF-B的平面角,在△KHG中,由KH=HG=1,∠KHG=120°,可解得KG=.11.【解题指南】可以根据几何的有关性质转化为点A1到直线D1E的距离,利用三角形的面积可求;或建立空间直角坐标系,利用平面的法向量来求.【解析】选D.方法一:∵A1B1∥EF,G在A1B1上,∴G到平面D1EF的距离即为A1到平面D1EF的距离,也就是A1到D1E的距离.∵D1E=,∴由三角形面积可得h==.方法二:以AB,AD,AA的方向作为x轴,y轴,z轴的正方向建立空间直角坐标系,1则E(0,0,),F(1,0,),D1(0,1,1),G(λ,0,1),∴=(1,0,0),=(0,1,),=(-λ,1,0),设平面EFD1的一个法向量是n=(x,y,z),则解得取y=1,则n=(0,1,-2).∴点G到平面EFD1的距离是:h===.12.【解析】选 D.如图建立空间直角坐标系,则B(2,2,0),D1(0,0,1),C1(0,2,1),∴=(0,0,1),=(2,2,0),=(-2,0,1).设平面BB1D1D的一个法向量n=(x,y,z),由可得∴可取n=(1,-1,0).cos<n,>===,∴BC1与平面BB1D1D所成角的正弦值为.13.【解析】∵a∥b,∴存在实数k,使得a=k b,即(λ+1,0,2λ)=k(6,2μ-1,2),∴解得k=λ=,μ=.答案:14.【解析】=(1,-3,-),=(-2,-1,-),∵∴∴x∶y∶z=y∶y∶(-y)=2∶3∶(-4).答案:2∶3∶(-4)15.【解析】如图所示,建立空间直角坐标系,不妨设O(0,0,0),P(1,2,3),∴|OP|==(cm).答案:16.【解析】∵=-,=-++=-++,∴·= (-)·(-++)=4-2=2.||2=(-++)2=6,∴||=,||=2,∴cos<,>= ==,即异面直线EF与BD所成角的余弦值为.答案:【一题多解】如图所示,建立空间直角坐标系Axyz,∴E(0,0,1),F(1,2,0),B(2,0,0),D(0,2,0),∴=(1,2,-1),=(-2,2,0),∴cos<,>==,∴异面直线EF与BD所成角的余弦值为.17.【解析】(1)∵=(-2,-1,3),=(1,-3,2),∴cos∠BAC==,∴∠BAC=60°,∴S=||||sin 60°=7. (2)设a=(x,y,z),则a⊥⇒-2x-y+3z=0,a⊥⇒x-3y+2z=0,|a|=⇒x2+y2+z2=3,解得x=y=z=1或x=y=z=-1,∴a=(1,1,1),或a=(-1,-1,-1).18.【解析】存在.以CA,CB,CC1所在的直线为x轴,y 轴和z轴,建立如图所示的空间直角坐标系,则A(2,0,0),A1(2,0,2),D(0,0,1),B(0,2,0),设=λ,λ∈(0,1),则E(2λ,2(1-λ),2λ).又=(-2,0,1),=(2(λ-1),2(1-λ),2λ),设n=(x,y,z)为平面AED的法向量,则即取x=1,则y=,z=2,即n=(1,,2).由于d==,∴=,又λ∈(0,1),解得λ=,∴当点E为A1B的中点时,A1到平面AED的距离为.【拓展提升】探索性问题的解法在立体几何中,经常会遇到点、线、面处在什么位置时结论成立,或某一结论成立时需要具备什么条件,或某一结论在某一条件下,某个元素在某个位置时是否成立等类似的问题.这些问题都属探索性问题,解决这些问题仅凭几何手段有时会十分困难,我们借助向量将“形”转化为“数”,把点、线、面的位置数量化,通过对代数式的运算就可得出相应的结论.这样可以使许多几何问题进行类化,公式化,使问题的解决变得有“法”可依,有路可寻.19.【解析】以A为原点,,,的方向分别为x轴、y轴、z轴的正方向建立空间直角坐标系.设AB=a,则A(0,0,0),D(0,1,0),D1(0,1,1),E(,1,0),B1(a,0,1),(1)=(0,1,1),=(-,1,-1),∵·=-×0+1×1+(-1)×1=0,∴B1E⊥AD1.(2)假设在棱AA1上存在一点P(0,0,z0),使得DP∥平面B1AE,此时=(0,-1,z0),又设平面B1AE的法向量为n=(x,y,z).∵n⊥平面B1AE,=(a,0,1),=(,1,0),∴n⊥,n⊥,得取x=1,得平面B1AE的一个法向量n=(1,-,-a),要使DP∥平面B1AE,只需n⊥,有-az0=0,解得:z0=.∴AP=,∴在棱AA1上存在点P,使得DP∥平面B1AE,且P为AA1的中点.20.【解题指南】要证明EF⊥B'C,只需要证明·=0;要求EF,C'G所成角的余弦值,只要求出,所成角的余弦值;要求FH的长,只要求出|即可. 【解析】(1)设=a,=b,=c,则c·b=b·a=c·a=0,|a|2=a2=1,|b|2=b2=1,|c|2=c2=1.∵=+=-c+(a-b)=(a-b-c),=-=b-c,∴·=(a-b-c)·(b-c)=(c2-b2)=×(1-1)=0.∴EF⊥B'C.(2)∵=(a-b-c),=+=-c-a,∴·=(a-b-c)·(-c-a)=(-a2+c2)=,||2=(a-b-c)2=(a2+b2+c2)=,||2=(-c-a)2=c2+a2=,∴||=,||=,cos<,>==,∴EF,C'G所成角的余弦值为.(3)∵=+++=(a-b)+b+c+=(a-b)+b+c+(-c-a)=a+b+c, ∴||2=(a+b+c)2=a2+b2+c2=,∴FH的长为.21.【解析】方法一:(1)∵O,D分别为AC,PC的中点,∴OD∥PA.又PA⊂平面PAB,OD⊄平面PAB,∴OD∥平面PAB.(2)设PA=2a,∵AB⊥BC,OA=OC,∴OA=OB=OC= a.又∵OP⊥平面ABC,∴PA=PB=PC=2a.取BC中点E,连接PE,则BC⊥平面POE.作OF⊥PE于F,连接DF,则OF⊥平面PBC.∴∠ODF是OD与平面PBC所成的角.∵PA=2a,OA=a,∴OP= a.又∵OE=,∴OF= a.在Rt△ODF中,sin∠ODF==,∴OD与平面PBC所成角的正弦值为.方法二:∵OP⊥平面ABC,OA=OC,AB=BC,∴OA⊥OB,OA⊥OP,OB⊥OP.以O为原点,建立空间直角坐标系Oxyz(如图), 设AB=a,则A(a,0,0),B(0,a,0),C(-a,0,0).设OP=h,则P(0,0,h).(1)∵D为PC的中点,∴=(-a,0,h).又=(a,0,-h),∴=-.∴∥,又PA⊂平面PAB,OD⊄平面PAB,∴OD∥平面PAB.(2)∵PA=2a,∴h=a,∴=(-a,0,a).可求得平面PBC的一个法向量n=(-1,1,), ∴cos<,n>==.设OD与平面PBC所成的角为θ,则sinθ=|cos<,n>|=.∴OD与平面PBC所成角的正弦值为.22.【解析】方法一:以A为原点,以AD,AB,AP所在直线分别为x轴,y轴,z轴建立空间直角坐标系Axyz,由AB=2,CD=1,AD=,PA=4PQ=4,M,N分别是PD,PB的中点,可得A(0,0,0),B(0,2,0),C(,1,0),D(,0,0),P(0,0,4),Q(0,0,3),M(,0,2),N(0,1,2).(1)=(,-1,0),=(0,2,-4),=(-,0,1).设平面PBC的法向量为n0=(x,y,z),则有:n0⊥⇒(x,y,z)·(,-1,0)=0⇒x-y=0,n0⊥⇒(x,y,z)·(0,2,-4)= 0⇒2y-4z=0,令z=1,则x=,y=2⇒n0=(,2,1).∴·n0=(-,0,1)·(,2,1)=0,又MQ⊄平面PCB,∴MQ∥平面PCB.(2)设平面的MCN的法向量为n=(x',y',z'),又=(-,-1,2),=(-,0,2),则有:n⊥⇒(x',y',z')·(-,-1,2)=0⇒-x'-y'+2z'=0,n⊥⇒(x',y',z')·(-,0,2)=0⇒-x'+2z'=0,令z'=1,则x'=,y'=1⇒n=(,1,1).又=(0,0,4)为平面ABCD的一个法向量.∴cos<n,>===,又截面MCN与底面ABCD所成二面角为锐二面角,∴截面MCN与底面ABCD所成二面角的大小为.(3)∵=(-,-1,0),∴所求的距离d=CAnn==.方法二:(1)取AP的中点E,连接ED,则ED∥CN,依题有Q为EP的中点,所以MQ∥ED,所以MQ∥CN,又MQ⊄平面PCB,CN⊂平面PCB,∴MQ∥平面PCB.(2)易证:平面MEN∥底面ABCD,所以截面MCN与平面MEN所成的二面角即为平面MCN与底面ABCD所成的角, 因为PA⊥平面ABCD,所以PA⊥平面MEN,过E作EF⊥MN,垂足为F,连接QF,则由三垂线定理可知QF⊥MN,由(1)可知M,C,N,Q四点共面,所以∠QFE为截面MCN与平面MEN所成的二面角的平面角.在Rt△MEN中,ME=,NE=1,MN=,故EF=,所以:tan∠QFE=,∠QFE=.即所求二面角大小为.(3)因为EP的中点为Q,且平面MCN与PA交于点Q,所以点A到平面MCN的距离是点E到平面MCN的距离的3倍,由(2)知:MN⊥平面QEF,则平面MCNQ⊥平面QEF且交线为QF,作EH⊥QF,垂足为H,则EH⊥平面MCNQ,故EH即为点E到平面MCN的距离.在Rt△EQF中,EF=,∠QFE=,故EH=,即原点A到平面MCN的距离是.关闭Word文档返回原板块。
立体几何大题综合(含答案)
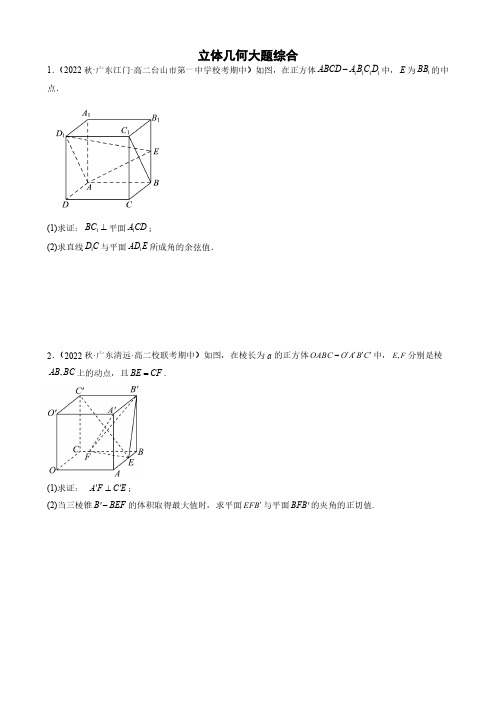
立体几何大题综合1.(2022秋·广东江门·高二台山市第一中学校考期中)如图,在正方体1111ABCD A B C D -中,E 为1BB 的中点.(1)求证:1BC ⊥平面1ACD ;(2)求直线1D C 与平面1AD E 所成角的余弦值.2.(2022秋·广东清远·高二校联考期中)如图,在棱长为a 的正方体OABC O A B C ''''-中,,E F 分别是棱,AB BC 上的动点,且BE CF =.(1)求证:A F C E ''⊥;(2)当三棱锥B BEF '-的体积取得最大值时,求平面EFB '与平面BFB '的夹角的正切值.3.(2022秋·广东肇庆·高二校考期中)如图在棱长为1的正方体1111ABCD A B C D -中,E 为11A B 的中点,F 为AB 的中点,H 为1DD 的中点,K 为1BB 的中点.(1)求直线1A H 到直线KC 的距离;(2)求直线FC 到平面1AEC 的距离.4.(2022秋·广东江门·高二校考期中)如图,在四棱锥P -ABCD 中,PD ⊥底面ABCD ,底面ABCD 是边长为2的正方形,PD CD =,F ,G 分别是PB ,AD 的中点.(1)求证:FG //平面PCD ;(2)求点C 到平面PGB 的距离.5.(2022秋·广东清远·高二校联考期中)如图,在四棱锥P ABCD -中,底面ABCD 为矩形,AB ⊥平面PAD ,E 是AD 的中点,PAD 为等腰直角三角形,DP AP ⊥,2PA AB ==2(1)求证:PE BD ⊥;(2)求点A 到平面PBE 的距离.6.(2022秋·广东江门·高二新会陈经纶中学校考期中)如图,在直角梯形ABCD 中,,=90,AD BC ADC AE ∠︒⊥∥平面ABCD ,EF CD ∥,112BC CD AE EF AD =====.(1)求证:BE AF ⊥;(2)在线段BC 上是否存在点M ,使平面EMD 与平面AMD 的夹角的大小为π3若存在,求出CM 的长;若不存在,请说明理由.7.(2022秋·广东江门·高二台山市第一中学校考期中)如图,边长为1的正方形ABCD 所在平面与正方形ABEF 所在平面互相垂直,动点M 、N 分别在正方形对角线AC 和BF 上移动,且(0CM BN a a ==<<.(1)求证MN 与平面BCE 平行;(2)当a =A MN B --的余弦值.8.(2022秋·广东肇庆·高二肇庆市端州中学校考期中)如图在四棱锥P ABCD -中,侧面PAD ⊥底面ABCD ,侧棱PA PD ==ABCD 为直角梯形,其中BC AD ∥,AB AD ⊥,222AD AB BC ===,O 为AD 的中点.(1)求证:PO ⊥平面ABCD ;(2)求二面角C PD A --的正弦值.9.(2022秋·广东江门·高二江门市第二中学校考期中)如图,已知PA ⊥平面ABCD ,底面ABCD 为矩形,2,,PA AD AB M N ===分别为,AB PC 的中点.(1)求证:MN 平面PAD ;(2)求平面PMC 与平面PAD 的夹角的余弦值.10.(2022秋·广东阳江·高二校联考期中)图1是直角梯形ABCD ,//AB DC ,90,2,3,2D AB DC AD CE ED ︒∠====.以BE 为折痕将BCE 折起,使点C 到达C 1的位置,且1AC = 2.(1)证明:平面1BC E ⊥平面ABED ;(2)求直线1BC 与平面1AC D 所成角的正弦值.11.(2022秋·广东深圳·高二深圳外国语学校校考期中)如图所示,在四棱锥P ABCD -中,底面ABCD 为正方形,E 为侧棱PC的中点.(1)设经过A 、B 、E 三点的平面交PD 于F ,证明:F 为PD 的中点;(2)若PA ⊥底面ABCD ,且2PA AD ==,求点P 到平面ABE 的距离.12.(2022秋·广东阳江·高二校联考期中)如图,在四棱柱ABCD -A 1B 1C 1D 1中,四边形ABCD 是一个边长为2的菱形,∠DAB =60°.侧棱DD 1⊥平面ABCD ,DD 1=3.(1)求二面角B -D 1C -D 的平面角的余弦值;(2)设E 是D 1B 的中点,在线段D 1C 上是否存在一点P ,使得AE ∥平面PDB ?若存在,请求出11D P D C的值;若不存在,请说明理由.13.(2022秋·广东茂名·高二统考期中)在直四棱柱1111ABCD A B C D -中,四边形ABCD 为平行四边形,M为1AA 的中点,1BC BD ==,1AB AA ==(1)求证:DM ⊥平面1BDC ;(2)求平面1MBC 与平面1D B C 夹角的余弦值.14.(2022秋·广东揭阳·高二惠来县第一中学校考期中)已知四棱锥P ABCD -中,底面ABCD 是矩形,且2=AD AB ,PAD 是正三角形,CD ⊥平面PAD ,E 、F 、G 、O 分别是PC 、PD 、BC 、AD 的中点.(1)求平面EFG 与平面ABCD 所成角的大小;(2)线段PA 上是否存在点M ,使得直线GM 与平面EFG 所成角的大小为π6,若存在,求出PM PA的值;若不存在,说明理由.15.(2022秋·广东佛山·高二顺德一中校考期中)如图,在直棱柱1111ABCD A B C D -中,底面ABCD 是边长为4的菱形,60BAD ∠= ,14AA =,P 是1AD 上的动点(不含端点).(1)当P 为1AD 的中点时,求直线AD 到平面PBC 的距离;(2)求直线1AD 和平面BCP 所成角的正弦值的取值范围.16.(2022秋·广东佛山·高二顺德一中校考期中)如图,在直角梯形ABED 中,//BE AD ,DE AD ⊥,BC AD ⊥,4AB =,BC =BE =.将矩形BEDC 沿BC 翻折,使得平面ABC ⊥平面BCDE .(1)求DB 与平面ADE 所成角的正弦值.(2)求平面ADE 与平面ABC 所成的锐二面角的余弦值.17.(2022秋·广东珠海·高二珠海市第二中学校考期中)如图1,在MBC 中,24BM BC BM BC ==⊥,,,A D 分别为棱,BM MC 的中点,将△MAD 沿AD 折起到PAD 的位置,使90PAB ∠=︒,如图2,连接,PB PC .(1)求证:平面PAD ⊥平面ABCD ;(2)若E 为PC 中点,求直线DE 与平面PBD 所成角的正弦值;(3)线段PC 上是否存在一点G ,使二面角G AD P --求出PG PC 的值;若不存在,请说明理由.18.(2022秋·广东广州·高二广州市第八十九中学校考期中)如图,已知梯形ABCD ,AB //CD ,,120AD DC BC ADC ︒==∠=,四边形ACFE 为正方形,且平面ACFE ⊥平面ABCD .(1)求证:BC ⊥平面ACFE ;(2)点M 在线段EF 上运动,求平面MAB 与平面ADE 夹角余弦值的取值范围.19.(2022秋·广东东莞·高二校考期中)如图,在长方体ABCD-A 1B 1C 1D 1中,E ,M 分别是BC ,AE 的中点,AD=AA 1=1,AB=2.(1)试问在线段CD 1上是否存在一点N ,使MN ∥平面ADD 1A 1?若存在,确定N 的位置;若不存在,请说明理由;(2)在(1)中,当MN ∥平面ADD 1A 1时,试确定直线BB 1与平面DMN 的交点F 的位置,并求BF 的长.20.(2022秋·广东湛江·高二湛江二十一中校考期中)如图,在长方体1111ABCD A B C D -中,11AD AA ==,2AB =,点E 在棱AB 上移动.(1)证明:11D E A D ⊥;(2)求平面1ACD 的法向量.(3)当E 为AB 的中点时,求点E 到面1ACD 的距离.21.(2022秋·广东广州·高二统考期中)如图,在四棱锥P —ABCD 中,PA ⊥平面ABCD ,底面ABCD 是边长为2的正方形,PA =,G 为CD 的中点,E ,F 是棱PD 上两点(F 在E 的上方),且2EF =.(1)若BF //平面AEG ,求DE ;(2)当点F 到平面AEC 的距离取得最大值时,求直线AG 与平面AEC 所成角的正弦值.22.(2022秋·广东广州·高二校联考期中)在多面体ABCDEF 中,平面ABCD 为正方形,2AB =,3AE =,DE =E AD C --//EF BD .(1)证明:平面ABCD ⊥平面DCE ;(2)若()0EF DB λλ=> ,求平面ABF 与平面CEF 所成锐二面角的余弦值的取值范围.23.(2022秋·广东佛山·高二佛山市顺德区容山中学校考期中)如图,圆柱的轴截面ABCD 为正方形,点E 在底面圆周上,且,BE CE M =为AE 上的一点,且,BM AC N ⊥为线段AC 上一动点(不与,A C 重合)(1)若2AN NC =,设平面BMN ⋂面BEC l =,求证://MN l ;(2)当平面BMN 与平面DEC 夹角为π3,试确定N 点的位置.24.(2022秋·广东肇庆·高二肇庆市端州中学校考期中)如图,四棱锥P ABCD -的底面为菱形,,23ABC AB AP π∠===,PA ⊥底面ABCD ,,E F 分别是线段,PB PD 的中点,G 是线段PC 上的一点.(1)若G 是直线PC 与平面AEF 的交点,试确定PG CG的值;(2)若直线AG 与平面AEF 所成角的正弦值为35,求三棱锥P EFG -体积.25.(2022秋·广东江门·高二校考期中)如图甲,在矩形ABCD 中,2AB AD E ==为线段DC 的中点,ADE V 沿直线AE 折起,使得DC .(1)求证:BE ⊥平面ADE ;(2)线段AB 上是否存在一点H ,使得平面ADE 与平面DHC 所成的角为π4若不存在,说明理由;若存在,求出H 点的位置.26.(2022秋·广东惠州·高二统考期中)如图,在四棱锥P ABMN -中,PNM △是边长为2的正三角形,AN NP ⊥,AN BM ∥,3AN =,1BM =,AB =C ,D 分别是线段AB ,NP 的中点.(1)求证:平面ANMB ⊥平面NMP ;(2)求直线CD 与平面ABP 所成角的正弦值.27.(2022秋·广东广州·高二校联考期中)如图,在四棱锥P ABCD -中,平面PAD ⊥平面,2,4,ABCD PA AD BD AB ====,BD 是ADC ∠的平分线,且BD BC ⊥.(1)若点E 为棱PC 的中点,证明:BE 平面PAD ;(2)已知二面角P AB D --的大小为60 ,求平面PBD 和平面PCD 的夹角的余弦值.28.(2022秋·广东珠海·高二珠海市斗门区第一中学校考期中)如图,等腰直角△ACD 的斜边AC 为直角△ABC 的直角边,E 是AC 的中点,F 在BC 上.将三角形ACD 沿AC 翻折,分别连接DE ,DF ,EF ,使得平面DEF ⊥平面ABC .已知2AC =,30B ∠=︒,(1)证明:EF ∥平面ABD ;(2)若DF =A BC D --的余弦值.29.(2022秋·广东阳江·高二统考期中)如图,在四面体ABCD 中,ABC 是正三角形,ACD 是直角三角形,ABD CBD ∠=∠,AB =BD .(1)求证:平面ACD ⊥平面ABC ;(2)若DE mDB = ,二面角D AE C --的余弦值为17,求m .30.(2022春·广东广州·高二执信中学校考期中)已知△ABC 是边长为6的等边三角形,点M ,N 分别是边AB ,AC 的三等分点,且13AM AB =,13CN CA =,沿MN 将△AMN 折起到A MN '△的位置,使90A MB '∠=︒.(1)求证:A M '⊥平面MBCN ;(2)在线段BC 上是否存在点D ,使平面A ND '与平面A MB '所成锐二面角的余弦值为13若存在,设()0BD BC λλ=> ,求λ的值;若不存在,说明理由.立体几何大题综合答案1.(2022秋·广东江门·高二台山市第一中学校考期中)如图,在正方体1111ABCD A B C D -中,E 为1BB 的中点.(1)求证:1BC ⊥平面1ACD ;(2)求直线1D C 与平面1AD E 所成角的余弦值.(2)以AD 方向为x 轴正方向,妨设正方体边长为1,则()0,0,0A 面1AD E 的法向量为(),,n x y z = ,则设直线1D C 与平面1AD E 所成角为2.(2022秋·广东清远·高二校联考期中)如图,在棱长为a 的正方体OABC O A B C ''''-中,,E F 分别是棱,AB BC 上的动点,且BE CF =.(1)求证:A F C E ''⊥;(2)当三棱锥B BEF '-的体积取得最大值时,求平面EFB '与平面BFB '的夹角的正切值.则()()()0,0,0,1,0,0,0,1,0,C O B B (,1,0),(0,,0)E m F m ,(1,A F '=- 则(1)(1)11A F C E m m ''⋅=-+-⨯+ ∴A F C E ''⊥ ,故A F C E ''⊥.(2)由(1)知1BB '=,而B BEF V '-故当S 取到最大值时,三棱锥111111的中点,F 为AB的中点,H为1DD的中点,K为1BB的中点.(1)求直线1A H到直线KC的距离;(2)求直线FC到平面1AEC的距离.【详解】(1)长为2的正方形,PD CD =,F ,G 分别是PB ,AD 的中点.(1)求证:FG //平面PCD ;(2)求点C 到平面PGB 的距离.【详解】(1)以D 为原点,DA ,DC ,DP 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系,则(1,0,0),(0,0,2),(2,0,0),(2,2,0),(0,2,0),(1,1,1),G P A B C F 明显面PCD 的一个法向量为()1,0,0n =r ,又()0,1,1GF = ,()()1,0,00,1,10n GF ∴⋅=⋅= ,GF n ∴⊥ ,又GF ⊄面PCD ,//GF ∴面PCD ;(2)(1,0,2),(2,2,2)PG PB =-=- ,设平面PGB 的一个法向量为(,,)m a b c = ,00m PB m PG ⎧⋅=⎪∴⎨⋅=⎪⎩ ,即222020a b c a c +-=⎧⎨-=⎩,令1c =,则2,1a b ==-所以平面PGB 的一个法向量为(2,1,1)m =- ,又()2,0,0CB = ,所以点C 到平面PGB 的距离4263||411CB m d m ⋅===++ 5.(2022秋·广东清远·高二校联考期中)如图,在四棱锥P ABCD -中,底面ABCD 为矩形,AB ⊥平面PAD ,E 是AD 的中点,PAD 为等腰直角三角形,DP AP ⊥,2PA AB ==2(1)求证:PE BD ⊥;(2)求点A 到平面PBE 的距离.【详解】(1)∵AB ⊥平面PAD ,PE ⊂平面PAD ,∴PE AB ⊥,又∵PAD 是等腰直角三角形,E 是斜边AD 的中点,∴PE AD ⊥,又∵AD ⊂平面ABCD ,AB ⊂平面ABCD ,AB AD A ⋂=,∴PE ⊥平面ABCD又∵BD ⊂平面ABCD ,∴PE BD ⊥;因为22PA AB ==,则()000E ,,,(0,1,1)B ,()010A ,,则(0,1,1)EB = ,(1,0,0)EP = ,PA 设平面PBE 的一个法向量为(n = 00EB n y z EP n x ⎧⋅=+=⎪⎨⋅==⎪⎩ ,取1y =,则z 设点A 到平面PBE 的距离为h ,则∴点A 到平面PBE 的距离为226.(2022秋·广东江门·高二新会陈经纶中学校考期中)如图,在直角梯形,=90,AD BC ADC AE ∠︒⊥∥平面ABCD ,EF CD ∥,112BC CD AE EF AD =====.(1)求证:BE AF ⊥;(2)在线段BC 上是否存在点M ,使平面EMD 与平面AMD 的夹角的大小为π3若存在,求出CM 的长;若不存在,请说明理由.【详解】(1)如图,作,FG EA AG EF ,连接EG ,AF ,BG ,∵EF CD ∥且EF AG ∥,AG CD ∴ ,即点G 在平面ABCD 内,所以四边形CDAG 为平行四边形,四边形AEFG 为平行四边形.又90ADC ∠=︒,BG AG ∴⊥,因为⊥AE 平面ABCD ,BG ⊂平面ABCD ,所以AE BG ⊥,又因为AG AE A = ,,AG AE ⊂平面AEFG ,∴BG ⊥平面AEFG ,因为AF ⊂平面AEFG ,BG AF ∴⊥.AE AG ⊥ ,所以平行四边形AEFG 为矩形,又因为AE EF =,所以矩形AEFG 为正方形,所以AF EG ⊥,又因为BG EG G = ,,BG EG ⊂平面BGE ,所以AF ⊥平面BGE ,因为BE ⊂平面BGE ,所以AF BE ⊥.(2)由(1)知AG ,AD ,AE 为三条两两互相垂直的直线,所以以A 为原点,AG 为x 轴,AD 为y 轴,AE 为z 轴建立空间直角坐标系A xyz -,如图,则(0,0,0),(1,0,0),(0,0,1),(0,2,0)A G E D ,设()001,,0,[1,2]M y y ∈,∴(0,2,1)ED =- ,()01,2,0DM y =- ,设平面EMD 的法向量为(,,)n x y z = ,则00n ED n DM ⎧⋅=⎪⎨⋅=⎪⎩,即()02020y z x y y -=⎧⎨+-=⎩,令1y =,得02,2z x y ==-,所以平面EMD 的法向量为()02,1,2n y =- ,又⊥AE 平面ABCD ,即⊥AE 平面AMD ,ABEF 所在平面互相垂直,动点M 、N 分别在正方形对角线AC 和BF 上移动,且(0CM BN a a ==<<.(1)求证MN 与平面BCE 平行;(2)当a =A MN B --的余弦值.8.(2022秋·广东肇庆·高二肇庆市端州中学校考期中)侧棱2PA PD ==,底面ABCD 为直角梯形,其中BC AD ∥,AB AD ⊥,222AD AB BC ===,O 为AD 的中点.(1)求证:PO ⊥平面ABCD ;(2)求二面角C PD A --的正弦值.【详解】(1)PA PD = ,O 为AD 的中点,PO AD ∴⊥,侧面PAD ⊥底面ABCD ,侧面PAD ⋂底面ABCD AD =,PO ⊂平面PAD ,PO ∴⊥平面ABCD ;(2) 底面ABCD 为直角梯形,其中BC AD ∥,AB AD ⊥,222AD AB BC ===,OC AD ∴⊥,又PO ⊥平面ABCD ,∴以O 为原点,OC 所在直线为x 轴,OD 所在直线为y 轴,OP 所在直线为z 轴,建立空间直角坐标系,易得平面PAD 的法向量(1,0,0m =设平面PCD 的法向量(,,n x y z = 设二面角C PD A --夹角为θ,则1cos 3m n m n θ⋅==⋅ ,则sin θ2,,PA AD AB M N ===分别为,AB PC 的中点.(1)求证:MN 平面PAD ;(2)求平面PMC 与平面PAD 的夹角的余弦值.(2)由题意,可构建如下图示的空间直角坐标系,令2x =,故(2,1,1)m =- ,又(1,0,0)n = 是面PAD 的一个法向量,所以26cos ,3||||6m n m n m n ⋅<>=== 故平面PMC 与平面PAD 的夹角的余弦值10.(2022秋·广东阳江·高二校联考期中)图90,2,3,2D AB DCAD CE ED ︒∠====.以BE 为折痕将BCE 折起,使点C 到达C 1的位置,且1AC = 2.(1)证明:平面1BC E ⊥平面ABED ;(2)求直线1BC 与平面1AC D 所成角的正弦值.(2)如图②,以D 为坐标原点,DA ,DE 的方向分别为空间直角坐标系.D xyz -则(0,0,0),(3,0,0),(3,2,0),(0,1,0)D A BE ,F 33(,,0)22,133(,,3)22C ,31(,,3)BC =-- ()3,0,0DA = ,DC = 正方形,E 为侧棱PC 的中点.(1)设经过A 、B 、E 三点的平面交PD 于F ,证明:F 为PD 的中点;(2)若PA ⊥底面ABCD ,且2PA AD ==,求点P 到平面ABE 的距离.【详解】(1)因为底面ABCD 为矩形,所以//AB CD .又AB ⊄平面PCD ,且CD ⊂平面PCD ,所以//AB 平面PCD .又AB ⊂平面ABE ,且平面ABE ⋂平面PCD EF =,所以//AB EF .又因为//AB CD ,所以//CD EF因为E 为PC 的中点,所以F 为PD 的中点.(2)如图所示,以A 为原点,,,AB AD AP 所在的直线分别为x 轴、y 轴、z 轴,建立如图所示的空间直角坐标系.则(2,0,0),(2,2,0),(0,0,2),(1,1,1)B C P E ,设(,,)n x y z = 是平面ABE 的法向量,则0,0n AE n AB ⋅=⋅= ,即200x x y z =⎧⎨++=⎩令1y =,则平面ABE 的一个法向量为(0,1,1)n =- 又因为(0,0,2)AP = ,所以点P 到平面ABE 的距离为222|||00+01+21|2||011AP n n ⋅⨯⨯⨯==++ (-),即点P 到平面ABE 的距离为2.12.(2022秋·广东阳江·高二校联考期中)如图,在四棱柱ABCD -A 1B 1C 1D 1中,四边形ABCD 是一个边长为2的菱形,∠DAB =60°.侧棱DD 1⊥平面ABCD ,DD 1=3.(1)求二面角B -D 1C -D 的平面角的余弦值;(2)设E 是D 1B 的中点,在线段D 1C 上是否存在一点P ,使得AE ∥平面PDB ?若存在,请求出11D P D C 的值;若不存在,请说明理由.【详解】(1)如图1,连接BD ,由题意,△ADB 是正三角形,设M 是AB 的中点,则DM ⊥AB ,所以DM ⊥DC ,又DD 1⊥平面ABCD ,所以DM ⊥平面DD 1C 1C.以D 为原点,建立如图所示的空间直角坐标系,则D (0,0,0),D 1(0,0,3),C (0,2,0),B (3,1,0),则BC =(-3,1,0),1BD =(-3,-1,3).显然,平面D 1CD 的一个法向量是()1,0,0m = ,设平面BD 1C 的法向量为n = (x ,y ,z ),则1=30,330,n BC x y n BD x y z ⎧⋅-+=⎪⎨⋅=--+=⎪⎩ 令x =3,得n = (3,3,2),设二面角B -D 1C -D 的平面角为θ,由几何体的特征可知θ为锐角,则cos ||||m n m n θ⋅=⋅=33941++⨯=34.故二面角B -D 1C -D 的平面角的余弦值为34.(2)设11D P D C=λ,即有11λD P D C =,其中01λ≤≤由(1)知D 1(0,0,3),C (0,2,0),则()10,2,3D C =- ,所以P (0,2,33)λλ-+,又D (0,0,0),B (3,1,0),1111为1AA的中点,1BC BD==,1AB AA==(1)求证:DM⊥平面1BDC;(2)求平面1MBC与平面1D B C夹角的余弦值.则()0,0,0D,21,0,2M⎛⎫⎪⎪⎝⎭,2=AD AB ,PAD 是正三角形,CD ⊥平面PAD ,E 、F 、G 、O 分别是PC 、PD 、BC 、AD 的中点.(1)求平面EFG 与平面ABCD 所成角的大小;(2)线段PA 上是否存在点M ,使得直线GM 与平面EFG 所成角的大小为π6,若存在,求出PMPA的值;若不存在,说明理由.【详解】(1)解:因为PAD 是正三角形,O 为AD 的中点,所以PO AD ⊥,因为CD ⊥平面PAD ,PO ⊂平面PAD ,PO CD ∴⊥,,,AD CD D AD CD Q Ç=Ì平面ABCD ,PO ∴⊥平面ABCD ,因为AD BC ∥且AD BC =,O 、G 分别为AD 、BC 的中点,所以AO BG ∥且AO BG =,所以四边形ABGO 为平行四边形,15.(2022秋·广东佛山·高二顺德一中校考期中)如图,在直棱柱1111为4的菱形,60BAD ∠= ,14AA =,P 是1AD 上的动点(不含端点).(1)当P 为1AD 的中点时,求直线AD 到平面PBC 的距离;(2)求直线1AD 和平面BCP 所成角的正弦值的取值范围.则()0,0,0O ,()23,0,0A ,()10,2,4D -,()1123,2,0B C =-∴- ,AB P 为1AD 的中点,则(P()3,3,2BP =∴- ,(BC =- 则33202320n BP x y z n BC x y ⎧⋅=-+=⎪⎨⋅=--=⎪⎩4AB =,BC =BE =.将矩形BEDC 沿BC 翻折,使得平面ABC ⊥平面BCDE .(1)求DB 与平面ADE 所成角的正弦值.(2)求平面ADE 与平面ABC 所成的锐二面角的余弦值.【详解】(1) 平面ABC ⊥平面BCDE ,平面ABC ⋂平面BCDE BC =,CD BC ⊥,BE ⊂平面BCDE ,CD \^平面ABC ,则以C 为原点,,,CA CB CD正方向为,,x y z 轴,可建立如图所示的空间直角坐标系,则()0,0,0C ,()22,0,0A()22,0,23AD ∴=- ,DE设平面ADE 的法向量为n =则2223220AD n x z DE n y ⎧⋅=-+=⎪⎨⋅==⎪⎩DB n ⋅ ,A D 分别为棱,BM MC 的中点,将△MAD 沿AD 折起到PAD 的位置,使90PAB ∠=︒,如图2,连接,PB PC .(1)求证:平面PAD ⊥平面ABCD ;(2)若E 为PC 中点,求直线DE 与平面PBD 所成角的正弦值;(3)线段PC 上是否存在一点G ,使二面角G AD P --的余弦值为10若存在,求出PG PC 的值;若不存在,请说明理由.由题意得(0,1,0),(0,0,2),(2,0,0),(2,2,0),D P B C 所以(1,0,1)DE = ,(2,0,2),PB PD =-=设平面PBD 的法向量(,,)n x y z =,则22020PB n x z PD n y z ⎧⋅=-=⎪⎨⋅=-=⎪⎩ ,解得(1,2,1)n = 设直线DE 与平面PBD 所成角为θ,n DE ⋅,120AD DC BC ADC ︒==∠=,四边形ACFE 为正方形,且平面ACFE ⊥平面ABCD .(1)求证:BC ⊥平面ACFE ;(2)点M 在线段EF 上运动,求平面MAB 与平面ADE 夹角余弦值的取值范围.令(03)FM λλ=≤≤,则(3,0,0),(0,1,0),(,0,3),(3,0,A B M E λ1111AD=AA 1=1,AB=2.(1)试问在线段CD 1上是否存在一点N ,使MN ∥平面ADD 1A 1?若存在,确定N 的位置;若不存在,请说明理由;(2)在(1)中,当MN ∥平面ADD 1A 1时,试确定直线BB 1与平面DMN 的交点F 的位置,并求BF 的长.延长DM交AB于点G,可证点G是线段再过点G作GF//AB1与线段BB1交于点20.(2022秋·广东湛江·高二湛江二十一中校考期中)如图,在长方体11111 AB=,点E在棱AB上移动.2(1)证明:11D E A D ⊥;(2)求平面1ACD 的法向量.(3)当E 为AB 的中点时,求点E 到面1ACD 的距离.【详解】(1)以D 为坐标原点,分别以1DA DC DD 、、所在直线为x y z 、、轴,建立如图的坐标系,则()()()()()110,0,0,1,0,1,0,0,1,1,0,00,2,0D A D A C ,,所以()11,0,1DA = ,设()1,,0E t ,所以()11,,1D E t =- ,所以11110DA D E ⋅=-= ,故11DA D E ⊥ 所以11D E A D ⊥;(2)设平面1ACD 的法向量为(),,n x y z =r,则()()11,0,1,1,2,0AD AC =-=-,由10,0n AD n AC ⋅=⋅=,得020x z x y -+=⎧⎨-+=⎩,令1x =得11,,12n ⎛⎫= ⎪⎝⎭;(3)当E 为AB 的中点时,()1,1,0E ,则()11,1,1D E =-,由点到平面的距离公式,得()12221111111231112n D E d n ⨯+⨯+⨯-⋅===⎛⎫++ ⎪⎝⎭,边长为2的正方形,PA=,G为CD的中点,E,F是棱PD上两点(F在E的上方),且2EF=.(1)若BF//平面AEG,求DE;(2)当点F到平面AEC的距离取得最大值时,求直线AG与平面AEC所成角的正弦值.则()0,0,0A ,()2,2,0C ,()1,2,0G ,因为2EF =,所以EFC 的面积为定值,又点A 到平面EFC 的距离为定值,所以三棱锥A -EFC 的体积为定值,即三棱锥所以要使点F 到平面AEC的距离最大,则AEC △即E 到AC 的距离最小时,点F 到平面AEC 的距离最大,设()0,2,3E t t -,则()0,2,3AE t t =- ,AC22AE AC⎛⎫⋅ DE =E AD C --//EF BD .(1)证明:平面ABCD ⊥平面DCE ;(2)若()0EF DB λλ=>,求平面ABF 与平面CEF 所成锐二面角的余弦值的取值范围.【详解】(1)∵2AB AD ==,3AE =,5DE =,∴222AD DE AE +=,即AD DE ⊥,又∵在正方形ABCD 中,AD DC ⊥,且DE DC D ⋂=,DE ⊂平面EDC ,DC ⊂平面EDC ,∴AD ⊥平面EDC ,又AD ⊂平面ABCD ,∴平面ABCD ⊥平面EDC ;(2)由(1)知,EDC ∠是二面角E AD C --的平面角,作OE CD ⊥于点O ,则cos 1OD DE EDC =⋅∠=,2OE =,且平面ABCD ⊥平面EDC ,平面ABCD ⋂平面EDC CD =,OE ⊂平面EDC ,∴OE ⊥平面ABCD ,取AB 中点M ,连接OM ,则OM CD ⊥,如图,建立空间直角坐标系,则()2,1,0A -,()2,1,0B ,()0,1,0D -,()0,1,0C ,()0,0,2E ,()2,2,0DB = ,()2,2,0EF λλ=,()0,1,2EC =- ,设平面CEF 的一个法向量为(),,m x y z=,则20220m EC y z m EF x y λλ⎧⋅=-=⎪⎨⋅=+=⎪⎩ ,取11,1,2m ⎛⎫=-- ⎪⎝⎭ ,()22,21,2BF λλ=--,()0,2,0AB = ,设平面ABF 的一个法向量为(),,n a b c =,在底面圆周上,且,BE CE M =为AE 上的一点,且,BM AC N ⊥为线段AC 上一动点(不与,A C 重合)(1)若2AN NC =,设平面BMN ⋂面BEC l =,求证://MN l ;(2)当平面BMN 与平面DEC 夹角为π3,试确定N 点的位置.【详解】(1)由题知AB ⊥面,BEC EC ⊂面BEC ,则AB EC ⊥,由BC 为底面圆的直径,则EC BE ⊥,由BE AB B =I ,,BE AB ⊂面ABE ,则(220,,,1,33BM CA ⎛⎫=-=-+ ⎪ ⎪⎝⎭设()(,,2,CN CA λλλλλ==-∈设面BMN 的法向量为(,,n x y z =r 13λ-⎛⎫,23ABC AB AP π∠===,PA ⊥底面ABCD ,,E F 分别是线段,PB PD 的中点,G 是线段PC 上的一点.(1)若G 是直线PC 与平面AEF 的交点,试确定PGCG的值;(2)若直线AG 与平面AEF 所成角的正弦值为35,求三棱锥P EFG -体积.则()()(0,0,0,3,1,0,3,1,0A BC-()31,,1,0,1,122AE AF ⎛⎫=-= ⎪ ⎪⎝⎭ (0,0,AG AP PG AP PC λ=+=+=设平面AEF 的法向量(,,m a b =ADE V 沿直线AE 折起,使得DC .(1)求证:BE ⊥平面ADE ;(2)线段AB 上是否存在一点H ,使得平面ADE 与平面DHC 所成的角为π4若不存在,说明理由;若存在,求出H 点的位置.【详解】(1)证明:连接BE ,取线段AE 的中点O ,连接,DO OC ,在Rt ADE V 中,DA DE ==,1DO AE DO ∴⊥=,在OEC △中,11,2OE AE ==()()()1,0,1,1,1,0,2,0,0,D C A B -平面ADE 的法向量()10,1,0n =,在平面直角坐标系xOy 中,直线设H 的坐标为(),2,0t t -,()(。
2021级人教版数学科目+立体几何综合训练(一)

2021 级数学科自主学习提升课程(一)立体几何综合训练1、如图,在三棱锥 A - BCD 中,平面 ABD ⊥ 平面 BCD , AB = AD , O 为 BD 的中点. (1)证明: OA ⊥ CD ;(2)若 OCD 是边长为 1 的等边三角形,点 E 在棱 AD 上, DE = 2EA ,且二面角 E - BC - D 的大小为 45︒ , 求三棱锥 A - BCD 的体积.2、如图,四棱锥 P - ABCD 的底面是矩形, PD ⊥ 底面 ABCD ,M 为 BC 的中点,且 PB ⊥ AM .(1)证明:平面 PAM ⊥ 平面 PBD ;(2)若 PD = DC = 1 ,求四棱锥 P - ABCD 的体积.3、如图,在四棱锥 P - ABCD 中,底面 ABCD 是平行四边形, ∠ABC = 120︒, AB = 1, BC = 4, PA = N 分别为 BC, PC 的中点, PD ⊥ DC , PM ⊥ MD . (1)证明: AB ⊥ PM ;(2)求直线 AN 与平面 PDM 所成角的正弦值.M ,4、如图,在四棱锥P﹣ABCD 中,PC⊥底面ABCD,底面ABCD 是直角梯形,AB⊥AD,AB∥CD,AB=2,AD=CD=1,E 是PB 的中点.(Ⅰ)求证:平面EAC⊥平面PBC;(Ⅱ)若PC>1,直线PA 与平面EAC 所成角的正弦值为,求二面角P﹣AC﹣E 的余弦值.5、如图,在四棱锥P﹣ABCD 中,AB∥CD,且∠BAP=∠CDP=90°.(1)证明:AD⊥CD;(2)已知CD=PD=4,AB=AD=3,∠ADP=90°.在棱AB 上是否存在一点E,使得平面PAD 与平面PCE 所成的锐二面角的余弦值为?若存在,求出的值,若不存在,请说明理由.6、如图,在四棱锥P﹣ABCD 中,AB∥CD,且∠BAP=∠CDP=90°.(1)证明:平面PAD⊥平面ABCD;(2)若PA=PD=AB=CD=2,∠APD=90°,求点C 到平面BDP 的距离.7、如图,在梯形ABCD 中,AB∥CD,AD=DC=CB,∠ABC=60°,四边形ACEF 是矩形.(Ⅰ)求证:AC⊥EB;(Ⅱ)若CE=BC,且CE⊥BC,求EB 与平面FBD 所成角的正弦值.8、如图,在四棱锥P﹣ABCD 中,PA=PB=AB,且∠PBC=2∠PAD=90°.(1)求证:平面PAD⊥平面ABCD;(2)求平面PAB 与平面PBC 所成锐二面角的余弦值.9、如图,在四棱锥P﹣ABCD 中,PA⊥平面ABCD,AD∥BC,PA=AD=CD=3,E为PD 的中点,点F 在PC 上,且;(Ⅰ)求证:CD⊥平面PAD;(Ⅱ)求二面角F﹣AE﹣P 的余弦值;(Ⅲ)设点G 在PB 上,且,判断直线AG 是否在平面AEF 内,说明理由.10、如图,四棱锥P﹣ABCD 中,平面PCD⊥平面ABCD,AB∥CD,AB=3DC=6,BM=2MP.(1)求证:CM∥平面PAD;(2)若AD=1,AD⊥DC,PD⊥PC 且PD=PC.求直线CM 与平面PAB 所成的角.11、已知平面四边形ABCD 中,AB⊥AC,AB=AC=AD=CD=2,现将△ABC沿AC 折起,使得点B 移至点P 的位置(如图),且PC=PD.(1)求证:CD⊥PA;(2)若M 为PD 的中点,求点D 到平面ACM 的距离.12、在四棱锥P﹣ABCD 中,四边形ABCD 为平行四边形,以BC 为直径的圆O(O 为圆心)过点A,且AO=AC =AP=2,PA 底面ABCD,M 为PC 的中点.(1)证明:平面OAM⊥平面PCD;(2)求二面角O﹣MD﹣C 的余弦值.13、在三棱柱ABC﹣A1B1C1 中,M,N 分别为BC,AB1 的中点.(Ⅰ)证明:MN∥平面ACC1A1;(Ⅱ)若AB=AC=AA=,BC=2,且A1 在底面ABC 上的正投影恰为点M,求二面角N﹣BC﹣C1 的正弦值.114、如图,在多面体ABCDE 中,平面ACDE⊥平面ABC,四边形ACDE 为直角梯形,CD∥AE,AC⊥AE,∠ABC=60°,CD=1,AE=AC=2,F 为BE 的中点.(1)当BC 的长为多少时,DF⊥平面ABE.(2)求平面ABE 与平面BCD 所成的锐二面角的大小.15、在四棱台ABCD﹣A1B1C1D1 中,底面为矩形,平面AA1D1D⊥平面CC1D1D,且CC1=CD=DD1=C1D1=1.(1)证明:AD⊥平面CC1D1D;(2)若AC 与平面CC1D1D 所成角为,求二面角C﹣AA1﹣D 的余弦值.116、在如图所示的几何体中,EA⊥平面ABCD,四边形ABCD 为等腰梯形,AD∥BC,AD=BC,AD=1,∠ABC=60°,EF∥AC,EF=AC.(1)证明:AB⊥CF;(2)当二面角B﹣EF﹣D 的余弦值为时,求线段CF 的长.17、如图,在四棱锥P﹣ABCD 中,BC⊥平面PAB,AB∥CD,若DC=DP=2,BC=,AP=1,AB=3.(Ⅰ)求证:AP⊥AB;(Ⅱ)求直线PC 与平面ADP 所成的角的正弦值.18、如图1,在梯形ABCD 中,AD∥BC,AB⊥AD,AD=AB=BC=2,将△ABD沿BD 折起,使得A 到P 的位置,且二面角P﹣BD﹣C 是直二面角,如图2.(1)求证:CD⊥PB.(2)求二面角P﹣BC﹣D 的余弦值.19、在直角梯形ABCD 中,∠ABC=90°,BC∥AD,AD=4,AB=BC=2,M为线段AD 中点.将△ABC沿AC 折起,使平面ABC⊥平面ACD,得到几何体B﹣ACD.(Ⅰ)求证:AB⊥平面BCD;(Ⅱ)求直线BD 与平面BCM 所成角的正弦值.20、如图所示,四棱锥S﹣ABCD 中,△SAB为等边三角形,四边形ABCD 为菱形,,二面角S﹣AB﹣C 为直二面角,点E 为线段AB 的中点.(1)求证:SC⊥CD;(2)求直线BC 与平面SCD 所成角的余弦值.21、已知正△ABC的边长为3,点D、E 分别是AB、AC 上的三等分点(点E 靠近点A,点D 靠近点B)(如图1),将△ADE沿DE 折起到△ADE的位置,使二面角A1﹣DE﹣B 的平面角为90°,连接A1B,A1C(如图2).1(1)求证:AE⊥平面BCED;1(2)在线段BC 上是否存在点P,使得直线PA1 与平面A1EC 所成的角为60°?若存在,求出CP 的长;若不存在,请说明理由.22、如图,AB⊥平面ADE,AB∥CD,AD=CD=AB=AE=3,∠DAE=120°,四边形ABCD 的对角线交于点M,N 为棱DE 上一点,且MN∥平面ABE.(1)求的值;(2)求二面角B﹣AC﹣N 的余弦值.23、如图,在四棱锥P﹣ABCD 中,△PBC为正三角形,底面ABCD 为直角梯形,AD∥BC,∠ADC=90°,AD=CD=3,BC=4,点M,N 分别在线段AD 和PC 上,且.(1)求证:PM∥平面BDN;(2)设二面角P﹣AD﹣B 为θ.若,求直线PA 与平面PBC 所成角的正弦值.24、如图:P⊥平面ABCD,四边形ABCD 为直角梯形,��//��,∠���= 90 ∘,P = P = 2P = 2A = 2.求证:平面���⊥平面PBC;求二面角�−��−�的余弦值;在棱PA 上是否存在点Q,使得��//平面PBC?若存在,求��的值,若不存在,请说明理由.��25、如图,AB 是半圆O 的直径,C 是半圆O 上除A,B 外的一个动点,DC 垂直于半圆O 所在的平面,DC∥EB,DC=EB=1,AB=4.(1)证明:平面ADE⊥平面ACD;(2)当C 点为半圆的中点时,求二面角D﹣AE﹣B 的余弦值.。
【小升初培优专题】 立体几何综合训练

立体几何综合训练1. 一个长方体仓库从里面量约长10米,宽5米,高6米,如果放入棱长是2米的正方体木箱,至多可以放进多少个?【解答】分别从长、宽、高三个方向进行考虑:10÷2=5(个)长这个方向可以放5个;5÷2=2(个)……1(米),宽这个方向可以放2个;6÷2=3(个),高这个方向可以放3个,5×2×3=30(个),所以至多可以放30个。
2. 如图,用棱长是1厘米的立方体拼成如图所示的立体图形,这个立体图形的表面积是多少平方厘米?上、下底面:3×5×2=30(平方厘米)左、右侧面:6×2=12(平方厘米)前、后侧面:8×2=16(平方厘米)立体图形的表面积:30+12+16=58(平方厘米)3. 如图(单位:厘米),要将一个圆锥形的零件用一个长方体硬纸板的盒子包装起来,至少需要多少平方厘米的硬纸板?(接头处忽略不计)。
5×2=10(厘米),长=宽=高10(厘米)硬纸板面积=10×10×6=600(平方厘米)立体几何综合训练4. 如图,甲圆柱体容器是空的,乙长方体容器中水深6.28厘米,将容器乙中的水全部倒入甲容器后水深8厘米,则甲容器的底面半径是多少厘米?【解答】水从乙容器倒入甲容器体积不变,找准这一点。
水的体积=10×10×6.28=628(立方厘米)S甲=V÷h=628÷8=78.5(平方厘米)因为S甲=78.5=πr²,那么r²=78.5÷3.14=25=5²,则r=5(厘米)5. 用铁皮做一个如图所示的水管(单位:厘米),需用铁皮多少平方厘米?铁皮围成的物体的体积是多少?如图,把两根一样的水管拼接成一根圆柱形水管,r=18÷2=9(厘米),h=45+55=100(厘米)S铁皮=2mrh÷2=2×3.14×9×100÷2=2826(平方厘米)V=πr²h÷2=3.14×9²×100÷2=12717(立方厘米)立体几何综合训练 6. 如图是一个棱长为6厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个棱长1厘米的正方体,做成一种零件,问它的表面积是多少?体积是多少?原表面积=6×6×6=216(平方厘米)新增表面积=1×1×4×6=24(平方厘米) 零件的表面积=216+24=240(平方厘米) 原体积=6×6×6=216(立方厘米)减少的体积=1×1×1×6=6(立方厘米) 零件的体积=216-6=210(立方厘米)答:它的表面积是240平方厘米,体积是 210立方厘米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何综合性训练一、单选题1.下列说法中不正确...的是( ) A .圆柱的侧面展开图是一个矩形B .直角三角形绕它的一条边所在直线旋转一周形成的曲面围成的几何体是圆锥C .圆锥中过轴的截面是一个等腰三角形D .圆台中平行于底面的截面是圆面 2.下列命题中错误的是:( )A .如果α⊥β,那么α内一定存在直线平行于平面β;B .如果α⊥β,那么α内所有直线都垂直于平面β;C .如果平面α不垂直平面β,那么α内一定不存在直线垂直于平面β;D .如果α⊥γ,β⊥γ,α∩β=l,那么l⊥γ.3.已知,m n 是两条不同的直线,,αβ是两个不同的平面.在下列条件中,可得出αβ⊥的是( )A .,,//m n m n αβ⊥⊥B .//,//,m n m n αβ⊥C .,//,//m n m n αβ⊥D .//,,m n m n αβ⊥⊥4.一个几何体的三视图如图所示,则该几何体的体积为( )A .103B .3C .83 D .735.用一个平面去截正方体,则截面不可能是( ) A .直角三角形B .等边三角形C .正方形D .正六边形6.如图,长方体1111ABCD A B C D -中,12AA AB ==,1AD =,点,,E F G 分别是1DD ,AB ,1CC 的中点,则异面直线1A E 与GF 所成的角是A .90oB .60oC .45oD .30o7.已知点,E F 分别是正方体1111ABCD A B C D -的棱1,AB AA 的中点,点,M N 分别是线段1D E 与1C F 上的点,则与平面ABCD 平行的直线MN 有( )条A .0B .1C .2D .无数个8.已知正三棱锥S ABC -的侧棱长为3底面边长为6,则该正三棱锥外接球的表面积是( ) A .16πB .20πC .32πD .64π9.如图示,三棱锥P ABC -的底面ABC 是等腰直角三角形,90ACB ∠=︒,且2PA PB AB ==3PC =,则PC 与面PAB 所成角的正弦值等于( )A .13B 6B .C .33D .2310.如图,在棱长为1的正方体1111ABCD A B C D -中,P 为线段1BC 上的动点(不含端点),则下列结论错误的是( )A .平面11D C P ⊥平面1C CPB .三棱锥1A D DP -的体积为定值C .11AD D P ⊥ D .DP ⊥平面11D C P11.如图,棱长为1的正方体1111ABCD A B C D -中,P 为线段1AB 的中点,,M N 分别为线段1AC 和 棱 11C D 上任意一点,则2PM +的最小值为( ) A 2 B 2C .1D 212.如图,四边形ABCD 为矩形,沿AB 将⊥ADC 翻折成'AD C V .设二面角'D AB C --的平面角为θ,直线'AD 与直线BC 所成角为1θ,直线'AD 与平面ABC 所成角为2θ,当θ为锐角时,有 A .21θθθ≤≤ B .21θθθ≤≤C .12θθθ≤≤D .21θθθ≤≤二、填空题13. 如图,边长为1的正方形''''D C B A 是在斜二测画法下所得图形,则原平面图形的面积为_________,周长为__________.14.如图,三棱锥S ABC -中,ABC ∆与SBC ∆均为等边三角形,且平面SBC ⊥平面ABC ,若4AB =,则三棱锥S ABC -的体积为__________________.15.如图所示,在直角梯形BCDF 中,90CBF BCE ∠=∠=o ,A 、D 分别是BF 、CE 上的点,//AD BC ,且22AB DE BC AF ===(如图⊥).将四边形ADEF 沿AD 折起,连接BE 、BF 、CE (如图⊥).在折起的过程中,则下列表述: ⊥//AC 平面BEF ;⊥四点B 、C 、E 、F 可能共面;⊥若EF CF ⊥,则平面ADEF ⊥平面ABCD ; 其中正确的是__________.16.已知点,,A B C 在半径为2的球面上,满足1AB AC ==,3BC =,若S 是球面上任意一点,则三棱锥S ABC -体积的最大值为____________. 三.解答题17. 在三棱柱中,平面,,且,平面. (1)证明:点是的中点; (2)证明:平面平面.111ABC A B C -1AA ⊥ABC 1AB BC AA ==2AC BC 1//AC 1B CD D AB 1ABC ⊥1B CD 1C 1B 1A ADBCFDCBA P18. 如图,直三棱柱111C B A ABC -,CB AC =,点M 是11B A 的中点. (1)求证:⊥M C 1平面11A ABB ; (2)求证:C B 1//平面M AC 1. (3)若︒=∠90ACB ,AC AA =1,1°求1AC 与平面B B AA 11所成角的大小;2°求二面角M AC A --11的余弦值19. 如图,平面SAB ⊥平面ABC ,ο90=∠=∠ABC SAB ,,点A 在SB 和SC 上的射影分别为N M 、,求证:SC MN ⊥.20.如图,四棱锥P ABCD -的底面是直角梯形,其中22,12AB DC AD ===,AD AB ⊥,顶点P 在底面ABCD 的射影落在线段AC 上,F 是PC 的中点.(1)求证:BF P 平面PAD ;(2)求证:平面PAC ⊥平面PDB ;(3)若1PA PC ==,求三棱锥P DBF -的体积。
MC 11A 1C五一作业(1)参考答案BBBAA ADDAD CB 13. 22,8 14.8 15.⊥⊥ 16323+ 9. 由题知ABC V 是等腰直角三角形且90ACB ∠=︒,ABP △是等边三角形, 设AB 中点为O ,连接PO ,CO ,可知6PO =,22CO =,同时易知AB PO ⊥,AB CO ⊥,所以AB ⊥面POC ,故POC ∠即为PC 与面PAB 所成角,有22222cos 2PO CO PC POC PO CO +-∠==⋅, 故1sin 1cos 3POC POC ∠=-∠=. 10.在正方体中,显然有11D C ⊥平面1C CP ,又11D C ⊂平面11D C P , 所以平面11D C P ⊥平面1C CP ,故A 正确;三棱锥1A D DP -的体积满足11A D DP P D DA V V --=,因为P 到平面1D DA 的距离不变,1D DA △的面积不变,三棱锥1A D DP 一的体积为定值,故B 正确;在正方体中,显然有111A D D C ⊥,11A D BC ⊥,所以1A D ⊥平面11D C P , 因为1D P ⊂平面11D C P ,所以11A D D P ⊥,故C 正确;若DP ⊥平面11D C P ,则1DP BC ^,结合1DC BC ⊥可得1BC ⊥平面DCP ,所以1BC CP ⊥,但1BC CP ⊥不是一直成立,故D 不正确.11.连接1C D ,过M 作1MH C D ⊥,连接HN ,过H 作111HH C D ⊥. 因为平面1AC D ⊥平面111CC D D C D =,1MH C D ⊥ 所以MH ⊥平面11CC D D .因为AD ⊥平面11CC D D ,所以//MH AD .所以11C HMH AD C D=.又因为11//HH DD ,所以1111HH C HDD C D=. 即11HH MH AD DD =. 因为1AD DD =,所以1MH HH =. 在RT MHN V 中,222MN MH HN =+.因为1HN HH ≥,所以2222212MH HN MH HH MH +≥+=.即222MN MH ≥,2MN MH ≥.所以212PM MN PM MH +≥+≥. 即2PM MN +的最小值为1 12. 设三棱锥D -ABC 是棱长为2的正四面体,取AB 中点E ,DC 中点M ,AC 中点M ,连结DE 、CE 、MN 、EN ,过D 作DO ⊥CE ,交CE 于O ,连结AO ,则12DEC DAO MNE ∠θ∠θ∠θ===,,, 413DE CE =-= ,DC =2,⊥1cos 3233θ==⨯⨯, 222341333AO CO CE ===-=,⊥2233323AO cos AD θ===, 取BC 中点E ,连结DE 、AE ,则DE ⊥BC ,AE ⊥BC ,又DE AE E ⋂=,⊥BC ⊥平面AED ,⊥190BC AD θ⊥∴=︒,. ⊥21θθθ≤≤.故选:B .15. 对于命题⊥,连接AC 、BD 交于点M ,取BE 的中点M 、N ,连接MN 、FN , 如图所示:则12AF DE =且//AF DE ,四边形ABCD 是矩形,且AC BD M =I ,M ∴为BD 的中点,N Q 为BE 的中点,//MN DE ∴且12MN DE =,//MN AF ∴且MN AF =,∴四边形AFNM 为平行四边形,//AM FN ∴,即//AC FN ,AC ⊄Q 平面BEF ,FN ⊂平面BEF ,//AC ∴平面BEF ,命题⊥正确;对于命题⊥,//BC AD Q ,BC ⊄平面ADEF ,AD ⊂平面ADEF ,//BC ∴平面ADEF , 若四点B 、C 、E 、F 共面,则这四点可确定平面α,则BC α⊂,平面αI 平面ADEF EF =,由线面平行的性质定理可得//BC EF ,则//EF AD ,但四边形ADEF 为梯形且AD 、EF 为两腰,AD 与EF 相交,矛盾. 所以,命题⊥错误;对于命题⊥,连接DF 、CF ,设AD AF a ==,则2DE a =, 在Rt ADF ∆中,AD AF a ==,2DAF π∠=,则ADF ∆为等腰直角三角形,且4AFD ADF π∠=∠=,2DF a =,4EDF π∴∠=,且2DE a =,由余弦定理得22222cos 2EF DE DF DE DF EDF a =+-⋅∠=,222DF EF DE ∴+=,DF EF ∴⊥,又EF CF ⊥Q ,DF CF F =I ,EF ∴⊥平面CDF ,CD ⊂Q 平面CDF ,CD EF ∴⊥,CD AD ⊥Q ,AD 、EF 为平面ADEF 内的两条相交直线,所以,CD ⊥平面ADEF ,CD ⊂Q 平面ABCD ,∴平面ADEF ⊥平面ABCD ,命题⊥正确;16.设ABC V 外接圆圆心为O ',三棱锥S ABC -外接球的球心为O ,1AB AC ==,设D 为BC 中点,连AD ,则AD BC ⊥,且O '在AD 上,221()22BC AD AB =-=, 设ABC V 外接圆半径为r ,222231()()()242BC r AD r r =+-=+-, 解得221,||23r OO r '=∴=-=要使S ABC -体积的最大,需S 到平面ABC 距离, 即S 为O O '32, 所以三棱锥S ABC -体积的最大值为11112)2)3322ABC S ⨯+=⨯⨯⨯=V故答案为:312+. 17. 略(easy )18.(1)依题意有1111C B C A =,又M 为11B A 的中点所以⊥M C 111B A由题意知1AA ⊥平面111C B A ,⊂M C 1平面111C B A , 所以⊥M C 11AA 而1111A AA B A =I 所以⊥M C 1平面11A ABB ;(2)连接C A 1交1AC 于O ,则O 为C A 1中点,连接MO ,因为M 为11B A 中点,则有C B MO 1// 而⊂MO 平面M AC 1,⊄C B 1平面M AC 1 所以C B 1//平面M AC 1. (3)设211=C A根据平面几何知识可得221111==B A MC 221=AC 由(1)知 ⊥M C 1平面11A ABB所以1AC 与平面11A ABB 所成角为AM C 1∠21sin 111==∠AC M C AM C所以1AC 与平面11A ABB 所成角为30°过点M 作MN 11C A ⊥于N ,又1AA ⊥平面111C B A 所以MN ⊥1AA所以MN ⊥平面11C AA所以MN ⊥1AC过点N 作NK ⊥1AC 于K ,连接MK所以1AC ⊥平面MKN所以1AC ⊥MK所以MKN ∠为所求二面角的平面角在直角三角形MKN 中,MN=1,NK=22=所以33cos ==∠MK NK MKN19:因为平面SAB ⊥平面ABC ,又平面SAB I 平面AB ABC =,SA AB ⊥,SA SAB 平面⊂……2分 所以⊥SA 面ABC ,……3分又⊂BC 平面ABC ,∴BC SA ⊥……4分∵ο90=∠B ,即BC AB ⊥,A SA BA =I ,……5分 ∴⊥BC 平面SAB .……6分∵⊂AN 平面SAB .∴AN BC ⊥.……7分又∵SB AN ⊥,……8分(射影的概念转化为垂直关系占1分) B BC SB =I ,∴⊥AN 平面SBC .……9分 ∵⊂SC 平面SBC ,∴SC AN ⊥,……10分 又∵SC AM ⊥,A AN AM =I , ∴⊥SC 平面AMN .……11分∵⊂MN 平面AMN .∴MN SC ⊥.……12分 20.解答:(1)取PD 中点E ,连结EA EF 、,∵E F 、分别是PD PC 、的中点,∴//EF DC ,又//DC AB ,且12EF DC AB ==, ∴//EF AB ,且EF AB =∴四边形EFBA 是平行四边形, ∴//AE BF ……1分 又∵AE PAD ⊂面,BF PAD ⊄面, ……2分 ∴EF P 平面PAD ……3分(2)顶点P 在底面ABCD 的射影落在线段AC 上,设为H ,则PH ABCD ⊥面 ∵BD ABCD ⊂面,∴PH BD ⊥ ……4分∵Rt ABD ∆中,2AB AD =, Rt DAC ∆中,2AD DC ==, ……5分 ∴Rt ABD ∆∽Rt DAC ∆,∴DAC ABD ∠=∠,故90ABD CAB ∠+∠=︒即AC BD ⊥又∵PH AC H =I ,PH AC PAC ⊂、面,∴BD PAC ⊥面 ……7分BD PBD ⊂面,∴PBD PAC ⊥面面 ……8分(3) ∵1PA PC ==,∴顶点P 在底面ABCD 的射影H 落在线段AC的中点上,且由AC ==12PH == ……9分 ∵F 分别是PC 的中点,∵F 到面PDB 的距离是C 到面PDB 的距离的12……10分 1122P DBF C PDB P DBC V V V ---==1111(1)2322=⨯⨯⨯24=……12分HO PABCDF。
