高二数学定积分曲边梯形面积(教案)
曲边梯形的面积和定积分的概念和微积分基本定理

4.5.1曲边梯形的面积【教学目标】1、通过问题情景,经历求曲面梯形的形成过程,了解定积分概念的实际背景。
理解求曲面梯形的一般步骤。
2、通过问题的探究体会以直代曲、以不变代变及无限逼近的思想。
通过类比体会从具体到抽象、从特殊到一般的数学思想方法。
3、体验和认同“有限和无限对立统一”的辩证观点,接受用运动变化的辩证唯物主义思想处理数学问题的积极态度。
【教学重难点】教学重点:求一般曲面梯形面积的方法。
教学难点:对以直代曲、无限逼近思想的理解。
【教学过程】(一)情景导入、展示目标教师:我们在小学、初中就学习过求平面图形面积的问题。
但基本是规则的平面图形,如矩形、三角形、梯形。
而现实生活中更多的是不规则的平面图形。
对于不规则的图形我们该如何求面积?比如我们重庆市的国土面积?通过实际问题引发学生思考,可结合问题:“在‘割圆术’中, 是如何利用正多边形的面积得到圆的面积的?具体步骤如何?”做进一步引导,并给出本节目标。
(二)合作探究、精讲点拨 (1)提出概念概念:如图,由直线,,x a x b x ==轴,曲线()y f x =所围成的图形称为曲边梯形。
(2)引导探究问题:对于由()2101y x x =+≤≤,x 轴所围成的面积该怎样求?(该图形为曲边梯形,教材第54页) (3)自主探究探究1:分割,怎样分割?分割成多少个?分成怎样的形状?有几种方案? (分割) 探究2:采用哪种好?把分割的几何图形变为代数的式子。
(近似代替)、(求和) 探究3:如何用数学的形式表达分割的几何图形越来越多? (取极限)由学生结合已有的知识,提出自己的看法,同伴之间进行交流。
老师及时点评指导,最后归纳、总结,讲评。
(教材第55-57页)(三)反馈测评练习1:求直线x=0,x=1,y=0与曲线y=x2所围成的曲边梯形的面积。
练习2:求直线x=1,x=4,y=0与曲线y=x2所围成的曲边梯形的面积。
(四)课堂总结思考:1、对于一般曲边梯形,如何求面积?用化归为计算矩形面积和逼近的思想方法求出曲边梯形的面积。
(完整版)1.5.1曲边梯形的面积(优秀教案)

1.5.1 曲边梯形的面积一、教学目标1、知识与技能目标:(1)通过问题情景,经历求曲边梯形面积的过程,初步了解、感受定积分概念的实际背景。
(2)理解求曲边梯形面积的“四步曲”——分割、近似代替、求和、取极限。
2、过程与方法目标:(1)通过问题的探究体会“以直代曲、无限逼近”的思想。
(2)通过类比体会从具体到抽象、从特殊到一般的数学思想方法。
3、情感、态度与价值观目标:在探究中进一步感受极限的思想,体会直与曲虽然是对立矛盾的,但它们可以相互转化,体现对立统一的辩证关系,在问题解决中体验成功的愉悦,感受数学的魅力。
二、学情分析本节课的教学对象是民语班的学生。
学生在本节课之前已经具备的认知基础有:一是学生已学习过如何通过割补的方法计算不规则直边图形的面积;学生在必修3的阅读与思考内容中对刘徽的“割圆术”求圆面积的方法已经有所了解。
二是学生虽然未学习过极限的有关知识,但通过导数的学习,对极限有了初步的认识。
学生在本节课学习中将会面临的难点:一是部分学生汉语程度相对较为薄弱,一些数学名词难以准确理解,因此需要借助民语教材对部分名词做民语标注,帮助学生准确掌握和学习;此外,学生的汉语表达能力较差,需要即时引导学生进行准确表述和学习。
二是本节课的学习过程中如何“以直代曲”,即学生如何将割圆术中“以直代曲,无限逼近”的思想灵活地迁移到一般的曲边梯形上.具体说来就是:如何选择适当的直边图形(矩形、三角形或梯形)代替曲边梯形,并使细分的过程程序化且便于操作和计算。
三、重点难点教学重点:探究求曲边梯形面积的方法。
教学难点:把“以直代曲”的思想方法转化为具体可操作的步骤,理解“无限逼近”的思想方法。
四、教学过程一、问题情境—生活中的数学原型【教师提问】观察下面的图片,从图片中截取一个平面图形,观察图形,如何求图形的面积?图片一:图形一:【教师提问】观察下面的图片,从图片中截取一个平面图形,观察图形,如何求图形的面积?图片二:图形二:【教师提问】观察下面的图片,从图片中截取一个平面图形,观察图形,如何求图形的面积?图片三:图形三:【思考】“曲边梯形”与“直边图形”的主要区别是什么?【设计意图】1.从生活实际出发,让学生充分感受数学与生活息息相关,生活中处处都能找到数学的原型。
曲边梯形面积,定积分求体积以及在物理中应用教学设计25

学 科
数学
年 级
高三
教学形式
教 师
单 位
课题名称
学情分析
建议
1.学生的学习特征,能力基础。
2.学生对之前相关知识的掌握程度,知识基础。
3.学生形成本节课知识时可能存在非科学或前科学概念的干扰。
4.学生对所学内容的兴趣、情感、态度、愿望、需求、重视等状况。
教材分析
本节课在整本教材中的地位和作用,知识结构或新旧知识的关联等。
③由两条曲线 与直线
图(1) 图(2) 图(3)
所围成的曲边梯形的面积: (如图(3));
(2) 型区域:①由一条曲线 与直线 以及 轴所围成
总结
板书设计提示:设计一套测试或练习题,用于检验通过微课学习,学生是否化解了“重难点”。这套题分:易、中、难三个层次,每个层次一道题(三道题围绕该重难点)
易1求直线 与抛物线 所围成的图形面积。
复习旧知,产生碰撞
过程
例1.计算由两条抛物线 和 所围成的图形的面积.
【分析】两条抛物线所围成的图形的面积,可以由以两条曲线所对应的曲边梯形的面积的差得到。
解: ,所以两曲线的交点为(0,0)、(1,1),面积S= ,所以 =
【点评】在直角坐标系下平面图形的面积的四个步骤:
1.作图象;2.求交点;3.用定积分表示所求的面积;4.微积分基本定理求定积分。
教学目标
知识目标、能力目标、情感态度与价值观目标。
教学重难点
重点:曲边梯形面积,定积分求体积以及在物理中应用
难点:曲边梯形、面积、体积
教学策略:
建议:
1、信息技术手段的使用
2、通过实例体会定积分在几何中及物理中的应用
教学过程与方法
曲边梯形的面积(教案)

《曲边梯形的面积》教学设计
课题:曲边梯形的面积
教材:人教A版选修2-2第1章第5节第1课时
课程标准
通过实例(如求曲边梯形的面积、变力做功等),从问题情境中了解定积分的实际背景;借助几何直观体会定积分的基本思想,初步了解定积分的概念.
教学目标
虽然函数的导数和积分可以用极限概念“纯数量”地去定义,但在中学阶段新课标强调在实际背景下直观地、实质地去给出导数和积分的描述,因而我们宁愿把两个概念看成是数形结合的产物.作为定积分概念的背景课,让学生在感受数学文化的同时获得数学思想方法.(1)认知目标:通过探求曲边梯形的面积,使学生了解定积分的实际背景,了解“以直代曲”“逼近”的思想方法,建立定积分概念的认知基础,为理解定积分概念及几何意义奠定基础.(2)能力目标:通过这部分内容的教学,逐步培养学生分析问题、解决问题的能力和思维能力.(3)情感目标:让学生感受数学文化,体验认识数学本质的快乐,收获探究活动的乐趣.
教学重点、难点
重点:了解定积分的基本思想方法——以直代曲、逼近的思想,初步掌握求曲边梯形面积的步骤——“四步曲”.
难点:“以直代曲”“逼近”思想的形成过程;求和符号∑.
教学基本流程
教学过程
板书设计
教学后记
今天(2007年12月25日)上午的公开课有幸请到三水区数学特级教师卢肇荣点评.以下是卢老师的点评:
(1)本堂课充分体现了新课标的理念,以学生为主体;
(2)驾驭课堂的能力很强;
(3)计算机多媒体使用恰当,没有喧宾夺主;
(4)时间把握准确;
(5)以问题的形式小结,值得肯定;
(6)难点重点把握得当;
(7)可能没有布置学生预习,如果让学生预习,本节课的效果还会更好.。
高中数学1.4.1曲边梯形的面积与定积分教案理新人教B版选修2_2

1.4.1曲边梯形的面积与定积分【教学目标】1.理解求曲边梯形面积的过程和步骤—分割、以直代曲、求和、取极限;了解定积分的概念及几何意义;2.体会化曲为直的极限思想;3.渗透“质量互变、对立统一”的观点.【教学重点】定积分的概念 【教学难点】以曲代直一、课前预习:阅读教材36页—38页,完成下列问题例1:求曲线2x y =与直线0,1==y x 所围成区域的面积.(1)分割:将区间[0,1]等分成n 个小区间,第一个小区间为[0,n 1],第二个小区间为[nn 2,1],第三个小区间为 …,第个i 小区间为 ,…,第n 个小区间为 .每个小区间的长度为=∆x(2)以直代曲:过各分点做轴的垂线,再分别用小区间左端点的纵坐标为高,为底作小矩形,则第一个小矩形的高为 ,第二个小矩形的高为 ,第三个小矩形的高为 ,…,第i 个小矩形的高为 ,…,第n 个小矩形的高为 .它们的面积分别为 .(3)近似求和:所有个小矩形的面积的和记为n S ,则n S =(4)取极限:==→∆n x S S lim 0 二、课上学习:1.定积分的概念: 设函数)(x f y =定义在区间],[b a 上,用分点b x x x x x a n n =<<<<<=-1210...思考:将教材例1,例2的结果用定积分如何表示?2.定积分的几何意义说明:一般情况下,定积分的几何意义是介于x 轴、函数的图形以及直线之间各部分面积的代数和,在轴上方的面积取正号,在轴下方的面积取负号.3.(1)⎰⎰=b a b a dx x f c dx x cf )()( (c 为常数)(2)设)(),(x g x f 可积,则=±⎰dx x g x f ba )]()([ 精美句子1、善思则能“从无字句处读书”。
读沙漠,读出了它坦荡豪放的胸怀;读太阳,读出了它普照万物的无私;读春雨,读出了它润物无声的柔情。
读大海,读出了它气势磅礴的豪情。
高中数学定积分第一课时曲边梯形的面积学案新人教A版选修Word版

定积分第一课时曲边梯形的面积学案一、学习目标1、知识与技能:通过曲边梯形的面积,了解定积分的实际背景;初步掌握求曲边梯形面积的步骤——四步曲2、过程与方法:了解“以直代曲”、“逼近”的思想方法;3、情感态度与价值观:逐步培养学生分析问题、解决问题的能力和思维能力。
二、学习重难点重点:掌握过程步骤:分割、以直代曲、求和、逼近(取极限)难点: 对过程中所包含的基本的微积分 “以直代曲”的思想的理解三、学法指导:阅读教材38---41页四、知识链接1你会求哪些平面图形的面积?这些平面图形有什么特点?2如何求曲线围成的平面图形的面积呢?这就是定积分要解决的问题。
定积分在科学研究和实际生活中都有非常广泛的应用。
本节我们将学习定积分的基本概念以及定积分的简单应用,初步体会定积分的思想及其应用价值。
五、学习过程(一)连续函数与曲边梯形问题1:函数()y f x =________________________ _____________________________,那么我们称函数()y f x =为在区间I 上的连续函数.问题2:在图1.5-1中,由____________________ _________________围成的图形称为曲边梯形.问题3:画出由2y x =与直线1,0x y ==围成的曲边梯形.(二)求曲边梯形面积的步骤——四步曲在由2y x =与直线1,0x y ==所围成的曲边梯形中:问题4:把区间[0,1]等间隔地插入1n -个点,将它等分为____个小区间,则第i 个小区间为________,其区间长度为x ∆=___________,当n →+∞时,x ∆→___.练习1:把区间[2,5]n 等分,所得n 个小区间的长度x ∆=( )A .1nB .2nC .3nD .4n练习2:在区间[1,8]中插入6个等分点,则所分的小区间长度x ∆=_____,第3个小区间是__________.问题5:在区间1[,]i i n n-上,函数2()f x x =的值()f x ≈______,曲边梯形在这个小区间的面积'i i S S ∆≈∆=_____________________,即小矩形的面积'i S ∆近似地代替i S ∆,即以直代曲.问题6:求图1.5-4中阴影部分面积n S (写出过程).问题7:2222123n ++++=__________.练习3:用符号“∑”表示下列运算:(1)123n ++++=___________.(2)2222135(21)n ++++-=____________.问题8:从图 1.5-5及表1-1中,当,n n S S →+∞→,即S =__________=_______________________=_______________. 问题9:把区间[0,1]不进行等分可以吗?分割的目的是什么?问题10:若函数()f x 在区间1[,](1,2,,)i i i n n n-=上的值近似地等于右端点i n 处的函数值()i f n ,用这种方法能求出S 的值吗?若能求出,这个值也是13吗?取任意1[,]i i i n n ξ-∈处的函数值()i f ξ作为近似值,情况又怎么样? (三)典型例题例1:求由2y x =与直线1,0x y ==围成的曲边梯形的面积.解:在区间[0,1]等间隔地插入1n -个点,将它n 等分,第i 个小区间为________,区间长度x ∆=___.'i i S S ∆≈∆=111'n n n n i i i i i S S S ===∴=∆≈∆==∑∑∑_____________________________________lim n S →+∞∴==.六、达标训练求直线0,2,0x x y ===与曲线2y x =所围成的曲边梯形的面积.七、【课堂小结】1.求曲边梯形面积的四步曲是________________.2.0lim lim ()n i n x S S f x ξ→∞∆→==∆=_____________.八、课后反思曲边梯形的面积当堂检测1.下列函数在定义域上不是连续函数的是( )A .2()f x x =B .()f x x =C .()f x =D .1()f x x= 2.在区间[2,5]上等间隔地插入n 个点,所得小区间长度x ∆=( )A .3n B .5n C .31n + D .51n + 3.把区间[,]()a b a b n <等分后,第i 个小区间是( ) A .1[,]i i n n- B .1[(),()]i i b a b a n n--- C .1[,]i i a a n n-++ D .1[(),()]i i a b a a b a n n -+-+- 4计算: 21[2(1)3]ni i =-+=∑________;5求20,0,22≤≤=-=x y x x y 围成图形面积(注:可编辑下载,若有不当之处,请指正,谢谢!)。
选修2-2第一章1.4.1曲边梯形面积与定积分-教案
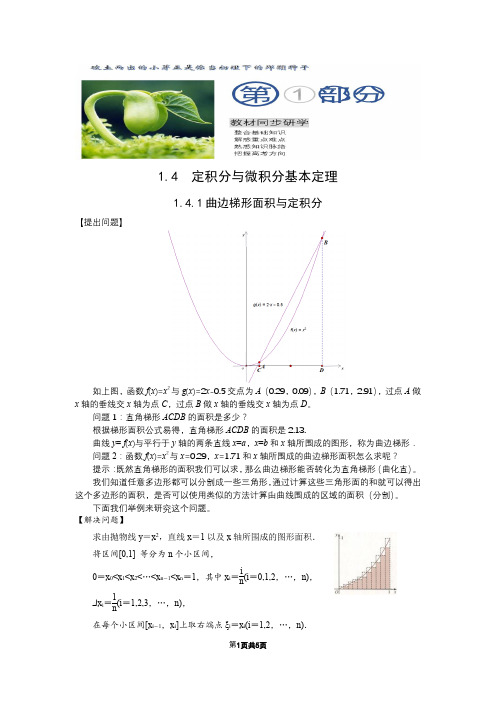
1.4 定积分与微积分基本定理1.4.1曲边梯形面积与定积分【提出问题】如上图,函数f(x)=x2与g(x)=2x-0.5交点为A(0.29,0.09),B(1.71,2.91),过点A做x轴的垂线交x轴为点C,过点B做x轴的垂线交x轴为点D。
问题1:直角梯形ACDB的面积是多少?根据梯形面积公式易得,直角梯形ACDB的面积是2.13.曲线y=f(x)与平行于y轴的两条直线x=a,x=b和x轴所围成的图形,称为曲边梯形.问题2:函数f(x)=x2与x=0.29,x=1.71和x轴所围成的曲边梯形面积怎么求呢?提示:既然直角梯形的面积我们可以求,那么曲边梯形能否转化为直角梯形(曲化直)。
我们知道任意多边形都可以分割成一些三角形,通过计算这些三角形面的和就可以得出这个多边形的面积,是否可以使用类似的方法计算由曲线围成的区域的面积(分割)。
下面我们举例来研究这个问题。
【解决问题】求由抛物线y=x2,直线x=1以及x轴所围成的图形面积.将区间[0,1] 等分为n个小区间,0=x0<x1<x2<…<x n-1<x n=1,其中x i=in(i=0,1,2,…,n),Δx i=1n(i=1,2,3,…,n),在每个小区间[x i-1,x i]上取右端点ξi=x i(i=1,2,…,n).于是曲线之下小矩形的面积为ξi 21n (i =0,1,2,…,n-1)所以曲线之下小矩形的面积和为S n =(0n ) 2∙1n +(1n ) 2∙1n +(2n ) 2∙1n +…+(n−1n ) 2∙1n=02+12+22+⋯+(n−1)2n 3=16(1−1n )(2−1n )由此得到S =lim n →∞S n =lim n →∞16(1−1n)(2−1n)=13.从图形上看,当n 越来越大时,划分越来越细,阴影部分的面积与曲边梯形面积相差越来越小,当n 趋于正无穷时,阴影部分趋近于曲边三角形,因此可以将13视为此曲边三角形的面积。
曲边梯形面积,定积分求体积以及在物理中应用教学设计22

学 科
数学
年 级
高三
教学形式
教 师
单 位
课题名称
曲边梯形面积,定积分求体积以及在物理中应用
学情分析
建议
1.学生的学习特征,能力基础。
2.学生对之前相关知识的掌握程度,知识基础。
3.学生形成本节课知识时可能存在非科学或前科学概念的干扰。
4.学生对所学内容的兴趣、情感、态度、愿望、需求、重视等状况。
教材分析
本节课在整本教材中的地位和作用,知识结构或新旧知识的关联等。
教学目标
知识目标、能力目标、情感态度与价值观目标。
教学重难点
重点:曲边梯形面积,定积分求体积以及在物理中应用
难点:曲边梯形、面积、体积
教学策略:
建议:
1、信息技术手段的使用
2、通过实例体会定积分在几何中及物理中的应用
教学过程与方法
教学环节
2、求曲边梯形面积的方法与步骤:
(1)画图,并将图形分割为若干个曲边梯形;
(2)对每个曲边梯形确定其存在的范围,从而确定积分的上、下限;
(3)确定被积函数;
(4)求出各曲边梯形的面积和,即各积分的绝对值的和。
3、几种常见的曲边梯形面积的计算方法:
(1) 型区域:①由一条曲线 与直线 以及 轴所围成的曲边梯形的面积: (如图(1));
易1求直线 与抛物线 所围成的图形面积。
中2求由抛物线 及其在点M(0,-3)
和N(3, 0)处的两条切线所围成的图形的面积。
难3求曲线 与曲线 以及 轴所围成的图形面积。
【点评】在直角坐标系下平面图形的面积的四个步骤:
1.作图象;2.求交点;3.用定积分表示所求的面积;4.微积分基本定理求定积分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
曲边梯形的面积(教案)
杭州市源清中学徐骋【教学目标】
1、知识与技能目标:
通过问题情景,经历求曲面梯形的形成过程,了解定积分概念的实际背景。
理解求曲面梯形的一般步骤。
2、过程与方法目标:
通过问题的探究体会以直代曲、以不变代变及无限逼近的思想。
通过类比体会从具体到抽象、从特殊到一般的数学思想方法。
3、情感、态度与价值观目标:
体验和认同“有限和无限对立统一”的辩证观点,接受用运动变化的辩证唯物主义思想处理数学问题的积极态度。
【教学重点】
求一般曲面梯形面积的方法。
【教学难点】
对以直代曲、无限逼近思想的理解。
【教学准备】
多媒体电脑、课件等。
【教学过程】
此问题在学生九年级中已有涉及,在九
问题二:户型图不完全是不规则的,有一边是曲线,其他边是直线,提出房屋面积的测量问题。
概念:如图,由直线x=a,x=b,x轴,曲线y=f(x)
y
y=f(x)
曲边梯形的面积(学案)
杭州市源清中学徐骋【学习目标】
1、理解“以直代曲”的意义;
2、理解求曲边梯形面积的四个步骤;
3、了解“近似代替”时取点的任意性。
【课堂程序】
问题一:我们在小学、初中就学习求平面图形面积的问题。
有的是规则的平面图形,但现实生活中更多的是不规则的平面图形。
对于不规则的图形我们该如何求面积,比如浙江省的面积?
问题二:户型图不完全是不规则的,有一边是曲线,其他边是直线,这样的面积又该怎样得出?
概念:如图,由直线x=a,x=b,x 轴,曲线y=f(x)所围成的图形称为曲边梯形。
问题三:对于由y=x 2与x 轴及x=1所围成的面积该怎样求?
【知识应用】
1、求直线x=0,x=2,y=0与曲线y=x 2所围成的曲边梯形的面积。
x
y
O y=x 2
图3
图4
2、求直线x=1,x=4,y=0与曲线y=x 2所围成的曲边梯形的面积。
【总结归纳】
1、对于一般曲边梯形,如何求面积?
2、求曲边梯形面积的方法步骤是什么? 【曲边梯形的面积 作业】
1、求由y=x 2+1,和x=0,x=3,x 轴围成的曲边梯形面积。
2、求由y=2x 2+1,和x=1,x=3,x 轴围成的曲边梯形面积。
特别帮助:12+22+32+…+n 2=16
n(n+1)(2n+1)。
