换元积分与分部积分
积分的换元法与分部积分法

积分的换元法与分部积分法积分作为微积分中重要的概念和工具,被广泛应用于数学、物理、工程等领域。
积分可以通过不同的方法来求解,其中换元法和分部积分法是常见且重要的两种方法。
本文将介绍积分的换元法和分部积分法,并对其原理和应用进行详细讨论。
一、换元法换元法又被称为变量代换法,其核心思想是通过引入新的变量来简化被积函数的形式。
具体步骤如下:1. 选择合适的变量代换。
2. 计算新变量关于原变量的导数,确定微元的变换关系。
3. 将被积函数和微元用新变量表示,进行积分计算。
4. 将结果用原变量表示,得到最终的积分结果。
举例来说,如果要计算∫(2x+1)^2 dx,可以选择变量代换u = 2x + 1。
根据导数的链式法则,有du/dx = 2,从而dx = du/2。
将被积函数和微元用新变量表示,得到∫u^2 (du/2)。
对该表达式进行积分计算,并将结果用原变量表示,即可得到∫(2x+1)^2 dx的积分结果。
换元法在解决一些形式复杂的积分问题时非常有用,可以将原函数变换为更简单的形式,进而实现积分的计算。
二、分部积分法分部积分法是对求导和求积分的相互关系的一种应用。
其基本原理是根据乘积的求导法则,将被积函数分解为两个函数的乘积的导数形式,从而利用求导法进行积分的计算。
具体步骤如下:1. 选择合适的分解形式。
2. 对乘积中的一个函数求导。
3. 对另一个函数进行积分。
4. 将结果用原变量表示,得到最终的积分结果。
举例来说,如果要计算∫x*sin(x) dx,可以将被积函数分解为两个函数的乘积形式,即f(x) = x和g(x) = sin(x)。
根据导数的乘法法则,有(fg)' = f'g + fg',其中f'和g'分别表示f(x)和g(x)的导数。
将该等式与积分的相互关系结合,得到∫f(x)g'(x)dx = fg - ∫f'(x)g(x)dx。
利用该等式进行计算,即可得到∫x*sin(x) dx的积分结果。
换元积分法与分部积分法

d
xn
(3) 统一函数: 利用三角公式 ; 配元方法
(4) 巧妙换元或配元
2022年9月29日8时31分
21
上一页 下一页 主 页 返回 退机出动 目录 上页 下页 返回 结束
思考与练习 1. 下列各题求积方法有何不同?
(1)
dx 4 x
(2)
4
d
x x
2
(3)
x 4 x2
dx
1 2
d(4 x2 ) 4 x2
13
上一页 下一页 主 页 返回 退出
例10 求
解法1
cos x cos2 x
dx
1
d
sin x sin2 x
1 2
1 1 sin
x
1 1 sin
x
d
sin
x
1 ln 1 sin x ln 1 sin x C
2 1 ln 1 sin x C
2 1 sin x
2022年9月29日8时31分
ax t
a2 x2
26
例17 求
解
令
x
a
tan
t
,
t
(
2
,
2
)
,
则
x2 a2 a2 tan2 t a2 a sect
dx a sec2 t d t
∴ 原式
a sec2 a sec t
t
d
t
sec t
d
t
ln sect tan t C1
ln
x2 a2
x a
C1
x2 a2
不定积分是求导运算的逆运算, 相应 于复合函数求导数的链式法则和乘法 求导公式, 不定积分有换元积分法和分 部积分法.
换元积分法和分部积分法

对于含有根式的函数的 积分,原则上是设法去 掉根式。
有些含有根式的函数的 积分,直接令根式为新 变量 即可将问题转化为一般 的不含根式的函数的积 分。
补充例题11 计算
解:
1 6
dx . 3 x x
xx ,
1 2
3
xx ,
1 3
它们的指数部分的 分母的最小公倍数 为6 .
令 t x , t 0,
则 x t , d x 6 t d t, 故
6 5
t 3 1 1 dx 6 t3 dt d t 6 3 t 1 x x t 1
1 6 ( t t 1 )dt t 1
2
2 t 3 3 t 2 6 t 6 ln | t 1 | C 2 x 33 x 66 x 6 ln( 6 x 1) C .
第二类换元法常见类型:
(1)
(2)
f ( x , n ax b ) dx , 令
a x b n ( x , c x d ) dx ,
f
令 或
第 三 节 讲
(3) (4) (5)
f ( x , a 2 x 2 ) dx , 令 f ( x , a 2 x 2 ) dx , 令 f ( x , x 2 a 2 ) dx , 令
求
f (tan x)sec 2 xdx
补充例题4
1 解: 原式 = 1 2 ln x 2 1 2 ln x
自主学习课本P141例4.2.6、例4.2.7、例4.2.8
例4.2.9 求
tan xdx 和 cot xdx
.
解: cot xdx cos x dx 1 d sin x = ln sinx + C sin x sin x
换元积分法和分部积分法

1 2 x 2 2 a arcsin x a x C . 2 a
例8 求
a2 x2 π 解 设 x a tan t , | t | . 2 dx a sec2 tdt a 2 x 2 a sec t
sec tdt ln | sec t tan t | C
(解法二) sec xdx
sec x(sec x tan x ) dx sec x tan x
d(sec x tan x ) ln | sec x tan x | C . sec x tan x
f (a 2 x 2 ), f (a 2 x 2 ), 第二类换元积分法常用在
例2 解
x d( ) x dx 1 a (令 u ) 2 2 x a a a x 1 ( )2 a 1 du 1 arctan u C 2 a a 1 u
dx a 2 x 2 (a 0).
对换元积分法较熟练后,可以不写出换元变量 , 而直接使用公式(1) 例3 求
一、 换元积分法
由复合函数求导法,可以导出换元积分法。 设 g( u)在 [ , ] 上有定义, u ( x ) 在 [a , b]上可导,且 ( x ) , x [a, b] 并记 f ( x ) g( ( x )) ( x ), x [a, b]. (i) 若 g ( u) 在 [ , ] 上存在原函数 G( u) ,则 f ( x ) 在 [a , b] 上也存在原函数F ( x ), F ( x ) G( ( x )) C , 即
第一换元积分法亦称为凑微分法, 即
g( ( x )) ( x )dx g( ( x ))d ( x ) G( ( x )) C ,
5.3 定积分的换元法和分部积分法

= − න (π − )(sin(π − ))d
则 d = −d
0
0
π
= න (π − )(sin )d
0
π
π
= π න (sin )d − න (sin )d
0
π
0
π
= π න (sin )d − න (sin )d ,
0
+ න () d
0
= න [(−) + ()] d
0
2 න () d , (−) = (),
=
0
0,
− = − .
奇、偶函数在对称区间上的定积分性质 偶倍奇零
第三节 定积分的换元法和分部积分法
定积分
第五章
1
2 2 + cos
例6 计算 න
0
解
1
d.
( > 0)
π
令 = sin , d = cos d, = ⇒ = , = 0 ⇒ = 0.
2
π
2
cos
d
原式 = න
2
2
0 sin + (1 − sin )
=න
π
2
0
cos
1
d = න
sin + cos
1
=
6
6
1
อ
第三节 定积分的换元法和分部积分法
0
cos 5 sin d
= − න cos 5 d(cos )
= 0 ⇒ = 1.
原式 = − න
π
2
1
= .
第五章 第4节定积分的换元法和分部积分法

sin
3
x sin
5
5
x cos x sin x 2
3
0
sin
3
x sin
3
x dx
0
cos x sin x 2 dx
3
3
0
2
cos x sin x 2 dx
3
cos x sin x 2 dx
2 3
0 sin x 2 d sin
3
( t 3) d t
2
1
3 1 1 3 22 ( t 3t ) 2 3 3 1
6
例3
计算 0
x 2
cos
0
5
2
cos
5
x sin xdx .
解
令 t cos x ,
2
dt sin xdx ,
t 0,
x sin xdx
5
x 0 t 1,
a
a x d x (a 0).
2 2
0
解: 令 x a sin t , 则 d x a cos t d t , 且当 x 0 时 t 0 , x a 时 t
2
∴ 原式 = a
2
2
2
cos t d t
(1 cos 2 t ) d t 1 2
2
0
2
a
2 a
则 有 f ( x )dx
a
b
f [ ( t )] ( t )dt .
2
证
积分的换元积分与分部积分

积分的换元积分与分部积分积分是微积分中的重要概念,它可以理解为对连续函数在一定区间上的求和运算。
在积分的计算过程中,换元积分和分部积分是常用的两种技巧。
本文将介绍积分的换元积分和分部积分,并分析它们在求解积分问题中的应用。
一、积分的换元积分积分的换元积分,也被称为变量代换法,是通过引入新的变量来简化积分表达式。
它在求解某些复杂的积分问题时非常有效。
我们先来看一个具体的例子来介绍换元积分的基本思想。
例子1:计算∫(x^2+1)^2·2x dx首先,我们观察到被积函数中的(x^2+1)的导数为2x,因此我们可以设u=x^2+1来进行变量代换。
接下来,我们需要计算du/dx以及dx/du。
由于u=x^2+1,对其求导得到du/dx=2x,即dx/du=1/(2x)。
接下来,将被积函数中的x dx用u du来表示,即将被积函数中的2x dx替换为2u du/(2x),化简得到u^2du。
最后,将变量代换后的积分表达式进行求解即可得到结果。
∫(x^2+1)^2·2x dx = ∫u^2 du = u^3/3 = (x^2+1)^3/3 + C通过这个例子,我们可以看到变量代换法在积分计算中的简化作用。
二、积分的分部积分分部积分是求解积分问题中另一个重要的技巧。
它基于积分的乘法法则,将一个复杂的积分转化为两个较简单的积分之和。
下面,我们来看一个例子来介绍分部积分的基本思想。
例子2:计算∫x·sinx dx对于这个积分,我们可以将其视为两个函数x和sinx的乘积,然后应用分部积分法进行求解。
分部积分的公式为∫u·v dx = u·∫v dx - ∫u'·(∫v dx) dx首先,我们需要选择u和v。
一般情况下,选择u为一个函数,其导数在求导后形式上简化,选择v为一个函数,其积分形式上比较简化。
对于这个例子,我们选择u=x,v=sinx。
接下来,计算u'和∫v dx。
定积分的换元法和分部积分法
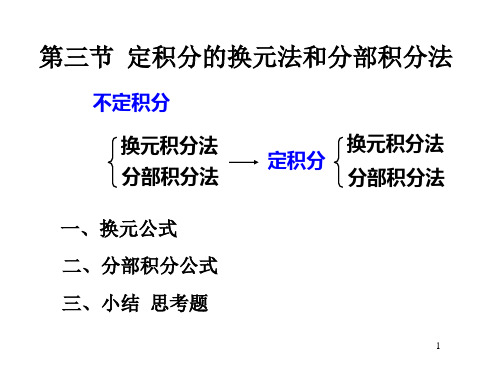
2
0
1
1 cos2
x
d (cos
x)
arctan(cos
2
x )0
( ) 2 . 2 44 4
15
二、分部积分公式
设函数u( x) 、v( x)在区间 a,b 上具有
连续导数,则有
b
a udv
uv b a
b
a vdu
.
定积分的分部积分公式
推导
uv uv uv,
b
a (uv
第三节 定积分的换元法和分部积分法
不定积分
换元积分法 分部积分法
换元积分法 定积分
分部积分法
一、换元公式 二、分部积分公式 三、小结 思考题
1
一、换元公式
定理 假设 f ( x)在[a,b]上连续,函数x (t )
满足条件:
(1) ( ) a , ( ) b;
(2) (t)在[ , ](或 , )上具有连续导数, 且其值域R a, b;
14
0 xf (sin x)dx 0 f (sin t)dt 0 tf (sin t)dt
0 f (sin x)dx 0 xf (sin x)dx,
xf (sin x)dx
f (sin x)dx.
0
20
0
1
x
sin x cos2
x
dx
2
0
1
sin x cos2
x
dx
2) 必需注意换元必换限 , 原函数中的变量不必代回 .
3) 换元公式也可反过来使用 , 即
(t) (t)
b
f (x)d x
(令 x (t))
a
或配元
(t) (t)
