《流体力学》徐正坦主编课后答案第五章要点
《流体力学》徐正坦主编课后答案第五章
第五章习题简答5-１有一薄壁圆形孔口，直径d= １0ｍm ，水头H 为2m 。
现测得射流收缩断面的直径d c 为8m ｍ,在３2.8s 时间内，经孔口流出的水量为0.０1ｍ3，试求该孔口的收缩系数ε，流量系数μ,流速系数φ及孔口局部损失系数ζ。
解: 64.010822=⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛==d d A A c c εs m d Q v /06.6008.08.32/01.04422=⨯⨯==ππ 62.097.064.006.0197.011197.028.9206.62222=⨯===-=-==⨯⨯==⇒=εϕμϕζϕϕgHvgH v5-2薄壁孔口出流,直径ｄ=2cm,水箱水位恒定H ＝2ｍ，试求:(1)孔口流量Q ；(2）此孔口外接圆柱形管嘴的流量Ｑn ；(3)管嘴收缩断面的真空高度。
题5-２图解:(1）孔口出流流量为s L s m gH A Q /219.1/10219.128.9202.0462.02332=⨯=⨯⨯⨯⨯⨯==πϕ（2)s L gH A Q n /612.128.9202.0482.022=⨯⨯⨯⨯⨯==πμ(３)真空高度：m H gpg p C Cv 48.1274.074.0=⨯==-=ρρ ５-3 水箱用隔板分为A 、B 两室,隔板上开一孔口,其直径ｄ1=４cm ，在B 室底部装有圆柱形外管嘴,其直径d 2=3cm 。
已知Ｈ=３m ，ｈ3＝0.5m 试求:(1）ｈ 1,h 2;(2)流出水箱的流量Q 。
题５-3图解:隔板孔口的流量 112gh A Q μ=圆柱形外管嘴的流量()()132222h H g A h h g A Q -=+=μμ由题意可得Q 1=Q ２,则()()1212122212111211303.082.004.062.022h h h H d h d h H g A gh A -⨯⨯=⨯⨯-=-=μμμμ解得m h 07.11=sL s m gh A Q mh h H h /56.3/1056.307.18.9204.0462.0243.15.007.1333211312=⨯=⨯⨯⨯⨯⨯==∴=--=--=∴-πμ5－4 有一平底空船，其船底面积Ω为8m ２,船舷高ｈ为０.5m ，船自重G 为9．8kN 。
流体力课后学习题解答
流体力学习题参考及答案第1 绪论1.1 若某种牌号的汽油的重度γ为7000N/m 3，求它的密度ρ。
解：由g γρ=得，3327000N/m 714.29kg/m 9.8m /m γρ===g1.2 已知水的密度ρ=997.0kg/m 3，运动黏度ν=0.893×10-6m 2/s ，求它的动力黏度μ。
解：ρμ=v 得，3624997.0kg/m 0.89310m /s 8.910Pa s μρν--==⨯⨯=⨯⋅ 1.3 一块可动平板与另一块不动平板同时浸在某种液体中，它们之间的距离为0.5mm ，可动板若以 0.25m/s 的速度移动，为了维持这个速度需要单位面积上的作用力为2N/m 2，求这两块平板间流体的动力黏度μ。
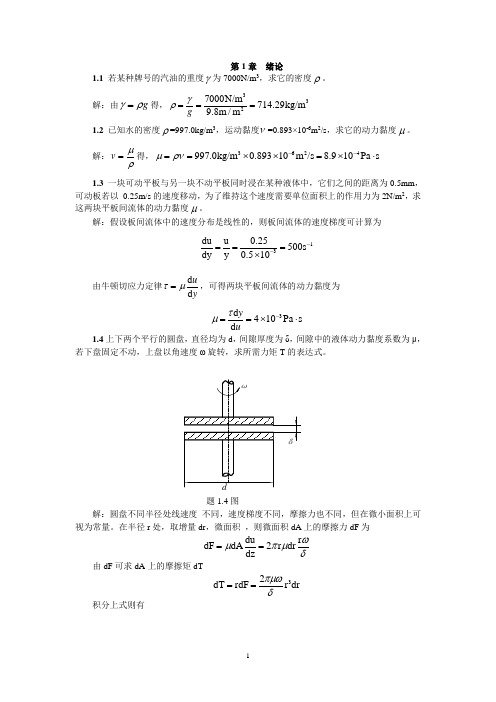
解：假设板间流体中的速度分布是线性的，则板间流体的速度梯度可计算为13du u 0.25500s dy y 0.510--===⨯ 由牛顿切应力定律d d uyτμ=，可得两块平板间流体的动力黏度为 3d 410Pa s d yuτμ-==⨯⋅1.4上下两个平行的圆盘，直径均为d ，间隙厚度为δ，间隙中的液体动力黏度系数为μ，若下盘固定不动，上盘以角速度ω旋转，求所需力矩T 的表达式。
题1.4图解：圆盘不同半径处线速度 不同，速度梯度不同，摩擦力也不同，但在微小面积上可视为常量。
在半径r 处，取增量dr ，微面积 ，则微面积dA 上的摩擦力dF 为du r dF dA2r dr dz ωμπμδ== 由dF 可求dA 上的摩擦矩dT32dT rdF r dr πμωδ==积分上式则有d 43202d T dT r dr 32πμωπμωδδ===⎰⎰1.5 如下图所示，水流在平板上运动，靠近板壁附近的流速呈抛物线形分布，E 点为抛物线端点，E 点处0d d =y u ，水的运动黏度ν=1.0×10-6m 2/s ，试求y =0，2，4cm 处的切应力。
（提示：先设流速分布C By Ay u ++=2，利用给定的条件确定待定常数A 、B 、C ）题1.5图解：以D 点为原点建立坐标系，设流速分布C By Ay u ++=2，由已知条件得C=0,A=-625,B=50则2u 625y 50y =-+ 由切应力公式du dyτμ=得du(1250y 50)dy τμρν==-+ y=0cm 时，221510N /m τ-=⨯；y=2cm 时，222 2.510N /m τ-=⨯；y=4cm 时，30τ= 1.6 某流体在圆筒形容器中。
《流体力学》课后习题答案.pdf
得：T1 = t1 + 273 = 50 + 273 = 323K ，T2 = t2 + 273 = 78 + 273 = 351K
根据
p
=
mRT V
，有：
p1
=
mRT1 V1
，
p2
=
mRT2 V2
得： V2 V1
=
p1 p2
T2 T1
=
9.8067 104 5.8840 105
351 323
=
0.18
设管段长度 l，管段表面积： A = dl
单位长度管壁上粘滞力： = A u = dl u − 0 = 3.14 0.025 0.03
l y l
0.001
1-8 解： A = 0.8 0.2 = 0.16m2 ，u=1m/s， = 10mm ， = 1.15Pa s
T = A u = A u − 0 = 1.15 0.16 1 = 18.4N
1
=
T1 b
=
A b
u
−0 −h
=
0.7 0.06b b
15 − 0 0.04 − 0.01
=
21N
/m，方向水平向左
下表面单位宽度受到的内摩擦力：
2
=
T2 b
=
Au−0 b h−0
=
0.7 0.06b 15 − 0
b
0.01− 0
= 63N
/m，方向水平向左
平板单位宽度上受到的阻力：
= 1 + 2 = 21+ 63 = 84N ，方向水平向左。
h1 = 5.6m
2.4 解：如图 1-2 是等压面，3-4 是等压面，5-6 段充的是空气，因此 p6 = p5 ，6-7 是等压面，
流体力学课后答案
流体力学课后答案(共112页) -本页仅作为预览文档封面，使用时请删除本页-第一章 流体及其物理性质1－1 已知油的重度为7800N/m 3，求它的密度和比重。
又，此种油的质量和重量各为多少已已知知：：γ＝7800N/m 3；V ＝。
解解析析：：(1) 油的密度为 3kg/m 79581.97800===g γρ；油的比重为 795.01000795OH 2===ρρS (2) 的油的质量和重量分别为 kg 1592.0795=⨯==V M ρ N 15602.07800=⨯==V G γ1－2 已知300L(升)水银的质量为4080kg ，求其密度、重度和比容。
已已知知：：V ＝300L ，m ＝4080kg 。
解解析析：：水银的密度为 33kg/m 13600103004080=⨯==-V m ρ水银的重度为 3N/m 13341681.913600=⨯==g ργ 水银的比容为 kg /m 10353.7136001135-⨯===ρv 1－3 某封闭容器内空气的压力从101325Pa 提高到607950Pa ，温度由20℃升高到78℃，空气的气体常数为kg ·K 。
问每kg 空气的体积将比原有体积减少多少减少的百分比又为多少已已知知：：p 1＝101325Pa ，p 2＝607950Pa ，t 1＝20℃，t 2＝78℃，R ＝kg ·K 。
解解析析：：由理想气体状态方程(1－12)式，得kg /m 83.0101325)27320(06.2873111=+⨯==p RT v kg /m 166.0607950)27378(06.2873222=+⨯==p RT v kg /m 664.0166.083.0321=-=-v v%80%10083.0166.083.0%100121=⨯-=⨯-v v v每kg 空气的体积比原有体积减少了；减少的百分比为80％。
1－4 图示为一水暖系统，为了防止水温升高时体积膨胀将水管胀裂，在系统顶部设一膨胀水箱，使水有膨胀的余地。
(完整word版)流体力学习题及答案-第五章
第五章 势流理论5-1流速为u 0=10m/s 沿正向的均匀流与位于原点的点涡叠加。
已知驻点位于(0，-5)，试求： (1)点涡的强度；(2) (0,5)点的流速以及通过驻点的流线方程。
答：（1）求点涡的强度Γ：设点涡的强度为Γ，则均匀流的速度势和流函数分别为：x u 01=ϕ，y u 01=ψ；点涡的速度势和流函数为：xy arctg πϕ22Γ-=，r y x ln 2)ln(221222ππψΓ=+Γ=； 因此，流动的速度势和流函数为：θπθπϕϕϕ2cos 20021Γ-=Γ-=+=r u x y arctg x u ， r y u y x y u ln 2sin )ln(202122021πθπψψψΓ+=+Γ+=+=；则速度分布为：2202y x yu y x u +⋅Γ+=∂∂=∂∂=πψϕ， 222yx x x y v +⋅Γ=∂∂-=∂∂=πψϕ； 由于)5,0(-为驻点，代入上式第一式中则得到：0)5(052220=-+-⋅Γ+πu ， 整理得到：ππ100100==Γu 。
（2）求)5,0(点的速度：将π100=Γ代入到速度分布中，得到：222222050102100102y x y y x y y x y u u ++=+⋅+=+⋅Γ+=πππ，2222225021002y x x y x x y x x v +=+⋅=+⋅Γ=πππ； 将0=x 、5=y 代入上述速度分布函数，得到：201010505501022=+=+⨯+=u （m/s ），05005022=+⨯=v （m/s ）；（3）求通过)5,0(点的流线方程：由流函数的性质可知，流函数为常数时表示流线方程C =ψ，则流线方程为：C y x y u =+Γ+21220)ln(2π；将0=x 、5=y 代入，得到：5ln 5050)50ln(21005102122+=+⨯+⨯=ππC ；则过该点的流线方程为：5ln 5050)ln(2100102122+=++y x y ππ，整理得到：5ln 55)ln(52122+=++y x y5-2 平面势流由点源和点汇叠加而成，点源位于（-1，0），其流量为θ1=20m 3/s ，点汇位于（2,0）点，其流量为θ2=40m 3/s ，已知流体密度为ρ=1.8kg/m 3，流场中（0，0）点的压力为0，试求点（0,1）和（1,1）的流速和压力。
流体力学课后答案.
第1章 绪论1.1 若某种牌号的汽油的重度γ为7000N/m 3，求它的密度ρ。
解：由g γρ=得，3327000N/m 714.29kg/m9.8m /m γρ===g1.2 已知水的密度ρ=997.0kg/m 3，运动黏度ν=0.893×10-6m 2/s ，求它的动力黏度μ。
解：ρμ=v 得，3624997.0kg/m 0.89310m /s 8.910Pa s μρν--==⨯⨯=⨯⋅ 1.3 一块可动平板与另一块不动平板同时浸在某种液体中，它们之间的距离为0.5mm ，可动板若以 0.25m/s 的速度移动，为了维持这个速度需要单位面积上的作用力为2N/m 2，求这两块平板间流体的动力黏度μ。
解：假设板间流体中的速度分布是线性的，则板间流体的速度梯度可计算为13du u 0.25500s dy y 0.510--===⨯ 由牛顿切应力定律d d uyτμ=，可得两块平板间流体的动力黏度为 3d 410Pa s d yuτμ-==⨯⋅1.4上下两个平行的圆盘，直径均为d ，间隙厚度为δ，间隙中的液体动力黏度系数为μ，若下盘固定不动，上盘以角速度ω旋转，求所需力矩T 的表达式。
题1.4图解：圆盘不同半径处线速度 不同，速度梯度不同，摩擦力也不同，但在微小面积上可视为常量。
在半径r 处，取增量dr ，微面积 ，则微面积dA 上的摩擦力dF 为du r dF dA2r dr dz ωμπμδ== 由dF 可求dA 上的摩擦矩dT32dT rdF r dr πμωδ==积分上式则有d 43202d T dT r dr 32πμωπμωδδ===⎰⎰1.5 如下图所示，水流在平板上运动，靠近板壁附近的流速呈抛物线形分布，E 点为抛物线端点，E 点处0d d =y u ，水的运动黏度ν=1.0×10-6m 2/s ，试求y =0，2，4cm 处的切应力。
（提示：先设流速分布C By Ay u ++=2，利用给定的条件确定待定常数A 、B 、C ）题1.5图解：以D 点为原点建立坐标系，设流速分布C By Ay u ++=2，由已知条件得C=0,A=-625,B=50则2u 625y 50y =-+ 由切应力公式du dyτμ=得du(1250y 50)dy τμρν==-+ y=0cm 时，221510N/m τ-=⨯；y=2cm 时，222 2.510N/m τ-=⨯；y=4cm 时，30τ= 1.6 某流体在圆筒形容器中。
流体力学第五章习题答案
第五章习题答案选择题（单选题）5.1 速度v ，长度l ，重力加速度g 的无量纲集合是：（b ）（a ）lv g ；（b ）v gl ；（c ）l gv ；（d ）2v gl。
5.2 速度v ，密度ρ，压强p 的无量纲集合是：（d ）（a ）p v ρ；（b ）v p ρ；（c ）2pv ρ；（d ）2p v ρ。
5.3 速度v ，长度l ，时间t 的无量纲集合是：（d ）（a ）v lt ；（b ）t vl ；（c ）2l vt ；（d ）lvt。
5.4 压强差p ，密度ρ，长度l ，流量Q 的无量纲集合是：（d ）（a ）2Qpl ρ；（b ）2lpQ ρ；（c ）plQρ；（d 。
5.5 进行水力模型实验，要实现明渠水流的动力相似，应选的相似准则是：（b ）（a ）雷诺准则；（b ）弗劳德准则；（c ）欧拉准则；（d ）其他。
5.6 进行水力模型实验，要实现有压管流的动力相似，应选的相似准则是：（a ）（a ）雷诺准则；（b ）弗劳德准则；（c ）欧拉准则；（d ）其他。
5.7 雷诺数的物理意义表示：（c ）（a ）粘滞力与重力之比；（b ）重力与惯性力之比；（c ）惯性力与粘滞力之比；（d ）压力与粘滞力之比。
5.8 明渠水流模型实验，长度比尺为4，模型流量应为原型流量的：（c ）（a ）1/2；（b ）1/4；（c ）1/8；（d ）1/32。
5.9 压力输水管模型实验，长度比尺为8，模型水管的流量应为原型输水管流量的：（c ）（a ）1/2；（b ）1/4；（c ）1/8；（d ）1/16。
5.10 假设自由落体的下落距离s 与落体的质量m 、重力加速度g 及下落时间t 有关，试用瑞利法导出自由落体下落距离的关系式。
解： ∵s Km g t αβγ=[]s L =；[]m M =；[]2g T L -=；[]t T =∴有量纲关系：2L M TL T αββγ-=可得：0α=；1β=；2γ= ∴2s Kgt =答：自由落体下落距离的关系式为2s Kgt =。
中南大学流体力学课后答案
中南大学流体力学课后答案第1章 绪论1.1 解：339005.08.94410m kg m kg gV G V m =⨯===ρ 1.2 解：3132-⎪⎭⎫ ⎝⎛=h y h u dy du m 当25.0=h y 时，此处的流速梯度为h uh u dy du m m0583.1413231=⎪⎭⎫⎝⎛=-当50.0=h y 时，此处的流速梯度为huhu dy du m m8399.0213231=⎪⎭⎫ ⎝⎛=-1.3 解：N N A dy du A T 1842.08.0001.0115.1=⨯⨯⨯===μτ 1.4 解：充入内外筒间隙中的实验液体，在外筒的带动下做圆周运动。
因间隙很小，速度可视为近似直线分布，不计内筒端面的影响，内桶剪切应力由牛顿内摩擦定律推得：δδωμδμμτ)(0+===r u dy du 作用于内筒的扭矩：h r r Ar M 22)(πδδωμτ+==()()s Pa s Pa hr r M ⋅=⋅+⨯⨯⨯⨯⨯=+=3219.4003.02.04.02.060102003.09.4222πδπωδμ1.5 解：体积压缩系数：dpV dV -=κmlPa ml N m VdpdV 8905.1)1011020(2001075.456210-=⨯-⨯⨯⨯⨯-=-=-κ（负号表示体积减少） 手轮转数：122.0418905.1422≈⨯⋅==πδπd dV n 1.6 解：νρμ=1()()νρρνμ035.1%101%1512=-+= 035.112=μμ，即2μ比1μ增加了3.5％。
1.7 解：测压管内液面超高：mm d h O H 98.28.292==mm dh Hg05.15.10-=-=当测压管内液面标高为5.437m 时，若箱内盛水，水箱液面高程为：m m m 34402.5100098.2347.5=-若箱内盛水银，水箱液面高程为：m m m 34805.5)100005.1(347.5=-- 1.8 解：当液体静止时，它所受到的单位质量力：{}}{g f f f f z y x -==,0,0,,。
[适合打印]中南大学流体力学课后答案
![[适合打印]中南大学流体力学课后答案](https://img.taocdn.com/s3/m/c3a1a1e8856a561252d36f82.png)
T
2
c1
根据量纲一致性原则：
M ： 1 c1
L ： 1 a1 b1 3c1 T ： 2 a1
得： a1 2, b1 0, c1 1 ，
根据帕斯卡原理，p 将等值的传递到液体当中各点，大活塞底部亦如此。
G p
D 2
4
T ( a b) D 2 ad 2
以基本量纲（ M 、 L 、 T ）表示各物理量量纲：
锅炉
ML2T 3 ML 2T 2
L T L
a 3 1 b
c
ln
V V T T0 0.00051 80 0.0408 V0
V V0 e V T T0 10e 0.0408 10 1.0416 10.4164m 3
N KQH KgQH
2
切应力 —— M LT
2
2
体积模量 —— LT 功 E —— ML2 T 2
2
M
1.15
表面张力系数 —— M T 2 1.12 答：① 1.13 解：
动量 p —— ML T ③
解： 列出有关物理量的关系式：
p
v 2
Eu （欧拉数） ②
T A
1.4 解：
du 1 A 1.15 0.8 0.2 N 184 N dy 0.001
5.347m
δ
油
若箱内盛水银，水箱液面高程为：
充入内外筒间隙中的实验液体，在外筒的带动下做圆周运 动。因间隙很小，速度可视为近似直线分布，不计内筒端面的 影响，内桶剪切应力由牛顿内摩擦定律推得：
流体力学课后作业答案
流 体 力 学
yD 2
(1.8 / sin 60 ) 1 (2 / sin 60 )
2.292m
由力矩平衡
yD F1 yD1 F2 ( yD 2 (1 0.8) / sin 60 ) F
油 h1 F1 F yD2 θ
yD1 yD
2.35m
F2 水 h2
46
解： 阀关时，由静力学方程
z1 p1
流 体 力 学
g
z2
p2
g
5mH 2O
阀开时，由伯努利方程
1 1 2 2
z1
p1
g
v1
2
2g
z2
p2
g
v
2
v2
2
2g
hl
5 0 0.1
1
2g
v 8.74m/s
50
3.28 管末端喷嘴d =10cm，D =40cm，Q=0.4m3/s，12 个螺栓固定法兰，不计质量，求每个螺栓的受力。 解：v1
l
hf
13.6 0.92
2
h 1.24m
又 h l v f
0.92
0.2
d 2g 设为层流 Re 64 320 2000 成立
h
vd Re
1 0.025 320
7.8 10 m /s
2
5
若反向流动，Q不变，Re不变，λ不变，hf不变， 所以h不变，只是反向高差为9cm。
第一章习题解答
1-3 水的密度ρ=1000kg/m3，μ=0.599×10-3Pa· s，求运动粘 度ν。 解： / 0.599 103 /1000 5.99 106 m2 /s 1-7 20º C的空气在直径为2.5cm的管中流动，距管壁上1mm 处的空气速度为3cm/s。求作用于单位长度管壁上的粘性切 力为多少？ 解：T=20º C时， μ=0.0183×10-3Pa· s 空气层厚度很小（1mm），速度可认为是线性分布
水力学第五章习题答案
6 • 12水管直径d= 10 cm 管中流速v 二1 m/s ?K 温为10°C .试判别流态口又流速等于多少时,流态将发生变化？解:查 P5 表 14 知 t=10r C T 1^1.31 xlO-em^/sRe -空"-―=.6> 104 > 2300紊流V 131XL0-6 R 轧二也二 2300二 2300x ］二 2丸0」引"" 二 O03m, v d 0*16 - 14有一矩形断面的小排水沟,水深15 cm ,底宽20 cm , 流速0.15 m/s ,水温1O C C ,试判别流态。
： R =—=―——二一 、-—_ _o o^H ；/ b + 2/i 0.2,22 汁uR 0.15x0.06 “F __r w + R" 一 二—品=^/0>575 緊流v 1 j1xiQ 6 - 16应用细管式粘度计测定油的粘浇系数。
已知细管直径d 二8nim .测量段长匸2 m .实测油的流MQ = 70 cm^/s ,水银压解： u = = — = 13 9c tn i s 901bh 0 2 0.15 差计读值h = 30cm ，油的密度尸=901kg/m 3o 试求油的运动粘変計和动力粘H 0 一. 4 • "0A, = zd 2g urJ d 2頁打型=422.8 ・咖心=2.9S K 1 Of% Mu(W*200V139139^0.008校核流态2乎-冷"璋层流.假设成立6・13油管［8径了5伽渺的密度901 kg/m3运动粘滯系数0,9 cm2/s , 在管轴位置安放连接水银压差计的皮托管，水银面高差hp= 20 mm ,试求油的流量。
此图有误解：恥込也厂】塑空怙心⑴撷H901n = ^IgAii = 71^ 6 > 0.282 =2.3 5tnJs设为层流v=u/2V 2 4 2 4校核心卩沿釜髓"层流6 - 23输水管道中设有阀门.已知管道直径为50 mu ,通过流量为3,34闻冰银压差计读值Ah = 150 m，沿程水头损失不计，试求阀门的局部阻力系数。
《流体力学》课后习题详细解答
1-8解:
或，由 积分得
1-9解:法一：5atm
10atm
=0.537 x 10-9x (10-5) x98.07 x 103= 0.026%
法二： ,积分得
1-10解：水在玻璃管中上升高度
h =
水银在玻璃管中下降的高度
H= mm
第二章流体静力学
2-1解：已知液体所受质量力的x向分量为–a ,z向分量为-g。液体平衡方程为
重心C位于浮心之上，偏心距
沉箱绕长度方向的对称轴y轴倾斜时稳定性最差。浮面面积A=15m2。浮面关于y
轴的惯性矩和体积排量为
定倾半径
可见， >e,定倾中心高于重心，沉箱是稳定的。
第三章流体运动学
3-1解：质点的运动速度
质点的轨迹方程
3-Байду номын сангаас解：
由 和 ,得
故
3-3解：当t=1s时，点A（1,2）处的流速
线速度u = 0r,速度环量
(2)半径r+dr的圆周封闭流线的速度环量为
得
忽略高阶项2 0dr2，得d
（3）设涡量为 ，它在半径r和r+dr两条圆周封闭流线之间的圆环域上的积分为d 。因为 在圆环域上可看作均匀分布，得
将圆环域的面积dA=2 rdr代入该式，得
可解出 =2 + dr/r。忽略无穷小量 dr/r，最后的涡量
沉箱绕长度方向的对称轴y倾斜时稳定性最差。浮面面积A=15m2.浮面关于y轴的惯性矩和体积排量为
定倾半径
可见， ，定倾中心低于重心，沉箱是不稳定的。
(2)沉箱的混凝土体积
沉箱的重量
沉箱水平截面面积
设吃水深度为h,取水的密度 =1000kg/m3.浮力F等于重量G。有
流体力学 课后答案
流体力学课后答案一、流体静力学实验1、同一静止液体内的测压管水头线是根什么线？答：测压管水头指，即静水力学实验仪显示的测压管液面至基准面的垂直高度。
测压管水头线指测压管液面的连线。
从表1.1的实测数据或实验直接观察可知，同一静止液面的测压管水头线是一根水平线。
2、当时，试根据记录数据确定水箱的真空区域。
答：以当时，第2次B点量测数据（表1.1）为例，此时，相应容器的真空区域包括以下3三部分：（1）过测压管2液面作一水平面，由等压面原理知，相对测压管2及水箱内的水体而言，该水平面为等压面，均为大气压强，故该平面以上由密封的水、气所占的空间区域，均为真空区域。
（2）同理，过箱顶小杯的液面作一水平面，测压管4中该平面以上的水体亦为真空区域。
（3）在测压管5中，自水面向下深度为的一段水注亦为真空区。
这段高度与测压管2液面低于水箱液面的高度相等，亦与测压管4液面高于小水杯液面高度相等，均为。
3、若再备一根直尺，试采用另外最简便的方法测定。
答：最简单的方法，是用直尺分别测量水箱内通大气情况下，管5油水界面至水面和油水界面至油面的垂直高度和，由式，从而求得。
4、如测压管太细，对测压管液面的读数将有何影响？答：设被测液体为水，测压管太细，测压管液面因毛细现象而升高，造成测量误差，毛细高度由下式计算式中，为表面张力系数；为液体的容重；为测压管的内径；为毛细升高。
常温（）的水，或，。
水与玻璃的浸润角很小，可认为。
于是有一般说来，当玻璃测压管的内径大于10mm时，毛细影响可略而不计。
另外，当水质不洁时，减小，毛细高度亦较净水小；当采用有机玻璃作测压管时，浸润角较大，其较普通玻璃管小。
如果用同一根测压管测量液体相对压差值，则毛细现象无任何影响。
因为测量高、低压强时均有毛细现象，但在计算压差时。
相互抵消了。
5、过C点作一水平面，相对管1、2、5及水箱中液体而言，这个水平是不是等压面？哪一部分液体是同一等压面？答：不全是等压面，它仅相对管1、2及水箱中的液体而言，这个水平面才是等压面。
《流体力学》课后习题答案
流体力学课后习题答案习题【1】1-1 解：已知：120t =℃，1395p kPa '=，250t =℃ 120273293T K =+=，250273323T K =+= 据p RT ρ=，有：11p RT ρ'=，22p RT ρ'= 得：2211p T p T '='，则2211323395435293T p p kPa T ''=⋅=⨯=1-2 解：受到的质量力有两个，一个是重力，一个是惯性力。
重力方向竖直向下，大小为mg ；惯性力方向和重力加速度方向相反为竖直向上，大小为mg ，其合力为0，受到的单位质量力为01-3 解：已知：V=10m 3，50T ∆=℃，0.0005V α=℃-1根据1V V V Tα∆=⋅∆，得：30.000510500.25m V V V T α∆=⋅⋅∆=⨯⨯=1-4 解：已知：419.806710Pa p '=⨯，52 5.884010Pa p '=⨯，150t =℃，278t =℃ 得：1127350273323T t K =+=+=，2227378273351T t K =+=+= 根据mRT p V =，有：111mRT p V '=，222mRT p V '=G ＝mg自由落体： 加速度a ＝g得：421251219.8067103510.185.884010323V p T V p T '⨯=⋅=⨯='⨯，即210.18V V = 体积减小了()10.18100%82%-⨯=1-5 解：已知：40mm δ=，0.7Pa s μ=⋅，a =60mm ，u =15m/s ，h =10mm根据牛顿内摩擦力定律：uT Ayμ∆=∆ 设平板宽度为b ，则平板面积0.06A a b b =⋅= 上表面单位宽度受到的内摩擦力：1100.70.06150210.040.01T A u b N b b h b μτδ-⨯-==⋅=⨯=--/m ，方向水平向左 下表面单位宽度受到的内摩擦力：2200.70.061506300.010T A u b N b b h b μτ-⨯-==⋅=⨯=--/m ，方向水平向左 平板单位宽度上受到的阻力：12216384N τττ=+=+=，方向水平向左。
流体力学课后答案
流体力学课后答案1. 流体什么是？流体是一种拥有自由度的物质，在受到外力作用下具有变形能力的物质。
物质由多个粒子组成，而且这些粒子之间可以相互作用。
流体可以通过管道或其他特定设备进行流动，其实质就是利用能量带动各个粒子运动，实现流动状态。
2. 流体力学是什么流体力学是一门利用物理学和数学原理研究物质运动的学科，也叫流体流动，它涉及物质几种物理性质，其重点是研究物质随着时间、空间变化的规律。
从而获得物质微观和宏观的运动都体现出来的流体流动技术方程。
3. 流体力学的应用有哪些1）气体外壳力学：涉及气体在外壳中的运动，主要用于火箭、飞机发动机等高空环境中气体运动的分析模拟；2）流体传动力学：是涉及多种形式流体传动装置上流体的运动，如液压传动和气动传动涉及的纵向、横向流动状态、机械传动装置的运动等方面的研究；3）流体控制力学：涉及流体的控制，主要是涉及流量和压力的控制，如气动控制系统与液压控制系统的运用；4）流体噪声控制力学：主要研究流体流动产生的噪声控制，如气体管道中流动噪声的控制等；5）流体流动热力学：涉及流体在特定条件下流动产生的热量及其物理性质研究，如沸腾、冷却、冷凝和过热等；6）流体自动控制力学：涉及某一流体力学系统的自动控制技术，如工业过程控制、气体排放控制系统的设计等。
4. 流体力学的基本原理1）牛顿第二定律：流体动力学的最基本原理，指流体受外力的冲击下，它的线性运动量发生改变的程度与外力的大小成正比。
2）守恒定律：指在流体动力学实验中，物质在时间和空间上的总量不变，称为物质守恒定律。
3）流体动量定律：指受力体在经过时间及空间上的变化后，其运动能量的变化量等于外力对其作用的积分，即动量理论。
4）几何形变定律：主要指在空间和时间上的几何形变，如流体的剪切变形率、旋转变形率、切应力以及物质应变等，是流体运动变形中的重要参数。
5）流体动量守恒定律：即物质在通道中流动时，流速在其内部保持一致，流体动量与时间和空间改变量保持一致。
《流体力学》徐正坦主编课后答案解析第五章
第五章习题简答5-1有一薄壁圆形孔口，直径d= 10mm ，水头H为2m。
现测得射流收缩断面的直径d e为8mm，在32.8s时间内，经孔口流出的水量为0.01m 3,试求该孔口的收缩系数&，流量系数□，流速系数0及孔口局部损失系数Z。
解：2 2A c 1 10.64A d 104Q 4 0.01/32.8 厂“, v 2 2 6.06m/ sd20.0082v 6.06v 2gH 0.97v'2gH V2 9.8 21 11 21 0.0620.9720.64 0.97 0.625-2薄壁孔口出流，直径d=2em，水箱水位恒定H=2m，试求：(1 )孔口流量Q ; (2) 此孔口外接圆柱形管嘴的流量Q n；(3)管嘴收缩断面的真空高度。
解：(1 )孔口出流流量为Q A. 2gH(2) Q n A 2gH2 13 30.62 0.02 2 9.8 2 1.219 10 m /s 1.219L/S4(3)真空高度：卫型g5-3水箱用隔板分为有圆柱形外管嘴，其直径出水箱的流量Q。
0.82 — 0.022 2 9.8 2 1.612L/S4-P C 0.74H 0.74 2 1.48mgA、B两室，隔板上开一孔口，其直径d 1=4cm，在B室底部装d2=3cm。
已知H=3m , h3=0.5m 试求：(1) h 1 , h 2; (2)流题5-3图解：隔板孔口的流量Q i A 2gh i圆柱形外管嘴的流量Q2 A 2g h2 h3 h i由题意可得Q i=Q 2,1A 2gh11d12 h12A 2g H h12d f . H h120.62 0.04-- 2+ 0.82 0.03 ,3 h i解得hh21.07mH h1h33 1.07 0.5 1.43m5-41A2gh120.62 — 0.04242 9.8 1.07 3.56 103 33m3/s 3.56L/S 有一平底空船，其船底面积Q为8m2，船舷高h题5-4图为0.5m，船自重G为9.8kN。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第五章习题简答5-1有一薄壁圆形孔口，直径d= 10mm ，水头H 为2m 。
现测得射流收缩断面的直径d c为8mm ，在32.8s 时间内，经孔口流出的水量为0.01m 3，试求该孔口的收缩系数ε，流量系数μ，流速系数φ及孔口局部损失系数ζ。
解: 64.010822=⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛==d d A A c c εs m d Q v /06.6008.08.32/01.04422=⨯⨯==ππ 62.097.064.006.0197.011197.028.9206.62222=⨯===-=-==⨯⨯==⇒=εϕμϕζϕϕgHvgH v5-2薄壁孔口出流，直径d=2cm ，水箱水位恒定H=2m ，试求：（1）孔口流量Q ；（2）此孔口外接圆柱形管嘴的流量Q n ；（3）管嘴收缩断面的真空高度。
题5-2图解：（1）孔口出流流量为s L s m gH A Q /219.1/10219.128.9202.0462.02332=⨯=⨯⨯⨯⨯⨯==πϕ（2）s L gH A Q n /612.128.9202.0482.022=⨯⨯⨯⨯⨯==πμ（3）真空高度：m H gpg p C Cv 48.1274.074.0=⨯==-=ρρ 5-3 水箱用隔板分为A 、B 两室，隔板上开一孔口，其直径d 1=4cm ，在B 室底部装有圆柱形外管嘴，其直径d 2=3cm 。
已知H=3m ，h 3=0.5m 试求：（1）h 1，h 2；（2）流出水箱的流量Q 。
题5-3图解：隔板孔口的流量 112gh A Q μ=圆柱形外管嘴的流量 ()()132222h H g A h h g A Q -=+=μμ由题意可得Q 1=Q 2，则()()1212122212111211303.082.004.062.022h h h H d h d h H g A gh A -⨯⨯=⨯⨯-=-=μμμμ解得m h 07.11=sL s m gh A Q mh h H h /56.3/1056.307.18.9204.0462.0243.15.007.1333211312=⨯=⨯⨯⨯⨯⨯==∴=--=--=∴-πμ5-4 有一平底空船，其船底面积Ω为8m 2，船舷高h 为0.5m ，船自重G 为9.8kN。
现船底破一直径10cm 的圆孔，水自圆孔漏入船中，试问经过多少时间后船将沉没。
题5-4图解：在船沉没的过程中存在（浮力定律）Ω+=Ω21gh G gh ρρ得 m g G h h h 125.089800980021=⨯=Ω=-=∆ρ s m h g A Q /1062.7125.08.921.0462.02332-⨯=⨯⨯⨯⨯⨯=∆=πμ∴船沉没过程中水自圆孔漏入的流量是不变的。
另外，当h 2=0时，h 1’=0.125，则s Q h h t 3941062.7)125.05.0(8)'(31=⨯-⨯=-Ω=-5-5游泳池长25m ，宽10m ，水深1.5m ，池底设有直径10cm 的放水孔直通排水地沟，试求放净池水所需的时间。
解：设孔口在某时间t 的作用水头为h ，dt 时间内经孔口流出的水的体积dt gh A Qdt 2μ=又∵dt 时间内游泳池水面下降dh ，则体积减少为dV=-Ωdh 由连续方程可得dV Qdt =hs g μA H Ωgh μA Ωdh t ghμA Ωdh dt Ωdh dt gh μA H89.7284068.921.0462.05.1102522222220==⨯⨯⨯⨯⨯⨯⨯==-=∴-=∴-=⎰π即5-6 油槽车的油槽长度为l ，直径为D ，油槽底部设有卸油孔，孔口面积为A ，流量系数为μ，试求该车充满油后所需卸空时间。
题5-6图解：在某时间t 时，油槽中油面高度为h,dt 时间内经孔口泄出的油的体积为dt gh A Qdt 2μ=又∵dt 时间内游泳池水面下降dh ，则体积减少为dh h hD l dh D h D l dh dV 2222222--=⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-=Ω-=由连续方程可得dVQdt =即 dh h hD l dt gh μA 222--=gμA lD g μA dh h D l t g μA dhh D l gh μA dh h hD l dt H2342222222302=--=--=--=∴⎰5-8 虹吸管将A 池中的水输入B 池，已知长度l 1=3m ，l 2=5m 直径d=75mm ，两池水面高差H=2m ， 最大超高h=1.8m ，沿程阻力系数λ=0.02，局部损失系数：进口ζa =0.5，转弯ζb =0.2，出口ζc = 1.0，试求流量及管道最大超高断面的真空度。
题5-8图解：这是简单短管道水力计算，应用公式有:sL s m gHdl l AgH d lAvA Q /13.14/01413.028.920.12.05.0075.05302.0075.042)(23232121==⨯⨯++++⨯⨯=++++=+==∑∑πζζζλζλs m d A Q v /2.3075.001413.04401413.022=⨯⨯=⨯==ππ 取断面0-0、1-1伯努利方程l h gv g p z +++=2021ρ又 c p p -=1m g v d l g v h h g v z g p b a l c 11.38.922.3)2.05.0075.0302.0(8.922.38.12)(22222122=⨯⨯++⨯+⨯+=++++=++=ζζλρ得5-9 如图所示，用水泵自吸水井向高位水箱供水。
已知吸水井水面高程为155.0m ，水泵轴线的高程为159.6m ，高位水箱水面高程为179.5m ，水泵的设计流量为0.034m 3/s ，水泵吸、压水管均采用铸铁管，其长度分别为8m 和50m ，吸水管进口带底阀滤网的局部阻力系数ζ1=5.2 ，管路中三个弯头的局部阻力系数均为ζ2=0.2，水泵出口断面逆止阀和闸阀的局部阻力系数分别为ζ3=6.5和ζ4=0.1，水泵进口断面的允许真空度〔h v 〕=6.0mH 2O 。
试确定：（1）水泵吸、压水管直径d 吸和d 压；（2）校核水泵进口断面的真空度是否满足允许值；（3）若该水泵能够正常工作，其扬程H 为多少？（4）绘制水泵管路系统的测压管水头线和总水头线。
（ 经济流速；吸水管路v 允许=1.2m/s 、压水管路v 压=2m/s ）题5-9图解：（1）吸水管路v 允许=1.2m/sm v Qd 190.02.1034.044=⨯⨯==ππ吸 取d 吸=200mm压水管路v 压=2m/sm v Qd 147.02034.044=⨯⨯==ππ压 取d 压=150mm（2）034.02.0021.0021.03.03.01===吸d λ m d Q v 082.12.0034.044221=⨯⨯==ππ 列0-0、1-1截面的伯努利方程；l h gvg p z +++=20211ρ又 c p p -=1[]OmH h m gv d l g v h h g v z g p g p v l c 2222121112216064.58.92082.1)2.02.52.08034.0(8.92082.10.1556.1592)(22=<=⨯⨯++⨯+⨯+-=++++=++=-=ζζλρρ则所以水泵进口断面的真空度是满足允许值（3）037.015.0021.0021.03.03.02===压d λ m d Q v 924.115.0034.044222=⨯⨯==ππ mh h H H mH m g v d l h mg v d l h l l l l 55.285.2465.34.0'5.241555.179'65.38.92924.1)1.05.62.0215.050037.0(2)2(4.08.92082.1)2.02.52.08034.0(2)(2122243222222121111=++=++==-==⨯⨯++⨯+⨯=+++==⨯⨯++⨯=++=ζζζλζζλ(4)5-10 风动工具的送风系统由空气压缩机、贮气筒、管道等组成，已知管道总长l=100m ，直径d=75mm ，沿程阻力系数λ=0.045，各项局部水头损失系数之和∑ζ=4.4，压缩空气密度ρ=7.86kg/m 3，风动工具要风压650kPa ，风量0.088m 3/s ，试求贮气筒的工作压强。
题5-10图解： s m d Q v /92.19075.0088.04422=⨯⨯==ππ kPagh v p mg v d l h l l 75265010008.986.768.130********.1986.7650268.13038.9292.194.4075.0100045.0222122221=+⨯⨯+⨯⨯=++=∴=⨯⎪⎭⎫ ⎝⎛+⨯=⎪⎭⎫ ⎝⎛+=--∑ρρζλ5-11 水从密闭容器A ，沿直径d=25mm ，长l=10m 的管道流入容器B ，已知容器A 水面的相对压强p 1=2at ，水面高H 1=1m ，H 2 =5m ，沿程阻力系数λ=0.025，局部损失系数：阀门ζV =4.0，弯头ζb =0.3，试求流量。
题5-11图解：列两液面的伯努力方程l h H gp H +++=++000211ρ 其中g vdlh l 22⎪⎭⎫ ⎝⎛+=∑ζλ，代入上式得 gvd lH g p H 20002211⎪⎭⎫ ⎝⎛++++=++∑ζλρ sm d v Q s m d l g p H H g v /1025.2025.0458.44/58.43.034025.010025.09800980002518.9223322121-⨯=⨯⨯=⋅=∴=⎪⎭⎫⎝⎛⨯++⨯⎪⎭⎫ ⎝⎛⨯+-⨯⨯=⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛+-=∑ππζλρ 5-12 由水塔向水车供水，水车由一直径d=150mm ，长l=80m 的管道供水，该管道中共有两个闸阀和4个90°弯头（λ= 0.03，闸阀全开ζa =0.12，弯头ζb =0.48）。
已知水车的有效容积V 为25m 3，水塔具有水头H=18m ，试求水车充满水所需的最短时间。
题5-12图解：列水塔液面及管道出流断面的伯努利方程sm d l gH v g v d l h g v z z H h gv z z l l/29.4)48.0412.0215.08003.01(188.92)1(22)1(220002221221=⨯+⨯+⨯+⨯⨯=++=++=+=-=+++=++∑∑ζλζλs d v Vt 33015.0429.425422=⨯⨯=⋅=∴ππ5-13 自闭容器经两段串联管道输水，已知压力表读值p M =1at ，水头H=2m ，管长l 1=10m ，l 2 =20m ，直径d 1 =100mm ，d 2 =200mm ，沿程阻力系数λ1=λ2=0.03，试求流量并绘总水头线和测压管水头线。