移位寄存器 第三章答案
计算机组成原理第3章习题参考答案
第3章习题参考答案1、设有一个具有20位地址和32位字长的存储器，问 (1) 该存储器能存储多少字节的信息？(2) 如果存储器由512K ×8位SRAM 芯片组成，需要多少片？ (3) 需要多少位地址作芯片选择？ 解：(1) 该存储器能存储：字节4M 832220=⨯ (2) 需要片8823228512322192020=⨯⨯=⨯⨯K (3) 用512K ⨯8位的芯片构成字长为32位的存储器，则需要每4片为一组进行字长的位数扩展，然后再由2组进行存储器容量的扩展。
所以只需一位最高位地址进行芯片选择。
2、已知某64位机主存采用半导体存储器，其地址码为26位，若使用4M ×8位的DRAM 芯片组成该机所允许的最大主存空间，并选用内存条结构形式，问； (1) 若每个内存条为16M ×64位，共需几个内存条? (2) 每个内存条内共有多少DRAM 芯片?(3) 主存共需多少DRAM 芯片? CPU 如何选择各内存条? 解：(1) 共需条4641664226=⨯⨯M 内存条 (2) 每个内存条内共有32846416=⨯⨯M M 个芯片(3) 主存共需多少1288464648464226=⨯⨯=⨯⨯M M M 个RAM 芯片， 共有4个内存条，故CPU 选择内存条用最高两位地址A 24和A 25通过2：4译码器实现；其余的24根地址线用于内存条内部单元的选择。
3、用16K ×8位的DRAM 芯片构成64K ×32位存储器，要求： (1) 画出该存储器的组成逻辑框图。
(2) 设存储器读/写周期为0.5μS ，CPU 在1μS 内至少要访问一次。
试问采用哪种刷新方式比较合理?两次刷新的最大时间间隔是多少?对全部存储单元刷新一遍所需的实际刷新时间是多少? 解：(1) 用16K ×8位的DRAM 芯片构成64K ×32位存储器，需要用16448163264=⨯=⨯⨯K K 个芯片，其中每4片为一组构成16K ×32位——进行字长位数扩展(一组内的4个芯片只有数据信号线不互连——分别接D 0~D 7、D 8~D 15、D 16~D 23和D 24~D 31，其余同名引脚互连)，需要低14位地址(A 0~A 13)作为模块内各个芯片的内部单元地址——分成行、列地址两次由A 0~A 6引脚输入；然后再由4组进行存储器容量扩展，用高两位地址A 14、A 15通过2：4译码器实现4组中选择一组。
单片机原理及应用习题答案第三
第一章习题参考答案1-1：何谓单片机？与通用微机相比，两者在结构上有何异同？答：将构成计算机的基本单元电路如微处理器(CPU)、存储器、I/O接口电路和相应实时控制器件等电路集成在一块芯片上，称其为单片微型计算机，简称单片机。
单片机与通用微机相比在结构上的异同：(1)两者都有CPU，但通用微机的CPU主要面向数据处理，其发展主要围绕数据处理功能、计算速度和精度的进一步提高。
例如，现今微机的CPU都支持浮点运算，采用流水线作业，并行处理、多级高速缓冲(Cache)技术等。
CPU的主频达到数百兆赫兹(MHz)，字长普遍达到32位。
单片机主要面向控制，控制中的数据类型及数据处理相对简单，所以单片机的数据处理功能比通用微机相对要弱一些，计算速度和精度也相对要低一些。
例如，现在的单片机产品的CPU大多不支持浮点运算，CPU还采用串行工作方式，其振荡频率大多在百兆赫兹范围内;在一些简单应用系统中采用4位字长的CPU，在中、小规模应用场合广泛采用8位字长单片机，在一些复杂的中、大规模的应用系统中才采用16位字长单片机，32位单片机产品目前应用得还不多。
(2) 两者都有存储器，但通用微机中存储器组织结构主要针对增大存储容量和CPU 对数据的存取速度。
现今微机的内存容量达到了数百兆字节(MB)，存储体系采用多体、并读技术和段、页等多种管理模式。
单片机中存储器的组织结构比较简单，存储器芯片直接挂接在单片机的总线上，CPU对存储器的读写按直接物理地址来寻址存储器单元，存储器的寻址空间一般都为64 KB。
(3) 两者都有I/O接口，但通用微机中I/O接口主要考虑标准外设(如CRT、标准键盘、鼠标、打印机、硬盘、光盘等)。
用户通过标准总线连接外设，能达到即插即用。
单片机应用系统的外设都是非标准的，且千差万别，种类很多。
单片机的I/O 接口实际上是向用户提供的与外设连接的物理界面。
用户对外设的连接要设计具体的接口电路，需有熟练的接口电路设计技术。
数字电子技术(山东联盟-潍坊学院)知到章节答案智慧树2023年
数字电子技术(山东联盟-潍坊学院）知到章节测试答案智慧树2023年最新第一章测试1.十进制数25对应的八进制数为（）。
参考答案:312.八进制数34.5对应的二进制数为（）。
参考答案:011100.1013.与十进制数53.5等值的8421BCD码为（）。
参考答案:0101 0011.01014.与十进制数（12.5）10等值的二进制数为（）。
参考答案:1100.15.与八进制数(47.3)8等值的二进制数为（）。
参考答案:100111.0116.不同的数码只能用来表示数量的不同大小。
参考答案:错7.带有符号位的二进制负数的补码与原码相同。
参考答案:错8.格雷码具有任何相邻码只有一位码元不同的特性。
参考答案:对9.正数的反码是将符号位保持不变，其它各位都取反。
参考答案:错10.将8421BCD码加0011得到余3码，所以余3码也是一种恒权码。
参考答案:错第二章测试1.当逻辑函数有n个变量时,共有( )个变量取值组合?参考答案:2.逻辑函数F=A+B'+CD'的反函数F'= ( ）。
参考答案:A'B(C'+D)3.用卡诺图化简下列逻辑函数，最简表达式为（）。
参考答案:F(A,B,C,D)=A′B′+AC′+C′D +B′D′4.已知逻辑函数的真值表表所示,列出该函数的最小项表达式（）。
0 0 0 00 0 1 00 1 0 00 1 1 11 0 0 01 0 1 11 1 0 11 1 1 1参考答案:F=A'BC+AB'C+ABC'+ABC5.求一个逻辑函数F的对偶式,可将F中的( )。
参考答案:“·”换成“+”,“+”换成“·”;变量不变; 常数中“0”换成“1”,“1”换成“0”6.逻辑代数的三个重要规则是( ）。
参考答案:对偶规则; 代入规则; 反演规则7.逻辑代数最基本的逻辑关系有( )三种。
参考答案:非运算; 与运算; 或运算8.逻辑函数最小项的性质有（）。
微机原理第三章习题参考答案
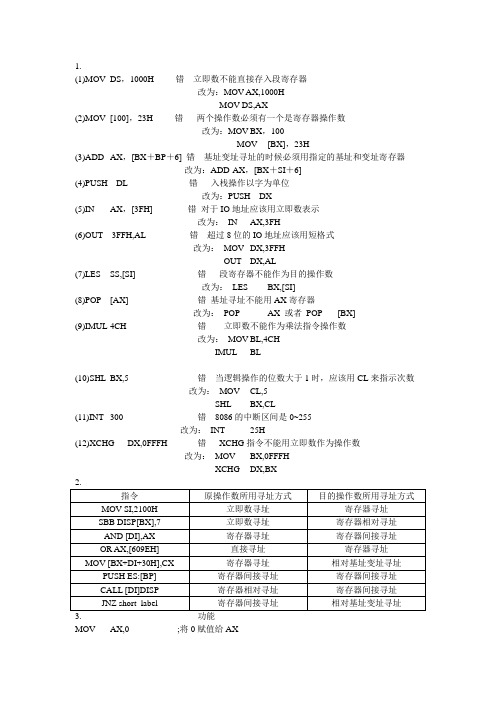
1.(1)MOV DS，1000H 错立即数不能直接存入段寄存器改为：MOV AX,1000HMOV DS,AX(2)MOV [100]，23H 错两个操作数必须有一个是寄存器操作数改为：MOV BX，100MOV [BX]，23H(3)ADD AX，[BX＋BP＋6] 错基址变址寻址的时候必须用指定的基址和变址寄存器改为：ADD AX，[BX＋SI＋6](4)PUSH DL 错入栈操作以字为单位改为：PUSH DX(5)IN AX，[3FH] 错对于IO地址应该用立即数表示改为：IN AX,3FH(6)OUT 3FFH,AL 错超过8位的IO地址应该用短格式改为：MOV DX,3FFHOUT DX,AL(7)LES SS,[SI] 错段寄存器不能作为目的操作数改为：LES BX,[SI](8)POP [AX] 错基址寻址不能用AX寄存器改为：POP AX 或者POP [BX](9)IMUL 4CH 错立即数不能作为乘法指令操作数改为：MOV BL,4CHIMUL BL(10)SHL BX,5 错当逻辑操作的位数大于1时，应该用CL来指示次数改为：MOV CL,5SHL BX,CL(11)INT 300 错8086的中断区间是0~255改为：INT 25H(12)XCHG DX,0FFFH 错XCHG指令不能用立即数作为操作数改为：MOV BX,0FFFHXCHG DX,BX3.功能MOV AX,0 ;将0赋值给AXLEA AX,[0000H] ;将偏移地址0000H 送到AX 中LDS AX,MEM32 ;mem32中的低地址中的值是0000HLES AX,MEM32 ; mem32中的低地址中的值是0000HSUB AX,AX ;AX 自己减自己AND AX,0000H ；AX 与0000相与XOR AX,AX ；AX 和自己异或SAL AX,CL ；当CL=16时清零。
功能是将AX 左移16位SAR AX,CL ；当CL=16且AX 最高位为0时清零。
微型计算机原理答案 第三章
第三章课后题答案注：存储单元或寄存器名用“（）”，表示存储单元或寄存器的内容寄存器名用“[]”，表示寄存器内容为一个内存单元的地址习题答案：1、指出指令中源操作数的寻址方式1)立即数寻址2)直接寻址3)寄存器间接寻址4)寄存器相对寻址5)寄存器寻址6)基址变址相对寻址7)寄存器寻址8)段内间接寻址9)端口间接寻址10)寄存器相对寻址11)立即数寻址12)立即数寻址2、指令是否正确，若不正确说明原因1)错误，立即数不能直接传送到段寄存器，可以用MOV AX,0100H MOVDS,AX两条指令实现2)错误，数据类型不匹配源操作数字节操作，目的操作数字操作数3)正确4)错误，端口地址>0FFH时，必须使用端口间接寻址方式。
可以用下两条指令实现：MOV DX,310H OUT DX,AL5)正确6)正确7)错误，没有同时用两个变址寄存器寻址内存单元的指令。
8)正确允许段超越9)错误，数据类型不匹配10)错误，BP不能作为间址寄存器11)正确12)错误，立即数不能作为目的操作数13)错误，堆栈指令不能用立即数14)错误，不能在两个内存单元之间直接用MOV指令传送数据。
15)错误，数据类型不匹配16)正确17)错误，CS段寄存器不能做目的操作数18)错误，没有指明操作数类型是字还是字节19)错误，端口间接寻址时，间址寄存器只能是DX不能是其它寄存器20)错误，移位指令和循环指令当操作次数大于1时，只能用CL存储操作次数。
21)错误，交换指令中不能用段寄存器22)错误，堆栈操作只能是字类型3、写出物理地址的计算表达式1)PA= (DS) * 10H + (DI)2)PA= (DS) * 10H + (BX) + (SI)3)PA= (DS) * 10H + (BX) + (DI) +54)PA= (ES) * 10H + (BX)5)PA= (DS) * 10H + 1000H6)PA= (DS) * 10H + (BX)+(DI)+2000H7)PA= (SS) * 10H + (BP)+(SI)8)PA= (DS) * 10H + (DI)4、计算物理地址1)PA= (DS) * 10H + (BX)=30000H+2000H=32000H2)PA= (DS) * 10H + (BX)+(SI)+1000H=30000H+2000H+0100H+1000H=33100H3)PA= (DS) * 10H + (BX)+(SI)=32100H4)PA= (ES) * 10H + (BX)=40000H+2000H=42000H5、代码段可寻址的空间范围：0E0000H~0EFFFFH6、(SP)=1FFEH，(AX)=5000H, (BX)=5000H7、两条指令的相同点：同为减法指令，均执行（AX）-09H操作；不同点：SUB指令有返回结果，而CMP指令没有返回结果。
第三章课后习题（1）参考答案
第三章 课后习题（1）参考答案P1111、 试说明串行进位和并行进位方式的不同之处。
（P .61.） 答：串行进位中进位是逐级形成的，每一级的进位直接依赖于前一级的进位，延迟时间较长，但节省器件，成本低。
并行进位中，各位进位信号都有独自的进位形成逻辑，每位进位信号的产生时间都相同，与低位进位无关，可有效地减少进位延迟时间。
但这是以增加逻辑线路为代价的。
2、 用74181和74182芯片构成一个64位的ALU ，采用分级分组并行进位链。
画出逻辑框图，并注明输入、输出等。
参考（P .63. 图3-6）答：P .63. 图3-6 画出了一个16位的并行进位ALU 结构 （每个74181芯片处理4位，16位需要4片74181芯片，组间用1片74182芯片产生组间并行进位。
）64位ALU ，可采用4组图3-6 的结构，每组处理16位，再用1片74182，处理组间进位。
A 3~0B 3~0A 7~4B 7~4A 11~8B 11~8A 15~12B 15~12__ __Cn16位并行进位ALU结构A 15~0B 15~0A 31~16B 31~16A 47~32 B 47~32A 63~48B 63~48__ __Cn64位并行进位ALU结构3、 用变形补码计算[X]补+[Y]补，并指出是否溢出，说明是正溢还是负溢。
（P .66.） 答：（1）[X]补=00,110011 [Y]补=00,101101 [X]补+[Y]补 = 01,100000，正溢出 （2）[X]补=00,010110 [Y]补=00,100101 [X]补+[Y]补 = 00,111011 无溢出 （3）[X]补=00,1110011 [Y]补=11,101101 [X]补+[Y]补 = 11,100000，无溢出 （4）[X]补=11,001101 [Y]补=11,010011[X]补+[Y]补 = 10,100000，负溢出4、 用变形补码计算[X]补-[Y]补，并指出是否溢出。
微机原理 第三章答案
第三章作业1答案思考题：1、简述80C51的指令寻址方式。
答：80C51的指令寻址方式有：寄存器寻址、立即寻址、寄存器间址、直接寻址、变址寻址、相对寻址、位寻址2、访问特殊功能寄存器SFR，可使用哪些寻址方式？答SFR只能直接寻址3、若访问外部RAM单元，可使用哪些寻址方式？答：外间RAM单元，只能通过MOVX指令进行寄存器间接寻址。
4、若访问内部RAM单元，可使用哪些寻址方式？答：片内RAM低128字节，可直接寻址、寄存器间接寻址。
（只能使用R0, R1作为间址寄存器。
片内RAM20~2FH单元，可以位寻址。
5、MOV、MOVC、MOVX指令有什么区别？分别用于哪些场合？答：MOV指令用于对内部RAM的访问。
MOVC指令用于对程序存储器的访问，从程序存储器中读取数据（如表格、常数等）。
MOVX指令采用间接寻址方式访问外部数据存储器，有Ri和DPTR两种间接寻址方式。
执行MOVX 指令时，在P3.7引脚上输出RD有效信号，或在P3.6 引脚上输出WR有效信号，可以用做外部数据存储器或I/O的读／写选通信号，与单片机扩展电路有关。
作业：1．给下段汇编语句加注释，汇编成机器语言，并说明该段程序的作用ORG 0000H 机器码MOV SP,#5FH ;栈顶指针指向内部RAM5FH单元C:0X0000 75815FMOV R7,#08H ；R7<- 08H,R7为计数器0X0003 7F08MOV R0,#3FH ；R0指向内部RAM3FH单元0X0005 783FCLOOP: POP ACC ; ACC<- (SP), SP<- SP-1 0X0007 D0E0 MOV @R0,A;把A中内容送入R0指向的单元（3FH）0X0009 F6DEC R0 ；R0<- R0-1 0X000A 18DJNZ R7,CLOOP ；R7<-R7-1 ，R7不为0跳转0X000B DFFASJMP $ ；原地踏步0X000D 80FE程序段作用：把内部RAM中58H-5FH单元的内容依次存入从38H-3FH的八个单元2．阅读下列程序，分析其功能。
数字电子技术(山东科技大学)智慧树知到课后章节答案2023年下山东科技大学
数字电子技术（山东科技大学）智慧树知到课后章节答案2023年下山东科技大学山东科技大学第一章测试1.一位十六进制数可以用（）位二进制数来表示。
答案:42.十进制数43可转换为（）8421BCD码。
答案:010000113.二进制数+1011的反码为（）。
答案:010114.有符号二进制数-89的补码为（）。
答案:101001115.与模拟电路相比，数字电路主要的优点有（）。
答案:抗干扰能力强; 保密性好; 通用性强6.与八进制数(47.3)8等值的数为（）。
答案:(27.6)16;(100111.011)27.以下代码中为恒权码的为（）。
答案:5421BCD码; 8421BCD码8.与十进制数（53.5）10等值的数或代码为（）。
答案:(65.4)8; (35.8)16; (110101.1)2; (0101 0011.0101)8421BCD9.在一个8位的存储单元中，能够存储的最大无符号整数是（）。
答案:（255）10;（FF）1610.矩形脉冲信号的参数有（）。
答案:占空比; 周期; 脉宽11.常用的BCD码有（）。
答案:余三码; 8421码12.以下几种编码中，可靠性编码是（）。
答案:奇偶校验码; 格雷码第二章测试1.利用约束项化简逻辑函数时，约束项应看成( )。
答案:能使圈组大的看成1，其它看成02.下面的卡诺图化简，应画（）个包围圈。
答案:43.已知两输入逻辑变量AB和输出结果Y的真值表如下表，则AB的逻辑关系为（）。
A B Y0 0 00 1 11 0 11 1 0答案:异或4.利用卡诺图化简逻辑函数时,8个相邻的最小项可消去（）个变量。
答案:35.在函数L（A，B，C，D）=AB+CD的真值表中，L=1的状态有（）。
答案:76.在同一逻辑函数式中，下标号相同的最小项和最大项是（）关系。
答案:互补7.F=ABCD'+ABD+BCD'+ABC+BD+BC' 化简为最简与或式（）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第三章习题参考答案1．画出以1)(246+++=x x x x f 为联接多项式的线性移位寄存器逻辑框图，及其对应的状态图。
解：由1)(246+++=x x x x f ，得反馈函数为531621),,,(x x x x x x f ++=Λ，故（1）逻辑框图：（2）状态图：状态圈-1： 状态圈-2：状态圈-3： 状态圈-4：状态圈-5： 状态圈-6：状态圈-7： 状态圈-8：状态圈-9： 状态圈-10：状态圈-11： 状态圈-12：2．已知图3-2所示的7级线性反馈移位寄存器：图3-2（1）绘出该移位寄存器的线性递推式，联接多项式及特征多项式。
（2）给出状态转移矩阵。
（3）设初态为（1 1 1 1 1 1 1），给出输出序列a 。
解：(1)由逻辑框图得，递推式为：k k k k a a a a ++=+++357 ()0≥k 。
联接多项式为：7421)(x x x x f +++=。
特征多项式为：7531)(~x x x x f +++=（2）状态转移矩阵：⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛0100000101000000010001000100000001000000011000000。
（3）输出序列：)111111111(ΛΛ=-a 。
3．设5级线性反馈移位寄存器的联接多项式为1)(25++=x x x f ，初态为（10101）。
求输出序列a 。
解：由联接多项式得，反馈函数为：41521),,,(x x x x x f +=Λ。
故以)10101(为初态的状态转移图为：1010101010001010001000001100000100000100100100100110100110100110100110100111100111100111101111101111001110001110001110000110010110110111110101110101110101110101→→→→→→→→→→→→→→→→→→→→→→→→→→→→→→→ 由此可得，输出序列为：=a 44444443444444421一个周期0110100100000011111001010111011…。
4．证明：n 级线性反馈移位寄存器的状态转移变换是n 维线性空间nF 2上的线性变换。
证明：设f T 为n 级线性移位寄存器的状态转移变换，对nF 2,∈∀βα，令),,,(110-=n a a a Λα，),,,(110-=n b b b Λβ，有：),,,(),,,()(121110∑=--==ni i n i n f f a c a a a a a T T ΛΛα，),,,(),,,()(121110∑=--==n i i n i n f f b c b b b b b T T ΛΛβ。
)()(),,,(),,,())(,,,(),,,()(12112112211111100βαβαf f i n ni i i n n i i ni i n i n i n n f f T T b c b b a c a a b a c b a b a b a b a b a T T +=+=+++=+++=+-=-==----∑∑∑ΛΛΛΛ对 2F k ∈∀，))((),,,(),,,()(121110ααf i n ni i n f f T k a c k ka ka ka ka ka T k T ===-=-∑ΛΛ。
故n 级线性反馈移位寄存器的状态转移变换是n 为线性空间nF 2上的线性变换。
5．设二元周期序列a 0≠的极小多项式为，T 是对应的状态转换矩阵，则S ，ST ，…，1)(-a p ST必两两不同。
其中),,,(120-=n a a a S Λ。
证明：若∃j i ,，1)(0-≤≠≤a p j i ，使得j i ST ST = （不妨设 j i <）。
令 j i -=τ，则 S ST =τ。
于是，对k S ∀，有 ττT S T ST ST S k k k k ===，即k k a a =+τ ，0≥k 。
从而τ（)(a p <）为序列a 的周期，与)(a p 为最小周期矛盾。
故S ，ST ，…，1)(-a p ST必两两不同。
6．证明：若a )(f G ∈的极小多项式次数为)1(≥n ，则a ，a L ，…，a L n 1-必线性无关。
证明：由题知0≠a ，假设a ，a L ，…，a L n 1-线性相关，则存在不全为零一组数110,,,-n c c c Λ使得0)(011101110=+++==+++----a L c L c c a L c a L c a c n n n n ΛΛ令：)(~x g 1110--+++=n n x c x c c Λ，则)(x g 也产生序列a ，而1)(0-≤∂n x g ，与a 的极小多项式)(x f 的次数为n 矛盾，故假设不成立，因此，a ，a L ，…，a Ln 1-必线性无关。
7．证明：若a )(f G ∈，n x f =∂)(0，0≠a ，则a ，a L ，…，a L n 1-构成)(f G 的一组基当且仅当a 以)(x f 为极小多项式。
证明：充分性：由n x f o=∂)(知)(f G 是n 维的。
又a )(f G ∈，a 以)(x f 为极小多项式，由上题结论可知a ，a L ，…，a Ln 1-线性无关，故构成)(f G 的一组基。
必要性：设a 的极小多项式为)(x m a ，m x m a o =∂)(，则)(|)(x f x m a ，n m ≤。
令：m m m a x x c x c x c x m +++++=--112211)(Λ，则0)(~=a L m a，从而， a ，a L ，…，a L m线性相关。
而a ，a L ，…，a Ln 1-为)(f G 的一组基，所以1->n m ，即n m ≥，故)()(x f x m a =。
即a 以)(x f 为极小多项式。
8．证明：若a )(f G ∈，n x f =∂)(0，a 以)(x f 为极小多项式，则)(f G 中每个序列均可唯一地表成a D g )(，并且a D g )(的极小多项式为))(),(()(x f x g x f ，其中n x g <∂)(0，D 为延迟变换。
从而)(f G 中有)(f ϕ个序列以)(x f 为极小多项式，其中)(f ϕ是次数f 0∂≤，且和)(x f 互素的多 项式的个数。
证明：（1）上题结论知，)(f G b ∈∀，都可由a ，a L ，…，a L n 1-为线性表出，则存在一组数110,,,-n c c c Λ 使得：a L c L c c a L c a L c a cb n n n n )(011101110----+++==+++=ΛΛ令：112210)(~--++++=n n x c x c x c c x g Λ，则有a D g b a L g b )()(~=⇔=，即)(f G b ∈∀均可唯一的表示成a D g )(的形式。
（2）令：)())(),((x d x g x f =，则)()()(1x f x d x f =，)()()(1x g x d x g =，1))(),((11=x g x f 。
设a D g )(的极小多项式为)(2x f ，则只须证明))(),(()()()(12x g x f x f x f x f ==。
)()()()()()()())()((11111====a D f D g a D g D f aD g D d D f a D g D f Θ∴)(1x f 为a D g )(的联接多项式，从而)(|)(12x f x f 。
又，由0)()()()()((122==a D g D d D f a D g D f 知，)()()(|)(12x g x d x f x f ，从而)()(|)(121x g x f x f ，而1))(),((11=x g x f ，故)(|)(21x f x f ，所以)()(12x f x f =，即 ))(),(()(x g x f x f 为-a D g )(的极小多项式。
（3）当1))(),((=x f x g 时，-a D g )(以)(x f 为极小多项式，而次数n <且与)(x f 互素的多项式)(x g 共有)(f ϕ个。
9．设)(x f ][2x F ∈，0)0(≠f 。
（1）证明)(f G 中任一平移等价类中序列有相同的极小多项式与周期。
（2）)(f G 中有相同的极小多项式的序列是否一定在同一平移等价类中？为什么？在什么条件下，序列的极小多项式相同当且仅当序列属于同一平移等价类？证明：（1）设a )(f G ∈，a L b t=（1)(0-≤≤a p t ）是其平移等价序列，且有t k k a b +=，0≥k 。
因为k t k a p t k a p k b a a b ===++++)()(，0≥k 。
故)(|)(a p b p ，同理可证)(|)(b p a p ，所以)()(a p b p =。
设a 的极小多项式为)(x m a ，b 的极小多项式为)(x m b ，则 0)(~=a L m a，从而 0)(0)(~)(~)(~=⇔===b D m a L m L a L L m b L m aa t t a a ， 即)(x m a 是b 的联接多项式，于是)(|)(x m x m a b ，同理可证)(|)(x m x m b a 。
因此)()(x m x m b a =。
（2）不一定。
例如，1)(234++++=x x x x x f 是4次不可约多项式，)(f G 中非零序列都以)(x f 为的极小多项式，但f G 中有3个周期为5的圈，显然这3个圈对应3个不同的平移等价类。
（或令Λ11000=a ，Λ10111=b ，)(,f G b a ∈，但a 与b 不在同一等价类中。
）当)(x f 是本原多项式时，序列的极小多项式相同当且仅当序列属于同一平移等价类。
10．设)(x f )()(21x f x f =，其中311)(x x x f ++=，221)(x x f +=][2x F ∈。
（1）证明以0 1 1 1 1 0 0 1 0 0 0 0 1 1为一个周期段的二元序列属于)(f G 。
（2）将上述序列分解成两个序列a 和b 之和，使得)(1f G a ∈，)(2f G b ∈。
证明：（1）1)()()(2521+++==x x x x f x f x f ， 令初态为=0S （01111），则)(x f 产生的序列为：Λ,00110111100100故以0 1 1 1 1 0 0 1 0 0 0 0 1 1为周期段的二元序列属于)(f G 。