数学实验题库--选择题
数学实验_重庆大学中国大学mooc课后章节答案期末考试题库2023年

数学实验_重庆大学中国大学mooc课后章节答案期末考试题库2023年1.无向图中边的端点地位是平等的、边是无序点对。
而有向图中边的端点的地位不平等,边是有序点对,不可以交换。
参考答案:正确2.人口数量与下列因素都有关,人口基数、出生率、死亡率、年龄结构、性别比例、医疗水平、工农业生产水平、环境、生育政策等等。
参考答案:正确3.一元5次代数方程在复数范围内有多少个根?参考答案:54.任何贪心算法都能求出最优解。
参考答案:错误5.二维插值函数z=interp2(x0,y0,z0,x,y,’method’)中,method的缺省值是()参考答案:linear6.在当前文件夹和搜索路径中都有文件ex1.m,在命令行窗口输入ex1时,则执行的文件是当前文件夹中的ex1.m参考答案:正确7.下列关于Dijkstra算法的哪些说法正确参考答案:Dijkstra算法是求加权图G中从某固定起点到其余各点最短路径的有效算法;_Dijkstra算法的时间复杂度为O(n2),其中n为顶点数;_Dijkstra算法可用于求解无向图、有向图和混合图的最短路径问题;8.如果x=1: 2 : 10,则x(1)和x(5)分别是( )参考答案:1,99.人口是按指数规律无限增长的。
参考答案:错误10.在包汤圆问题的整个建模过程,包括了如下几个步骤(1)找出问题涉及的主要因素(变量),重新梳理问题使之更明确(2)作出简化、合理的假设(3)用数学的语言来描述问题(4)用几何的知识解决问题(5)模型应用参考答案:正确11.下面程序所解的微分方程组,对应的方程和初始条件为:(1)函数M文件weif.m:function xdot=weif(t, x)xdot=[3*x(1)+x(3);2*x(1)+6;-3*x(2)^2+2*x(3)];(2)脚本M文件main.m:x0=[1,2,3] ;[t,x]=ode23(‘weif’,[0,1],x0),plot(t,x’),figure(2),plot3(x( :,1),x( :,2),x( :,3)参考答案:___12.某公司投资2000万元建成一条生产线。
科研方法试题库

科研方法试题库一、选择题1.试验设计中强调必须遵守“随机、对照、重复、均衡”四大原则,其目的就是为了( a )。
A.减少过失误差、降低随机误差、消除系统误差;B.便于收集资料、便于统计处理、便于撰写论文;C.纯化“信号”、降低“噪音”、多快好省;D.仅用一、二次,最多十几次试验,就可得到可靠结果;2.已知A、B、C都是三水平因素,且根据试验得知:A⨯B、B⨯C不可忽视。
若希望试验次数尽可能少一些,试验设计时最好选择( b )。
A.拉丁方B.正交设计C.析因设计D.交叉设计3.为了研究一组因素X1,X2,……,X g对一组肺癌患者生存时间长短的影响,对病人进行追踪随访观察,观察结果分为两档,,即病人生存时间≤2年和>2年,考察的危险因素有治疗方法(4种)、治疗前病人的状态(6种)、病人的年龄、癌细胞的类型(3种)等。
问这种资料最适合选用什么统计方法分析(c )。
A.方差分析B.多元线性回归分析C.COX回归分析D.Logistic回归分析4.为了研究一组因素X1,X2,……,X g对一组肺癌患者生存时间长短的影响,对病人进行追踪随访观察,观察结果为病人的生存时间(年),含终检数据,考察的危险因素有治疗方法(4种)、治疗前病人的状态(6种)、病人的年龄、癌细胞的类型(3种)等。
问这种资料最适合选用什么统计方法分析( c )。
A.方差分析B.多元线性回归分析C.COX回归分析D.Logistic回归分析5.某试验需在5%和15%两种氧浓度下进行,每种氧浓度分别使用甲、乙、丙、丁四种类似的药物对K562细胞进行抑制,每个试验条件下均重复4次试验(独立的4个样品,所含细胞的质和量都相同)。
观察的指标为计量资料,此设计称为(c )。
A.拉丁方B.配对设计C.析因设计D.交叉设计6.良好的实验设计,能减少人力、物力,提高实验效率,还有助于消除或减少( b )。
A.系统误差(偏性)B.随机误差C.抽样误差D.责任事故7.对于由一个错误的实验设计所产生的实验数据,在进行数据处理之前,其补救方法靠( d )。
大物实验理论题库

⼤物实验理论题库⼤物实验理论题库及答案Metaphor1⼀、填空题PART11.依照测量⽅法的不同,可将测量分为和两⼤类。
2.误差产⽣的原因很多,按照误差产⽣的原因和不同性质,可将误差分为疏失误差、和。
3.测量中的视差多属误差;天平不等臂产⽣的误差属于误差。
4.已知某地重⼒加速度值为9.794m/s2,甲、⼄、丙三⼈测量的结果依次分别为:9.790±0.024m/s2、9.811±0.004m/s2、9.795±0.006m/s2,其中精密度最⾼的是,准确度最⾼的是。
5.累加放⼤测量⽅法⽤来测量物理量,使⽤该⽅法的⽬的是减⼩仪器造成的误差从⽽减⼩不确定度。
若仪器的极限误差为0.4,要求测量的不确定度⼩于0.04,则累加倍数N>。
6.⽰波器的⽰波管主要由、和荧光屏组成。
7.已知y=2X1-3X2+5X3,直接测量量X1,X2,X3的不确定度分别为ΔX1、ΔX2、ΔX3,则间接测量量的不确定度Δy= 。
8、对于0.5级的电压表,使⽤量程为3V,若⽤它单次测量某⼀电压U,测量值为2.763V,则测量结果应表⽰为U= ,相对不确定度为B= 。
9、滑线变阻器的两种⽤法是接成线路或线路。
⼆、判断题(“对”在题号前()中打√,“错”打×)(10分)()1、误差是指测量值与真值之差,即误差=测量值-真值,如此定义的误差反映的是测量值偏离真值的⼤⼩和⽅向,既有⼤⼩⼜有正负符号。
()2、残差(偏差)是指测量值与其算术平均值之差,它与误差定义⼀样。
()3、精密度是指重复测量所得结果相互接近程度,反映的是随机误差⼤⼩的程度。
()4、测量不确定度是评价测量质量的⼀个重要指标,是指测量误差可能出现的范围。
()5、在验证焦⽿定律实验中,量热器中发⽣的过程是近似绝热过程。
()6、在落球法测量液体粘滞系数实验中,多个⼩钢球⼀起测质量,主要⽬的是减⼩随机误差。
()7、分光计设计了两个⾓游标是为了消除视差。
知识与能力综合考试题库

知识与能力综合考试题库# 知识与能力综合考试题库一、选择题(每题2分,共20分)1. 以下哪项不是科学研究的基本方法?A. 观察法B. 实验法C. 调查法D. 猜测法2. 根据达尔文的进化论,生物进化的驱动力是:A. 突变B. 自然选择C. 遗传D. 环境适应3. 在数学中,勾股定理适用于:A. 所有三角形B. 直角三角形C. 等边三角形D. 等腰三角形4. 以下哪个不是计算机编程语言?A. PythonB. JavaC. HTMLD. C++5. 根据牛顿第三定律,作用力与反作用力:A. 总是相等B. 总是相反C. 总是垂直D. 总是相等且相反6. 经济学中的边际效用递减法则指的是:A. 随着商品数量的增加,其总效用增加B. 随着商品数量的增加,其总效用减少C. 随着商品数量的增加,每增加一个单位商品带来的额外效用减少D. 随着商品数量的增加,每增加一个单位商品带来的额外效用增加7. 在化学中,化合物是由:A. 单一元素组成B. 两种或以上的元素组成C. 同种元素的不同同位素组成D. 同种元素的不同同分异构体组成8. 以下哪个不是文学创作的基本手法?A. 比喻B. 拟人C. 排比D. 翻译9. 在物理学中,能量守恒定律指的是:A. 能量可以被创造或消灭B. 能量在封闭系统中总量保持不变C. 能量总是从高温物体转移到低温物体D. 能量总是从低温物体转移到高温物体10. 以下哪个是心理学中的防御机制?A. 观察B. 投射C. 记忆D. 学习二、填空题(每题2分,共20分)11. 根据相对论,光速在真空中的速度是_______。
12. 在生物学中,细胞分裂的过程称为_______。
13. 计算机操作系统的主要功能是_______和管理计算机资源。
14. 经济学中的供求法则表明,商品的_______与其需求量成反比。
15. 在数学中,一个数的平方根是指一个数乘以自己等于原数的数。
16. 牛顿的第二定律指出,力等于_______乘以加速度。
中考数学题库(含答案和解析)

中考数学题库(含答案和解析)一、选择题(共10小题.每小题3分.满分30分)1.(3分)﹣5的绝对值为()A.﹣5 B.5 C.﹣D.2.(3分)当x=1时.代数式4﹣3x的值是()A.1 B.2 C.3 D.43.(3分)4的算术平方根是()A.±2 B.2 C.﹣2 D.4.(3分)若一个圆锥的侧面展开图是半径为18cm.圆心角为240°的扇形.则这个圆锥的底面半径长是()A.6cm B.9cm C.12cm D.18cm 5.(3分)已知一组数据的方差是3.则这组数据的标准差是()A.9 B.3 C.D.6.(3分)如图.已知在△ABC中.CD是AB边上的高线.BE平分∠ABC.交CD于点E.BC=5.DE=2.则△BCE的面积等于()A.10 B.7 C.5 D.47.(3分)一个布袋内只装有1个黑球和2个白球.这些球除颜色外其余都相同.随机摸出一个球后放回并搅匀.再随机摸出一个球.则两次摸出的球都是黑球的概率是()A.B.C.D.8.(3分)如图.以点O为圆心的两个圆中.大圆的弦AB切小圆于点C.OA交小圆于点D.若OD=2.tan∠OAB=.则AB的长是()A.4 B.2C.8 D.49.(3分)如图.AC是矩形ABCD的对角线.⊙O是△ABC的内切圆.现将矩形ABCD按如图所示的方式折叠.使点D与点O重合.折痕为FG.点F.G分别在边AD.BC上.连结OG.DG.若OG⊥DG.且⊙O的半径长为1.则下列结论不成立的是()A.CD+DF=4 B.CD﹣DF=2﹣3 C.BC+AB=2+4 D.BC﹣AB=210.(3分)如图.已知在平面直角坐标系xOy中.O是坐标原点.点A 是函数y=(x<0)图象上一点.AO的延长线交函数y=(x>0.k是不等于0的常数)的图象于点C.点A关于y轴的对称点为A′.点C关于x轴的对称点为C′.交于x轴于点B.连结AB.AA′.A′C′.若△ABC的面积等于6.则由线段′.C′A′.A′A所围成的图形的面积等于()A.8 B.10 C.3D.4二、填空题(共6小题.每小题4分.满分24分)11.(4分)计算:23×()2=.12.(4分)放学后.小明骑车回家.他经过的路程s(千米)与所用时间t(分钟)的函数关系如图所示.则小明的骑车速度是千米/分钟.13.(4分)在“争创美丽校园.争做文明学生”示范校评比活动中.10位评委给某校的评分情况下表所示:80859095评分(分)评委人1252数则这10位评委评分的平均数是分.14.(4分)如图.已知C.D是以AB为直径的半圆周上的两点.O是圆心.半径OA=2.∠COD=120°.则图中阴影部分的面积等于.15.(4分)如图.已知抛物线C1:y=a1x2+b1x+c1和C2:y=a2x2+b2x+c2都经过原点.顶点分别为A.B.与x轴的另一交点分别为M.N.如果点A与点B.点M与点N都关于原点O成中心对称.则称抛物线C1和C2为姐妹抛物线.请你写出一对姐妹抛物线C1和C2.使四边形ANBM恰好是矩形.你所写的一对抛物线解析式是和.16.(4分)已知正方形ABC1D1的边长为1.延长C1D1到A1.以A1C1为边向右作正方形A1C1C2D2.延长C2D2到A2.以A2C2为边向右作正方形A2C2C3D3(如图所示).以此类推….若A1C1=2.且点A.D2.D3.….D10都在同一直线上.则正方形A9C9C10D10的边长是.三、解答题(本题有8个小题.共66分)17.(6分)计算:.18.(6分)解不等式组.19.(6分)已知y是x的一次函数.当x=3时.y=1;当x=﹣2时.y =﹣4.求这个一次函数的解析式.20.(8分)如图.已知BC是⊙O的直径.AC切⊙O于点C.AB交⊙O于点D.E为AC的中点.连结DE.(1)若AD=DB.OC=5.求切线AC的长;(2)求证:ED是⊙O的切线.21.(8分)为了深化课程改革.某校积极开展校本课程建设.计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团.要求每位学生都自主选择其中一个社团.为此.随机调查了本校各年级部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):选择意向所占百分比文学鉴赏a科学实验35%音乐舞蹈b手工编织10%其他c根据统计图表中的信息.解答下列问题:(1)求本次调查的学生总人数及a.b.c的值;(2)将条形统计图补充完整;(3)若该校共有1200名学生.试估计全校选择“科学实验”社团的学生人数.22.(10分)某工厂计划在规定时间内生产24000个零件.若每天比原计划多生产30个零件.则在规定时间内可以多生产300个零件.(1)求原计划每天生产的零件个数和规定的天数;(2)为了提前完成生产任务.工厂在安排原有工人按原计划正常生产的同时.引进5组机器人生产流水线共同参与零件生产.已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%.按此测算.恰好提前两天完成24000个零件的生产任务.求原计划安排的工人人数.23.(10分)问题背景已知在△ABC中.AB边上的动点D由A向B运动(与A.B不重合).点E与点D同时出发.由点C沿BC的延长线方向运动(E不与C 重合).连接DE交AC于点F.点H是线段AF上一点.(1)初步尝试如图1.若△ABC是等边三角形.DH⊥AC.且点D.E的运动速度相等.求证:HF=AH+CF.小五同学发现可以由以下两种思路解决此问题:思路一:过点D作DG∥BC.交AC于点G.先证GH=AH.再证GF =CF.从而证得结论成立;思路二:过点E作EM⊥AC.交AC的延长线于点M.先证CM=AH.再证HF=MF.从而证得结论成立.请你任选一种思路.完整地书写本小题的证明过程(如用两种方法作答.则以第一种方法评分);(2)类比探究如图2.若在△ABC中.∠ABC=90°.∠ADH=∠BAC=30°.且D.E 的运动速度之比是:1.求的值;(3)延伸拓展如图3.若在△ABC中.AB=AC.∠ADH=∠BAC=36°.记=m.且点D.E运动速度相等.试用含m的代数式表示(直接写出结果.不必写解答过程).24.(12分)已知在平面直角坐标系xOy中.O为坐标原点.线段AB 的两个端点A(0.2).B(1.0)分别在y轴和x轴的正半轴上.点C为线段AB的中点.现将线段BA绕点B按顺时针方向旋转90°得到线段BD.抛物线y=ax2+bx+c(a≠0)经过点D.(1)如图1.若该抛物线经过原点O.且a=﹣.①求点D的坐标及该抛物线的解析式;②连结CD.问:在抛物线上是否存在点P.使得∠POB与∠BCD互余?若存在.请求出所有满足条件的点P的坐标.若不存在.请说明理由;(2)如图2.若该抛物线y=ax2+bx+c(a≠0)经过点E(1.1).点Q 在抛物线上.且满足∠QOB与∠BCD互余.若符合条件的Q点的个数是4个.请直接写出a的取值范围.参考答案与试题解析一、选择题(共10小题.每小题3分.满分30分)1.【分析】根据绝对值的概念:数轴上某个数与原点的距离叫做这个数的绝对值可直接得到答案.【解答】解:﹣5的绝对值为5.故选:B.【点评】此题主要考查了绝对值.关键是掌握绝对值规律总结:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.2.【分析】把x的值代入原式计算即可得到结果.【解答】解:当x=1时.原式=4﹣3=1.故选:A.【点评】此题考查了代数式求值.熟练掌握运算法则是解本题的关键.3.【分析】根据开方运算.可得一个数的算术平方根.【解答】解:4的算术平方根是2.故选:B.【点评】本题考查了算术平方根.注意一个正数只有一个算术平方根.4.【分析】利用弧长公式可得圆锥的侧面展开图的弧长.除以2π即为圆锥的底面半径.【解答】解:圆锥的弧长为:=24π.∴圆锥的底面半径为24π÷2π=12.故选:C.【点评】考查了圆锥的计算.用到的知识点为:圆锥的侧面展开图的弧长等于圆锥的底面周长;5.【分析】根据标准差是方差的算术平方根.即可得出答案.【解答】解:∵数据的方差是S2=3.∴这组数据的标准差是;故选:D.【点评】本题考查了标准差.关键是掌握标准差和方差的关系.标准差即方差的算术平方根;注意标准差和方差一样都是非负数.6.【分析】作EF⊥BC于F.根据角平分线的性质求得EF=DE=2.然后根据三角形面积公式求得即可.【解答】解:作EF⊥BC于F.∵BE平分∠ABC.ED⊥AB.EF⊥BC.∴EF=DE=2.∴S△BCE=BC•EF=×5×2=5.故选:C.【点评】本题考查了角的平分线的性质以及三角形的面积.作出辅助线求得三角形的高是解题的关键.7.【分析】列表将所有等可能的结果列举出来.利用概率公式求解即可.【解答】解:列表得:黑白白黑(黑.黑)(黑.白)(黑.白)白(黑.白)(白.白)(白.白)白(黑.白)(白.白)(白.白)∵共9种等可能的结果.两次都是黑色的情况有1种.∴两次摸出的球都是黑球的概率为.故选:D.【点评】本题考查了列表法与树状图法的知识.解决本题时采用了两个独立事件同时发生的概率等于两个独立事件单独发生的概率的积.难度不大.8.【分析】连接OC.利用切线的性质知OC⊥AB.由垂径定理得AB =2AC.因为tan∠OAB=.易得=.代入得结果.【解答】解:连接OC.∵大圆的弦AB切小圆于点C.∴OC⊥AB.∴AB=2AC.∵OD=2.∴OC=2.∵tan∠OAB=.∴AC=4.∴AB=8.故选:C.【点评】本题主要考查了切线的性质和垂径定理.连接过切点的半径是解答此题的关键.9.【分析】设⊙O与BC的切点为M.连接MO并延长MO交AD于点N.证明△OMG≌△GCD.得到OM=GC=1.CD=GM=BC﹣BM ﹣GC=BC﹣2.设AB=a.BC=b.AC=c.⊙O的半径为r.⊙O是Rt △ABC的内切圆可得r=(a+b﹣c).所以c=a+b﹣2.在Rt△ABC 中.利用勾股定理求得(舍去).从而求出a.b的值.所以BC+AB=2+4.再设DF=x.在Rt△ONF中.FN=.OF=x.ON=.由勾股定理可得.解得x=4.从而得到CD﹣DF=.CD+DF=.即可解答.【解答】解:如图.设⊙O与BC的切点为M.连接MO并延长MO交AD于点N.∵将矩形ABCD按如图所示的方式折叠.使点D与点O重合.折痕为FG.∴OG=DG.∵OG⊥DG.∴∠MGO+∠DGC=90°.∵∠MOG+∠MGO=90°.∴∠MOG=∠DGC.在△OMG和△GCD中.∴△OMG≌△GCD.∴OM=GC=1.CD=GM=BC﹣BM﹣GC=BC﹣2.∵AB=CD.∴BC﹣AB=2.设AB=a.BC=b.AC=c.⊙O的半径为r.⊙O是Rt△ABC的内切圆可得r=(a+b﹣c).∴c=a+b﹣2.在Rt△ABC中.由勾股定理可得a2+b2=(a+b﹣2)2.整理得2ab﹣4a﹣4b+4=0.又∵BC﹣AB=2即b=2+a.代入可得2a(2+a)﹣4a﹣4(2+a)+4=0.解得(舍去).∴.∴BC+AB=2+4.再设DF=x.在Rt△ONF中.FN=.OF=x.ON=. 由勾股定理可得.解得x=4.∴CD﹣DF=.CD+DF=.综上只有选项A错误.故选:A.【点评】本题考查了三角形的内切圆和内心.切线的性质.勾股定理.矩形的性质等知识点的综合应用.解决本题的关键是三角形内切圆的性质.10.【分析】过A作AD⊥x轴于D.连接OA′.设A(a.).C(b.).由△OAD∽△BCO.得到==.根据反比例函数的系数k的几何意义得到S△ADO=.S△BOC=.求出k2=.得到k=﹣.根据S△ABC=S△AOB+S△BOC=(﹣)•b+=6.列出关于k的方程k2+k﹣12=0.求得k=3.由于点A关于y轴的对称点为A′.点C关于x轴的对称点为C′.得到OA′.OC′在同一条直线上.于是得到由线段′.C′A′.A′A所围成的图形的面积=S△+S△OBC′+S△OAA′=10.OBC【解答】解:过A作AD⊥x轴于D.连接OA′.∵点A是函数y=(x<0)图象上一点.∴设A(a.).∵点C在函数y=(x>0.k是不等于0的常数)的图象上.∴设C(b.).∵AD⊥BD.BC⊥BD.∴△OAD∽△OCB.∴==.∵S△ADO=.S△BOC=.∴k2=.∵S△ABC=S△AOB+S△BOC=(﹣)•b+=6.∴k2﹣=12.①当k>0时.k=﹣.∴k2+k﹣12=0.解得:k=3.k=﹣4(不合题意舍去).②当k<0时.k=.∴k2﹣k﹣12=0.解得:k=﹣3.k=4(不合题意舍去).∴k2=9∵点A关于y轴的对称点为A′.点C关于x轴的对称点为C′. ∴∠1=∠2.∠3=∠4.∴∠1+∠4=∠2+∠3=90°.∴OA′.OC′在同一条直线上.∴S△OBC′=S△OBC==.∵S△OAA′=2S△OAD=1.∴由线段′.C′A′.A′A所围成的图形的面积=S△OBC+S△+S△OAA′=10.OBC′故选:B.【点评】本题考查了反比例函数的图象的性质.系数k的几何意义.相似三角形的判定和性质.轴对称的性质.正确的理解轴对称图形的性质是解题的关键.二、填空题(共6小题.每小题4分.满分24分)11.【分析】根据有理数的乘方.即可解答.【解答】解:23×()2=8×=2.故答案为:2.【点评】本题考查了有理数的乘方.解决本题的关键是熟记有理数乘方的定义.12.【分析】根据函数图象的纵坐标.可得路程.根据函数图象的横坐标.可得时间.根据路程与时间的关系.可得答案.【解答】解:由纵坐标看出路程是2千米.由横坐标看出时间是10分钟.小明的骑车速度是2÷10=0.2(千米/分钟).故答案为:0.2.【点评】本题考查了函数图象.观察函数图象的纵坐标得出路程.观察函数图象的横坐标得出时间.利用了路程与时间的关系.13.【分析】平均数的计算方法是求出所有数据的和.然后除以数据的总个数.【解答】解:这10位评委评分的平均数是:(80+85×2+90×5+95×2)÷10=89(分).故答案为89.【点评】本题考查的是加权平均数的求法.本题易出现的错误是求80.85.90.95这四个数的平均数.对平均数的理解不正确.14.【分析】图中阴影部分的面积=半圆的面积﹣圆心角是120°的扇形的面积.根据扇形面积的计算公式计算即可求解.【解答】解:图中阴影部分的面积=π×22﹣=2π﹣π=π.答:图中阴影部分的面积等于π.故答案为:π.【点评】考查了扇形面积的计算.求阴影面积的主要思路是将不规则图形面积转化为规则图形的面积.15.【分析】连接AB.根据姐妹抛物线的二次项的系数互为相反数.一次项系数相等且不等于零.常数项都是零.设抛物线C1的解析式为y=ax2+bx.根据四边形ANBM恰好是矩形可得△AOM是等边三角形.设OM=2.则点A的坐标是(1.).求出抛物线C1的解析式.从而求出抛物线C2的解析式.【解答】解:连接AB.根据姐妹抛物线的定义.可得姐妹抛物线的二次项的系数互为相反数.一次项系数相等且不等于零.常数项都是零.设抛物线C1的解析式为y=ax2+bx.根据四边形ANBM恰好是矩形可得:OA=OM.∵OA=MA.∴△AOM是等边三角形.设OM=2.则点A的坐标是(1.).则.解得:则抛物线C1的解析式为y=﹣x2+2x.抛物线C2的解析式为y=x2+2x.故答案为:y=﹣x2+2x.y=x2+2x(答案不唯一).【点评】此题考查了二次函数的图象与几何变换.用到的知识点是姐妹抛物线的定义、二次函数的图象与性质、矩形的判定.关键是根据姐妹抛物线的定义得出姐妹抛物线的二次项的系数、一次项系数、常数项之间的关系.16.【分析】延长D4A和C1B交于O.根据正方形的性质和三角形相似的性质即可求得各个正方形的边长.从而得出规律.即可求得正方形A9C9C10D10的边长.【解答】解:延长D4A和C1B交于O.∵AB∥A2C2.∴△AOB∽△D2OC2.∴=.∵AB=BC1=1.C2=C1C2=2.∴==∴OC2=2OB.∴OB=BC2=3.∴OC2=6.设正方形A2C2C3D3的边长为x1.同理证得:△D2OC2∽△D3OC3.∴=.解得.x1=3.∴正方形A2C2C3D3的边长为3.设正方形A3C3C4D4的边长为x2.同理证得:△D3OC3∽△D4OC4.∴=.解得x2=.∴正方形A3C3C4D4的边长为;设正方形A4C4C5D5的边长为x3.同理证得:△D4OC4∽△D5OC5.∴=.解得x=.∴正方形A4C4C5D5的边长为;以此类推….C n﹣1∁nD n的边长为;正方形A n﹣1∴正方形A9C9C10D10的边长为.故答案为.【点评】本题考查了正方形的性质.相似三角形的判定和性质.求得前五个正方形的边长得出规律是解题的关键.三、解答题(本题有8个小题.共66分)17.【分析】原式利用同分母分式的减法法则计算.约分即可得到结果.【解答】解:原式===a+b.【点评】此题考查了分式的加减法.熟练掌握运算法则是解本题的关键.18.【分析】先求出每个不等式的解集.再根据找不等式组解集的规律找出不等式组的解集即可.【解答】解:∵解不等式①得:x<6.解不等式②得:x>1.∴不等式组的解集为1<x<6.【点评】本题考查了解一元一次不等式组的应用.解此题的关键是能根据不等式的解集求出不等式组的解集.难度适中.19.【分析】一次函数解析式为y=kx+b.将x与y的两对值代入求出k与b的值.即可确定出一次函数解析式.【解答】解:设一次函数解析式为y=kx+b.将x=3.y=1;x=﹣2.y=﹣4代入得:.解得:k=1.b=﹣2.则一次函数解析式为y=x﹣2.【点评】此题考查了待定系数法求一次函数解析式.熟练掌握待定系数法是解本题的关键.20.【分析】(1)连接CD.由直径所对的圆周角为直角可得:∠BDC =90°.即可得:CD⊥AB.然后根据AD=DB.进而可得CD垂直平分AB.进而可得AC=BC=2OC=10;(2)连接OD.先由直角三角形中线的性质可得DE=EC.然后根据等边对等角可得∠1=∠2.由OD=OC.根据等边对等角可得∠3=∠4.然后根据切线的性质可得∠2+∠4=90°.进而可得:∠1+∠3=90°.进而可得:DE⊥OD.从而可得:ED是⊙O的切线.【解答】(1)解:连接CD.∵BC是⊙O的直径.∴∠BDC=90°.即CD⊥AB.∵AD=DB.OC=5.∴CD垂直平分AB.∴AC=BC=2OC=10;(2)证明:连接OD.如图所示.∵∠ADC=90°.E为AC的中点.∴DE=EC=AC.∴∠1=∠2.∵OD=OC.∴∠3=∠4.∵AC切⊙O于点C.∴AC⊥OC.∴∠1+∠3=∠2+∠4=90°.即DE⊥OD.∴ED是⊙O的切线.【点评】此题考查了切线的判定与性质.解题的关键是:熟记切线的判定定理与性质定理.经过半径的外端.并且垂直于这条半径的直线是圆的切线;圆的切线垂直于过切点的直径.21.【分析】(1)先计算出本次调查的学生总人数.再分别计算出百分比.即可解答;(2)根据百分比.计算出文学鉴赏和手工编织的人数.即可补全条形统计图;(3)用总人数乘以“科学实验”社团的百分比.即可解答.【解答】解:(1)本次调查的学生总人数是:70÷35%=200(人). b=40÷200=20%.c=10÷200=5%.a=1﹣(35%+20%+10%+5%)=30%.(2)文学鉴赏的人数:30%×200=60(人).手工编织的人数:10%×200=20(人).如图所示.(3)全校选择“科学实验”社团的学生人数:1200×35%=420(人).【点评】本题考查条形统计图.解决本题的关键是读懂图形.获取相关信息.22.【分析】(1)可设原计划每天生产的零件x个.根据时间是一定的.列出方程求得原计划每天生产的零件个数.再根据工作时间=工作总量÷工作效率.即可求得规定的天数;(2)可设原计划安排的工人人数为y人.根据等量关系:恰好提前两天完成2400个零件的生产任务.列出方程求解即可.【解答】解:(1)设原计划每天生产的零件x个.依题意有=.解得x=2400.经检验.x=2400是原方程的根.且符合题意.∴规定的天数为24000÷2400=10(天).答:原计划每天生产的零件2400个.规定的天数是10天;(2)设原计划安排的工人人数为y人.依题意有[5×20×(1+20%)×+2400]×(10﹣2)=24000.解得y=480.经检验.y=480是原方程的根.且符合题意.答:原计划安排的工人人数为480人.【点评】考查了分式方程的应用.一元一次方程的应用.分析题意.找到关键描述语.找到合适的等量关系是解决问题的关键.此题等量关系比较多.主要用到公式:工作总量=工作效率×工作时间.23.【分析】(1)过点D作DG∥BC.交AC于点G.先证明△ADG 是等边三角形.得出GD=AD=CE.再证明GH=AH.由ASA证明△GDF≌△CEF.得出GF=CF.即可得出结论;(2)过点D作DG∥BC.交AC于点G.先证出AH=GH=GD.AD=GD.由题意AD=CE.得出GD=CE.再证明△GDF≌△CEF.得出GF=CF.即可得出结论;(3)过点D作DG∥BC.交AC于点G.先证出DG=DH=AH.再证明△ADG∽△ABC.△ADG∽△DGH.△DGH∽△ABC.得出=m.=m.△DGH∽△ABC.得出=m.=m.证明△DFG∽△EFC.得出=m.=m.=.即可得出结果.【解答】(1)证明(选择思路一):过点D作DG∥BC.交AC于点G.如图1所示:则∠ADG=∠B.∠AGD=∠ACB.∵△ABC是等边三角形.∴∠A=∠B=∠ACB=60°.∴∠ADG=∠AGD=∠A.∴△ADG是等边三角形.∴GD=AD=CE.∵DH⊥AC.∴GH=AH.∵DG∥BC.∴∠GDF=∠CEF.∠DGF=∠ECF.在△GDF和△CEF中..∴△GDF≌△CEF(ASA).∴GF=CF.∴GH+GF=AH+CF.即HF=AH+CF;(2)解:过点D作DG∥BC.交AC于点G.如图2所示:则∠ADG=∠B=90°.∵∠BAC=∠ADH=30°.∴∠HGD=∠HDG=60°.∴AH=GH=GD.AD=GD.根据题意得:AD=CE.∴GD=CE.∵DG∥BC.∴∠GDF=∠CEF.∠DGF=∠ECF.在△GDF和△CEF中..∴△GDF≌△CEF(ASA).∴GF=CF.∴GH+GF=AH+CF.即HF=AH+CF.∴=2;(3解:.理由如下:过点D作DG∥BC.交AC于点G.如图3所示:则∠ADG=∠B.∠AGD=∠ACB.∵AB=AC.∠BAC=36°.∴∠ACB=∠B=∠ADG=∠AGD=72°.∵∠ADH=∠BAC=36°.∴AH=DH.∠DHG=72°=∠AGD.∴DG=DH=AH.△ADG∽△ABC.△ADG∽△DGH. ∴=m.=m.∴△DGH∽△ABC.∴=m.∴=m.∵DG∥BC.∴△DFG∽△EFC.∴=m.∴=m.即=m.∴=.∴===.【点评】本题是相似形综合题目.考查了等边三角形的判定与性质、相似三角形的判定与性质、全等三角形的判定与性质、等腰三角形的判定与性质等知识;本题难度较大.综合性强.特别是(2)(3)中.需要通过作辅助线证明三角形全等或三角形相似才能得出结果.24.【分析】(1)①过点D作DF⊥x轴于点F.先通过三角形全等求得D的坐标.把D的坐标和a=﹣.c=0代入y=ax2+bx+c即可求得抛物线的解析式;②先证得CD∥x轴.进而求得要使得∠POB与∠BCD互余.则必须∠POB=∠BAO.设P的坐标为(x.﹣x2+x).分两种情况讨论即可求得;(2)若符合条件的Q点的个数是4个.则当a<0时.抛物线交于y轴的负半轴.当a>0时.最小值得<﹣1.解不等式即可求得.【解答】解:(1)①过点D作DF⊥x轴于点F.如图1.∵∠DBF+∠ABO=90°.∠BAO+∠ABO=90°.∴∠DBF=∠BAO.又∵∠AOB=∠BFD=90°.AB=BD.在△AOB和△BFD中..∴△AOB≌△BFD(AAS)∴DF=BO=1.BF=AO=2.∴D的坐标是(3.1).根据题意.得a=﹣.c=0.且a×32+b×3+c=1.∴b=.∴该抛物线的解析式为y=﹣x2+x;②∵点A(0.2).B(1.0).点C为线段AB的中点.∴C(.1).∵C、D两点的纵坐标都为1.∴CD∥x轴.∴∠BCD=∠ABO.∴∠BAO与∠BCD互余.要使得∠POB与∠BCD互余.则必须∠POB=∠BAO.设P的坐标为(x.﹣x2+x).(Ⅰ)当P在x轴的上方时.过P作PG⊥x轴于点G.如图2. 则tan∠POB=tan∠BAO.即=.∴=.解得x1=0(舍去).x2=.∴﹣x2+x=.∴P点的坐标为(.);(Ⅱ)当P在x轴的下方时.过P作PG⊥x轴于点G.如图3则tan∠POB=tan∠BAO.即=.∴=.解得x1=0(舍去).x2=.∴﹣x2+x=﹣.∴P点的坐标为(.﹣);综上.在抛物线上是否存在点P(.)或(.﹣).使得∠POB 与∠BCD互余.(2)如图3.∵D(3.1).E(1.1).抛物线y=ax2+bx+c过点E、D.代入可得.解得.所以y=ax2﹣4ax+3a+1.分两种情况:①当抛物线y=ax2+bx+c开口向下时.若满足∠QOB与∠BCD互余且符合条件的Q点的个数是4个.则点Q在x轴的上、下方各有两个.(i)当点Q在x轴的下方时.直线OQ与抛物线有两个交点.满足条件的Q有2个;(ii)当点Q在x轴的上方时.要使直线OQ与抛物线y=ax2+bx+c有两个交点.抛物线y=ax2+bx+c与x轴的交点必须在x轴的正半轴上.与y轴的交点在y轴的负半轴.所以3a+1<0.解得a<﹣;②当抛物线y=ax2+bx+c开口向上时.点Q在x轴的上、下方各有两个.(i)当点Q在x轴的上方时.直线OQ与抛物线y=ax2+bx+c有两个交点.符合条件的点Q有两个;(ii)当点Q在x轴的下方时.要使直线OQ与抛物线y=ax2+bx+c 有两个交点.符合条件的点Q才两个.根据(2)可知.要使得∠QOB与∠BCD互余.则必须∠QOB=∠BAO. ∴tan∠QOB=tan∠BAO==.此时直线OQ的斜率为﹣.则直线OQ的解析式为y=﹣x.要使直线OQ与抛物线y=ax2+bx+c有两个交点.所以方程ax2﹣4ax+3a+1=﹣x有两个不相等的实数根.所以△=(﹣4a+)2﹣4a(3a+1)>0.即4a2﹣8a+>0.解得a>.a<(舍去).综上所示.a的取值范围为a<﹣或a>.【点评】本题是二次函数的综合题.考查了待定系数法求二次函数的解析式.正切函数.最小值等.分类讨论的思想是本题的关键.。
实验试题库参考答案
实验二 美沙拉嗪的制备1. 如何控制硝化反应条件?硝基还可以采用哪些还原方法?并加以比较。
温度的控制、搅拌速度的控制、混酸滴加的速度方法:催化氢化法、水合肼还原、氢化铝锂还原催化氢化:干净、方便、成本高;水合肼还原:产率高、后处理方便、还原反应较为剧烈、水合肼碱性较强;氢化铝锂还原:还原能力强、易爆炸,不安全2. 硝化反应时产生的气体是什么?是否有毒?除了使用排风系统外,还有什么方法能除去?NO 、NO 2等氮氧化物 有毒溶液吸收法;氧化吸收法;利用活性炭、分子筛或硅胶吸附3. 硝基还原反应时,除了用铁作还原剂外还能用什么试剂作为还原剂?氢气、水合肼、氢化铝锂、锡4. 保险粉和亚硫酸氢钠的作用分别是什么?防氧化5. 保险粉又称连二亚硫酸钠,使用它时需要注意什么?由于保险粉易燃、易爆,与水分解,与空气氧化分解,在使用过程中需要防止明火,无水操作,少于空气接触。
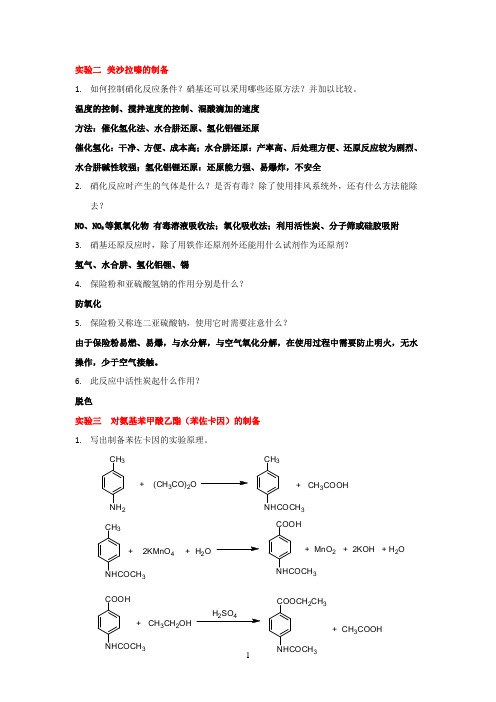
6. 此反应中活性炭起什么作用?脱色实验三 对氨基苯甲酸乙酯(苯佐卡因)的制备1. 写出制备苯佐卡因的实验原理。
CH 32+(CH 3CO)2O CH 33+CH 3COOH CH 3NHCOCH 3+2KMnO 4+H 2O COOHNHCOCH 3+MnO 2+2KOH +H 2OCOOH+CH 3CH 2OH24COOCH 2CH 3+CH 3COOH2.在反应过程中高锰酸钾为什么要分批加入?避免氧化剂浓度过高,破坏产物,并且使反应在比较温和的条件下进行,提高反应收率。
3.如何选择重结晶时的溶剂?(1)所选溶剂不与被提纯物质起化学反应(2)在较高温度时能溶解大量的被提纯物质;而在室温或更低温度时,只能溶解很少量的该种物质。
使被提纯物质热易溶,冷难溶。
(3)对杂质的溶解非常大或者非常小(前一种情况是使杂质留在母液中不随被提纯物晶体一同析出;后一种情况是使杂质在热过滤时被滤去)(4)容易挥发(溶剂的沸点较低),易与结晶分离除去(5)能给出较好的晶体(6)无毒或毒性很小,便于操作(7)价廉易得,回收率高(8)适当时候可以选用混合溶剂4.在第二步中为何加入稀硫酸酸化后就会析出固体?因为之前反应后形成的是对乙酰氨基苯甲酸钠,水溶性较好,但是加入稀硫酸酸化后,变成了对乙酰氨基苯甲酸,水溶性较差,从而使其析出得到需要的中间体产物。
黑龙江大专考试题库

黑龙江大专考试题库黑龙江大专考试题库涵盖了多个学科领域,包括但不限于数学、英语、计算机科学、工程学等。
以下是一些模拟题目,供学生复习和练习使用。
# 数学部分1. 选择题:下列哪个选项是方程 \( ax^2 + bx + c = 0 \) 的判别式?- A. \( b^2 - 4ac \)- B. \( 4ac - b^2 \)- C. \( 4ab - c^2 \)- D. \( b^2 + 4ac \)2. 填空题:函数 \( f(x) = 2x^3 - 5x^2 + 3x - 1 \) 的导数是\[ f'(x) = \] _______。
3. 解答题:求解不等式 \( |x - 2| + |x + 3| < 7 \)。
# 英语部分1. 词汇题:根据句子的意思,选择正确的单词填空。
- The _______ of the new bridge will greatly improve the traffic conditions.- A. construction- B. destruction- C. instruction- D. function2. 阅读理解:阅读下面的文章,回答以下问题。
- 文章 - 问题:根据文章,技术如何改变了教育方式?3. 写作题:写一篇不少于150词的短文,描述你对未来教育的展望。
# 计算机科学部分1. 选择题:以下哪个是数据库管理系统(DBMS)的特点?- A. 数据共享- B. 数据冗余- C. 数据不一致性- D. 数据独立性2. 填空题:在面向对象编程中,封装是指将对象的实现细节隐藏起来,只暴露出一个可以被外界访问的接口,这个过程称为 \[ \] _______。
3. 编程题:编写一个函数,实现对一个整数列表进行排序,并返回排序后的列表。
# 工程学部分1. 选择题:在结构工程中,下列哪个因素不是影响结构稳定性的因素? - A. 材料强度- B. 结构形式- C. 外部温度- D. 载荷大小2. 计算题:给定一个简单的梁结构,计算在特定载荷下的弯矩和剪力。
教科版小学六年级下册数学实验题

教科版小学六年级下册数学实验题
本文档主要介绍教科版小学六年级下册数学实验题,内容涵盖以下几个方面:
实验目的
通过开展数学实验,激发学生的数学兴趣,提高学生的数学思维能力和创新意识。
实验内容
本册的数学实验包含以下几个方面:
1. 图形的旋转和对称性实验
2. 三角形的分类实验
3. 平行四边形与梯形的性质实验
4. 角的度量实验
5. 直角三角形的性质实验
每个实验都有详细的实验步骤和实验方法,帮助学生更好地理解和掌握数学知识。
实验意义
数学实验是数学教学的一种创新型教学方法,它能使学生在探究中研究,在实践中提高,加深学生对数学知识的理解和记忆,能够更好地培养学生的观察能力、动手能力和创新能力。
实验操作要求
为了保证实验的顺利进行和实验结果的准确可靠,学生在进行数学实验时,需要注意以下几点:
1. 仔细阅读实验操作方法,按照操作步骤进行实验。
2. 注意实验器材的使用和存放,保持实验桌面整洁。
3. 将实验结果记录在实验桌面上的实验记录表上,并认真分析实验结果。
4. 实验过程中要注意安全,遵守实验室安全规定,防止意外事故的发生。
实验总结
通过进行数学实验,学生能够更直观地感受和理解数学知识,培养学生的数学思维和创新意识,有利于提高学生的数学成绩和科学素养,同时也有利于激发学生对数学的兴趣和热爱。
希望本文档能够对教师和学生在进行数学实验时有所帮助。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学实验题库选择题实验1 Matlab概述121.MATLAB系统运行时,内存中有包括X和Y在内的多个变量(数据),要删除所有变量(数据),应该使用的命令是(A )A clear;B clc;C home;D clear X Y2.下面有关MATLAB函数的说法,哪一个是错误的(D )A 函数文件的第一行必须由function开始,一般应有返回参数,函数名和输入参数;B MATLAB的函数可以有多个返回参数和多个输入参数;C 如果函数文件内有多个函数,则只有第一个函数可以供外部调用;D 在函数中可以用nargin检测用户调用函数时的输出参数个数3.有关sym和syms的用法不正确的是(C)A sym 一次只能定义一个变量;B syms一次可以定义一个或多个变量C sym一次可以定义一个或多个变量 D syms 不可以定义符号常量4. MA TLAB系统运行时,要清除屏幕(命令窗口)中的所有内容,应该使用的命令是(B )A clear;B clc;C home;D clear X Y5.在MATLAB中,who命令用于( B )A 重构工作区B 显示当前内存变量列表C 显示矩阵大小D 查询给定函数的路径6. 在MATLAB中下列数值的表示不正确的是(C)A.+99 B.1.3e-5 C.2-3*e^2 D.3-2*pi7.下列变量中比0大的最小数是( B )A.i B.realmin C.realmax D.pi8.将带小数的实数处理为整数称为取整,常用四种取整法则是:向正无穷大方向取整、向负无穷大方向取整、向零方向取整和四舍五入取整。
MA TLAB提供了如下四个取整函数,若a = -1.4,对a 取整的结果是-1,则不应该选用下面哪个函数。
(A )(A)floor;(B)round;(C)ceil;(D)fix;9.下列哪个变量的定义是不合法的( A )A abcd-3B xyz_3C abcdefD x3yz10. 在循环结构中跳出循环,执行循环后面代码的命令为( B )A returnB breakC continueD keyboard11. 用round函数四舍五入对数组[2.48 6.39 3.93 8.52]取整,结果为(C )A [2 6 3 8]B [2 6 4 8]C [2 6 4 9]D [3 7 4 9]x ,计算其正弦函数的运算为( D )12. 角度[30,45,60]1A SIN(x*pi/180)B SIN(x)C sin(x)D sin(x*pi/180)13.i=2; a=2i; b=2*i; c=2*sqrt(-1); 程序执行后;a, b, c的值分别是多少?( C )A a=4, b=4, c=2.0000iB a=4, b=2.0000i, c=2.0000iC a=2.0000i, b=4, c=2.0000iD a=2.0000i, b=2.0000i, c=2.0000i14. MA TLAB命令theta=0:0.5:2*pi;length(theta),显示计算结果为( C )Aans=11; B ans=12; C ans=13; D ans=14。
15. 要退出MA TLAB软件可在命令窗口中键入命令( D )A helpB cdC pwdD quit16. Matlab系统中的基本命令what的作用是(A )A 列出当前目录中文件清单B 显示当前目录C 改变当前目录D 显示文件内容17. 关于函数m文件下列说法正确的是(B )A. 文件名可以和函数名不一致B文件名必须和函数名一致C 文件名可以以数字开头D 文件名中不能有数字18. 图形窗口操作命令hold on的作用是(D )A 显示当前图形窗口B 将图形窗口分成若干个子窗口C 将图形窗口设定为单窗口模式D 保持当前图形并允许在当前图形中加入另一个图形19. 命令k=mod(2008,12)+1的结果是( B )A 4B 5C 6D 720.绘制条形图的命令是(A )A barB pieC polarD grid实验2函数图形绘图321. 下列命令不能绘制平面图形的是(A )A plot3B plotC polarD fplot22. 极坐标作图的命令是(C )A plot3B plotC polarD fplot23. 绘制空间曲线的命令是(A )A plot3B plotC meshD surf24. 绘制空间曲面着色图的命令是(C )A plot3B ezsurfC meshD surf25. MA TLAB命令[x,y]=meshgrid(1:3);得到的x和y是(C )23A 两个长度为3的行向量B 两个长度为3的列向量C 两个3阶方阵;D 一个向量一个矩阵26. 关于grid 的作用下列说法正确的是( D )A. 绘制图形窗口的网格B.清除图形中的网格C. 保持图形D. 在grid on 和grid off 间切换27. 用mesh(x,y,z)绘制空间曲面(,)=z f x y 在xOy 平面上的投影时只需令( C )A .x=0 B. y=0 C. z=0 D. x=y=028. MATLAB 语句[x,y]=meshgrid(-2:2) 的数据结果中(D )A x 是行向量,y 是列向量;B x 是五行五列的矩阵;C x 是行元素相同的矩阵;D y 是列向量相同的矩阵29. 极坐标绘图命令polar(theta,rho)中的theta 是指( B )A 以角度为单位的极角B 以弧度为单位的极角C 极径D 长度实验3 数列极限与函数极限 230. 关于Matlab 中求极限命令limit ,下列说法正确的是 (A )A. limit 命令可以求左右极限 B limit 不能求负无穷大处的极限C. limit 命令只能求有限点处的极限D. 使用limit 时变量不需要定义成符号变量31. 代码syms x ;limit(2^(1/x),x,0,’right ’)的执行结果是( B )A -InfB InfC 0D NaN32.代码limit('2^x','x',0)的执行结果是(A )A. 语法错误,不能执行B. 0 C 1 D Inf33. 在做生物种群的数量增长模型实验时,循环语句for i=2:30;p(i)=k*p(i-1)*(1-p(i-1)); end 中使用的递推公式是( C )A 2=⨯+⨯i n n p k p k pB 2=⨯-⨯i n n p k p k pC 2=⨯-⨯i i i p k p k pD 21+=⨯-⨯i i i p k p k p4实验4 导数与偏导数的计算 234. 在MA TLAB 命令窗口中,键入命令syms x,F=1/(2+cos(x));ezplot(diff(F)),结果是( D )A 绘出函数F 在[0,2π ]的图形;B 绘出函数F 在[–2π,2π ]的图形;C 绘函数F 的导函数在[0,2π ]的图形;D 绘函数F 的导函数在[–2π,2π ]的图形 35 . 在MA TLAB 命令窗口中,键入命令syms x ;diff(x*sin(x))。
结果是( C )A ans= sin(x)-x*cos(x);B ans= cos(x)+x*sin(x);C ans= sin(x)+xcos(x);D ans= -1/2*cos(x)*sin(x)+1/2*x36.在MATLAB 命令窗口中,键入命令syms x ;diff(x*cos(x))。
结果是( B )A ans= cos(x)+x*sin(x);B ans= cos(x) - x*sin(x);C ans= sin(x) - cos(x);D ans= sin(x) - x*cos(x)37.在MA TLAB 命令窗口中,键入命令syms x ; diff(x*exp(x))。
结果是( B )A ans= exp(x)*(x - 1);B ans= exp(x)+ x*exp(x);C ans= x – exp(x);D ans= x +exp(x)38. MA TLAB 命令syms a b x y ,f=exp(a*x)*sin(b*y),diff(f,x,2) 的功能是( C )A 计算函数f 关于a 的二阶导数;B 计算函数f 关于b 的高阶导数;C 计算函数f 关于x 的二阶偏导数;D 计算函数f 关于y 的二阶偏导数。
39 MA TLAB 命令syms t ,f=cos(t)/(2*t+6);df=diff(f) ;subs(df,t,2)的功能是( D )A 计算函数f 关于t 的二阶导数;B 计算函数f 关于t 的二阶偏导数;C 计算函数f 在2处的二阶导数;D 计算函数f 在2处的导数。
实验5 方程近似解的求法 340.求方程近似解中牛顿迭代法的迭代公式是( A ) A 111()'()---=-n n n n f x x x f x B 111()'()---=+n n n n f x x x f x C 111'()()---=-n n n n f x x x f x D 111'()()---=+n n n n f x x x f x 41 设区间[,]a b 是()f x 的一个隔离区间,用二分法求()f x 根的近似值时误差不超过( C )A 2-b aB 2+b aC 2-n b aD 2+n b a 42. 求方程近似解中弦截法的迭代公式是( D )5 A 111()()()()+--=-+-n n n n n n n f x x x x x f x f x B 111()()()()+--=+--n n n n n n n f x x x x x f x f x C 111()(()())+--=---n n n n n n n f x x x f x f x x x D 111()()()()+--=---n n n n n n n f x x x x x f x f x 43. 求单变量非线性方程的近似根可以用下列哪个命令( D )A fsolveB dsolveC solveD fzero44. 求方程(组)的代数解(精确解)用下列哪个命令( A )A fsolveB dsolveC solveD fzero45 关于求方程解的两个命令roots 和fsolve 下列说法正确的是( C )A roots 求得的是方程的精确解B roots 和fsolve 的调用格式一样C fsolve 求得的是方程的精确解D fsolve 求得的是方程的数值解46. 用Matlab 软件求方程43-4+12-9 = 0x x x 的所有解的代码为( D )A root('x^4-4*x^3+12*x-9')B root([1,-4,0,12,-9])A roots('x^4-4*x^3+12*x-9')B roots([1,-4,0,12,-9])47.MATLAB 命令syms e2;f=sqrt(1-e2*cos(t)^2);S=int(f,t,0,pi/2)功能是( D )A 计算f(x)在[0,pi/2]上的积分;B 计算f(t)不定积分符号结果;C 计算f(x)积分的数值结果;D 计算f(t)定积分的符号结果。
