相对论2-4
第4章 狭义相对论
第4章 狭义相对论一、基本要求1．掌握运动时间延缓和运动长度收缩原理； 2．理解质速关系和质能关系。
二、基本内容（一）本章重点和难点：重点：狭义相对论时空观中运动时间延缓和运动长度收缩。
难点：相对论动力学中质能关系。
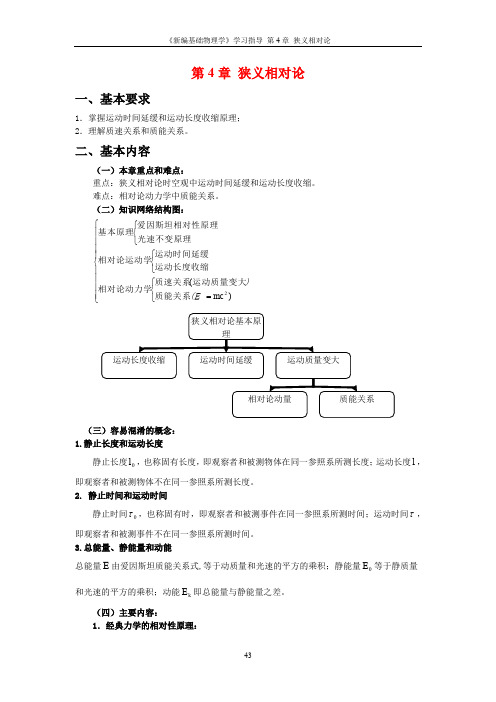
（二）知识网络结构图：⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎩⎨⎧=⎩⎨⎧⎩⎨⎧)(2mc （E ）质能关系运动质量变大质速关系相对论动力学运动长度收缩运动时间延缓相对论运动学光速不变原理爱因斯坦相对性原理基本原理（三）容易混淆的概念： 1.静止长度和运动长度静止长度0l ，也称固有长度，即观察者和被测物体在同一参照系所测长度；运动长度l ，即观察者和被测物体不在同一参照系所测长度。
2. 静止时间和运动时间静止时间0τ，也称固有时，即观察者和被测事件在同一参照系所测时间；运动时间τ，即观察者和被测事件不在同一参照系所测时间。
3.总能量、静能量和动能总能量E 由爱因斯坦质能关系式,等于动质量和光速的平方的乘积；静能量0E 等于静质量和光速的平方的乘积；动能k E 即总能量与静能量之差。
（四）主要内容：1．经典力学的相对性原理：一切彼此相对作匀速直线运动的诸惯性系中的力学规律是一样的。
即力学规律的数学形式都是相同的。
2．狭义相对论基本原理：（1）爱因斯坦相对性原理：物理定律在所有惯性参考系内都是等价的。
（2）光速不变原理：在所有惯性系中，光在真空中的速度恒等于c 。
3．洛伦兹变换：若S S 、'分别为两惯性系，S 系相对S '系以v 沿x 轴运动，在0='=t t 时两系重合，则一质点（或一事件）在S 系中的时空坐标（x 、y 、z 、t ）与在S '系中的时空坐标（x '、y '、z '、t '）之间的关系为洛伦兹时空变换。
（1）洛伦兹时空变换同一事件在S 系中时空坐标（x 、y 、z 、t ）与在S '系中的时空坐标（x '、y '、z '、t '）之间的关系为：⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧='='--='--='z z y y c v vt x x c v x c v t t 222)(1)(1逆变换为：⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧'='=-+'=-+=z z y y c v vtx x c v x c v t t 222)(1)(1（2）洛伦兹速度变换某质点相对于S 系速度u ，与相对S '系速度u '之间的关系为：PcE 021c vu v u u x x x--='；221)(1c v u c v u u x y y --='；221)(1c v u cvu u x z z --='逆变换为：21c vu v u u x xx '++'=；221)(1c v u c v u u x y y '+-'=；221)(1c v u c v u u x z z '+-'=4．狭义相对论时空观：（为简化公式，可令：22221,11c v cv -=-=βγ） （1）运动时间延缓公式：2201c v -=ττ其中：0τ为静止时间，也称固有时，即观察者和被测事件在同一参照系所测时间；τ为运动时间，即观察者和被测事件不在同一参照系所测时间。
4-2 相对论速度变换公式 modified
2 ′ 1 v u / c − ⋅ dt x , = dt 1 − v2 / c2
1− β 2 . u’ 和u 之间的变换关系 y y v 1 − 2 ux c
1− β 2 同 理 ， u ′z = . u’z和uz之间的变换关系 v 1 − 2 ux c uz
5/16
洛仑兹速度变换式
u = (ux , u y , uz )
x
u = u '+ v
x′
在 K′系来看，P的速度为： u ' = ( u ' x , u ' y , u ' z ) 在经典伽利略变换下，速度满足：
速度分量满足：？….
问题: 在洛仑兹坐标变换下， u 和 u’ 之间满 足什么关系？
2/16
洛仑兹速度变换
从最根本的定义出发，进行推导。
洛仑兹速度变换式讨论
d . 在洛仑兹速度变换下，光速不变。 K’系相对K系沿X轴 正向以v运动， 设在K系中, 光沿x轴传播， 即光速ux＝c, uy＝0, uz＝0, 根据洛仑兹速度变换，
O
y K
y′
K'
v
c
O′
x′ x
ux − v c−v u′x = = 2 2 1 − v ⋅ ux / c 1 − v ⋅ c / c
例题：设想一飞船以0.80c 的速度在地球上空飞行（沿x 轴），如果在飞船上沿y方向发射一光子， 问：从地面上看，光子速度如何？
K'
解： 选择地面参考系为K系， 飞船参考系为K’系
K
v
c
∴ v = 0 .8 0 c
在飞船（K’系）中，光子速度：
v
uz ' = 0.
广义相对论之4_协变导数、联络与度规的关系
6
7
8
可得
证明见下页
9
逆变矢量的协变导数表达式的证明
10
11
12
13
14
15
16
17
18
说明，g是权为2的标量密度。 但到目前为止我们还没定义张量密度的协变导数。 而在后面我们将看到，对张量密度的协变导数的定义需要用到 “g的协变导数为零”这个结论。 把“g的协变导数为零”当作一种约定来看也是可以的。
19Байду номын сангаас
20
21
22
将联络的上下指标收缩后的一些等价的表达式
23
24
证明：根据
25
26
证明：
27
广义相对论之四协变导数联络与度规的关系由上式可求得联络的坐标变换关系为证明见下页可得证明见下页10逆变矢量的协变导数表达式的证明111213141516171819说明g是权为2的标量密度
广义相对论之四 协变导数、联络与度规的关系
张宏浩
2
3
4
由上式可求得联络的坐标变换关系为
证明见下页
5
联络的坐标变换关系的证明
(人教)高中物理选修34课件：15.12相对论的诞生 时间和空间的相对性
都是_一__样__的___．
(2)两个基本假设
狭义相对性 在不同的_惯__性___参考系中，一切
原理
物理规律都是_相__同___的
光速不变原 真空中的光速在不同的惯性参考
理
系中都是_相__同___的
二、时间和空间的相对性 1．“同时”的相对性 在经典物理学上，如果两个事件在一个参考系中认为是同 时的，在另一个参考系中一定也是同时的；而根据爱因斯坦的 两个假设，同时是_相__对___的． 2．长度的相对性 (1)经典物理学认为，一条杆的长度不会因为观察者是否与 杆做__相__对__运__动___而不同．
(2)如果与杆相对静止人认为杆长是 L0，与杆相对运动的 人认为杆长是 L，则两者之间的关系为 L＝L0 1－vc2.
(3)一条沿自身长度方向运动的杆，其长度总比杆静止时的 长度小．
3．时间间隔的相对性 (1)经典的时空观：某两个事件，在不同的惯性系中观察， 它们的时间间隔总是_相__同___的． (2)相对论的时空观：某两个事件，在不同的惯性参考系中 观察，它们的时间间隔是_不__同___的． 设 Δτ 表示相对事件发生地静止的惯性系中观测的时间间 隔，Δt 表示相对事件发生地以 v 高速运动的参考系中观察同样
A．飞船正前方地面上的观察者看到这一光速为 1.5c B．飞船正后方地面上的观察者看到这一光速为 0.5c C．在垂直飞船前进方向地面上的观察者看到这一光速是 c D．在地面上任何地方的观察者看到的光速都是 c
解析： 答案： CD
样理解“动尺变短”和“动钟变慢” 1．怎样理解“动尺变短”？ 狭义相对论中的长度公式：l＝l0 1－vc2中，l0 是相对于 杆静止的观察者测出的杆的长度，而 l 可以认为是杆沿自己的长 度方向以速度 v 运动时，静止的观察者测量的长度．还可以认 为是杆不动，而观察者沿杆的长度方向以速度 v 运动时测出的 杆的长度．
《现代科学技术概论》提纲第二章到第四章
现代科学技术概论提纲第二章1.现代物理学包括狭义相对论、广义相对论、量子力学与基本粒子理论。
2.两朵乌云：第一朵是黑体辐射问题；第二朵是关于光速的迈克耳逊-莫雷实验。
3.牛顿力学把绝对空间做匀速直线运动的参照系称为“惯性系”。
4.爱因斯坦采取的态度是：先确定宇宙中相互联系的基本过程——光速，这是一个宇宙常数，然后定义异地时间。
5.时间间隔与空间距离的相对性：两事件的时间间隔相对性、空间距离的相对性。
6.广义相对性原理：惯性系与非惯性系不可区分。
7.等效原理：引力质量与惯性质量无法区分。
8.英国物理学家汤姆逊把广义相对论称作为人类历史上最伟大的成就之一，一方面是由于这个理论的立论基础如此简单与完美，另一方面是因为它引起了人类思想的全面变革。
9.霍金与广义相对论：他被认为当代最重要的广义相对论专家和宇宙论家，被称为在世的最伟大的科学家。
10.霍金代表作《时间简史》11.黑洞面积：随时间增加，面积不变12.相对论的意义（论述）13.如果说迈克耳逊-莫雷实践等引起的光速之谜导致了相对论的提出，那么，关于黑体辐射的“紫外灾难”则导致了量子力学的创建14.所谓“绝对黑体”指的是百分之百吸收照射到其上的物体15.绝对黑体内高于某一频率的无限多的驻波，其能量总和将必然是无限的！这就是著名的“紫外灾难”16.老三论：世界系统结构的科学（解释名词）●信息概念与信息论●“可能性空间”与控制论●整体性与系统论17.申农的“最小努力量原理”——人们总是力图用最小的力量来完成既定事件18.传播信息的通道称为信道。
某一信道1秒内能够通过的信息量（比特）是信道的传播速率，称比特率19.用信息论的观点来分析事物、理解事物和改造事物的方法，称为“信息方法”20.控制论的最基本的思想要素是“可能性空间”。
维纳—“可能性空间”21.负反馈（课本71页图）22.“新三论”又称“自组织理论”23.耗散结构理论—普利高津、哈肯的协同学理论、艾根的超循环理论。
高中物理 第六章 相对论 第4节 相对论的速度变换公式 质能关系课件 教科版选修3-4.ppt
7
活动三 相对论质量 物体的能量和质量之间存在
密切的联系，他们的关系是：
Emc2
这就是著名的爱因斯坦质能方程
8
具体推导过程如下：
Ek EE0 Emc2
E0 m0c2
v 1 c
Ek
m0c2 1 v 2
m0c2
c
1v2 11v2
判天地之美，析万物之理
物理学家费尔德曾指出： 当你领悟一个出色的公式时，你会得到
如同听巴哈的乐曲一样的感受。
1
4
相对论的速度变换公式 质能关系
2
活动一 相对论的速度变换
u
v
车对地的速度为v，人对车的速度为v′
地面上的人看到车上人相对 地面的速度为：
v
u v
1
uv c2
3
v
u v
1
uv c2
c
2c
Ek
m0c2
m0c2
1 2
m0c2
v
2
c
1
1
v
2
2c
1 2
m0v 2
9
Ek
1 2
m0v2
这就是我们过去熟悉的动能表达式，这也能让 我们看出，牛顿力学是相对论力学在低速情况下的 特例．
10
如果车上人运动方向与火车运动方向相反，则v′取负 值
4
活动二 相对论质量
物体的运动速度不能无限增加，那么物体的质量是否随 着速度而变化？
严格的论证表明，物体高速（与光速相比）运动时的质 量与它静止时的质量之间有下面的关系：
m
Hale Waihona Puke m01v2
原子物理学杨福家第四版课后答案
目 录第一章 原子的位形 ............................................................................. - 1 - 第二章 原子的量子态：波尔模型 ..................................................... - 7 - 第三章 量子力学导论 ....................................................................... - 12 - 第四章 原子的精细结构：电子的自旋 ........................................... - 16 - 第五章 多电子原子 ......................................................................... - 23 - 第六章 X 射线 ................................................................................... - 28 -第一章 原子的位形 1-1)解：α粒子与电子碰撞，能量守恒，动量守恒，故有：⎪⎩⎪⎨⎧+'='+=e e v m v M v M v M mv Mv 222212121 ⎪⎪⎩⎪⎪⎨⎧='-='-⇒222e e v M m v v v Mm v ve v m p=∆e p=mv p=mv ∴∆∆，其大小： (1) 222(')(')(')e m v v v v v v v M-≈+-=近似认为：(');'p M v v v v ∆≈-≈22e m v v v M∴⋅∆=有 212e p p Mmv ⋅∆=亦即： (2)(1)2/(2)得22422210e e m v m p Mmv M -∆===p 亦即：()ptg rad pθθ∆≈=-4～101-2) 解：① 22a b ctg Eθπε=228e ；库仑散射因子：a=4)2)(4(420202EZ e E Ze a πεπε==22279()() 1.44()45.545eZ a fmMev fm E Mev πε⨯=== 当901θθ=︒=时，ctg2122.752b a fm ∴== 亦即：1522.7510b m -=⨯② 解：金的原子量为197A =；密度：731.8910/g m ρ=⨯ 依公式，λ射α粒子被散射到θ方向，d Ω立体角的内的几率： nt d a dP 2sin16)(42θθΩ=(1)式中，n 为原子核数密度，()AA m n n N ρ∴=⋅= 即：A V n Aρ=(2)由（1）式得：在90º→180 º范围内找到α粒子得几率为：(θP 18022490a nt 2sin ()164sin 2d a nt πθθπρθθ︒︒=⋅=⎰将所有数据代入得)(θP 5()9.410ρθ-=⨯这就是α粒子被散射到大于90º范围的粒子数占全部粒子数得百分比。
相对论基本公式
相对论基本公式
相对论的基本公式包括：
1. 相对速度公式：△v=v1-v2/√(1-v1v2/c^2)，其中v1和v2是两个物体的速度，△v是它们之间的速度差，c是光速。
2. 相对长度公式：L=Lo √(1-v^2/c^2)，其中Lo是物体静止时的长度，L
是物体的运动时的长度，v是物体速度，c是光速。
这个公式表明，速度越大，物体长度越压缩。
3. 相对质量公式：M=Mo/√(1-v^2/c^2)，其中Mo是物体静止时的质量，M是物体的运动时的质量，v是物体速度，c是光速。
4. 相对时间公式：t=to √(1-v^2/c^2)，其中to是物体静止时的时间流逝
的快慢，t是物体的运动时的时间流逝快慢，v是物体速度，c是光速。
这个公式表明，速度越大，物体时间走得越慢。
当物体以光速运动，物体的时间就不再流逝，从而时间停止。
这些公式都与光速有关，表明光速在相对论中是一个恒定的、不变的速度上限。
这些公式适用于任何惯性参考系，是狭义相对论的基本原理。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
有
0 2 3 R00 = 0 Γ1 + Γ1 Γ 0 Γ1 Γ10 Γ1 Γ1 Γ1 Γ12 Γ1 Γ13 00,1 00 01 00 00 11 00 00
=
e ν
ν ′′ ν′ ν ′ ′ + ( ν ′) 2 r 4
0 3 0 0 3 3 1 2 1 1 1 2 2 R 11 = Γ10,1 + Γ11,1 + Γ12,1 + Γ13,1 Γ11,1 + Γ10 Γ10 + Γ11Γ11 + Γ12 Γ12 + Γ13Γ13
ds 2 = g 00 (dx 0 ) 2 + 2g 0i dx 0 dx i + g ijdx i dx j
g 00 g10 = g 20 g30 g 01 g11 g 21 g31 g 02 g12 g 22 g 32 g 03 g13 对称张量 10个独立分量 g 23 g33
0 Γ12
=
0 Γ21
1 00 = g (g 02,1 + g10, 2 g12,0 ) = 0 2
1 0 0 Γ13 = Γ31 = g 00 (g 03,1 + g10,3 g13,0 ) = 0 2 1 1 1 Γ00 = g11 (g10,0 + g 01,0 g 00,1 ) = e ν ν′ 2 2 1 = Γ1 = 1 g11 (g Γ01 10 11, 0 + g 01,1 g 01,1 ) = 0 2
r r = e sin 2 θ e sin 2 θ + e ν′ sin 2 θ + e u ′ sin 2 θ + e sin 2 θ 2 2 r = sin 2 θe 1 e + (ν′ ′) = R 22 sin 2 θ 2
对真空情形， Tν = 0 故有
ν′′ ν′ ν′ + (′ ν′) = 0 2 r 4 ν′′ ′ ν′ (′ ν′) = 0 2 r 4 r 1 e + (ν′ ′) = 0 2 (1) ( 2) (3)
ds 2 = eν ( r ) dt 2 + e ( r ) dr 2 + r 2 (dθ 2 + sin 2 θ d 2 )
∴
及
g 00 = e ν g11 = e 2 g 22 = r g 33 = r 2 sin 2 θ
g 00 = e ν g11 = e 22 g = r 2 33 g = r 2 sin 2 θ
（1）－（2） ν′ + ′ = 0 + ν = λ = const （1）代入（3）中
1 e ru ′ = 0
(re )′ = 1
re = r + c
e = 1 + c r
令c=-2k 有 又
e
k=const.
2k = 1 , r
λ
ν=λ
∴ e =e
2k = e (1 ) r
1 r 1 1 1 2 2 Γ22 = re , Γ33 = re sin 2 θ, Γ12 = Γ21 = r
1 1 2 2 Γ22 = re , Γ33 = re sin 2 θ, Γ12 = Γ21 =
式中，撇“，”意指对r求导
λ 将以上不为零的 Γν 代入方程：
ρ λ λ λ λ ρ R ν = Γλ,ν Γν,λ + Γλ Γνρ Γν Γλρ
第四章
球对称解
爱因斯坦方程是非线性的偏微分方程：
R ν 1 g ν R = 8πGTν 2
其精确求解非常困难，到目前为止，有物理意义 的精确解只有几个。
史瓦西尔时空（1916年） §4-1 史瓦西尔时空
1.时空度规的球对称结构 取球坐标，（对球对称空间）（ r ,θ , , t ） 使 x 0 = t , x 1 = r , x 2 = θ, x 3 = 则度规可写为
r = e 1 e + (ν′ ′) 2
3 3 1 3 0 1 2 1 2 1 1 1 1 2 R 33 = 0 Γ33 ,1 Γ33, 2 + Γ33 Γ31 + Γ31 Γ33 + Γ32 Γ33 Γ33 Γ10 Γ33 Γ11 Γ33 Γ12
1 2 2 3 Γ33 Γ13 Γ33Γ23
1 1 1 Γ11 = g11 (g11,1 + g11,1 g11,1 ) = u ′ 2 2
1 1 1 Γ12 = Γ21 = g11 (g12,1 + g11, 2 g12,1 ) = 0 2
因此，不为零的联络分量仅有9个
1 1 1 0 0 1 1 Γ01 = Γ10 = ν′, Γ11 = u ′, Γ01 = e ν ν′ 2 2 2
——史瓦西尔解 or
ds 2 = (1 2GM 2 2GM 1 2 )dt + (1 ) dr + r 2 (dθ 2 + sin 2 θd 2 ) r r
3．伯克霍夫（Birkhoff）定理 伯克霍夫（ 定理：所有球对称的真空时空都是静态的。 该定理的意义——不论球对称的引力源如何变化， 其外部时空都是球对称静态时空，即都可用 Schwarzschild度规描述。 4．史瓦西尔坐标的物理意义 ① ∵ g 0i = 0 固有距离为
g ν
又因球对称性，作适当变换，有
ds 2 = e ν ( r ,t ) dt 2 + e ( r ,t ) dr 2 + r 2 (dθ 2 + sin 2 θd 2 )
——球对称度规的一般表达式。 2．史瓦西尔解（1916年，德国数学家，对球对称 真空情形第一个求出爱因斯坦场方程之解） 对 R ν = 0 由于是静态（静止球对称引力源外部）则有
1 0 1 1 1 2 1 3 Γ11Γ10 Γ11Γ11 Γ11Γ12 Γ11Γ13
ν′′ 2 ν′ 2 2 ′ν′ ′ ν′′ ′ ν′ ′ = 2+ + 2 = + (ν ′) 2 r 4 r 4 r 2 r 4
3 3 3 0 3 1 1 2 2 2 1 1 1 1 2 1 R 22 = Γ23, 2 Γ22 ,1 + Γ22 Γ12 + Γ21Γ21 + Γ23 Γ23 Γ22 Γ10 Γ22 Γ11 Γ22 Γ12 Γ22 Γ13
1 00 = g (g 01,1 + g10,0 g11,0 ) = 0 2
1 0 0 Γ02 = Γ20 = g 00 (g 02,0 + g 00, 2 g 02,0 ) = 0 2 1 0 0 Γ03 = Γ30 = g 00 (g 03,0 + g 00,3 g 03,0 ) = 0 2
λ
又∵ g 00 = e ν ， 可令 λ = 0 （相当于作时间尺度变换） 2k ν 则 g 00 = e = (1 ) r 2k 1 g11 = e = (1 ) r
故最后解得球对称真空解（度规）为
ds 2 = (1 2k 2 2k )dt + (1 ) 1 dr 2 + r 2 (dθ 2 + sin 2 θd 2 ) r r
l 2 = (1 2GM 1 2 ) dr + r 2 dθ 2 + r 2 ν 2 θd 2 r②r=2GM,源自ds 2 → ∞ 发散——视界
③ r＜2GM，坐标无意义（非物理的）
其余分量为零，将之代入场方程中便可求解
∵
1 λ Γαβ = g λτ (g τβ,α + g ατ,β g αβ,τ ) 2
2 1 1 0 0 Γ01 = Γ10 = g 00 (g 00,1 + g10,0 g10,0 ) = ν′ 2 2
0 Γ11
0 ∴ 有 Γ00 = 1 g 00 (g 00,0 + g 00,0 g 00,0 ) = 0