2012自控原理试题_A_答案
2012年云南昆明理工大学自动控制原理考研真题A卷
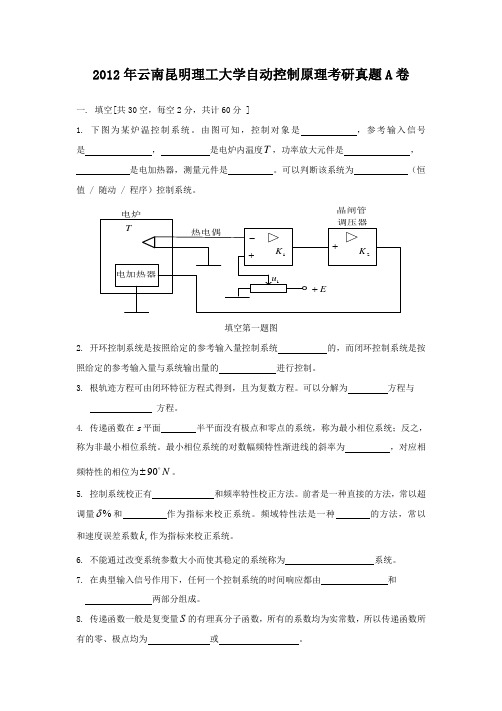
2012年云南昆明理工大学自动控制原理考研真题A 卷一. 填空[共30空,每空2分,共计60分 ]1. 下图为某炉温控制系统。
由图可知,控制对象是 ,参考输入信号是 , 是电炉内温度T ,功率放大元件是 , 是电加热器,测量元件是 。
可以判断该系统为 (恒值 / 随动 / 程序)控制系统。
晶闸管填空第一题图2. 开环控制系统是按照给定的参考输入量控制系统 的,而闭环控制系统是按照给定的参考输入量与系统输出量的 进行控制。
3. 根轨迹方程可由闭环特征方程式得到,且为复数方程。
可以分解为 方程与 方程。
4. 传递函数在s 平面 半平面没有极点和零点的系统,称为最小相位系统;反之,称为非最小相位系统。
最小相位系统的对数幅频特性渐进线的斜率为 ,对应相频特性的相位为N90±。
5. 控制系统校正有 和频率特性校正方法。
前者是一种直接的方法,常以超调量%δ和 作为指标来校正系统。
频域特性法是一种 的方法,常以 和速度误差系数v k 作为指标来校正系统。
6. 不能通过改变系统参数大小而使其稳定的系统称为 系统。
7. 在典型输入信号作用下,任何一个控制系统的时间响应都由 和 两部分组成。
8. 传递函数一般是复变量S 的有理真分子函数,所有的系数均为实常数,所以传递函数所有的零、极点均为 或 。
9. 在进行系统校正时,PI 控制器相当于 ,PD 控制器相当于 , 控制器相当于滞后—超前校正。
10. 线性定常系统具有这样的性质:① 一个输入信号导数的时域响应等于该信号时域响应的 ; ② 一个输入信号积分的时域响应等于该信号时域响应的 。
11. 是开环控制方式与闭环控制方式的某种组合。
当闭环控制系统不能取得满意的稳态性能(精度)和动态性能时,可在闭环控制的基础上,引入按 或按扰动的开环控制通道,形成该控制方式,以提高系统类型或 。
二. 在保持系统闭环传递函数不变的情况下,将下图(a )所示系统框图变换成图(b ),并求)(s H 的表达式。
中南大学10、11、12级自控原理试题A及答案

专业年级: 自动化、电气工程、测控、智能科学、物联网等专业 2011 级
总分 100 分,占总评成绩 70 %
姓名:
班级:
学号:
第一题、是非题(15 分,每题 3 分)
1. 经典控制理论以传递函数为基础,它主要研究 单输入-单输出、线性定常系 统的分析和设计问题;而现代控制理论则以状态空间法为基础,它主要研究 具有高性能、高精度的多变量、变参数系统的最优控制问题。
第四题(15 分)、系统结构如第四题图所示,其中 K > 0 , β ≥ 0 ,
(1)试分析β 值对系统稳定性的影响;(5 分)
(2)在 K 一定且系统阻尼比 0 < ξ < 1的情况下,试分析β 值变化(如增
大)对系统动态性能的影响;在斜坡输入作用下,分析β 值变化(如增大)对
系统稳态性能的影响;(5 分)
(1)对√
(2)错
第1页共7页
第二题(10 分)、某一非线性系统,其线性部分的奈奎斯特曲线 G(jω)和非线 性环节的负倒描述函数曲线 − 1 如第二题图所示,试分析该系统是否存在
N ( A) 周期运动(自激振荡)?若有,试分析周期运动(自激振荡)的稳定性?
自控原理习题全部解答

第九章 现性系统的状态空间分析与综合习题解答9-1 已知电枢控制的直流伺服电机的微分方程组及传递函数 b aaa a a E dtdi L I R U ++= dtd K E mbb θ= a m m i C M =dt d f dtd J M mm m m m θθ+=22 )()([)()(2m b m a a m m a m a ma m C K f R s R J f L s J L s C s U s ++++=Θ (1) 设状态变量mm m x x x θθθ ===321及输出量m y θ=,试建立其动态方程;(2) 设状态变量mm a x x i x θθ ===321,,及 m y θ=,试建立其动态方程 (3) 设,x T x =确立两组状态变量间的变换阵解:(1)由题意可知: ⎪⎪⎩⎪⎪⎨⎧=======123121xy xx x x x m m mmθθθθ ,由已知 ⎪⎪⎩⎪⎪⎨⎧+===++=m m m m ma m m mb ba a a a a f J M i C M K E E i L i R U θθθ可推导出 ⎪⎪⎪⎩⎪⎪⎪⎨⎧=++-+-===12333221x y U J L C x J L C K f R x J L R J L f x x x x xa ma mm a m b m a m a a m a m由上式,可列动态方程如下=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321x x x ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+-+-m a a m m a m a m b m a J L R J f L J L C K f R 0100010⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321x x x +⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡m a m J L C 00a Uy =[]001⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321x x x(2)由题意可知:,1a i x =mm m y x x θθθ===,,32 可推导出⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧==-=-====+--=+--==23133231111x y x J f x J C J f i J C x x x U L x L K x L R U L L K i L R i x m m m m m m m m a m m m m a aa b a a a a m a b a a a aθθθθθ可列动态方程如下[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=321010x x x y由⎪⎩⎪⎨⎧===mm mx x x θθθ 321和⎪⎩⎪⎨⎧===mm a x x i x θθ 321得 aa m m mm a b a aU L x x x J f JC L K L R x x x ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡00101000321321⎪⎪⎪⎩⎪⎪⎪⎨⎧-=-======3133221x J f x J C J f i J C x x x x x m m m m m m m a m m m m m θθθθ由上式可得变换矩阵如下⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-=m m mm J f J C T 010010 9-2设系统微分方程为 u x x x =++23式中 u 为输入量,x 为输出量(1)设取状态变量 xx x x ==21, 试列写动态方程 (2) 设有状态变换2122112,x x x x x x --=+=,试确定变换矩阵及变换后的动态方程 解:(1) 由题意可知⎩⎨⎧+--===u x x x x x x1222123动态方程即为(2) 即⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡21213210x x x xU x x U x x x xx x ⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--⎥⎦⎤⎢⎣⎡--⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡---112001102111211132102111211121121121121 9-3 设系统微分方程为u y y y y 66116=+++式中u ,y 分别为系统输入,输出量。
2012年南京航空航天大学820自动控制原理考研初试真题(A卷)

820 自动控制原理 第 3 页 共 4 页
πA 1.分析周期运动的稳定性; 2.求出稳定周期运动的振幅 A 和频率 ω 以及 c(t) 表达式。
图6
九. (本题 15 分) 某系统的状态空间模型为 x&1(t) = −x1(t) + 5x2 (t) x&2 (t) = −6x1(t) + u(t) y(t) = x1(t)
现采用状态反馈控制策略,即 u(t) = −k1x1(t) − k2x2 (t) + r(t) ,其中 k1,k2 为实常数,
R(s)
Gc(s)
K1 s(Ts + 1)
K 2 C分) 已知采样系统的结构图如图 5 所示,要求:
1.若使系统在 r(t) = t 作用时稳态误差为 0.1,试确定采样周期 T 的值;
2.求系统在上述采样周期下的单位阶跃响应 c* (t) (写出前三项即可)。
提示:Z[
四. (本题 15 分) 某系统的结构图如图 3,若要求输入信号 r(t) = t 时,稳态 误差 ess ≤ 2.25 ,同时系统单位阶跃响应无超调,试确定 K1 的值。
R(s)
1
C(s)
K1
s(s + 3)2
图3
五. (本题 15 分) 某单位负反馈系统的开环传递函数为
G(s)
=
K (0.2s +1)(0.1s +1) s2(s +1)(0.01s +1)
2012届毕业生补考-自控原理

2012届毕业生毕业前补考试卷课程名称《自动控制原理》任课教师签名徐利新出题教师签名徐利新审题教师签名王利恒
考试方式(开)卷适用专业 08智能
考试时间( 120 )分钟
题号一二三四五六七总分
得分
评卷
人
一、计算题(15分)
已知系统的状态结构如图所示,试求系统的传递函数。
二、计算题(20分)
求下列系统的闭环传递函数
三、计算题(20分)
求图示系统的稳态误差。
其中:,
,
四、分析题(20分)
已知单位反馈系统的开环传递函数为,试绘制闭环系统的根轨迹();并确定使系统稳定的值范围。
五、问答题 (25分)
1.什么是开环控制系统?它与闭环控制系统的区别在哪里?
2.日常生活中你见到的控制系统有哪些?说明它们是属于开环控制系统?还是闭环控制系统,并说明理由。
期末《自控》试题及解答

浙江工业大学2010/2011(1)期终考试《自动控制原理》试题课程自动控制原理姓名班级学号第一部分简答题(共5题,每题3分,共15分。
答题必须简明扼要。
)1滞后—超前串联校正改善系统性能的原因。
(1)降低截止频率,(2)中频段提高相位裕度,(3)避免了单独采用超前校正或单独采用滞后校正的不足。
2惯性环节在什么条件下可以近似为比例环节。
在惯性时间常数很小的情况下。
3列举3种非线性系统与线性系统特性的不同之处。
(1)是否满足叠加原理(2)是否有可能产生自激振荡,(3)系统的特性(如稳定性)与初始状态是否有关。
4现实中,真实的系统都具有一定程度的非线性特性和时变特性,但是理论分析和设计经常采用线性时不变模型的原因。
(1)通常系统工作在平衡点附近的小范围内,(2)近似的精度通常满足工程要求,(3)线性系统的分析与设计方法成熟、方便。
(4)对于本质非线性,或者非线性明显的情况,或者要求比较高的情况,必须采用非线性的方法5零阶保持器传递函数1()TsheG ss--=中是否包含积分环节?为什么?不包含积分环节,因为s趋向0时,G(s)并不趋向无穷。
第二部分 填空题(共25分。
)6图示调节器的传递函数()/()o i U s U s 为 。
(图中运放器为理想运算放大器)(4分) 12111120010()(1)(1),,,()o i U s T s T s R KK T R C T R C U s T sR ++==-==其中C o第6题图7零初始条件下,某系统在单位脉冲()t δ作用下的响应为))(()(1211212T t eT T T t T T K t k ---=δ,该系统的输入输出间的传递函数为11)(12++=s T s T Ks G ,该系统输入输出间的微分方程为12()()(()())T y t y t K T u t u t +=+ 。
(每空3分)8 已知单位负反馈系统的开环传递函数为2(1)()()K s G s H s s+=,0,K >在单位阶跃1()t 、单位斜坡t 、单位加速度2t 作用下系统的稳态误差分别为 0 , 0 , 2/K 。
(完整版)自动控制原理试题及答案,推荐文档

自动控制原理:参考答案及评分标准一、单项选择题(每小题1分,共20分)1. 系统和输入已知,求输出并对动态特性进行研究,称为(C)A. 系统综合B.系统辨识C.系统分析D.系统设计2. 惯性环节和积分环节的频率特性在(A )上相等。
A. 幅频特性的斜率B.最小幅值C.相位变化率D.穿越频率3. 通过测量输出量,产生一个与输出信号存在确定函数比例关系值的元件称为(C)A.比较元件B.给定元件C.反馈元件D.放大元件4. 3从0变化到时,延迟环节频率特性极坐标图为(A )A.圆B.半圆C椭圆 D.双曲线5. 当忽略电动机的电枢电感后,以电动机的转速为输出变量,电枢电压为输入变量时,电动机可看作一个(B )A.比例环节B.微分环节C.积分环节D.惯性环节6.若系统的开环传递函数为10s(5s 2)则它的开环增益为(A.1B.2C.5D.107.二阶系统的传递函数G(s)5~2s 2s 5则该系统是(A.临界阻尼系统B.欠阻尼系统8. 若保持二阶系统的Z不变,提咼3n,A.提高上升时间和峰值时间C.提高上升时间和调整时间9. 一阶微分环节G(s) 1 Ts,当频率A. 45 °B.-45°10. 最小相位系统的开环增益越大,其(A.振荡次数越多C. 过阻尼系统D.零阻尼系统则可以(B )B. 减少上升时间和峰值时间D. 减少上升时间和超调量卡时,则相频特性G(j )为(A )C. 90 °D.- 90°D )B. 稳定裕量越大D. 稳态误差越小11设系统的特征方程为D s s4 8s3217s 16s 50,则此系统(A )A.稳定B.临界稳定C.不稳定D.稳定性不确定。
12某单位反馈系统的开环传递函数为: G ss(s 1)(s 5),当k= ( C )时,闭环系统临界稳定。
B.20 C.30 D.4013.设系统的特征方程为Ds 3s310s 5s2s 2 0,则此系统中包含正实部特征的个数有(C )A.0B.1C.2D.316.稳态误差e ss 与误差信号E (s )的函数关系为(B )A.(-3,x )B.(0宀)C.(- x ,-3)D.(-3,0)20.在直流电动机调速系统中,霍尔传感器是用作( B )反馈的传感器。
自控原理习题解答

②R(s)和N(s)同时作用时系统的输出
∴ C(s) = CR (s) + CN (s)
=
G1G2 + G1G3 + G1G2G3H1
R(s) +
1+ G1G3 + G2H1 + G1G2 + G1G2G3H1
+ 1+ G2H1 + G1G2G4 + G1G3G4 + G1G2G3G4H1 N (s) 1+ G1G3 + G2H1 + G1G2 + G1G2G3H1
s(s + 1)
Kts
1.试分析速度反馈系数Kt对系统稳定性的影响。 2.试求KP、Kv、Ka并说明内反馈对稳态误差的影响。 解: 1.如果没有内反馈,系统的开环和闭环传递函数为
解:将系统开环传递函数与二阶系统典型开环传递函
数比较: 所以:
G(s) =
ωn2
s(s + 2ζωn )
ωn = 10K
2ζωn = 10 ζωn = 5
ζ= 5
10K
−πζ
σ = e 1−ζ 2 ×100%
tp
=π ωd
=
ωn
π 1−ζ 2
tS
(5%)
≈
3
ζωn
分别将K=10 ,K=20代入计算,结果如下:
10K1 = 10 1 + 10 K 2
解之得:K2=0.9 K1=10
Ø 3-4 单位反馈系统的开环传递函数为
G(s) = K = 10K s(0.1s + 1) s(s +10)
试分别求出K=10s–1和K=20s–1时,系统的阻尼比ζ 和
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作根轨迹如右图所示。
(2)将分离点 s1 = −21.13 代入幅值条件:
m
∏(s − Z j)
K * j=1 n
= −1
∏(s − Pi )
i =1
∏ ∴ K * = | s − Pi | =| s1 || s1 + 50 || s1 +100 |= K ×100× 50 i =1
求出临界阻尼比相应的开环增益: K = 21.13× 28.87 × 78.87 = 9.62
= =
ωn2 2ξωn
,
得
⎧⎪ ⎨
ωn =
K
⎪⎩ξ = K β / 2
K 一定, β > 0 且 0 < ξ < 1 时,ωn 一定,则β 增大( β ↑ )时:
第3页共7页
① 系统的动态性能: ξ ↑
→
σ
o o
↓ ,平稳性提高;
ξ↑
→ ts
=
3.5 ξωn
=
7 Kβ
↓ ,快速性提高;
② 系统的稳态性能:
G(s)H (s) =
K
,
s(0.01s +1)(0.02s +1)
(1)作系统的根轨迹;(10 分) (2)确定与系统临界阻尼比相对应的开环增益 K。(5 分)
【解】(1)作出系统准确的根轨迹: G(s)H (s) = K ×100×50 ; K * = K ×100× 50
s(s +100)(s + 50)
4 2
可得:①
⎩⎨⎧βK
=4 = 0.707
②
σ
0 0
=
e −ξπ
1−ξ 2
= 4.32 00 , ts
=
3.5 ξωn
= 3.5 = 2.48 (秒) 2
③
在斜坡输入
r(t)
=
2t
作用下系统的稳态误差为:
e ss
= Aβ
=
2β =1.414
第4页共7页
第五题(15 分)、设负反馈系统的开环传递函数为:
K
【解】(1)
Φ(s)
=
C(s) R(s)
=
1+
s2 Kβ
s
+
K s2
=
K
s 2 + Kβ s + K
=
ω
2 n
s2
+
2ξωn s
+
ω
2 n
系统特征方程: s2 + K β s + K = 0
可见,当 β > 0 时,系统稳定;当 β = 0 时,系统临界稳定,也即不稳定。
(2)
由
⎧ ⎨ ⎩
K
K β
(1)对√
(2)错
2. 按反馈控制方式组成的反馈控制系统,具有抑制任何内、外扰动对被控量产 生影响的能力。所有反馈控制系统在任何输入信号作用下的稳态误差都会等 于零。
(1)对
(2)错 √
3. 对于一个线性系统来说,两个输入信号同时加于系统所产生的总输出,等于 这两个输入信号单独作用时分别产生的输出之和;且输入信号的数值增大或 减小若干倍时,系统的输出亦相应地增大或减小同样的倍数。
中南大学考试试卷(A)答案
2011—2012 学年 下 学期 时间 100 分钟 2012 年 6 月 14 日
自动控制理论 课程 64 学时 4 学分 考试形式:闭卷
专业年级: 自动化 10 级 总分 100 分,占总评成绩 70 %
姓名:
班级:
学号:
第一题、是非题(15 分,每题 3 分)
1. 反馈控制是自动控制系统最基本的控制方式。在反馈控制系统中,控制装置 对被控对象施加的控制作用,是取自被控量的反馈信息,用来不断修正被控 量与输入量之间的偏差,从而实现对被控对象进行控制的任务,这就是反馈 控制的原理。
第5页共7页
第六题图
⎜⎛ s +1⎟⎞⎜⎛ s +1⎟⎞
【解】(1)
Gc (s)
=
G(s) Go (s)
=
⎜⎛
⎝3 s
⎠⎝ 10 +1⎟⎞⎜⎛ s
⎠ + 1⎟⎞
⎝ 0.3 ⎠⎝100 ⎠
(2) G ( s ) ==
Hale Waihona Puke 100 ⎜⎛ s + 1 ⎟⎞ ⎝3 ⎠
s ⎜⎛ s + 1 ⎟⎞⎜⎛ s + 1 ⎟⎞ 2
K
方法 1:
系统的开环传函为:
Gk
(s)
=
1
s2 +K
β
s
=
s(s
K +K
β
)
=
1
β
s(
1 Kβ
s +1)
则系统开环放大系数为: KK = 1 β ,系统的型为: v = 1
A
在斜坡输入 r(t) =
At
作用下系统的稳态误差为:
e ss
=
K
= Aβ
K
方法 2:系统的误差传函为: Φe (s) =
E(s) R(s)
第三题(15 分)、试用梅森增益公式求第三题图所示系统信号流图的传递函数 C(s)/R(s)。
G6
−H3
R(s) 1
G1
G2
G3
G4
G5
−H1
1 C(s)
−H2
第三题图
第2页共7页
【 解 】 上 述 信 号 流 图 存 在 两 条 前 向 通 路 : P1 和 P2 ; 三 个 回 路 : −G3H1 、 −G2G3H2、−G3G4H3。
(1)对√
(2)错
第1页共7页
第二题(10 分)、某一非线性系统,其线性部分的奈奎斯特曲线 G(jω)和非线 性环节的负倒描述函数曲线 − 1 如第二题图所示,试分析该系统是否存在
N ( A) 周期运动(自激振荡)?若有,试分析周期运动(自激振荡)的稳定性?
j G(jω)
N10· · 0
−1 N ( A)
=
1+
Kβ s
1+
Kβ s
+
K s2
=
s2 + Kβs s2 + Kβs + K
或: Φe (s)
=
E(s) R(s)
=
1+
1 Gk
(s)
=
s2 s2 +
+ Kβs Kβs+ K
在斜坡输入 r(t) = At 作用下系统的稳态误差为:
ess
=
lim
t→∞
ess
(t
)
=
lim sE(s)
s→0
=
lim
s→0
sΦ
e
(s)
⋅
R(s)
= lim s ⋅ s 2 + Kβs ⋅ A = Aβ s→0 s 2 + Kβs + K s 2
所以:β增大( β ↑ ),ess↑,稳态性能(精度)降低。
(3)要使系统满足条件:ξ = 0.707 ,ωn = 2
则有:
⎧K ⎩⎨Kβ
=
ω
2 n
=
22
= 2ξωn =
= 2
(3)要使系统满足条件: ξ = 0.707 , ωn = 2 ,试确定相应的参数 K 和
β
;求此时系统由单位阶跃输入产生的超调量 σ
0 0
和调节时间
ts , 以 及 由
r(t) = 2t 产生的稳态误差 ess (∞) ;(5 分)
R (s) + E (s)
K
C (s)
_
s(s + Kβ )
第四题图
Δ = 1 + G3 H1 + G2G3 H 2 + G3G4 H 3 P1 = G1G2G3G4G5 , Δ1 = 1 P2 = G6 , Δ 2 = Δ
所以, C(s) R(s)
=
P1Δ1 + P2Δ 2 Δ
= G6
+
G1G2G3G4G5
1 + G3 H1 + G2G3 H 2 + G3G4 H 3
⎝ 0 .3 ⎠⎝ 100 ⎠
, ωc = 10 rad/s
γ = 180° + arctan 10 − 90° − arctan 10 − 2 × arctan 10 = 63.6°
3
0.3
100
第七题(15 分)、某离散系统如第七题图所示,采样周期 T=1s。
第6页共7页
R (s) +
_
T=1s
50 ×100
第六题(15 分)、单位负反馈系统的开环对数幅频特性如第六题图所示,其中 实线表示校正前的 L0 (ω) ,虚线表示校正后的 L(ω) 。(1)写出串联校正装置的 传递函数 Gc (s) ,在图中绘制校正装置的对数幅频特性曲线 Lc (ω) ;(10 分) (2)当校正后系统截止频率ωc = 10 rad / s 时,求相应的相角裕度 γ 。(5 分)
(n+2)T 时刻,依次类推,从而把一个脉冲序列变成一个连续的阶梯信号。
(2)
G(z)
=
(1 −
z−1)Ζ[G0 (s)] s
=
(1 −
z
−1
)Ζ[
1 s2
−
1 s
+
s
1] +1
=
(1 −
z −1 )[ (z
z −1)2
−
z
z+ −1
z
z − e−1
]
=
