高中数学第二章基本初等函数(Ⅰ)2(20190226195708)
高中数学 第二章 基本初等函数(Ⅰ)2.1 指数函数 2.1.1 第2课时 指数幂及运算讲义教案

学习资料第2课时指数幂及运算学习目标核心素养1.理解分数指数幂的含义,掌握根式与分数指数幂的互化.(重点、难点)2.掌握实数指数幂的运算性质,并能对代数式进行化简或求值.(重点)1.通过分数指数幂、运算性质的推导,培养逻辑推理素养.2.借助指数幂的运算性质对代数式化简或求值,提升数学运算素养.1.分数指数幂的意义分数指数幂正分数指数幂规定:a错误!=错误!(a〉0,m,n∈N*,且n〉1)负分数指数幂规定:a错误!=错误!=错误!(a〉0,m,n∈N*,且n>1) 0的分数指数幂0的正分数指数幂等于0,0的负分数指数幂没有意义提示:①若a=0,0的正分数指数幂恒等于0,即错误!=a错误!=0,无研究价值.②若a<0,a错误!=错误!不一定成立,如(-2)错误!=错误!无意义,故为了避免上述情况规定了a>0。
2.有理数指数幂的运算性质,(1)a r a s=a r+s(a>0,r,s∈Q).(2)(a r)s=a rs(a〉0,r,s∈Q).(3)(ab)r=a r b r(a〉0,b>0,r∈Q).3.无理数指数幂一般地,无理数指数幂aα(a〉0,α是无理数)是一个确定的实数.有理数指数幂的运算性质同样适用于无理数指数幂.1.下列运算结果中,正确的是()A.a2a3=a5B.(-a2)3=(-a3)2C.(错误!-1)0=1 D.(-a2)3=a6A[a2a3=a2+3=a5;(-a2)3=-a6≠(-a3)2=a6;(a-1)0=1,若成立,需要满足a≠1,故选A.]2.4错误!等于()A.25 B.错误!C。
错误!D。
错误!B[4错误!=错误!=错误!,故选B。
]3.已知a〉0,则a错误!等于()A.错误!B。
错误!C.错误!D.-错误!B[a错误!=错误!=错误!。
]4.(m错误!)4+(-1)0=________.m2+1[(m错误!)4+(-1)0=m2+1。
高中数学 第二章 基本初等函数(Ⅰ)2.1.1 函数的概念和图象(二)课件 苏教版必修1.pptx

3.若函数y=f(x)的图象经过点(0,1),则函数y=f(x-1)的图象必经过点 __(1_,_1_)__.
12345
26 答案
4.某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了再走余 下的路程,建立坐标系,其中纵轴表示离学校的距离,横轴表示出发后的 时间,则下图中较符合此学生走法的是____④____.(填序号)
6
知识点二 函数图象的初步应用
思考
如图是一个函数f(x)的图象,那么函数f(x)的定义域、值域是 什么?f 12和 f 13谁大?
7 答案
梳理
如果已知函数图象,可以从中知道函数的定义域、值域、上升、下降趋 势、某些特殊点的坐标等性质.
9
题型探究
10
类型一 画函数的图象
例1 画出下列函数的图象.
12 解答
(3)y=x2+x,x∈[-1,1). 解 y=x2+x,x∈[-1,1)的图象是y=x2+x,x∈R的图象上x∈[-1,1) 的一段,其中点(-1,0)在图象上,用实心点表示;点(1,2)不在图象上, 用空心点表示:
解答
反思与感悟
函数图象受对应法则和定义域的双重影响,故画图时要关注定义域, 另外画图时要标明关键点坐标,如最高点、最低点、与x轴、y轴交点, 点的虚实要分清.
5 答案
梳理
将自变量的一个值x0作为横坐标,相应的函数值f(x0)作为纵坐标,就 得到坐标平面上的一个点(x0,f(x0)).当自变量取遍函数定义域A中的 每一个值时,就得到一系列这样的点.所有这些点组成的集合(点集) 为{(x,f(x))|x∈A},即{(x,y)|y=f(x),x∈A},所有这些点组成的图 形就是函数y=f(x)的图象.
值域:[1,10).
高中数学第二章基本初等函数(Ⅰ)2.2对数函数2.2.1第1课时对数练习新人教A版必修1(2021

2018-2019学年高中数学第二章基本初等函数(Ⅰ)2.2 对数函数2.2.1 第1课时对数练习新人教A版必修1编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018-2019学年高中数学第二章基本初等函数(Ⅰ)2.2 对数函数2.2.1 第1课时对数练习新人教A版必修1)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018-2019学年高中数学第二章基本初等函数(Ⅰ)2.2 对数函数2.2.1 第1课时对数练习新人教A版必修1的全部内容。
1 / 31第二章 2.2 2。
2。
1 第1课时对数1.下列指数式与对数式互化不正确的一组是()A.e0=1与ln 1=0 B.log39=2与9错误!=3C.8-错误!=错误!与log8错误!=-错误!D.log77=1与71=7解析:log39=2可化为指数式32=9,9错误!=3可化为对数式log93=错误!.答案:B2.若log a错误!=c,则a,b,c之间满足( )A.b7=a c B.b=a7cC.b=7a c D.b=c7a解析:由已知可得错误!=a c,∴b=a7c.答案:B3.有以下四个结论:①lg(lg 10)=0;②ln(ln e)=0;③若10=lg x,则x=10;④若e =ln x,则x=e2.其中正确的是()A.①③B.②④C.①②D.③④解析:lg(lg 10)=lg 1=0;ln(ln e)=ln 1=0,故①②正确.若10=lg x,则x=1010,③错误;若e=ln x,则x=e e,故④错误.答案:C4.已知4a=2,lg x=a,则x=______。
高中数学第二章基本初等函数(Ⅰ)2.1.1.1根式课件新人教A版必修13

(2)已知 x7=6,则 x=____6____. (3)若4 x-2有意义,则实数 x 的取值范围是__[2_,__+__∞__)__.
[解析] (1)∵(±4)2=16, ∴16 的平方根为±4.-27 的 5 次方根为5 -27. (2)∵x7=6,∴x=7 6. (3)要使4 x-2有意义, 则需 x-2≥0,即 x≥2. 因此实数 x 的取值范围是[2,+∞).
5.已知 a<b<0,n>1,n∈N*,化简n a-bn+n a+bn.
解:∵a<b<0,∴a-b<0,a+b<0. 当 n 是奇数时,原式=(a-b)+(a+b)=2a; 当 n 是偶数时,原式=|a-b|+|a+b| =(b-a)+(-a-b)=-2a. ∴n a-bn+n a+bn=2-a, 2an,为n奇 为数 偶, 数.
知识点一 a 的 n 次方根和根式
1.a 的 n 次方根 (1)定义:如果 xn=a n>1,且 n∈N*. (2)表示:
[填一填] ,那么 x 叫做 a 的 n 次方根,其中
2.根式 式子 n a 是 a.
叫做根式,其中根指数是 n ,被开方数
[答一答] 1.3 8是根式吗?根式一定是无理式吗?
(2)原式=-8+|3-π|=-8+π-3=π-11.
(3)原式=(a-b)+|b-a|=a-b+b-a=0.
[变式训练 2] (1)化简3 a3+4 1-a4的结果是( C )
A.1
B.2a-1
C.1 或 2a-1 D.0
解析:3 a3+4 1-a4=a+|1-a|
=12, a-1,
a≤1, a>1.来自n (2)an是实数
最新人教版高中数学必修1第二章“基本初等函数(Ⅰ)”本章概述

《基本初等函数(Ⅰ)》本章概述本章主要内容本章共有三大节:2.1指数函数,2.2对数函数,2.3幂函数.(1)为学习指数函数,首先要将指数的取值范围扩充到实数.由于在初中学习了数的开平方、开立方以及二次根式的概念,又学习了整数指数幂的概念以及整数指数幂的运算法则.有了这些知识作准备,通过实际问题引入分数指数幂,说明了扩张指数范围的必要性,为此先将平方根与立方根的概念扩充到n次方根,将二次根式的概念扩充到一般根式的概念,然后进一步介绍了分数指数幂及其运算性质,最后结合一个实例,通过有理指数幂逼近无理指数幂的方法介绍了无理指数幂的意义,从而将指数的取值范围扩充到了实数.在此基础上再学习指数函数及其图象和性质.(2)为学习对数函数,首先学习对数和对数的运算法则、换底公式,然后再学习对数函数及其图象和性质.(3)为学习幂函数,首先以简单的幂函数为主要例子,通过图象分析了幂函数的性质.本章地位作用本章是在上一章学习函数及其性质的基础上,具体研究指数函数、对数函数、幂函数这三个高中阶段重要的函数.这是高中函数学习的第二个阶段,目的是使学生在这一阶段获得较为系统的函数知识,并逐步培养函数应用意识,为今后函数的应用这一章的学习打下坚实的基础,同时使学生对函数的认识由感性上升到理性.可以说这一章起到了承上启下的重要作用,本章所涉及的一些重要思想方法,如推广的思想,逼近的思想,数形结合的思想等,对学生掌握基础的数学语言,学好高中数学起到重要的作用.本章重点难点本章的重点是指数函数和对数函数的性质;难点是无理指数幂的含义以及指数和对数的关系.指数函数是高中新引进的第一个基本初等函数,因此,教科书先给出了指数函数的实际背景,然后对指数函数概念的建立、指数函数图象的绘制、指数函数的基本性质的发现与指数函数的初步应用,作了完整的介绍.指数函数是本章的重点内容之一.对数函数同指数函数一样,是以对数概念和运算法则作为基础展开的.对数函数的研究过程也同指数函数的研究过程一样,目的是让学生对建立和研究一个具体函数的方法有较完整的认识.对数函数是本章的另一个重点内容.无理指数幂是通过有理指数幂无限逼近无理指数幂的方法引入的,体现了无限逼近的思想,在理解时有可能会有难度.教材强调“对数源于指数”,以及指数运算与对数运算的互逆关系.在学习了指数函数与对数函数后,以两个底数相同的指数函数与对数函数介绍了反函数.这也可能是教学上的难点.本章知识结构本章教学建议(1)充分挖掘结合学生生活实际的素材,创设丰富的现实情境,重视学生直观感知的作用,加强数学与现实的联系,让学生体会数学的广泛应用.为了让学生在学习之初就感受到所要学习的函数的实际背景,可以先给出实际例子,让学生体会其中的函数模型的同时,激发学生探究的兴趣与欲望,为新知识的学习作了铺垫.(2)注意运用类比的方法,注重将新知识与旧知识进行联系与类比.新旧知识的联系与类比有利于学生建立新的知识体系,同时也能在一定程度上培养学生的合情推理能力.比如通过复习回顾初中所学整数幂运算,用类比的方法来完成实数指数幂的学习;在学习了指数函数后,运用类比的方法来学习对数函数.(3)要注意发挥信息技术的力量,尽量利用计算器或计算机等创设教学情境,为学生的数学探究与数学思维提供支持.如在无理指数幂的学习中,用计算器或计算机来帮助学生体会“用有理数逼近无理数”的思想;在研究函数图象和性质时,借助图形计算器或计算机来研究函数的性质.(4)要注意渗透一些数学思想方法.如推广的思想(指数幂运算律的推广),逼近的思想(有理指数幂逼近无理指数幂),数形结合的思想(通过函数的图象探究函数的性质)等.(5)鼓励学生的自主探索和合作交流.在函数概念引入及其图象、性质及其应用等学习过程中,教师应引导学生主动地观察、操作、交流、归纳等探索活动,应给予学生足够的活动时间和空间,而不要以教师的讲解代替学生的探索.。
高中数学第二章基本初等函数(Ⅰ)2.1指数函数2.1.1指数与指数幂的运算(3)教案数学教案
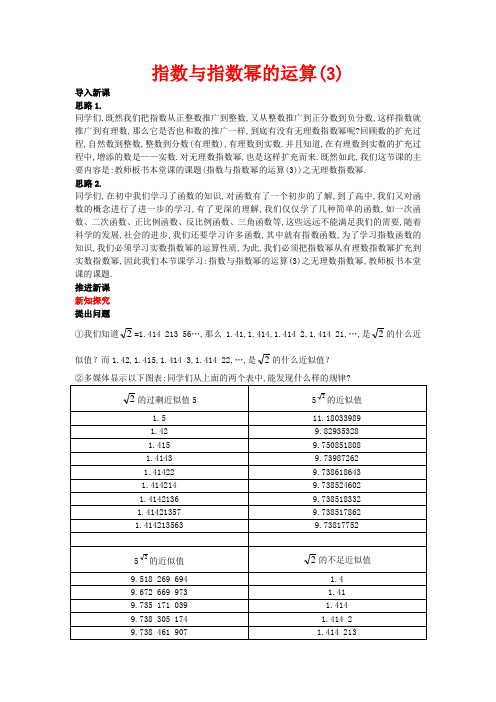
指数与指数幂的运算(3)导入新课思路1.同学们,既然我们把指数从正整数推广到整数,又从整数推广到正分数到负分数,这样指数就推广到有理数,那么它是否也和数的推广一样,到底有没有无理数指数幂呢?回顾数的扩充过程,自然数到整数,整数到分数(有理数),有理数到实数.并且知道,在有理数到实数的扩充过程中,增添的数是——实数.对无理数指数幂,也是这样扩充而来.既然如此,我们这节课的主要内容是:教师板书本堂课的课题(指数与指数幂的运算(3))之无理数指数幂.思路2.同学们,在初中我们学习了函数的知识,对函数有了一个初步的了解,到了高中,我们又对函数的概念进行了进一步的学习,有了更深的理解,我们仅仅学了几种简单的函数,如一次函数、二次函数、正比例函数、反比例函数、三角函数等,这些远远不能满足我们的需要,随着科学的发展,社会的进步,我们还要学习许多函数,其中就有指数函数,为了学习指数函数的知识,我们必须学习实数指数幂的运算性质,为此,我们必须把指数幂从有理数指数幂扩充到实数指数幂,因此我们本节课学习:指数与指数幂的运算(3)之无理数指数幂,教师板书本堂课的课题.推进新课新知探究提出问题①我们知道2=1.414 213 56…,那么1.41,1.414,1.414 2,1.414 21,…,是2的什么近似值?而1.42,1.415,1.414 3,1.414 22,…,是2的什么近似值?③你能给上述思想起个名字吗?④一个正数的无理数次幂到底是一个什么性质的数呢?如52,根据你学过的知识,能作出判断并合理地解释吗?⑤借助上面的结论你能说出一般性的结论吗?活动:教师引导,学生回忆,教师提问,学生回答,积极交流,及时评价学生,学生有困惑时加以解释,可用多媒体显示辅助内容:问题①从近似值的分类来考虑,一方面从大于2的方向,另一方面从小于2的方向.问题②对图表的观察一方面从上往下看,再一方面从左向右看,注意其关联.问题③上述方法实际上是无限接近,最后是逼近.问题④对问题给予大胆猜测,从数轴的观点加以解释.问题⑤在③④的基础上,推广到一般的情形,即由特殊到一般.讨论结果:①1.41,1.414,1.414 2,1.414 21,…这些数都小于2,称2的不足近似值,而1.42,1.415,1.414 3,1.414 22,…,这些数都大于2,称2的过剩近似值.②第一个表:从大于2的方向逼近2时,52就从51.5,51.42,51.415,51.4143,51.41422,…,即大于52的方向逼近52.第二个表:从小于2的方向逼近2时,52就从51.4,51.41,51.414,51.414 2,51.414 21,…,即小于52的方向逼近52.从另一角度来看这个问题,在数轴上近似地表示这些点,数轴上的数字表明一方面52从51.4,51.41,51.414,51.414 2,51.414 21,…,即小于52的方向接近52,而另一方面52从51.5,51.42,51.415,51.4143,51.41422,…,即大于52的方向接近52,可以说从两个方向无限地接近52,即逼近52,所以52是一串有理数指数幂51.4,51.41,51.414,51.414 2,51.414 21,…,和另一串有理数指数幂51.5,51.42,51.415,51.4143,51.41422,…,按上述变化规律变化的结果,事实上表示这些数的点从两个方向向表示52的点靠近,但这个点一定在数轴上,由此我们可得到的结论是52一定是一个实数,即51.4<51.41<51.414<51.414 2<51.41421<…<52<…<51.41422<51.4143<51.415<51.42<51.5.充分表明52是一个实数.③逼近思想,事实上里面含有极限的思想,这是以后要学的知识. ④根据②③我们可以推断52是一个实数,猜测一个正数的无理数次幂是一个实数.⑤无理数指数幂的意义:一般地,无理数指数幂a α(a>0,α是无理数)是一个确定的实数.也就是说无理数可以作为指数,并且它的结果是一个实数,这样指数概念又一次得到推广,在数的扩充过程中,我们知道有理数和无理数统称为实数.我们规定了无理数指数幂的意义,知道它是一个确定的实数,结合前面的有理数指数幂,那么,指数幂就从有理数指数幂扩充到实数指数幂. 提出问题(1)为什么在规定无理数指数幂的意义时,必须规定底数是正数?(2)无理数指数幂的运算法则是怎样的?是否与有理数指数幂的运算法则相通呢? (3)你能给出实数指数幂的运算法则吗?活动:教师组织学生互助合作,交流探讨,引导他们用反例说明问题,注意类比,归纳. 对问题(1)回顾我们学习分数指数幂的意义时对底数的规定,举例说明.对问题(2)结合有理数指数幂的运算法则,既然无理数指数幂a α(a>0,α是无理数)是一个确定的实数,那么无理数指数幂的运算法则应当与有理数指数幂的运算法则类似,并且相通. 对问题(3)有了有理数指数幂的运算法则和无理数指数幂的运算法则,实数的运算法则自然就得到了.讨论结果:(1)底数大于零的必要性,若a=-1,那么a α是+1还是-1就无法确定了,这样就造成混乱,规定了底数是正数后,无理数指数幂a α是一个确定的实数,就不会再造成混乱. (2)因为无理数指数幂是一个确定的实数,所以能进行指数的运算,也能进行幂的运算,有理数指数幂的运算性质,同样也适用于无理数指数幂.类比有理数指数幂的运算性质可以得到无理数指数幂的运算法则: ①a r ·a s =a r+s(a>0,r,s 都是无理数).②(a r )s =a rs(a>0,r,s 都是无理数).③(a·b)r =a r b r(a>0,b>0,r 是无理数).(3)指数幂扩充到实数后,指数幂的运算性质也就推广到了实数指数幂. 实数指数幂的运算性质:对任意的实数r,s,均有下面的运算性质: ①a r ·a s =a r+s(a>0,r,s∈R ).②(a r )s =a rs(a>0,r,s∈R ).③(a·b)r =a r b r(a>0,b>0,r∈R ). 应用示例思路1例1利用函数计算器计算.(精确到0.001) (1)0.32.1;(2)3.14-3;(3)3.143;(4)33.活动:教师教会学生利用函数计算器计算,熟悉计算器的各键的功能,正确输入各类数,算出数值,对于(1),可先按底数0.3,再按键,再按幂指数2.1,最后按,即可求得它的值; 对于(2),先按底数3.14,再按键,再按负号键,再按3,最后按即可;对于(3),先按底数3.1,再按键,再按34,最后按即可;对于(4),这种无理指数幂,可先按底数3,其次按键,再按键,再按3,最后按键.有时也可按或键,使用键上面的功能去运算.学生可以相互交流,挖掘计算器的用途.答案:(1)0.32.1≈0.080;(2)3.14-3≈0.032; (3)3.143≈2.336;(4)33≈6.705.点评:熟练掌握用计算器计算幂的值的方法与步骤,感受现代技术的威力,逐步把自己融入现代信息社会;用四舍五入法求近似值,若保留小数点后n 位,只需看第(n+1)位能否进位即可.例2求值或化简. (1)3224ab ba -(a>0,b>0); (2)(41)21-213321)()1.0()4(---b a ab (a>0,b>0);(3)246347625---+-.活动:学生观察,思考,所谓化简,即若能化为常数则化为常数,若不能化为常数则应使所化式子达到最简,对既有分数指数幂又有根式的式子,应该把根式统一化为分数指数幂的形式,便于运算,教师有针对性地提示引导,对(1)由里向外把根式化成分数指数幂,要紧扣分数指数幂的意义和运算性质,对(2)既有分数指数幂又有根式,应当统一起来,化为分数指数幂,对(3)有多重根号的式子,应先去根号,这里是二次根式,被开方数应凑完全平方,这样,把5,7,6拆成(3)2+(2)2,22+(3)2,22+(2)2,并对学生作及时的评价,注意总结解题的方法和规律.解:(1)3224ab ba -=2224b a -(a 31b 32)21=a -2ba 61b 31=a611-b 34=61134ab .点评:根式的运算常常化成幂的运算进行,计算结果如没有特殊要求,就用根式的形式来表示.(2)(41)21-2133231)()1.0()4(---b a ab =223211044•a 23a 23-b 23-b 23=254a 0b 0=254.点评:化简这类式子一般有两种办法,一是首先用负指数幂的定义把负指数化成正指数,另一个方法是采用分式的基本性质把负指数化成正指数.(3) 246347625---+- =222)22()32()23(---+- =3-2+2-3-2+2=0.点评:考虑根号里面的数是一个完全平方数,千万注意方根的性质的运用.例3已知x=21(5n 1-5n 1-),n∈N *,求(x+2x 1+)n 的值.活动:学生思考,观察题目的特点,从整体上看,应先化简,然后再求值,要有预见性,5n1与5n1-具有对称性,它们的积是常数1,为我们解题提供了思路,教师引导学生考虑问题的思路,必要时给予提示.x 2=41(5n 1-5n 1-)2=41(5n 2-2·50+5n 2-)=41(5n 2+2+5n 2--4) =41(5n 1+5n 1-)2-1. 这时应看到1+x 2=1+41(n 1-5n 1-)2=41(5n 1+5n 1-)2,这样先算出1+x 2,再算出2x 1+,带入即可.解:将x=21(5n 1-5n 1-)代入1+x 2,得1+x 2=1+41(5n 1-5n 1-)2=41(5n 1+5n 1-)n ,所以(x+2x 1+)n=[21(5n 1-5n 1-)+211)55(41n n-+]n=[21(5n 1-5n 1-)+21(5n 1+5n 1-)]n =(5n 1)n=5.点评:运用整体思想和完全平方公式是解决本题的关键,要深刻理解这种做法.思路2 例1计算:(1)105432)(0625.0833416--+++π;(2)12532+(21)-2+34331-(271)31-;(3)(-2x 41y31-)(3x 21y 32);(4)(x 21-y 21)÷(x 41-y 41).活动:学生观察、思考,根式化成分数指数,利用幂的运算性质解题,另外要注意整体的意识,教师有针对性的提示引导,对(1)根式的运算常常化成幂的运算进行,对(2)充分利用指数幂的运算法则来进行,对(3)则要根据单项式乘法和幂的运算法则进行,对(4)要利用平方差公式先因式分解,并对学生作及时的评价. 解:(1)105432)(0625.0833416--+++π =(425)21+(827)31+(0.062 5)41+1-21=(25)2×21+(23)313⨯+(0.5)414⨯+21 =25+23+0.5+21 =5;(2)12532+(21)-2+34331-(271)31-=(53)32+(2-1)-2+(73)31-(3-3)31-=5323⨯+2-2×(-1)+7313⨯-3)31(3-⨯-=25+4+7-3=33; (3)(-2x 41y 31-)(3x 21y 32)=(-2×3)(x 41x 21·y31-y 32)=323121416+-+•-yx=-6x 43y 31=3436y x-;(4)(x 21-y 21)÷(x 41-y 41)=((x 41)2-(y 41)2)÷(x 41-y 41) =(x 41+y 41)(x 41-y 41)÷(x 41-y 41) =x 41+y 41.点评:在指数运算中,一定要注意运算顺序和灵活运用乘法公式.例2化简下列各式: (1)323222323222--------+--++yxy x yxy x ;(2)(a 3+a -3)(a 3-a -3)÷[(a 4+a -4+1)(a-a -1)].活动:学生观察式子的特点,特别是指数的特点,教师引导学生考虑题目的思路,这两题要注意分解因式,特别是立方和和立方差公式的应用,对有困难的学生及时提示:对(1)考查x 2与x 32的关系可知x 2=(x 32)3,立方关系就出来了,公式便可运用,对(2)先利用平方差,再利用幂的乘方转化为立方差,再分解因式,组织学生讨论交流. 解:(1)原式=323222323222--------+--++yxy x yxy x=])())(()[()()(23232322322323232232--------++-+-yyx x yy x x=343234343234)()(---------+-yxy xy xy x=xyxy xy 3322)(2-=--; (2)原式=[(a 3)2-(a -3)2]÷[(a 4+a -4+1)(a-a -1)]=))(1()()(1442222----++-a a a a a a =))(1()1)((1444422-----++++-a a a a a a a a =1212)(----a a a a =a+a -1.点评:注意立方和立方差公式在分数指数幂当中的应用,因为二项和、差公式,平方差公式一般在使用中一目了然,而对立方和立方差公式却一般不易观察到,a 23=(a 21)3还容易看出,对其中夹杂的数字m 可以化为m·a 21a 21-=m,需认真对待,要在做题中不断地提高灵活运用这些公式的能力.知能训练课本P 59习题2.1A 组 3.利用投影仪投射下列补充练习: 1.化简:(1+2321-)(1+2161-)(1+281-)(1+241-)(1+221-)的结果是( )A.21(1-2321-)-1B.(1-2321-)-1C.1-2321- D.21(1-2321-) 分析:根据本题的特点,注意到它的整体性,特别是指数的规律性,我们可以进行适当的变形. 因为(1+2321-)(1-2321-)=1-2161-,所以原式的分子分母同乘以(1-2321-),依次类推,所以321212121)21)(21(----+-=32112121----=21(1-2321-)-1. 答案:A2.计算(297)0.5+0.1-2+(22710)32--3π0+9-0.5+490.5×2-4.解:原式=(925)21+100+(6427)32-3+4921×161=53+100+169-3+31+167=100.3.计算1212--+-+a a a a (a≥1). 解:原式=|11|11)11()11(22--++-=--++-a a a a (a≥1).本题可以继续向下做,去掉绝对值,作为思考留作课下练习.4.设a>0,x=21(a n 1-a n 1-),则(x+2x 1+)n 的值为_______.分析:从整体上看,应先化简,然后再求值,这时应看到解:1+x 2=1+41(a n 1-a n 1-)2=41(a n 1+a n 1-)2.这样先算出1+x 2,再算出2x 1+,将x=21(a n 1-a n 1-)代入1+x 2,得1+x 2=1+41(a n 1-a n 1-)2=41(a n 1+a n 1-)2.所以(x+2x 1+)n=[21(a n 1-a n 1-)+41(a n 1+a n 1-)2]n=[21(a n 1-a n 1-)+21(a n 1+a n 1-)]n=a.答案:a 拓展提升参照我们说明无理数指数幂的意义的过程,请你说明无理数指数幂32的意义.活动:教师引导学生回顾无理数指数幂52的意义的过程,利用计算器计算出3的近似值,取它的过剩近似值和不足近似值,根据这些近似值计算32的过剩近似值和不足近似值,利用逼近思想,“逼出”32的意义,学生合作交流,在投影仪上展示自己的探究结果.我们把用2作底数,3的不足近似值作指数的各个幂排成从小到大的一列数 21.7,21.72,21.731,21.7319,…,同样把用2作底数, 3的过剩近似值作指数的各个幂排成从大到小的一列数: 21.8,21.74,21.733,21.7321,…,不难看出3的过剩近似值和不足近似值相同的位数越多,即3的近似值精确度越高,以其过剩近似值和不足近似值为指数的幂2α会越来越趋近于同一个数,我们把这个数记为32. 即21.7<21.73<21.731<21.7319<…<32<…<21.7321<21.733<21.74<21.8.也就是说32是一个实数,32=3.321 997 …也可以这样解释:当3的过剩近似值从大于3的方向逼近3时,32的近似值从大于32的方向逼近32; 当3的不足近似值从小于3的方向逼近3时,32的近似值从小于32的方向逼近32.所以32就是一串有理指数幂21.7,21.73,21.731,21.7319,…,和另一串有理指数幂21.8,21.74,21.733,21.7321,…,按上述规律变化的结果,即32≈3.321 997.课堂小结(1)无理指数幂的意义.一般地,无理数指数幂a α(a>0,α是无理数)是一个确定的实数. (2)实数指数幂的运算性质:对任意的实数r,s,均有下面的运算性质: ①a r ·a s =a r+s(a>0,r,s∈R ).②(a r )s =a rs(a>0,r,s∈R ).③(a·b)r =a r b r(a>0,b>0,r∈R ).(3)逼近的思想,体会无限接近的含义. 作业课本P 60习题2.1 B 组 2.设计感想无理数指数是指数概念的又一次扩充,教学中要让学生通过多媒体的演示,理解无理数指数幂的意义,教学中也可以让学生自己通过实际情况去探索,自己得出结论,加深对概念的理解,本堂课内容较为抽象,又不能进行推理,只能通过多媒体的教学手段,让学生体会,特别是逼近的思想、类比的思想,多作练习,提高学生理解问题、分析问题的能力.。
高中数学第二章基本初等函数(Ⅰ)2.1.1.1根式课件新人教A版必修1

【解析】 (2a 1) 2 =|2a-1|, 3 (1 2a)3 =1-2a.
因为|2a-1|=1-2a,故2a-1≤0,所以a≤ 1 .
2
【延伸探究】
1.若将条件“ (2a 1) 2 3 (1 2a)3 ”换为“ (2a 1) 2 =
的运算结果是±2;③当n为大于1的奇数时, n a 对任意
a∈R都有意义;④当n为大于1的偶数时, n a 只有当a≥0 时才有意义.其中正确的是 ( )
A.①③④
B.ห้องสมุดไป่ตู้③④
C.②③
D.③④
(2)已知64的平方根为a,a的立方根为b,求a+b的值.
【解题指南】(1)由根式的概念及运算性质对每一说法
2.如果xn=a,则x叫做a的什么?如何表示?
提示:若xn=a,则x叫做a的n次方根,若n为奇数,则x= n a ; 若n为偶数,则x=〒 n a (a≥0).
结论: 1.n次方根的定义及表示
xn=a 那么x叫做a的n次方根,其中n>1,且 (1)定义:如果____,
n∈N*.
x n (2)表示:x =a⇔ n x a (n为奇数). n a (n为偶数且a 0),
【预习自测】
1.若x5=2017,则x等于 ( A. 5 2017 B.- 5 2017 )
C.± 5 2017
D. 20175
【解析】选A.由根式的定义知由x5=2017,得x= 5 2017 .
2.若m是实数,则下列式子中可能没有意义的是
A. 4 m 2 B. 3 m C. 6 m
(
)
D. 5 m
作出判断. (2)先由平方根的定义求出a的值,再由立方根的定义求
高中数学第二章基本初等函数(Ⅰ)2.2对数函数2.2.2第1课时对数函数的图象及性质练习新人教A版

2018-2019学年高中数学第二章基本初等函数(Ⅰ)2.2 对数函数2.2.2 第1课时对数函数的图象及性质练习新人教A版必修1编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018-2019学年高中数学第二章基本初等函数(Ⅰ)2.2 对数函数2.2.2 第1课时对数函数的图象及性质练习新人教A版必修1)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018-2019学年高中数学第二章基本初等函数(Ⅰ)2.2 对数函数2.2.2 第1课时对数函数的图象及性质练习新人教A版必修1的全部内容。
1 / 31第二章2。
2 2。
2.2 第1课时对数函数的图象及性质1.函数f(x)=ln(x2+1)的图象大致是()解析:f(-x)=ln((-x)2+1)=ln(x2+1)=f(x),所以f(x)的图象关于y轴对称.又x∈(0,+∞)时,f(x)是增函数,且过点(0,0),所以A图符合,选A.答案:A2.函数f(x)=log2(3x+1)的值域为()A.(0,+∞)B.[0,+∞)C.(1,+∞)D.[1,+∞)解析:∵3x+1>1,∴log2(3x+1)〉0。
答案:A3.函数f(x)=错误!的定义域为()A.错误!B.(2,+∞)C.错误!∪(2,+∞)D.错误!∪[2,+∞)解析:根据题意得,错误!解得错误!故选C。
答案:C4.已知函数f(x)=log5x,则f(3)+f错误!=______.解析:f(3)+f错误!=log53+log5错误!=log525=2.答案:25.函数y=log a(2x-3)+1的图象恒过定点P,则点P的坐标是____________.解析:当2x-3=1,即x=2时,对任意的a>0,且a≠1都有y=log a1+1=0+1=1,所以函数图象y=log a(2x-3)+1恒过定点(2,1),故点P的坐标是(2,1).答案:(2,1)6.函数f(x)=(a2-a+1)log(a+1)x是对数函数,求实数a的值及f(x)的解析式.2 / 32解:a2-a+1=1,解得a=0,1.又a+1>0,且a+1≠1,∴a=1。
