Spinor Gravity

合集下载

回形针浮在水面上的英语作文

回形针浮在水面上的英语作文Paper clips are one of the most ubiquitous and versatile office supplies in the world Today these small metal fasteners serve a multitude of purposes beyond their original function of holding papers together They have become an integral part of our daily lives and have even found their way into popular culture and art However one of the most intriguing and captivating properties of the paper clip is its ability to float on water This simple yet mesmerizing phenomenon has fascinated people for generations and has inspired countless experiments and explorationsThe ability of a paper clip to float on water is a testament to the principles of surface tension and buoyancy At its core the floating of a paper clip is a result of the cohesive forces between the water molecules on the surface of the liquid This cohesion creates a thin yet strong film that can support the weight of a lightweight object like a paper clip As the paper clip is gently placed on the water surface the surface tension of the water supports the weight of the clip preventing it from sinking The shape and orientation of the paper clip also play a crucial role in its ability to float Some paperclips with a more curved or rounded shape tend to float more easily as they distribute their weight more evenly across the water surfaceInterestingly the floating of a paper clip is not limited to just water but can also be observed in other liquids with high surface tension such as mercury or even some oils However the specific behavior of the paper clip may vary depending on the properties of the liquid For example in mercury the paper clip may float at a different angle or exhibit different movements compared to when floating on waterThe phenomenon of a paper clip floating on water has long captured the imagination of scientists and curious minds alike Countless experiments have been conducted to better understand the underlying principles and to explore the limits of this captivating behavior One common experiment involves carefully placing the paper clip on the water surface and observing its behavior over time Researchers have found that the paper clip can remain afloat for extended periods often hours or even days depending on the environmental conditions and the care with which the experiment is conductedSome researchers have also explored the factors that can influence the floating ability of a paper clip For instance the surface tension of the water can be altered by adding various substances such as detergents or salts which can disrupt the cohesive forces and causethe paper clip to sink Similarly the temperature of the water can also affect the surface tension and the buoyancy of the paper clip with colder water generally allowing the paper clip to float more easilyBeyond the scientific exploration the floating paper clip has also found its way into the realm of art and popular culture Artists have long been fascinated by the elegant and graceful movements of the paper clip as it dances on the water surface and have incorporated this imagery into their works Some have even created kinetic sculptures that mimic the floating behavior of the paper clip using various mechanisms and materialsIn the world of popular culture the floating paper clip has also become a symbol of ingenuity and resourcefulness In some instances the paper clip has been used as a makeshift tool for various purposes such as picking locks or repairing broken electronics The ability of the paper clip to float on water has also been referenced in various media such as films television shows and even in the design of everyday objectsDespite its seemingly simple nature the floating paper clip continues to captivate and inspire people around the world Its ability to defy gravity and seemingly defy the laws of physics has made it a symbol of wonder and curiosity for generations Whether it is being studied in a laboratory or serving as a source of inspiration for artists thefloating paper clip remains a testament to the incredible complexity and beauty of the natural world。

LOCTITE 5452 商品说明书

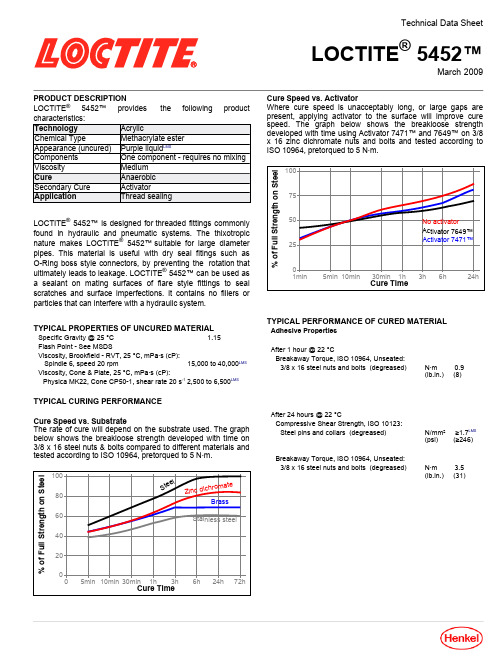
Technical Data SheetLOCTITE®5452™March2009 PRODUCT DESCRIPTIONLOCTITE®5452™provides the following productLOCTITE®5452™is designed for threaded fittings commonlyfound in hydraulic and pneumatic systems.The thixotropicnature makes LOCTITE®5452™ suitable for large diameterpipes.This material is useful with dry seal fitings such asO-Ring boss style connectors,by preventing the rotation thatultimately leads to leakage.LOCTITE®5452™can be used asa sealant on mating surfaces of flare style fittings to sealscratches and surface imperfections.It contains no fillers orparticles that can interfere with a hydraulic system.TYPICAL PROPERTIES OF UNCURED MATERIALSpecific Gravity@ 25°C 1.15Flash Point-See MSDSViscosity,Brookfield -RVT, 25°C,mPa·s(cP):Spindle6,speed20rpm15,000 to40,000LMSViscosity,Cone&Plate,25°C,mPa·s(cP):Physica MK22,Cone CP50-1,shear rate20s-12,500 to6,500LMSTYPICAL CURING PERFORMANCECure Speed vs.SubstrateThe rate of cure will depend on the substrate used. The graphbelow shows the breakloose strength developed with time on3/8x16steel nuts&bolts compared to different materials andtested according to ISO10964,pretorqued to5N·m.%ofFullStrengthonSteelCure Time1008060402005min10min30min1h3h6h24h72hS t ee lBrassZ i n c d i ch r o m a t eSta inle ss s teelCure Speed vs.ActivatorWhere cure speed is unacceptably long,or large gaps arepresent,applying activator to the surface will improve curespeed.The graph below shows the breakloose strengthdeveloped with time using Activator 7471™and7649™on3/8x16zinc dichromate nuts and bolts and tested according toISO10964,pretorqued to5N·m.%ofFullStrengthonSteelCure Time1007550251min5min10min30min1h3h6h24hActivator 7471™Activator 7649™No activatorTYPICAL PERFORMANCE OF CURED MATERIALAdhesive PropertiesAfter 1 hour @22°CBreakaway Torque,ISO10964,Unseated:3/8x 16steel nuts and bolts (degreased)N·m 0.9(lb.in.) (8)After 24 hours @22°CCompressive Shear Strength, ISO10123:Steel pins and collars (degreased) N/mm² ≥1.7LMS(psi) (≥246)Breakaway Torque,ISO10964,Unseated:3/8x 16steel nuts and bolts (degreased)N·m 3.5(lb.in.) (31)TYPICAL ENVIRONMENTAL RESISTANCECured for 1 week @22°CBreakloose Torque,ISO 10964,Pre-torqued to 5N·m:3/8x 16zinc phosphate nuts and boltsHeat AgingAged at temperature indicated and tested @22°C% I n i t i a l S t r e n g t h @ 22 °CExposure Time, hours1501251007550250010050010003000120 °C 150 °C 180 °CChemical/Solvent ResistanceAged under conditions indicated and tested @22°C.%of initial strength Environment °C 100h500h 1000h Motor oil125100100100Unleaded gasoline 22100100100Brake fluid 22100100100Ethanol 87100100100Acetone22858585GENERAL INFORMATIONThis product is not recommended for use in pure oxygen and/or oxygen rich systems and should not be selected as a sealant for chlorine or other strong oxidizing materials For safe handling information on this product,consult the Material Safety Data Sheet (MSDS).Where aqueous washing systems are used to clean the surfaces before bonding,it is important to check for compatibility of the washing solution with the adhesive. In some cases these aqueous washes can affect the cure and performance of the adhesive.This product is not normally recommended for use on plastics (particularly thermoplastic materials where stress cracking of the plastic could result). Users are recommended to confirm compatibility of the product with such substrates.Directions for use:For Assembly1.For best results,clean all surfaces (external and internal)with a LOCTITE ® cleaning solvent and allow to dry.2.If quicker service time is required,use Activator 7471™ or7649™prior to application of sealant and allow to dry.3.For NPT or other taper joint fittings apply a 360°band ofsealant to leading threads of the male fitting.For larger threads and gaps,adjust the volume of sealant accordingly.4.For ORB &O-Ring Fittings apply a 360°band of sealantto the threads for the male fitting.Ensure product is applied into roots of the threads and adequate coverage.5.For JIC Fittings coat the face of the male JIC with thesealant.This is applicable for new and damaged fittings.Also apply to threads for vibration resistance.For Disassembly1.Remove with standard hand tools.2.Where hand tools do not work because of excessiveengagement length or large diameters (over 25mm),apply localized heat to approximately 250°C. Disassemble while hot.For Cleanup1.Cured product is most easily removed with mechanicalabrasion such as a wire brush and wiped clean with a cotton cloth.2.Fittings if mechanically acceptable can normally bereused once cleaned.Loctite Material Specification LMSLMS dated October 17,2008. Test reports for each batch are available for the indicated properties. LMS test reports include selected QC test parameters considered appropriate to specifications for customer use. Additionally,comprehensive controls are in place to assure product quality and consistency. Special customer specification requirements may be coordinated through Henkel Quality.StorageStore product in the unopened container in a dry location. Storage information may be indicated on the product container labeling.Optimal Storage: 8°C to 21°C. Storage below 8°C or greater than 28°C can adversely affect product properties .Material removed from containers may be contaminated during use. Do not return product to the original container. Henkel Corporation cannot assume responsibility for product which has been contaminated or stored under conditions other than those previously indicated.If additional information is required,please contact your local Technical Service Center or Customer Service Representative.Conversions(°C x1.8)+32=°FkV/mm x25.4=V/milmm/25.4=inchesµm/25.4=milN x0.225=lbN/mm x5.71=lb/inN/mm²x145=psiMPa x145=psiN·m x 8.851= lb·inN·m x0.738=lb·ftN·mm x0.142=oz·inmPa·s=cPNoteThe data contained herein are furnished for information only and are believed to be reliable. We cannot assume responsibility for the results obtained by others over whose methods we have no control. It is the user's responsibility to determine suitability for the user's purpose of any production methods mentioned herein and to adopt such precautions as may be advisable for the protection of property and of persons against any hazards that may be involved in the handling and use thereof.In light of the foregoing,Henkel Corporation specifically disclaims all warranties expressed or implied, including warranties of merchantability or fitness for a particular purpose,arising from sale or use of Henkel Corporation’s products. Henkel Corporation specifically disclaims any liability for consequential or incidental damages of any kind,including lost profits.The discussion herein of various processes or compositions is not to be interpreted as representation that they are free from domination of patents owned by others or as a license under any Henkel Corporation patents that may cover such processes or compositions. We recommend that each prospective user test his proposed application before repetitive use,using this data as a guide. This product may be covered by one or more United States or foreign patents or patent applications.Trademark usageExcept as otherwise noted,all trademarks in this document are trademarks of Henkel Corporation in the U.S.and elsewhere. ®denotes a trademark registered in the U.S. Patent and Trademark Office.Reference0.0。

我做了一个小实验矿泉瓶扎眼不漏水英文作文

我做了一个小实验矿泉瓶扎眼不漏水英文作文全文共2篇示例，仅供读者参考我做了一个小实验矿泉瓶扎眼不漏水英文作文1:Title: My Experiment: Poking Holes in a Water Bottle Without LeakageIntroduction:Have you ever wondered if it's possible to poke holes in a water bottle without it leaking? This question intrigued me, so I decided to conduct a small experiment to find out. In this essay, I will detail the process, results, and implications of my experiment.Experiment Setup:To conduct this experiment, I gathered the following materials:1. A plastic water bottle2. A sharp needle3. A bowl of waterMethodology:1. I filled the plastic water bottle to its maximum capacity with water.2. Carefully, I inserted the sharp needle into the side of the water bottle, near the bottom.3. I observed the bottle closely to check for any signs of leakage.4. After a few minutes, I examined the area around the puncture to see if any water had leaked out.Results:Surprisingly, the water bottle did not leak, despite the puncture made by the needle. Even after several minutes, there was no noticeable leakage. I repeated the experiment multiple times, and each time, the result was the same: no leakage.Discussion:The outcome of this experiment raises interesting questions about the properties of plastic and the behavior of water under pressure. It appears that the plastic material ofthe water bottle has some degree of self-healing ability, allowing it to seal small punctures on its own. Additionally, the surface tension of water may play a role in preventing leakage, as it forms a barrier that prevents water from escaping through the puncture.Implications:The findings of this experiment could have practical applications in various fields, such as packaging and engineering. Understanding how plastic materials behave under different conditions can help in the development of more durable and resilient products. Furthermore, exploring the properties of water under pressure can lead to innovations in leak-proofing technology.Conclusion:In conclusion, my experiment demonstrated that it is possible to poke holes in a water bottle without it leaking. This unexpected result opens up new avenues for research and innovation in material science and engineering. By further investigating the underlying mechanisms behind this phenomenon, we can gain valuable insights that may benefitvarious industries in the future.我做了一个小实验矿泉瓶扎眼不漏水英文作文2:Title: My Experiment: Does Piercing a Mineral Water Bottle Prevent Leakage?Introduction:In our daily lives, we often encounter situations where we need to improvise solutions to everyday problems. One such dilemma I faced was whether piercing a hole in a mineral water bottle could prevent leakage. To satisfy my curiosity, I conducted a simple experiment. This essay details the process, observations, and conclusions drawn from my experiment.Experiment Design:For this experiment, I used a standard mineral water bottle and a sharp object to pierce a small hole near the bottom. I filled the bottle with water and observed whether the pierced bottle would leak when tilted or turned upside down. Additionally, I compared the leakage rate between the pierced and intact bottles to determine the effectiveness of piercing in preventing water leakage.Observations:Initially, I carefully pierced a small hole in the designated area of the water bottle. Upon filling the bottle with water and tilting it, I observed that water began to leak steadily from the pierced hole. The rate of leakage was relatively slow, but noticeable. In contrast, the intact bottle did not exhibit any leakage when tilted or turned upside down.As the experiment progressed, I noticed that the size of the pierced hole influenced the rate of leakage. A larger hole resulted in faster and more pronounced leakage, while a smaller hole led to slower leakage. Despite this, the pierced bottle consistently leaked water, albeit at varying rates.Analysis:The presence of a hole in the water bottle compromised its integrity, allowing water to escape through the opening. When the bottle was tilted or inverted, gravity acted upon the water, exerting pressure on the pierced area and facilitating leakage. Furthermore, the size of the hole played a significant role in determining the rate of leakage, with larger holes allowing for faster water flow.Conclusion:Based on the observations and analysis, it can be concluded that piercing a hole in a mineral water bottle does not prevent leakage. On the contrary, it accelerates the process by providing an outlet for water to escape. Therefore, if the objective is to contain water without leakage, it is advisable to keep the bottle intact and free from any punctures or perforations.Implications:While the experiment focused on the specific scenario of piercing a mineral water bottle, the findings have broader implications. They underscore the importance of maintaining the structural integrity of containers to prevent leakage. Whether it's a water bottle, storage tank, or pipeline, any compromise in integrity can lead to unintended leaks and potential wastage.Furthermore, the experiment highlights the value of curiosity-driven inquiry and experimentation in everyday life. By questioning conventional wisdom and conducting simpleexperiments, we can gain valuable insights and deepen our understanding of the world around us. This spirit of inquiry and experimentation is essential for fostering innovation and problem-solving skills.In conclusion, my experiment yielded valuable insights into the behavior of pierced mineral water bottles and emphasized the importance of structural integrity in preventing leakage. Through curiosity-driven inquiry and experimentation, we can uncover hidden truths and enhance our understanding of everyday phenomena.。

实验室仪器or试剂耗材中英文对照

实验室仪器or试剂耗材中英文对照收藏起来，以后再也不用暗搓搓地搞个小本本记录了~ 容器与耗材 vessel & consumablematerial小瓶——vial量杯——measuring cup烧杯——beaker量筒——measuring flask/measuring cylinderer坩埚——crucible坩埚钳——crucible clamp试管——test tube漏斗——funnel比色皿——cuvette鱼缸——aquarium烧瓶——flask锥形瓶——conical flask塞子——stopper/plug洗瓶——plastic wash bottle玻璃活塞——stopcock试剂瓶——reagent bottles玻棒——glass rod搅拌棒——stirringrod容量瓶——volumetric flask/measuring flask移液管——(one-mark) pipette吸液管——pipette滤器——filter滤纸——filter paper培养皿——culture dish移液枪——pipette移液枪枪头——pipette tips剃刀刀片——razorblade手术刀——scalpel垃圾袋——disposablebag垃圾桶——garbagebin橡皮筋——rubber band托盘——Tray铝箔——aluminiumfoil洗耳球——rubber suction bulb保鲜膜——preservativefilm研磨钵——mortar研杵——pestle小滴管——dropper蒸馏装置——distillingapparatus 桶——bucket广口瓶——wide-mouth bottle离心机转子——rotor试管架——test tube holder/rack酒精灯——alcoholburner酒精喷灯——blastalcohol burner搅拌装置——stirring device石蜡封口膜——Parafilm微量离心管（EP管）——Eppendorf tube 载玻片——Slide盖玻片——Cover glass离心管——Centrifugetube电泳槽——Geltank电线——Electricalleads牙签——Toothpick螺丝钉——Screw锁紧螺母——Nut,Cap nut复印纸——Copypaper复写纸——Carbonpaper 钉——Nail试管刷——test-tube brush计时器——Timer闹钟——AlarmclockU形钉——Staple衣服挂钩——Coathanger电泳用的梳子——Comb扳手——Shiftingspanner订书机——Stapler订书钉——staple圆珠笔芯——Refill灯泡——Globe记号笔——marker pen注射器——syringe注射器活塞——plunger铁架台——ironsupport万能夹——extensionclamp止水夹——flatjawpinchcock圆形漏斗架——cast-ironring橡胶管——rubbertubing药匙——labspoon镊子——forceps/tweezers蜂鸣器——buzzer架子——shelf剪刀——scissor打孔器——stopperborer移液吸管——serological pipette 血球计数板hemocytometerpH试纸——universal ph indicatorpaper 称量纸——weighingpaper透明胶带——sellotape筛子——sieve网眼——mesh格子——grid擦镜纸——wiperfor lens水银温度计——mercury-filledthermometer 白大褂——white gown真空泵——vacuumpump水浴锅——waterbath kettle口罩——respirator电极——electrode阳极,正极——anode阴极,负极——cathode实验操作——（manipulation）丢弃——discard转移容器——decant吸出——aspirate吹吸——blowing and suction离心收集——pellet重悬——resuspend絮状沉淀——flocculent precipitate浑浊的——turbid烘——bake灭菌——sterilize均质化——homogenize分装——aliquot培养——foster通风——ventilate冷却——chill down稀释——dilute洗脱——elute孵育——incubate超声破碎——ultrasonication 淬灭——quench裂解物——Lysate沉淀物——Sediment上清——Supernatant小滴——droplet一批——batch色谱——chromatograph沉淀——precipitate接种——inoculate探针——probe蒸馏——distil/distill搅拌——Stir/agitate旋转——swirl/ spin中和——neutralize校准——calibrate平衡——equilibrate结块、块状沉淀——clump 粘稠的——viscous漂洗——rinse脱水——dehydrate发酵——fermentation溶解——dissolve燃烧——combustion水解——hydrolysis过滤——filtrate浓缩——condense催化剂——catalyst研磨——grind破碎——crush催化作用——catalysis分解——dissolution涡旋震荡——Vortex电泳——Electrophoresis抽滤——suctionfiltration电转化——electro-transformation收菌——harvest切碎——chop/mince灌注——perfusion浆液——slurry仪器——（apparatus）恒温循环仪——Thermostaticcirculator空调机——AirconditionerpH计——pHmeter照度计(测量荧光素酶酶活)——luminometer 磁力搅拌器——magneticstirrer烘箱——oven微波炉——microwaveoven电磁炉——electromagneticoven凝胶系统——Gelsystem电子天平——Electronicbalance转接器——Adapter离心机——centrifuge盖子——lid/ cap封口设备——Sealingequipment复印机——Duplicator,copying machine超净工作台——superclean bench通风橱——fume cupboard药柜——Cupboard高压蒸汽灭菌器——autoclave电泳电源——Electrophoresispower supply紫外灯——Ultravioletillumination真空泵——Vacuumpump天平——balance/scale分析天平——analytical balance台秤——platform balance涡旋振荡器——VortexingmachineCO2培养箱——CO2Incubators电子显微镜——ElectroMicroscopy电泳仪——ElectrophoresisSystem恒流泵——constantflow pump解剖镜——anatomicallensPCR仪——Thermocycler倒置显微镜——InvertedMicroscope核磁共振波谱仪——NuclearMagnetic Resonance Spectrometer光学显微镜——OpticalMicroscopy摇床——Shaker培养箱——incubator超滤器——UltrahighPurity Filter超低温冰箱——Ultra-lowTemperature Freezer超声破碎仪——UltrasonicCell Disruptor紫外观察灯——UltravioletLamp紫外-可见光分光光度计——UV-isibleSpectrophotometer计算器——calculator/numerator容器类量杯——measuringcup烧杯——beaker不锈钢杯——stainless-steelbeaker量筒——measuringflask/measuring cylinder 量筒——graduatedflask/measuring cylinder 坩埚——crucible坩埚钳——crucibleclamp坩埚——cruciblepot，meltingpot试管——testtube试管架——testtube holder漏斗——funnel分液漏斗——separatoryfunnel烧瓶——flask锥形瓶——conicalflask塞子——stopper洗瓶——plasticwash bottle滴定管——burette玻璃活塞——stopcock冷凝器——condenser试剂瓶——reagentbottles玻棒——glassrod搅拌棒——stirringrod蒸馏烧瓶——distillingflask碘量瓶——iodineflask表面皿——watchglass蒸发皿——evaporatingdish容量瓶——volumetricflask/measuring flask 移液管——(one-mark)pipette刻度移液管——graduatedpipettes称量瓶——weighingbottle吸液管——pipette滤管——filter天平——balance/scale分析天平——analyticalbalance台秤——platformbalance游码——crossbeamsand sliding weights酒精灯——alcoholburner酒精喷灯——blastalcohol burner搅拌装置——stirringdevice洗耳球——rubbersuction bulb研磨钵——mortar研磨棒——pestle玛瑙研钵——agatemortar瓷器——porcelain白细口瓶——flintglass solution bottle with stopper 滴瓶——droppingbottle小滴管——dropper蒸馏装置——distillingapparatus蒸发器——evaporator试验用器材升降台——labjack铁架台——ironsupport万能夹——extensionclamp蝴蝶夹——double-buretclamp双顶丝——clampregular holder止水夹——flatjawpinchcock圆形漏斗架——cast-ironring移液管架——pipetrack试管架——tuberack沸石——boilingstone橡胶管——rubbertubing药匙——labspoon镊子——forceps坩埚钳——crucibletong剪刀——scissor打孔器——stopperborer石棉网——asbestos-freewire gauze电炉丝——wirecoil for heater脱脂棉——absorbentcottonphph试纸——universal ph indicator paper滤纸——filter paper称量纸——weighingpaper擦镜纸——wiperfor lens秒表——stopwatch量杯——glassgraduates with scale白滴定管（酸）——flintglass burette with glass stopcock棕色滴定管（酸）——brownglass burette with glass stopcock 白滴定管（碱）——flintglass burette for alkali棕色滴定管（碱）——brownglass burette for alkali比重瓶——specificgravity bottle水银温度计——mercury-filledthermometerpH计——pHmeter折光仪——refractometer真空泵——vacuumpump冷、热浴——bath离心机——centrifuge口罩——respirator防毒面具——respirator、gasmask磁力搅拌器——magneticstirrer电动搅拌器——powerbasic stirrer烘箱——oven闪点仪——flashpoint tester马弗炉——furnace电炉——heater微波炉电热套——heatingmantle本生灯——Bunsen burner化学反应产物——product设备——apparatuspH值指示剂，氢离子(浓度的)负指数指示剂——pH indicator 卵形瓶——matrass石蕊——litmus石蕊试纸——litmus paper滴定管——burette曲颈甑——retort蒸馏釜——still烤钵——cupel化学反应analysis——分解fractionation ——分馏endothermicreaction ——吸热反应exothermicreaction——放热反应precipitation ——沉淀to precipitate ——沉淀to distil，todistill——蒸馏distillation ——蒸馏to calcine——煅烧to oxidize——氧化alkalinization——碱化to oxygenate，tooxidize ——脱氧,氧化to neutralize ——中和to hydrogenate ——氢化to hydrate——水合，水化to dehydrate——脱水fermentation——发酵solution——溶解combustion——燃烧fusion，melting——熔解alkalinity——碱性isomerism，isomery——同分异物现象hydrolysis——水解electrolysis——电解electrod——e电极anode——阳极，正极cathode——阴极，负极catalyst——催化剂catalysis——催化作用oxidization，oxidation——氧化reducer——还原剂dissolution——分解synthesis——合成reversible——可逆的仪器中英文对照Aging PropertyTester——老化性能测定仪；Amino AcidAnalyzer——氨基酸组成分析仪；Analyzer forClinic Medicine Concentration——临床药物浓度仪；AtomicAbsorption Spectroscopy——原子吸收光谱仪；Atomic EmissionSpectrometer——原子发射光谱仪；AtomicFluorescence Spectroscopy——原子荧光光谱仪；AutomaticTitrator——自动滴定仪；Basic Physics——基本物理量测定；BiochemicalAnalyzer——生化分析仪；Biochemicalanalysis——生物技术分析；Bio-reactor——生物反应器；Blood-gasAnalyzer——血气分析仪；Centrifuge——离心机；ChemiluminescenceApparatus——化学发光仪；CHN Analysis——环境成分分析仪；CO2Incubators ——CO2培养箱；CombustionPropertyTester——燃烧性能测定仪；ConductivityMeter——电导仪；ConstantT emperature Circulator——恒温循环泵；Direct CurrentPlasma Emission Spectrometer——直流等离子体发射光谱仪；DNA Sequencers——DNA测序仪；DNA synthesizer——DNA合成仪；ElectricalProperty Tester——电性能测定仪；ElectroMicroscopy——电子显微镜；ElectrolyticAnalyzer——电解质分析仪；Electron EnergyDisperse Spectroscopy——电子能谱仪；ElectronParamagnetic Resonance Spectrometer——电子顺磁共振波谱仪；Electrophoresis ——电泳ElectrophoresisSystem ——电泳仪ELIASA ——酶标仪Energy DisperseSpectroscopy ——能谱仪Fermenter ——发酵罐Flow Analyticaland Process AnalyticalChemistry——流动分析与过程分析FractionCollector ——部分收集器FreezeDryingEquipment ——冻干机FT-IRSpectrometer ——傅里叶变换红外光谱仪FT-RamanSpectrometer——傅里叶变换拉曼光谱仪Gas Analysis ——气体分析GasChromatograph ——气相色谱仪GC-MS ——气相色谱-质谱联用仪GelPermeationChromatograph——凝胶渗透色谱仪HighPressure/PerformanceLiquid Chromatography ——高压/效液相色谱仪HybridizationOven ——分子杂交仪ICP-MS ——ICP-质谱联用仪InductiveCoupled Plasma Emission Spectrometer ——电感偶合等离子体发射光谱仪Instrument forNondestructive Testing ——无损检测仪Instrument forPolymerase Chain Reaction—— PCR仪InvertedMicroscope ——倒置显微镜IonChromatograph ——离子色谱仪Isotope X-RayFluorescence Spectrometer ——同位素X荧光光谱仪LC-MS ——液相色谱-质谱联用仪MassSpectrometer ——质谱仪MechanicalProperty Tester ——机械性能测定仪Metal/materialelemental analysis ——金属/材料元素分析仪MetallurgicalMicroscopy ——金相显微镜MicrowaveInductive Plasma Emission Spectrometer ——微波等离子体光谱仪Nuclear MagneticResonance Spectrometer ——核磁共振波谱仪OpticalMicroscopy ——光学显微镜Optical PropertyT ester——光学性能测定仪Particle SizeAnalyzer ——粒度分析仪PCR Amplifier——PCR仪Peptidesynthesizer ——多肽合成仪Physical PropertyAnalysis ——物性分析Polaro-graph——极谱仪ProteinSequencer ——氨基酸测序仪Rheo-meter——流变仪Sample Handling ——样品处理Scanning ProbeMicroscopyFG|8oU——扫描探针显微镜Sensors ——传感器Sequencers andSynthesizers for DNA and Protein—— DNA 及蛋白质的测序和合成仪Shaker ——摇床Size ExclusionChromatograph ——体积排阻色谱Surface Science ——表面科学Surface Analyzer——表面分析仪Thermal Analyzer——热分析仪Thermal PhysicalProperty Tester ——热物理性能测定仪Ultrahigh PurityFilter ——超滤器Ultra-lowTemperature Freezer ——超低温冰箱Ultrasonic CellDisruptor ——超声破碎仪UltravioletDetector ——紫外检测仪Ultraviolet Lamp——紫外观察灯Urine Analyzer——尿液分析仪UV-VisibleSpectrophotometer ——紫外-可见光分光光度计Viscometer ——粘度计Voltam-merter——伏安仪Water Test Kits ——水质分析仪X-RayFluorescence Spectrometer ——X射线荧光光谱仪X-Ray Diffractomer——X射线衍射仪分子生物学实验室常用仪器物品英文词汇口罩——respirator试验管——tube耐酸橡胶手套——rubber gloves试管架——test tube rack药匙——lab spoon洗瓶——plastic wash bottle钳子——pliers玻璃搅棒——glass stirring stick扳子——spanne研钵——mortars螺丝刀——screw driver研棒——pestles多用电源插座——multi-purpose socket 冰盒——ice box复印纸——copy paper液氮罐——Dewar flask笔记本——note book记号笔——marker pen培养皿——culture dish夹子——clip皮氏培养皿——petri dish擦镜纸——wiper for lens培养三角瓶——culture flask标签纸——paper label接种环——inoculating loop打火机——lighter接种针——inoculating needle温度计——thermometer过滤灭菌器——syringe filters定时器——timer镊子——forceps棉线（细绳）——cotton rope剪刀——scissors橡皮圈——rubber band解剖刀片——scalpel blade清洁布——rag解剖刀柄——scalpel handle牛皮纸——kraftpaper酒精灯——alcohol burner塑料筐——plastic basker样品推车——lab cart塑料桶——plastic basin保温桶——thermos封口膜——parafilmwrap and dispenser 不锈钢盘——stainless steel tray塑料膜——plastic film搪瓷盘——enamel tray保鲜膜——cling film铝箔纸——aluminum foil烧杯——beaker脱脂棉——absorbent cotton三角瓶、烧瓶——flask容量瓶——volumetric flask铁架台——iron support量筒——graduated cylinder石棉网——asbestos board移液器——pipette玻璃干燥器——glass desiccator移液管——serological pipette三角漏斗——funnel吸耳球——bulb for pipet布氏漏斗——buchnerfunnel移液管架——pipet rack玻璃漏斗——glass funnel离心管架——centrifuge tube rack酸碱滴定管——Burette天平——balance安全帽——safety helmet分析天平——analytical balance工作服——lab coat称量瓶——weighting bottle工作鞋——footware称量纸——weighing paper隔热手套——heat insulation gloves比重计——hydrometer体重计——body weight scales酸度计——pH meterpH试纸——pH indicator paper升降台——lab jack电磁搅拌器——magnetic stirring电磁搅棒——magnetic stirring bar匀浆器——homo-genixe摇床——shaker水浴摇床——reciprocating shaker bath 涡旋振荡器——vortex mixer离心机——centrifuge烘箱——oven低温水浴——refrigerating circulator 冰箱——refrigerator超低温冰箱——ultra-low temperature freezer 培养箱——incubator分光光度计——spectrophotometer石英比色杯——quartz cuvette超声波清洗器——ultrasonic cleaner杂交炉——hybridization oven。

氧化钙盐产品说明书

Product # (s)_7160__________________Page 1 of 2MATERIAL SAFETY DATA SHEET Section I – Product InformationProduct Name or Identity:Thioglycollate Medium W/O Indicator Manufacturer’s Name:Acumedia Manufacturers, Inc.Emergency Phone No.517/372-9200740 East ShiawasseeFax No.:517/372-2006Lansing, Michigan 48912e-mail:*********************Date Prepared or Revised: 10/10/04Section II – Hazardous Ingredients / Identity InformationHazardous Components:(Specific Chemical Identity: Common Names)OSHA PEL (Permissible Exposure Limits)ACGIH TLV (Threshold Limit Value)Toxicity Data LD 50Sodium Chloride, NaCl, Common saltN/A N/A ORL-RAT, 3000 mg/kg Sodium Thioglycollate N/AN/A ORL-MSE, 504 mg/kg Section III – Physical CharacteristicsBoiling Point: 1413ºC (Sodium Chloride)Specific Gravity (H 2O = 1): 2.16 g/cm 3 (Sodium Chloride)Vapor Pressure (mm Hg.): 1.0 @ 865ºC (Sodium Chloride)Melting Point: 804ºC (Sodium Chloride) 300ºC (Sodium Thioglycollate)Vapor Density (AIR = 1): N/A Evaporation Rate (Butyl Acetate = 1): N/A Solubility in Water: 35.7 g/100g at 0ºC (Sodium Chloride), Soluble at 20ºC (Sodium Thioglycollate)Appearance and Odor: Colorless crystals or white powder. Characteristic odor. (Sodium Chloride).Powder, faintly beige (Sodium Thioglycollate)Section IV – Fire and Explosion Hazard DataFlash Point (Method Used ): Not applicable Flammable Limits: LEL (Lower Explosive Limit) - N/AUEL (Upper Explosive Limit) - N/AExtinguishing Media: Suitable extinguishing agents. CO 2, extinguishing powder, or water spray .Special Fire Fighting Procedures: Fight larger fires with water or alcohol resistant foam. Firefighters should wear protective equipment and self-contained breathing apparatus.Unusual Fire and Explosion Hazards: During heating or in case of fire, poisonous gases are produced.Section V – Reactivity Data Stability:Unstable Conditions to Avoid: Stable under ordinary conditions of use and storage.Hygroscopic. Protect from moisture.Stable XIncompatibility (Materials to Avoid): Reacts with acids, alkalis, bases, oxidizing agents, Lithium, and Bromine trifluoride.Hazardous Decomposition or Byproducts: Phosphorous oxides, Sodium oxides, Carbon monoxide, Carbon dioxide,and Sulfur oxides. When heated to above 801°C it emits toxic fumes of chloride and sodium oxide.HazardousPolymerization:May Occur Conditions to Avoid: Dust generation, exposure to air, excess heat, and incompatible materials.Will Not Occur XProduct # (s)_7160_______________Page 2 of 2Rev 03, 10/04Section VI – Health Hazard DataRoute(s) of Entry:Inhalation? Yes Skin? Yes Ingestion? Yes Health Hazards:(Acute and Chronic)Harmful. Harmful if swallowed, inhaled, or absorbed through the skin. Irritating to eyes, respiratory system, and skin.Carcinogenicity: NTP? No (National Toxicology Program)IARC Monographs? No(International Agency for Research in Cancer)OSHA Regulated? NoSigns and Symptoms of Exposure: Irritant to skin and mucous membranes. Irritating effect to eye. May cause irritation to respiratory tract and mucous membranes.Medical Conditions Generally Aggravated by Exposure: If ingested, large doses can cause vomiting, diarrhea, and prostration. Can produce delayed pulmonary edema. Effects may be delayed.Ingestion: If swallowed, seek medical attention.Inhalation: Supply fresh air or oxygen. Seek medical attention.Eye Contact: Rinse opened eye for at least 15 minutes under running water. Seek medical attention.Emergency /First AidProcedures:Skin Contact: Wash with plenty of soap and water for 15 minutes. Seek medical attention if irritationdevelops.Section VII – Precautions for Safe Handling and UseAccidental Release Measures: Ventilate spill area. Wear suitable protective clothing. Wipe up with damp sponge or mop. Avoid inhalation, contact with eyes, skin, and clothing.Waste Disposal Method: Dispose in accordance with all applicable federal, state, and local environmental regulations.Handling and Storing: Keep container tightly closed. Protect from moisture and physical damage. Suitable for any general chemical storage area. Store away from oxidizing agents.Other Precautions: Prevent formation of dust. Ensure good ventilation / exhaustion at the workplace. Avoid prolonged or repeated exposure.Section VIII – Control MeasuresRespiratory Protection (Specify Type): None required where adequate ventilation conditions exist. If airborne concentration is high, use an appropriate respirator or dust mask.Ventilation:Local Exhaust: 50 – 100 CFM Special: N/AMechanical (General): N/AOther: N/A Protective Gloves: Proper disposable gloves Eye Protection: Chemical resistant safety gogglesOther Protective Clothing or Equipment: Uniform, lab coat, or disposable lab wear.Work / Hygienic Practices: Follow the usual precautionary measures for handling chemicals / powder. Keep away from food and beverages. Immediately remove all soiled and contaminated clothing. Avoid contact with eyes, skin, and clothing.This document is believed to be correct, but does not purport to be all inclusive and shall be used only as a guide.Acumedia shall not be held liable for any damage resulting from handling or from contact with the above product. These suggestions should not be confused with state, municipal or insurance requirements, and constitute NO WARRANTY.。

物理专业词汇S2

specific binding energy 比结合能
specific conductance 导电率
specific electronic charge 电子的比电荷
specific gravity 比重
specific gravity bottle 比重瓶
specific heat 比热
spectroscopic parallax 分光视差
spectroscopic photography 分光摄影术
spectroscopy 光谱学
spectrum 光谱
spectrum locus 光谱轨迹
spectrum selector 光谱选挥器
spectrum variable 光谱变星
source of light 光源
source of sound 声源
south pole 南极
space 空间
space astronomy 空间天文学
space charge 空间电荷
space charge density 空间电荷密度
space charge effect 空间电荷效应
spectrohelioscope 太阳光谱观测镜
spectrometer 光谱仪
spectrometry 光谱测定法
spectrophotofluorometer 荧光分光光度计
spectrophotography 光谱摄影学
spectrophotometer 分光光度计
spectrophotometry 光谱测定法
spark chamber 火花室
spark counter 火花计数器

第四届冷原子会议会议安排July 5

40
[P16]
Jing Qian（钱静）
Efficient production of polar molecular Bose–Einstein condensates via an all-optical R-type atom–molecule adiabatic passage
41
[P17]
31
[P07]
Haichao Zhang（张海潮）
Demonstration of Neutral Atom Guiding via Radio-Frequency Field
32
[P08]
Shuyu Zhou（周蜀渝）
Double-well Array Trapping Atoms Based on Binary Optics ethod
会议安排July 5, Monday
Opening Ceremony
Presider
Liang Liu（刘亮）
8:30-9:00
Yuzhu Wang（王育竹）and Chaohui Ye（叶朝辉）
Opening Remarks
Sec. A
Presider
Li You（尤力）
9:00-9:30
Jun Ye（叶军）
Xing-Dong Zhao（赵兴东）
A magical polarization orientation for canceling the dipole-dipole
interaction in ultracold Bosonic dipolar gases
42
[P18]
Cheng-ling Bian（边成玲）
46
[P22]
K. Zhang（张可烨）

有关重力的英语作文

有关重力的英语作文Title: Exploring the Phenomenon of Gravity。

Gravity is a fundamental force of nature thatinfluences every aspect of our lives, yet its intricate workings continue to fascinate scientists and researchers worldwide. In this essay, we delve into the depths of gravity, exploring its significance, its effects, and its implications for our understanding of the universe.Firstly, let us define gravity. In simple terms,gravity is the force of attraction between objects with mass. It is what keeps our feet firmly planted on theground and governs the motions of celestial bodies in space. Sir Isaac Newton famously described gravity as a force that acts between any two masses, pulling them together with a strength proportional to their masses and inversely proportional to the square of the distance between them.Gravity plays a pivotal role in shaping the structureof the universe. On a cosmic scale, it governs the formation and movement of galaxies, stars, and planets. Without gravity, stars would not ignite, planets would not orbit, and galaxies would not coalesce. Indeed, it is the gravitational pull of the sun that keeps Earth and the other planets in our solar system in their respective orbits.On a more terrestrial level, gravity influences the behavior of objects in our everyday lives. It determines the weight of an object and the force required to lift it. It dictates the trajectory of a thrown ball and the descent of a falling leaf. From the tides in the ocean to the sway of a pendulum, gravity manifests itself in myriad phenomena that shape our experiences on Earth.One of the most intriguing aspects of gravity is its universality. Unlike some forces that only operate under specific conditions, gravity is omnipresent, affecting all matter regardless of its composition or state. Whether it's a feather floating gracefully to the ground or a massive boulder hurtling through space, gravity exerts itsinfluence with unwavering consistency.Yet, despite centuries of study, gravity remains one of the least understood forces in physics. While Newton's laws provided a groundbreaking framework for understanding gravity's effects on Earth, they were eventually superseded by Albert Einstein's theory of general relativity. According to Einstein's theory, gravity arises from the curvature of spacetime caused by the presence of mass and energy. In other words, massive objects like planets and stars warp the fabric of spacetime, creating agravitational field that governs the motion of other objects within it.Einstein's theory revolutionized our understanding of gravity, providing a more comprehensive explanation for phenomena such as the bending of starlight by massive objects and the existence of black holes. However, despite its success in explaining these phenomena, generalrelativity is not without its limitations. At the quantum level, where gravity interacts with the other fundamental forces of nature, physicists struggle to reconcileEinstein's theory with the principles of quantum mechanics. The quest for a unified theory of gravity—one that seamlessly integrates the principles of general relativity and quantum mechanics—remains one of the greatest challenges in modern physics.In addition to its theoretical implications, gravity also has practical applications that shape our daily lives. From the design of buildings and bridges to the navigation of spacecraft, an understanding of gravity is essential for engineers and designers across a wide range of disciplines. Without accounting for the effects of gravity, structures would collapse, and spacecraft would veer off course, jeopardizing both human lives and valuable resources.In conclusion, gravity is a force of nature that permeates every aspect of our existence. From the grandeur of the cosmos to the minutiae of everyday life, its influence is profound and far-reaching. Yet, despite centuries of study, there is still much we have yet to learn about this enigmatic force. As we continue to unravelits mysteries, we inch closer to a deeper understanding of the universe and our place within it.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

a r X i v :h e p -t h /0307109v 3 11 A u g 2003Spinor GravityA.Hebecker ∗,C.Wetterich ∗∗∗Deutsches Elektronen-Synchrotron,Notkestraße.85,D-22603Hamburg,Germany ∗∗Institut f¨u r Theoretische Physik,Philosophenweg 16,D-69120Heidelberg,GermanyA uniﬁed description of all interactions could be based on a higher-dimensional theory involvingonly spinor ﬁelds.The metric arises as a composite object and the gravitational ﬁeld equations contain torsion-corrections as compared to Einstein gravity.Lorentz symmetry in spinor space is only global,implying new goldstone-boson-like gravitational particles beyond the graviton.However,the Schwarzschild and Friedman solutions are unaﬀected at one loop order.Our generalized gravity seems compatible with all present observations.The physical description of our world is based on fermionic and bosonic degrees of freedom,corresponding to particles with diﬀerent statistical properties.In par-ticular,bosons mediate the interactions between fermions as well as between themselves.One may consider two al-ternative approaches to a fundamental uniﬁed theory.Ei-ther one treats bosons and fermions on equal footing,at-tempting to link them by some symmetry principle -this is the road of supersymmetry.Alternatively,one consid-ers the fermions as fundamental and explains the bosons as composite objects of an even number of fermions.The second approach is commonly followed in the treatment of strongly correlated electrons in statistical physics and is familiar from the Nambu-Jona-Lasinio [1]and Gross-Neveu [2]models 1.In this letter we explore the hypothesis that a funda-mental uniﬁed theory of the gravitational,electroweak and strong interactions can be formulated in terms of only fermionic degrees of freedom.Given that all bosons arise as composite ﬁelds,one immediately faces the fun-damental challenge of describing the metric in terms of fermionic variables.In particular,one has to realize the symmetry of general coordinate transformations or dif-feomorphisms by a purely fermionic functional integral without the use of a fundamental metric degree of free-dom.The metric of space-time can then be associated with the expectation value of a suitable fermion bilinear.Our formulation uses the notion of d -dimensional coordi-nates x µ,µ=0,...,d −1,only in order to describe spinor ﬁelds ψ(x )in some local coordinate patch and for the deﬁnition of a derivative ∂µψ.The geometric and topo-logical properties of space-time arise a posteriori as a consequence of the dynamics of the system,reﬂected in the fermion correlators.This realizes the idea of obtain-ing geometry from general statistics [4].The idea of a purely fermionic fundamental theory has previously been explored on the basis of proposals for “pregeometry”[5,6]or “metric from matter”[7],whereSpinors are Grassmann variables and our basic tool is the Grassmann functional integral for the partition func-tionZ[J]= Dψexp −(S+S J) .(1)The dynamics is described by the“classical action”S[ψ] which has to be a polynomial functional of the spinor ﬁelds.As a technical tool we have added to the action a source term S J.It is linear in suitable sources J and fa-cilitates the computation of expectation values of spinor bilinears.We will set J=0in the end to obtain ex-pectation values in the vacuum.Ourﬁrst task is toﬁnd a polynomial action S which is invariant under diﬀeo-morphisms,so that no particular choice of coordinates is singled out.For this purpose we may use as a basic building block the“real”local fermion bilinears˜E m µ(x)=id! d d xǫµ1...µdǫm1...m d˜E m1µ1...˜E m dµd.(3)Clearly,no metric is needed in order to realize diﬀeomor-phism invariance in a fundamental fermionic theory[6]. Since we demand that the action is polynomial inψ,no inverse of˜E mµcan appear and all lower world indices from derivatives∂µhave to be contracted with the totally an-tisymmetric d-dimensionalǫ-tensor.This also ensures the cancellation of the Jacobian of reparameterizations.The action of Eq.(3)is invariant under global but not under local Lorentz rotations.More general forms of invariant actions can be found in an accompanying paper[14].As explained above,they have to contain precisely d derivatives by reparameteriza-tion invariance.The number of spinorﬁelds contained inδJµm(x).(4)Here we have speciﬁed the source term S J=− d d x Jµm(x)˜E mµ(x).Usingηmn=diag(−1,1...1),the metric can be constructed in the standard waygµν(x)=E mµ(x)Eνm(x)=E mµ(x)E nν(x)ηmn.(5) The inverse metric gµνexists whenever E=det(E mµ) =0and can be used to“raise indices”.As required,the metric transforms as a symmetric tensorﬁeld.We will argue that the metric obeysﬁeld equations similar to the Einstein equations.It can be associated with a massless, composite graviton(see also[15]for some of the early as well as more recent related ideas).However,we expect the resulting eﬀective gravity theory to be a generaliza-tion of Einstein gravity.Since the action of Eq.(3)is invariant under global but not under local Lorentz rota-tions,the vielbein describes additional massless degrees of freedom not associated with the metric.(This distin-guishes our approach from earlier attempts to realize lo-cal Lorentz symmetry[5–7].)The resulting“generalized gravity”[16]will lead to a speciﬁc version of torsion.In suitable dimensions and for a suitable“ground state”E mµ,our fundamental spinor theory will describe bothmassless spinors and massless gravitationalﬁelds.In order to get aﬁrst glance at the dynamics of the the-ory,we employ the method of partial bosonization[17].Without a perturbative expansion in a small parameter we do not expect quantitatively accurate results,but the structural elements deriving from the eﬀective degrees of freedom and symmetries will become visible.Up to an irrelevant normalization constant,we can write the par-tition function as an equivalent functional integral over fermionsψand bosonﬁeldsχ(cf.[2]),Z[J]= DψDχnνexp −S B+ d d xJµmχmµ , S B[ψ,χ]=α d d x det(˜E mµ)−det(˜E mµ−χmµ) .(6)The equivalent purely fermionic theory can be recovered by performing the Gaussian functional integral for the bosonicﬁeldsχnν.It diﬀers from the theory deﬁned by Eqs.(1)and(3)only in the connected correlation func-tions of at least order d in˜E mµ[14].With E mµ= χmµ , the eﬀective actionΓ[E]is deﬁned as2Γ[E]=−W+ d d xJµm(x)E mµ(x),(7)δW[J]δE mµ=Jµm,(9)where Jµm=0in the vacuum.Contributions from matter and radiation can be associated to an energy momentum tensor Tµν=E−1E mµJνm.The latter accounts for the incoherentﬂuctuations ofψand of bosonic composite ﬁelds as well as for possible expectation values of bosonic compositeﬁelds other than E mµ.At one loop order in the fermionicﬂuctuations,Γ[E] is given by(˜α=(−1)d+1α)Γ[E]=˜α d d xE−12EE mµ∂ν(EEνm).(12)The evaluation of the one loop term can be performed by standard techniques(see, e.g.,[19]and references therein).We expand in the number of derivatives and ﬁnd(see below)for the term with two derivativesΓ(2)=µ2(hµν+aµν)ηνm,(15)where hµνand aµνare the symmetric and antisymmet-ric part.The former accounts for the metricﬂuctuations(gµν=ηµν+hµν)and can be decomposed in the usualmanner,hµν=bµν+1∂2 σ+∂µ∂ν8 d d x∂µbνρ∂µbνρ−d−2long ago[13]and it would be very interesting to see how such a construction could emerge from the generalization of gravity proposed in this letter.We assume that,after compactiﬁcation,the gravita-tional part of the eﬀective four-dimensional action still has the form of Eq.(13),now with new eﬀective coeﬃ-cientsµ4,τ4.The general form of the action is restricted by the symmetries,even if additional invariants are added to the classical action of Eq.(3).In this context we note that the two terms multiplyingτin Eq.(13)could,from the point of view of global Lorentz and diﬀeomorphism invariance,have coeﬃcients with a ratio other than−2. In other words,there are really three independent invari-ants only two of which are actually generated by the loop calculation.If present,the third invariant would lead to more drastic deviations from Einstein gravity[14]than the invariant∼τgenerated in the one loop approxima-tion.In this letter we assume that some deeper reason (symmetry?)protects the structure of the one loop ex-pression Eq.(13)at higher-loop order.As a working hy-pothesis we take the coeﬃcient of the other allowed in-variant to be zero(or very small).As a test of the viability of a generalized gravity theory with only global Lorentz symmetry,we therefore compare theﬁeld equations ob-tained from the eﬀection action Eq.(13)in d=4with observations.In this context we also assume that the cos-mological constant in the eﬀective4-dimensional theory (almost)vanishes.Postponing a more detailed investiga-tion of this interesting issue,we note that the classical cosmological term in Eq.(10)can be chosen to cancel the one-loop contribution,which amounts to the usual ﬁne-tuning.This cancellation also depends on the inter-nal compact space and extends to a more general form of the fundamental spinor action which could involve other invariants beyond Eq.(3).For weak gravity the linearﬁeld equations follow from the variation ofΓ(2)in Eq.(18)in presence of an energy momentum tensor Tµν.With energy density T00=ρand Newtonian potentialφ=−12µ.(19)This associatesµwith the reduced Planck mass¯M2p= M2p/8π=(8πG N)−1=µ.The newﬁeld cµνonly couples to the antisymmetric part of the energy momentum tensor,(T A)µν,deﬁned by the variation of the action with respect to the anti-symmetric part of E mµ.As will become clear below,for spinors this corresponds to a coupling to the spin.Point-like particles without internal structure(including mass-less particles)generate a symmetric energy momentum tensor.Therefore(T A)µνcan only be related to the inter-nal structure–in our case it involves the spin vector.The “spin contribution”to the gravitational interactions me-diated by the exchange of cνρdoes not contain a rotation invariant part since c0i andǫijk c jk transform as vectors.Only for macroscopic objects with a nonzero macroscopic spin vector the modiﬁcations of gravity would become observable.It has been checked[14]that even beyond the linear approximation the modiﬁcations of gravity∼τneither aﬀect the Schwarzschild solution nor the Friedmann cos-mological solution.We conclude that our proposal of gen-eralized gravity is compatible with all present tests of general relativity.Nevertheless,it is conceivable that the presence of new long rangeﬁelds beyond the graviton may lead to new interesting cosmological solutions,pos-sibly accounting for quintessence[23].To make the relation of spinor gravity to conventional general relativity more explicit,it is useful to introduce nonlinearﬁelds with local Lorentz invariance.We write the global vielbein as E mµ=e nµH n m,where e nµis a con-ventional“local vielbein”with local Lorentz index.The SO(1,d−1)matrix H n m has one local and one global index.The new local Lorentz transformations present in the nonlinear formulation correspond to a reparameteri-zation of the decomposition of E mµin e nµand H n m,leav-ing E mµinvariant.The nonlinearﬁeld H mncharacterizes the new degrees of freedom that are present in addition to those of conventional gravity.We deﬁne here the co-variant derivative Dµby the requirement of a covariantly constant local vielbein e mµ.This implies that the covari-ant derivative of E mνis given by DµE mν=e nνDµH n m.Here the action of Dµon theﬁrst index of H makes use of the spin connection deﬁned by e mµ,while the second, global index is inert.Given that E=e=det(e mµ),it is now obvious that Eq.(13)describes conventional gravity covariantly coupled to the non-linearﬁeld H.Geometrically,the new degrees of freedom can be char-acterized by a further connection˜Γ,which is present in addition to the Riemannian connectionΓ,˜Γµνλ=(∂µE mν)Eλm.(20)This connection is deﬁned by demanding that E mµbe covariantly constant.The existence of a covariantly con-stant basis of vectorﬁelds implies that our new connec-tion is curvature-free.It has,however,non-vanishing tor-sionTµνρ=(∂µE mν−∂νE mµ)Eρm.(21) Thus,in the bosonic formulation,we are dealing with general relativity with torsion,where the torsion ten-sor is restricted by the requirement of a curvature-free Riemann-Cartan connection.More precisely,given a met-ric and a torsion tensor such that the Riemann-Cartan connection has zero curvature,we can always deﬁne a global vielbein E mµby parallel transporting a frame de-ﬁned at an arbitrary butﬁxed point of the manifold.One can easily check that E mµwill then automatically satisfy Eq.(21).Note that such a theory is very diﬀerent from general relativity with a generic(unconstrained)torsion tensor.4In the above geometrical formulation,the one-loop cal-culation leading to Eq.(13)is particularly easy to un-derstand.The leading fermionic term in the lagrangianof Eq.(6)readsLψ∼¯ψEµmγm∂µψ+h.c.(22)Using the local Lorentz invariance introduced above,wechoose e mµ=E mµ.In this local frame,the coeﬃcientsof the spin connection going with our Riemann-Cartanconnection vanish,˜ωµab=0.Thus,we haveLψ∼¯ψeµmγm˜Dµψ+h.c.,(23)and the problem is reduced to evaluating the eﬀective ac-tion induced by integrating out a fermion in a Riemann-Cartan background.In fact,we can introduce a newfermionic variableψ′deﬁned to coincide withψin theframe where e mµ=E mµand to transform like a usualgeneral-relativity spinor under local Lorentz transforma-tions of e mµ.(This corresponds to theﬁeld redeﬁnitionψ=S(H−1)ψ′,where S denotes the spinor representa-tion.)Now we have a formulation of partially bosonizedspinor gravity with full local Lorentz invariance:The vari-ables areψ′,e mµand Tµνρ(constrained by the require-ment of a curvature-free Riemann-Cartan connection).The quadratic part of the fermionic action is given byEq.(23)withψ→ψ′,which has local Lorentz-invariance.The fermionic one-loop contribution to the eﬀectiveaction for e mµand Tµνρis calculated from the square ofthe Dirac operator deﬁned by Eq.(23).More speciﬁcally,the leading divergences are characterized by the DeWittcoeﬃcients[12]of the relevant operator(see,e.g.,[24]).While the highest divergence comes with the cosmologi-cal constant,the next contribution contains the leadingterms with vielbein derivatives and torsion.Given thatonly the totally antisymmetric part of the torsion couplesto fermions,it has to be of the formµΓ(2)=[1]Y.Nambu and G.Jona-Lasinio,Phys.Rev.122(1961)345and124(1961)246.[2]D.J.Gross and A.Neveu,Phys.Rev.D10(1974)3235.[3]T.H.Skyrme,Proc.Roy.Soc.Lond.A262(1961)237.[4]C.Wetterich,Nucl.Phys.B397(1993)299.[5]K.Akama,Y.Chikashige,T.Matsuki and H.Terazawa,Prog.Theor.Phys.60(1978)868.5[6]K.Akama,Prog.Theor.Phys.60(1978)1900.[7]D.Amati and G.Veneziano,Phys.Lett.B105(1981)358.[8]J.Lukierski,Phys.Lett.B121(1983)135.[9]A.D.Sakharov,Sov.Phys.Dokl.12(1968)1040[Dokl.Akad.Nauk Ser.Fiz.177(1967)70].[10]S.L.Adler,Rev.Mod.Phys.54(1982)729.[11]T.Kaluza,Sitzungsber.Preuss.Akad.Wiss.Berlin(Math.Phys.)K1(1921)966;O.Klein,Z.Phys.37(1926)895.[12]B.S.DeWitt,Dynamical Theory of Groups and Fields,Gordon and Breach,New York,1965.[13]C.Wetterich,Nucl.Phys.B244(1984)359;B261(1985)461.[14]C.Wetterich,arXiv:hep-th/0307145.[15]J.D.Bjorken,Annals Phys.24(1963)174;H.C.Ohanian,Phys.Rev.184(1969)1305;C.Barcelo,M.Visser and S.Liberati,Int.J.Mod.Phys.D10(2001)799[arXiv:gr-qc/0106002];P.Kraus and E.T.Tomboulis,Phys.Rev.D66(2002)045015[arXiv:hep-th/0203221].[16]C.Wetterich,Nucl.Phys.B242(1984)473.[17]J.Hubbard,Phys.Rev.Lett.3(1959)77R.Stratonovich,Dokl.Akad.Nauk.SSR115(1957)1097. [18]L.Alvarez-Gaume and E.Witten,Nucl.Phys.B234(1984)269.[19]V.P.Gusynin,E.V.Gorbar and V.V.Romankov,Nucl.Phys.B362(1991)449.[20]S.Yajima,Prog.Theor.Phys.79(1988)535.[21]C.Wetterich,Nucl.Phys.B211(1983)177.[22]C.Wetterich,Nucl.Phys.B223(1983)109;E.Witten,in Proc.of the1983Shelter Island ConferenceII(MIT Press,Cambridge,Mass.,1984).[23]C.Wetterich,Nucl.Phys.B302(1988)668;B.Ratra and P.J.Peebles,Phys.Rev.D37(1988)3406.[24]S.W.Hawking,Commun.Math.Phys.55(1977)133.6。