投入产出分析报告论文设计
项目投入产出分析报告

项目投入产出分析报告目录1. 项目投入分析1.1 投入成本1.2 投入时间2. 项目产出分析2.1 产出效益2.2 产出质量1. 项目投入分析1.1 投入成本在进行项目投入分析时,首先要考虑的就是项目的投入成本。
投入成本包括直接成本和间接成本两部分。
直接成本主要包括人力成本、物资成本、设备成本等,而间接成本则包括水电费、租金、管理费用等。
通过对投入成本的详细分析,可以有效地评估项目的经济性和可行性。
1.2 投入时间除了金钱上的投入,项目还需要投入大量的时间。
投入时间包括项目规划阶段、执行阶段和总结阶段。
在规划阶段,需要制定详细的时间表和计划,合理安排各项工作的时间节点。
在执行阶段,要及时跟进项目进展,避免时间延误导致项目进度延迟。
总结阶段则需要对整个项目的时间投入进行评估和反思,以提高未来项目的时间管理效率。
2. 项目产出分析2.1 产出效益项目的产出效益是评估项目成果的重要标准之一。
产出效益包括经济效益、社会效益和环境效益等多个方面。
经济效益主要是指项目是否能够带来利润或盈利,社会效益则是指项目对社会的积极影响,环境效益则是指项目对环境的保护与改善。
通过对项目产出效益进行综合评估,可以全面了解项目的成果和影响力。
2.2 产出质量除了产出效益外,项目的产出质量也是评估项目成果的重要指标。
产出质量包括项目成果的可靠性、稳定性和持久性等方面。
可靠性指项目成果能否按照设计要求正常运行,稳定性则指项目成果的稳定程度,持久性则是指项目成果的影响能否持续较长时间。
通过对项目产出质量进行评估,可以判断项目成果的实用性和可持续性。
项目投入产出分析报告

项目投入产出分析报告一、项目背景近年来,随着我国经济快速发展和市场竞争加剧,项目投资成为企业获取新的增长点和提升竞争力的重要途径。
本报告将对某项目的投入产出进行分析,以评估项目的可行性和潜在风险。
二、项目目标本项目旨在开发一款新型智能家电产品,提升用户的居家生活品质,并在市场上获得竞争优势。
该产品具有独特的设计理念和技术优势,预计可满足不同消费群体对智能家居的需求。
三、项目投入项目投入主要包括人力资源、资金、技术研发和市场推广等方面。
人力资源投入涉及项目团队的组建与培训,资金投入包括研发费用、设备购置和生产线建设等,技术研发投入涉及专利申请与技术迭代,市场推广投入包括宣传推广与销售渠道建设。
四、项目产出项目产出主要体现在产品销售和品牌价值方面。
产品销售是项目最直接的反映,通过市场推广和销售渠道建设,预计项目可得到一定的销售额。
品牌价值是项目的长期收益,通过产品质量和品牌溢价,项目将增强市场竞争力和品牌影响力。
五、投入产出分析进行投入产出分析是评估项目可行性和风险的重要手段。
根据现有数据和市场调研,我们进行了详细的分析。
1. 人力资源投入和产出:项目需要一支高效的团队来推动研发和市场推广,通过培训和合理激励机制,合理投入人力资源可提升项目效能,但过度的人力资源投入可能会增加成本而无法带来相应的产出。
2. 资金投入和产出:合理投入资金可支持项目的研发和生产,确保产品质量和市场竞争力,但过度投入资金可能会导致资金链紧张和回报周期延长。
3. 技术研发投入和产出:适度的技术研发投入能够使产品技术达到市场领先水平,增强产品吸引力和竞争力。
但技术迭代过多可能增加运营成本,而技术投入少则可能无法满足市场需求。
4. 市场推广投入和产出:充分的市场推广和销售渠道建设有助于扩大市场份额,提升产品销售额。
但过度的推广投入可能导致成本过高而无法得到相应的市场回报。
六、风险分析项目投入产出分析的同时,需要对项目的潜在风险进行评估。
投入产出分析报告

投入产出分析报告1. 引言投入产出分析是一种经济学方法,用于评估投资项目或经济活动的效益。
它通过比较投入和产出之间的关系,帮助我们了解资源的利用效率和效果。
本文将介绍投入产出分析的基本原理和应用,并通过实例分析展示其实际应用。
2. 投入产出分析的基本原理投入产出分析以一个经济系统为对象,将其划分为若干个部门,并考虑各个部门之间的投入和产出关系。
基本原理可以概括为以下几点:2.1 投入和产出投入是指用于生产的资源,如人力、资金、原材料等。
产出是指生产活动的结果,如产品、服务等。
投入和产出之间的关系可以用数学模型表示,从而进行分析。
2.2 投入产出系数投入产出系数表示单位产出所需的投入量。
例如,如果某个部门在生产一个单位的产品时需要10个单位的原材料和5个单位的人力资源,那么该部门的投入产出系数为10和5。
2.3 直接效益和间接效益直接效益是指投入产出关系中直接可观察到的效益,即产出与投入之间的比例。
间接效益是指投入产出关系中隐含的效益,即通过间接影响其他部门的效益。
3. 投入产出分析的应用投入产出分析在实际应用中可以帮助我们评估各种经济活动的效益,例如政府投资项目、企业生产决策等。
以下是两个案例的分析:3.1 政府投资项目假设某地政府决定投资修建一条高速公路,投入产出分析可以帮助评估该项目的效益。
首先,我们需要确定各个部门的投入产出系数,例如土木工程部门的投入产出系数为10和5。
然后,计算投入和产出之间的关系,并综合考虑直接效益和间接效益,得出该项目的总体效益。
3.2 企业生产决策假设某企业考虑引进一项新的生产技术,投入产出分析可以帮助评估该决策的可行性。
首先,我们需要确定该技术的投入产出系数,例如该技术所需的人力资源和资金投入量。
然后,计算投入和产出之间的关系,并综合考虑直接效益和间接效益,得出该决策的效益。
4. 结论投入产出分析是一种有效的经济分析方法,可以帮助我们评估投资项目或经济活动的效益。
投入产出分析论文

投入产出分析课程论文投入产出模型应用与分析投入产出模型应用与分析一、投入产出分析简介投入产出分析,是研究经济系统各个部分间表现为投入与产出的相互依存关系的经济数量方法。
投入是进行一项活动的消耗。
如生产过程的消耗包括本系统内各部门产品的消耗(中间投入)和初始投入要素的消耗(最初投入)。
产出是指进行一项活动的结果。
如生产活动的结果是为本系统各部分生产的产品(物质产品和劳务)。
瓦西里·列昂剔夫(Wassily W.Leontief,1906—1999)是投入产出账户的创始人。
投入产出表同时表现了社会产品的实物分配和价值构成,全面反映了社会再生产中各部门的经济联系。
利用投入产出表及其数学模型,通过确定一些十分重要的经济参数,可以深入分析国民经济的各种重大比例和经济结构,这就对社会再生产过程进行系统的经济分析提供了非常有用的工具。
价值型投入产出表是根据国民经济各产品部门本期生产活动的产品与服务的分配去向和消耗来源排列而成的一张棋盘式平衡表。
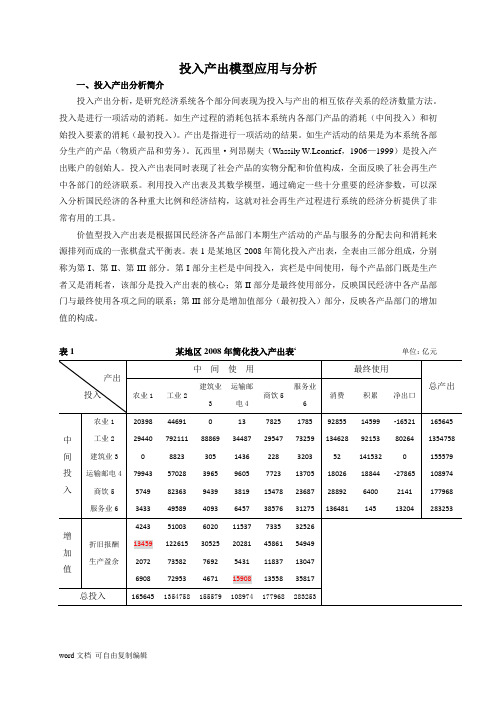
表1是某地区2008年简化投入产出表,全表由三部分组成,分别称为第I、第II、第III部分。
第I部分主栏是中间投入,宾栏是中间使用,每个产品部门既是生产者又是消耗者,该部分是投入产出表的核心;第II部分是最终使用部分,反映国民经济中各产品部门与最终使用各项之间的联系;第III部分是增加值部分(最初投入)部分,反映各产品部门的增加值的构成。
表1 某地区2008年简化投入产出表i单位:亿元二、投入产出模型(一)建立模型 1.行模型(1)建立行模型:i i X y nj ij x =+∑=1 (i =1,2,...,n) 引入直接消耗系数 ij a ,即:ij a =ij x /j X可得:i i X y jX nj ij a =+∑=1即用矩阵表示为: AX+Y=X化简后可得价值型行数学模型: X=(I-A)-1Y 或 X=B Y (2)计算相关矩阵A ,B=(I-A)-1-I ,B =(I-A)-1 =B+I直接消耗系数矩阵:A=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.1104 0.21680.05930.0263 0.0366 0.0207 0.0836 0.0870 0.0350 0.0607 0.0608 0.0347 0.0484 0.0434 0.0881 0.0255 0.0421 0.4826 0.0113 0.00130.0132 0.0020 0.0065 0.0000 0.2586 0.1660 0.3165 0.5712 0.5847 0.1777 0.0063 0.04400.0001 0.0000 0.03301231.0完全消耗系数矩阵:B=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.22350.34120.16110.1660 0.1902 0.1696 0.1885 0.1958 0.1385 0.2087 0.2227 0.1731 0.1508 0.1664 0.1908 0.1689 0.2174 0.7095 0.02270.0133 0.0250 0.0178 0.0240 0.0197 1.00730.87641.11911.7485 1.8655 1.25510.0562 0.0955 0.0504 0.0775 0.12040.1976完全需要系数矩阵:B =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 1.2235 0.3412 0.1611 0.1660 0.1902 0.1696 0.1885 1.1958 0.1385 0.2087 0.2227 0.1731 0.1508 0.1664 1.1908 0.1689 0.2174 0.7095 0.0227 0.0133 0.0250 1.0178 0.0240 0.0197 1.0073 0.8764 1.1191 1.7485 2.8655 1.25510.0562 0.0955 0.0504 0.0775 0.12041.1976(3)价值型行数学模型 X=(I-A)-1Y=B Y⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛654321X X X X X X =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 1.2235 0.3412 0.1611 0.1660 0.1902 0.1696 0.1885 1.1958 0.1385 0.2087 0.2227 0.17310.1508 0.1664 1.1908 0.1689 0.2174 0.7095 0.0227 0.0133 0.0250 1.0178 0.0240 0.0197 1.0073 0.8764 1.1191 1.7485 2.8655 1.25510.0562 0.0955 0.0504 0.0775 0.1204 1.1976⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛654321Y Y Y Y Y Y2列模型 (1)建立列模型j j j j j X s t v d ni ij x =++++∑=1 (j =1,2,...,n)引入直接消耗系数 ij a 可得:j j j j j X s t v d j X ni ij a =++++∑=1即用矩阵表示为:AcX+N=X化简后可得价值型列数学模型: X=(I-Ac)-1N (2)计算相关矩阵A C ,(I-Ac)-1物耗系数矩阵:Ac=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.5187000000 0.5584000000 0.5122000000 0.6856000000 0.76370000000.8389增加值系数矩阵:(I-Ac)-1=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 2.0775*******.26440000002.0500000003.181********.231590000006.2081(3)价值型列数学模型 X=(I-Ac)-1N⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛654321X X X X X X =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛ 2.0775*******.26440000002.05000000003.181********.231590000006.2081⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛654321N N N N N N ij x :第i 部门(行部门)生产的产品或服务分配给第j 部门(列部门)用于生产消耗的产品产值;第j 部门(列部门)生产过程中直接消耗第i 部门的产品或服务的产品产值;i y :第i 部门在本期产品中提供的最终使用额,包括消费和积累;j d 、j v 、j t 、j s :分别为第j 部门的折旧,劳动报酬,生产税净额,和营业盈余; j m :为第j 部门的社会纯收入,等于j t +j s ; j N :为第j 部门的增加值,等于j d +j v +j t +j s ;i X :第i 部门总产出 ;j X :第j 部门总投入;A :直接消耗系数矩阵(ij a )n n ⨯X=(X 1 X 2.......X N )T —总产出的列向量;Y=(y 1 y 2.......y N )T —最终使用的列向量;j i ,=1,2,3,4,5,6分别表示农业部门、工业部门、建筑业部门、运输邮电部门、商饮部门和服务业部门;n =6。
投入产出分析论文 投入产出模型应用与分析
投入产出模型应用与分析一、投入产出分析简介投入产出分析,是研究经济系统各个部分间表现为投入与产出的相互依存关系的经济数量方法。
投入是进行一项活动的消耗。
如生产过程的消耗包括本系统内各部门产品的消耗(中间投入)和初始投入要素的消耗(最初投入)。
产出是指进行一项活动的结果。
如生产活动的结果是为本系统各部分生产的产品(物质产品和劳务)。
瓦西里·列昂剔夫(Wassily W.Leontief,1906—1999)是投入产出账户的创始人。
投入产出表同时表现了社会产品的实物分配和价值构成,全面反映了社会再生产中各部门的经济联系。
利用投入产出表及其数学模型,通过确定一些十分重要的经济参数,可以深入分析国民经济的各种重大比例和经济结构,这就对社会再生产过程进行系统的经济分析提供了非常有用的工具。
价值型投入产出表是根据国民经济各产品部门本期生产活动的产品与服务的分配去向和消耗来源排列而成的一张棋盘式平衡表。
表1是某地区2008年简化投入产出表,全表由三部分组成,分别称为第I、第II、第III部分。
第I部分主栏是中间投入,宾栏是中间使用,每个产品部门既是生产者又是消耗者,该部分是投入产出表的核心;第II部分是最终使用部分,反映国民经济中各产品部门与最终使用各项之间的联系;第III部分是增加值部分(最初投入)部分,反映各产品部门的增加值的构成。
表1 某地区2008年简化投入产出表i单位:亿元二、投入产出模型(一)建立模型 1.行模型(1)建立行模型:i i X y nj ij x =+∑=1 (i =1,2,...,n) 引入直接消耗系数 ij a ,即:ij a =ij x /j X可得:i i X y jX nj ij a =+∑=1即用矩阵表示为: AX+Y=X化简后可得价值型行数学模型: X=(I-A)-1Y 或 X=B Y (2)计算相关矩阵A ,B=(I-A)-1-I ,B =(I-A)-1 =B+I直接消耗系数矩阵:A=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.1104 0.21680.05930.0263 0.0366 0.0207 0.0836 0.0870 0.0350 0.0607 0.0608 0.0347 0.0484 0.0434 0.0881 0.0255 0.0421 0.4826 0.0113 0.00130.0132 0.0020 0.0065 0.0000 0.2586 0.1660 0.3165 0.5712 0.5847 0.1777 0.0063 0.04400.0001 0.0000 0.03301231.0完全消耗系数矩阵:B=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.22350.34120.16110.1660 0.1902 0.1696 0.1885 0.1958 0.1385 0.2087 0.2227 0.1731 0.1508 0.1664 0.1908 0.1689 0.2174 0.7095 0.02270.0133 0.0250 0.0178 0.0240 0.0197 1.00730.87641.11911.7485 1.8655 1.25510.0562 0.0955 0.0504 0.0775 0.12040.1976完全需要系数矩阵:B =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 1.2235 0.3412 0.1611 0.1660 0.1902 0.1696 0.1885 1.1958 0.1385 0.2087 0.2227 0.1731 0.1508 0.1664 1.1908 0.1689 0.2174 0.7095 0.0227 0.0133 0.0250 1.0178 0.0240 0.0197 1.0073 0.8764 1.1191 1.7485 2.8655 1.25510.0562 0.0955 0.0504 0.0775 0.12041.1976(3)价值型行数学模型 X=(I-A)-1Y=B Y⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛654321X X X X X X =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 1.2235 0.3412 0.1611 0.1660 0.1902 0.1696 0.1885 1.1958 0.1385 0.2087 0.2227 0.17310.1508 0.1664 1.1908 0.1689 0.2174 0.7095 0.0227 0.0133 0.0250 1.0178 0.0240 0.0197 1.0073 0.8764 1.1191 1.7485 2.8655 1.25510.0562 0.0955 0.0504 0.0775 0.1204 1.1976⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛654321Y Y Y Y Y Y2列模型 (1)建立列模型j j j j j X s t v d ni ij x =++++∑=1 (j =1,2,...,n)引入直接消耗系数 ij a 可得:j j j j j X s t v d j X ni ij a =++++∑=1即用矩阵表示为:AcX+N=X化简后可得价值型列数学模型: X=(I-Ac)-1N (2)计算相关矩阵A C ,(I-Ac)-1物耗系数矩阵:Ac=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.5187000000 0.5584000000 0.5122000000 0.6856000000 0.76370000000.8389增加值系数矩阵:(I-Ac)-1=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 2.0775*******.26440000002.0500000003.181********.231590000006.2081(3)价值型列数学模型 X=(I-Ac)-1N⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛654321X X X X X X =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛ 2.0775*******.26440000002.05000000003.181********.231590000006.2081⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛654321N N N N N N ij x :第i 部门(行部门)生产的产品或服务分配给第j 部门(列部门)用于生产消耗的产品产值;第j 部门(列部门)生产过程中直接消耗第i 部门的产品或服务的产品产值;i y :第i 部门在本期产品中提供的最终使用额,包括消费和积累;j d 、j v 、j t 、j s :分别为第j 部门的折旧,劳动报酬,生产税净额,和营业盈余; j m :为第j 部门的社会纯收入,等于j t +j s ; j N :为第j 部门的增加值,等于j d +j v +j t +j s ;i X :第i 部门总产出 ;j X :第j 部门总投入;A :直接消耗系数矩阵(ij a )n n ⨯X=(X 1 X 2.......X N )T —总产出的列向量;Y=(y 1 y 2.......y N )T —最终使用的列向量;j i ,=1,2,3,4,5,6分别表示农业部门、工业部门、建筑业部门、运输邮电部门、商饮部门和服务业部门;n =6。
企业投入产出比分析报告

企业投入产出比分析报告1.引言1.1 概述概述企业投入产出比分析是对企业经营活动中投入与产出之间关系的深入研究和评估。
在企业经营管理中,对于投入成本和产出效益的分析是至关重要的,它直接关系到企业的盈利能力和竞争力。
通过对企业投入产出比的分析,可以帮助企业更好地调整资源配置,优化生产流程,提高效益和竞争力。
本报告将通过对企业投入和产出两个方面的分析,结合计算投入产出比的方法,对企业的经营状况进行全面评估,为企业经营决策提供有力的数据支持。
同时,本报告还将探讨投入产出比的意义和评价,以期为企业提供科学的经营指导,促进企业的可持续发展。
文章结构部分的内容可以包括对整篇文章的结构进行简要介绍,以便读者能够更好地理解文章的内容和逻辑。
例如:"文章结构部分将会对本文的组织结构进行简要介绍,包括引言、正文和结论部分的内容。
通过明确的结构布局,读者将更容易理解本文的内容和逻辑线索。
".2 如何计算投入产出比":{},"2.3.3 投入产出比的意义":{}}},"3.结论":{"3.1 总结投入分析":{},"3.2 总结产出分析":{},"3.3 投入产出比的评价":{}}}}请编写文章1.2 文章结构部分的内容1.3 目的本报告的目的在于对企业的投入产出比进行深入分析和评估。
通过对企业投入和产出的要素、成本、价值以及效益进行系统性的研究和对比,旨在帮助企业管理者更好地了解和评判企业经营的效率和盈利能力。
同时,通过对投入产出比的计算和意义进行阐述,为企业提供科学的决策依据,指导企业实现投入和产出的平衡和优化,提高经营绩效和竞争力。
"3.2 总结产出分析":{},"3.3 投入产出比的评价":{}}}}请编写文章1.3 目的部分的内容2.正文2.1 企业投入分析企业的投入分析是指对企业在生产经营过程中所投入的要素、成本以及投入所带来的效益进行分析。
企业投入产出分析报告

企业投入产出分析报告一、引言企业投入产出分析是一种通过对企业投入和产出进行量化和比较的方法,以评估企业的经济效益、生产效率和资源利用,从而为企业的决策和管理提供数据支持。
本文将对某企业的投入产出情况进行分析,并提出相应的建议。
二、投入分析1. 人力资源投入根据企业提供的数据,该企业共有100名员工,其中管理人员20名,技术人员30名,劳动力50名。
按照市场平均工资标准,计算得出该企业的人力资源成本为150万元。
2. 生产设备投入该企业购置了先进的生产设备,设备总投资为200万元,设备预计寿命10年,每年的折旧费用为20万元。
3. 原材料投入根据企业的生产数据,每年需要购买原材料50吨,原材料的购买价格为每吨5000元,因此每年的原材料投入为25万元。
三、产出分析1. 产品产出根据企业提供的生产数据,该企业每年生产5000个产品,产品的售价为每个1000元,因此每年的产品产出为500万元。
2. 销售收入根据产品的售价和每年生产的产品数量,该企业的销售收入为500万元。
四、投入产出比较1. 人力资源产出比人力资源产出比=销售收入/人力资源投入= 500万元/ 150万元≈3.332. 设备产出比设备产出比=销售收入/设备投入= 500万元/ 200万元= 2.53. 原材料产出比原材料产出比=销售收入/原材料投入= 500万元/ 25万元= 20五、分析及建议通过投入产出比较分析可知,该企业人力资源产出比较高,设备产出比和原材料产出比较低。
由此可以得出以下分析和建议:1. 人力资源投入产出比较高,说明该企业的员工绩效相对较高,但也需要加强管理人员的培训和激励,以保持良好的团队合作和高效的生产。
2. 设备产出比较低,可能是由于设备的使用效率不高或者已经进入到使用寿命的后期。
建议对设备进行维护和升级,提高设备的生产效率,减少折旧费用。
3. 原材料产出比较低,可能是因为采购成本较高或者原材料的使用不够合理。
投入产出分析报告

投入产出分析报告1. 引言投入产出分析是一种经济学方法,用于评估各种经济活动的效果和影响。
它通过分析投入(如资金、劳动力)和产出(如产品、服务)之间的关系,帮助决策者做出合理的决策。
本报告将对某公司的投入产出进行分析,并提出相应的建议。
2. 背景介绍2.1 公司简介某公司是一家中小型制造业企业,主要生产电子产品。
公司拥有自己的工厂和研发团队,同时也有自己的销售渠道。
在充满竞争的市场环境下,公司不断寻求提高生产效率和产品质量的方法。
2.2 问题陈述由于市场竞争激烈,公司希望减少生产成本,并提高产品的市场竞争力。
因此,公司希望通过投入产出分析来评估各种生产因素对产品产出的影响,进而推动公司的相关决策。
3. 数据收集和方法为了进行投入产出分析,我们首先收集了以下数据:•生产员工的人数和工资•生产所需的材料和设备成本•公司销售的产品数量和售价我们采用了以下方法进行投入产出分析:1.计算总投入和总产出:将所有投入(如工资、材料成本)进行总和,同时计算总产出(产品的数量乘以售价)。
2.计算平均投入和平均产出:将总投入和总产出除以生产的产品数量,得到平均投入和平均产出。
3.计算边际投入产出比:根据前一步计算的平均投入和平均产出,计算增加或减少1单位投入所带来的产出变化。
4.进行敏感性分析:通过调整投入的数量或价格,观察产出的变化,并评估其对公司决策的影响。
4. 结果分析4.1 总投入和总产出根据数据收集和计算,我们得到了以下结果:•总投入:XXXXX元•总产出:XXXXX个产品4.2 平均投入和平均产出基于总投入和总产出的数据,计算得到了以下结果:•平均投入:XXXXX元/个产品•平均产出:XXXXX元/个产品4.3 边际投入产出比根据平均投入和平均产出的数据,计算得到了以下结果:•边际投入产出比:XXXXX(1单位投入所带来的产出变化)5. 建议根据我们的投入产出分析结果,我们提出以下建议来改善公司的效益:1.提高生产员工的效率:通过培训和激励措施,提高员工的生产效率,减少对劳动力的需求,从而降低平均投入和提高边际投入产出比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
投入产出模型应用与分析一、投入产出分析简介投入产出分析,是研究经济系统各个部分间表现为投入与产出的相互依存关系的经济数量方法。
投入是进行一项活动的消耗。
如生产过程的消耗包括本系统各部门产品的消耗(中间投入)和初始投入要素的消耗(最初投入)。
产出是指进行一项活动的结果。
如生产活动的结果是为本系统各部分生产的产品(物质产品和劳务)。
瓦西里·列昂剔夫(Wassily W.Leontief,1906—1999)是投入产出账户的创始人。
投入产出表同时表现了社会产品的实物分配和价值构成,全面反映了社会再生产中各部门的经济联系。
利用投入产出表及其数学模型,通过确定一些十分重要的经济参数,可以深入分析国民经济的各种重大比例和经济结构,这就对社会再生产过程进行系统的经济分析提供了非常有用的工具。
价值型投入产出表是根据国民经济各产品部门本期生产活动的产品与服务的分配去向和消耗来源排列而成的一棋盘式平衡表。
表1是某地区2008年简化投入产出表,全表由三部分组成,分别称为第I、第II、第III部分。
第I部分主栏是中间投入,宾栏是中间使用,每个产品部门既是生产者又是消耗者,该部分是投入产出表的核心;第II部分是最终使用部分,反映国民经济中各产品部门与最终使用各项之间的联系;第III部分是增加值部分(最初投入)部分,反映各产品部门的增加值的构成。
表1 某地区2008年简化投入产出表i单位:亿元二、投入产出模型(一)建立模型 1.行模型(1)建立行模型:i i X y nj ij x =+∑=1 (i =1,2,...,n) 引入直接消耗系数 ij a ,即:ij a =ij x /j X可得:i i X y jX nj ij a =+∑=1即用矩阵表示为: AX+Y=X化简后可得价值型行数学模型: X=(I-A)-1Y 或 X=B Y (2)计算相关矩阵A ,B=(I-A)-1-I ,B =(I-A)-1 =B+I直接消耗系数矩阵:A=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.1104 0.21680.05930.0263 0.0366 0.0207 0.0836 0.0870 0.0350 0.0607 0.0608 0.0347 0.0484 0.0434 0.0881 0.0255 0.0421 0.4826 0.0113 0.00130.0132 0.0020 0.0065 0.0000 0.2586 0.1660 0.3165 0.5712 0.5847 0.1777 0.0063 0.04400.0001 0.0000 0.03301231.0完全消耗系数矩阵:B=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.22350.34120.16110.1660 0.1902 0.1696 0.1885 0.1958 0.1385 0.2087 0.2227 0.1731 0.1508 0.1664 0.1908 0.1689 0.2174 0.7095 0.02270.0133 0.0250 0.0178 0.0240 0.0197 1.00730.87641.11911.7485 1.8655 1.25510.0562 0.0955 0.0504 0.0775 0.12040.1976完全需要系数矩阵:B =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 1.2235 0.3412 0.1611 0.1660 0.1902 0.1696 0.1885 1.1958 0.1385 0.2087 0.2227 0.1731 0.1508 0.1664 1.1908 0.1689 0.2174 0.7095 0.0227 0.0133 0.0250 1.0178 0.0240 0.0197 1.0073 0.8764 1.1191 1.7485 2.8655 1.25510.0562 0.0955 0.0504 0.0775 0.12041.1976(3)价值型行数学模型 X=(I-A)-1Y=B Y⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛654321X X X X X X =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 1.2235 0.3412 0.1611 0.1660 0.1902 0.1696 0.1885 1.1958 0.1385 0.2087 0.2227 0.17310.1508 0.1664 1.1908 0.1689 0.2174 0.7095 0.0227 0.0133 0.0250 1.0178 0.0240 0.0197 1.0073 0.8764 1.1191 1.7485 2.8655 1.25510.0562 0.0955 0.0504 0.0775 0.1204 1.1976⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛654321Y Y Y Y Y Y2列模型 (1)建立列模型j j j j j X s t v d ni ij x =++++∑=1 (j =1,2,...,n)引入直接消耗系数 ij a 可得:j j j j j X s t v d j X ni ij a =++++∑=1即用矩阵表示为:AcX+N=X化简后可得价值型列数学模型: X=(I-Ac)-1N (2)计算相关矩阵A C ,(I-Ac)-1物耗系数矩阵:Ac=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.5187000000 0.5584000000 0.5122000000 0.6856000000 0.76370000000.8389增加值系数矩阵:(I-Ac)-1=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 2.0775*******.26440000002.0500000003.181********.231590000006.2081(3)价值型列数学模型 X=(I-Ac)-1N⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛654321X X X X X X =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛ 2.0775*******.26440000002.05000000003.181********.231590000006.2081⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛654321N N N N N N ij x :第i 部门(行部门)生产的产品或服务分配给第j 部门(列部门)用于生产消耗的产品产值;第j 部门(列部门)生产过程中直接消耗第i 部门的产品或服务的产品产值;i y :第i 部门在本期产品中提供的最终使用额,包括消费和积累;j d 、j v 、j t 、j s :分别为第j 部门的折旧,劳动报酬,生产税净额,和营业盈余; j m :为第j 部门的社会纯收入,等于j t +j s ; j N :为第j 部门的增加值,等于j d +j v +j t +j s ;i X :第i 部门总产出 ;j X :第j 部门总投入;A :直接消耗系数矩阵(ij a )n n ⨯X=(X 1 X 2.......X N )T —总产出的列向量;Y=(y 1 y 2.......y N )T —最终使用的列向量;j i ,=1,2,3,4,5,6分别表示农业部门、工业部门、建筑业部门、运输邮电部门、商饮部门和服务业部门;n =6。
.(二)主要系数计算与分析: 1分配系数分配系数是第i 部门提供的产品和服务在各种用途之间的分配使用比例。
中间产品分配系数为ij h =ijx /i X ,根据数据计算H=(66)(⨯=ij h H ,Hi (主对角线为∑=61j ij h 的对角矩阵)。
H =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.1104 0.13620.0228 0.0144 0.1751 0.0121 0.1331 0.0870 0.0215 0.0530 0.4628 0.0323 0.1258 0.0709 0.08810.0364 0.5233 0.7336 0.206 0.00150.0092 0.0020 0.0567 0.0000 0.0541 0.0218 0.0255 0.0656 0.5847 0.0217 0.0108 0.04720.0001 0.0000 0.2698 0.1231H i =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.4710000000 0.7897000000 1.5781000000 0.0900000000 0.77340000000.4510 可用中间分配系数矩阵建立投入产出模型: 行模型:HiX+Y=X 即X=(I-Hi)-1Y 列模型:H T X+N=X 即X=(I-H T )-1N 2增加值系数: (1)折旧系数直接折旧系数dj a = j d /j X ,完全折旧系数dj b =dj a + ∑=ni ij a di b 1 (j i ,=1,2,...,n)直接折旧系数行向量61)(⨯=dj d a A ,完全折旧系数B d = A d (I-A)-1 ,计算结果如下: 直接折旧系数行向量A d =()0.11480.04120.10580.03860.03760.0256完全折旧系数行向量B d =A d (I-A)-1 =() 0.0896 0.1008 0.0888 0.1140 0.1283 0.1548(2)劳动者报酬系数直接劳动者报酬系数行向量A v =(0.0813 0.0905 0.1962 0.1861 0.2577 0.1940)完全劳动者报酬系数行向量B v = Av(I-A)-1 =(0.3431 0.3181 0.2855 0.2127 0.2373 0.2202) (3)生产税净额系数:直接生产税净额系数行向量A t =(0.0125 0.0543 0.0494 0.0498 0.0665 0.0461) 完全生产税净额系数行向量B t = At(I-A)-1 =(0.1263 0.1384 0.1268 0.0888 0.0865 0.0869) (4)营业盈余系数:直接营业盈余系数行向量As =(0.0417 0.0538 0.0300 0.1460 0.0762 0.1264) 完全营业盈余系数行向量Bs= As(I-A)-1 =(0.2146 0.1790 0.1595 0.1219 0.1339 0.1219) 劳动报酬、社会纯收入等完全系数又称为影响乘数,可以分析调整措施的影响程度。
3 综合直接消耗系数:cj a =∑=ni ij a 1(j =1,2,3,4,5,6)混合直接消耗系数:ei a =∑=nj ij a 1(i =1,2,3,4,5,6)分析:下标1,2,3,4,5,6分别表示农业部门、工业部门、建筑业部门、运输邮电部门、商饮部门和服务业部门。
从计算结果中分析,农业的综合直接消耗系数最大,说明农业对所有部门的直接依存强度最高,其他服务部门次之。
