材料力学期中试题2014-2017
材料力学试卷试题(附答案)
5．如图所示为矩形截面悬臂梁，在梁的自由端突然加一个重为 的物块，求梁的最大弯曲动应力。（4分）
6．如图所示为两根材料相同的简支梁，求两梁中点的挠度之比 。（4分）
7．两块相同钢板用5个铆钉连接如图所示，已知铆钉直径d，钢板厚度t，宽度b，求铆钉所受的最大切应力，并画出上钢板的轴力图。（6分）
（14分）
五、圆截面直角弯杆ABC放置于图示的水平位置，已知 ，水平力 ，铅垂均布载荷 ，材料的许用应力 ，试用第三强度理论设计杆的直径 。（14分）
8．超静定结构如图所示，所有杆件不计自重，AB为刚性杆，试写出变形协调方程。（4分）
二、作图示梁的剪力图与弯矩图。（10分）
三、不计剪力的影响，已知EI，试用能量法求图示悬臂梁自由端的挠度 。
（12分）
四、铸铁梁的载荷及截面尺寸如图所示，其中 。已知许用拉应力 ，许用压应力 。试按正应力条件校核梁的强度。若载荷不变，但将截面倒置，问是否合理？为什么？
材料力学试卷试题(附答案)
一、简单计算题（共38分）
1．如图所示是一枚被称为“孔方兄”的中国古钱币，设圆的直径为 ，挖去的正方形边长为 ，若 ，求该截面的弯曲截面系数 。（6分）
2. 已知某点处的应力状态如图所示， 弹性模量 ，泊松比 ，求该点处的三个主应力及最大正应变。
（6分）
3．试画出低碳钢的拉伸应力－应变曲线，并在图上标出4个极限应力。（4分）
(完整版)材料力学试题及答案
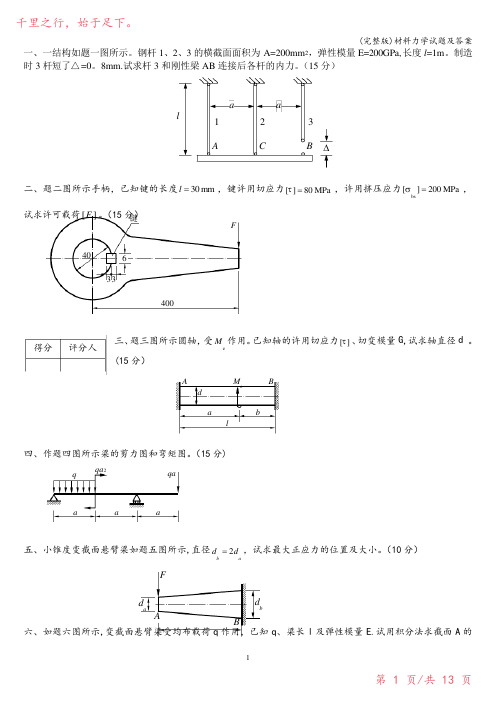
一、一结构如题一图所示。
钢杆1、2、3的横截面面积为A=200mm 2，弹性模量E=200GPa,长度l =1m 。
制造时3杆短了△=0。
8mm.试求杆3和刚性梁AB 连接后各杆的内力。
（15分）aalABC123∆二、题二图所示手柄，已知键的长度30 mm l =，键许用切应力[]80 MPa τ=，许用挤压应力bs[]200 MPa σ=，试求许可载荷][F 。
（15分）三、题三图所示圆轴，受eM 作用。
已知轴的许用切应力[]τ、切变模量G ,试求轴直径d 。
(15分）四、作题四图所示梁的剪力图和弯矩图。
（15分)五、小锥度变截面悬臂梁如题五图所示,直径2bad d =，试求最大正应力的位置及大小。
（10分）六、如题六图所示,变截面悬臂梁受均布载荷q 作用，已知q 、梁长l 及弹性模量E .试用积分法求截面A 的得分评分人F键40633400Aal bM eBd a a aqqaqa 2dbBda AF挠度w A 和截面C 的转角θC .（15分)七、如图所示工字形截面梁AB ,截面的惯性矩672.5610zI -=⨯m 4，求固定端截面翼缘和腹板交界处点a 的主应力和主方向。
（15分）一、（15分)（1）静力分析（如图（a）)1N F2N F3N F图(a)∑=+=231,0N N N yF F F F（a)∑==31,0N N CF F M(b)（2）几何分析（如图（b)）1l∆2l∆3l∆∆图（b）wql /3x lhb 0b (x )b (x )BAC 50kN AB0.75m303030140150zya∆=∆+∆+∆3212l l l(3）物理条件EA l F l N 11=∆，EA l F l N 22=∆，EAl F l N 33=∆ （4）补充方程∆=++EAlF EA l F EA l F N N N 3212 （c） （5）联立（a）、（b）、(c)式解得:kN FkN FF N N N 67.10,33.5231===二、(15分）以手柄和半个键为隔离体，S0, 204000OM F F ∑=⨯-⨯=取半个键为隔离体，bsS20F F F ==由剪切：S []s FA ττ=≤，720 N F = 由挤压:bs bs bs bs[][], 900N FF Aσσ=≤≤取[]720N F =.三、（15分）eABM M M +=0ABϕ=， A B M a M b ⋅=⋅得 e B a M M a b =+, e A b MM a b=+当a b >时 e316π ()[]M ad a b τ≥+；当b a >时 e316π ()[]M bd a b τ≥+。
材料力学期中试题及答案
一、判断题（共20分，每题2分）1．杆件受扭时，横截面上的最大切应力发生在距截面形心最远处。
（ × ） 2．切应力互等定理，仅适用于纯剪切情况。
（ × ) 3．受扭杆件的扭矩，仅与杆件受到的转矩（外力偶矩）有关，而与杆件的材料及其横截面的大小、形状无关。
( √ ) 4．受扭圆轴在横截面上和包含轴的纵向截面上均无正应力。
（ √ ) 5．因为构件是变形固体，在研究构件平衡时，应按变形后的尺寸进行计算。
（ × ） 6．杆件的基本变形只是拉(压)、剪、扭和弯四种，如果还有另一种变形，必定是这四种变形的某种组合。
（ √ )7. 在非均质材料的等截面梁中，最大正应力maxσ不一定出现在maxM的截面上。
（ × ）8.梁产生纯弯曲时，过梁内任一点的任一截面上的剪应力都等于零。
（ × ） 9. 中性轴是梁横截面与中性层的交线。
梁发生平面弯曲时，其横截面绕中性轴旋转。
（√） 10.横力弯曲时，横截面上的最大切应力不一定发生在截面的中性轴上。
（ √ ）二、填空题（共20分，每空2分）1．材料力学的任务是满足 强度 ， 刚度 ， 稳定性 的要求下，为设计经济安全的构件提供必要的理论基础和计算方法。
2． 当实心圆轴的直径增加1培时，其抗扭强度增加到原来的（ 8 ）倍，抗扭刚度增加到原来的（ 16 ）倍。
3. 如图所示的矩形截面悬臂梁，其高为h 、宽为b 、长为l ，则在其中性层的水平剪力=S FbhF23 。
4. 如图3所示的外伸梁，已知B 截面转角θB =EI Fl 162，则C 截面的挠度y C =EIFl 323。
x5.梁的三种截面形状和尺寸如图所示，则其抗弯截面系数分别为226161bH BH -、 H Bh BH 66132- 和 Hbh BH 66132- 。
三、 选择题（共16分，每题2分）1． 梁在集中力偶作用的截面处，它的内力图为（ C )。
材料力学期中试卷答案
b，若解：192)13(12)2/(64444d d d I I I zr zc z -=-=-=ππ96)13()2//(3d d I W z z -==π03. 阶梯轴尺寸及受力如图所示，试求AB 段的最大切应力1max τ与BC 段的最大切应力2max τ之比，以及AC 截面之间的相对扭转角。
解：16/)2(31d W p π=，16/32d W p π=1111max /3/p p W m W T ==τ，2222max //p p W m W T ==τ，8/3/3/122max 1max ==p p W W ττ 44422113832/32/)2(3d G mld G ml d G ml GI l T GI l T GI l T p p pi i i AC πππϕ=+=+=∑= 04. 已知某点处的应力状态如图所示，MPa 60=τ，MPa 100=σ，弹性模量GPa 200=E ，泊松比25.0=ν，求该点处的三个主应力及最大正应变。
解：MPa 60MPa,60MPa,100321--=====τστσσσ 3313211105.0)10200/(100/)]([1-⨯=⨯==+-=E Eσσσνσε05. 直径为d 的圆柱放在直径为D =3d 、厚为t 的圆形基座上，地基对基座的支反力为均匀分布，圆柱承受轴向压力P ，试求基座剪切面的剪力。
解： PF Pd D P F F s s y 98)2()2(:022==⨯+=∑则：ππy二、圆轴直径56mm d =，长2m l =，64110m p I -=⨯，533.610m p W -=⨯左端固定，右端有一直径400mm D =的鼓轮。
轮上绕以钢绳，绳的端点A 悬挂吊盘。
绳长110m l =，横截面面积2100mm A =，弹性模量200GPa E =。
重量17.36kN W =的物体放置在吊盘中，轴的切变模量80GPa G =，求轴内最大切应力和绳内最大正应力。
材料力学试题(含答案)
材料力学试题（含答案）一、选择题1.图示结构中，AB 杆将发生的变形为：（）A.弯曲变形B.拉压变形C.弯曲与压缩的组合变形D.弯曲与拉伸的组合变形2．图示简支梁上作用有集中力F 和均布载荷q ，则C 截面处（）。
A ．剪力图有突变，弯矩图光滑连续B ．剪力图有尖角，弯矩图光滑连续C ．剪力图有尖角，弯矩图有尖角D ．剪力图有突变，弯矩图有尖角3．以下说法错误的是（）。
A 构件材料的极限应力由计算可得B 塑性材料已屈服极限为极限应力C 脆性材料以强度极限作为极限应力D 材料的破坏形式主要有2种4．图示梁上a 点的应力状态有下列四种答案，正确的是（）。
二、填空题1．（2分）一受扭圆轴如图示，其截面m-m 上的扭矩T 等于。
2．（4分，每空1分）在拉伸试验中，低碳钢材料试件屈服时试件表面会出现与轴线约成的滑移线，这是因为该面上作用有最大应力；铸铁材料试件将沿着被拉断，断裂发生在最大应力作用面。
3．（4分，每空1分）梁在发生对称弯曲时，横截面上正应力沿截面高度按分布；中性轴上点的正应力为；矩形截面梁横截面上的切应力沿截面高度按FqABC 题1－2图A B C D题1－4图题2－1图分布；截面边缘上点的切应力为；4.（5分）已知AB 杆直径d ＝30mm ，a ＝1m ，E ＝210GPa 。
若测得AB 杆应变ε＝7.15×10–4时，则载荷P 的值为。
三、计算题1．（15分）已知外伸梁AB 的载荷图、弯矩图和截面图，C 为截面形心。
B 截面上边缘处的应力为MPa 60=σ，求（1）全梁上的最大拉应力max t σ；(2)全梁上的最大压应力max c σ。
题3－1图2.（15分）平行杆系1、2、3悬吊着刚性横梁AB 如图所示。
在横梁上作用有荷载G 。
如杆1、2、3的截面积、长度、弹性模量均相同，分别为A 、l 、E 。
试求三根杆的轴力N1、N2、N3。
题3-2图3.（15分）如图所示圆轴，已知直径100d mm =，4T kN m =⋅，400F kN =，15e mm =，屈服极限200s MPa σ=，安全系数2n =，试求：（1）指出危险点并画出相应微单元体的应力状态图；（2）按第三强度理论校核轴的强度。
材料力学考试试题及答案
材料力学考试试题及答案一、选择题（每题2分，共20分）1. 材料力学中，下列哪一项不是材料的基本力学性能？A. 弹性B. 塑性C. 韧性D. 硬度2. 材料在拉伸过程中，若应力超过屈服点后继续增加，材料将进入：A. 弹性阶段B. 塑性阶段C. 断裂阶段D. 疲劳阶段3. 材料的弹性模量E表示的是：A. 材料的硬度B. 材料的韧性C. 材料的弹性程度D. 材料的屈服强度4. 根据材料力学理论，下列哪一项不是材料的疲劳破坏特点？A. 疲劳破坏是局部的B. 疲劳破坏是突然的C. 疲劳破坏是可预测的D. 疲劳破坏是累积的5. 在材料力学中，下列哪一项不是材料的失效模式？A. 屈服B. 断裂C. 腐蚀D. 疲劳6. 材料的屈服强度和抗拉强度之间的关系是：A. 屈服强度总是大于抗拉强度B. 屈服强度总是小于抗拉强度C. 屈服强度等于抗拉强度D. 两者之间没有固定关系7. 材料的疲劳寿命与下列哪一项无关？A. 应力水平B. 材料的微观结构C. 环境温度D. 材料的密度8. 材料的冲击韧性通常用下列哪一项来表示？A. 抗拉强度B. 屈服强度C. 硬度D. 冲击吸收能量9. 材料的疲劳寿命与加载频率的关系是：A. 正相关B. 负相关C. 无关D. 先正相关后负相关10. 在材料力学中，下列哪一项不是材料的应力-应变曲线的特点？A. 弹性阶段B. 屈服阶段C. 塑性阶段D. 线性阶段二、简答题（每题10分，共20分）1. 请简述材料的弹性模量和屈服强度的区别和联系。
2. 材料的疲劳破坏与静载下的破坏有何不同？三、计算题（每题15分，共30分）1. 已知一材料的弹性模量E=200 GPa，泊松比ν=0.3。
若材料受到拉伸力F=10 kN，试计算材料的应变ε和应力σ。
2. 某材料的疲劳寿命S-N曲线已知，当应力水平为σ=200 MPa时，疲劳寿命N=1000次。
若应力水平降低到150 MPa，根据Basis Goodman关系，计算新的疲劳寿命。
材料力学期中考试试卷及答案
acting on a length dx of the shaft is t dx, so that the total torque applied to the shaft is
TA
∫
A L
L
o
tdx
∫
L
o
tdx . The maximum torque in the shaft
B
x
is TA, which occurs at the fixed support. From the FBD we get
(a)
∑M
x
=0
∫
L
o
L
tdx − TA = 0
L
Therefore
TA = ∫ tdx = ∫ t B
o o
t L 1 x dx = B = (200)(1.5) = 150N ⋅ m L 2 2
The maximum shear stress in the shaft is
τ max =
16TA 16(150) = = 48.9 × 10 6 Pa = 48.9MPa 3 3 πd π (0.025)
B B
maximum shear stress in the shaft; and (2) the angle of twist. (Use G=80 GPa for steel) (20 points)
Solution: (1) Figure (a) shows the FBD(free-body diagram) of the shaft. The applied torque
∫
TA A x
L
o
tdx
T x
Which gives
【材料力学精品课件】材料力学期中试卷答案
12013～2014学年第二学期材料力学期中试卷答案（港航、海洋专业12级）一、概念题（6小题，共6×5分＝30分）1．试画图说明，塑性材料分别在弹性和强化两个阶段，卸载与重新加载的工作路径。
并据此解释“冷作硬化”的含义。
冷作硬化：在强化阶段卸载后再加载时，材料的比例极限提高了，且不再有屈服现象；拉断后的塑性变形减少了。
2．图示结构中，杆1、2、3各发生什么变形？卸载重新加载卸载重新加载杆1：轴向拉伸； 杆2：轴向压缩； 杆3：平面弯曲。
3．图示薄壁截面梁，若剪力F S方向向下，试画出各截面上切应力流的方向，并标出各截面弯曲中心点A的大致位置。
AA234．画出图示梁的挠曲线大致形状。
5．已知平面图形的形心为C ，面积为A ，对z 轴的惯性矩为z I ，图形对1z 轴的惯性矩有四种答案：(A)A b I z 2+；(B)A b a I z 2)(++；(C)A b a I z )(22-+； (D)A a b I z )(22-+。
正确答案是 (D ) 。
lll q2ql 2z C bz 1az C2ql＋2ql 2F M 图46．若y S 、z S 、yz I 分别是平面图形对坐标轴y 、z 的面积矩和惯性积，则轴y 、z 是形心主惯性轴的条件为 S y =0 ，S z =0 ，I yz =0 。
5二、计算题（共70分）1．梁受力如图，已知［σt ］＝40 MPa,［σc ］＝70 MPa, ［τ］＝40 MPa ，M B ＝1.6 kN ·m (上拉下压)，M D ＝2.45 kN ·m (下拉上压)，F S ＝3.6 kN 。
D 截面：MPa 5.29t =⋅='zD I y M 下σ，MPa 78.54c=⋅='z D I yM 上σ； B 截面：MPa 78.35t =⋅=''z B I y M 上σ，cc σσ'<⋅=''zB I y M 下 。
材料力学期中考试复习题
材料力学期中考试复习题绪论1.各向同性假设认为，材料内部各点的（）是相同的。
（A）力学性质；（B）外力；（C）变形；（D）位移。
2.根据小变形条件，可以认为( )。
（A）构件不变形；（B）构件不变形；（C）构件仅发生弹性变形；（D）构件的变形远小于其原始尺寸。
3.在一截面的任意点处，正应力σ与切应力τ的夹角( )。
(A)α＝900；（B）α＝450；（C）α＝00；（D）α为任意角。
4.根据材料的主要性能作如下三个基本假设___________、___________、-___________。
5.材料在使用过程中提出三个方面的性能要求，即___________、___________、-___________。
6.构件的强度、刚度和稳定性（）。
（A）只与材料的力学性质有关；（B）只与构件的形状尺寸关（C）与二者都有关；（D）与二者都无关。
7.用截面法求一水平杆某截面的内力时，是对( )建立平衡方程求解的。
(A) 该截面左段; (B) 该截面右段;(C) 该截面左段或右段; (D) 整个杆。
8.如图所示，设虚线表示单元体变形后的形状，则该单元体的剪应变为( )。
(A)α; (B) π/2-α; (C) 2α; (D) π/2-2α。
答案1（A）2（D）3（A）4 均匀性假设，连续性假设及各向同性假设。
5 强度、刚度和稳定性。
6（A）7（C）8（C）拉压1. 轴向拉伸杆，正应力最大的截面和切应力最大的截面（）。
(A）分别是横截面、45°斜截面；（B）都是横截面，（C）分别是45°斜截面、横截面；（D）都是45°斜截面。
2. 轴向拉压杆，在与其轴线平行的纵向截面上（）。
（A）正应力为零，切应力不为零；（B）正应力不为零，切应力为零；（C）正应力和切应力均不为零；（D）正应力和切应力均为零。
3. 应力－应变曲线的纵、横坐标分别为σ＝F N /A，ε＝△L / L，其中（）。
材料力学试卷试题(附参考答案)
材料力学试卷试题(附参考答案)材料力学试卷试题一、选择题（每题共10分，共5题，计50分）1. 下面哪项不属于材料力学的基本假设？A. 弹性材料的应力-应变关系符合胡克定律。
B. 材料的体积不随外力的作用发生改变。
C. 在材料的应力达到极限时将发生塑性变形。
D. 材料在外力作用下会发生应变。
2. 受力体系中，若要使物体保持静止，则下面哪个条件必须满足？A. 所有受力的合力为零。
B. 所有受力的合力的矩为零。
C. 所有受力的合力和合力矩皆为零。
D. 所有受力的大小均为零。
3. 弹簧常数为k，弹簧长度为l，当受到外力F时，弹簧发生形变Δl，弹性势能为U。
则下面哪个公式正确？A. U = F/ΔlB. U = F·ΔlC. U = 1/2k(Δl)^2D. U = k/2Δl4. 一根弹性绳子的上端系在固定点，下端挂着一个质量为m的小球，长度为l。
如果小球偏离平衡位置的距离为x，则绳子受力的大小为多少？A. mgx/lB. mg/lxC. mx/lgD. mg/l5. 压力是物体受到的外力作用面积单位所计算出的量。
压力的计算公式为？A. P = F/AB. P = F×AC. P = F-AD. P = A/F二、简答题（共10分，计20分）1. 什么是材料力学的研究对象？并介绍材料力学的主要内容。
（要求回答清晰明了，条理清晰）2. 说明静力平衡的条件，并举例说明其应用。
（要求回答准确，能说明条件的必要性，并给出具体应用例子）三、计算题（共15分，计30分）1. 一个质量为2kg的物体受到两个力的作用，分别为10N和20N。
这两个力的夹角为60°，求物体所受合力的大小和方向。
（要求列出计算步骤，有清晰的计算过程和结果）2. 一个弹簧的斜率为k，长度为l，质量为m的物体悬挂在该弹簧下方，当物体达到平衡时，弹簧的形变为Δl。
求物体所受重力的大小。
（要求列出计算步骤，有清晰的计算过程和结果）3. 一个桥梁的两个支座分别承受20kN和30kN的垂直压力，支座之间的距离为4m。
期中《材料力学》参考答案及评分标准.doc
（2011年5月）机密襄樊学院理工学院期中考试试卷《材料力学》一、选择题（共24分，每题3分）1 .工程上区分塑性材料和脆性材料的标准是看其延伸率5大于等于 还是小于（C ）A. 1%B. 3%C. 5%D. 10%2. 使材料丧失正常工作能力的应力称为极限应力，低碳钢的极限应力是（C ） A.比例极限。
P B.弹性极限。
e C.屈服极限。
sD.强度极限。
b3. 如下图示空心圆轴扭转时，受扭矩T 作用，其横截面切应力分布的正确表达应为 （B ）A.最大切应力相同，而扭转角不同C.最大切应力不同，而扭转角相同 5.横截面上最大弯曲拉应力等于压应力的条件是（B.最大切应力相同，扭转角也相同 D.最大切应力不同，扭转角也不同B ）A.梁材料的拉、压强度相等 C.同时满足A 、B 两条6. 梁在弯曲变形时，其中性层的曲率（A.与弯矩成反比，与抗弯刚度成正比B.截面形状对称于中性轴D.除了满足A 、B 以外，还TT 条件 B ）B.与弯矩成正比，与抗弯刚度成反比D.与弯矩及抗弯刚度均成反比1 1 / A2 =——bh , 1 hl 2 A 12 y 12 B .= — /?/?, 12 L =—bh 2 12 C .= — /?/?, 12 Jy =—/?/?312 D.= —bh\ 12 fy 12 A.挠度为零，转角也为零 B.挠度为零，转角不为零 C.挠度不为零，转角为零 D.挠度不为零，转角也不为零7. 图示矩形截面对z 、y 两形心轴的惯性矩分别为（D ）8. 用积分法求一悬臂梁受力后的变形时，边界条件为：在梁的固定端处（ A ）本题 得二、填空题（共24分，每题3分）4.直径和长度相同而材料不同的圆轴，在相同扭矩作用下，它们的（ A ）1. 在材料力学中，显示和确定内力的基本方法称为 截面法 °2. 构件承载能力包括三个方面，即强度、 刚度、稳定性。
3. 材料力学中，变形固体的基本假设有连续性假设、均匀性假设、各向同性假设和 小变形假设。
《材料力学》期中考试试题
2023年年春季学期《材料力学》期中考试试题（开卷）
姓名：学号：年级：
(考试时光为120分钟)
1、(a)外伸梁如图1所示，写出内力方程，并画内力图。
（10分）
图1
(b)梁AB和梁AC在B点由铰链衔接，载荷及几何尺寸如图2所示，其中a，q，m和F为已知量。
求该梁的内力方程，并画出剪力图和弯矩图。
（10分）
图2
2、矩形截面如图3所示，已知：q=2kN/m，P0=240kN，P1=160kN，P2=4kN，b=12cm，
l=2m，h=16cm。
求梁内的最大拉应力和压应力以及危险截面上中性轴的位置（20分）。
第 1 页/共 4 页
图3
3、如图4所示，材料相同、宽度相等、厚度12/1/2h h 的两块板，组成一简支
梁，其上承受均布载荷q 。
（1）若两块板只是互相重叠在一起，求此时两块板内的最大正应力之比。
（2）若两块板胶合在一起，不互相滑动，问此时的最大正应力比前一种情况减少了多少？（20分）
q l b h 1 2
4、试推导如图5所示薄壁圆环受扭矩M时的切应力公式。
（20分）
图5
5、不对称工字型截面悬臂梁受力以及横截面上的剪力方向如图6所示。
请分析：
（20分）
(1) 横截面的腹板上的随意点处是否存在水平方向的切应力；
(2) 翼缘的切应力流的方向；
(3) 判断弯曲中央的大致位置。
第 3 页/共 4 页。
材料力学(4)期中考试题解答共16页文档
zC
Si 2a 422a1a 222.5a5a
Ai
2a 421a 22
3
Iy (1)Iy1A 1(z2(a)2 3
34.66a4
Iy (2)Iy2A 2(z2Czc)24a1 (3a2)3
12a2(5a)2 6
17.33a4
Iy Iy(1) Iy(2) 17.33a4
F 2a
F/2
F
2a
a F F/2
2a
2a
a
FF
F F
2a
2a
a
解毕
3. (4分)
解:
1
2
3
2kN
2kN 3kN
1
2
3
3kN
N1 2kN N2 0 N3 3kN
解毕
4. (4分)
MAC 0 a ?
x
A l
解:
NA
M A C NAx0
F a
B Cl
NB
NA 0
mB 0
2 N A l F (l a ) 0
al
解毕
5. (4分)
a?
I
最小
B
a
B
yC C
Z
解: IBICA (ayC)2
I B要最小，应有：a yC
d
D
yC
Si Ai
S1
R2
2
4 3R23 R3
S2
r2
2
3 4r 23 r3
yC ((2//32))((R R32rr32))
a 23D1123
d D
解毕
6. (4分)
0.6 A1 A2
F 5A[ ]
6
许可载荷为: [F] 5d2 []
材料力学期中测验（含答案）
材料⼒学期中测验（含答案）材料⼒学基础测试题（1⾄6章）⼀、判断题：（对“√”，错“X ”各1分共10分）1、E 的⼤⼩与杆的材料和长度⽆关。
（X ）2、求超静定问题时要由⼏何关系和物理关系建⽴补充⽅程。
（√）3、胡克定理的适⽤条件是ρσσ≤对吗？（√ ）4、提⾼梁的强度主要是改变L 和E 。
（ X ）5、⼀般细长梁弯曲正应⼒强度满⾜则剪应⼒强度必满⾜。
（√）6、图⽰结构为2次超静定桁架。
（ X ）7、图⽰直梁在截⾯C 承受eM 作⽤。
则截⾯C 转⾓不为零，挠度为零。
（√）8、等直传动轴如图所⽰，轮B 和轮D 为主动轮，轮A ，轮C 和轮E 为从动轮。
若主动轮B 和D 上的输⼊功率相等，从动轮A ,C 和E 上的输出功率也相等，如只考虑扭转变形⽽不考虑弯曲变形，危险截⾯的位置在AB 区间和DE 区间。
（√）9、等截⾯直杆受轴向拉⼒F 作⽤发⽣拉伸变形。
已知横截⾯⾯积为A的正应⼒的结果为AF，A F2问正确否？（√）10、低碳钢拉伸试验进⼊屈服阶段以后，只发⽣线弹性变形。
（X ）⼆、填空题（每空1分，共12分。
）1、表⽰塑性材料的强度极限应⼒是______；2、表⽰脆性材料的强度极限应⼒是_______。
3、剪切应⼒互等定理是：。
4、⽤积分法求图⽰梁的挠曲线时，确定积分常数使⽤的边界条件是________________；使⽤的连续条件是___________________。
7、已知图（a ）梁B 端挠度为 q 4l / (8 E I ) ，转⾓为 q 3l /（6 E I ），则图（b ）梁C 截⾯的转⾓为。
8、当L/h ＞的梁为细长梁。
三、选择题：（各2分，共28分）1、任意截⾯形状的等直梁在弹性纯弯曲条件下，中性轴的位置问题有四种答案： (A) 等分横截⾯积； (B) 通过横截⾯的形⼼； (C) 通过横截⾯的弯⼼； (D) 由横截⾯上拉⼒对中性轴的⼒矩等于压⼒对该轴的⼒矩的条件确定。
正确答案是 B 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
哈工大2014年春季学期材料力学期中考试试题（开卷）题号 一 二 三 四 五 六 七 八 九 十 总分 分数班号 姓名 学号(注意: 本次期中考试成绩卷面分值为100分, 得分将按25%计入最终成绩。
)1．如图所示外伸梁，q 、a 已知，试作其剪力sy F 图和弯矩z M 图。
（20分）解：支反力qa F A 41=（向上） qa F B 47= （向上）○2分 ○8分10分D C B Aqa F =q 2qa m =a a 2 a)(Z M 221qa23217qa 2qaqa )(sy Fqa 41qa 472．图示构件内某点处的应力状态为（a ）、（b ）两种应力状态的叠加结果，试求叠加后该点的主应力、最大切应力。
（20分）解：图(b)经过变换为纯剪切应力状态 ○5与（a ）图应力状态相叠加Mpa x 30=σ , Mpa y 20-=σ, xy 20=τMpa z 80=='''σσ22)2(2xy y x y x τσσσσσσ+-±+=⎭⎬⎫''' Mpa ⎩⎨⎧-=2737○10分Mpa 801=σ Mpa 372=σ Mpa 273-=σ ○3分Mpa 5.53max =τ ○2分3.图示实心圆截面杆，直径为D ,两端受外力偶m 作用，测得该杆表面与轴线成o 45方向上的线应变o 45ε,试求：（1）该杆材料的剪切弹性模量G 的表达式；（2）若m N m .50=，mm D 20=，64510200-⨯=o ε，计算G 的数值。
（22分）解：圆轴扭转表面任意点均为纯剪切应力状态 316DmW m t πτ==)1(2ν+=EG ○7分(1) 方法1：τσ=o 45 ， τσ-=o 135 ][11354545o o o νσσε-=E )1(ντ+=EG2τ= ○10分3454582D m G πεετoo==○2分 (2)代入已知数据 Mpa G 6.79= ○3分【方法2：0=x ε，0=y ε，Gxy τγ=o o 90sin 0045Gxyγε++=G2τ= 10分 】4.图示等直杆，其抗拉、压刚度N EA 61022⨯=。
A 端固定，B 端距基础为mm 2.0=δ。
套在杆上的弹簧其刚度系数m kN k /300=、长度为mm 250，向左压缩弹簧至mm 200长时，固定在C 截面。
杆CB 段作用沿轴线且集度m kN q /5=的均布载荷。
要求画出杆的轴力图。
（23分）解：弹簧作用于C 截面上的力310)200250(-⨯-=k F C kN 15=⎰+=∆1xdx EA qEA l F L AC NAC mm 296.0=＞δ○6分 设A 处反力为A F 、B 处反力为B F 均向左 1、力学方面 01=--⨯+B A C F F q F (1) 2、几何方面 δ=∆+∆CB AC l l (2) 3、物理方面 EA lF l AC A AC=∆, EA l F xdx EA q l CB B CB -=∆⎰1（3）（3）式代入（2）式 EA F ql F B AC A δ=-+2(4) ○10分 联立求解得 kN F A 25.18=(←)kN F B 75.1= (←) ○2分○5分5. 单项选择题 (共5小题，每小题3分，合计15分)(1)图示三个单元体，变形后如虚线所示。
（a ）、(b)、(c)三单元体的切应变用a γ、b γ、c γ来表示，则其切应变分别为 C 。
A ）αγ2=a ，αγ2=b ，0=c γ；B ）0=a γ，αγ2=b ，αγ=c ；C ）0=a γ，αγ=b ，αγ2=c ；D ）αγ2=a ，αγ2=b ，αγ2=c 。
（2）图示等截面圆轴，若截面B 相对截面A 的扭转角0=AB φ，则外力偶1m 和2m 的关系为 B 。
A ）21m m =；B ）212m m =；）122m m =； D ）213m m = 。
（3）现有钢和铸铁两种圆截面杆材，其直径相同。
从承载能力和经济效益两个 方面考虑，图示结构中两杆的合理选材方案是 A 。
杆为钢，2杆为铸铁； B)1杆为铸铁，2杆为钢； C)两杆均为钢；D)两杆均为铸铁。
（a ）(b) (c)（4）一圆截面轴向拉杆，若其直径增加一倍，则抗拉 D 。
A ）强度和刚度分别是原来的2倍、4倍；B ）强度和刚度分别是原来的4倍、2倍；C ）强度和刚度均是原来的2倍；D ）强度和刚度均是原来的4倍。
（5）图示(a)、(b)、(c)三个图形对形心轴的惯性矩分别为a I 、b I 、c I ，惯性半径分别为a i 、b i 、c i ，则 C 。
A ）C b a I I I -=, c b a i i i -=；B ）C b a I I I -≠, c b a i i i -=； C ）C b a I I I -=, c b a i i i -≠；D ）C b a I I I -≠, c b a i i i -≠。
哈尔滨工业大学 2015 学年 春 季学期材料力学期末 试 题题号 一 二 三 四 五 六 七 八 九 十 总分 得分 阅卷人院系学号 姓名主管领导审核签字……………………………密………………………封………………………线……………………………一、图示简支梁AB ，其抗弯刚度为EI ，由A 至B 受分布载荷作用，载荷集度3)(kx x q -=，k 为已知常数。
试求：1）梁的挠曲线方程)(x v ；2）A 截面的转角A θ。
（20分）解：挠曲线近似微分方程 )(x M v EI ='' （a ）3)()(kx x q x M -==''积分两次 A x k x M +-='4)(4B Ax x k x M ++-=20)(5由边界条件 00==x M，0==lx M求出 0=B , 204l k A =)(20)(45x l x k x M --= (b) （10分） 式（a ）代入式(b))(2045x l x k v EI --='' 积分两次 C x l x k v EI +--=')26(20246D Cx x l x k EIv ++--=)642(20347 （c ）由边界条件 00==x v，0==l x v得出 0=D , 1406kl C -= 代入（c ）式)67(8406347x l x l x EIkv +--= （8分）EIkl A 1406-=θ （2分）二、图示结构，各杆的刚度已知（标在图中），受力F ，且102Al I =。
试求：1）CD 杆的内力；2）画出结构的轴力图、弯矩图。
（20分）院系学号 姓名…………………………………………密………………………………封………………………………线…………………………………………… --------------------------------------------------------------------------------------------------------------------------------相当系统解：一次静不定问题， 断开CD 杆，其内力为1X （2分） 力法正则方程01111=∆+F X δ (a) （2分）]112121[1]232221[411⨯⨯+⨯⨯+⨯⨯⨯⨯=l l EA l l l EI δEA l1255=（4分）]2221[11Fl ll EI F ⨯⨯⨯-=∆ EA Fl5-= （3分）代入式(a)，得F F X 09.111121==(拉) （3分）1﹢﹣1画出弯矩图、轴力图如下：（4分）（2分）三、图示结构，AB 为刚性杆，杆1、杆2材料相同，均为Q235钢，其弹性模量GPa E 200=，比例极限MPa p 200=σ，屈服极限MPa s 230=σ。
杆1为正方形截面，边长mm a 20=；杆2为圆形截面，直径mm d 36=。
求结构失效时的F 值。
（20分）—﹢第5页（共8页）院系学号 姓名…………………………………………密………………………………封………………………………线…………………………………………………解：一次静不定问题 杆1、杆2均为二力杆杆1受拉，强度问题； 杆2受压，稳定问题由于是静不定结构，1、2均失效结构才失效杆1失效时的极限轴力 9210202010230661=⨯⨯⨯⨯==-A F s s σ KN （5分）计算杆2的临界轴力15743610213=⨯⨯==ilμλ3.99102001020014.369=⨯⨯⨯==pp Eσπλp λλ>，大柔度杆，用欧拉公式4.811036414.31571020014.362292222=⨯⨯⨯⨯⨯==-A E F cr λπ KN （10分） 由AB 杆的平衡0=∑AM032sin 145sin =⨯-⨯+⨯F F F s cr αo6.46)221122(3122=⨯+⨯+⨯=s cr F F F KN （5分）四、图示圆截面杆，受横向力F 和绕轴线的外力偶e M 作用。
已知杆的直径mm d40=，尺寸mm a 160=，材料弹性模量GPa E 200=，泊松比3.0=ν，许用应力MPa 140][=σ。
由实验测得距B 端为2a的上表面处沿轴线方向的线应变6010200-⨯=o ε，CD 段某截面最前侧表面沿o45方向的线应变64510380-⨯=oε。
要求：1）确定F 、e M 的值；2）按第三强度理论校核杆的强度。
（20分）第6页（共8页）解：弯、扭组合问题 1、求F 和e M距B 端为2a的上表面处，为平面应力状态oεσE = (a)ZZ W aF W M 2⨯==σ (b) (a)= (b) 解出 14.320==aE WF Z oε KN （6分）CD 段最前侧表面处，为纯剪切应力状态τσ=o 45τσ-=o135][1][11354545νττνσσε+=-=EE oo oτνE+=1 νετ+=145o E (c)teW M =τ (d) (c) = (d) 解出 3.734145=+=νεt e W E M o KN （6分）2、校核强度CD 段危险，4.502==Fa M N.m3.734==e M T N.m （2分）1421223=+=T M W Zr σ MPa >][σ 或（6分）不安全安全第7页（共8页）院系 学号 姓名…………………………………………密………………………………封………………………………线…………………………………………………五、受水平冲击的刚架如图所示。