信号与线性系统题解第二章
信号与系统课后题解第二章

⑺
对⑺式求一阶导,有:
de(t ) d 2 i 2 (t ) di (t ) du (t ) =2 +2 2 + c 2 dt dt dt dt de(t ) d 2 i2 (t ) di (t ) =2 + 2 2 + 2i1 (t ) + 2i 2 (t ) 2 dt dt dt
⑻
将⑸式代入⑻式中,有:
λ 2 + 2λ + 1 = 0
可解得特征根为 微分方程齐次解为
λ1, 2 = −1
y h (t ) = C1e −t + C2 te− t
由初始状态为 y (0 ) = 1, y ' (0 ) = 0 ,则有:
C1 = 1 − C 1 + C 2 = 0
由联立方程可得 故系统的零输入响应为:
由联立方程可得 故系统的零输入响应为:
A1 = 2, A2 = −1
y zi (t ) = 2e − t − e −2 t
(2)由原微分方程可得其特征方程为
λ 2 + 2λ + 2 = 0
可解得特征根为 微分方程齐次解为
λ1, 2 = −1 ± i
y h (t ) = e −t (C1 cos t + C2 sin t )
(− 3C1 + 3C2 )δ (t ) + (C1 + C2 )δ ' (t ) − (− 2C1 + C 2 )δ (t ) = δ (t )
(
(
( + C e )δ (t ) + (C e
2 1
)
−2 t
+ C2 e t δ ' (t )
信号与系统 第二章习题 王老师经典解法(青岛大学)小白发布
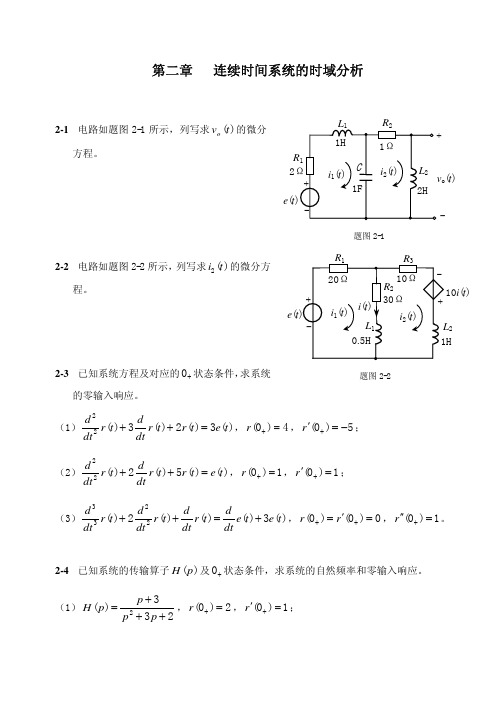
2-16 已知 f1 (t ) =
画出下列各卷积的波形。 (1) s1 (t ) = f1 (t ) ∗ f 2 (t ) ; (2) s2 (t ) = f1 (t ) ∗ f 2 (t ) ∗ f 2 (t ) ; (3) s3 (t ) = f1 (t ) ∗ f 3 (t ) 。
2-17 求题图 2-17 所示电路在 e(t ) = (1 + 2e
第二章
连续时间系统的时域分析
2-1 电路如题图 2-1 所示,列写求 vo (t ) 的微分 方程。
L1 1H R1 2Ω + e(t) i 1 (t )
R2 1Ω + L2 2H 题图 2-1
C
1F
i 2 (t )
vo(t)
2-2 电路如题图 2-2 所示, 列写求 i2 (t ) 的微分方 程。
题图 2-18
−2 t
− 1)U (t ) , 试利用卷积的性质求题
1 0 -1
e2(t)=tU(t) 1 t 0
e3(t)
t 0 1
2-19 一线性时不变的连续时间系统,其初始状态一定,当输入 e1 (t ) = δ (t ) 时,其全响应
r1 (t ) = −3e − tU (t ) ; 当 输 入 e2 (t ) = U (t ) 时 , 其 全 响 应 r2 (t ) = (1 − 5e − t )U (t ) 。 求 当 输 入 e(t ) = tU (t ) 时的全响应。
2-14 计算卷积 f (t ) = f 1 (t ) ∗ f 2 (t ) ,其中 f1 (t ) = sgn(t − 1) , f 2 (t ) = e 2-15 求下列卷积 (1) f1 (t ) = e
信号与线性系统_习题答案(有错版)

2.1 (1) 已知连续时间信号 x(t ) 如图 P2.1(a)所示。试画出下列各信号的波形图,并加以标 注。 (a) x(t − 2) (b) x(1 − t ) (c) x(2t + 2) (2) 根据图 P2.1(b)所示的信号 h(t ) ,试画出下列各信号的波形图,并加以标注。 (a) h(t + 3) (b) h( − 2) (c) h(1 − 2t ) (3) 根据图 P2.1(a)和(b)所示的 x(t ) 和 h(t ) ,画出下列各信号的波形图,并加以标注。 (a) x(t )h(−t ) (b) x(1 − t )h(t − 1) (c) x(2 − ) h(t + 4)
其基波周期 T0 是 T1 , T2 的最小公倍数。 (b) x(n) 和 y ( n) 是周期的, x(n + = N1 ) x(n), y (n + N = y ( n) 2) 令 f= (n) x(n) + y (n) ,欲使 f (n) 是周期的,必须有
= N 0 kN = mN 2 1
πn
4
,对所有 n ,
7
1 n , n奇 显然 x(n) 是非周期的,但 y1 (n) 是周期的。 h(n) = 3 0, n偶
(c) 正确。若 x(n) 的周期为 N ,则 y2 (n) 的周期为 2 N 。 (d) 正确。若 y2 (n) 的周期为 N ,则 N 只能是偶数。 x(n) 的周期为 N / 2 。 2.7 判断下列各信号是否是周期信号,如果是周期信号,求出它的基波周期。 (a) = x(t ) 2 cos(3t + π / 4) (c) x(t ) = e (e) = x ( n)
1
信号与系统第二章习题与答案

第二章习题与答案1.求以下序列的z 变换并画出零极点图和收敛域。
分析:Z 变换概念∑∞-∞=-==n nzn x z X n x Z )()()]([,n 的取值是)(n x 的有值范围。
Z 变换的收敛域 是知足∞<=∑∞-∞=-M zn x n n)(的z 值范围。
解:(1) 由Z 变换的概念可知:∞====<<<<z z az a z az a z a az ,0 1, 11,1 零点为:极点为:即:且收敛域:)(21)()2(n u n x n⎪⎭⎫⎝⎛=)1(21)()3(--⎪⎭⎫⎝⎛-=n u n x n)1(,1)()4(≥=n nn x 为常数)00(0,)sin()()5(ωω≥=n n n n x 10,)()cos()()6(0<<+=r n u n Ar n x n Φω)1||()()1(<=a an x nnn nzaz X -∞-∞=⋅=∑)(nn n nn n z a za-∞=---∞=-∑∑+=1nn n nn n z a z a -∞=∞=∑∑+=01))(1()1()1)(1(1111212a z az a z a az az a za az az ---=---=-+-=-解:(2) 由z 变换的概念可知:n n nz n u z X -∞-∞=∑=)()21()( ∑∞=-=0)21(n n n z 12111--=z 211121><⋅z z 即:收敛域: 0 21==z z 零点为:极点为:解:(3)nn n z n u z X -∞-∞=∑---=)1()21()(∑--∞=--=1)21(n n n z∑∞=-=12n n n z zz212--= 12111--=z 21 12 <<z z 即:收敛域:0 21 ==z z 零点为:极点为: 解: (4) ∑-⋅∞==11)(n nz n z X∑∞--=-=•••11)(1)(n n z n n dz z dX 21)(11z z z n n -=-=∑∞=-- ,1||>z。
信号与系统课后习题与解答第二章
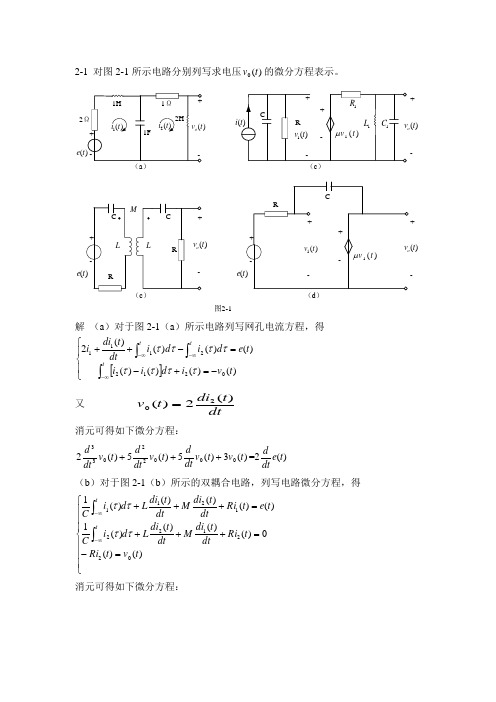
2-1 对图2-1所示电路分别列写求电压)(0t v 的微分方程表示。
2(t ei )(t +-(e )(e )(t +-图2-1解 (a )对于图2-1(a )所示电路列写网孔电流方程,得[]⎪⎩⎪⎨⎧-=+-=-++⎰⎰⎰∞-∞-∞-t t t t v i d i i t e d i d i dt t di i )()()()()()()()(202122111ττττττττ 又 dtt di t v )(2)(20= 消元可得如下微分方程:)(3)(5)(5)(200022033t v t v dt dt v dtd t v dt d +++=2)(te dt d(b )对于图2-1(b )所示的双耦合电路,列写电路微分方程,得⎪⎪⎪⎩⎪⎪⎪⎨⎧=-=+++=+++⎰⎰∞-∞-)()(0)()()()(1)()()()()(10221221211t v t Ri t Ri dt t di M dt t di L d i Ct e t Ri dtt di M dt t di L d i C ttττττ 消元可得如下微分方程:)()(1)(2)(2)(2)()(22020022203304422t e dtd MR t v C t v dt d C R t v dtd R R L t v dtd RL t v dt d M L =++⎪⎭⎫ ⎝⎛+++- (c )对于图2-1(c )所示电路列写电路方程,得⎪⎪⎩⎪⎪⎨⎧=⎥⎦⎤⎢⎣⎡+++=⎰∞-)()()(1)()()()(10101011t v t v dt d C dt t v L R t v R t v t v dt d C t i t μ 消元可得如下微分方程:)()(1)(1)()(101011022110331t i dt dR t v RL t v dt d R R L C t v dt d R C R C t v dt d CC μ=+⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛++ (d )对图2-1(d )所示电路列写电路方程,电流)(t i 如图2-2所示,得⎪⎪⎩⎪⎪⎨⎧==+=++⎰∞-)()()()()()()()(1)(1011t v t v t e t v t Ri t e t v d i C t Ri t μμττ 消元可得如下微分方程:(t e )(t +-图2-2)()(1)()1(00t e Rt v R t v dt d Cμμ=+-2-2 图2-3所示为理想火箭推动器模型。
信号与系统-第2章例题

d2y dy 5 6 y (t ) 4 f (t ) 2 dt dt
ቤተ መጻሕፍቲ ባይዱ
t0
系统的特征方程为 系统的特征根为
s 2 5s 6 0 s1 2,s2 3
yx (t ) K1e—2t K2e—3t
y(0)=yx(0)=K1+K2=1 y' (0)= y'x(0)= 2K13K2 =3
r2 (t ) rzi (t ) 2rzs (t ) [e3t 2sin(2t )]u(t )
解得
rzi (t ) 3e3t u(t )
rzs (t ) [e3t sin(2t )]u(t )
r3 (t ) rzi (t ) rzs (t t0 )
冲激平衡法 冲激平衡法是指为保持系统对应的动态方程式的 恒等,方程式两边所具有的冲激信号函数及其各阶导 数必须相等。根据此规则即可求得系统的冲激响应h(t)。
例:
已知某线性非时变系统的动态方程式为
dy (t ) 3 y (t ) 2 f (t ) dt
试求系统的冲激响应h(t)。
(t 0)
[解] 系统的特征方程为 系统的特征根为 y(0)=yx(0)=K1=1; y'(0)= y'x(0)= 2K1+K2 =3
s 2 4s 4 0
s1 s2 2
(两相等实根)
yx (t ) K1e—2t K2te—2t
解得 K1 =1, K2=5
yx (t ) e2t 5te2t , t 0
2) 求非齐次方程y‘’(t)+6y‘(t)+8y(t) = f(t)的特解yp(t) 由输入f (t)的形式,设方程的特解为
信号与系统课后答案 第2章 习题解

第2章 习 题2-1 求下列齐次微分方程在给定起始状态条件下的零输入响应(1)0)(2)(3)(22=++t y t y dt d t y dt d ;给定:2)0(,3)0(==--y dt dy ; (2)0)(4)(22=+t y t y dt d ;给定:1)0(,1)0(==--y dtd y ;(3)0)(2)(2)(22=++t y t y dt d t y dt d ;给定:2)0(,1)0(==--y dt dy ; (4)0)()(2)(22=++t y t y dt d t y dt d ;给定:2)0(,1)0(==--y dtdy ; (5)0)()(2)(2233=++t y dt d t y dt d t y dt d ;给定:2)0(,1)0(,1)0(22===---y dt d y dt d y 。
(6)0)(4)(22=+t y dt d t y dt d ;给定:2)0(,1)0(==--y dtdy 。
解:(1)微分方程的特征方程为:2320λλ++=,解得特征根:121, 2.λλ=-=- 因此该方程的齐次解为:2()t th y t Ae Be --=+.由(0)3,(0)2dy y dt--==得:3,2 2.A B A B +=--=解得:8, 5.A B ==- 所以此齐次方程的零输入响应为:2()85tty t e e--=-.(2)微分方程的特征方程为:240λ+=,解得特征根:1,22i λ=±.因此该方程的齐次解为:()cos(2)sin(2)h y t A t B t =+.由(0)1,(0)1d y y dx --==得:1A =,21B =,解得:11,2A B ==. 所以此齐次方程的零输入响应为:1()cos(2)sin(2)2y t t t =+.(3)微分方程的特征方程为:2220λλ++=,解得特征根:1,21i λ=-± 因此该方程的齐次解为:()(cos()sin())th y t e A t B t -=+.由(0)1,(0)2dy y dx--==得:1,2,A B A =-= 解得:1,3A B ==.所以齐次方程的零输入响应为:()(cos()3sin())ty t e t t -=+.(4)微分方程的特征方程为:2210λλ++=,解得二重根:1,21λ=-.因此该方程的齐次解为:()()th y t At B e -=+. 由(0)1,(0)2dy y dx--==得:1,2,B A B =-=解得:3, 1.A B == 所以该方程的零输入响应为:()(31)ty t t e -=+.(5)微分方程的特征方程为:3220λλλ++=,解得特征根: 1,21λ=-,30λ=. 因此该方程的齐次解为:()()th y t A Bt C e -=++.由22(0)1,(0)1,(0)2d d y y y dx dt---===得:1,1,22A C B C C B +=-=-=. 解得:5,3,4A B C ==-=-.所以方程的零输入响应为:()5(34)ty t t e -=-+.(6)微分方程的特征方程为:240λλ+=,解得特征根:120,4λλ==-. 因此该方程的齐次解为:4()th y t A Be -=+.由(0)1,(0)2d y y dx --==得:1,42A B B +=-=.解得:31,22A B ==-. 所以此齐次方程的零输入响应为:431()22ty t e -=-.2-2 已知系统的微分方程和激励信号,求系统的零状态响应。
线性系统课后答案第2章
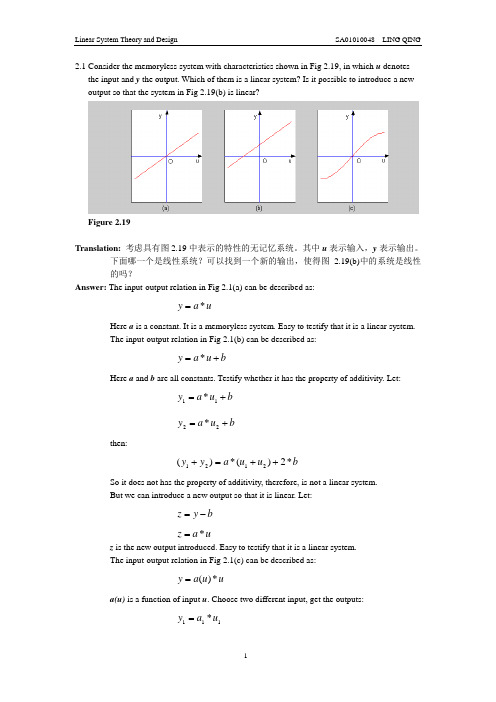
2.1 Consider the memoryless system with characteristics shown in Fig 2.19, in which u denotes the input and y the output. Which of them is a linear system? Is it possible to introduce a new output so that the system in Fig 2.19(b) is linear?Figure 2.19Translation: 考虑具有图2.19中表示的特性的无记忆系统。
其中u 表示输入,y 表示输出。
下面哪一个是线性系统?可以找到一个新的输出,使得图2.19(b)中的系统是线性的吗?Answer: The input-output relation in Fig 2.1(a) can be described as:u a y *=Here a is a constant. It is a memoryless system. Easy to testify that it is a linear system. The input-output relation in Fig 2.1(b) can be described as:b u a y +=*Here a and b are all constants. Testify whether it has the property of additivity. Let: b u a y +=11*b u a y +=22*then:b u u a y y *2)(*)(2121++=+So it does not has the property of additivity, therefore, is not a linear system.But we can introduce a new output so that it is linear. Let:b y z -=u a z *=z is the new output introduced. Easy to testify that it is a linear system.The input-output relation in Fig 2.1(c) can be described as:u u a y *)(=a(u) is a function of input u . Choose two different input, get the outputs:111*u a y =222*u a y =Assure:21a a ≠then:221121**)(u a u a y y +=+So it does not has the property of additivity, therefore, is not a linear system.2.2 The impulse response of an ideal lowpass filter is given by)(2)(2sin 2)(00t t t t t g --=ωωω for all t , where w and to are constants. Is the ideal lowpass filter causal? Is is possible to built the filter in the real world?Translation: 理想低通滤波器的冲激响应如式所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章习题答案收集自网络2.1 (1) 已知连续时间信号()x t 如图P2.1(a)所示。
试画出下列各信号的波形图,并加以标注。
(a) (2)x t - (b) (1)x t - (c) (22)x t +(2) 根据图P2.1(b)所示的信号()h t ,试画出下列各信号的波形图,并加以标注。
(a) (3)h t + (b) (2)2t h -(c) (12)h t -(3) 根据图P2.1(a)和(b)所示的()x t 和()h t ,画出下列各信号的波形图,并加以标注。
(a) ()()x t h t - (b) (1)(1)x t h t -- (c) (2)(4)2t x h t -+图P2.1 解:(1) 各信号波形如下图所示:(a)(b)(c)12(2)x t -(1)x t -(22)x t +ttt22221111121001-1-1-2-2-35(2) 各信号波形如下图所示:(a)(b)(c)1212-32(3)h t +(2)2t h -(12)h t -t tt111124681-2-3-4-5-(3) 各信号波形如下图所示:()()x t h t -(1)(1)x t h t --(2)2t x -(a)(b)(c)ttt∴(2/2)(4)0x t h t -+=0111112222221-1-462-2.2 已知信号(52)x t -的波形图如图P2.2所示,试画出()x t 的波形图,并加以标注。
(52)x t -t32521123图P2.2解:波形如下图所示:3252(52)x t -(5)x t -(5)x t +()x t tttt0001111111222334561-2-3-4-5-6-2.3 (1) 已知离散时间信号()x n 如图P2.3(a)所示,试画出下列各信号的波形图,并加以标注。
(a) (4)x n - (b) (21)x n +(c) (),ˆ()30,nx nx n n ⎧⎪=⎨⎪⎩其他(2) 对图P2.3(b)所示的信号()h n ,试画出下列个信号的波形,并加以标注。
(a) (2)h n - (b) (2)h n +(c) (2)(1)h n h n ++--(3) 根据图P2.3(a)和(b)所示的()x n 和()h n ,画出下列各信号的波形图,并加以标注。
(a) (2)(12)x n h n +- (b) (1)(4)x n h n -+ (c) (1)(3)x n h n --()x n n()h n n1212-3232-12(a)(b)4-1-1-1-2-0011122334421图P2.3 解:(1) 各信号波形图如下图所示:(4)x n -n(a)1/22-1-01123456(21)x n+ˆ()xn nn(b)(c)2-1-1-0011112233(2) 各信号波形图如下图所示:(2)(1)h n h n ++--n1/2(c)6-5-4-3-2-2-2-1-0123(3) 各信号波形如下图所示:(2)(12)x n h n +-(1)(4)x n h n -+(a)(b)nn1/21/2-3/23/21/43/4-1-1-001112232(1)(3)x n h n --(c)n1/21/2-3/2-1-1-012345672.4 画出图P2.4所给各信号的奇部和偶部。
()x t t()x t t(a)(b)00112112-1-图P2.4 解:(a)1212{}()d x t O tt12-1-1-2-2-01122{}()u E x t(b){}()d x t O tt12122-2-1-1-00112212-1{}()u E x t(c)()e x n ()o x n nn4-3-2-2-1-1-0011223344111-(d)1/23/21/21/2-1/2-1/2-1/2-1/2-3/21/21/21/23/2-()o x n ()e x n nn3-2-1-0011232.5 已知()x n 如图P2.5所示,设:12()(2)(/2),()0,y n x n x n n y n n =⎧=⎨⎩偶奇画出1()y n 和2()y n 的波形图。
()x n n4-1-0112234图P2.5 解:2.6 判断下列说法是否正确?如果正确,则求出每个信号基波周期之前的关系,如果不正确,则举出一个反例。
(1) (a) 若()x t 是周期的,则(2)x t 也是周期的。
(b) 若(2)x t 是周期的,则()x t 也是周期的。
(c) 若()x t 是周期的,则(/2)x t 也是周期的。
(d) 若(/2)x t 是周期的,则()x t 也是周期的。
(2) 定义12(/2),()(2),()0,x n n y n x n y n n ⎧==⎨⎩偶奇(a) 若()x n 是周期的,则1()y n 也是周期的。
(b) 若1()y n 是周期的,则()x n 也是周期的。
(c) 若()x n 是周期的,则2()y n 也是周期的。
(d) 若2()y n 是周期的,则()x n 也是周期的。
解:(1) (a) 正确。
若()x t 的周期为T ,则(2)x t 的周期为/2T 。
(b) 正确。
若(2)x t 的周期为T ,则()x t 的周期为2T 。
(c) 正确。
若()x t 的周期为T ,则(/2)x t 的周期为2T 。
(d) 正确。
若(/2)x t 的周期为T ,则()x t 的周期为/2T 。
(2) 由12(/2),()(2),()0,x n n y n x n y n n ⎧==⎨⎩偶奇 (a) 正确。
设()x n 的周期为N 。
如果N 为偶数,则1()y n 的周期为/2N ;如果N为奇数,则必须有022N N =,才能保证周期性,此时1()y n 的周期为0N N =。
(b) 不正确。
设()()()x n g n h n =+,其中()sin4ng n π=,对所有n ,1,()30,n n h n n ⎧⎛⎫⎪ ⎪=⎨⎝⎭⎪⎩奇偶显然()x n 是非周期的,但1()y n 是周期的。
(c) 正确。
若()x n 的周期为N ,则2()y n 的周期为2N 。
(d) 正确。
若2()y n 的周期为N ,则N 只能是偶数。
()x n 的周期为/2N 。
2.7 判断下列各信号是否是周期信号,如果是周期信号,求出它的基波周期。
(a) ()2cos(3/4)x t t π=+ (b) ()cos(8/72)x n n π=+ (c) (1)()j t x t e π-= (d) (/8)()j n x n e π-=(e) []0()(3)(13)m x n n m n m δδ∞==----∑(f) ()cos 2()x t t u t π=⨯ (g) ()cos(/4)cos(/4)x n n n π=⨯ (h) []()cos 2()v x t E t u t π=⨯ (i) []()cos(2/4)()v x t E t u t ππ=+⨯ (j) ()2cos(/4)sin(/8)2sin(/2/6)x n n n n ππππ=+-+ 解:(a) ()2cos(3/4)x t t π=+,周期信号,23T π=。
(b) ()cos(8/72)x n n π=+,周期信号,087πΩ= ,7N ∴=(c) (1)()j t x t e π-=,周期信号,2T =。
(d) (/8)()j n x n eπ-=,非周期信号,因为0/2πΩ是无理数。
(e) []()(3)(13)m x n n m n m δδ∞=-∞=----∑,设周期为N,则有[]()(3)(13)m x n N n N m n N m δδ∞=-∞+=+--+--∑,令3N k =,(k 为整数) 则()()(3)3()13()m x n k n m k n m k δδ∞=-∞+=------⎡⎤⎣⎦∑,令m k l -=则有()()(3)313m x n k n l n l δδ∞=-∞+=----⎡⎤⎣⎦∑显然,()x n 是周期信号,其周期为3N =。
(f) ()cos 2()x t t u t π=⨯,非周期信号。
(g) cos4n 是非周期的,∴()x n 是非周期信号。
(h) [][]1()cos 2()(cos 2)()(cos 2)()2v x t E t u t t u t t u t πππ=⨯=⨯+⨯-,周期的,周期1T =。
(i) []()cos(2/4)()v x t E t u t ππ=+⨯,非周期信号。
(j) ()x n 是周期信号,其周期就是cos sin 48n n ππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭、和sin 26n ππ⎛⎫+⎪⎝⎭的公共周期。
∴ 周期为16N =。
2.8 (a) 设()x t 和()y t 都是周期信号,其基波周期分别为1T 和2T 。
在什么条件下,和式()()x t y t +是周期的?如果该信号是周期的,它的基波周期是什么?(b) 设()x n 和()y n 都是周期信号,其基波周期分别为1N 和2N 。
在什么条件下,和式()()x n y n +是周期的?如果该信号是周期的,它的基波周期是什么?解: (a) ()x t ,()y t 是周期的,1()()x t kT x t +=,2()()y t kT y t += 令()()()f t x t y t =+,欲使()f t 是周期的,必须有00()()()()()()s t T x t T y tT x ty t f t+=+++=+= 012T k T l T ∴== 即12T l T k=,其中,k l 为整数。
这表明:只要()x t 和()y t 的周期之比12T T 是有理数,()()x t y t +就一定是周期的。
其基波周期0T 是12,T T 的最小公倍数。
(b) ()x n 和()y n 是周期的,12()(),()()x n N x n y n N y n +=+= 令()()()f n x n y n =+,欲使()f n 是周期的,必须有 012N k N m N == (,k m 为整数) 即''11121''22122gcd(,)gcd(,)N N N N N m N kN N N N ==='1N 与'2N 无公因子, ''12,m N k N ∴=='0211212/g c d (,)N N N N N N N== 2.9 画出下列各信号的波形图:(a) ()(2)()t x t e u t -=- (b) []()cos10(1)(2)tx t e t u t u t π-=---(c) 2()(9)x t u t =- (d) 2()(4)x t t δ=- 解:各信号波形如下图所示:图PS2.92.10 已知信号()()()sin x t t u t u t π=⨯--⎡⎤⎣⎦,求: (a) 212()()()d x t x t x t dt=+ (b) 2()()t x t x d ττ-∞=⎰解: ()()()sin x t t u t u t π=⨯--⎡⎤⎣⎦()()()()()()()cos sin cos dx t t u t u t t t t dtt u t u t πδδππ=⨯--+⨯--⎡⎤⎡⎤⎣⎦⎣⎦=⨯--⎡⎤⎣⎦()()()()()()()()()()()()22()sin cos sin cos 0cos sin d x t t u t u t t t t dtt u t u t t t t u t u t t t πδδππδδπππδδπ=-⨯--+⨯+-⎡⎤⎡⎤⎣⎦⎣⎦=-⨯--++-⎡⎤⎣⎦=-⨯--+--⎡⎤⎣⎦ ∴ (a) 212()()()()()d x t x t x t t t dtδδπ=+=--(b) 200()()1cos 02t t x t x d t t t ττππ-∞≤⎧⎪==-<≤⎨⎪>⎩⎰2.11 计算下列各积分: (a) sin ()2t t dt πδ∞-∞⨯-⎰(b)(2)te t dt δ∞--∞⨯+⎰(c) 3(2)(1)t t t dt δ∞-∞++-⎰ (d) 00()()2t u t t t dt δ∞-∞-⨯-⎰(e) ()e dt τδτ∞--∞⎰(f)121(4)t dt δ--⎰解: (a) sin ()sin122t t dt ππδ∞-∞⨯-==⎰(b)(2)2(2)t e t dt e e δ∞----∞⨯+==⎰(c) 同(b),4 (d) 00000()()()()222t t t u t t t dt u t u δ∞-∞-⨯-=-=⎰(e)()1e dt e τδτ∞--∞==⎰(f) 02.12 根据本章的讨论,一个系统可能是或者不是:①瞬时的;②时不变的;③线性的;④因果的;⑤稳定的。
