第十四届华罗庚金杯数学初一赛决赛(C组)试题
第十六届“华杯赛”初一组决赛试题C(含答案)

内
线
封
密
-1-
5
7
(2010) 2011
5
7
(2009) 2011
5
7 (1) 2011
5 7 1
2011
5
7 2
2011Biblioteka 5 73 2011
其中 n, m 为非负整数, 则这两串单项式中共有多少对同类项?
10. 求所有满足方程组 ab c 13, a bc 23的正整数解 (a, b, c) .
11. 如图, M、N 分别为四边形 ABCD 对角线 AC、BD 的 中点, 过 M、N 的直线分别交 CD、AB 于 E、F . 如 果三角形 ABE 的面积为 45, 求三角形 CDF 的面积.
-3-
第十六届华罗庚金杯少年数学邀请赛
决赛试题 C 参考答案(初中组)
一、 填空题 (每小题 10 分,共 80 分)
题号 1
2
3
4
5
6
7
8
答案 11 25721 57
1
420
6
2010 10
2
二、解答下列各题 (每题 10 分,共 40 分, 要求写出简要过程)
9. 答案:402. 理由:依照同类项之定义,若3n 1 5m 2 ,自然会有3n 2 5m 3,则 x3n1 y3n2
12. 答案:9 解:第一次从前向后加注红圈时,设加红圈的页面号码为 m,则 m 1 1 1k , k 1 , 2 , 3 , m 2 0 1 1(1)
第十四届华罗庚金杯数学初一赛决赛(C组)试题

第十四届华罗庚金杯数学初一赛决赛试题(时间:2009年4月11日10:00~11:30)一、填空(每题l0分,共80分)1.计算:2614(3)( 6.5)(2)(6)313--⨯-+-÷-= . 2.设有理数,,a b c 在数轴上的对应点如右图所示,则代数式b a a c c b -+-+-= . 3.设,m n 是非负整数且1m n <-,则三个m 次多项式之积与一个(32)n -次多项式之和是 次多项式.4.如果关于,x y 的方程组37362ax y x y +=⎧⎨+=⎩无解,则a 等于 . 5.某企业投入资金制造某种产品,按照当时的产品价格,可以有20%的利润.由于金融危机,产品价格平均下降了30%,企业亏损了160万元.那么企业投入的资金是 万元.6.已知a b 、是有理数.下列各式:① a b a b +<-, ② 222210a b a b +--+<,③ 2210a b a b ++++< 中一定不成立的是 (填写序号).7.将一张长20厘米、宽12厘米的长方形纸片沿对角线对折,生成的图形如图1;再将该图形过图l 所标示的B 点对折,并使得A 与A '重合(同时C 与C '重合),得到四边形ABDC ,如图2.则四边形ABDC 的面积为 平方厘米.8.已知32525n m n +=-是正整数,那么n 可取 个不同的正整数值. 二、解答下列各题(每题l0分,共40分,要求写出简要过程) 9.在直角三角形ABC 中,090C ∠=.如果M 和N 分别为AC 和BC 的中点,AN=19和BM=22,求AB 的长.10.甲、乙两车同时由A 地出发,当甲车到达C 地时,乙车到达B 地;当乙车到达C 地时,甲车到达D 地.已知甲、乙两车的速度之和是每小时220千米,2536AB AD =,求甲车的速度.A C 'A 'D CB B AC 图2图1AB C M 192211.已知关于x 的方程2x ax =+只有负数根,求a 的取值范围.12.天津和上海之间有四种交通工具:飞机、火车、轮船与长途汽车.假期里,几位同学去上海旅游了一次,对于其中的任意三位同学,要么去上海时所选用的交通工具各不相同,要么从上海回来时所选用的交通工具各不相同.则这些同学最多有多少位?三、解答下列各题(每题l5分,共30分,要求写出详细过程)13.在下面的乘法竖式中,每个数字被纸片盖住,纸片上只标出盖住的数字的奇偶,请写出该乘法竖式.14.下图中,平行四边形ABCD 的面积是1,E 、F 分别是AB 、CD 上的点,AF 与DE 交于G .已知,DF b AE d FC a EB c ==,问:三角形DFG 的面积是多少?奇⨯偶偶偶偶偶偶奇偶偶奇偶奇奇偶偶A BC D E F G。
惠州市2009年华杯赛决赛成绩通报

七
刘志辉
叁
华罗庚中学
林嘉麒
七
吴政先
叁
惠高附属实验学校
刘欣
七
邓洪波
叁
惠阳高级中学初中部
刘达贤
七
温海雄
叁
惠州市第一中学
王燕
七
胡昌莲、彭高阳、郑志慧
叁
惠阳高级中学初中部
徐严妍
七
朱洁
叁
澳头中学
许贺芳
七
曾琪瑛
叁
惠阳高级中学初中部
胡璟
七
朱洁
叁
华罗庚中学
叶仕安
七
吴政先
叁
惠阳第一中学
周文盛
七
刘翠玲
叁
惠州市外国语学校
叁
惠州市第一中学
成勇
七
胡昌莲、彭高阳、郑志慧
叁
惠阳高级中学初中部
戴育成
七
温海雄
叁
惠城区水口中学
邓代昭
七
余志刚
叁
惠阳第一中学
董仲维
七
吴恒华
叁
惠州市第五中学
韩帅
七
黄文英
叁
惠城区水口中学
胡伟兵
七
杨英俊
叁
惠州市第一中学
黄熙
七
胡昌莲、彭高阳、郑志慧
叁
惠阳崇雅中学初中部
黄华坤
七
林旭明
叁
惠阳中山中学
黄俊龙
七
黎密梅、聂瑞秀
六
徐红英
壹
惠州市实验小学
陈正胤
六
叶秋莲
壹
惠州市第十一小学
刘弘斌
六
林秋蓉
壹
博罗实验学校
2019年香港华罗庚金杯少年数学邀请赛(决赛)初中二年级、初一年级组试题含答案

一小時三十分鐘完卷 (上午 10:00 至上午 11:30) 比賽須知:
1. 全卷共 10 題,滿分 100 分。包括填空題 6 道,每題 10 分;詳答題 4 道,每題 10 分。 2. 參賽學生必須全部作答,所有答案寫在答題紙上。 3. 填空題無需書寫步驟,只須填寫答案;詳答題要求寫出詳細過程。 4. 比賽時使用自備文具,例如鉛筆、原子筆及橡皮擦膠等。不准使用計算器。違規者將被
若 | x1-x2|=2 2,則 k 的值為
.
答案:1. 解:令 x+2=kxx2+2x-k=0,△=22+4k≥0k≥-1.
x1+x2=-2,x1x2=-k,|x1-x2|= (x1+x2)2-4x1x2= 4+4k=2 2 k=1.
9. 如圖,方格紙中的每個小正方形的邊長為 1.記圖中陰影部分的面積 A
中二組 F.2 (10 marks for each question)
1. (3x-1)2=0x=3,故3x+3x=2
2.
24+1=4( 2-1),3-4 5=3+ 5即滿足要求的 m 可以取 2,3,4,
5,共 4 個數
3. 取(0,2)關於直線 y=x 的對稱點(2,0),過(-4,-2),(2,0)的直線為 y= 13(x-2),與 y=x 交於點(-1,-1).即為周長最小時的點 C.故 a=-1
二、解答下列各題 (每小題 10 分,共 40 分,要求寫出詳細過程。)
7. 求 − 2 + 2 (− 2 )2 − 4 (− 2 )4 的值。
2
2
2
8. 設 k 為非零實數, 兩個函數 y = x + 2 與 y = k 的圖像相交於 A(x1,y1)、B(x2,y2) x
历届“华杯赛”初赛决赛试题汇编【小中组(附答案)】

二、简答题(每小题 15 分, 共 60 分, 要求写出简要过程)
9. 用 4 个数码 4 和一些加、减、乘、除号和小括号, 写出值分别等于 2、3、4、 5、6 的五个算式. 10. 右图是 U, V, W, X 四辆不同类型的汽车每百千米的耗油 量. 如果每辆车都有 50 升油, 那么这四辆车最多可行驶 的路程总计是多少千米? 11. 某商店卖出一支钢笔的利润是 9 元, 一个小熊玩具的进 价为 2 元. 一次, 商家采取 “买 4 支钢笔赠送一个小熊玩具”的打包促销, 共 获利润 1922 元. 问这次促销最多卖出了多少支钢笔? 12. 编号从 1 到 10 的 10 个白球排成一行, 现按照如下方法涂红色: 1)涂 2 个球; 2)被涂色的 2 个球的编号之差大于 2. 那么不同的涂色方法有多少种?
四百米比赛进入冲刺阶段,甲在乙前面 30 米,丙在丁后面 60 米,乙在丙前面 20 米. 这时,跑在最前面的两位同学相差( (A)10 (B)20 )米. (D)60
(C)50
5.
在右图所示的两位数的加法算式中, 已知 A B C D 22 , ). (B)4 (C)7 (D)13
一、选择题 (每小题 10 分, 满分 60 分. 以下每题的四个选项中, 仅 有一个是正确的, 请将表示正确答案的英文字母写在每题的圆括号 内.)
华杯赛决赛第13~16届(初一组)试题及答案

y 的, 而当 y 1时, 由第一个等式得到 2x 1, 所以 x 1 .
2 评分参考: 1) (1)之前给 2 分; 2) (1)和(2)各给 4 分.
三、解答下列各题(每题 15 分,共 30 分,要求写出详细过程)
1 k
4k 2 9
4k
2
9
,
其中,
对于有理数
x,
x= x x.
所以有1 k2
,
9
1
1
k
4k 9
2
0.
当 k 取不同整数时, 1 k 4k 2 的情况如下表: 9
k
2
1
0
=1
=2
xy 0 . 因此, 三个相等的式子只有两种可能:
(1) x y xy x . 由后一等式得到, y 1或 y 1, 而 y 1是不可能的, 因为 y
此时由第一个等式得到 x 1 x , 矛盾. 当 y 1 时, 由第一个等式得到 x 1 x , 即 2x 1 , 所以 x 1 .
第十三届全国“华罗庚庚金杯”少年数学邀请赛决赛试卷(初一组)
第十三届“华罗庚金杯”少年数学邀请赛 决赛试卷(初一组)
(建议考试时间:2008 年 4 月 19 日 10:00~11:30)
一、填空(每题 10 分,共 80 分)
1. 某地区 2008 年 2 月 21 日至 28 日的平均气温为-1℃,2 月 22 日至 29 日的平
枚围棋
第十三届全国“华罗庚庚金杯”少年数学邀请赛决赛试卷(初一组)
第十四届全国“华罗庚金杯”少年数学邀请赛决赛
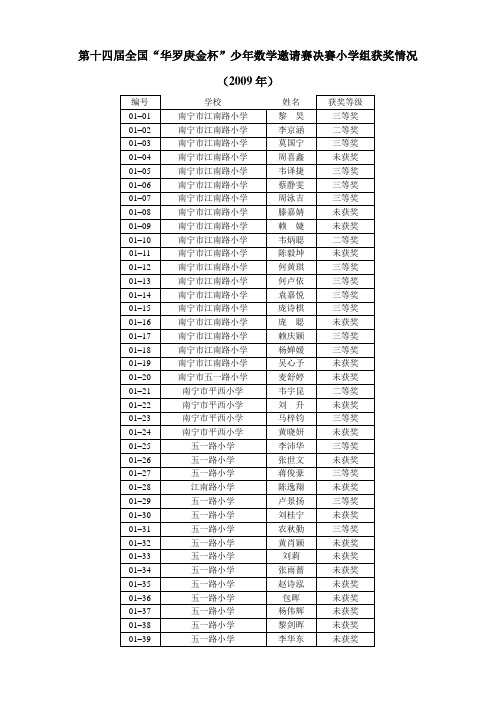
05–16 05–17 05–18 05–19 05–20 05–21 05–22 05–23 05–24 05–25 05–26 05–27 05–28 05–29 05–30 05–31 05–32 05–33 05–34 05–35 05–36 05–37 05–38 05–39 05–40 05–41 05–42 05–43 05–44 05–45 05–46 05–47 05–48 05–49 05–50 06–01 06–02 06–03 06–04 06–05 06–06 06–07 06–08 06–09
玉国圣 谭喜校 巫柳柳 廖小莹 覃 敏
未获奖 未获奖 未获奖 三等奖 未获奖 未获奖 未获奖 未获奖 三等奖 未获奖 一等奖 未获奖 二等奖 二等奖 未获奖 未获奖 二等奖 未获奖 三等奖 二等奖 一等奖 未获奖 未获奖 二等奖 未获奖 未获奖 未获奖 未获奖 未获奖 未获奖 三等奖 三等奖 未获奖 三等奖 三等奖 三等奖 三等奖 二等奖 三等奖 三等奖 三等奖 未获奖 三等奖 未获奖
南宁市荣和实验学校 南宁市荣和实验学校 南宁市荣和实验学校 南宁市菠萝岭小学 南宁市菠萝岭小学 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 白沙路学校 五一中路学校 五一中路学校 五一中路学校 五一中路学校 五一中路学校 五一中路学校 五一中路学校 江南区淡村小学 江南区淡村小学 江南区淡村小学 江南区淡村小学 江南区淡村小学 南宁市壮锦学校 南宁市壮锦学校 南宁市壮锦学校 南宁市壮锦学校 南宁市壮锦学校 南宁市壮锦学校 南宁市五一西路学校 白沙小学 白沙小学
第十四届华罗庚金杯少年数学邀请赛决赛试题C(初一组)参考答案

第十四届华罗庚金杯少年数学邀请赛决赛试题C参考答案(初一组一、填空(每题l0分,共80分题号 1 2 3 4 5 6 7 8③答案二、解答下列各题(每题l0分,共40分,要求写出简要过程9.答案:26.解答:因为和是直角三角形且AC=2MC、BC=2NC,我们有:,,等式两边对应相加,结合也是直角三角形,得到:,所以:,.评分参考:1列出前两个等式得4分;2列出第三个等式得4分;3给出正确结果得2分.10.答案:每小时120千米.解答:设甲和乙车速度分别是每小时和千米,甲和乙到达C地的时间分别是小时和小时.则:,化简得:,,.所以甲车速度是每小时l20千米.评分参考:1列出一个方程给2分,共6分;2给出正确结果得4分.11.答案:.解答:设有负数根,则,进而.要保证为负数,必须满足.设有正数根,则,进而.要保证为正数,必须满足.综合上面的讨论,要保证只有负数根,必须满足.评分参考:1讨论清楚有正数根的条件得4分;2讨论清楚有负数根的条件得4分;3给出正确结果得2分.12.答案:6解答:用A、B、C、D表示四种交通工具,分情况进行讨论.1如果去(或返回时,大家选择的工具没有相同的,则最多4位同学.2如果去(或返回时,恰有两位选择的工具相同,其他几位都与别人不同,则最多有5位同学.3如果去(或返回时,恰有三位选择的工具相同,其他几位都与别人不同,则最多有6位同学.4如果去(或返回时,有四位或更多选择的工具相同,则最多有4位同学.否则,假设有5位或更多同学.不妨设前四位选择了A,则他们返回(或去时选的工具一定互不相同,分别是A、B、C、D.返回(或去时,前四位之外的任何一位选择的工具一定与前四位中的某位相同.在这两位和前四位中的另外一位三人中,去(或返回时以及返回(或去时都至少有两位选择了相同交通工具.矛盾.上面的讨论说明,至多有6位同学.下表说明6位同学可以满足题设条件.1 2 3 4 5 6去 A A A B C D回 B C D A A A评分参考:1给出正确答案得2分;2说明6位同学可以得4分.3说明多于6人不可得4分.三、解答下列各题(每题l5分,共30分,要求写出详细过程13.解答:若被乘数“奇偶偶”<200,那么,偶奇偶偶=奇偶偶×偶<188×8=1504<偶奇偶偶.矛盾.所以,被乘数不小于300.被乘数的百位与乘数的十位的乘积应该小于8,否则加一个非0偶数就应该进位了,最后的结果应该是5位数,与竖式不符.所以,被乘数的百位是3,乘数的十位是2.因此:3偶偶×2=偶奇偶,被乘数的个位数只能6或8,否则不能进位;而被乘数的十位数只能是0,2或4,否则就要进位.因此,被乘数只可能是306,308,326,328,346,348.这些数乘以4或6都得不到“偶奇偶偶”,而348乘以8时,得“偶奇偶偶”,所以,最后得到右式.评分参考:1给出正确答案得8分;2给出理由得7分.14.答案:.解答1.如图1,连接AC.则三角形ACD的面积为,易知,,同法,连接BD,求得:……①如图2,连接EF,则ADFE是个梯形,设,则因为:,所以:……②即:.也就是:,所以:.即:.评分参考:1画出辅助线得2分;2讨论到①式得4分;3讨论到②式得6分;4得到正确答案得3分.解答2.如图3,记,,,.∵且,∴,∵,∴,求得:,∴.∴.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十四届华罗庚金杯数学初一赛决赛试题
(时间:2009年4月11日10:00~11:30)
一、填空(每题l0分,共80分)
1.计算:2614(3)( 6.5)(2)(6)313
--⨯-+-÷-= . 2.设有理数,,a b c 在数轴上的对应点如右图所示,
则代数式b a a c c b -+-+-= . 3.设,m n 是非负整数且1m n <-,则三个m 次多项式之积与一个(32)n -次多项式之和是 次多项式.
4.如果关于,x y 的方程组37362ax y x y +=⎧⎨+=⎩
无解,则a 等于 . 5.某企业投入资金制造某种产品,按照当时的产品价格,可以有20%的利润.由于金融危机,产品价格平均下降了30%,企业亏损了160万元.那么企业投入的资金是 万元.
6.已知a b 、是有理数.下列各式:
① a b a b +<-, ② 222210a b a b +--+<,
③ 2210a b a b ++++< 中一定不成立的是 (填写序号).
7.将一张长20厘米、宽12厘米的长方形纸片沿对角线对折,生成的图形如图1;再将该图形过图l 所标示的B 点对折,并使得A 与A '重合(同时C 与C '重合),得到四边形ABDC ,如图2.则四边形ABDC 的面积为 平方厘米.
8.已知32525
n m n +=
-是正整数,那么n 可取 个不同的正整数值. 二、解答下列各题(每题l0分,共40分,要求写出简要过程) 9.在直角三角形ABC 中,090C ∠=.如果M 和N 分别为AC 和BC 的中点,AN=19和BM=22,求AB 的长.
10.甲、乙两车同时由A 地出发,当甲车到达C 地时,乙车到达B 地;当乙车到达C 地时,甲车到达D 地.已知甲、乙两车的速度之和是每小时220千米,
2536
AB AD =,求甲车的速度.
A C 'A 'D C
B B A
C 图2图1
A
B C M 1922
11.已知关于x 的方程2x ax =+只有负数根,求a 的取值范围.
12.天津和上海之间有四种交通工具:飞机、火车、轮船与长途汽车.假期里,几位同学去上海旅游了一次,对于其中的任意三位同学,要么去上海时所选用的交通工具各不相同,要么从上海回来时所选用的交通工具各不相同.则这些同学最多有多少位?
三、解答下列各题(每题l5分,共30分,要求写出详细过程)
13.在下面的乘法竖式中,每个数字被纸片盖住,纸片上只标出盖住的数字的奇偶,请写出该乘法竖式.
14.下图中,平行四边形ABCD 的面积是1,E 、F 分别是AB 、CD 上的点,AF 与DE 交于G .已知
,DF b AE d FC a EB c ==,问:三角形DFG 的面积是多少?
奇⨯偶偶偶偶偶偶奇偶偶奇偶奇奇偶偶A B
C D E F G。
