圆锥形及阶梯型变幅杆模态分析教案资料
模态分析经典课件

隔离体受 力分析
kx
k
x(t)
m
O
第二十八页,共110页。
运动微分方程
运动微分方程
mx kx 0
x(0)
x0 ,
x(0)
x0
x n2 x 0
x(0) x0, x(0) x0
n
k m
第二十九页,共110页。
运动微分方程
解
x A1 cosnt A2 sin nt
Acos(nt )
an bn
把谐波分析 的结果形象化:An,n和之间的 关系用图形来表示,称为频谱
第二十五页,共110页。
单自由度系统
自由振动 简谐振动 非周期强迫振动
第二十六页,共110页。
自由振动
振动系统在初始激励下或外加激励消失后的运动状态。
自由振动时系统不受外界激励的影响,其运动时 的能量来自于初始时刻弹性元件和惯性元件中存 储的能量。
运动学
把一个周期函数展开成傅立叶级数,亦即展开成一系列简谐函数之和 一般的周期振动可以通过谐波分析分解成简谐振动
第二十三页,共110页。
运动学
傅立叶级数
F
t
a0 2
a1
cos 1t
a2
cos 21t
...
b1 sin 1t b2 sin 21t ...
1:基频
a0 2
an
n1
cos n1t
)2
0
0.2
0.7
0.1
0.5
1
2
0 0 1
2
3
第四十五页,共110页。
全解
简谐强迫振动
第四十六页,共110页。
简谐强迫振动
全解
圆锥摆模型

专题:圆锥摆模型(水平面内的圆周运动)教学目标物理观念:通过圆锥摆模型的分析,会在具体问题中分析向心力的来源,会寻找圆心,计算半径,列出方程求解物理量。
科学思维:运用函数思想构建所求物理量的函数关系,并利用函数关系处理物理问题。
科学探究:通过圆锥摆模型的分析,体会物理模型的重要性,并能将相关模型等效成圆锥摆模型。
科学态度与责任:通过圆锥摆模型的分析,培养学生将物理知识应用于生活的意识。
教学重难点:重点:通过圆锥摆模型的分析,会在具体问题中分析向心力的来源,会寻找圆心,计算半径,列出方程求解物理量。
难点:1.运用函数思想构建所求物理量的函数关系,并利用函数关系处理物理问题。
2.通过圆锥摆模型的分析,体会物理模型的重要性,并能将相关模型等效成圆锥摆。
模型。
教学过程:复习导入:向心力的表达式。
新课教学一.圆锥摆模型的受力特点受两个力,且两个力的合力沿水平方向,物体在水平面内做匀速圆周运动。
二.圆锥摆的相关规律1.摆球的加速度2.摆球的线速度3.摆球的周期和角速度4.摆线得拉力5.两种圆锥摆分析对甲:由a =g tan θ知A 、B 的向心加速度大小相等。
由a =ω2r 知ωA <ωB ,由a =v 2r 知v A >v B 对乙:由T =2πhg 知摆高h 相同,则ωA =ωB ,由v =ωr 知v A >v B ,由a =ω2r知a A >a B 。
三.案例分析例1、如图所示,两根长度相同的细线分别系有两个完全相同的小球,细线的上端都系于O 点.设法让两个小球均在各自的水平面上做匀速圆周运动.已知L 1跟竖直方向的夹角为60°,L 2跟竖直方向的夹角为30°,下列说法正确的是( )A .细线L 1和细线L 2所受的拉力大小之比为1:√3B .小球m 1和m 2的角速度大小之比为1:1C .小球m 1和m 2的向心力大小之比为3:1D .小球m 1和m 2的线速度大小之比为3√3:1练习1、A 、B 两质量相同的质点用轻质细线悬挂在同一点O ,在同一水平面上做匀速圆周运动,如图所示,则( ) A .A 的加速度一定比B 的加速度小 B .A 的线速度一定比B 的线速度小 C .A 的角速度一定等于B 的角速度D .A 所受细线的拉力一定等于B 所受的细线的拉力例2:如图所示,用一根质量不计、不可伸长的细绳,一端系一可视为质点的小球,另一端固定在O 点。
模态分析教程及实例讲解PPT学习教案

② 假定为自由振动(忽略阻尼):M u Ku 0
③ 假定为谐运动: K2M u 0
④
这相个应方的程向的量根 是是{u}Ii,,即即特特征征向值量,。i 的范围从1到自由度的数目,
注意:
•模态分析假定结构是线性的(如, [M]和[K]保持为常数) •简谐运动方程u = u0cos(t), 其中 为自振圆周频率(rad/s)
有预应力的结构进行模态分析。例如旋转的涡轮叶片。 循环对称结构模态分析。允许对循环对称结构的一部分进行建模,
而分析产生整个结构的振型。 ANSYS的模态分析都是线性分析。 ANSYS中的模态提取方法:
Block Lanzos(默认)、子空间、PowerDynamics、缩减法、非对称法、阻 尼法和QR 阻尼法。后两种允许结构中包含阻尼。
第18页/共74页
频率分析的相关知识
频率分析就是计算结构的共振频率及对应振动模态,不计 算位移和应力
固有频率:结构趋向于振荡的频率,固有的振动频率。 基本频率:最低的固有频率
固有振动模态:特定的固有频率对应唯一的振动形式。 每种模态对应着特定的固有频率
第19页/共74页
频率分析的相关知识
振幅:大 振幅:小
振动频率:是单位时间里摆动的次数。 1秒钟内的次数用Hz(赫兹)来表示。 周期:摆动1次所需要的时间。
钟摆的形状(长度)决定了其固有的数值。 钟摆越长周期越长,钟摆越短周期越短。
第11页/共74页
频率分析的相关知识
固有频率(以钟摆为例) 钟摆的振动所经过的时间越来越小,最后停了下来。 这是因为空气的阻碍、磨擦的阻碍等的阻力妨碍了钟摆的摆动(振动)。 因为这样的阻力作用使振动衰减的力而起作用,被称为衰减力。 钟摆在没有外部而来的强迫它摆动的力(重力除外)作用下的振动称为自由振动。 与此相对应,地震和汽车因为地基能、发动机等的强迫力作用下的振动称为强迫振动。
阶梯轴ANSYS静态分析与模态分析
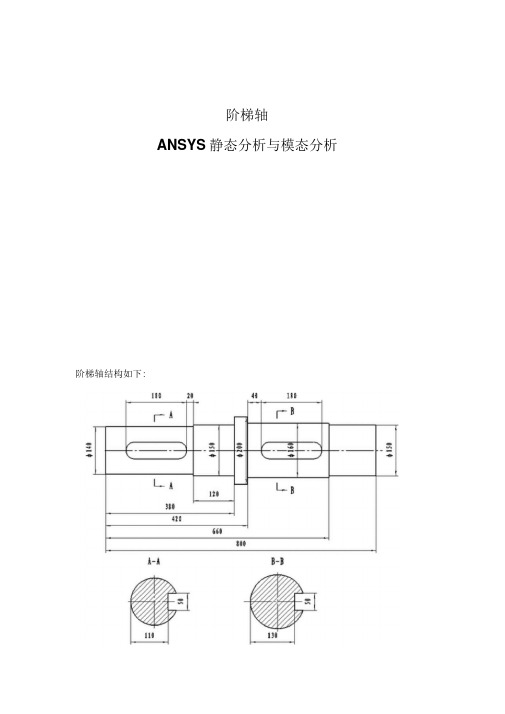
阶梯轴ANSYS静态分析与模态分析阶梯轴结构如下:F面来做轴的静态分析:1定义工作文件名和工作标题(过程略)2显示工作平面(过程略)3利用矩形面素生成面1) 生成矩形面:Main Menu>Preprocessor>Create>Rectangle>By Dimensions ,在对话框的“ X-coordinates ”和“丫-coordinates ”后面输入栏中分别输入下列数据:X1=0, X2=260, Y1=0,Y2=70,单击“ Aplay ” X仁260, X2=380, 丫仁0,Y2=75, 单击“ Aplay ”;XI=380 , X2=420 , 丫仁0 ,丫2=100 ,单击“ Aplay ”;X仁420 , X2=660 , 丫仁0 ,丫2=80 ,单击“ Aplay ”;X仁660, X2=800, 丫仁0,丫2=75,单击“ ok”;生成的结果如图两WX2)矩形面相加操作:Ma in Men u>Preprocessor>Operate>Add>Area§出现一个拾取框,单击“ Pick All ”,则完成相加操作,生成的结果如图AREASANSYS311010^667 张旭4由面绕轴线生成体1)面绕轴线操作:Main Menu>Preprocessor>Operate> Extrude>About Axis , 出现一个拾取框,单击“ Pick All ”又出现第二个拾取轴心线两端点的拾取 框,用鼠标在图形上分别拾取编号为“ 1、18”的关键点,然后单击“ OK ,又弹出一个对话框单击“ OK .TYPE NUM丸跟lfi 201420:51:533110104667张旭2)保存到 文件中:Main Menu> File>Save As, 弹出一个对话框,在 “Save Database to ”下面的输入栏中输入用户自定义的文件名 “shaft.DB ”, 单击“0K .5生成A-A 键槽1) 移动工作平面:在“ Offset WP by In creme nts ” 中的“ X ,Y ,Z Offset ”下面的输入栏中输入“85, 0, 40”(A-A 键槽左侧圆弧中心),并按“Enter ” 键确认。
模态分析方法与步骤

模态分析方法与步骤模态分析方法与步骤一、模态分析包括下列6种方法:1.降阶法(reduced householder method):该方法为一般结构最常用的方法之一。
其原理是在原结构中选取某些重要的节点为自由度,称为主自由度(master degree of freedom),再用该主自由度来定义结构的质量矩阵及刚度矩阵并求出其频率及振动模态,进而将其结果扩展至全部结构。
在解题过程中该方法速度较快,但其答案较不准确。
主自由度的选择依照所探讨的模态、结构负载的情况而定:a. 主自由度的个数至少为所求频率个数的两倍。
b. 选择主自由度的方向为结构最可能振动的方向。
c. 主自由度节点位于较大质量或转动惯量处及刚性较低位置。
d. 如果弯曲模态为主要探讨模态,则可省略旋转自由度。
e. 主自由度的节点位于施力处或非零位移处。
f. 位移限制为零的位置不能选为主自由度节点,因为这种节点具有高刚性的特性。
可以用M命令来定义主自由度。
此外,也可由ANSYS自动选择自由度。
2. 次空间法(subspace method):通常用于大型结构中,仅探讨前几个振动频率,所得到结果较准确,不需要定义主自由度,但需要较多的硬盘空间及CPU时间。
求取的振动模态数应该小于模型全部自由度的一半。
3. 非对称法(unsymmetrical method):该方法用于质量矩阵或刚度矩阵为非对称时,例如转子系统。
其特征值(eigenvalue)为复数,实数部分为自然频率;虚数部分为系统的稳定度,正值表示不稳定,负值表示稳定。
4. 阻尼法(damped method):该方法用于结构系统具有阻尼现象时,其特征值为复数,虚数部分为自然频率;实数部分为系统的稳定度,正值表示不稳定,负值表示稳定。
5. 区块法(block lanczos method):该方法用于大型结构对称的质量及刚度矩阵,和次空间方法相似,但收敛性更快。
6. 快速动力法(power dynamics method):该方法用于非常大的结构(自由度大于100,000)且仅需最小几个模态。
精选有限元分析模态分析讲义

精选有限元分析模态分析讲义有限元分析(Finite Element Analysis,FEA)是一种工程分析方法,通过将连续体离散化为若干个有限单元,建立有限元模型,以求解结构的力学性能和振动特性。
模态分析是有限元分析的重要应用之一,主要用于研究和预测结构的固有频率、振型和模态势能的分布。
以下是一份精选的有限元分析模态分析讲义,包括了模态分析的基本原理、建立有限元模型的步骤和模态分析的结果解读。
一、模态分析的基本原理:1.结构固有频率的定义和意义;2.结构的振型和模态势能的物理意义;3.模态分析的数学模型和假设;4.模态方程的推导和求解方法;5.模态分析的应用示例。
二、建立有限元模型的步骤:1.结构的几何建模和网格划分;2.材料的力学性质和边界条件的定义;3.单元类型和单元参数的选择;4.单元刚度矩阵和质量矩阵的生成;5.结构的总刚度矩阵和总质量矩阵的组装;6.结构的边界约束处理;7.求解结构的固有频率和振型。
三、模态分析的结果解读:1.结构的固有频率和振型的意义及影响因素;2.模态势能的计算和分析;3.结构的频率响应和模态叠加法;4.模态分析结果的验证和灵敏度分析;5.模态分析在结构设计和优化中的应用。
此外,讲义还可以包括以下内容:1.不同类型结构的模态分析实例和案例分析;2.常见的模态分析方法和软件工具的介绍;3.模态分析结果的后处理和可视化方法;4.模态分析中的常见问题和解决方法;5.模态分析在结构健康监测和故障诊断中的应用。
总之,一份精选的有限元分析模态分析讲义应当全面介绍模态分析的基本原理和方法,包括模态分析的建模步骤和结果解读,同时提供实例和案例分析,为学习者提供理论基础和实践指导,使他们掌握有限元模态分析的基本原理和应用技能。
材料力学第04章 杆件变形分析ppt课件

中北大学理学院力学系
第一节 杆件轴向拉压变形 第二节 圆轴改动变形 第三节 积分法求梁弯曲变形叠加法求梁弯曲变形 第四节 提高梁弯曲刚度的措施 总结与讨论
杆件在载荷作用下都将发生变形〔deformation〕。在 有些构造或实践工程中,杆件发生过大的变形将影响杆件或 构造的正常运用,必需对杆件的变形加以限制,如工程中运 用的传动轴、车床主轴等变形过大会呵斥机器不能正常任务; 而有些构造又需求杆件有较大的变形,如汽车上所运用的叠 板弹簧,只需当弹簧有较大变形时,才干起缓冲作用。在构 造的设计中,无论是限制杆件的变形,还是利用杆件的变形, 都必需掌握计算杆件变形的方法。本章将详细讨论杆件轴向 拉伸〔或紧缩〕、圆轴改动和弯曲三种情况下的杆件变形。 研讨杆件变形的目的,一方面是为了分析杆件的刚度问题, 另一方面那么是为了求解超静定问题。
根据平面假设,横截面在梁弯曲变形后,仍与梁轴垂直,那
么横截面会发生角位移,即绕中性轴转过一个角度,称为转
角〔slope of cross section〕,用q表示。由几何关系可知,
横截面的转角q与挠曲线在该截面处的切线与坐标轴x的夹角
q′相等,即
由于梁的变形普通很小,这时转角q也很小,于是有挠曲线与 转角之间的近似关系为
那么轴的总改动角为 A C A B B C 1 . 5 0 1 0 2 ( 1 . 1 7 1 0 2 ) 0 . 3 3 1 0 2 r a d
〔2〕刚度轴校为核等。截面轴,AB段的扭矩最大,所以,应校核 该段轴的改动刚度。
AB段的改动角变化率,即单位长度改动角为
d d x G T A I B P 1 8 0 8 0 1 0 9 3 1 . 0 8 0 1 0 5 1 0 1 2 1 8 0 0 . 4 3 /m < [ ]
阶梯轴教案

阶梯轴的车削加工§1 工作任务描述1.加工零件项目工作任务名称:阶梯轴的车削加工。
2.零件类型描述:该零件属于较简单的阶梯轴类零件,是使用数控车床加工的基本零件轮廓形状。
是数控车削加工中难度较低的基本零件之一。
3.任务内容描述:已知毛坯材料为LY12,毛坯尺寸为Ф40mm×70mm的棒料。
制定零件加工工艺,编写零件加工程序,并在仿真软件上进行虚拟操作加工,最后在数控车床上进行实际操作加工,并对加工后的零件进行检测、评价。
§2 学习情境教学设计§3 教学内容与教学设计学习方法设计:1.教师采用引导文教学法引导学生进入学习情境;教师布置工作任务,提出问题,进行资讯;教师当学生,分组讨论,学生决策;教师讲述、演示、解惑2. 学生根据零件图完成学习环境的实施;学生对加工后的零件进行自检互评3 .由教、学、做逐渐过渡为做、学、教,做中学,学中做,边学、边做、边修正§3.1制定工艺方案引导文设计:1.选择合适的毛坯应注意哪些事项?。
2.从保证加工表面的加工精度和表面粗糙度的要求出发,选择备选加工方法。
3.分析轴类零件所要求的加工精度、尺寸公差等是否可以得到保证?4.有无引起矛盾的多余尺寸或缺尺寸?3.1.1分析零件图工艺信息:教师布置工作任务,学生资讯,教师解惑,学生填写零件图工艺信息分析卡片,见表1-1。
3.1.2确定加工顺序:小组讨论,听取学生的决策意见,学生填写卡片,见表1-2。
表1-2 加工顺序卡片单位名称爱尔福特手工业协会班级学号姓名成绩零件图号零件名称使用设备场地001 阶梯轴CK6136S数控车床数控加工实训中心程序编号零件材料LY12 数控系统HNC-21T工步序号工步内容确定理由量具选用备注名称量程1 车端面车平端面,建立长度基准,保证工件长度要求。
车削完的端面在后续加工中不需再加工。
0.02mm游标卡尺0-150mm 手动2 粗车各外圆表面较短时间内去除毛坯大部分余量,满足精车余量均匀性要求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆锥形及阶梯型变幅杆模态分析 超声波变幅杆的设计及修正 摘 要: 超声变幅杆是超声波振动系统中一个重要的组成部分。本文结合超声变幅杆理论对设计变幅杆进行结果分析及参数修正,采用ANSYS 12.1对变幅杆进行了有限元模态分析,在此基础上,设计并加工了一个应用于超声显微切割系统中的、谐振频率为70 kHz的半波长圆锥型变幅杆,和用于超声波近场悬浮的、谐振频率是20kHz的阶梯型变幅杆,并进行了相关实验。实验结果表明,利用ANSYS软件辅助设计方法得到的超声变幅杆,其谐振频率与模态分析值非常接近,修正理论也可以让变幅杆谐振频率更加接近设计值,为超声变幅杆的设计、校核和优化提供了一种新途径。 关键词:变幅杆;有限元;模态分析
Design and Revise of Ultrasonic horn
Abstract:Ultrasonic horns apply widely in ultrasonic processing. Combined with ultrasonic horn theory, correct the ultrasonic horn by formula, analysis the modal of horn by ANSYS 12.1, on this basis, design a half-wavelength conical horn which resonant frequency is 60kHz, used by a ultrasonic micro dissection system, and a stepped ultrasonic horn which resonant frequency is 20kHz, used by a near-field acoustic levitation system, then make the related experiment. The results show that the resonant frequency of the ultrasonic horn designed by ANSYS is approaching the theory value, the correction coefficient also can make the resonant frequency approach the theory value, that provides a new way to design, checking or optimization. Key word: Ultrasonic horn; Finite element; Modal analysis
引 言 超声变幅杆是超声振动系统的重要组成部件,它在振动系统中的主要作用是把机械振动的质点位移量或运动速度放大,并将超声能量集中在较小的面积上[1]。在高强度超声应用中,如超声加工、超声焊接、超声切割、超声波悬浮等场合,所需要的振幅大约为几十至几百微米,但是超声换能器辐射面所产生的振动幅度较小,一般只有几微米,所以必须借助变幅杆将机械振动质点的位移或速度放大至满足工程应用要求。目前,有关超声变幅杆的设计,国内外主要采用传统解析法、等效电路法与替代法等,但是这些方法普遍存在计算量大而且设计精度不高的缺陷。运用有限元分析软件ANSYS,可以有效地解决传统设计方法中存在的不足[2]。因此,运用ANSYS,通过对超声变幅杆进行模态分析和参数优化,可以大大提高设计效率和精度。本研究结合ANSYS软件,设计一个在超声显微切割系统应用的、谐振频率为60 kHz的半波长圆锥型变幅杆和超声波悬浮中应用的谐振频率为20kHz圆柱型变幅杆。
1 超声变幅杆的理论分析与设计 1. 1 变截面杆纵向振动的理论分析 物体在弹性介质中发生振动时会引起介质的振动。在研究振动波时,假设把弹性介质分成若干层,每一层看作是由许多彼此紧密相连的质点组成,一旦介质中的某个质点受到某种扰动,此质点便产生偏离其平衡位置的运动[3],由于介质各点之间存在着弹性的联系,这一运动势必推动与其相邻的质点也开始运动,这样,物体的振动就在弹性介质中传播出去,这种物体的振动在弹性介质中的传播被称为波动。以质点和简单机械振动系统的振动及超声波的传播原理为理论基础,建立数学模型,根据牛顿定理可以确定变截面杆纵向振动的波动方程。 为了便于研究,设定理想状态,假定变截面杆是由均匀、各向同性材料所构成的,略去机械损耗,当杆的横截面尺寸远小于波长时,可以认定,平面纵波沿杆轴向传播,在杆的横截面上应力分布是均匀的[4]。 图1 变截面杆纵向振动 任一变横截面杆(如图1所示),其对称轴为X轴,作用在任意的一小体积元,dxxx
上的张应力为dxx,根据牛顿定律可以得出动力学方程:
22()ddSxSxxx (1) 为变幅杆纵向振动位移,ssx为面积函数,kc为波数,为材料的密度。为应力函数,Ex,E是杨氏模量。 按照经典的一维变截面细杆纵振理论,假定变幅杆是由密度均匀且各向同性的材料制成,不计机械损耗,在杆的横截面上应力分布均匀且平面波沿轴向传播,此时平面波的传播方程为:
22210skxsxx (2) kc为圆波数,是圆频率,c是纵波在细杆中的传播速度,cE[5]。 1.2 圆锥型变幅杆的设计 1.2.1 变幅杆的理论分析 变幅杆各性能参数是根据纵向振动的波动方程、杆的面积函数及边界条件推导出的公式确定的,如图2所示。
图2 圆锥型变幅杆结构图 以变幅杆的纵向为x轴,l为长度,()Sx为截面面积,设坐标原点x=0处的横截面积
为1S,xl处的横截面积为2S;作用在1S,2S上的力及位移分别为1F、1和2F、2,两端自由的时候,边界条件为:
11000:,|,|0xxxtxg (3) 22:,|,|0xlxlxltx
g
(4)
根据边界条件可以得到变幅杆的谐振长度: 2l (5) 这就是变幅杆的设计长都都是半波长的原因[6]。 1.2.2 变幅杆谐振频率修正 假设变幅杆纵振时沿轴线方向上的位移为x,则应变为xxx,纵振速度为xxddt。
根据瑞利近似理论[9],横向应变为xrx(为泊松比),横向位移为xrrrrx(r为半径),横向振动速度为xrrdrdtx。变幅杆上任意一个微分单元的质量为2dmrdrdx,故沿轴向方向的纵向振动动能xE和沿径向方向的横向振动动能rE分别为: 22201()22lxxxEdmRxdx (6)
222401()24lxrrEdmRxdxx (7) 忽略横向振动后的系统总动能降低,等效质量eqm 减小,因为12KfM,故变幅杆计算出的谐振频率比实际谐振频率高[7]。增加横向振动后的纵振谐振频率'f与忽略横向振动时的频率f比值为:
'xxrEffEE (8) 这里称为频率修正系数。为了让变幅杆实际频率与设计频率一致,需要对未考虑横向振动时的杆长l进行修正,经修正后的杆长'l为: 'll (9)
对于圆柱杆,两端自由时cosxAl,所以222200llxxdxdxxl,故222212杆杆杆xxrEREEl
,于是圆柱杆的频率修正公式为:
2222'112杆fRlf (10) 对于常用的粗细两段等长阶梯型变幅杆,令粗细两段半径分别为R和r,质点的纵向振动速度分别为xa和xb。两端自由时,变幅杆两端应力为0,在0x的截面处力和位移连
续,由这些边界条件可知120AA,1122BSBS,所以22122baSRNSr,2xbbxaaN。计算阶梯型变幅杆的纵振动能阶梯xE和横振动能阶梯rE时,可以按照半径为R长度为l的等效圆柱杆来计算,只是在计算阶梯rE时,应加上阶梯面对变幅杆两端速度的影响。于是阶梯xE、阶梯rE分别为:
22222
002阶梯llxaxaxERdxRdx
(11)
22
2
0442
0232442220414
阶梯lxaxblrlxaERdxRdx
xx
NRdxl
(12)
故阶梯型变幅杆频率修正公式为[8]: 4222
211122阶梯N
R
l
(13)
1.2.3 变幅杆的设计 分别为超声显微切割系统和超声波近场悬浮系统设计一个半波长的变幅杆,要求工作频
率60fkHz和20fkHz,材料选用45号钢。
根据系统结构要求,设定圆锥型变幅杆的大端直径120Dmm,小端直径25Dmm,得到124NDD,可知纵波声速(在45号钢中)65.1710/cmms,根据式(5)、式(6)和式(7)计算可得: 143lmm,019xmm。同时,考虑到其与外界的装配问题,在节面处增加了一厚度为4mm,外径为28mm的法兰盘,具体尺寸如图3所示。
图3圆锥型变幅杆 而对于设计频率是20kHz的近场悬浮变幅杆,型状是一个圆柱上面一个圆盘,可以把圆盘考虑成弯曲振动,这样设计的时候只需考虑圆柱杆。同上面的步骤,最后得到变幅杆尺寸
为:长度2129lmm,取大端直径338Dmm,小端直径420Dmm。如图4所示。
图4 阶梯型变幅杆 2 超声变幅杆的有限元分析 根据圆锥型变幅杆的理论完成设计,并进行有限元分析。这里采用美国ANSYS公司设计开发的大型通用有限元分析软件ANSYS 12.1进行分析。
