小学三年级数学上册 找规律思维训练
三年级数学思维训练[1]1
![三年级数学思维训练[1]1](https://img.taocdn.com/s3/m/3be3bb9eba4cf7ec4afe04a1b0717fd5370cb27a.png)
整数计算综合
还原问题
数阵图初步
竖式问题
几何图形简拼
路程、时间、速度
01-整数计算综合(1)
02-整数计算综合(2)
03-还原问题(1)
04-还原问题(2)
05-数阵图初步(1)
06-数阵图初步(2)
07-竖式问题(1)
08-竖式问题(2)
09-竖式问题(3)
10-竖式问题(4)
37-长度计算1
38-长度计算2
39-长度计算3
40-角度的计算1
41-角度的计算2
42-角度的计算3
43-找位置1
44-找位置2
火柴棍算式与生活趣题
三年级期末复习与检测
45-火柴棍算式与生活趣题1
46-火柴棍算式与生活趣题2
47-三年级期末复习与检测1
48-三年级期末复习与检测2
49-三年级期末复习与检测3
11-几何图形简拼(1)
12-几何图形简拼(2)
13-几何图形简拼(3)
14-几何图形简拼(4)
15-路程、时间、速度(1)
16-路程、时间、速度(2)
17-路程、时间、速度(3)
18-路程、时间、速度(4)
行程中的线段图
简单抽屉原理
基本直线形面积公式
底、高的选取与组合
变倍问题
和差倍中的分组比较
19-行程中的线段图(1)
复杂数阵图
有特殊要求的挑选
捆绑法与插空法
最值问题一
40-多次往返相遇与追与1
41-多次往返相遇与追与2
42-多次往返相遇与追与3
43-多次往返相遇与追与4
44-从洛书到幻方1
45-从洛书到幻方2
三年级上册思维训练题

三年级上册数学思维第一单元:时、分、秒1、利用间隔数解决爬楼梯问题明明从1楼走到3楼需要16秒。
照这样的速度计算,他从1楼走到7楼需要多少秒?思路分析:可以这样想:明明从1楼走到3楼走了2层,需要16秒,则平均每层需要走8秒。
照这样的速度计算,他从1楼走到7楼走了6层,一共需要走48秒。
正确解答:一层:16÷(3-1)=8(秒)到7楼:8×(7-1)=48(秒)举一反三:(1)公路的一侧每隔10米种1棵树,小丽从第1棵树走到第5棵树需要28秒,照这样的速度计算,她从第1棵树走到第10棵树需要多少秒?(2)芳芳从四楼到一楼用了 24秒,玲玲从八楼到一楼用了 56秒,她们下楼的速度一样吗?(3)从田边到池塘有9米,青蛙从田边跳到池塘、每跳3米要用5 秒,休息1秒后继续跳,青蛙从田边跳到池塘需要多长时间?2.求等车时间间隔的问题例题:去人民公园的公共汽车每15分钟发一班车。
小明早上7: 10到达车站,发现7:05时已经发了一班车,他还要等多长时间才能坐上车?思路分析:方法一:可以先求出下一班车的发车时间,再减去小明到达车站的时间,就是等车的时间。
方法二:可以求出距离上一班车的发车时间经过了几分钟,再用两班车发车的间隔时间减去经过的时间,就是等车的时间。
正确解答: 方法一 7时5分+15分钟=7时20分7时20分-7时10分=10分钟方法二 7时10-7时5分=5分钟 15- 5=10(分钟) 举一反三:(1)去图书馆的公共汽车每15分钟发一班车。
小明上午9: 05到达车站,发现9:00时已经发了一班车,他还要等多长时间才能坐上车?(2)小红从家到学校要走20分钟,她每天早晨要8:40到学校。
小红最迟几时从家出发?(3)火车8:15发车,小东7:00从家出发坐车去火车站,从他家到火车站乘车需45分钟,从进站口到检票完需要20分钟,他能赶上这趟火车吗?3.利用分段计时法计算经过的时间例题:永辉超市营业时间,开门:早上7:30,关门:晚上10:00。
三年级数学思维训练第1讲 寻找规律(一)

【知识要点】三年级数学思维训练第1 讲寻找规律(一)观察是解决问题的依据。
通过观察,可以揭示出事物的发展和变化规律,在一般情况下,我们可以从以下几个方面来找规律:1.根据每相邻两个数之间的关系,找出规律,推断出所要填的数。
2.根据相隔的每两个数之间的关系,找出规律,推断出所要填的数。
3.要善于从整体上把握数据之间的联系,从而很快找出规律。
4.数据之间的联系往往可以从不同的角度来理解,只要言之有理,所得出的规律都可以认为是正确的。
【例题 1】先找出下列数排列的规律,然后在括号里填上适当的数。
(1)1,4,7,10,(),16,19答案:13;【解析】在这列数中,相邻的两个数的差都是 3,即每一个数加上 3 都等于后面的数。
根据这一规律,括号里应填的数为:10+3=13 或16-3=13。
(2)2,4,8,16,(),(),()答案:32 64 128【解析】按照一定顺序排列的一串数叫作数列。
在这列数中,相邻的两个数的比都是 2,即每一个数乘 2 都等于后一个数。
根据这一规律,括号里应填的数为16×2=32,32×2=64,64×2=128。
像这样,从第二个数起,每一个数与前一个数的比都相等的数列,叫作等比数列。
(1)2,6,10,14,(),22,26(2)3,6,9,12,(),18,21(3)33,28,23,(),13,(),3(4)55,49,43,(),31,(),19(5)3,6,12,(),48,(),192(6)2,6,18,(),162,()(7)128,64,32,(),8,(),2(8)768,(),48,12,3【例题2】先找出下列数的排列规律,然后在括号里填上适当的数。
1,2,4,7,(),16,22答案:11。
【解析】在这列数中,前4个数每相邻的两个数的差依次是1,2,3。
由此可以推算7比括号里的数少4,括号里应填:7+4=11。
(1)10,11,13,16,20,(),31(2)1,4,9,16,25,(),49,64(3)18,19,21,24,(),33,(),()(4)53,44,36,29,(),18,(),11,9,8 (5)81,64,49,36,(),16,(),4,1,0 (6)1,4,8,13,19,(),()(7)1,3,7,13,(),()(8)3,4,6,10,18,(),()【例题3】先找出规律,然后在括号里填上适当的数。
三年级上册数学思维拓展图形找规律
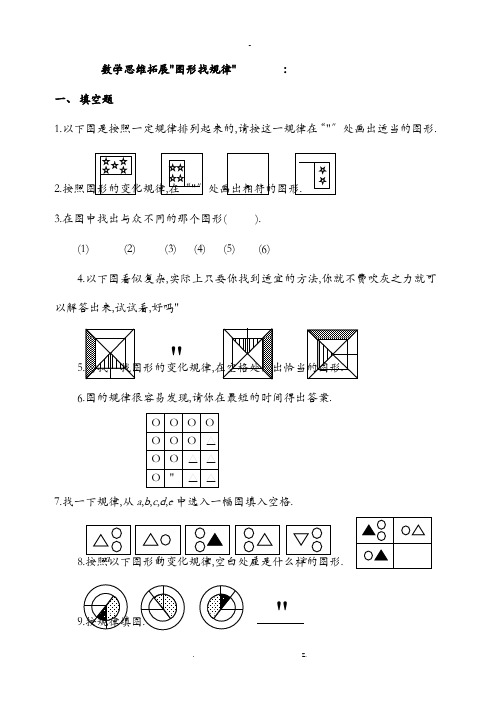
数学思维拓展"图形找规律" :一、 填空题1.以下图是按照一定规律排列起来的,请按这一规律在“"〞处画出适当的图形.2.〞处画出相符的图形3.在图中找出与众不同的那个图形( ).(1)(2)(3) (4)(5) (6)4.以下图看似复杂,实际上只要你找到适宜的方法,你就不费吹灰之力就可以解答出来,试试看,好吗",6.图的规律很容易发现,请你在最短的时间得出答案.7.找一下规律,从a ,b ,c ,d ,e 中选入一幅图填入空格...""如果 变成 则 应变为10.下面一组图形的阴影变化是有规律的,请根据这个规律把第四幅图的阴影局部画出来.二、解答题11.图中,哪个图形与众不同"(1) (2) (3) (4) (5)12.有一个立方体,每个面上分别写上数字1、2、3、4、5、6、,有3个人 从不同的角度观察的结果如以下图所示,这个立方体的每一个数字的对面各是什么数字" 13.下面是由几何图形组成的帆船图形,请按照一定的规律,在标序号处画出符合规律的小帆船."1 2 61 3 4 ① ②③———————————————答案——————————————————————1. 这一组图形我们应该从两方面来看:一是旗子的方向,二是旗子上星星的颗数.首先我们看一下旗子的方向.第1面旗子向右,第2面向上,第4面向下,可以发现,旗子的方向是按逆时针旋转的,并依次旋转︒90,所以第3面旗子应是第2面逆时针旋转︒90得来的,旗子应向下倒立.其次我们看旗上星星的颗数.第1面是5颗,第2面是4颗,第4面是2颗,1颗,所以第3面旗上应是3颗星星.所以“"〞处的图形应为:2. 这组图形的变化只在于正方形中阴影局部的位置.通过观察,我们可以发现阴影局部是按照逆时针方向依次旋转︒90得到的.所以“"〞处的图形应为:3. 选(4).因为变化规律是从左到右依次逆时针旋转︒90.4. 在这组图形中,不变的有以下几点:大小正方形不变,两条对角线不变.所以“"〞处也应有大小两个正方形和两条对角线.发生变化的有:一、阴影局部和黑色局部的位置.通过观察,我们可以看出这两局部都是按逆时针方向依次旋转︒90得到的,所以“"〞处的阴影局部应是小正方形的右边,黑色局部应在大正方形的下部.二、小竖线的位置.小竖线是从图形中心到相应的边所作的一条垂线.它的变化规律是按逆时针方向依次旋转︒90,这样,整个图形我们就分析完了,下面看一看你画出的图形和书上的一样吗"如果一样,就做对了.5. 因为要填的是第1幅图,我们可以从后往前看.首先三角形的个数是发生变化的,依次是7、5、3.可以发现是从后向前依次减少2个的.所以第1幅图中应有1个三角形.其次三角形的方向也是有变化的,从后面观察,三角形是按逆时针方向依次旋转︒90,所以第1幅图中的三角形应向上,阴影局部在右边.如以下图所示:6. 横行观察,圆的个数逐次减少1个,所以到第4行,圆的个数应为1,所以“"〞处应是“△〞.或者从三角形考虑,三角形的个数为0、1、2,是逐次增加1,所以第4行中三角形的个数应为3,所以“.〞处应为“△〞所以最后的图形为:7. 选a.根据对角图形规律,可知右下角图形是a图.8. 分析:先看不变的局部.在整个变化过程中,图形、小两个圆圈没有变化,因此可以肯定空白处的图形一定也有大、小两个圆圈,位置一里一外.变化的局部可为两局部:①图形中的直线局部,其变化规律是每次顺时针旋转︒90,黑色局部交90;②图形中的阴影局部,其变化规律是每次逆时针旋转︒替出现.解:根据上面的分析,可画出空白处的图形如下图.9. 先应找出变化的规律,然后再依此规律,在空白处填画出所缺的图形.从第一行可以看到,当左边的图形变成右边的图形时,下部图形移到上面,里面的图形移到下面,上面的外部图形移到里面,各局部的颜色都没有变.根据这一规律,我们可以把下面图形变为:10. 先看第1行,阴影局部所在的位置是1、2、3.是逐次向后一个,所以第四幅图中第1行的阴影局部应在第4格.同样,第2行是2、3、4.4再向后应是5了,但没有第5个格,所以折回到第1个格.同理可推出第3行的阴影局部在第2格,第4行的阴影局部在第3格.还可以这样想:在同一行中,阴影局部都不在同一位置,所以第1行已经被占去了第1、2、3格,所以第四幅图的第一行阴影局部一定是第4格,同理推出第2、3、4行中阴影局部的位置.最后的答案如以下图所示.11. 分析:这五辆汽车车窗一致,车轮一致,车底一致,差异就只能在车头、车身局部去寻找.从车身看,(3)与众不同,只用一笔画成,可是它的车头与(1)同;从车头看:(2)与众不同,(因车头(1)与(3)同,(4)与(5)同),但是(2)的车身与(1)、(4)、(5)类似.所以从车头、车身这些特征比拟出来的图形,理由缺乏以说服人.我们把目光转移到笔划多少上,就可以找到与众不一的车辆了.解:与众不同的汽车是(1).其他四车均是由一个矩形、两个圆以及四条直线段、一段弧线画成,而(1)多一条直线段.12. 这个题目并不难.但是,推理方法不正确的话,也很难看出答案.直接考虑数字1的对面是什么数,想不出来.不妨换一种思维方式,想一想1的对面不是什么数.从第1个图看出1的对面不是4和6;从第2个图看出1的对面不是2和3,所以1的对面只能是5.同样的方法可以得到,4的对面是2;3的对面是6.13.因为正锥体的每个顶点连接三个面.当正锥体在雪花格纸上按顺时针方向旋转时,只有写有1、2、4三面所围出的顶点一直在雪花格的中心,所以只有1、2、4贴纸面旋转,雪花格有6个小格,正好可以转两圈,所以回到原地各面数字仍是原样分布.14.每一只小帆船都由三局部组成:船体、帆和小旗.这三局部都是变化的,另外船体的颜色也是变化的.下面我们逐一来分析.。
三年级数学思维训练(1)

思维训练一1、★×2+7-20=25 ★=()(54-★)×9=72 ★=()2、A乘4,再加上20,然后除以5,等于8,A是()。
3、篮子里有一些苹果,5个5个的数多1个,7个7个的数也多一个。
篮子里至少有()个苹果。
4、甲仓库存粮80吨,乙仓库存粮56吨,每天从甲仓库运出8吨粮食,从乙仓库运出5吨粮食。
那么()天之后两个仓库剩下的粮食就同样多了。
5、把一根木头锯成3段要4分钟,把这根木头锯成4段要()分钟。
6、名华奥校今年招收二年级新生80人,其中男生比女生多10人,男人有()人女生()人7、一年一班和一年二班共有学生46人,一年二班转到一年一班2人,两个班人数相等,原来一班有()人二班有()人8、一位数加一位数,最小是(),最大是(),两位数加两位数,最小是(),最大是(),三位数加三位数,最小是(),最大是(),从以上的解题中你是否发现规律了呢请完成下面挑战题:四位数加四位数,最小是(),最大是()。
9、小李、小华比赛爬楼梯,小李跑到第2层时,小华正好跑到第4层。
照这样计算,小李跑到第5层时,小华到第()层。
10、直接写出得数(1)42+71+29+58= (2)526-73-27-26=(3)1457-(185+457)= (4)729+154+271=(5)516-56-44-16=11、小明和小强原有书和相等,后来小明把书送给小强12本,这时小明和小强,()的书多多()本。
12、一只鸭、一只鹅共重12千克。
如果知道一只鸡和一只鸭共重7千克;一只鹅和一只鸭共重9千克,那么一只鸭是()千克。
13、把两张纸贴接在一起用一分钟,把同样6张纸连接贴成一张大纸,共用()分钟14、甲是乙的哥哥,丙是丁的弟弟,丁是甲的父亲,丙是乙的什么人()思维训练二1、先找规律,再填数1×9+2=1112×9+3=111123×9+4=11111234×9+5=()12345×9+6=()123456×9+7=()×9+9=()2、算式谜□ 9 1 □ 8 2 □□□□□□+ □ 1 □ + □ 1 □ - □ 8 5 - □ 8 7□ 9 1 □□ 9 0 □ 6 3 7 7 3 73、小推理(1)已知□+○=28,□=○+○+○,那么□=()○=()(2)☆+☆+□+□+□=61,☆+☆+□+□=52,那么☆=()□=()4、在一个减法算式里,被减数、减数、差这三个数的和是120,则被减数是()。
(完整版)三年级数学思维训练入门
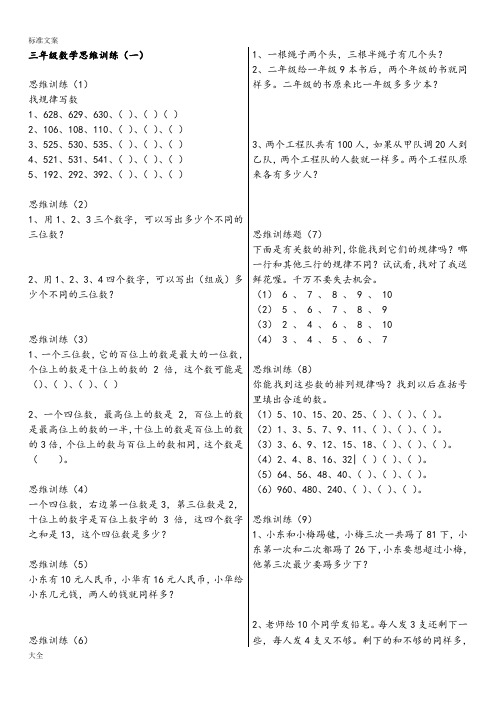
三年级数学思维训练(一)思维训练(1)找规律写数1、628、629、630、()、()()2、106、108、110、()、()、()3、525、530、535、()、()、()4、521、531、541、()、()、()5、192、292、392、()、()、()思维训练(2)1、用1、2、3三个数字,可以写出多少个不同的三位数?2、用1、2、3、4四个数字,可以写出(组成)多少个不同的三位数?思维训练(3)1、一个三位数,它的百位上的数是最大的一位数,个位上的数是十位上的数的2倍,这个数可能是()、()、()、()2、一个四位数,最高位上的数是2,百位上的数是最高位上的数的一半,十位上的数是百位上的数的3倍,个位上的数与百位上的数相同,这个数是()。
思维训练(4)一个四位数,右边第一位数是3,第三位数是2,十位上的数字是百位上数字的 3 倍,这四个数字之和是13,这个四位数是多少?思维训练(5)小东有10元人民币,小华有16元人民币,小华给小东几元钱,两人的钱就同样多?思维训练(6)1、一根绳子两个头,三根半绳子有几个头?2、二年级给一年级9本书后,两个年级的书就同样多。
二年级的书原来比一年级多多少本?3、两个工程队共有100人,如果从甲队调20人到乙队,两个工程队的人数就一样多。
两个工程队原来各有多少人?思维训练题(7)下面是有关数的排列,你能找到它们的规律吗?哪一行和其他三行的规律不同?试试看,找对了我送鲜花喔。
千万不要失去机会。
(1) 6 、 7 、 8 、 9 、 10(2) 5 、 6 、 7 、 8 、 9(3) 2 、 4 、 6 、 8 、 10(4) 3 、 4 、 5 、 6 、 7思维训练(8)你能找到这些数的排列规律吗?找到以后在括号里填出合适的数。
(1)5、10、15、20、25、()、()、()。
(2)1、3、5、7、9、11、()、()、()。
(3)3、6、9、12、15、18、()、()、()。
完整)三年级数学思维训练

完整)三年级数学思维训练1.第一题:求解符号的值,第一个式子中有两个符号,第二个式子中有一个符号,需要先计算出符号的值,再代入求解。
第二题:先算出A的值,再代入求解。
第三题:需要找到最小的满足条件的数,可以通过列举法得到。
第四题:需要算出每天两个仓库的总共运出的粮食,然后计算剩下的粮食是否相等。
第五题:可以通过列举法得到答案。
第六题:可以通过列方程解得到男生和女生的数量。
第七题:可以通过列方程解得到一年一班和一年二班原来的人数。
第八题:需要找到每个位数的最小和最大值,可以通过列举法得到。
第九题:可以通过比例关系得到答案。
第十题:需要进行简单的加减法运算。
第十一题:需要列方程解得到每个人现在的书的数量。
第十二题:需要列方程解得到每种动物的重量。
第十三题:可以通过列举法得到答案。
第十四题:需要通过家庭关系推理得到答案。
2.第一题:需要找到每个数与九的关系,可以通过列举法得到。
第二题:需要将数字填入算式中,使得等式成立,可以通过代入法得到。
第三题:需要通过已知条件推理出未知数的值,可以通过代入法得到。
2、4、6、15、9、8、8、3、44、27、36、甲、15、150、100、31、4、8、20、16、6、18、8、28、4、7、29.2、已知两个等式,求解其中的未知数。
第一个等式为:☆+☆+□+□+□=61,☆+☆+□+□=52,求解出☆和□的值。
第二个等式为:被减数+减数+差=120,求解出被减数的值。
第三个问题是一个简单的代数问题,求解出两个数的和,已知其中一个加数增加12,另一个加数增加18,和应为多少。
6、XXX在XXX吃东西,可以用不同的食品进行交换。
已知1个汉堡可以换2个鸡翅,1个鸡翅可以换3个冰淇淋,求解出1个汉堡可以换多少个冰淇淋。
7、有20名三年级同学参加竞赛,其中15人参加数学竞赛,13人参加作文竞赛,求解出既参加数学竞赛又参加作文竞赛的人数。
8、这个问题给出了一些算式,要求求解出其中的未知数。
三年级数学思维训练(1)

思维训练一1、★×2+7-20=25 ★=()(54-★)×9=72 ★=()2、A乘4,再加上20,然后除以5,等于8,A是()。
3、篮子里有一些苹果,5个5个的数多1个,7个7个的数也多一个。
篮子里至少有()个苹果。
4、甲仓库存粮80吨,乙仓库存粮56吨,每天从甲仓库运出8吨粮食,从乙仓库运出5吨粮食。
那么()天之后两个仓库剩下的粮食就同样多了。
5、把一根木头锯成3段要4分钟,把这根木头锯成4段要()分钟。
6、名华奥校今年招收二年级新生80人,其中男生比女生多10人,男人有()人?女生()人?7、一年一班和一年二班共有学生46人,一年二班转到一年一班2人,两个班人数相等,原来一班有()人?二班有()人?8、一位数加一位数,最小是(),最大是(),两位数加两位数,最小是(),最大是(),三位数加三位数,最小是(),最大是(),从以上的解题中你是否发现规律了呢?请完成下面挑战题:四位数加四位数,最小是(),最大是()。
9、小李、小华比赛爬楼梯,小李跑到第2层时,小华正好跑到第4层。
照这样计算,小李跑到第5层时,小华到第()层。
10、直接写出得数(1)42+71+29+58= (2)526-73-27-26=(3)1457-(185+457)= (4)729+154+271=(5)516-56-44-16=11、小明和小强原有书和相等,后来小明把书送给小强12本,这时小明和小强,()的书多?多()本。
12、一只鸭、一只鹅共重12千克。
如果知道一只鸡和一只鸭共重7千克;一只鹅和一只鸭共重9千克,那么一只鸭是()千克。
13、把两张纸贴接在一起用一分钟,把同样6张纸连接贴成一张大纸,共用()分钟?14、甲是乙的哥哥,丙是丁的弟弟,丁是甲的父亲,丙是乙的什么人?()思维训练二1、先找规律,再填数1×9+2=1112×9+3=111123×9+4=11111234×9+5=()12345×9+6=()123456×9+7=()12345678×9+9=()2、算式谜□ 9 1 □ 8 2 □□□□□□+ □ 1 □ + □ 1 □ - □ 8 5 - □ 8 7□ 9 1 □□ 9 0 □ 6 3 7 7 3 73、小推理(1)已知□+○=28,□=○+○+○,那么□=()○=()(2)☆+☆+□+□+□=61,☆+☆+□+□=52,那么☆=()□=()4、在一个减法算式里,被减数、减数、差这三个数的和是120,则被减数是()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
找规律(一)
这一讲我们先介绍什么是“数列”,然后讲如何发现和寻找“数列”的规律。
按一定次序排列的一列数就叫数列。
例如,
(1) 1,2,3,4,5,6,⋯
(2) 1,2,4,8,16,32;
(3) 1,0,0,1,0,0,1,⋯
(4) 1,1,2,3,5,8,13。
一个数列中从左至右的第n 个数,称为这个数列的第n 项。
如,数列(1)的第3 项是3,数列(2)的第3 项是4。
一般地,我们将数列的第n 项记作a n。
数列中的数可以是有限多个,如数列(2)(4),也可以是无限多个,如数列(1)(3)。
许多数列中的数是按一定规律排列的,我们这一讲就是讲如何发现这些规律。
数列(1)是按照自然数从小到大的次序排列的,也叫做自然数数列,其规律是:后项=前项+1,或第n 项a n =n。
数列(2)的规律是:后项=前项×2。
数列(3)的规律是:“1,0,0”周而复始地出现。
数列(4)的规律是:从第三项起,每项等于它前面两项的和,即a3=1+1=2,a4=1+2=3,a5=2+3=5,a6=3+5=8,a7=5+8=13。
常见的较简单的数列规律有这样几类:
第一类是数列各项只与它的项数有关,或只与它的前一项有关。
例如数列(1)(2)。
第二类是前后几项为一组,以组为单元找关系才可找到规律。
例如数列(3)(4)。
第三类是数列本身要与其他数列对比才能发现其规律。
这类情形稍为复杂些,我们用后面的例3、例4 来作一些说明。
例1 找出下列各数列的规律,并按其规律在( )内填上合适的数:
(1)4,7,10,13,( ); (2)84,72,60,( ),( );
(3)2,6,18,( ),( ),(4)625,125,25,( ),( );
(5)1,4,9,16,( ),(6)2,6,12,20,( ),( ),
解:通过对已知的几个数的前后两项的观察、分析,可发现
(1)的规律是:前项+3=后项。
所以应填16。
(2)的规律是:前项-12=后项。
所以应填48,36。
(3)的规律是:前项×3=后项。
所以应填54,162。
(4)的规律是:前项÷5=后项。
所以应填5,1。
(5)的规律是:数列各项依次为1=1×1, 4=2×2, 9=3×3, 16=4×4,
所以应填5×5=25。
(6)的规律是:数列各项依次为2=1×2,6=2×3,12=3×4,20=4×5,
所以,应填 5×6=30, 6×7=42。
例2 找出下列各数列的规律,并按其规律在( )内填上合适的数:
(1)1,2,2,3,3,4,( ),( );
(2)( ),( ),10,5,12,6,14,7;
(3) 3,7,10,17,27,( );
(4) 1,2,2,4,8,32,( )。
解:通过对各数列已知的几个数的观察分析可得其规律。
(1)把数列每两项分为一组,1,2,2,3,3,4,不难发现其规律是:前一组每个数
加1 得到后一组数,所以应填4,5。
(2)把后面已知的六个数分成三组:10,5,12,6,14,7,每组中两数的商都是2,且由5,6,7 的次序知,应填8,4。
(3) 这个数列的规律是:前面两项的和等于后面一项,故应填(17+27=)44。
(4)这个数列的规律是:前面两项的乘积等于后面一项,故应填(8×32=)256。
例3 找出下列各数列的规律,并按其规律在( )内填上合适的数:
(1)18,20,24,30,( );
(2)11,12,14,18,26,( );
(3)2,5,11,23,47,( ),( )。
解:(1)因20-18=2,24-20=4,30-24=6,说明(后项-前项)组成一新数列2,4,6,⋯其规律是“依次加2”,因为6 后面是8,所以,a5-a4=a5-30=8,故a5=8+30=38。
(2)12-11=1,14-12=2, 18-14=4, 26-18=8,组成一新数列1,2,4,8,⋯按此规律,8 后面为16。
因此,a6-a5=a6-26=16,故a6=16+26=42。
(3)观察数列前、后项的关系,后项=前项×2+1,所以a6=2a5+1=2×47+1=95,
a7=2a6+1=2×95+1=191。
例4 找出下列各数列的规律,并按其规律在( )内填上合适的数:
(1)12,15,17,30, 22,45,( ),( );
(2) 2,8,5,6,8,4,( ),( )。
解:(1)数列的第1,3,5,⋯项组成一个新数列12,17, 22,⋯其规律是“依次加5”,22 后面的项就是27;数列的第2,4,6,⋯项组成一个新数列15,30,45,⋯其规律是“依次加15”,45 后面的项就是60。
故应填27,60。
(2)如(1)分析,由奇数项组成的新数列2,5,8,⋯中,8 后面的数应为11;由偶数项组成的新数列8,6,4,⋯中,4 后面的数应为2。
故应填11,2。
练习5
按其规律在下列各数列的( )内填数。
1.56,49,42,35,( )。
2.11, 15, 19, 23,( ),⋯
3.3,6,12,24,( )。
4.2,3,5,9,17,( ),⋯
5.1,3,4,7,11,( )。
6.1,3,7,13,21,( )。
7.3,5,3,10,3,15,( ),( )。
8.8,3,9,4,10,5,( ),( )。
9.2,5,10,17,26,( )。
10.15,21,18,19,21,17,( ),( )。
11.数列1,3,5,7,11,13,15,17。
(1)如果其中缺少一个数,那么这个数是几?应补在何处?
(2)如果其中多了一个数,那么这个数是几?为什么?。
