4.Lagrangian网格
Ls-Dyna_负体积问题

LS-DYNA FAQ 中英文版-Negative Volume 负体积2007年09月13日星期四下午 10:26泡沫材料的负体积(或其它软的材料)对于承受很大变形的材料,比如说泡沫,一个单元可能变得非常扭曲以至于单元的体积计算得到一个负值。
这可能发生在材料还没有达到失效标准前。
对一个拉格朗日(Lagrangian)网格在没有采取网格光滑(mesh smoothing)或者重划分(remeshing)时能适应多大变形有个内在的限制。
LS-DYNA中计算得到负体积(negative volume)会导致计算终止,除非在*control_timestep卡里面设置ERODE选项为1,而且在*control_termination里设置DTMIN项为任何非零的值,在这种情况下,出现负体积的单元会被删掉而且计算继续进行(大多数情况)。
有时即使ERODE和DTMIN换上面说的设置了,负体积可能还是会导致因错误终止。
有助于克服负体积的一些方法如下:* 简单的把材料应力-应变曲线在大应变时硬化。
这种方法会非常有效。
* 有时候修改初始网格来适应特定的变形场将阻止负体积的形成。
此外,负体积通常只对非常严重的变形情况是个问题,而且特别是仅发生在像泡沫这样的软的材料上面。
* 减小时间步缩放系数(timestep scale factor)。
缺省的0.9可能不足以防止数值不稳定。
* 避免用全积分的体单元(单元类型2和3),它们在包含大变形和扭曲的仿真中往往不是很稳定。
全积分单元在大变形的时候鲁棒性不如单点积分单元,因为单元的一个积分点可能出现负的Jacobian而整个单元还维持正的体积。
在计算中用全积分单元因计算出现负的Jacobian而终止会比单元积分单元来得快。
* 用缺省的单元方程(单点积分体单元)和类型4或者5的沙漏(hourglass)控制(将会刚化响应)。
对泡沫材料首先的沙漏方程是:如果低速冲击type 6,系数1.0; 高速冲击type 2或者3。
计算固体力学 第2章 一维Lagrangian和Eulerian有限元

Xa
uA0 P, X u, X
A0 PdX
Xb
Xb
Xa
u A0 P , X dX uA0 n 0 P uA0 t x0
Xb Xa
t
Xa
u , X A0 P dX
u , X A0 P dX
在指定位移边界处变分项 u 消失,第二行服从边界互补条件 和力边界条件。
b-单位质量的力-体力 应力在坐标方向的分量
如果初始横截面面积在空间保持常数,则动量方程成为
( P),X 0b 0u
2 完全的Lagrangian格式
不计惯性力,则动量方程成为平衡方程
平衡方程 能量守恒
( A0 P),X 0 A0b 0
平衡意味着物体处于静止或者以匀速运动
尽管TL和UL表面看来有很大区别,两种格式的力学本质 是相同的;因此,TL可以转换为UL,反之亦然。
TSINGHUA UNIVERSITY
1 引言
对于每一种公式,将建立动量方程的弱形式,已知为虚 功原理(或虚功)。这种弱形式是通过对变分项与动量方程 的乘积进行积分来建立。在 TL格式中,积分在所有材料坐标 上进行;在 Eulerian 和 UL格式中,积分在空间坐标上进行。 也将说明如何处理力边界条件,因此近似(试)解不需要满 足力边界条件。这个过程与在线性有限元分析中的过程是一 致的,在非线性公式中的主要区别是需要定义积分赋值的坐 标系和确定选择应力和应变的度量。 推导有限元近似计算的离散方程。对于考虑加速度(动 力学)或那些包含率相关材料的问题,推导离散有限元方程 为普通微分方程( ODEs )。这个空间的离散过程称为半离散 化,因为有限元仅将空间微分运算转化为离散形式,而没有 对时间导数进行离散。对于静力学与率无关材料问题,离散 方程独立于时间,有限元离散将导致一组非线性代数方程。
拉格朗日,欧拉,ALE网格解释

6 Y" @' w: g3 A
7 o1 N9 e, b0 RALE、Lagrange、Euler是数值模拟中处理连续体的广泛应用的三种方法。
0 n$ g% v) N! Z
* z% ^7 N, r$ GLagrange方法多用于固体结构的应力应变分析,这种方法以物质坐标为基础,其所描述的网格单元将以类似“雕刻”的方式划分在用于分析的结构上,即是说采用Lagrange方法描述的网格和分析的结构是一体的,有限元节点即为物质点。采用这种方法时,分析结构的形状的变化和有限单元网格的变化完全是一致的(因为有限元节点就为物质点),物质不会在单元与单元之间发生流动。这种方法主要的优点是能够非常精确的描述结构边界的运动,但当处理大变形问题时,由于算法本身特点的限制,将会出现严重的网格畸变现象,因此不利于计算的进行。
! e1 w# f& Z" r% J2 |( m6 D2 b4 V) P1 ^# u
Euler方法以空间坐标为基础,使用这种方法划分的网格和所分析的物质结构是相互独立的,网格在整个分析过程中始终程始终是不变的。很显然由于算法自身的特点,网格的大小形状和空间位置不变,因此在整个数值模拟过程中,各个迭代过程中计算数值的精度是不变的。但这种方法在物质边界的捕捉上是困难的。多用于流体的分析中。使用这种方法时网格与网格之间物质是可以流动的。
/ q# @ }) Y0 {) s/ M6 kALE方法最初出现于数值模拟流体动力学问题的有限差分方法中。这种方法兼具Lagrange方法和Euler方法二者的特长,即首先在结构边界运动的处理上它引进了Larange方法的特点,因此能够有效的跟踪物质结构边界的运动;其次在内部网格的划分上,它吸收了Euler的长处,即是使内部网格单元独立于物质实体而存在,但它又不完全和Euler网格相同,网格可以根据定义的参数在求解过程中适当调整位置,使得网格不致出现严重的畸变。这种方法在分析大变形问题时是非常有利的。使用这种方法时网格与网格之间物质也是可以流动的。
Lagrange、Euler、ALE三种方法的简单介绍

Lagrange、Euler、ALE三种方法的简单介绍ALE、Lagrange、Euler是数值模拟中处理连续体的广泛应用的三种方法。
Lagrange方法多用于固体结构的应力应变分析,这种方法以物质坐标为基础,其所描述的网格单元将以类似“雕刻”的方式划分在用于分析的结构上,即是说采用Lagrange方法描述的网格和分析的结构是一体的,有限元节点即为物质点。
采用这种方法时,分析结构的形状的变化和有限单元网格的变化完全是一致的(因为有限元节点就为物质点),物质不会在单元与单元之间发生流动。
这种方法主要的优点是能够非常精确的描述结构边界的运动,但当处理大变形问题时,由于算法本身特点的限制,将会出现严重的网格畸变现象,因此不利于计算的进行。
Euler方法以空间坐标为基础,使用这种方法划分的网格和所分析的物质结构是相互独立的,网格在整个分析过程中始终保持最初的空间位置不动,有限元节点即为空间点,其所在空间的位置在整个分析过程始终是不变的。
很显然由于算法自身的特点,网格的大小形状和空间位置不变,因此在整个数值模拟过程中,各个迭代过程中计算数值的精度是不变的。
但这种方法在物质边界的捕捉上是困难的。
多用于流体的分析中。
使用这种方法时网格与网格之间物质是可以流动的。
ALE方法最初出现于数值模拟流体动力学问题的有限差分方法中。
这种方法兼具Lagrange方法和Euler方法二者的特长,即首先在结构边界运动的处理上它引进了Larange方法的特点,因此能够有效的跟踪物质结构边界的运动;其次在内部网格的划分上,它吸收了Euler 的长处,即是使内部网格单元独立于物质实体而存在,但它又不完全和Euler网格相同,网格可以根据定义的参数在求解过程中适当调整位置,使得网格不致出现严重的畸变。
这种方法在分析大变形问题时是非常有利的。
使用这种方法时网格与网格之间物质也是可以流动的。
固体结构分析中一般都选用lagrange坐标,实际上lagrange euler法在有限元中体现的节点意义正如楼主所述,但是本质牵扯的是参考什么样的坐标来描述应力应变关系。
Abaqus中三种自适应网格介绍及对比
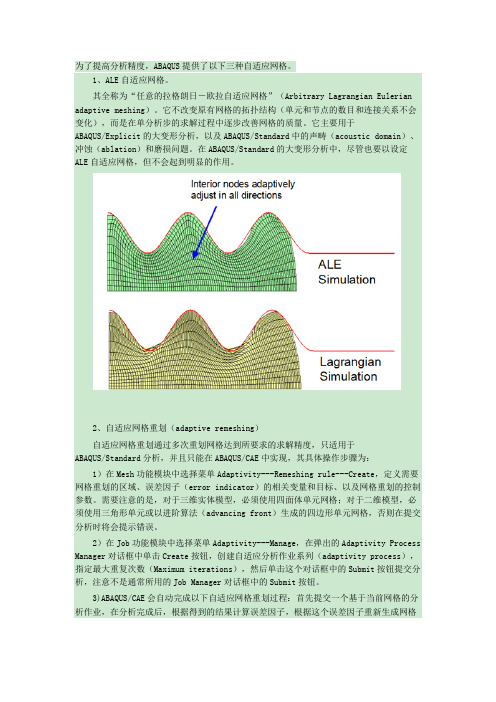
为了提高分析精度,ABAQUS提供了以下三种自适应网格。
1、ALE自适应网格。
其全称为“任意的拉格朗日-欧拉自适应网格”(Arbitrary Lagrangian Eulerian adaptive meshing)。
它不改变原有网格的拓扑结构(单元和节点的数目和连接关系不会变化),而是在单分析步的求解过程中逐步改善网格的质量。
它主要用于ABAQUS/Explicit的大变形分析,以及ABAQUS/Standard中的声畴(acoustic domain)、冲蚀(ablation)和磨损问题。
在ABAQUS/Standard的大变形分析中,尽管也要以设定ALE自适应网格,但不会起到明显的作用。
2、自适应网格重划(adaptive remeshing)自适应网格重划通过多次重划网格达到所要求的求解精度,只适用于ABAQUS/Standard 分析,并且只能在ABAQUS/CAE中实现,其具体操作步骤为:1)在Mesh功能模块中选择菜单Adaptivity---Remeshing rule---Create,定义需要网格重划的区域、误差因子(error indicator)的相关变量和目标、以及网格重划的控制参数。
需要注意的是,对于三维实体模型,必须使用四面体单元网格;对于二维模型,必须使用三角形单元或以进阶算法(advancing front)生成的四边形单元网格,否则在提交分析时将会提示错误。
2)在Job功能模块中选择菜单Adaptivity---Manage,在弹出的Adaptivity Process Manager对话框中单击Create按钮,创建自适应分析作业系列(adaptivity process),指定最大重复次数(Maximum iterations),然后单击这个对话框中的Submit按钮提交分析,注意不是通常所用的Job Manager对话框中的Submit按钮。
3)ABAQUS/CAE会自动完成以下自适应网格重划过程:首先提交一个基于当前网格的分析作业,在分析完成后,根据得到的结果计算误差因子,根据这个误差因子重新生成网格(在JOB功能模块中可以看到新的网格),然后重新提交分析。
FLAC3D基础介绍

GeoHohai
命令栏
18/74
菜单驱动(Plot)
GeoHohai
19/74
Case-2 一个最简单的例子
gen zon bri size 3 3 3 ;建立网格
model elas
;材料参数
prop bulk 3e8 shear 1e8
ini dens 2000
;初始条件
fix z ran z -.1 .1
GeoHohai
38/74
接触面单元的用途
岩体介质中的解理、断层、岩层面 地基与土体的接触 箱、槽及其内充填物的接触 空间中无变形的固定“障碍”
GeoHohaiΒιβλιοθήκη 39/74接触面的原理
如:井
孔隙压力,孔隙率,饱和度和流体属性的初始分 布可以用INITIAL命令或者PROPERTY命令定义。
GeoHohai
29/74
单渗流计算及渗流耦合计算
时间比例 完全耦合分析方法 孔压固定分析(有效应力分析) 单渗流得到孔压分布 无渗流计算——孔压的力学响应 流-固耦合计算
GeoHohai
PROP biot_c 0 (or INI fmod 0)
GeoHohai
33/74
无渗流计算——孔压的力学响应
不排水短期响应 两种分析方法:干法和湿法
干法:Ku=K+a2M 两种破坏形式
WATER或INI获得常孔压,不排水的c,φ (孔压改变较小) φ=0,c=cu (M>>K+4/3G)
GeoHohai
16/74
FLAC3D的前后处理
命令驱动(推荐)
程序控制 图形界面接口 计算模型输出 指定本构模型及参数 指定初始条件及边界条件,指定结构单元 指定接触面 指定自定义变量及函数(FISH) 求解过程的变量跟踪 进行求解 模型输出
计算固体力学7_ALE公式
结论是,在弱形式中的材料速度的时间导数为
v dv I (t ) N I (ξ) c(ξ, t ) N I (ξ ) v I (t ) dt
对于密度的材料时间导数,应用同样的过程,给出
d I (t ) N I (ξ ) c(ξ, t ) N I (ξ ) I (t ) dt
[X ]
x j i
wi f , t [ ] f , j c j
(7.2.17)
利用空间梯度建立材料时间导数的表达式
Df f , t [Χ ] c grad f f , t [Χ ] c f Dt
f 若代表是速度,上式为加速度
i vi ,t[ ] vi , j c j v
4 ALE控制方程
连续方程(质量守恒)
vk , k 0
动量方程
或者
,t[ ] ,i ci vk , k 0
i (vi , t[ ] vi , j c j ) ji , j bi v
能量方程
(E,t[ ] E,i ci ) ij Dij bi vi (kij , j ),i s
[X ]
材料速度和网格速度的差
xi (χ , t ) j (X, t ) xi (χ , t ) ˆi ci vi v wj j t j
2 ALE连续介质力学
代入
Df f x j i f , t[ ] Dt x j i t f , t[ ] f , j
解决:在发生严重大变形的模拟中,重新划分网格是不 可避免的,工作量大,而且由于网格投影引入了误差。
1 引言
一个 Lagrangian 网格像在材料上的 蚀刻:当材料变形 时,蚀刻(和单元) 随着变形。 一个 Eulerian 网 格像放在材料前面 一薄片玻璃上的蚀 刻:当材料变形时, 蚀刻不变形,而材 料横穿过网格。
lagrangian方程
lagrangian方程Lagrangian方程是经典力学中一种重要的数学工具,用于描述物体在给定势能下的运动。
它是由法国数学家和天文学家拉格朗日于18世纪提出的,被广泛应用于多个学科领域。
本文将介绍Lagrangian 方程的基本概念、应用以及其在物理学中的重要性。
Lagrangian方程是经典力学中的一种描述物体运动的数学表达式。
它是由Lagrangian函数L定义的,L是物体的动能T与势能V之差,即L = T - V。
对于一个物体在给定势能下的运动,其Lagrangian 函数可以用物体的广义坐标q和广义速度q'来表示。
Lagrangian方程的形式为d/dt (∂L/∂q') - ∂L/∂q = 0,其中∂L/∂q'表示对广义坐标q'求偏导数,∂L/∂q表示对广义坐标q求偏导数。
这个方程实际上是一个运动方程,描述了物体在给定势能下的运动规律。
Lagrangian方程的出现是为了解决经典力学中的动力学问题。
与牛顿力学相比,Lagrangian方程的优势在于它能够同时处理多个自由度的问题,而无需像牛顿力学那样引入大量的约束方程。
在Lagrangian方程的框架下,可以使用变分法来求解运动方程,得到物体的运动轨迹。
Lagrangian方程的应用范围非常广泛。
在物理学中,它被用于描述各种力学系统,如刚体、弹性体和流体力学等。
此外,Lagrangian方程还可以推广到相对论力学和量子力学领域,成为了研究这些领域中物体运动规律的重要工具。
在天体力学中,Lagrangian方程也有着重要的应用。
通过建立天体系统的Lagrangian函数,可以推导出描述行星、卫星等天体运动的方程。
这些方程不仅可以用于预测天体的运动轨迹,还可以揭示天体系统中的动力学规律,为天文学家研究宇宙中的各种现象提供了重要的理论基础。
除了物理学和天文学领域,Lagrangian方程在工程学和应用数学中也有着广泛的应用。
ABAQUS的CEL分析
ABAQUS的CEL分析什么是ABAQUSABAQUS是一种强大的有限元分析软件,常被用于求解结构力学和热力学问题。
它可以帮助工程师和科学家进行复杂结构的建模和分析,提供了多种功能模块,如静力学、动力学、热力学和电磁学等。
其中,CEL (Coupled Eulerian-Lagrangian)分析是ABAQUS中的一种特殊分析方法,用于模拟固体或液体中相对运动的结构。
CEL分析的原理CEL方法将物体划分为Eulerian网格和Lagrangian粒子,分别用于描述固体和流体的运动。
Eulerian网格是一种固定的网格,在整个分析过程中不发生变形,用于描述流体介质的运动。
Lagrangian粒子则随物体表面的移动而移动,用于描述固体物体的运动。
这种耦合的方法可用于模拟多种情况,如液体冲击、爆炸、钣金成形等。
CEL分析的步骤要进行CEL分析,需要执行以下步骤:1. 准备模型首先,需要准备一个包含所有几何和材料属性的模型。
这个模型可以是由CAD软件创建的几何模型,也可以是ABAQUS中的几何建模工具创建的模型。
在模型中,需要定义材料的本构关系、初始应力状态和初始速度等信息。
2. 离散网格在进行CEL分析之前,需要进行离散网格的划分。
将模型划分为适当的单元(element),以便进行数值计算。
在CEL分析中,需要同时划分Eulerian网格和Lagrangian粒子。
3. 定义物理耦合CEL分析的核心是定义Eulerian网格和Lagrangian粒子之间的物理耦合关系。
这通常包括流体与固体之间的接触、传热、质量传输等。
通过定义这些物理耦合关系,可以模拟出复杂的物理现象。
4. 定义加载条件加载条件是指施加在模型上的外部力和约束条件。
在CEL分析中,外部力可以是流体的冲击、爆炸力等,约束条件可以是固体的几何限制或边界条件。
5. 求解模型在进行CEL分析之前,需要设置求解器的参数和时间步长。
然后,通过ABAQUS的求解器对模型进行求解。
代数多重网格算法
代数多重网格算法代数多重网格算法(algebraic multigrid method,简称AMG)是一种用于求解线性代数方程组的数值方法,特别适用于大规模的、稀疏的线性方程组。
AMG算法结合了代数方法和多重网格技术,能够快速、高效地求解线性方程组,是一种非常强大的求解器。
AMG算法的核心思想是通过构建粗网格模型来近似细网格上的线性代数方程组,从而实现高效的求解。
该算法可以分为以下几个步骤:1.建立粗网格模型:根据细网格的结构,构造一个粗略的网格模型。
这个模型通常比原始网格拥有更少的节点和单元,因此粗网格上的方程组规模更小。
2.选择插值算子:通过插值算子将细网格上的解插值到粗网格上,从而在粗网格上构造一个近似解。
插值算子的选择非常关键,一般有线性插值、加权平均等方法。
3. 求解粗网格方程组:在粗网格上使用传统的迭代方法(如Jacobi迭代、Gauss-Seidel迭代等)求解方程组。
由于粗网格上方程组规模较小,因此计算速度更快。
4.修正细网格解:通过使用插值算子将粗网格上的解修正到细网格上,从而在细网格上获得一个更准确的解。
修正的步骤通常与插值算子的方法相反。
通过以上四个步骤,AMG算法能够在较短的时间内求解原始的线性代数方程组。
相比于传统的直接解法和迭代法,AMG算法具有以下优点:1.高效的计算速度:AMG算法通过使用粗网格模型,将原始方程组规模缩小,因此计算速度更快。
2.高精度的解:AMG算法通过修正细网格解,能够得到更精确的解。
3.大规模问题的求解能力:AMG算法适用于大规模和稀疏的线性方程组,能够处理数百万乃至数十亿个未知数的问题。
4.并行计算的可扩展性:由于AMG算法的计算过程可以自然地分解成多个独立的任务,因此非常适合并行计算,具有良好的可扩展性。
综上所述,代数多重网格算法是一种高效、高精度、可扩展的线性代数方程组求解方法。
在科学计算、工程领域和计算机图形学中,AMG算法被广泛应用于各种领域的问题求解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
xQ t NI XQ xI t
n
为应力张量的独立分量数目,
在二维平面应力问题中,由于应力张量对称,n 在三维问题中,n
3 ;
6。
3 UL有限元离散
离散方程
半离散运动(动量)方程为关于时间的常微分方程
M ijI J v jJ f iIint f iIext
ij XQ ij Dkl XQ , etc.
初始条件:可以是速度和应力,或者是位移和速度。第一组初 始条件更适合于大多数工程问题,因为确定一个物体的初始位移通 常是很困难的。初始应力通常为已知的残余应力,有时候可以测量 或者通过平衡解答估算。例如,当一个钢件经过铸锭成型后确定其 位移几乎是不可能的。对于在工程部件中的残余应力场,经常能够 给出较准确的估计。类似地,在埋置管道中,靠近管道周围的土壤 或岩石的初始位移的概念是毫无意义的,而初始应力场可以通过平 衡分析估计出来。因此,以应力形式的初始条件更加实用。
一个单元的三个域:
1. 2. 母单元域 当前单元域 □
e e t
3.
初始(参考)单元域
e 0
3 UL有限元离散
单元坐标
相关的映射
通过映射的合成描述每一单元的运动
x xX, t x ξ e X, t
3 UL有限元离散
单元坐标
运动近似给出为
xi ξ , t xiI t N I ξ
M ijIJ ij N I N J d
内部节点力代表着物体的应力。以上这些表达式既可以应用于整体网格,也 可以应用于任意单元或单元集。这些表达式包含形状函数对应于空间坐标的 导数和在当前构形上的积分。在非线性有限元方法中,对于更新的 Lagrangian网格,这是一个关键的方程;它也应用于Eulerian和ALE网格。
2 UL控制方程
弱形式
2 UL控制方程
弱形式
边界条件:在二维问题中,面力或速度的每个分量都必须预先 指定在整个边界上;但是,在边界上同一点处不能同时指定面力和 速度分量。其分量可以指定在不同于总体坐标系的局部坐标系上。
速度边界条件等价于位移边界条件:如果给定了位移,可以通 过时间微分得到速度;给定了速度,可以通过时间积分得到位移。
2 UL控制方程
弱形式
虚功率原理是动量方程,面力边界条件和内部力连续性条件的弱 形式。微分方程的积分形式一般称为弱形式。 强形式或广义动量平衡,包括动量方程,力边界条件和力连续性 条件。微分方程一般称为强形式 。
3 UL有限元离散
有限元近似
在有限元方法中,运动 xX, t 近似地表示为
xi X, t N I XxiI t
i
N I ji d x j
i
外部节点力 惯性节点力
f iIext N I bi d N I t i d t
f iIkin N I vi d
f iIkin N I N J dviJ
f iIkin M ijI J v jJ
vi X, t
ui X, t uiI t N I X viI t N I X t
N I viI N I , j x j
变形率给出为
Dij 1 Lij L ji 1 viI N I , j v jI N I , i 2 2
在任何指定速度的地方,虚速度必须为零。
利用除
v
以外的节点上虚节点速度的任意性,则动量方程的弱形式为
i
nSD N I ji d N I bi d N I t i d N I vi d 0 ti i 1 x j
I,i v
3 UL有限元离散
有限元近似
当一个节点具有初始位置 X J ,有:
N I X J I J
xX J , t x I t N I X J x I t I J x J t
节点J总是对应于相同的材料点XJ ,在L网格中,节点总是和材料点保持一致
定义节点位移:
当前构形中的节点坐标
小写的下标表示分量,如三维 大写的下标表示节点号
xiI xI , y I , z I
I 1 ~ nN
默认对重复的指标求和;在小写指标的情况下,对空 间的维数进行求和,而在大写指标的情况下,对节点的编 号进行求和。 在求和中的节点数目取决于所考虑的域:当考虑整个 域时,对整个域中的所有节点求和;当考虑一个单元时, 对这个单元的所有节点求和。
vi X, t u i X, t u iI t N I X viI t N I X t
3 UL有限元离散
有限元近似
加速度是速度的材料时间导数
ui X, t uiI t N I X
速度梯度为
Lij vi , j viI
计算固体力学
非线性有限元
第4章 Lagrangian网格
庄茁
2009.10
第4章 Lagrangian网格
1
2 3
4
5
6
引言 UL控制方程,弱形式 UL有限元离散 编制程序 旋转公式 TL格式,弱形式,有限元半离散化
1 引言
在Lagrangian网格中,节点和单元随着材料移动, 边界和接触面与单元边缘保持一致,处理较为简单。 积分点也随着材料移动,本构方程总是在相同材料点 处赋值,这对于历史相关材料是有利的。基于这些原 因,在固体力学中广泛地应用Lagrangian网格。 UL格式,Eulerian(空间)坐标和Cauchy应力; TL格式,名义应力,PK2应力,Green应变张量。
XQ
i
Dij X Q
1 Lij L ji 2
Lij N I , j X Q viI
这是真正意义的离散平衡方程。如果本构方程是率无关 的,那么离散平衡方程是关于应力和节点位移的非线性代数 方程组。对于率相关材料,为了获得非线性代数方程组,任 何率形式都必须在时间上离散。
对于线性问题,控制方程也可以写成 KU=F 矩阵位移 法的刚度方程形式。
1 1 1 1 Q1 1 Q2 1 nQ nQ 1 2
4 编制程序
完全积分
在非线性分析中,采用积分点数的规则一般基于在线性分析中的 相同规则;对于一个规则的单元,积分点数目的选择是能恰好积分内 部节点力。一个单元的规则形式,是指仅通过母单元的拉伸而不是剪 切能得到的形式;例如,二维等参单元的一个矩形。
在 Voigt 标记中,将应力和变形率表示为列向量的形式。 从指标表示到矩阵形式的转换是比较任意的,并取决于个人 的偏爱。在大多数情况下,将单指标的变量解释为列矩阵;当 解释为行矩阵时,其过程就会有所不同。
4 编制程序
4 编制程序
数值积分
节点力、质量矩阵和其它单元矩阵的积分不是解析计算的, 而是应用数值解答,称为数值积分。最广泛应用的是Gauss积分
3 UL有限元离散
单元坐标
单元坐标是时间不变的,可以将位移、速度和加速度表示 为形状函数的形式:
ui ξ , t uiI t N I ξ uξ , t u I t N I ξ
ui ξ , t vi ξ , t viI t N I ξ , uξ , t vξ , t v I t N I ξ
3 UL有限元离散
离散方程
半离散运动(动量)方程
MijI J v jJ fiIint fiIext
是关于节点速度的 n DOF 个常微分方程系统。
n DOF 是不受约束的节点速度分量的数目,称作自由度的数目。
为了完成这个方程系统,要附加上单元积分点处的本构方程 n nQ 和以节点速度形式表示的变形率。 在网格中nQ个积分点表示为 积分点与材料点是一致的。
通过任何常微分方程的积分方法,如Runge-Kutta法或中心差分 法,可以对这个常微分方程系统进行时间积分;见第6章。
3 UL有限元离散
离散方程
对于平衡问题,加速度为零,控制方程成为
f iIint f iIext
ij XQ ij Dkl XQ , etc.
I ,i v
f d w f
1 nQ 1 Q 1 Q Q
式中nQ个积分点的权重wQ 和坐标值ξQ有表可查;见附录3。
指定方程在母单元域上进行积分,其积分区间为[-1,1]。
一个二维单元的Gauss积分为
□ f d□ f , dd wQ1 wQ2 f Q1 ,Q2
形状函数仅是母单元坐标的函数;运动的时间相关性完全反映在节点 坐标上。上式为在单元的母域和当前构形之间的一个时间相关映射。
在t=0时写出这个映射,得到
X i ξ xi ξ ,0 xiI 0N I ξ X iI N I ξ
在L单元中,材料坐标和单元坐标之间的映射是时间不变的。 如果这个映射是一对一的,则在L网格中可以将单元坐标代替材料 坐标,因为在一个单元中的每一材料点具有唯一的单元坐标编号。 为了在Ω0中在单元坐标和材料坐标之间建立唯一的对应关系,单元 数目必须成为编号的一部分。如果单元坐标不能代替材料坐标,则 网格不是L格式(如ALE)。应用初始坐标X作为材料坐标主要源于解 析过程;在有限元中,应用单元坐标作为材料编号是更自然的。
2 UL控制方程
弱形式
考虑一个物体,占有域Ω,边界为Г。 连续体力学行为的控制方程是: 1 质量(或物质)守恒,标量方程; 2 线动量和角动量守恒,张量方程,包含n个偏微分方程(n-维数); 3 能量守恒,通常称作热力学第一定律,标量方程; 4 本构方程,应力-应变或应变率的关系,对称张量; 5 应变-位移方程。
i
离散运动(动量)方程为
M ijI J v jJ f iIint f iIext I ,i v
