13数列
压轴题型13 数列压轴大题的处理策略(原卷版)-2023年高考数学压轴题专项训练

压轴题13数列压轴大题的处理策略高考数列这类问题虽然没有解析几何那样大的计算量,没有太多需要理解的东西,也不需要立体几何中的空间想象力,然而数列中涉及到的的递推思想、函数思想、分类讨论思想以及数列求和、求通项公式的各种方法和技巧贯穿与整个高中数学之中,高中最常见的数列题型就是求通项公式和数列求和两种了,数列作为数学中的一个重要概念,常常出现在各种数学竞赛中,其重要性不言而喻。
在数列中,我们需要掌握其定义、性质和求和公式等知识点,才能够有效地解决各种数列相关的问题。
对于求和问题,我们可以通过数学归纳法或递推公式等方法进行求解。
同时,我们还需要掌握数列的通项公式,以便于我们更直观地理解数列的规律和性质。
而在数列压轴题中,我们需要将所学的数列知识灵活运用,解决各种复杂的数列问题。
例如,我们可能需要使用数学归纳法证明某个数列的性质,或者需要通过构造新的数列来解决问题。
总的来说,数列作为数学中的一个重要概念,在数学竞赛中经常出现,是我们必须掌握的知识点之一。
通过不断练习和总结,我们可以更好地掌握数列的求和、通项公式和数列压轴题等知识,从而在数学高考中获得好成绩。
○热○点○题○型1数列中的不动点问题○热○点○题○型2数列与数学史○热○点○题○型3数列与生活○热○点○题○型4数列与不等式1.已知数列{}n a 的前n 项和为n S ,()2*n S n n =∈N ,数列{}n b 为等比数列,且21a +,41a +分别为数列{}n b 第二项和第三项.(1)求数列{}n a 与数列{}n b 的通项公式;(2)若数列()()1322(1)11+⋅-=+-⋅--n nn n n n n c a b b b ,求数列{}n c 的前2n 项和2n T ;(3)求证:()2131n i i i b b =<-∑.2.已知有穷数列()*12:,,,,3N A a a a N N ∈≥N 满足{}()1,0,11,2,,i a i N ∈-= .给定正整数m ,若存在正整数s ,()t s t ≠,使得对任意的{}0,1,2,,1k m ∈- ,都有s k t k a a ++=,则称数列A 是m -连续等项数列.(1)判断数列:1,1,0,1,0,1,1A --是否为3-连续等项数列?是否为4-连续等项数列?说明理由;(2)若项数为N 的任意数列A 都是2-连续等项数列,求N 的最小值;(3)若数列12:,,,N A a a a 不是4-连续等项数列,而数列112:,,,,1N A a a a - ,数列212:,,,,0N A a a a 与数列312:,,,,1N A a a a 都是4-连续等项数列,且30a =,求N a 的值.3.已知数列{}n a 中,n S 是其前n 项的和,21511S S =,112n n na a a ++=-.(1)求1a ,2a 的值,并证明11n a ⎧⎫-⎨⎬⎩⎭是等比数列;(2)证明:11111222n n n n S n +-+<<-.4.已知数列{}n a ,设()12*n n a a a m n N n+++=∈ ,若{}n a 满足性质Ω:存在常数c ,使得对于任意两两不等的正整数i 、j 、k ,都有()()()k i j i j m j k m k i m c -+-+-=,则称数列{}n a 为“梦想数列”.(1)若()2*n n b n N =∈,判断数列{}n b 是否为“梦想数列”,并说明理由;(2)若()21*n c n n N =-∈,判断数列{}n c 是否为“梦想数列”,并说明理由;(3)判断“梦想数列”{}n a 是否为等差数列,并说明理由.5.马尔科夫链是概率统计中的一个重要模型,也是机器学习和人工智能的基石,在强化学习、自然语言处理、金融领域、天气预测等方面都有着极其广泛的应用.其数学定义为:假设我们的序列状态是…,2t X -,1t X -,t X ,1t X +,…,那么1t X +时刻的状态的条件概率仅依赖前一状态t X ,即()()1211,,,t t t t t t P X X X X P X X +--+⋅⋅⋅=.现实生活中也存在着许多马尔科夫链,例如著名的赌徒模型.假如一名赌徒进入赌场参与一个赌博游戏,每一局赌徒赌赢的概率为50%,且每局赌赢可以赢得1元,每一局赌徒赌输的概率为50%,且赌输就要输掉1元.赌徒会一直玩下去,直到遇到如下两种情况才会结束赌博游戏:一种是手中赌金为0元,即赌徒输光;一种是赌金达到预期的B 元,赌徒停止赌博.记赌徒的本金为()*N ,A A A B ∈<,赌博过程如下图的数轴所示.当赌徒手中有n 元(0n B ≤≤,N n ∈)时,最终输光的概率为........()P n ,请回答下列问题:(1)请直接写出()0P 与()P B 的数值.(2)证明(){}P n 是一个等差数列,并写出公差d .(3)当100A =时,分别计算200B =,1000B =时,()P A 的数值,并结合实际,解释当B →∞时,()P A 的统计含义.6.求符合条件的序列12,,n a a a L 的个数,满足如下条件:(1){}0,1,1,2,i a i n ∈= ;(2){}1,2,,2|i n i ∀∈ ,有{}11max ,i i i a a a -+≥.7.已知无穷数列A :1a ,2a ,…满足:①1a ,2a ,…N i a ∈且0(1,2,)i a i >= ;②(1,2,;1,2,;31)i j i j i j a a a a a i j i j ++≤≤+=+=+≥ ,设*i a 为(1,2,)i a i = 所能取到的最大值,并记数列*A :*1a ,*2a ,….(1)若数列A 为等差数列且11a =,求其公差d ;(2)若121a a ==,求*4a 的值;(3)若11a =,22a =,求数列*A 的前100项和.8.若数列{an }满足“对任意正整数i ,j ,i ≠j ,都存在正整数k ,使得ak =ai •aj ”,则称数列{an }具有“性质P ”.(1)判断各项均等于a 的常数列是否具有“性质P ”,并说明理由;(2)若公比为2的无穷等比数列{an }具有“性质P ”,求首项a 1的值;(3)若首项a 1=2的无穷等差数列{an }具有“性质P ”,求公差d 的值.9.已知数列A :1a ,2a ,…,n a 满足:{}0,1i a ∈(1i =,2,…,n ,2n ≥),从A 中选取第1i 项、第2i 项、…、第m i 项(12m i i i <<< ,2m ≥)称数列1i a ,2i a ,…,m i a 为A 的长度为m 的子列.记()T A 为A 所有子列的个数.例如A :0,0,1,其()3T A =.(1)设数列A :1,1,0,0,写出A 的长度为3的全部子列,并求()T A ;(2)设数列A :1a ,2a ,…,n a ,A ':n a ,1n a -,…,1a ,A '':11a -,21a -,…,1n a -,判断()T A ,()T A ',()T A ''的大小,并说明理由;(3)对于给定的正整数n ,k (11k n ≤≤-),若数列A :1a ,2a ,…,n a 满足:12n a a a k ++⋅⋅⋅+=,求()T A 的最小值.10.某辖区组织居民接种新冠疫苗,现有A ,B ,C ,D 四种疫苗且每种都供应充足.前来接种的居民接种与号码机产生的号码对应的疫苗,号码机有A ,B ,C ,D 四个号码,每次可随机产生一个号码,后一次产生的号码由前一次余下的三个号码中随机产生,张医生接种A 种疫苗后,再为居民们接种,记第n 位居民(不包含张医生)接种A ,B ,C ,D 四种疫苗的概率分别为(),(),(),()n n n n P A P B P C P D .(1)第2位居民接种哪种疫苗的概率最大;(2)证明:()()()n n n P B P C P D ==;(3)张医生认为,一段时间后接种A ,B ,C ,D 四种疫苗的概率应该相差无几,请你通过计算第10位居民接种A ,B ,C ,D 四种的概率,解释张医生观点的合理性.参考数据:910910553411115.110, 1.710, 2.010,9.810.3322----⎛⎫⎛⎫⎛⎫⎛⎫≈⨯≈⨯≈⨯≈⨯ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭11.在如图所示的平面四边形ABCD 中,ABD △的面积是CBD △面积的两倍,又数列{}n a 满足12a =,当2n ≥时,()()1122n n n n BD a BA a BC --=++- ,记2n n n a b =.(1)求数列{}n b 的通项公式;(2)求证:2221211154n b b b +++< .12.已知函数()y f x =是定义在()(),00,∞-+∞U 上的偶函数,当0x >时,()()121,0212,22x x f x f x x -⎧-<≤⎪=⎨->⎪⎩,()n a f n =(n 为正整数).(1)当20x -≤<时,求()y f x =的解析式;(2)若函数()()g x f x m =-存在零点,且零点个数不超过10,求实数m 的取值范围;(3)求数列{}n a 的前n 项和为,n n S S 是否存在极限?若存在,求出这个极限;若不存在,请说明理由13.设数列{}n a 的前n 项和为n S ,且n a 与4-n 的等差中项为n n S a -.(1)证明:数列{}2n a +是等比数列;(2)设32log 2n n a b +=,证明:1352111111111n b b b b -⎛⎫⎛⎫⎛⎫⎛⎫++++> ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ .14.已知数列:A 1a ,2a ,…,()3N a N ≥的各项均为正整数.设集合,{}|,1j i T x x a a i j N ==-≤≤≤记T 的元素个数为()P T .(1)若数列:A 1,1,3,2,求集合T ,并写出()P T 的值;(2)若A 是递增数列,求证:“()1P T N =-”的充要条件是“A 为等差数列”;(3)若23N =,数列A 由1,2,3,…,11,22这12个数组成,且这12个数在数列A 中每个至少出现一次,求()P T 的最大值.15.已知递增数列{}n a 的前n 项和为n S ,且满足211,441n n a S n a =-+=,设11n n n b a a +=,*n ∈N ,且数列{}n b 的前n 项和为n T .(1)求证:数列{}n a 为等差数列;(2)试求所有的正整数m ,使得222121m m m m m a a a a a ++++-为整数;(3)若对任意的*N n ∈,不等式118(1)n n T n λ+<+-恒成立,求实数λ的取值范围.16.若无穷数列{}n a 的各项均为整数.且对于,,i j i j *∀∈<N ,都存在k j >,使得k j i j i a a a a a =--,则称数列{}n a 满足性质P .(1)判断下列数列是否满足性质P ,并说明理由.①n a n =,1n =,2,3,…;②2n b n =+,1n =,2,3,….(2)若数列{}n a 满足性质P ,且11a =,求证:集合{}3∣n n a *∈=N 为无限集;(3)若周期数列{}n a 满足性质P ,请写出数列{}n a 的通项公式(不需要证明).17.在一个有穷数列的每相邻两项之间插入这两项的和,形成新的数列,我们把这样的操作称为该数列的一次“和扩充”.如数列1,2第1次“和扩充”后得到数列1,3,2,第2次“和扩充”后得到数列1,4,3,5,2.设数列a ,b ,c 经过第n 次“和扩充”后所得数列的项数记为n P ,所有项的和记为n S .(1)若1,2,3a b c ===,求2P ,2S ;(2)设满足2023n P ≥的n 的最小值为0n ,求0n 及03n S ⎡⎤⎢⎥⎣⎦(其中[x ]是指不超过x 的最大整数,如[]1.21=,[]2.63-=-);(3)是否存在实数a ,b ,c ,使得数列{n S }为等比数列?若存在,求,a b ,c 满足的条件;若不存在,请说明理由.18.已知函数2()x f x ax b =+,(1)1f =,1223f ⎛⎫= ⎪⎝⎭.令112x =,()1n n x f x +=.(1)求数列{}n x 的通项公式;(2)证明:12112en x x x +⋅⋅⋅>.19.已知有穷数列()*12:,,,,3N A a a a N N ∈≥N 满足{}()1,0,11,2,,i a i N ∈-= .给定正整数m ,若存在正整数s ,()t s t ≠,使得对任意的{}0,1,2,,1k m ∈- ,都有s k t k a a ++=,则称数列A 是m -连续等项数列.(1)判断数列:1,1,0,1,0,1,1A --是否为3-连续等项数列?是否为4-连续等项数列?说明理由;(2)若项数为N 的任意数列A 都是2-连续等项数列,求N 的最小值;(3)若数列12:,,,N A a a a 不是4-连续等项数列,而数列112:,,,,1N A a a a - ,数列212:,,,,0N A a a a 与数列312:,,,,1N A a a a 都是4-连续等项数列,且30a =,求N a 的值.。
按规律填数
序号 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 789 90 91 92 93 94 95 96 97 98 99
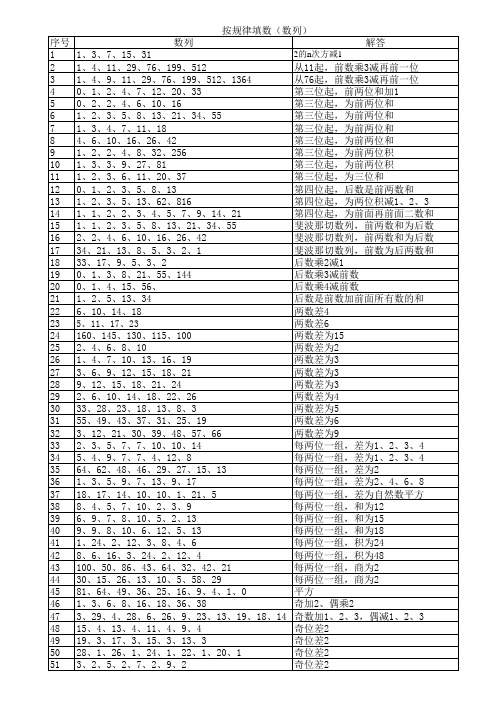
按规律填数(数列) 数列 解答 13、2、15、4、17、6、19、8 奇位差2、偶位差2 21、2、19、5、17、8、15、11 奇位差2、偶位差3 1、6、4、8、7、10、10、12、13、14 奇位差3、偶位差2 23、4、20、6、17、8、14、10、11、12 奇位差3、偶位差2 32、20、29、18、26、16、23、14、20、12 奇位差3、偶位差2 30、2、26、2、22、2、18、2、14、2 奇位差4 1、6、5、10、9、14、13、18、17 奇位差4、偶位差4 1、5、2、8、4、11、8、14、16、17 奇位乘2、偶位差3 2、3、4、6、8、9、16、12 奇位乘2、偶位加3 2、9、6、10、18、11、54、12、162、13、486 奇位乘3、偶位差1 320、1、160、3、80、9、40、27、20、81 奇位除2、偶位乘3 8、1、4、2、2、3 奇位除2偶位加1 2、1、4、1、7、1、11、1、16、1、22、1 奇位加2、3、4、5 8、15、10、13、12、11、14、9 奇位加2、偶位减2 2、32、4、24、6、16、8、8 奇位加2、偶位减8 8、6、10、5、12、4、14、3、16、2、18、1 奇位加2偶位减1 3、4、7、9、15、16、31、25 奇位加4、8、16偶位是2、3、4平方 1、6、7、12、13、18、19、 奇位加6、偶位加6(加5加1) 10、1、8、2、6、4、4、7、2、11、1 奇位减2偶位加1、2、3、4 15、2、12、4、9、6、6、8 奇位减3、偶位加2 35、42、30、39、25、36、20、33、15 奇位减5偶位减3 1、2、2、3、4、6、9、14、22、35 前两数和减1 10、8、6.4、5.12、4.096、3.2768 前数乘0.8 3、6、12、24、48、96、192 前数乘2 1、3、8、19、42、89、184 前数乘2后依次加1、2、3、4 3、7、15、31、63、127 前数乘2加1 2、6、18、54、162、486 前数乘3 2、5、14、41、122、365、1094 前数乘3减1 2、4、10、28、82、244、730 前数乘3减2 128、64、32、16、8、4、2 前数除2 1、4、9、16、25、36、49、64 数位的平方 1、8、27、64 位数的3次方 先乘3再减一 1、3、2、6、5、15、14、42、41 1、2、4、7、11、16、22 相邻数依次加1、2、3 10、11、13、16、20、25、31 相邻数依次加1、2、3 1、2、6、24、120 依次乘2、3、4、5 2、8、32、128、512 依次乘4(2的奇次方) 1、5、25、125 依次乘5 729、243、81、27、9、3 依次除3 11、12、14、18、26、42 依次加1、2、4、8、16 1、2、5、10、17、26、37 依次加1、3、5、7、9、11 45、55、66、78、91 依次加10、11、12、13 12、26、39、52、65、78 依次加13 1、3、6、10、15、21、28 依次加2、3、4、5、6 16、18、22、28、36、46、59 依次加2、4、6、8、10 1、4、3、6、5、8 依次加3减1 35、28、22、17、13、10 依次减7、6、5、4、3 53、44、36、29、23、18、14、11、9、8 由后向前依次加1、2、3
三年高考(2015-2017)高考数学试题解析13数列小题理

专题13数列小题1。
【2017课标1,理4】记nS 为等差数列{}na 的前项和.若4524a a +=,648S =,则{}na 的公差为A .1B .2C .4D .8 【答案】C 【解析】试题分析:设公差为d ,45111342724a a a d a d a d +=+++=+=,611656615482S ad a d ⨯=+=+=,联立112724,61548a d a d +=⎧⎨+=⎩解得4d =,故选C.秒杀解析:因为166346()3()482a a S a a +==+=,即3416aa +=,则4534()()24168a a a a +-+=-=,即5328a a d -==,解得4d =,故选C 。
【考点】等差数列的基本量求解【名师点睛】求解等差数列基本量问题时,要多多使用等差数列的性质,如{}na 为等差数列,若m np q +=+,则mnpqa a a a +=+。
2。
【2017课标3,理9】等差数列{}na 的首项为1,公差不为0.若a 2,a 3,a 6成等比数列,则{}na 前6项的和为A .24-B .3-C .3D .8 【答案】A 【解析】故选A 。
【考点】等差数列求和公式;等差数列基本量的计算【名师点睛】(1)等差数列的通项公式及前n 项和公式,共涉及五个量a 1,a n ,d ,n ,S n ,知其中三个就能求另外两个,体现了用方程的思想解决问题.(2)数列的通项公式和前n 项和公式在解题中起到变量代换作用,而a1和d是等差数列的两个基本量,用它们表示已知和未知是常用方法.3。
【2017课标II,理3】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯()A.1盏B.3盏C.5盏D.9盏【答案】B【解析】试题分析:设塔的顶层共有灯x盏,则各层的灯数构成一个首项为x,公比为2的等比数列,结合等比数列的求和公式有:()712381 12x⨯-=-,解得3x=,即塔的顶层共有灯3盏,故选B。
13数字推理解析

【解析】选D,1+1=2, 3+1=4 ,3+5=8 ,6+10=16,其中2,4 ,8 ,16等比。
【解析】选A,59-18=11;43-32=11;28-17=11。
【解析】选B,1=16/16 ,分子+分母=22=>19+13=32 ,16+16=32,10+22=32,7+25=32。
【解析】选A,3=22-1,8=32-1,24=52-1,48=72-1,120=112-1,168=132-1,其中2,3,5,7,11质数数列。
【解析】选B, 27-21=6=2×3,36-27=9=3×3,51-36=15=5×3,72-51=21=7×3,105-72=33=11×3,其中2、3、5、7、11质数列。
【解析】选C,1/2,1,1,( ),9/11,11/13 =>1/2,3/3, 5/5,7/7 ,9/11,11/13=>分子1,3,5,7,9,11等差;分母2,3,5,7,11,13 连续质数列。
【解析】选C,前后项相减得到1,2,2,4 第三个数为前两个数相乘,推出下一个数为8,所以11+8=19 【解析】D。
个位2,3,5,8,12=>作差1,2,3,4等差;其他位3,4,5,6等差【解析】C。
20/9,4/3,7/9,4/9,1/4,(5/36)=>80/36,48/36,28/36,16/36,9/36,5/36;分母36,36,36,36,36,36 等差;分子80,48,28,16,9,5 三级等差【解析】A。
5×3+2=17,5×4+1=21,5×5=0=25,5×6-1=29【解析】D,奇数项2,3,5,7连续质数列;偶数项4,9,20,44,前项除以后项=>4/9,9/20,20/44=>8/18,9/20,10/22.分子8,9,10等差,分母18,20,22等差。
1 3 7 13 21 31的规律公式讲解

关于数列中的规律公式,一直是数学领域中备受关注的重要话题。
今天,我们将要探讨的主题是“1 3 7 13 21 31的规律公式讲解”。
让我们从最简单的开始,逐步深入了解这个规律。
1. 从简单到复杂的探索我们首先来看这个数列:1, 3, 7, 13, 21, 31。
通过简单观察,我们可以发现相邻的两个数之间的差别分别是2, 4, 6, 8, 10。
这里的规律并不是很容易捉摸,所以我们需要更深入地进行探索。
2. 规律的发现与解释在进一步探索中,我们发现这个数列中的每个数都是前一个数加上一个递增的奇数得到的。
第一个数是1,第二个数是前一个数加上3得到的,第三个数是前一个数加上4得到的,依此类推。
这个规律也可以用一个简单的公式来表示:nth number = (n-1)th number + 2n-1。
3. 规律公式的推导和证明接下来,让我们来推导和证明这个规律公式。
我们可以通过数学归纳法来证明这个规律公式的正确性。
我们验证当n=2时,公式成立;然后假设当n=k时,公式也成立,即第k个数等于第k-1个数加上2k-1;接着通过代入n=k+1来验证当n=k+1时公式是否依然成立。
经过验证,我们可以得出这个规律公式在数列1, 3, 7, 13, 21, 31中是成立的。
4. 总结与回顾通过对1, 3, 7, 13, 21, 31这一数列规律的深入探讨,我们不仅发现了其中隐藏的规律,还成功地推导并证明了其规律公式。
这让我们对数列中规律的理解更加深入,也让我们意识到数学中隐藏的美妙之处。
5. 个人观点和理解对于我个人来说,探索数学中的规律是一件非常有趣且充满挑战的事情。
发现规律并推导出相应的公式,不仅需要逻辑思维,还需要创造性的思考和耐心的探索。
这种深入探讨数学规律的过程,也能够在某种程度上训练我们的思维能力和逻辑推理能力。
通过以上的探讨,我们对于“1 3 7 13 21 31的规律公式”这一主题有了更加深刻和全面的理解。
斐波那契数列

斐波那契数列(一)斐波纳契数列(Fibonacci Sequence),又称黄金分割数列。
斐波那契数列指的是这样一个数列:1、1、2、3、5、8、13、21、…… 这个数列从第三项开始,每一项都等于前两项之和。
斐波那契数列的发明者,是意大利数学家列昂纳多〃斐波那契(Leonardo Fibonacci,生于公元1170年,卒于1240年,籍贯大概是比萨)。
他被人称作“比萨的列昂纳多”。
1202年,他撰写了《珠算原理》(Liber Abacci)一书。
他是第一个研究了印度和阿拉伯数学理论的欧洲人。
他的父亲被比萨的一家商业团体聘任为外交领事,派驻地点相当于今日的阿尔及利亚地区,列昂纳多因此得以在一个阿拉伯老师的指导下研究数学。
他还曾在埃及、叙利亚、希腊、西西里和普罗旺斯研究数学。
在现代物理、准晶体结构、化学等领域,斐波纳契数列都有直接的应用,为此,美国数学会从1960年代起出版了《斐波纳契数列》季刊,专门刊载这方面的研究成果。
斐波那契数列在自然界中的出现是如此地频繁,人们深信这不是偶然的。
(1)细察下列各种花,它们的花瓣的数目具有斐波那契数:延龄草、野玫瑰、南美血根草、大波斯菊、金凤花、耧斗菜、百合花、蝴蝶花。
(2)细察以下花的类似花瓣部分,它们也具有斐波那契数:紫宛、大波斯菊、雏菊。
斐波那契数经常与花瓣的数目相结合:3………………………百合和蝴蝶花5………………………蓝花耧斗菜、金凤花、飞燕草8………………………翠雀花13………………………金盏草21………………………紫宛34,55,84……………雏菊(3)斐波那契数还可以在植物的叶、枝、茎等排列中发现。
例如,在树木的枝干上选一片叶子,记其为数0,然后依序点数叶子(假定没有折损),直到到达与那息叶子正对的位臵,则其间的叶子数多半是斐波那契数。
叶子从一个位臵到达下一个正对的位臵称为一个循回。
叶子在一个循回中旋转的圈数也是斐波那契数。
在一个循回中叶子数与叶子旋转圈数的比称为叶序(源自希腊词,意即叶子的排列)比。
13-等比数列(1)

2.4 等比数列(1)教材分析本节内容是《数列》第3小节的内容,是我们在认识了等差数列后,学生有接触的一个新的数列,是对数列知识的延伸,可以借助研究等差数列的方法类比来研究等比数列。
等比数列在实际生活中也有广泛的应用,因此等比数列的教学可以选择更多的有实际背景的例子。
等比数列与等差数列之间存在着很多类似的地方,但也有本质的区别,学生容易混淆。
一方面,建议在本节的教学中始终强调等比数列的定义和体现等比数列的本质的公比q ;另一方面,本节有利于培养学生的类比推理的能力。
课时分配本节内容用2课时的时间完成,主要讲解等比数列的定义,通项公式和性质.教学目标重点:等比数列的定义及通项公式.难点:灵活应用等比数列的定义式及通项公式解决一些相关问题. 知识点:等比数列定义和通项公式.能力点:类比等比数列的定义,并如何探寻等比数列的通项公式.教育点:经历由特殊到特殊的类比研究数学问题的过程,体会探究的乐趣,激发学生的学习热情.自主探究点:如何运用等比数列的通项公式.考试点:用等比数列的通项公式解决数列中的简单量. 易错易混点:运用等比数列通项公式时的项数. 拓展点:等比数列通项的变形形式mn m n qa a -=.教具准备 多媒体课件和三角板 课堂模式 学案导学 一、 引入新课前面几节课,我们共同探讨了等差数列,现在我们再来回顾一下等差数列的主要内容。
下面我们来看这样几个数列,看其又有何共同特点?1,2,4,8,16,…,263; ① 5,25,125,625,…; ②1,-12 ,14 ,-18,…;③思考:(1)是不是等差数列?(2)每一项与前一项之间有什么关系?【师生活动】教师分析:仔细观察数列,寻其共同特点.对于数列①,2;211==--n nn n a a a (2≥n ) 对于数列②,5;51==-n nnn a a a (2≥n ) 对于数列③,21;21)1(111-=-=--+n n n n n a a a (2≥n ) 学生总结共同特点:从第二项起,第一项与前一项的比都等于同一个常数.也就是说,这些数列从第二项起,每一项与前一项的比都具有“相等”的特点.教师总结: 1.等比数列定义一般地,如果一个数列从第二项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列.这个常数叫做等比数列的公比;公比通常用字母q 表示(q ≠0),即:a n ∶a n -1=q (q ≠0)如:数列①,②,③都是等比数列,它们的公比依次是2,5,-12 .与等差数列比较,仅一字之差.总之,若一数列从第二项起,每一项与其前一项之“差”为常数,则为等差数列,之“比”为常数,则为等比数列,此常数称为“公差”或“公比”.注意(1)公差“d ”可为0,(2)公比“q ”不可为0.【设计意图】 通过具学生对等比数列下定义,培养学生类比的数学思想.二、探究新知 (一)归纳通项公式等比数列的通项公式又如何呢? 写出上面三个数列的通项公式对于数列①,12-=n n a (2≥n )对于数列②,nn a 5=(2≥n ) 对于数列③,;21)1(11-+-=n n n a (2≥n )探究课本50页类比等差数列写出等比数列的通项公式的推导,请你补全首项是1a ,公比是q 的等比数列}{n a 的通项公式()1q a a n =[设计意图]培养学生由特殊到一般的总结问题的能力,在探究寻找中找到学习的兴趣。
数列全集

1、256 ,269 ,286 ,302 ,()解析: 2+5+6=13 256+13=269 2+6+9=17 269+17=286 2+8+6=16 286+16=302 302+3+2=3072、72 , 36 , 24 , 18 , ( )解析:(方法一)相邻两项相除,72 36 24 18\ / \ / \ /2/1 3/2 4/3(分子与分母相差1且前一项的分子是后一项的分母)接下来貌似该轮到5/4,而18/=5/4. 选C(方法二)6×12=72, 6×6=36, 6×4=24, 6×3 =18, 6×X 现在转化为求X12,6,4,3,X12/6 ,6/4 , 4/3 ,3/X化简得2/1,3/2,4/3,3/X,注意前三项有规律,即分子比分母大一,则3/X=5/4 可解得:X=12/5 再用6×12/5=3、8 , 10 , 14 , 18 ,()A. 24B. 32C. 26D. 20分析:8,10,14,18分别相差2,4,4,?可考虑满足2/4=4/?则?=8所以,此题选18+8=264、3 , 11 , 13 , 29 , 31 ,()分析:奇偶项分别相差11-3=8,29-13=16=8×2,?-31=24=8×3则可得?=55,故此题选D5、-2/5,1/5,-8/750,()。
A 11/375B 9/375C 7/375D 8/375解析: -2/5,1/5,-8/750,11/375=> 4/(-10),1/5,8/(-750),11/375=>分子 4、1、8、11=>头尾相减=>7、7分母 -10、5、-750、375=>分2组(-10,5)、(-750,375)=>每组第二项除以第一项=>-1/2,-1/2 答案为A1. 16 , 8 , 8 , 12 , 24 , 60 , ( )分析:相邻两项的商为,1,,2,,3,所以选1802. 2 ,3 ,6 ,9 ,17 ,()分析:6+9=15=3×53+17=20=4×5 那么2+?=5×5=25 所以?=23 所以选B3. 3 ,2 ,5/3 ,3/2 ,()5 6 5 4分析:通分 3/1 4/2 5/3 6/4 ----7/5所以选A4. 20 ,22 ,25 ,30 ,37 ,()分析:它们相差的值分别为2,3,5,7。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数列1、理解数列的概念,了解数列通项公式的意义.了解递推公式是给出数列的一种方法,并能根据递推公式写出数列的前几项.2、理解等差数列的概念,掌握等差数列的通项公式与前n项和的公式,并能解决简单的实际问题.3、理解等比数列的概念,掌握等比数列的通项公式与前n项和公式,并能解决简单的实际纵观近几年高考试题,对数列的考查已从最低谷走出,估计以后几年对数列的考查的比重仍不会减小,等差、等比数列的概念、性质、通项公式、前n项和公式的应用是必考内容,数列与函数、三角、解析几何、组合数的综合应用问题是命题热点.从解题思想方法的规律着眼,主要有:①方程思想的应用,利用公式列方程(组),例如等差、等比数列中的“知三求二”问题;②函数思想方法的应用、图像、单调性、最值等问题;③待定系数法、分类讨论等方法的应用.第1课时数列的概念数N*或其子集{1,2,3,……n}的函数f(n).数列的一般形式为a1,a2,…,a n…,简记为{a n},其中a n是数列{a n}的第项.2.数列的通项公式一个数列{a n}的与之间的函数关系,如果可用一个公式a n=f(n)来表示,我们就把这个公式叫做这个数列的通项公式.3.在数列{a n }中,前n 项和S n 与通项a n 的关系为:=n a⎪⎩⎪⎨⎧≥==21n n a n4.求数列的通项公式的其它方法⑴ 公式法:等差数列与等比数列采用首项与公差(公比)确定的方法.⑵ 观察归纳法:先观察哪些因素随项数n 的变化而变化,哪些因素不变;初步归纳出公式,再取n 的特珠值进行检验,最后用数学归纳法对归纳出的结果加以证明.⑶ 递推关系法:先观察数列相邻项间的递推关系,将它们一般化,得到的数列普遍的递推关系,再通过代数方法由递推关系求出通项公式.例1. 根据下面各数列的前n 项的值,写出数列的一个通项公式.⑴ -312⨯,534⨯,-758⨯,9716⨯…;⑵ 1,2,6,13,23,36,…;⑶ 1,1,2,2,3,3,解: ⑴ a n =(-1)n)12)(12(12+--n n n ⑵ a n =)673(212+-n n (提示:a 2-a 1=1,a 3-a 2=4,a 4-a 3=7,a 5-a 4=10,…,a n -a n -1=1+3(n -2)=3n -5.各式相加得)673(21)43)(1(211)]53(10741[12+-=--+=-++++++=n n n n n a n ⑶ 将1,1,2,2,3,3,…变形为,213,202,211+++,,26,215,204 +++∴4)1(1222)1(111++-++=-++=n n n n n a 变式训练1.某数列{a n }的前四项为0,2,0,2,则以下各式:① a n =22[1+(-1)n ] ② a n =n )(11-+③ a n =⎩⎨⎧)(0)(2为奇数为偶数n n 其中可作为{a n }的通项公式的是 ( )A .①B .①②C .②③D .①②③解:D例2. 已知数列{a n }的前n 项和S n ,求通项.⑴ S n =3n -2⑵ S n =n 2+3n +1解 ⑴ a n =S n -S n -1 (n≥2) a 1=S 1解得:a n =⎩⎨⎧=≥⋅-)1(1)2(321n n n ⑵ a n =⎩⎨⎧≥+=)2(22)1(5n n n 变式训练2:已知数列{a n }的前n 项的和S n 满足关系式lg(S n -1)=n ,(n ∈N *),则数列{a n }的通项公式为 .解:,110101)1lg(+=⇒=-⇒=-n n n n n S S n S 当n =1时,a 1=S 1=11;当n≥2时,a n =S n -S n -1=10n -10n -1=9·10 n -1.故a n =⎪⎩⎪⎨⎧≥⋅=-)2(109)1(111n n n 例3. 根据下面数列{a n }的首项和递推关系,探求其通项公式.⑴ a 1=1,a n =2a n -1+1 (n≥2)⑵ a 1=1,a n =113--+n n a (n≥2)⑶ a 1=1,a n =11--n a nn (n≥2)解:⑴ a n =2a n -1+1⇒(a n +1)=2(a n -1+1)(n≥2),a 1+1=2.故:a 1+1=2n ,∴a n =2n -1.⑵a n =(a n -a n -1)+(a n -1-a n -2)+…+(a 3-a 2)+(a 2-a 1)+a 1=3n -1+3n -2+…+33+3+1=)13(21-n .(3)∵nn a a n n 11-=-∴a n =⋅--⋅-=⋅⋅⋅⋅⋅-----12111232211n n n n a a a a a a a a a n n n n n n nn n 112123=⋅⋅⋅-- 变式训练3.已知数列{a n }中,a 1=1,a n +1=22+n na a (n ∈N *),求该数列的通项公式.解:方法一:由a n +1=22+n na a 得21111=-+n n a a ,∴{n a 1}是以111=a 为首项,21为公差的等差数列.∴na 1=1+(n -1)·21,即a n =12+n 方法二:求出前5项,归纳猜想出a n =12+n ,然后用数学归纳证明.例4. 已知函数)(x f =2x -2-x ,数列{a n }满足)(log 2n a f =-2n ,求数列{a n }通项公式.解:na f n a n a n 222)(log 2log 2log 2-=-=-n a a nn 21-=-得n n a n -+=12变式训练4.知数列{a n }的首项a 1=5.前n 项和为S n 且S n +1=2S n +n +5(n ∈N *).(1) 证明数列{a n +1}是等比数列;(2) 令f (x)=a 1x +a 2x 2+…+a n x n ,求函数f (x)在点x =1处导数f 1 (1).解:(1) 由已知S n +1=2S n +n +5,∴ n≥2时,S n =2S n -1+n +4,两式相减,得:S n +1-S n =2(S n -S n -1)+1,即a n +1=2a n +1从而a n +1+1=2(a n +1)当n =1时,S 2=2S 1+1+5,∴ a 1+a 2=2a 1+6,又a 1=5,∴ a 2=11∴111+++n n a a =2,即{a n +1}是以a 1+1=6为首项,2为公比的等比数列.(2) 由(1)知a n =3×2n -1 ∵ )(x f =a 1x +a 2x 2+…+a n x n∴ )('x f =a 1+2a 2x +…+na n x n -1从而)1('f =a 1+2a 2+…+na n=(3×2-1)+2(3×22-1)+…+n(3×2n -1)=3(2+2×22+…+n×2n )-(1+2+…+n)=3[n×2n +1-(2+…+2n )]-2)1(+n n =3(n -1)·2n +1-2)1(+n n +61.根据数列的前几项,写出它的一个通项公式,关键在于找出这些项与项数之间的关系,常用的方法有观察法、通项法,转化为特殊数列法等.2.由S n 求a n 时,用公式a n =S n -S n -1要注意n≥2这个条件,a 1应由a 1=S 1来确定,最后看二者能否统一.3.由递推公式求通项公式的常见形式有:a n +1-a n =f(n),nn a a 1+=f(n),a n +1=pa n +q ,分别用累加法、累乘法、迭代法(或换元法).第2课时 等差数列等差数列的定义: - =d (d 为常数).2.等差数列的通项公式:⑴ a n =a 1+ ×d ⑵ a n =a m + ×d3.等差数列的前n 项和公式:S n = = .4.等差中项:如果a 、b 、c 成等差数列,则b 叫做a 与c 的等差中项,即b = .5.数列{a n }是等差数列的两个充要条件是:⑴ 数列{a n }的通项公式可写成a n =pn +q(p, q ∈R)⑵ 数列{a n }的前n 项和公式可写成S n =an 2+bn (a, b ∈R)6.等差数列{a n }的两个重要性质:⑴ m, n, p, q ∈N *,若m +n =p +q ,则 .⑵ 数列{a n }的前n 项和为S n ,S 2n -S n ,S 3n -S 2n 成 数列.例1. 在等差数列{a n }中,(1)已知a 15=10,a 45=90,求a 60; (2)已知S 12=84,S 20=460,求S 28; (3)已知a 6=10,S 5=5,求a 8和S 8.解:(1)方法一:⎪⎪⎩⎪⎪⎨⎧=-=⇒⎩⎨⎧=+==+=38382904410141145115d a d a a d a a ∴a 60=a 1+59d =130. 方法二:3815451545=--=--=a a m n a a d m n ,由a n =a m +(n -m)d ⇒a 60=a 45+(60-45)d =90+15×38=130.(2)不妨设S n =An 2+Bn ,∴⎩⎨⎧-==⇒⎪⎩⎪⎨⎧=+=+172460202084121222B A B A B A∴S n =2n 2-17n∴S 28=2×282-17×28=1092 (3)∵S 6=S 5+a 6=5+10=15, 又S 6=2)10(62)(6161+=+a a a ∴15=2)10(61+a 即a 1=-5 而d =31616=--a a ∴a 8=a 6+2 d =16 S 8=442)(881=+a a 变式训练1.在等差数列{a n }中,a 5=3,a 6=-2,则a 4+a 5+…+a 10= . 解:∵d =a 6-a 5=-5, ∴a 4+a 5+…+a 10=49)2(72)(75104-=+=+d a a a 例2. 已知数列{a n }满足a 1=2a ,a n =2a -12-n a a (n≥2).其中a 是不为0的常数,令b n =aa n -1. ⑴ 求证:数列{b n }是等差数列.⑵ 求数列{a n }的通项公式.解:∵ ⑴ a n =2a -12-n a a (n≥2)∴ b n =)(11111a a a a a a a aa n n n n -=-=---- (n≥2)∴ b n -b n -1=aa a a a a a n n n 11)(111=------ (n≥2)∴ 数列{b n }是公差为a1的等差数列. ⑵ ∵ b 1=aa -11=a 1 故由⑴得:b n =a 1+(n -1)×a 1=an 即:aa n -1=a n 得:a n =a(1+n 1) 变式训练2.已知公比为3的等比数列{}n b 与数列{}n a 满足*,3N n b n an ∈=,且11=a , (1)判断{}n a 是何种数列,并给出证明; (2)若11+=n n n a a C ,求数列{}n C 的前n 项和解:1)1111333,13n n n na a a n n n a nb a a b ++-++===∴-=,即 {}n a 为等差数列。
