A1-1-10对数的概念与性质
对数的性质和运算法则

(一)对数的性质 先提问学生上节课书上P.109第17题答案. 第17题:把指数式化为对数式,或对数式化为指数式. (1)logaN=b→ab=N, (2)a0=1→loga1=0, (3)a1=a→logaa=1. 总结出对数两条性质: (1)1的对数为0. (2)底数的对数为1. 提问:0和负数有否对数?为什么? 总结出对数第三条性质:0和负数没有对数.
logaMn=(logaM)n. 指出错误的原因并举例说明. 例 lg2(8+8)≠lg28+log28. 五、作业 P.79中3、4、5、6;P.109中18、19. 六、板书设计
练习:P.78中2、3.
例3
计算:
(四)总结 本节学习的是对数的性质及运算法则,要求学生理解推 导这些运算法则的依据和推导过程,会用语言叙述,要 记住这些公式并能熟练应用.指出新学这四个法则容易 产生下面的错误: loga(M+N)=logaM+logaN; loga(MN)=logaMlogaN;
对数的性质和运算法则对数的性质与运算法则对数运算法则对数函数运算法则对数的运算法则对数函数的运算法则自然对数运算法则对数乘法运算法则指数对数运算法则对数运算法则的推导
1.15 .
对数的性质和运算法则
一、素质教育目标 (一)知识教学点 1.对数的性质. 2.对数运算法则. (二)能力训练点 1.利用对数式与指数式的关系研究证明对数的三条性质,培 养学生逻辑思维能力(观察、分析、归纳、类比). 2.掌握好积、商、幂、方根的对数运算法则,能根据公式法 则进行数、式、方程的正确运算及变形,进一步培养学生合理 的运算能力. (三)德育渗透点 1.利用指、对数式关系启发学生研究对数性质及运算法则培 养学生注意探索、研究、揭示事物的内在联系,培养分析问题、 解决问题的能力.
对数函数的概念对数函数ylogx的图像和性质(ppt)

(2)y log x
(4)y ( )x 2
(2)y x
(3)y log1.4x
(4)y log x
2
思考探究3:
你能用描点法画出对数函数
ylog2x和 ylog1x
2
的图像吗? 作图步骤: ①列表,
②描点,
③连线.
画y=log2x的图像
列 表
x
… 1 1 1 2 4…
4
2
y=log2x … -2 -1 0 1 2 …
y
描2
点
1 11
连 线
42
O
1
2
34
-1
若把对数函数的
-2
思考:
底数换成3,4, 7.6,10……图像 性质又会是怎样
与上相仿
的?
性质:
(1)定义域是 (0, )
(2)值域是 R x
(3)图像过特殊点 (1,0)
(4)在其定义域上是 增函数
画y=log 1 x的图像
2
列
x
1
1
12 4
4
2
表
y log 1 x
(2){x|x > 1 且x≠1}; 3
提升总结 对数函数的定义域即使对数式有意义的x的取值
范围,其中需真数大于0,底数大于0且不等于1
思考探究2:
指数函数 y a x 和对数函数 ylo g ax (a0 ,a1 ) 有什么关系?
指数函数 y a x 和对数函数 x loga y 刻画的是同
1. 掌握对数函数的概念、反函数的概念.(重点) 2. 知道对数函数与指数函数互为反函数.(易混点) 3. 会画具体的对数函数的图像. (难点)
底数 指数 幂
教学课件第1课时对数的定义与性质
[例 4] 对数式 loga-2(5-a)=b 中,实数 a 的取值范围是
()
A.(-∞,5)
B.(2,5)
C.(2,+∞)
D.(2,3)∪(3,5)
[错解] A
由题意,得 5-a>0,∴a<5.
[错因分析] 该解法忽视了对数的底数和真数都有范围
限制,只考虑了真数而忽视了底数.
[正解]
5-a>0, D 由题意,得a-2>0,
请同学们结合本节课的学习,说出你有什么收获? 1.对数的定义
一般地,如果a(a>0,且a≠1)的 x 次幂等于N, 即ax=N, 那么数x叫做以a为底N的对数, 记作
logaN=x (式中的a叫做对数的底数,N叫做真数). 2.掌握指数式与对数式的互化
loga N x ax N (a>0,且a≠1)
3.掌握对数的性质.
③∵log1
2
8=-3,∴(12)-3=8.
④∵log3217=-3,∴3-3=217.
[点评] 互化时,首先指数式与对数式的底数相同,其次 将对数式的对数换为指数式的指数(或将指数式的指数换为对 数式的对数).
探究二 对数与指数的关系
ab N 叫做指数式, loga N b 叫做对数式.
当 a 0, a 1, N 0 时,
第二章 基本初等函数(Ⅰ)
第二章
2.2 对 数 函 数
第二章
2.2.1 对数与对数运算
第二章
第 1 课时 对数的定义与性质
1.理解对数的概念;(重点) 2.能够说明对数与指数的关系; 3.掌握对数式与指数式的相互转化.(难点) 4.掌握对数的性质.(重点)
温故知新 1.在指数 ab=N 中,a 称为 底数,b 称为 指数 ,N 称为 幂值,在引入了分数指数幂与无理数指数幂之后,b 的取值范 围由初中时的限定为整数扩充到了实数 . 2.若 a>0 且 a≠1,则 a0= 1 ;a1= a ;对于任意 x∈R, ax>0.
对数函数知识点总结

对数函数知识点总结(共12页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--对数函数(一)对数1.对数的概念:一般地,如果N a x=)1,0(≠>a a ,那么数x 叫做以.a 为底..N 的对数,记作:N x a log =(a — 底数,N — 真数,N a log — 对数式)说明:○1 注意底数的限制0>a ,且1≠a ;○2 x N N a a x=⇔=log ;○3 注意对数的书写格式. 两个重要对数:○1 常用对数:以10为底的对数N lg ; ○2 自然对数:以无理数 71828.2=e 为底的对数的对数N ln .(二)对数的运算性质如果0>a ,且1≠a ,0>M ,0>N ,那么:○1 M a (log ·=)N M a log +N a log ; ○2 =N Ma log M a log -N a log ; ○3 na M log n =M a log )(R n ∈. 注意:换底公式abb c c a log log log =(0>a ,且1≠a ;0>c ,且1≠c ;0>b ).利用换底公式推导下面的结论(1)b mnb a n a mlog log =;(2)a b b a log 1log =.(二)对数函数1、对数函数的概念:函数0(log >=a x y a ,且)1≠a 叫做对数函数,其中x 是自变量,函数的定义域是(0,+∞).注意:○1 对数函数的定义与指数函数类似,都是形式定义,注意辨别。
如:x y 2log 2=,5log 5x y = 都不是对数函数,而只能称其为对数型函数.○2 对数函数对底数的限制:0(>a ,且)1≠a .对数函数·例题解析例1.求下列函数的定义域:(1)2log x y a =; (2))4(log x y a -=; (3))9(log 2x y a -=.解:(1)由2x >0得0≠x ,∴函数2log x y a =的定义域是{}0x x ≠;(2)由04>-x 得4<x ,∴函数)4(log x y a -=的定义域是{}4x x <;(3)由9-02>-x 得-33<<x ,∴函数)9(log 2x y a -=的定义域是{}33x x -<<.例2.求函数251-⎪⎭⎫ ⎝⎛=xy 和函数22112+⎪⎭⎫⎝⎛=+x y )0(<x 的反函数。
高三数学 第一轮复习 06:对数、对数方程

高中数学第一轮复习06对数、对数方程·知识梳理·模块01:对数1、对数的定义:在0a >,1a ≠,且0N >的条件下,唯一满足x a N =的数x ,称为N 以a 为底的对数(logarithm),并用符号log a N 表示,而N 称为真数。
注意:对数的底是不等于1的正数。
负数和零没有对数。
2、指数式与对数式的关系:log (0,1,0)b a a N N b a a N =⇔=>≠>要能灵活运用这个关系,能随时将二者互化。
由对数定义可知:log 1a a =(0,1)a a >≠。
3、对数恒等式:log a N a N =(0,01N a a >>≠且)。
4、对数的运算性质:对数性质1:当0,0M N >>成立,则log ()log log a a a MN M N =+。
对数性质2:当0,0M N >>成立,则log log log aa a MM N N=-。
对数性质3:当0N >,对任何给定得实数c 成立,则log log c a a N c N =。
特别的:log c a a c =公式拓展:b nmb a m a n log log =5、换底公式及衍生性质:换底公式:log log log m a m N N a=(0a >且1a ≠,0m >,1m ≠,0N >)换底公式推论:(1)ab b a log 1log =;(2)log log log a b a b c c ⋅=。
6、两种特殊的对数:①通常将以10为底的对数叫做常用对数。
N 的常用对数记作lg N 。
②另外在科学技术中,常使用无理数 2.71828e = 为底的对数,以e 为底的对数叫做自然对数,记为ln N 。
模块02:对数方程1、基本概念:在指数中含有未知数的方程叫指数方程。
2、解指数方程的基本思想:化同底或换元。
对数函数知识点总结
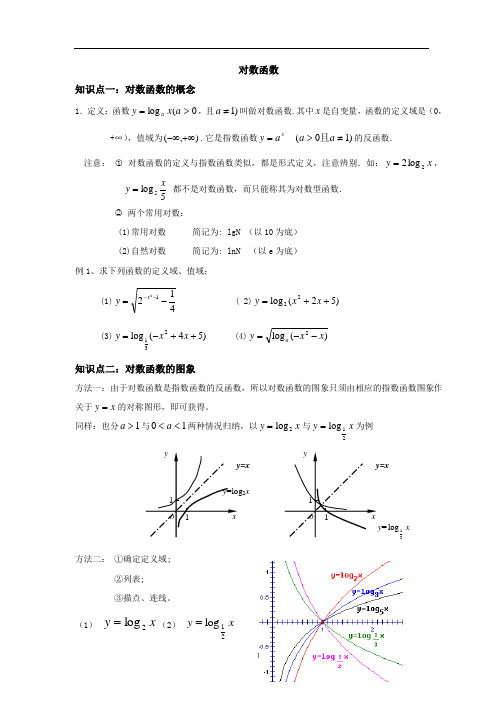
对数函数知识点一:对数函数的概念1.定义:函数0(log >=a x y a ,且)1≠a 叫做对数函数.其中x 是自变量,函数的定义域是(0,+∞),值域为),(+∞-∞.它是指数函数xa y = )10(≠>a a 且的反函数.注意: ○1 对数函数的定义与指数函数类似,都是形式定义,注意辨别.如:x y 2log 2=,5log 5xy = 都不是对数函数,而只能称其为对数型函数. ○2 两个常用对数: (1)常用对数 简记为: lgN (以10为底) (2)自然对数 简记为: lnN (以e 为底)例1、求下列函数的定义域、值域:(1)41212-=--xy ( 2))52(log 22++=x x y (3))54(log 231++-=x x y (4))(log 2x x y a --=知识点二:对数函数的图象方法一:由于对数函数是指数函数的反函数,所以对数函数的图象只须由相应的指数函数图象作关于x y =的对称图形,即可获得。
同样:也分1>a 与10<<a 两种情况归纳,以x y 2log =与x y 21log =为例方法二: ①确定定义域; ②列表; ③描点、连线。
(1)x y 2log =(2) x y 21log =y=x o 11 yxy =log 2x o 11 yxy=xy =x 21log(3)x y 3log =(4) x y 31log =思考:函数x y 2log =与y =3log x 与y对函数的相同性质和不同性质. 相同性质: 不同性质:例2、作出下列对数函数的图象:知识点三:对数函数的性质由对数函数的图象,观察得出对数函数的性质.思考:底数a 是如何影响函数x y a log =的.(学生独立思考,师生共同总结)规律:在第一象限内,自左向右,图象对应的对数函数的底数逐渐变大. 例3、比较下列各组数中两个值的大小:⑴ 5.8log ,4.3log 22; ⑵7.2log ,8.1log 3.03.0; ⑶)1,0(9.5log ,1.5log ≠>a a a a . 变式训练:(1)若3log 3log n m <,求n m 和的关系。
对数运算法则

故12y=1z-1x.
解法二3x=4y=6z=m,
则有3=m1x①,4=m1y②,6=m1z③,
③÷①,得m1z-1x=63=2=m12y.
∴1z-1x=12y.
9
logaMN=
logaMn=(n∈R)
(a>0,a≠1,M>0,N>0)
难点疑点突破
对数定义中,为什么要规定a>0,,且a≠1?
理由如下:
①若a<0,则N的某些值不存在,例如log-28
②若a=0,则N≠0时b不存在;N=0时b不惟一,可以为任何正数
③若a=1时,则N≠1时b不存在;N=1时b也不惟一,可以为任何正数
(2)中logbc能否也换成以a为底的对数.
(3)应用(1)将logab换成以b为底的对数.
(4)应用(1)将loganbm换成以a为底的对数.
解答(1)设logaN=b,则ab=N,两边取以c为底的对数得:b·logca=logcN,
∴b=logcNlogca.∴logaN=logcNlogca.
∴Δ=S2+4S≥0,解得S≤-4或S≥0,
故lg(xy)的取值范围是(-∞,-4〕∪〔0,+∞).
5
求值:
(1)lg25+lg2·lg50+(lg2)2;
(2)2log32-log3329+log38-52log53;
(3)设lga+lgb=2lg(a-2b),求log2a-log2b的值;
为了避免上述各种情况,所以规定对数式的底是一个不等于1的正数
高一数学对数函数题型及解题技巧

高一数学对数函数题型及解题技巧对数函数是高一数学中的一个重要概念,它的应用非常广泛。
下面我们来了解一些对数函数的题型及解题技巧。
一、基本概念对数函数的定义是:设a>0且a≠1,那么我们称y=loga(x)为以a为底,x的对数。
其中a称为底数,x称为真数,y称为以a为底,x的对数。
以10为底的对数函数常用符号是log(x),而以e(自然对数)为底的对数函数常用符号是ln(x)。
二、题型分类1. 求解对数函数的定义域和值域。
定义域是x>0,值域是R(实数集)。
2. 计算对数函数的值。
根据定义,可以用对数的转化公式来计算对数函数的值。
例如log3(81)=4,因为3的4次方等于81。
3. 求解对数方程。
对数方程一般可以转化为指数方程来求解。
例如,求解log2(x)=3,可以将其转化为2的3次方等于x,即x=8。
4. 求解等比数列。
等比数列的通项公式为an=a1*r^(n-1),其中a1为首项,r为公比,n为项数。
如果要求等比数列的第n项,则有an=a1*q^(n-1),其中q=loga(r),a是公比的底数。
5. 求解对数函数的性质。
对数函数有多种性质,如对称轴、单调性、奇偶性等。
可以根据对数函数的图像来分析求解。
三、解题技巧1. 掌握对数函数的基本概念,理解对数函数的定义、性质和应用。
2. 熟练掌握对数函数的计算方法,掌握对数的转化公式、对数方程的转化方法和等比数列的求解方法。
3. 学会对数函数的图像分析方法,掌握对数函数的对称轴、单调性、奇偶性等特点,从而更好地解决对数函数相关的问题。
以上是关于高一数学对数函数题型及解题技巧的介绍,希望能够帮助大家更好地掌握对数函数的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2. 2.1第一课时 对数的概念教案【教学目标】1.理解对数的概念,能够进行对数式与指数式的互化2.渗透应用意识,培养归纳思维能力和逻辑推理能力,提高数学发现能力【教学重难点】 重点:对数的概念难点:对数概念的理解. 【教学过程】一、预习检查、总结疑惑检查落实了学生的预习情况并了解了学生的疑惑,使教学具有了针对性。
二、情景导入、展示目标。
(一)复习引入:1庄子:一尺之棰,日取其半,万世不竭(1)取4次,还有多长?(2)取多少次,还有0.125尺?2假设2002年我国国民生产总值为a 亿元,如果每年平均增长8%,那么经过多少年国民生产总值是2002年的2倍?抽象出:1. =?,=0.125x=? 2. =2x=?也是已知底数和幂的值,求指数你能看得出来吗?怎样求呢?(二)新授内容:定义:一般地,如果 的b 次幂等于N, 就是,那么数 b 叫做 以a 为底 N 的对数,记作 ,a 叫做对数的底数,N 叫做真数例如: ;; 探究:⑴负数与零没有对数(∵在指数式中 N > 0 )⑵,∵对任意 且 , 都有 ∴同样易知: ⑶对数恒等式如果把 中的 b 写成 , 则有421⎪⎭⎫ ⎝⎛x⎪⎭⎫ ⎝⎛21⇒()x%81+⇒()1,0≠>a a a N a b=b N a =log 1642=⇔216log 4=100102=⇔2100log 10=2421=⇔212log 4=01.0102=-⇔201.0log 10-=01log =a 1log =a a 0>a 1≠a 10=a 01log =a 1log =a a N a b=N a log N aNa =log⑷常用对数:我们通常将以10为底的对数叫做常用对数为了简便,N 的常用对数简记作lgN例如:简记作lg5 ; 简记作lg3.5.⑸自然对数:在科学技术中常常使用以无理数e=2.71828……为底的对数,以e 为底的对数叫自然对数,为了简便,N 的自然对数简记作lnN例如:简记作ln3 ; 简记作ln10(6)底数的取值范围;真数的取值范围(三)合作探究,精讲点拨 探究一:指对互化例1将下列指数式写成对数式:(课本第87页) (1)=625 (2)=(3)=27 (4) =5.73解析:直接用对数式的定义进行改写. 解:(1)625=4; (2)=-6; (3)27=a ; (4)点评:主要考察了底真树与幂三者的位置. 变式练习1: 将下列对数式写成指数式: (1); (2)128=7;(3)lg0.01=-2; (4)ln10=2.303解:(1) (2)=128;(3)=0.01; (4)=10探究二:计算例2计算: ⑴,⑵,⑶,⑷解析:将对数式写成指数式,再求解. 解:⑴设 则 , ∴ ⑵设 则, , ∴N 10log 5log 105.3log 10N e log 3log e 10log e ),1()1,0(+∞ ,0(+∞4562-641a3m )(315log 2log 6413log m =73.5log 31416log 21-=2log 16)21(4=-72210-303.2e27log 981log 43()()32log 32-+625log 345=x 27log 9,279=x3233=x23=x =x 81log 43()8134=x4433=x 16=x⑶令 =,∴, ∴⑷令 , ∴, , ∴点评:考察了指数与对数的相互转化. (四)小结:本节主要学习了对数的概念,要熟练的进行指对互化. 【板书设计】 一、对数函数概念 二、例题例1 变式1 例2 变式2【作业布置】导学案课后练习与提高2.2.1对数的概念导学案课前预习学案一、预习目标了解对数的概念,知道常用对数与自然对数以及这两种对数符号的记法,了解对数恒等式,二、预习内容 对数概念:1.一般地,如果()的次幂等于,即,那么数叫做 ,记作.其中,叫做对数的 ,叫做 .例如:,读作:以3为底9的对数为2 .(1)概念分析:对数式中各字母的取值范围:: ; : ; : .(2)零和负数没有对数;1的对数为0,即(且);底数的对数为1,即(且).2.以10为底的对数称为 ,以e 为底的对数称为3.三、提出疑惑=x ()()32log 32-+()()13232log -++()()13232-+=+x1-=x =x 625log 345()625534=x43455=x 3=x a 0,1a a >≠b N b a N =b log a N b =a N 2339 log 92=⇒=log a b N =a 0,1a a >≠b b R ∈N 0N >log 10a =0a >1≠a log 1a a =0a >1≠a log ba a =log a Na =课内探究学案一、 学习目标1、 理解指数式与对数式的相互关系,能熟练进行指数式与对数式的互化。
2‘2、 并能运用恒等式进行计算。
学习重难点:理解对数的概念,能够进行对数式与指数式的互化、二、 学习过程 (一)合作探究探究一.指数式和对数式互化 1.将下列指数式写成对数式:解析:直接用对数式的定义进行改写.解:点评:主要考察了底真树与幂三者的位置.变1.将下列对数式写成指数式:探究二.求对数值2、⑴,⑵,⑶,⑷解析:将对数式写成指数式,再求解. 解:点评:考察了指数与对数的相互转化.变2.求下列对数的值(1) (2) (3)42115625 10 81 () 5.731003a m e -===①②③④=2121log 16 4 log 7 lg 0.01 2 ln10 2.303128=-=-=-①②③④=27log 981log 43()()32log 32-+625log 34572log4)381(log 3课后练习与提高1.对数式的值为 ( )(A ) 1(B )-1(C )(D )-2、若log [ log ( lo g x)] = 0,则x 为( ).(A). (B).(C).(D).3.计算 (1) (2)4.已知且,,,求的值。
73221-32133121423(2log 2)3+=52log 35=0a >1a ≠log 2a m =log 3a n =2m na +2. 2.1第二课时 对数的运算性质【教学目标】1.知识目标:掌握对数的运算性质,并能理解推导这些法则的依据和过程; 2.能力目标:能较熟练地运用法则解决问题; 【教学重难点】重点、对数运算性质难点:对数运算性质的证明方法. 【教学过程】(一)预习检查、总结疑惑检查落实了学生的预习情况并了解了学生的疑惑,使教学具有了针对性。
(二)情景导入、展示目标。
(一)、复习引入:1.对数的定义 其中 a 与 N2.指数式与对数式的互化3.重要公式:⑴负数与零没有对数; ⑵,⑶对数恒等式3.指数运算法则(二)、新授内容:积、商、幂的对数运算法则:如果 a > 0,a ≠ 1,M > 0, N > 0 有:证明:①设M=p, N=q b N a =log ∈),1()1,0(+∞ ∈,0(+∞01log =a log =a a N aNa =log )()(),()(),(R n b a ab R n m aa R n m a a a n n n mnnm n m n m ∈⋅=∈=∈=⋅+)()()(3R)M(n nlog M log 2N log M log NM log 1N log M log (MN)log a n a a a a a a a ∈=-=+=a log a log由对数的定义可以得:M=,N=∴MN= = ∴MN=p+q ,即证得MN=M + N ②设M=p ,N=q由对数的定义可以得M=,N=∴∴ 即证得 ③设M=P 由对数定义可以得M=,∴= ∴=np , 即证得=n M说明:上述证明是运用转化的思想,先通过假设,将对数式化成指数式,并利用幂的运算性质进行恒等变形;然后再根据对数定义将指数式化成对数式 ①简易语言表达:“积的对数 = 对数的和”……②有时逆向运用公式:如③真数的取值范围必须是:是不成立的是不成立的④对公式容易错误记忆,要特别注意:,(三)、合作探究,精讲点拨 例1 计算(1)25, (2)1, (3)(×), (4)lg 解析:用对数的运算性质进行计算.解:(1)25= =2(2)1=0(3)(×25)= +p a qa paq a q p a +a log a log a log a log a log a log p a qa q p q pa aa N M -==q p N M a -=log N M NMa a alog log log -=a log pa n M np a a log n M a log nM a log 10log 2log 5log 101010==+),0(+∞)5(log )3(log )5)(3(log 222-+-=--)10(log 2)10(log 10210-=-N M MN a a a log log )(log ⋅≠N M N M a a a log log )(log ±≠±5log 4.0log 2log 745251005log 5log 254.0log 2log 742log 742log 52= + = 2×7+5=19(4)lg = 点评:本题主要考察了对数性质的应用,有助于学生掌握性质. 例2 用,,表示下列各式:解析:利用对数的性质化简. 解:(1)=(xy )-z=x+y- z (2)=(= +=2x+点评:熟悉对数的运算性质. 变式练习、计算: (1)lg14-2lg+lg7-lg18 (2) (3) 说明:此题可讲练结合. (1)解法一:lg14-2lg+lg7-lg18 =lg(2×7)-2(lg7-lg3)+lg7-lg(×2) =lg2+lg 7-2lg7+2lg3+lg7-2lg3-lg2=0解法二:lg14-2lg +lg7-lg18=lg14-lg +lg7-lg18=lg评述:此题体现了对数运算性质的灵活运用,运算性质的逆用常被学生所忽视.2log 722⨯2log 52510052lg1052log10512==x a log y a log z a log 32log )2(;(1)log zyx zxyaa zxyalog a log a log a log a log a log 32log zyx aa log 2x3log )z y a -a log 2x a log 3log z y a -a log z y a a log 31log 21-379lg 243lg 2.1lg 10lg 38lg 27lg -+3723372)37(01lg 18)37(7142==⨯⨯23lg 23lg 53lg 3lg 9lg 243lg )2(25===评述:此例题体现对数运算性质的综合运用,应注意掌握变形技巧,如(3)题各部分变形要化到最简形式,同时注意分子、分母的联系.(2)题要避免错用对数运算性质. (四)、反思总结,当堂检测 1.求下列各式的值:(1)6-3 (2)lg 5+lg 22. 用lg x,lg y,lg z表示下列各式:(1) lg (xyz ); (2)lg ;【板书设计】一、对数概念及其运算性质 二、例题 例1 变式1 例2 变式2【作业布置】导学案课后练习与提高2.2.1对数的运算性质导学案1023lg)10lg(32lg )3lg(2.1lg 10lg 38lg 27lg )3(2213213⨯=+=-+212lg 23lg )12lg 23(lg 23=-+-+=2log 2log zxy 2课前预习学案一、预习目标初步了解对数的运算性质,知道推导这些法则的依据和过程; 二、预习内容1.对数的定义 其中 a 与 N2.指数式与对数式的互化3.重要公式:⑴负数与零没有对数;⑵ ,⑶对数恒等式3.指数运算法则 三、提出疑惑课内探究学案三、 学习目标1.掌握对数的运算性质,并能理解推导这些法则的依据和过程; 2.能较熟练地运用法则解决问题; 学习重点、对数运算性质学习难点:对数运算性质的证明方法.四、 学习过程 (一)合作探究探究一:积、商、幂的对数运算法则: 如果 a > 0,a ≠ 1,M > 0, N > 0 有:解析:利用对数的性质与对数式与指数式的关系证明. 点评:知道公式的推倒过程有利于学生掌握公式.探究二 例1 计算(1)25, (2)1, (3)(×), (4)lg 解析:用对数的运算性质进行计算.b N a =log ∈),1()1,0(+∞ ∈,0(+∞=1log a =a a log =Na alog )_______()(),______()(),_____(R n ab R n m a R n m a a n nm n m ∈=∈=∈=⋅)()()(3R)M(n nlog M log 2N log M log NM log 1N log M log (MN)log a n a a a a a a a ∈=-=+=5log 4.0log 2log 74525100解:点评:本题主要考察了对数性质的应用,有助于学生掌握性质.例2 用,,表示下列各式:解析:利用对数的性质化简. 解:点评:熟悉对数的运算性质.变式练习:计算: (1)lg14-2lg +lg7-lg18 (2) (3)(二)反思总结(三)当堂检测 1.求下列各式的值:(1)6-3 (2)lg 5+lg 2x a log y a log z a log 32log )2(;(1)log zyx zxyaa 379lg 243lg 2.1lg 10lg 38lg 27lg -+2log 2log2. 用lg x,lg y,lg z表示下列各式:(1) lg (xyz ); (2)lg ;课后练习与提高1.若3a =2,则log 38-2log 36用a 的代数式可表示为( ) (A )a-2 (B )3a-(1+a)2 (C )5a-2 (D )3a-a 22、已知lga ,lgb 是方程2x -4x +1 = 0的两个根,则(lg )的值是( ). (A).4 (B).3 (C).2 (D).1 3、下列各式中正确的个数是 ( ).① ② ③(A )0 (B )1 (C )2 (D )34.已知,,那么______.5、若lg2 = a ,lg3 = b ,则lg =_____________. 6. 用lg x,lg y,lg z表示下列各式: (1); (2) zxy 22ba 254zxy 3lgzy x 2lg2. 2.1第三课时 对数的运算性质的应用【教学目标】1.知识目标:掌握对数的运算性质,并能理解推导这些法则的依据和过程; 2.能力目标:能较熟练地运用法则解决问题; 【教学重难点】重点:对数运算性质难点:对数运算性质的应用. 【教学过程】(一)预习检查、总结疑惑检查落实了学生的预习情况并了解了学生的疑惑,使教学具有了针对性。
