一维CFD模拟仿真设计
CFD数值模拟实验指导书

(4) (5a) (5b) (5c) (6)
对于无法用解析方法求解的微分方程可以用数值方法求解, 所谓数值方法求解就是用近 似的数值解逼近微分方程的精确解。流动控制方程的精确解是流场计算域内流动参数(如速 度、压力、温度等)的连续分布,而数值解则是流场计算域内离散的点上的近似解对连续精 确解的逼近,换句话说,我们可以把连续的流场离散为一定数目的不连续的点,在这些离散 点上,守恒方程被近似满足,如果离散点之间的距离为无穷小,则近似解将无限趋近于精确 解,因此我们可以用近似解代替精确解。这就是流动微分方程数值求解的基本思想。 以数值方法求解流动微分方程,首先要把需要求解的流场的几何空间(或称为计算域) 离散为孤立的不连续的点,或者说用一定数量的点覆盖或代表要求解的连续的流场,然后将 流动控制方程的偏导数用离散点之间的有限变化来代替, 例如, 表示速度梯度的导数 ∂u / ∂x 用差商 Δu / Δx 来代替,其中 Δu 和 Δx 分别是 x 坐标方向的两个相邻的点的速度差和坐标 x 的增量。 可以想象, 如果控制微分方程中的所有导数或偏导数都被类似于差商的量代替的话, 偏微分方程将有可能变成一个线性方程,一个只包含离散点的坐标和待求函数值(如上述的 u)的线性方程。事实上,我们可以把流动控制方程组的每一个偏微分方程在每一个离散点 上转变为一个线性方程。假如我们用 100 个点离散一个计算域,那么对每个偏微分方程我们 将得到 100 个线性方程。至此,偏微分方程的求解已经转化为线性方程组的求解,如果得到 线性方程组的解,我们就得到了偏微分方程组的近似数值解。因此,我们也可以说,CFD 模 拟的过程本质上是在计算域上构建线性方程组并求解线性方程组的过程。 从上面的论述可以看出,数值方法求解流动微分方程至少包括三个步骤:首先,离散计 算域;其次,在离散后的计算域上离散控制方程;其三,求解离散得到的线性方程组。需要 补充的是,并不是所有的线性方程都需要求解,实际上有些特殊点上的流动变量值或其梯度 是已知的,这些特殊的点就是计算域边界上的点。通常为了限定微分方程的解,我们需要给
CFD模拟图(A-1)---模板
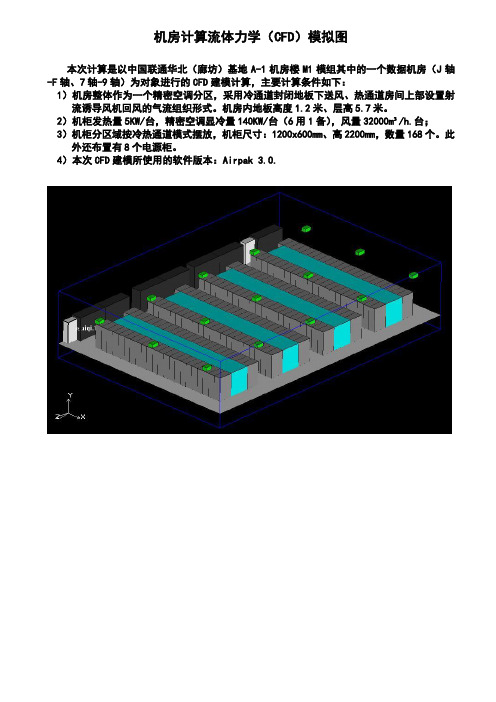
机房计算流体力学(CFD)模拟图
本次计算是以中国联通华北(廊坊)基地A-1机房楼M1模组其中的一个数据机房(J轴-F轴、7轴-9轴)为对象进行的CFD建模计算,主要计算条件如下:
1)机房整体作为一个精密空调分区,采用冷通道封闭地板下送风、热通道房间上部设置射流诱导风机回风的气流组织形式。
机房内地板高度1.2米、层高5.7米。
2)机柜发热量5KW/台,精密空调显冷量140KW/台(6用1备),风量32000m³/h.台;
3)机柜分区域按冷热通道模式摆放,机柜尺寸:1200x600mm、高2200mm,数量168个。
此外还布置有8个电源柜。
4)本次CFD建模所使用的软件版本:Airpak 3.0.
一、CFD模拟温度场计算结果:(1)地板上高度0.5米高度温度场分布
(2)地板上高度1.0米高度温度场分布
(3)地板上高度1.8米高度温度场分布
(4)地板上X轴向温度场分布
三、CFD 计算结果表明:机柜冷通道封闭,其温度场分布均匀,无局部过热情况出现。
冷量得到有效管理,避免了气流短路,效率高从而更为节能。
一维弹道修正理论与仿真

0引言弹道修正引信技术将引信的功能从安全控制、炸点控制和起爆控制拓宽到命中点控制,使引信不仅控制对目标实施有效的毁伤,而且还控制对目标的命中精度。
也就是说,弹道修正引信不仅具有传统引信系统保证弹药安全和控制战斗部起爆的功能,还具有感知及辨识弹道环境和修正弹道的功能。
它通过对弹丸实际弹道环境的辨识,预估弹道偏差,迅速产生弹道修正指令并传输给相应的执行机构,以达到对无控弹药的弹道修正。
发射后,炮弹即不受地面控制,因此抗干扰能力较强。
本文探讨的迫击炮一维弹道修正引信的基本目的是在不增加士兵后勤负担的情况下,提高步兵迫击炮间接射击的有效性。
一维弹道修正模块使之成为一个灵巧武器,能减小射程误差,提高其打击毁伤效率。
1一维弹道修正模块设计引信对弹道修正模块在各方面有严格的要求和限制,具体如下:(1)弹道修正模块必须在系统通过测量、计算得到的不定时刻t起,通过某种方式显著增加引信在飞行中所受的空气阻力;(2)在t时刻之前,弹道修正模块的附加不应对原弹道特性产生显著影响;(3)由于现实条件限制,引信提供给修正模块的最大空间仅为17 cm3,因此空间利用率愈高愈好;(4)目前技术条件下,引信无法为修正模块提供过多电能,以带动电机等耗能设备;(5)弹丸在飞行过程中不作任何旋转运动,不能提供任何大小的离心力。
基于以上要求,本设计选取可以存储能量的扭转弹簧作为机构打开的动力源。
如图1所示:8个叶片分别受起始角为0°,自然角为108°扭转弹簧作用;固定盘受起始角为0°,自然角为17.5°的扭转弹簧作用。
控制装置在一定时刻释放桨式叶片,通过增大飞行装置与空气的接触面积达到增大空气阻力的目的。
其工作过程如下:机构张开前,8个叶片紧贴飞行装置圆锥状外表面,以尽可能减小对飞行装置原飞行特性的影响。
固定盘由固定销固定于起始位置,其8个支爪则分别抵于8个叶片的底部,从而固定了叶片。
系统发出张开指令后,控制装置引爆微型雷管,利用其爆炸产生的能量拔出固定销,释放固定盘。
一维流体系统仿真平台Flowmaster简介

Flowmaster——系统压力分配(KPa)
15
Flowmaster——系统瞬态特性
16
Flowmaster——分析水锤现象,预测汽蚀
阀门瞬间关闭
气穴捕捉
17
Flowmaster——换热分析
换热发生在计算网络的流体之间 管道壁面的换热分析 热量在某一离散点输入或者输出 瞬态换热以及热量在元件中的蓄存 同种流体的混合 温度对流体物性的影响
1987,Flowmaster 正式投入市场,至今20多年的流体系统 仿真咨询的成功经验,成为该领域的领导者。
7
Flowmaster——完备的数据库
建立完善的用户数据库
8
Flowmaster——便捷的自定义专有特性曲线
9
Flowmaster——常用元件示例
类型完备的管道、弯管、三通、阀门、泵、风机、换热器、空调系统元件、稳 压器、油箱、弹簧、质量套筒、热桥、控制元件……,共计400多个族类
24
Flowmaster——可压供气系统
PID控制阀
25
PID控制 压力波捕捉
Flowmaster——通风系统
26
Flowmaster具备丰富的 通风系统元件库,例如 通气槽道、风机、接头、 驻点风压等
对于多层建筑的大型 通风系统,Flowmaster能 够轻松的进行建模和模 拟,帮助设计人员确保 通风系统的合理配置
Flowmaster专业版
Flowmaster——专业版
通用版 汽车版 航空版 燃气涡轮机版 能源电力版
42
Flowmaster——汽车版
43
Flowmaster——发动机冷却系统
软件中提供了冷却系统的标准元件,如 水泵、节温器、软管、散热器、用户自 定义冷却液、换热器、冷却风扇等
CFD仿真模拟【转】

一.介绍1.什么是CFD?简单地说,CFD就是利用计算机求解流体流动的各种守恒控制偏微分方程组的技术,这其中将涉及流体力学(尤其是湍流力学)、计算方法乃至计算机图形处理等技术。
因问题的不同,CFD技术也会有所差别,如可压缩气体的亚音速流动、不可压缩气体的低速流动等。
对于暖通空调领域内的流动问题,多为低速流动,流速在10m/s以下;流体温度或密度变化不大,故可将其看作不可压缩流动,不必考虑可压缩流体高速流动下的激波等复杂现象。
从此角度而言,此应用范围内的CFD和数值传热学NHT(Numerical Heat Transfer)等同。
另外,暖通空调领域内的流体流动多为湍流流动,这又给解决实际问题带来很大的困难。
由于湍流现象至今没有完全得到解决,目前HVAC内的一些湍流现象主要依靠湍流半经验理论来解决。
总体而言,CFD通常包含如下几个主要环节:建立数学物理模型、数值算法求解、结果可视化。
2.建立模型建立数学物理模型是对所研究的流动问题进行数学描述,对于暖通空调工程领域的流动问题而言,通常是不可压流体的粘性流体流动的控制微分方程。
另外,由于暖通空调领域的流体流动基本为湍流流动,所以要结合湍流模型才能构成对所关心问题的完整描述,便于数值求解。
如下式为粘性流体流动的通用控制微分方程,随着其中的变量f的不同,如f代表速度、焓以及湍流参数等物理量时,上式代表流体流动的动量守恒方程、能量守恒方程以及湍流动能和湍流动能耗散率方程。
基于该方程,即可求解工程中关心的流场速度、温度、浓度等物理量分布。
3.数值算法上述的各微分方程相互耦合,具有很强的非线性特征,目前只能利用数值方法进行求解。
这就需要对实际问题的求解区域进行离散。
数值方法中常用的离散形式有:有限容积,有限差分,有限元。
目前这三种方法在暖通空调工程领域的CFD技术中均有应用。
总体而言,对于暖通空调领域中的低速,不可压流动和传热问题,采用有限容积法进行离散的情形较多。
04.车辆冷却风道的一维CFD仿真分析

车辆冷却风道的一维CFD仿真研究 One Dimensional CFD Simulation Study for WindTunnel of Vehicle韩恺 赵长禄(北京理工大学机械与车辆学院军用车辆动力系统技术国防重点学科实验室)摘 要: 本文利用GT-Suite软件的Cool3D模块和GT-Cool模块离散了车辆冷却风道的3D模型,并采用边界耦合法建立了特殊冷却风道的一维CFD仿真模型。
在此基础上,利用主要部件的性能试验数据建立了某装甲车辆冷却系统模型,研究环境温度和散热器高度变化时对冷却风道主要设计参数之间的影响。
仿真结果为冷却风道的设计提供了理论依据。
关键词:车辆; Cool3D; 冷却风道; 一维CFDAbstract: 3D model of wind tunnel of vehicle is discrete by Cool3D module and GT-Cool module of GT-Suite Software, and One Dimensional CFD simulation model of special wind tunnel is built up by boundary coupling method.On the basis, the cooling system simulation model of the armored vehicle is created by utilizing performance experimental data of main components, and the main design parameters of the wind tunnel versus environment temperature and radiator high is investigated. Simulation results provide theory instruction for design of wind tunnel.Key words: Vehicle; Cool3D; Wind Tunnel; One Dimensional CFD1 引言冷却空气从进入车辆到从车辆排出的全流程所掠过的腔道,称为冷却风道【1】。
基于一维-三维耦合仿真的进气系统优化方法
第2期(总第229期) 2017年4月车用发动机VEHICLEENGINENo .2(Serial No .229)Apr .2017基于一维-三维耦合仿真的进气系统优化方法董江峰\孙淑慧2,仲蕾s 陈晋兵s 王尚学\牛海杰1(1.中国北方发动机研究所(天津),天津 300400; 2.天津市热电设计院有限公司,天津 300000 )摘要:提出了基于一维-三维耦合仿真的进气系统优化方法,此方法兼具CFD 对进气系统三维流动特性准确描述与一维仿真对内燃机进气系统全局控制的优点。
建立了进气歧管三维模型,采用GT-Power 软件进行缸内工作过程模型仿真,根据试验数据标定仿真模型。
通过一维-三维耦合仿真计算得到进气歧管各转速下的流动参数, 以此作为CFD 仿真的边界条件,优化进气歧管的结构参数。
通过整机试验对进气歧管流动性能进行了验证。
试验结果表明,该方法能够较好地指导进气歧管设计。
关键词:内燃机;仿真;进气歧管;进气均勻性DOI : 10.3969/j .issn .l 001-2222.2017.02.010中图分类号:TK 413.44 文献标志码:B文章编号:1001-2222(2017)02-0056-06油气混合的质量对发动机燃烧过程及整机性能 有着十分重要的影响,而进排气系统设计的优劣会 影响其流动特性,进而影响油气混合质量。
为提高 各缸进气均匀性,降低流通阻力,需要对进气歧管的 结构进行优化,在满足各缸进气均匀性的条件下,尽 可能减小流通阻力,增加进气量,从而增加有效功的 循环输出量,提高柴油机功率密度,同时满足排放法 规要求,这些在工程应用中也是重要的内容〜5]。
国内外在发动机进气系统的流动特性研究方面做了很多工作。
Hoong T T o h 等研究了进气歧管 几何结构对内燃机缸内气体流动的影响规律[6] ;Cui Y 等以整个进气系统作为研究对象,研究了多缸发 动机中间气缸与其他气缸的流量及总压变化[7] ;Y . L.Q i 等研究了在进气冲程时进气门上游漩涡对缸 内流动的影响规律,揭示了滚流率和充量系数的提 高途径[8];蓝志宝等应用C FD 方法进行了进气歧管 的开发研究[9# ;王文、王兴海等对进排气压力波对 缸内燃烧的影响规律进行了试验研究[11_12]。
CFD值模拟原理总结
CFD 数值模拟原理课程总结随着近代科学技术的进步,在绝大部分的研究领域内,人们对常见现象的理论研究已达到了一个崭新的境界,如力学、新材料设计的超分子建筑学、统计物理学、流体力学、传热学、化学反应流等。
与此同时,这些数学物理方程、理论模型或经验模型,在大量的实验研究及工程应用中得到证实。
为了在实际工程运用中能更加直观简洁的描述流体在流场中的流动情况,CFX 软件系列中的CFD ,PRO-E 等软件就能系统的解决流体的数值模拟问题。
CFD 的基本理论基础与流体力学理论基础相似,质量守恒方程,动量守恒方程(牛顿运动定律)和能量守恒方程(热力学第一定律)是CFD 理论的基石和核心。
以下为粘性流体流动的基本方程组:(1)连续性方程: (2)动量方程:(3)能量方程:(4)质量组分分数方程:在粘性流体流动的系统中,以上四个方程构成的方程组是叩开理论流体力学实际问题的基础,同时在CFD 软件运用开发过程中起着理论核心的作用。
二、网格计算中的对流——扩散方程的差分格式分析网格计算中的基本物理概念(1)节点:需要求解未知物理量的空间几何位置;(2)控制容积:空间实体的面积或体积;(3)界面:控制容积之间的分界面;(4)网格线:连接各节点之间的连线。
对于均匀网格,内节点与外节点在区域内的分布趋于一致,仅在坐标轴方向错位半个网格空间;对于不均匀网格计算,内节点永远在控制容积中心,而外节点的界面永远位于两相邻点的中间位置。
在实际工程运算中,内节点网格计算处理特变物理现象比较容易,外节点状态。
由能量守恒微分方程可以推出差分方程,根据工程应用数学所学知识,运用Taylor 展开得到差分方程。
在均匀的网格中,对一维方程,采用不同的离散形式,可以得到相同的差分方程。
但是,这不是普遍现象。
一般情况下,有差别,计算结果的准确度也不有差别。
运用Taylor 展开易于进行数学分析,其缺点是物理概念不清,计算()()0=⋅∇+i i i i i t u ρε∂ρε∂()()()i g s i i i i i i i i i Sc P t +-+∇-=⋅∇+u u u u u βερε∂ρε∂()()()i g s i i i i i i i i i Sc P t+-+∇-=⋅∇+u u u u u βερε∂ρε∂()()()()∑∑==-+-=∇Γ-⋅∇+Np j ik ji jk ij Np j ik i jk j k ij ik i ik ik i i i ik i i Y m Y m Y Y Y Y t Y 11ρρβαρα∂ρα∂u的结果可能违背基本的物理定律。
CFD的参数化和优化仿真过程
网格最小尺寸
体网格总数
体网格质量 最小值
求解器阶段的参数化
• • • 材料物性的参数化 边界条件数值的参数化 计算结果数据的参数化
– 力、力矩、通量、面积分值、体积分值等
压力出口的速度均匀性
速度入口的数值
优化
• 什么是优化? • 在设计空间中寻找最佳的合理设计点 优化是一个双重问题
• 对“参数化”的变量进行适当的规划 •
CFD的参数化和优化仿真过程
崔亮 行业专员
北京福思营销顾问有限公司呈送
目录
• 基于Workbench的参数化仿真流程
– 几何建模阶段的参数化 – 网格剖分阶段的参数化 – 求解器阶段的参数化
• 基于ANSYS DesignXplorer (DX)的优化仿真过程 • 培训案例
Workbench
• • • ANSYS Workbench是一个项目管理工具,它是连接所有ANSYS软件工具的 顶层接口。 Workbench控制着ANSYS不同工具(几何建模/网格剖分/求解器/后处理) 之间的数据传输。 Workbench为项目管理带来了极大的帮助,用户无需再担心独立的几何、网 格、求解数据等文件在硬盘上的存储位置,只需通过Workbench界面中的工 作流程图即可轻松管理整个项目。 由于Workbench能够管理每个ANSYS软件工具以及它们之前的数据传输, 因此可以很方便地实现自动化的仿真流程,从而实现参数化分析和设计优化 分析。
• B. Static Mixer边界条件和计算结果的参数化和优化仿真
Inlet 400 K
Outlet
Thanks
•
Workbench工作流程
• Workbench包含了一些预定义的分析系统流程,此外用户也可以通过拖拽各 个软件工具,组合出自定义的分析流程。
飞行器流动仿真讲稿第7章-拟一维喷管流动的数值模拟
参考量都是常数 化简为
A V A A V A V 化简为
V ln A V V t x x x 同理可得动量方程和能量方程的无量纲形式。
第7.2节 亚声速—超声速喷管等熵流动的CFD解法(1)
二、网格生成
对一维问题,网格生成非常简单,只需代数方法即可; 有限差分方法使用均匀网格,取网格点数为
第7.2节 亚声速—超声速喷管等熵流动的CFD解法(1) 2. 物理条件 气体为标准空气,γ=1.4; 进口给定总温和总压,无量纲值:p0=1,T0=1,ρ0=1 对出口达超声速的情况,环境反压必须很低。本计算不需要 反压的具体值,它不会影响喷管内部的流动。 3. 精确解 亚声速—超声速喷管等熵流动为定常流动; 临界状态出现在喉道截面,喉道截面积就是临界面积
(7-6) 面积比公式
1 1
1
(7-7)
1 2 1 Ma 0 2
(7-8)
T 1 2 1 Ma T0 2
1
(7-9)
V Ma RT (7-10a)
第7.1节 拟一维喷管流动的三个物理问题 等熵流动三类问题 ① 已知总温、总压和临界截面积A*——由(7-6)式解出待求 截面的马赫数Ma,再用(7-7)式~(7-9a)式求出其它参数;
温度:滞止温度T0 密度:滞止密度ρ0 内能:滞止内能e0= cvT0 长度:喷管全长L 速度:滞止声速a0
无量纲温度:T′=T/T0
无量纲密度:ρ′=ρ/ρ0 无量纲内能:e′=e/e0 无量纲长度:x′=x/L 无量纲速度:V′=V/a0 无量纲时间:t′=t/t0 无量纲面积:A′=A/At
a0 RT0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
CFD simulation in Laval nozzleSIAE 090441313AbstractWe aim to simulate the quasi one dimension flow in the Laval nozzle based on CFD computation in this paper .We consider the change of the temperature ,the pressure ,the density and the speed of the flow to study the flow.The analytic solution of the flow in the Laval nozzle is provided when the input velocity is supersonic.We use the Mac-Cormack Explicit Difference Scheme to slove the question.Key words :Laval nozzle ,CFD,throat narrow.ContentsAbstract .................................................. . (1)Introduction .............................................. .. (2)Simulation of one-dimensional steady flow (3)Basisequations ................................................. (3)Dimensionless .......................................... . (10)Mac -Cormack Explicit Difference Scheme (11)Boundaryconditions ................................................ (13)Reference .............................................. (13)Annex .................................................. .. (14)IntroductionLaval nozzle is the most commonly used components of rocket engines and aero-engine, constituted by two tapered tube, one shrink tube, another expansion tube.Laval nozzle is an important part of the thrust chamber. The first half of the nozzle from large to small contraction to a narrow throat to the middle. Narrow throat and then expandoutwards from small to big to the end. The gas in the rocket body by the front half of the high pressure into the nozzle, through the narrow throat to escape by the rear half. This architecture allows the speed of the air flow changes due to changes in the jet cross-sectional area, the airflow from subsonic to the speed of sound, until accelerated to transonic. So, people flared nozzle called transonic nozzle. Since it was invented by the Swedish Laval, also known as Laval nozzle. Analysis of the principle of the Laval nozzle. The rocket engines of the gas flow in the combustion chamber under pressure, after the backward movement of the nozzle into the nozzle . At this stage, the gas movement follow the principle of "the fluid moves in the tube , the small cross-section at the flow rate large sectional large flow velocity", thus accelerating airflow.Laval nozzleWhen you reach the narrow throat, the flow rate has exceededthe speed of sound. Transonic fluid movement they no longer follow the principle of "cross-section at small velocity, at a flow rate of small cross-section large", but on the contrary the larger cross-sectional flow faster. The gas flow speed is further accelerated to 2-3 km / sec,equivalent to 7-8 times the speed of sound, thus creating a great thrust. The Laval nozzle fact played the role of a "flow rate Enlargement Device". In fact, not just rocket engines, missile nozzle is this horn shape, so the Laval nozzle weapons has a very wide range of applications.Simulation of one-dimensional steady flow1.Basis equationsAs we know,Laval nozzle is a zooming nozzle flow channel to narrow further expansion.Allows the airflow to further accelerate to reach the speed of sound at the throat into a supersonic flow.Now,we want to simulate the quasione-dimension flowing.Firstly,we will analysis on theory.The flow is isentropic,so we can apply the following equations.(1)Continuity equation:In the flow, we need to consider the following physical quantities.The pression ,the temperature ,the speed of the fluid and the cross-section .They are respectively represented by P,T,u,A. We apply the conservation of the mass.we will obtain this equation.))()((du u dA A d uA +++=ρρρAnd then we get=++ρρd u du A dA(2)Equation of momentum(in the direction of the axis) According to the theory of momentum:dAdP P dA A dP P PA uAu du u uA )2())(()(++++-=-+ρρThe simplification of this equation isdP udu -=ρ(3)Energy equation)2(2=+=+=udu dh v h d dh tIdeal gas equation of stateRTMP ρ=R is ideal gas constant,R=8.314J/g/K. M is the masse per mole.(4)The equation of ThermodynamicsP dPRT dT C dP T V T dT C dS dT C dh VdP dh TdS P e h PdV de dS p p p -=-=⇒=-=+=+=;,;V ,T Because the flow is isentropic,sodS=0And we use the equation of momentum,we have1)(T P -∆=∆=∆γγT RC p)(Combine with others equations,we result withRTγ=2uWe called u the speed of sound,we noted a.RTγ=2aWe apply the continuity equation)1(A dA 22-=a uWe defined the Mach numbera u =MIf we have the relation as)48.0tanh(347.0398.1A -+=xWe have the figure ○1Sou du M A A )1(d 2-= M>1,supersonic If dA<0,we have du>0. If dA>0,we have du<0. M<1,subsonicIf dA<0,we have du>0. If dA>0,we have du<0.This is the reason why this architecture allows the speed of the air flow changes due to changes in the jet cross-sectional area, the airflow from subsonic to the speed of sound, until accelerated to transonic.We have the consequence as followsPAMRTMAMP T R t tγγγγγ=-+⋅=-+)1(212)2111(m&1)211(;)211(T 22--+=-+=γγγγM P P M T ttThen we replace P and T in this equation.The consequence will become122)211(211m--+⋅-+=γγγγγM AMP T M Rt t&To simplify)1(212)2111(m-+-+=γγγγMAM T P R tt &In this equation,the variable is the much number,as the speed of the flow is from subsonic to supersonic ,so we can suppose that there exist a critical section where M equal to 1.Then)1(212)21211(1-+*+-+=γγγγMM AAFigure ○2This section is called narrow throat.The same method,we can obtain121122)21121()21121(21121-*-**-++=-++=-++=γγγγγρργγγγM M P PM T TFigure ○3We know the section in narrow throat is minimum.])2111)()1())1(2)1(()111[()(1)1(212)1(212+-+-+++-⋅-+-+-+=γγγγγγγγγγMM M M K AmdM d &we can judge that the function attains the maximum or not)1(212)2111()(f -+-+=γγγMM M2 DimensionlessCombining CFD with one-dimension flow theory,we make the variables dimensionless.According to the condition initial which is given .We note0'0''0'0'0'u lt t A A A lx x u u u T T T ======ρρρWe use the variable dimensionless to represent theequations.And the equations have the following changes (1)Continuity equation'''''''''''''''''''''''ln t 0t x v x A v x v xv x A A v x v ∂∂-∂∂-∂∂-=∂∂⇒=∂∂+∂∂+∂∂+∂∂ρρρρρρρρ‘‘ (2)Equation of momentum)(1v '''''''''''x T x T x v v t ∂∂+∂∂-∂∂-=∂∂ρργ (3)Energy equation)ln ()1(T '''''''''''x A v x v T x T v t ∂∂+∂∂--∂∂-=∂∂γ3.Mac-Cormack Explicit Difference SchemeThen we use the Mac-Cormack Explicit Difference Scheme,theprincipal of this theory is using the surrounding points to present differential parts of a point and we consider the question with one dimension.The distance between two points is h.0222003022200103013003320022000)(2)()(2)()()(!31)()(!21))((f f(x)x f h x f h f f x f h x f h f f hx x hx x x x xf x x x f x f x x ∂∂+∂∂-=∂∂+∂∂+=-=+=-∂∂+-∂∂+∂∂-+≈So we can use two points adjacent to present the differential parts.20310223102)(2)(h f f f x f hf f x f -+=∂∂-=∂∂Using this method,we make an estimation and correct the error. Estimationx nA A v x v v x v t i i t i t i t i t i t i t i t i t i t i ∆-⋅-∆-⋅-∆--=∂∂+++111ln )(ρρρρρ correct the errorx v t t t i t t i t t i t t i ∆--=∂∂∆+-∆+∆+∆+1)(ρρρIntermediate valuet t t i t i t t i ∆∂∂+=∆+)(ρρρ Then the equation has the following change))()((21)(t ti ti av t t t ∆+∂∂+∂∂=∂∂ρρρAt the moment t ,we will know the value in the whole plan . And we define).....,,,,min(54321t N t t t t t ii ii t t t t t t t a v x c t ∆∆∆∆∆∆=∆+∆=∆4.Boundary conditionsHyperbola equation has two characteristics lines.When one of the characteristics lines enter the flow zone .We admit a parameter to be fixed ,otherwise when one of the characteristics go out the flow zone ,we admit a parameter to be a variable depends the time.Applying this theory ,we can determine the boundary conditions.Reference :[1]章利特,高铁瑜,夏庆锋,徐廷相.拉瓦尔喷管的准一维定常流动.中国科技论文在线。
