第6章 多重共线性
一、多重共线性的概念二、产生多重共线性的原因三、多重共

相关情况,大企业二者都大,小企业都小。
(2)滞后变量的引入 在经济计量模型中,往往需要引入滞后经济变量来反映真实的经济 关系。 例如,消费=f(当期收入, 前期收入),显然,两期收入间有较强的 线性相关性。
《计量经济学》,高教出版社,王 少平、杨继生和欧阳志刚等编著 5
(3)多项式项的引入
如研究企业的成本与产量之间的关系时,往往在成本模型中引
其 中 : ci 不全为 0 ,则称 为解 释变量 间存 在 完全 多重 共线性 ( perfect
即:
1 X 11 1 X 12 X 1 X 1n X 21 X k1 X 22 X k 2 X 2 n X kn
中,至少有一列向量可由其他列向量(不包括第一列)线性表出。如 X2=kX1,则X2对Y的作用可由X1代替。
进产量的三次方,即:
Yi 0 1 X1i 2 X12i 3 X13i ui
在这种模型中,解释变量之间可能存在一定程度的多重共线性。
(4)样本资料的限制
由于完全符合理论模型所要求的样本数据较难收集,特定范
围内抽取样本可能存在某种程度的多重共线性。 进一步地讲,如果在实际应用中我们有足够多的样本,解释 变量的多重共线性程度就会大大降低。这就再次说明,多重共线 性本质上是样本问题。
jjjjjkkxcxxxxx??121122j????knkfkrfj计量经济学高教出版社王少平杨继生和欧阳志刚等编著17计量经济学高教出版社王少平杨继生和欧阳志刚等编著18计量经济学高教出版社王少平杨继生和欧阳志刚等编著19计量经济学高教出版社王少平杨继生和欧阳志刚等编著20计量经济学高教出版社王少平杨继生和欧阳志刚等编著213
1 2 2 x 1 r 1i
多重共线性

多重共线性多重共线性(multicollinearity )的特征● 多重共线性是指一个回归模型中的一些或全部解释变量之间存在有一种“完全”或准确的线性关系:0...2211=+++k k X X X λλλ其中k λλλ,...,,21为常数,但不同时为零。
● 0...2211≈+++k k X X X λλλ, 近似的多重共线性● 通过巴伦坦图做简单的描述。
共线性部分可用两圆圈的重叠部分来衡量。
重叠部分越大,共线性程度越高。
● 我们定义的多重共线性仅对X 变量之间的线性关系而言,它们之间的非线性关系并不违反无多重共线性的假设i i i i u X X Y +++=2210βββ多重共线性的后果●如果多重共线性是完全的,诸X变量的回归系数将是不正确的,并且它们的标准误差为无穷大●如果多重共线性是不完全的,那末,虽然回归系数可以确定,却有较大的标准误差,意思是,系数不能以很高的精确或准精确加以估计,这会导致:-参数估计不精确,也不稳定-参数估计量的标准差较大,影响系数的显著性检验●多重共线性产生的后果具有一定的不确定性●在近似的多重共线性的情况下,只要模型满足CLRM 假定,回归系数就为BLUE,但特定的样本估计量并不一定等于真值。
多重共线性的来源(1)许多经济变量在时间上由共同变动的趋势,如:收入,投资,消费(2)把一些经济变量的滞后值也作为解释变量在模型中使用,而解释变量和滞后变量通常相关,如:消费和过去的收入多重共线性一般与时间序列有关,但在横截面数据中也经常出现多重共线性的检验● 多重共线性是普遍存在的,造成的后果也比较复杂,对多重共线性的检验缺少统一的准则- 对有两个解释变量的模型,作散点图,或相 关系数,或拟和优度R平方。
- 对有多个解释变量的模型,分别用一个解释 变量对其它解释变量进行线性回归,计算拟 和优度22221,...,,k R R R- 考察参数估计值的符号,符不符合理论 - 增加或减少解释变量,考察参数估计值的变 化- 对比拟和优度和t检验值多重共线性的修正方法● 增加样本观测值,如果多重共线性是由样本引起的,可以通过收集更多的观测值增加样本容量。
实验6 多重共线性问题,确定与鸡肉消费量相关的解释变量
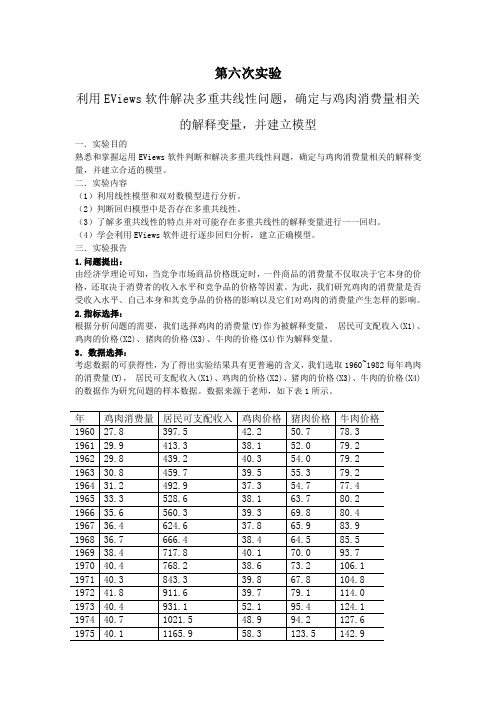
第六次实验利用EViews软件解决多重共线性问题,确定与鸡肉消费量相关的解释变量,并建立模型一.实验目的熟悉和掌握运用EViews软件判断和解决多重共线性问题,确定与鸡肉消费量相关的解释变量,并建立合适的模型。
二.实验内容(1)利用线性模型和双对数模型进行分析。
(2)判断回归模型中是否存在多重共线性。
(3)了解多重共线性的特点并对可能存在多重共线性的解释变量进行一一回归。
(4)学会利用EViews软件进行逐步回归分析,建立正确模型。
三.实验报告1.问题提出:由经济学理论可知,当竞争市场商品价格既定时,一件商品的消费量不仅取决于它本身的价格,还取决于消费者的收入水平和竞争品的价格等因素。
为此,我们研究鸡肉的消费量是否受收入水平、自己本身和其竞争品的价格的影响以及它们对鸡肉的消费量产生怎样的影响。
2.指标选择:根据分析问题的需要,我们选择鸡肉的消费量(Y)作为被解释变量,居民可支配收入(X1)、鸡肉的价格(X2)、猪肉的价格(X3)、牛肉的价格(X4)作为解释变量。
3.数据选择:考虑数据的可获得性,为了得出实验结果具有更普遍的含义,我们选取1960~1982每年鸡肉的消费量(Y),居民可支配收入(X1)、鸡肉的价格(X2)、猪肉的价格(X3)、牛肉的价格(X4)的数据作为研究问题的样本数据。
数据来源于老师,如下表1所示。
年鸡肉消费量居民可支配收入鸡肉价格猪肉价格牛肉价格1960 27.8 397.5 42.2 50.7 78.31961 29.9 413.3 38.1 52.0 79.21962 29.8 439.2 40.3 54.0 79.21963 30.8 459.7 39.5 55.3 79.21964 31.2 492.9 37.3 54.7 77.41965 33.3 528.6 38.1 63.7 80.21966 35.6 560.3 39.3 69.8 80.41967 36.4 624.6 37.8 65.9 83.91968 36.7 666.4 38.4 64.5 85.51969 38.4 717.8 40.1 70.0 93.71970 40.4 768.2 38.6 73.2 106.11971 40.3 843.3 39.8 67.8 104.81972 41.8 911.6 39.7 79.1 114.01973 40.4 931.1 52.1 95.4 124.11974 40.7 1021.5 48.9 94.2 127.61975 40.1 1165.9 58.3 123.5 142.91976 42.7 1349.6 57.9 129.9 143.6 1977 44.1 1449.4 56.5 117.6 139.2 1978 46.7 1575.5 63.7 130.9 165.5 1979 50.6 1759.1 61.6 129.8 203.3 1980 50.1 1994.2 58.9 128.0 219.6 1981 51.7 2258.166.4141.0221.61982表14.数据处理:数据可以直接应用于实验,不需要做其他处理。
多重共线性的四种检验方法

多重共线性的四种检验方法1. 协方差矩阵检验协方差矩阵检验是通过计算变量之间的协方差来检测变量之间是否存在多重共线性的一种方法。
当变量之间的协方差较大时,可以推断出变量之间存在多重共线性的可能。
另外,协方差矩阵检验还可以用来检测变量之间的相关性,以及变量之间的线性关系。
2. 因子分析检验因子分析检验是一种检验多重共线性的方法,它检验变量之间是否存在共同的共线性因子。
它通过对变量之间的相关性进行分析,以及对变量的因子负载度进行检验,来确定变量之间是否存在多重共线性。
因子分析检验可以帮助研究者识别变量之间的共同共线性因子,从而更好地理解数据的结构。
3. 相关系数检验相关系数检验是一种检验多重共线性的方法,它可以检测自变量之间的相关性。
它通过计算自变量之间的相关系数来检验,如果相关系数的绝对值较大,则可以认为存在多重共线性。
此外,相关系数检验还可以检测自变量与因变量之间的相关性,如果自变量与因变量之间的相关系数较大,则可以认为存在多重共线性。
方差分析检验:方差分析检验是一种检验多重共线性的有效方法,它可以用来检测自变量之间的关系。
它的思想是,如果自变量之间存在多重共线性,那么它们的方差应该会受到影响,而且这种影响会反映在回归系数上。
因此,方差分析检验的基本思想是,如果自变量之间存在多重共线性,那么它们的方差应该会受到影响,而且这种影响会反映在回归系数上。
为了检验这一点,可以使用方差分析检验,它可以用来检测自变量之间是否存在多重共线性。
5. 回归分析检验回归分析检验是一种用于检测多重共线性的方法,它可以用来确定变量之间是否存在多重共线性。
回归分析检验是通过比较模型的R-平方值和调整后的R-平方值来确定多重共线性存在的程度。
如果调整后的R-平方值明显低于R-平方值,则表明多重共线性存在。
另外,可以通过观察模型的拟合度来检测多重共线性。
如果拟合度较低,则可能存在多重共线性。
实验六 多重共线性
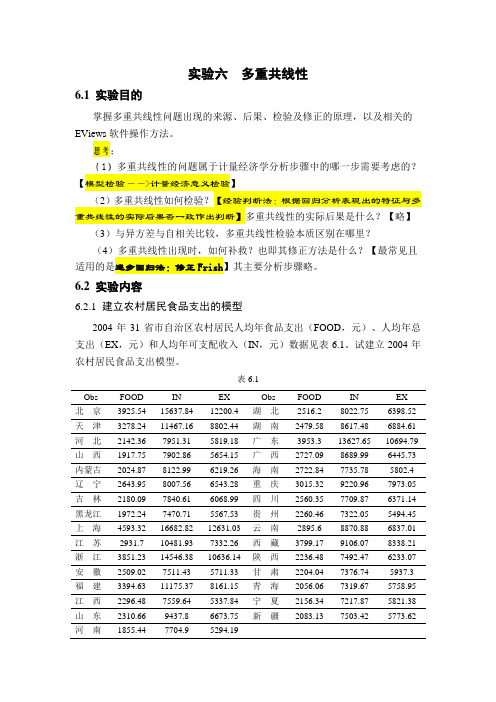
实验六多重共线性6.1 实验目的掌握多重共线性问题出现的来源、后果、检验及修正的原理,以及相关的EViews软件操作方法。
思考:(1)多重共线性的问题属于计量经济学分析步骤中的哪一步需要考虑的?【模型检验——>计量经济意义检验】(2)多重共线性如何检验?【经验判断法:根据回归分析表现出的特征与多重共线性的实际后果否一致作出判断】多重共线性的实际后果是什么?【略】(3)与异方差与自相关比较,多重共线性检验本质区别在哪里?(4)多重共线性出现时,如何补救?也即其修正方法是什么?【最常见且适用的是逐步回归法:修正Frish】其主要分析步骤略。
6.2 实验内容6.2.1 建立农村居民食品支出的模型2004年31省市自治区农村居民人均年食品支出(FOOD,元)、人均年总支出(EX,元)和人均年可支配收入(IN,元)数据见表6.1。
试建立2004年农村居民食品支出模型。
表6.1Obs FOOD IN EX Obs FOOD IN EX北京3925.54 15637.84 12200.4 湖北2516.2 8022.75 6398.52 天津3278.24 11467.16 8802.44 湖南2479.58 8617.48 6884.61 河北2142.36 7951.31 5819.18 广东3953.3 13627.65 10694.79 山西1917.75 7902.86 5654.15 广西2727.09 8689.99 6445.73 内蒙古2024.87 8122.99 6219.26 海南2722.84 7735.78 5802.4 辽宁2643.95 8007.56 6543.28 重庆3015.32 9220.96 7973.05 吉林2180.09 7840.61 6068.99 四川2560.35 7709.87 6371.14 黑龙江1972.24 7470.71 5567.53 贵州2260.46 7322.05 5494.45 上海4593.32 16682.82 12631.03 云南2895.6 8870.88 6837.01 江苏2931.7 10481.93 7332.26 西藏3799.17 9106.07 8338.21 浙江3851.23 14546.38 10636.14 陕西2236.48 7492.47 6233.07 安徽2509.02 7511.43 5711.33 甘肃2204.04 7376.74 5937.3 福建3394.63 11175.37 8161.15 青海2056.06 7319.67 5758.95 江西2296.48 7559.64 5337.84 宁夏2156.34 7217.87 5821.38 山东2310.66 9437.8 6673.75 新疆2083.13 7503.42 5773.62 河南1855.44 7704.9 5294.19资料来源:2005年中国统计年鉴,中国统计出版社6.2.2 建立中国私人轿车拥有量模型考虑到目前农村家庭购买私人轿车的现象还很少,在建立中国私人轿车拥有量模型时,主要考虑如下因素:(1)城镇居民家庭人均可支配收入;(2)城镇总人口;(3)轿车产量;(4)公路交通完善程度;(5)轿车价格。
多重共线性(统计累赘)的概念、特征及其测量方式和处理方式

试述多重共线性(统计累赘)的概念、特征及其测量方式和处理方式。
1、概念多重共线性是指自变量之间存在线性相关关。
倘若其中两个自变项的关系特别强,则在相互控制后就会使每者的效果减弱,而其他的变相的效果就会因此而增大。
2、特征3、产生原因产生多重相关性的原因主要包括四方面。
一是没有足够多的样本数据; 二是选取的自变量之间客观上就有共线性的关系; 还可能由其它因素导致, 如数据采集所用的方法, 模型设定, 一个过度决定的模型等。
但多数研究者认为共线性本质上是由于样本数据不足引起的。
4、测量方式(1)经验式的诊断方法通过观察,得到一些多重相关性严重存在的迹象。
①在自变量的简单相关系数矩阵中,有某些自变量的相关系数值较大。
②回归系数的代数符号与专业知识或一般经验相反;或者该自变量与因变量的简单相关系数符号相反。
③对重要自变量的回归系数进行t 检验,其结果不显著。
特别是当F 检验能在高精度下通过,测定系数R 2的值也很大,但自变量的t 检验却全都不显著,这时多重相关性的可能将会很大。
④如果增加或删除一个变量,或者增加或删除一个观测值,回归系数发生了明显的变化。
⑤重要自变量的回归系数置信区别明显过大。
⑥在自变量中,某一个自变量是另一部分自变量的完全或近似完全的线性组合。
⑦对于一般的观测数据,如果样本点的个数过少,比如接近于变量的个数或者少于变量的个数,样本数据中的多重相关性就会经常存在。
(2)统计检验方法共线性的诊断方法是基于对自变量的观测数据构成的矩阵X ’X 进行分析,使用各种反映自变量间相关性的指标。
共线性诊断常用的统计量有方差膨胀因子VIF 或容限TOL 、条件指数和方差比例等。
方差膨胀因子VIF 是指回归系数的估计量由于自变量的共线性使其方差增加的一个相对度量。
对于第i 个回归系数,它的方差膨胀因子定义为:VIF=1/1-R 2=1/TOL i 其中R2i 是自变量Xi 对模型中其余自变量线性回归模型的R 平方。
多重共线性解决方法
多重共线性解决方法
多重共线性是指在回归模型中,自变量之间存在高度相关性的情况,这会导致模型的解释能力下降,系数估计不准确,模型的稳定性受到影响。
以下是一些解决多重共线性问题的方法:
1.增加样本量:通过增加样本量可以减少模型中的抽样误差,从而减轻多重共线性的影响。
2.删除冗余变量:通过剔除高度相关的自变量,可以降低共线性的程度。
可以使用相关性矩阵或者变量膨胀因子(VIF)来判断哪些自变量之间存在高相关性,并选择保留一个或几个相关性较为弱的变量。
3.主成分分析(PCA):主成分分析可以将高度相关的自变量转换成一组无关的主成分,从而降低共线性的影响。
可以选择保留其中的几个主成分作为新的自变量,代替原始的自变量。
4.岭回归(Ridge Regression):岭回归是在普通最小二乘法的基础上加入一个正则化项,通过缩小系数估计的幅度,减少共线性对系数估计的影响。
岭回归可以通过交叉验证选择合适的正则化参数。
5.套索回归(Lasso Regression):套索回归也是在普通最小二乘法的基础上加入一个正则化项,不同的是套索回归使用L1范数作为正则化项,可以将一些系
数估计缩减为零,从而实现变量选择的效果。
6.弹性网回归(Elastic Net Regression):弹性网回归是岭回归和套索回归的结合,同时使用L1和L2范数作为正则化项,可以在预测准确性和变量选择之间进行权衡。
以上方法可以根据具体问题的特点和需求选择合适的方法来解决多重共线性问题。
多重共线性名词解释
多重共线性名词解释多重共线性多重共线性,是指同一条曲线在不同时期反映了同一经济行为。
从外部看来,这些具有相同特征或因素的影响在不同的经济行为中是互不相关的。
但是,这些事物之间却存在着内在联系:外在表象或因素之间存在的线性关系可以用一个概念进行解释,就是说,事物在不同时期的不同影响因素是有机整体。
从更广泛的意义上说,每一个影响因素都具有相同的行为,并且,与其他影响因素有机地结合起来,构成一个统一的模式,而该模式又反过来对另一类型的影响因素产生决定性的影响。
11、地方政府支出变动; 12、总统选举(赢者通吃); 13、结构变迁,也叫结构演化; 14、创新系统; 15、全球化; 16、文化遗产。
2、现代主义的城市设计理念,将都市视为由“住宅区—商业区—工业区”三部分组成的体系。
3、城市设计必须考虑城市空间的问题,即研究如何使人们的生活活动与各种建筑要素、城市的生态环境之间保持协调和融洽,从而达到舒适、安全、健康、卫生和高效率的目的。
4、城市形象是城市的面子。
5、美国城市设计师查尔斯·罗奇(Charles Lorich)最早提出这个概念,认为当代城市不仅需要考虑功能、技术和经济的问题,而且还应考虑空间和社会层面的问题。
6、区域化导致市场分割。
7、超大城市化正在发展。
8、现代主义强调标准化、简约化和功能性,注重形式逻辑、数字技术和系统分析,因此在城市设计领域颇受推崇。
9、我国正处于城镇化快速发展阶段。
10、“城乡规划是一门为公众利益服务的艺术。
”6、区域化导致市场分割,尤其在资本积累时期。
城市边缘化现象严重。
7、目前的城市空间扩张伴随着高成本、高风险和高消耗。
8、现代主义空间追求便捷、开放和轻松。
9、城市结构理论的发展与新城市主义思潮的兴起。
10、美国城市设计师查尔斯·罗奇(Charles Lorich)最早提出这个概念,认为当代城市不仅需要考虑功能、技术和经济的问题,而且还应考虑空间和社会层面的问题。
多重共线性
比如对于两个解释变量的模型
Yi 1 X 1i 2 X 2i ui
根据我们前面的讨论,参数的最小二乘估计为:
ˆ 1
2 ( yi x1i )( x2 i ) ( yi x2 i )( x1i x2 i ) 2 2 ( x12i )( x2 ) ( x x ) 1i 2i i
R 2 0.8101 ˆ , ˆ ) 0.00868 cov( 1 2
12 0.5523
df 2
ˆ 在单侧t检验的显著水平10%是显著的(1.886)。 1
第二组数据的回归结果
ˆ 1.2108 Y i se (0.7480) t (1.6187) 0.4014 X 1i (0.2721) (1.4752) 0.0270 X 2i (0.1252) (0.2158)
多重共线性
南开大学数学科学学院 白晓棠
多重共线性
在经典的线性回归模型中,我们假定回归模型中诸回归元 之间无多重共线性。
在本节中我们将放松此要求从而来研究: 1、什么是多重共线性? 2、它会引起什么样的后果? 3、怎样去发现它? 4、我们可以采取哪些补救措施来缓解多重共线性的问 题?
第一组数据
Y 1 2 3 4 5
X1 2 0 4 6 8
X2 4 2 12 0 16
第二组数据
Y 1 2 3 4 5
X1 2 0 4 6 8Leabharlann X2 4 2 0 12 16
第一组数据的回归结果
ˆ 1.1939 Y i se (0.7737) t (1.5431) 0.4463 X 1i (0.1848) (2.4151) 0.0030 X 2i (0.0851) (0.0358)
多重共线性问题的几种解决方法【最新】
多重共线性问题的几种解决方法在多元线性回归模型经典假设中,其重要假定之一是回归模型的解释变量之间不存在线性关系,也就是说,解释变量X1,X2,……,X k中的任何一个都不能是其他解释变量的线性组合。
如果违背这一假定,即线性回归模型中某一个解释变量与其他解释变量间存在线性关系,就称线性回归模型中存在多重共线性。
多重共线性违背了解释变量间不相关的古典假设,将给普通最小二乘法带来严重后果。
这里,我们总结了8个处理多重共线性问题的可用方法,大家在遇到多重共线性问题时可作参考:1、保留重要解释变量,去掉次要或可替代解释变量2、用相对数变量替代绝对数变量3、差分法4、逐步回归分析5、主成份分析6、偏最小二乘回归7、岭回归8、增加样本容量这次我们主要研究逐步回归分析方法是如何处理多重共线性问题的。
逐步回归分析方法的基本思想是通过相关系数r、拟合优度R2和标准误差三个方面综合判断一系列回归方程的优劣,从而得到最优回归方程。
具体方法分为两步:第一步,先将被解释变量y对每个解释变量作简单回归:对每一个回归方程进行统计检验分析(相关系数r、拟合优度R2和标准误差),并结合经济理论分析选出最优回归方程,也称为基本回归方程。
第二步,将其他解释变量逐一引入到基本回归方程中,建立一系列回归方程,根据每个新加的解释变量的标准差和复相关系数来考察其对每个回归系数的影响,一般根据如下标准进行分类判别:1.如果新引进的解释变量使R2得到提高,而其他参数回归系数在统计上和经济理论上仍然合理,则认为这个新引入的变量对回归模型是有利的,可以作为解释变量予以保留。
2.如果新引进的解释变量对R2改进不明显,对其他回归系数也没有多大影响,则不必保留在回归模型中。
3.如果新引进的解释变量不仅改变了R2,而且对其他回归系数的数值或符号具有明显影响,则认为该解释变量为不利变量,引进后会使回归模型出现多重共线性问题。
不利变量未必是多余的,如果它可能对被解释变量是不可缺少的,则不能简单舍弃,而是应研究改善模型的形式,寻找更符合实际的模型,重新进行估计。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第6章 多重共线性本章专门讨论古典假设中无多重共线性假定被违反的情况,主要内容包括多重共线性的概念、产生的原因和表现、产生的后果、多重共线性的检验方法及无多重共线性假定违反后的解决方法。
6.1多重共线性的概念在第三章的多元线性回归模型的建立中,强调了无多重共线性,即假定各解释变量之间不存在线性关系,或者各解释变量的观测值之间线性无关。
计量经济学中的多重共线性是指模型中各解释变量的线性关系,它不仅包括解释变量之间精确的线性关系,还包括解释变量之间近似的线性关系,因此多重共线性也就表现为完全多重共线性和近似多重共线性。
6.1.1完全多重共线性从数学意义上去说明多重共线性,就是对于解释变量k X 、、X X 32,如果存在不全为0的数k λλλ,2,1 ,能使得n ,2, ,1i033221 ==++++kik iiXXXλλλλ ( 6.1.1 )则称解释变量k X X X ,,,32 之间存在着完全的多重共线性 用矩阵表示,解释变量的数据矩阵为:X=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡kn nnk k X XXX XXXX X322322213121111(6.1.2) 当矩阵X 的秩小于k 时,表明其中至少有一个列向量可以用其余的列向量线性表示,则说明存在完全多重共线性。
6.1.2不完全的多重共线性在实际经济问题中,完全的多重共线性并不多见。
比较常见的是解释变量kXX X ,,,32 之间存在不完全的多重共线性。
所谓不完全的多重共线性,是指对于解释变量k X 、、X X 32,存在不全为0的数k λλλ,2,1 ,使得 n ,2, ,1i033221 ==+++++i kik iiu XXXλλλλ (6.1.3)其中,i u 为随机变量。
这表明解释变量k X 、、X X 32存在一种近似的线性关系。
如果k 个解释变量之间不存在完全或不完全的线性关系,则称无多重共线性①。
若用矩阵表示,这时X 为满秩矩阵,即Rank(X)=k 。
总之,回归模型中解释变量的关系用相关系数表示出来有三种情形:①0=j x i x r ,解释变量间不存在线性关系,变量间相互正交。
这时不需要作多元回归,可以通过Y 对X j 的多个一元回归来估计每个参数值βj 。
②1=j x i x r ,解释变量间存在完全共线性。
此时模型参数将无法估计。
当两变量按同一方式①解释变量之间不存在线性关系,并非不存在非线性关系,当解释变量存在非线性关系时,并不违反无多重共线性假定。
变化时,要区别每个解释变量对被解释变量的影响程度非常困难。
③10<<j x i x r ,解释变量间存在不同程度的线性关系。
随着共线性程度的加强,会对参数估计值的准确性、稳定性带来不同的影响。
因此分析多重共线性的程度是研究的重点问题。
6.2实际经济问题中的多重共线性在实际经济问题中,多重共线性的产生主要是由于经济现象变化的多个影响因素之间存在一定的相关性。
主要表现为以下几种情形: 1)经济变量之间具有共同变化趋势在时间序列中,反映经济总体状况的数据指标会出现同样的变化趋势。
例如,收入水平、消费水平和就业率在经济繁荣时期均呈现增长的趋势,而在经济衰退期都出现下降。
当这些变量同时作为模型中的解释变量时就会产生多重共线性。
2)滞后变量的引入在经济计量模型中,往往需要引入滞后变量来反映真实的经济状况。
例如,消费水平与人们的当期收入和前期收入密切相关,在建立模型时,就需要引入,,21--t t XX等多个滞后变量,它们与X 变量之间存在高度相关性,因此导致出现多重共线性。
3)截面数据的使用利用截面数据建模时,许多变量变化与发展规模相关,会呈现出共同增长的趋势,例如资本、劳动力、能源等投入与产出的规模相关,这时容易出现多重共线性。
有时如果部分因素的变化与另一部分因素的变化相关程度较高时,也容易出现共线性。
如钢铁产量与原材料用量、劳动力人数、厂房面积、生产投入资金建立回归模型,发现回归效果较差,原因是生产投入资金的影响已经通过原材料和劳动力两个因素体现出来,三者之间存在较严重的多重共线性。
4)样本资料自身的限制抽样选取的样本只是总体解释变量取值中的一个有限范围,会使得变量的变异不大;由于总体受限,多个解释变量的样本数据之间存在相关关系,也会造成样本的多重共线性;另外,客观上完全符合理论模型所要求的样本数据较难收集,也会使得特定样本存在某种程度的共线性。
这一点在时间序列数据模型中表现更加明显。
6.3多重共线性问题的后果6.3.1完全多重共线性下产生的后果 1)参数的估计值不存在完全共线性时,X 矩阵的秩小于k ,此时0='X X ,正规方程组的解不惟一,()1-'X X 不存在,回归参数的最小二乘估计表达式不成立。
例如,在两个解释变量的回归模型i iii u XXY +++=33221βββ中,假定iX2与iX3之间存在完全多重共线性,即iiXX32λ=,λ是一个非零常数,则有:()()()()()()()00ˆ2332232323332332=--=∑∑∑∑∑∑∑ii i i i iiiiiix x x x x xx y x x y λλλλβ (6.3.1)()()()()()()()0ˆ22322323223323233=--=∑∑∑∑∑∑∑ii iii i i i i x x x x x y x x y λλλλλβ (6.3.2)这说明当iiXX32λ=时,参数的估计值是不确定的。
例6.1:用商品价格和每周收入作某一商品需求量的回归分析表6.1Y(需求量)X2(价格)X3(每周收入) X4(每周收益)491 298 297.5 452 296 294.9 443 294 293.5 39 4 292 292.8 38 5 290 290.2 376 288 289.7 34 7 286 285.8 33 8 284 284.6 309 282 281.1 2910280278.8点击proc —make equation ,弹出如图6.1所示的对话框图6.1由此可见无法对Y 进行回归拟合,分析后发现这是因为iiXX122300-=,()122==rR,也就是说收入变量与价格变量完全线性相关,二者存在完全多重共线性。
2)参数估计值的方差无限大对两个解释变量的回归模型进行OLS 估计,其参数的方差为21V a r-C o v ()=()σ-'^βX X,在完全共线性情况下,iiXX32λ=,则有∞==-=-=∑∑∑∑∑∑∑∑∑2232233232322322322322232^)()())(()(σσλλσβx x x x x x x x x x x Var (6.3.3)同理 ∞==-=∑∑∑∑∑2222233232322323^)())(()(σσλλλβx x x x x x Var (6.3.4)这表明,当解释变量之间存在完全的共线性时,参数估计值的方差将变成无穷大。
这直接导致模型总体参数的置信区间变大,使回归方程的可决系数2R 很高,但对各个参数单独的 t 检验却可能不显著,甚至可能使估计的回归系数符号相反,得出完全错误的结论,从而使普通最小二乘估计量的精确度降低,使变量的显著性检验失败。
6.3.2不完全多重共线性下产生的后果在实际经济问题中,解释变量之间往往存在不完全共线性,在这种情况下,通过回归可以得到参数的估计值。
在例6.1中,作X2,X4对被解释变量Y 的回归方程,结果如图6.2所示:图6.2从理论上说,在接近共线性的情形下仍能进行最小二乘估计,而且该估计量是无偏的,能满足最小二乘估计量的最小方差性,但是实际上,共线性的存在对计量经济分析可能会产生一系列的影响。
1)参数估计值的方差增大以两个解释变量的回归模型为例,假设2X与3X存在不完全的共线性,即i i i v x x +=32λ,其中,0≠λ,i v 是满足∑=02i i v x 的随机误差项。
由此可得出OLS 法估计的回归系数:()()()()()()()2232232232233223233ˆ∑∑∑∑∑∑∑∑∑∑-++-+=iiiiiiiiiii i i x x v xx v y x y v xx y λλλλλβ(6.3.5)因此在2X 与3X 近似共线性时,3ˆβ还是可以估计的。
但是,如果2X 与3X 共线程度越高,i v 会充分地小,以至于非常接近于零,此时3ˆβ会愈加趋于不确定。
对于2ˆβ也可推出类似的表达式,并得到类似的结论。
在2X 与3X 为不完全的共线性时,2X 与3X 的相关系数的平方用离差形式可表示为 ∑∑∑=2322232223)(x x x x r可以证明得到22322322232^)())(()(σβ∑∑∑∑-=x x x x x Var()∑-=2232221r x i σ(6.3.6)()()∑-=22323231ˆvar r x i σβ (6.3.7)()()∑∑--=2322223223321ˆ,ˆcov ii x x r r σββ (6.3.8)从(6.3.7)和(6.3.8)式中可以看出,随着共线性增加,23r 趋于1,两个参数估计量的方差也将增大。
同样地,其协方差在绝对值上也会增大。
2)参数的置信区间趋于变大存在多重共线性时,参数估计值的方差增大,其标准误差也增大,导致总体参数的置信区间也随之变大。
同上例,假设方差已知,在置信度为95%的水平下,当23r 取不同的值时,置信区间也会相应发生变化,相关系数越高,3β的置信区间越大。
见表6.2所示:表6.2 增加共线性对3β的95%置信区间()33ˆe 1.96ˆββs ±的影响3)参数估计量经济含义不合理当模型中两个解释变量具有线性相关性,即i i i v x x +=32λ时,ii XX 32和前的参数32ββ和并不反映各自与被解释变量之间的结构关系,而是反映它们对被解释变量的共同影响,因此当二者呈现同方向变化时,无法准确地将二者的影响分离开来,这是估计的参数也失去了原有的经济意义。
4)严重多重共线时,假设检验容易作出错误的判断存在严重多重共线时,参数的置信区间扩大会使得接受一个本应拒绝的假设的概率增大;另外,在对回归系数进行t 检验中,)ˆ(ˆ33ββVar t =,在高度共线性时,参数估计值的方差增加较快,会使得t 值变小,从而容易产生接受原假设的结论。
5)模型的预测功能减弱在给定的置信水平α-1下,0Y 的置信区间为()'01'21XXXXt Y-∧+⨯±α显然,当解释变量之间存在多重共线性时,由于()1'-X X 非常大,所以其置信区间也很大,因此,模型的预测功能会减弱。
6.4多重共线性问题的检验由于多重共线性表现为解释变量之间具有相关关系,所以用于多重共线性的检验方法主要是采用统计方法以下我们采用中国电信业务总量的计量经济模型作为实例分析例6.2: 中国电信业务总量的计量经济模型②②案例来源: 张晓桐,《计量经济学基础(第3版)》,南开大学出版社,2007年9月表6.3年份电信业务总量y 邮政业务总量x1中国人口数x2市镇人口比重x3人均GDPx4人均消费水平x51991 1.5163 0.5275 11.5823 0.2637 1.879 0.896 1992 2.2657 0.6367 11.7171 0.2763 2.287 1.070 1993 3.8245 0.8026 11.8517 0.2814 2.939 1.331 1994 5.9230 0.9589 11.9850 0.2862 3.923 1.746 1995 8.7551 1.1334 12.1121 0.2904 4.854 2.236 1996 12.0875 1.3329 12.2389 0.2937 5.576 2.641 1997 12.6895 1.4434 12.3626 0.2992 6.053 2.834 1998 22.6494 1.6628 12.4810 0.3040 6.307 2.972 1999 31.3238 1.9844 12.5909 0.3089 6.534 3.1431)相关系数检验法相关系数检验法是利用解释变量之间的线性相关程度来判断是否存在严重多重共线性的一种简便方法。
