传感器动态建模的一种辨识法
基于BP神经网络的传感器非线性建模
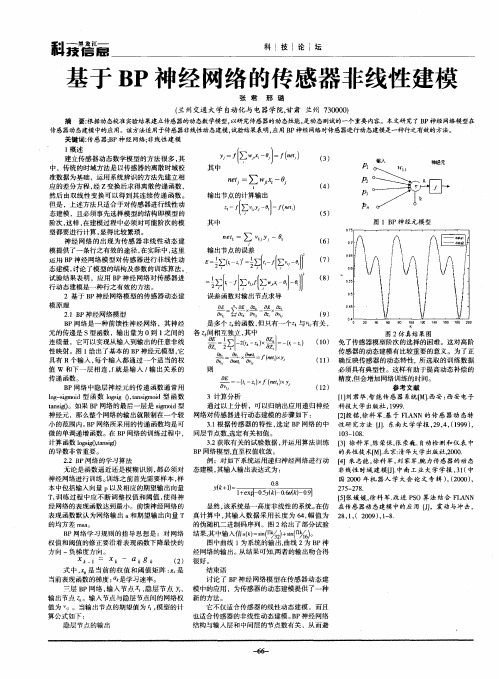
无论是函数逼近还是模 糊识别 , 都必须对 神经网络进行训练 。 训练之前首先需要样本 , 样 J 1 + = ) 丽8 而二 0 . 网 本 中包括输入向量 P以及相应 的期望输 出向量 2 5 7 7 —2 8 T 训练过程中应不断调整权值 和阈值 , , 使得神 【] 5张媛媛, 徐科 军. 改进 P O算 法结合 F A N S LN 经 网络的表现函数达到最小。前馈神经 网络的 显然 , 该系统是一高度非线性 的系统。 在仿 在 传感器动态建模 中的应用 l ,震动与冲击, J 】 表现函数默认为网络输出 a 和期望输 出向量 T 真计算 中 , 其输入 数据采用 长度为 6 , 4 幅值为 2 , , 0 9 , - . 8 1 (2 0 ) 1 8 的均 方 差 m a s。 的 伪 随 机 二进 制 码 序 列 。 图 2给 出 了部 分 试 验 B P网 络 学 习 规 则 的指 导 思 想 是 :对 网 络 结 ,中 人 (=n ) m 果其 输 信“)s“ 2 s ) i ( +( 。 权值和阈值的修正要沿着表现函数下降最快的 图中曲线 1为系统 的输 出, 曲线 2为 B P神 方 向 一负梯度方向。 经 网络的输出。 从结果可知, 两者的输 出吻合得 1 — a tg ( ) 很好。 2 结束语 式 中 , 是 当前的权 值和 阈值 矩阵 g 是 当前表现 函数的梯度 : 是学 习速率 。 讨论了 B P神经 网络模 型在传 感器动态建 j层 B P网络 , 输入节点 , 隐层节点 , 模中的应用 ,为传感器的动态建模提供 了一种 输出节点 。输人节点与隐层节点间的网络权 新 的 方法 。 它不仅适合传感器的线性动态建模 ,而且 值为 v 。当输出节点的期望值为 ‘, 型的计 模 算公式如下 : 也适合传感器的非线性 动态建模 。 P神经网络 B 隐层 节 点 的 输 出 结构与输入层和中问层 的节点数有关 ,从而避
一种非线性动态的传感器建模算法

w a s t a k e n a s t h e o b j e c t f u n c t i o n ,a n d t h e n t a r g e t i n d i v i d u a l s w e r e d e t e r mi n e d b y d y n a mi c a n d s t o c h a s t i c e x t r a c t i o n
ABS TRACT: T h e p a p e r p r o p o s e d a n o n l i n e r a s e n s o r d y n a mi c mo d e l i n g a l g o r i t h m f o r t h e r d y n a mi c o f S e n s o r .T h e p a r m e a t e s r o f L S S VM mo d e l we r e c o n s i d e r e d t h e p o s i t i o n v e c t o r o f a n t s w h i l e t h e a c c u r a c y o f s e n s o r d y n m i a c mo d e l
2 .郑州大学软件技术学院 , 河南 郑州 4 5 0 0 0 2 )
摘要 : 针对传感器动态 的非线性 、 动态特性 , 精确建模 比较难 。为此 , 提出一种非 线性 的传感器动态建模 方法。首先将 L S S . V M参数作为蚂蚁的位 置向量 , 传感器动态建模 精度作 为 目 标 函数 , 然后 采用动 态随机抽取 的方法来确定 目标个体 引导蚁 群进行全局搜索 , 并在最优蚂蚁邻域 内进行小步长局部搜索 , 找到算法的最优参数 , 最 后建立传感器动 态模 型。结果表 明, A C O— L S S V M所建模型具有较强的实用性 和可靠性 , 为改善传感器动态性 能及在线补偿提供了参考依 据。 关键词 : 传感器 ; 最小二乘支持 向量机 ; 蚁群优化算法 ; 动态建模
动态系统辨识导论与应用

动态系统辨识导论与应用动态系统辨识导论与应用什么是动态系统辨识?动态系统辨识是一种将观测数据与数学模型结合的方法,旨在通过统计分析和计算模拟来揭示系统的内在特性和行为。
通过辨识系统的动态特性和参数,我们可以更好地理解和掌握所研究的系统,进而进行预测、控制和优化的应用。
应用领域工业控制动态系统辨识在工业控制领域有着广泛的应用。
通过对工业过程中的传感器数据进行辨识,可以建立准确的数学模型,从而实现对工业过程的控制和优化。
例如,在化工工艺控制中,通过对反应控制器传感器数据的辨识,可以建立准确的反应动态模型,从而优化反应控制参数,提高反应过程的效率和安全性。
经济系统建模动态系统辨识在经济学中也有着重要的应用。
通过对经济变量的观测数据进行辨识,可以建立经济系统的数学模型,用于预测和分析经济变量的走势。
例如,在宏观经济领域,通过对国家经济指标的辨识,可以建立宏观经济系统的动态模型,用于预测和制定经济政策。
生物医学动态系统辨识在生物医学领域也有着广泛的应用。
通过对生物体内传感器数据的辨识,可以建立生物体的动态模型,用于分析和预测生物体的生理过程。
例如,在心脏病研究中,通过对心电图传感器数据的辨识,可以建立心脏的动态模型,从而提供心脏病的早期预警和诊断方法。
环境监测动态系统辨识在环境监测领域也有着重要的应用。
通过对环境传感器数据的辨识,可以建立环境系统的动态模型,用于监测和预测环境变化。
例如,在气象预测中,通过对气象传感器数据的辨识,可以建立气象系统的动态模型,用于准确预测未来的天气变化。
总结动态系统辨识在工业控制、经济学、生物医学和环境监测等领域都有着重要的应用。
通过对观测数据的辨识,可以建立准确的数学模型,从而实现对系统的控制、预测和优化。
动态系统辨识的研究和应用不仅能够推动科学的发展,也有着广阔的应用前景。
交通运输动态系统辨识在交通运输领域也有着广泛的应用。
通过对交通传感器数据的辨识,可以建立交通系统的动态模型,用于优化交通流量和减少拥堵。
机械系统的动态建模与参数辨识

机械系统的动态建模与参数辨识机械系统是指由各种机械元件组成的系统,如齿轮传动、弹簧系统等。
为了对机械系统进行分析和控制,我们需要对其进行动态建模和参数辨识。
动态建模是指通过数学模型来描述机械系统的运动规律。
首先,我们需要明确机械系统的输入和输出变量。
输入变量通常是外部施加的力、力矩或位移,而输出变量则是系统的状态或响应。
其次,我们可以根据机械系统的特性和工作原理选择合适的数学模型,如微分方程、差分方程或状态空间模型等。
最后,利用物理原理和运动学关系,我们可以建立起机械系统的动态模型。
在动态建模的过程中,参数辨识起着重要的作用。
参数辨识是指通过实验或数据分析,对机械系统中的参数进行估计和辨识。
由于机械系统中的参数通常很难直接测量或获取,我们需要借助于辨识方法来对这些参数进行估计。
常见的参数辨识方法包括最小二乘法、极大似然法等。
参数辨识的过程可以分为离线辨识和在线辨识。
离线辨识是指在事先收集好的实验数据基础上进行参数辨识,而在线辨识则是指在系统运行过程中不断对参数进行更新和辨识。
无论是离线辨识还是在线辨识,我们都需要选择合适的辨识算法和模型结构。
辨识算法的选择通常需要考虑辨识误差、计算复杂度和辨识时间等因素。
而模型结构的选择则需要结合机械系统的特性和实际需求。
机械系统的动态建模和参数辨识对于机械工程领域具有重要意义。
通过建立准确的数学模型,我们可以深入理解机械系统的工作原理和运动规律,为系统分析和控制提供有力支持。
同时,通过参数辨识,我们可以对机械系统的参数进行精确估计,为系统设计和优化提供依据。
然而,机械系统的动态建模和参数辨识也存在一些挑战和限制。
首先,机械系统的运动规律通常是非线性的,因此需要采用适当的非线性模型和辨识方法。
其次,机械系统中存在着各种不确定因素,如摩擦、载荷变化等,这些因素会对参数辨识的准确性和稳定性造成影响。
此外,由于机械系统的复杂性和多样性,动态建模和参数辨识的过程也需要一定的专业知识和经验。
基于MATLAB的传感器动态数学模型辨识系统

定 的 辨 识 算 法 确 定模 型 结 构 参 数 ,对 差 分 方 程 形 函数 s u : 成 多个 A tc 生 r RX模 型 结 构 参 数 , 以进
式的模型结构类 , 是要辨识 阶次和纯时延 。 就
2 MA AB系统 辨识 工具 箱 的主 要 函数 TL
( )数 据 预 处 理 1
其 目的 是 为 了提 高 辨 识 的精 度 。
函数 drn : 除 观 测 数 据 中 的 趋 势 项 。 t d消 e
函 数 if t di :计 算 相 应 的 B t r r l ut Wo h滤 波 器 参 e t 数 , 输 入 输 出数 据 进 行 滤 波 , 除 高 频 成 分 。 对 剔
中 图 分 类 号 : P 1 T37 文 献 识 别 码 : B
1 引 言
在 测 控 系统 中 ,最 重 要 的 部 件 是 传 感 器 。 为 了
形 式 完 全 相 同 ,不需 要 按 传 统 的方 法 重 新 编 程 。 由 于 使 用 MA L T AB编 程 运 算 的过 程 与 人 进 行 科 学 计 算 的思 路 和表 达 方 式 完 全 一 致 ,所 以 使用 者 很 快 就 能 够 初 步 掌 握 MA L B的 基 本 用 法 ,并 利 用 MA . TA T L B进 行 高 效 和 富有 创 造 性 的计 算 。 A
种 功 能 强 , 率 高 , 于进 行 科 学 和 工 程 计 算 的 交互 效 便 式 软件 包 ,采 用 直 译 式 语 言 进 行 编 程 。其 中 的功 能 模 块 包 括 : 般 数 值 分 析 、 阵运 算 、 字 信 号 处 理 、 一 矩 数 建模 和 系 统 控 制 、 化 设 计 、 经 网络 控 制 等 应 用 程 优 神 序 , 将 上 述 功 能 模 块 进 行 了集 成 。 在集 成 环 境 下 , 并 求 解 问 题 的 MA L B语 言 表 述 形 式 与 其 数 学 表 达 TA
基于SVM的传感器动态模型辩识方法

关键词 : 支持 向量机 ; 动态模 型; 传感器 ; 模型辩识
\ .colfIs u et c ne HeeU i r t cnl y Hee200 , hn 2Shoo t m n Si c, fi nv s y fthoo , f 309 C i nr e ei o e g i a
}
Ab ta t Th s p p rp e e t e m e h d f rd n m i mo e e tfc t n o e s r ,a d g v st e c r sr c : i a e r s n s a n w t o o y a c d l d n iia i f n o s n i e h o — i o s
W U ih i ,W a g Xi o h n De — u n a —o g
1C l g fEl to i E gneig,Juin nvri J uin mn  ̄ 32 0 ,C ia! . ol e e o e rnc n iern c ija gU iest y, ija gJ g 3 05 hn 、 /
rt m o v r s m a h n e r i g i t u d a i r g a ih c n e t c i e la n n n o q a r t p o r mm i g S m u a i n n x e i e t l r s l h w c n . i lt s a d e p r o m n a e u t s o s
维普资讯
第1 卷 9
第3 期
传 感 技 术 学 报
A nI 10 S A 1R
v0 . 9 No 3 11 .
2 0 ‘ 6月 0 6年
J n 2 0 u .06
无线传感器网络的时空动态建模与预测技术

无线传感器网络的时空动态建模与预测技术无线传感器网络(Wireless Sensor Network,WSN)是一种由大量分布在空间中的无线传感器节点组成的网络系统,用于采集、处理和传输环境信息。
WSN已广泛应用于环境监测、智能交通、农业、医疗等领域。
在这些应用中,时空动态建模与预测技术起着重要的作用。
本文将探讨WSN的时空动态建模与预测技术的原理、方法和应用。
一、时空动态建模技术时空动态建模是指根据WSN采集到的环境信息,对环境的时空变化进行建模和描述的过程。
时空动态建模技术可以帮助我们理解环境的演化规律,预测未来的变化趋势。
1. 数据采集与处理WSN通过传感器节点采集环境信息,如温度、湿度、光照等。
传感器节点将采集到的数据传输到基站或其他节点进行处理。
数据采集与处理是时空动态建模的基础,准确的数据采集和有效的数据处理能够提高建模的精度和效率。
2. 空间建模空间建模是将WSN采集到的环境信息在空间维度上进行建模和描述。
常用的空间建模方法包括插值法、克里金法等。
插值法通过已知点的观测值推断未知点的值,克里金法则通过对已知点的空间相关性进行建模来估计未知点的值。
空间建模可以帮助我们了解环境的空间分布规律,预测未来的空间变化趋势。
3. 时间建模时间建模是将WSN采集到的环境信息在时间维度上进行建模和描述。
常用的时间建模方法包括时间序列分析、回归分析等。
时间序列分析通过对时间序列数据的统计特性进行建模,来预测未来的变化趋势。
回归分析则通过建立环境变量与时间的函数关系来预测未来的变化趋势。
时间建模可以帮助我们了解环境的时间演化规律,预测未来的时间变化趋势。
二、时空动态预测技术时空动态预测是指根据WSN建模的结果,对未来的时空变化进行预测的过程。
时空动态预测技术可以帮助我们做出准确的决策,优化资源配置。
1. 预测模型建立预测模型建立是时空动态预测的关键步骤。
根据WSN建模的结果,可以选择合适的预测模型进行建立。
基于预测误差法的加速度传感器动态模型参数辨识

p e n s a t i o n .F o r t h e p a r a me t e r i d e n t i i f c a t i o n o f d y n a m i c mo d e l o f t h e a c c e l e r a t i o n s e n s o r ,a p a r a me t e r i d e n t i i f c a t i o n me t h o d u s i n g t h e p r e d i c — t i o n e r T o r me t h o d f o r t h e a c c e l e r a t i o n s e n s o r d y n a mi c mo de l i s p r o p o s e d .T h e me t h o d b u i l d s a l i n e r a a u t o r e g r e s s i v e mo v i n g a v e r a g e w i t h e x -
e x pr e s s i o n. Fi n a l l y,i t c a n a c hi e v e o p t i ma l p ra a m e t e r s o f t he a c c e l e r a t i o n s e n s o r d y n m i a c mo de l b y s o l v i n g t he s y s t e m o p t i ma l s t e p p r e d i c —
中 图分 类 号 : T H 8 2 4 文 献标 识 码 : A 国 家标 准 学 科 分 类 代 码 : 4 6 0 . 4 0 2 0
Dy na mi c mo d e l pa r a me t e r i d e n t i ic f a t i o n o f t h e a c c e l e r a t i o n s e ns o r ba s e d o n t he pr e d i c t i o n e r r o r me t h o d
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3. 204 1 # 10- 5
0. 071 34 s2+ 0. 608 1 s+ 0. 937 4 0. 733 9 s4+ 1. 581s 3+ 4. 483 s2+ 5. 007 s+ 1
2. 872 4 # 10- 5
当模型阶次为二阶以上时, 误差均较小, 增加模
型阶次对模型准确度提高影响很小, 可见, 所建模型
仿真实验取传递函数为
G ( s) =
1. 2s 4 +
0. 3s2 + 3. 1s3 +
1. 1s + 1. 5 7. 5s2 + 8. 1s +
1. 6 .
无噪声时辨识结果及误差计算如表 1 所示。
表 1 无噪声阶跃信号不同阶次辨识结果 Tab 1 Identificati on results of step signal i n noise free case
传递函数 G ( s )
误差 !
0. 956 3 4. 672 s+ 1
3. 068 4 # 10- 4
0. 935 8 1. 643 s2+ 4. 334s + 1
7. 838 3 # 10- 5
0. 939 6 0. 506 8 s3+ 1. 477 s2+ 4. 391s + 1
2. 862 5 # 10- 5
本文在研究现有各种建模方法的基础上, 借鉴 线性连续时延过程阶跃响应辨识思想[ 5] , 提出了一
收稿日期: 2003- 08- 18 * 基金项目: 国家自然科学基金资助项目( 50174021)
种基于数值积分的传感器动态建模方法, 该方法先
对所测数据进行积分, 再用辨识方法进行建模, 无需
迭代计算即可直接得出微分方程的系数, 减少转化
+ +
b1s + a1s +
b0 1
.
( 2)
( n)
t
! !! ! 定义
f=
n
[0, t]
00
2f ( 1) d 1 d n,
0
对式( 1) 两侧进行 n 次积分得
!( 1)
any ( t ) +
an- 1
y+
[ 0, t ]
! ! ( n- 1)
( n)
+ a1
y+
y=
[ 0, t]
[ 0, t ]
38
传感器技术( Journal of T ransducer T echnology)
2004 年 第 23 卷 第 1 期
计算与测试
传感器动态建模的一种辨识法*
张 华, 次 英, 谢 植
( 东北大学 信息科学与工程学院, 辽宁 沈阳 110004)
摘 要 : 提出一 种简单但鲁棒性强的传感器动态建模方法, 该方法基 于数值积分思想, 能有效克服测量 噪
an
dny ( t ) d tn
+
a n-
1
dn- 1 y ( t d tn- 1
)
+
a
1
d
y( t dt
)
+
y ( t)
=
bm
dmu ( t ) dtm
+
bm- 1
dm- 1 u ( t ) dt m- 1
+
+
b1
du( t) dt
+
b0u( t ),
( 1)
式中 u ( t ) 为输入量; y ( t ) 为输出量; m < n; a0,
- 0. 276 5 s+ 0. 938 7 0. 218 4s 2+ 4. 084 s+ 1
6. 678 2 # 10- 5
- 0. 178 6 s+ 0. 939 2 0. 177 8s 3+ 0. 659 3s 2+ 4. 196 s+ 1
5. 708 9 # 10- 5
0. 788 7 s+ 0. 937 3 0. 709 6 s4+ 1. 529s 3+ 5. 254 s2+ 5. 197 s+ 1
声, 无需迭代即可直接从微分方程辨 识出模 型参数, 所建 模型阶 次较低、准 确度 较高, 且较 易实现 递推 算 法, 为传感器改善动态特性、实现动态补偿提供一种有效方法。大量实验和仿真结果验证了该方法的有 效 性。
关键词: 传感器; 动态建模; 辨识; 积分
中图分类号: T P212
文献标识码 : A
! 7. 838 3 # 10- 5
0. 001 2
10
0. 950 63; 1
0. 004 8
30
0. 986 6 1. 318 s2+ 5. 388s + 1
0. 040 9
50
1. 004 0. 155 s2+ 5. 506s + 1
0. 116 7
70
1. 095 1. 642 s2+ 7. 237s + 1
Abstract: A simple and very robust met hod is proposed for sensors dynamic modeling . Based on numerical inte gr als, the model parameters are estimated from the differential equation without iterations, the method is very effective in overcoming large amounts of measurement noise in the output. T he model s order built by this method is lower and the accuracy is hig her. A n effectiv e met hod is proposed for improving sensors dynamic char acter istics and realizing sensors dynamic compensation. T he effectiveness of the identification method has been demonstrated throug h a number of simulations and tests. Key words: sensor ; dynamic modeling; identification; integrals
准确度较高、阶次较低。
通常, 传感器模型可近似为二阶线性系统, 故本
文仅以此为例分析其抗噪声能力。对上述传递函数 施加不同信噪比 R SN [ 5] 零均值正态分布的随机噪 声, R SN = 90% 的仿真曲线如图 1 所示。
图 1 阶跃信号( R SN= 90 %) 辨识结果 Fig 1 Identificati on resul ts of step signal( R SN= 90 %)
y,
[ 0, t ]
i
! ! ( n- 1)
( n- m)
-
y,
u,
[ 0, t]
[ 0, t i]
,
!( n)
,
u
[ 0, ti ]
.
非奇异, 则由最小二乘法( LS) 可得
最佳估计值为
^ = ( T )-1 TY .
( 5)
对于传感器而言, 测量信号虽经滤波和积分处理, 仍不可避免地存在测量噪声, 假定噪声为零均值且平
0. 248 1
90
0. 947 5 0. 113 2s 2+ 4. 91 s+ 1
0. 385 6
40
传 感器 技术
第 23 卷
从中可见, 当 R SN ∃ 10% 时, !∃ 0. 004 8, 能很 好满足一般应用场合需求, 可见, 该方法具有较好的 鲁棒性。
图 2 和图 3 分别给出仿真输入为斜坡信号 ( R SN = 50% ) 、正弦信 号( R SN = 50% ) 的辨识 结 果, 可见建模方法对输入信号无特殊要求。
稳随机, 则可采用辅助变量法( IV) 代替最小二乘法。 2 数值仿真
不失一般性, 输入取单位阶跃信号, 则
!( n) u [0, t ]
=
t
n i
n!
.
i
模型误差为
!=
1 N
i
N
∀(
=1
y(
ti)
-
y^ ( ti ) ) 2,
( 6)
其中 y ( ti ) , y^ ( ti ) 分别为实际值与模型计算值。
0引 言 传感器的动态建模是研究其机理、评价其性能
的有效手段, 是改善动态特性、实现动态补偿的重要 依据。目前常用的时域建模方法有[ 1] : 系统辨识方 法[ 2] 、沃尔什变换方法[ 3] 、最大熵谱法、自适应方法 和神经元方法[ 4] 等。其中, 系统辨识建模法应用较 广、发展较成熟; 与之相比, 沃尔什变换法所用数据 较少, 所建模型的阶数低, 可直接得出微分方程的系 数, 减少转化误差, 但不是递推算法, 且对数据个数 要求严格; 最大熵谱法属时间序列分析建模方法, 只 需传感器动态标定中的输出数据, 但它建模的准确 度不高; 在长序列建模中, 自适应方法比最大熵谱法 具有明显的优势; 神经元方法虽然具有所建模型阶 次低、准确度高的优点, 但离现场实际应用还有一段 距离。
图 2 斜坡信号( R SN = 50%) 辨识结果 Fig 2 Identification resul ts of ramp si gnal( R SN = 50%)
