21.4无理方程.ppt
§21.4 无理方程(2)

课堂练习 3: 下列方程中,有实数根的方程是: A、 x − 1 + 4 = 0 ; C、 x = − x ; B、 x + 1 = 0 ;
2
学生:C
D、 x + 2 +
x−2 = 0;
1、含一个“根号”的无理方 程的解法; 2、含两个“根号”的无理方 程的解法.
三、本课小结 通过这节课的学习,你有什么收获?
§21.4 无理方程(2) 21. 无理方程(2)
普陀区课题组
教学目标: 教学目标: 1.会解无理方程,并再次规范解题格式; 2.通过无理方程转化为有理方程,感受化归的数学思想. 教学重点: 教学重点:无理方程的解法. 教学难点 难点: 教学难点:含有两个关于未知数二次根式的无理方程的解法. 教学过程: 教学过程: 教师活动 一、复习引入 复习引入 1、解无理方程的一般步骤是什么? 学生活动 预设: (1) 设计意图
请 2 位同学板演.
及 时 练
3
(1) x − 4 x + 3 = 1 − x ;
2
习,巩固知 识.
(2) x − 2 • (3) x − 7 +
x−3− 2 =0; x = 7。
让学生来 观察和判断 预设: 无理方程有 不能 学生小组交流, 请几位同 无实数根,激 学汇报,并及时的给予评价. 发 学 生 从 另 外的角度来 x + 1 的值是一个非负 分析无理方 数,在加上个 1,和肯定大于 程,使学生养 0,所以原方程没有实数根. 成 良 好 的 观 察和分析习 惯。练习丰富 此方法的适 应类型,让学 生掌握方法, 从而能举一 反三.
x1 = 2, x 2 = 6
这两个解都是原方程的根吗? 经检验, x = 2 是原方程的 根; x = 6 是增根,舍去. 所以原方程的根是 x = 2. 适 时 小 结,让学生掌 握规律.
【数学课件】无理方程

最高级的技巧和艺术。——苏霍姆林斯基 5、没有时间教育儿子——就意味着没有时间做人。——(前苏联)苏霍姆林斯基 6、教育不是注满一桶水,而且点燃一把火。——叶芝 7、教育技巧的全部奥秘也就在于如何爱护儿童。——苏霍姆林斯基 8、教育的根是苦的,但其果实是甜的。——亚里士多德 9、教育的目的,是替年轻人的终生自修作准备。——R.M.H. 10、教育的目的在于能让青年人毕生进行自我教育。——哈钦斯 11、教育的实质正是在于克服自己身上的动物本能和发展人所特有的全部本性。——(前苏联)苏霍姆林斯基 12、教育的唯一工作与全部工作可以总结在这一概念之中——道德。——赫尔巴特 13、教育儿童通过周围世界的美,人的关系的美而看到的精神的高尚、善良和诚实,并在此基础上在自己身上确立美的品质。——苏霍姆林斯基 14、教育不在于使人知其所未知,而在于按其所未行而行。——园斯金 15、教育工作中的百分之一的废品,就会使国家遭受严重的损失。——马卡连柯 16、教育技巧的全部诀窍就在于抓住儿童的这种上进心,这种道德上的自勉。要是儿童自己不求上进,不知自勉,任何教育者就都不能在他的身
心就是流淌在班级之池中的水,时刻滋润着学生的心田。——夏丐尊 20、教育不能创造什么,但它能启发儿童创造力以从事于创造工作。——陶行知
一次方程
整式方程
有理方程
代数方程
分式方程
21.4无理方程(分层作业)(5种题型基础练+提升练)解析版

21.4无理方程(5种题型基础练+提升练)题型一:无理方程的概念2.下列方程是无理方程的是().A .20x -=B 9x=C 2=-D 45x +=【答案】D【解析】根据无理方程的概念,方程中含有根式,并且被开方数是含有未知数的代数式的方程叫做无理方程,可知D 是无理方程,故选D .【总结】考查无理方程的概念,方程中根号内含有未知数即可.题型二:不解方程,判断方程是否有实数根2.下列哪个方程有实数解()A 0+=B 30=C 2=D x=-【答案】D【解析】根据二次根式的双重非负性,对A 选项,1x ³³;对B330+³¹,可知方程无实数解;对C 选项,1040x x -³ìí--³î, x 无解,即方程无实数解;故选D .【总结】考查对无理方程解的判断,根据二次根式双重非负性即可进行简单判定.题型三:解无理方程题型四:无理方程的根的讨论一、填空题二、解答题检验:当m =2时,左边=右边;当m =3时,左边≠右边.∴m =2.【点评】本题考查了无理方程,把无理方程转化为整式方程是解题的关键,解无理方程最后要检验.题型五:无理方程的应用1.用一根56厘米的细铁丝弯折成一个直角三角形,使它的一条直角边长为7厘米,求这个直角三角形的另两条边的长度.【答案】24cm 和25cm .【解析】设另外一条直角边长为xcm ,依题意可得756x ++=,解得:24x =,经检验,24x =是原方程的根且符合25cm =,即另两边长分别为24cm 和25cm .【总结】考查直角三角形勾股定理的应用,用周长列式解题,注意应用题也要验根.2.建一块场地,用600块正方形的砖头铺成,如果把场地的面积扩大到原来面积的2倍还多0.6平方米,且正方形的砖头的边长增加10厘米,则需要铺540块方砖,求原场地的面积.【答案】224m .【解析】设原场地的边长为xm ,100.1cm m =,则扩大后场边长为()0.1x m +,依题意得()225400.126000.6x x +=´+,整理得22754520x x --=,解得:115x =,2255x =-(舍),由此得原场地面积为2221600600245x m æö=´=ç÷èø.【总结】考查根据题意找准等量关系列方程解应用题,注意单位的统一.3.如果y 轴上一点P 到两点A (3,5)、B (-1,-2)的距离相等,求P 点的坐标.【答案】29014P æöç÷èø,.【解析】设点()0P x ,=, 平方得22103445x x x x -+=++,解得:2914x =,经检验,2914x =是原方程的根,即29014P æöç÷èø,.【总结】考查利用两点间距离公式确定点的位置问题.一、单选题1.(2022春·上海·八年级校考期中)下列方程中,有实数解的是( )A 10=B .22111x x x =--C 1=D 2=故选:D .【点睛】本题考查了解无理方程,解分式方程和二次根式有意义的条件等知识点,能把解无理方程转化成有理方程和能把分式方程转化成整式方程是解此题的关键.2.(2022春·上海·八年级上海市市西初级中学校考期中)在下列方程中,无实数根的方程有( )40=; 0=; x -;0=; ⑤2240x x -+=; ⑥2236111x x x +=+--.A .2B .3C .4D .5二、填空题3.(2023春·八年级单元测试)有两个正方形纸片,较大纸片的面积比较小纸片的面积大28,较大纸片的边长比较小纸片的边长大2,若设较大纸片的面积为x,按题意可列方程为______.【答案】x1=【分析】方程两边同时平方,得到一个一元二次方程,解出x的值,再进行检验即可得出结果.【详解】解:方程两边同时平方得:()2322x x -=-,∴2210x x -+=,即()210x -=,∴x 1=x 2=1,经检验,x=1是原方程的根,故答案为:x=1.【点睛】本题考查了无理方程求解,先平方得到一元二次方程求解再验证根,掌握基本概念和解法是解题的关键.三、解答题5.(2022春·上海徐汇·八年级统考期末)解方程:2x =.28200--=x x(x-10)(x-2)=0x1=10,x2=-2经检验x=10是原方程的解,∴原方程的解为x=10.【点睛】本题考查无理方程的解法,解题关键是将无理方程转化为有理方程.7.(2022春·上海·1=【答案】点P 在两道路交点上下方【分析】建立平面直角坐标系,直接根据勾股定理列出方程即可求解.【详解】解:以公路n 、m 分别为依题意得()10A ,,()123B ,或()23B -,,设()0P y ,,依题意可得()22212325y y +++-=或()22212325y y ++++=,整理得2112440y y -+=或2112440y y ++=,解得:12y =,2211y =,32y =-,4211y =-,经检验均是原方程的解,但32y =-,4211y =-不符合题意,故舍去,2。
[正式版]无理方程ppt资料
![[正式版]无理方程ppt资料](https://img.taocdn.com/s3/m/808e57e352ea551811a68778.png)
八
方 年
级
程 第
二 学 期
无忧PPT整理发布
一、课前复习
1.解下列方程:
(1)x1 x+3 (2) x 6 2
解无理方程的一般步骤:
开始Biblioteka 去根号 他项放在方程的另一边,然后进行平方,这样求解比较简单.
再整理,这样可以简化解题过程. 思考:不解方程,你能判断出下列方程的根的情况吗?理 由是什么? 解无理方程必须要把求得的x的值代入原方程检验. 解含有两个“根号”的无理方程时,一般将两个“根号项”分别放在等号两边,两边平方后 解含有两个“根号”的无理方程时,一般将两个“根号项”分别放在等号两边,两边平方后
注2:
解无理方程必须要把求得的x的值代入原方程检验.
二、课堂学习
❖例题2:解下列方程
(1) x22 2x1 (2) x2 x1
注3:
解含有两个“根号”的无理方程时,一般将两个“根号项”分别放在等号两边,两边平 再整理,这样可以简化解题过程.
注4:
如果含两个“根号”的无理方程中还有其他“项”,通常要经过两次平方,才能把原方 转化为有理方程.
注1: 解含有两个“根号”的无理方程时,一般将两个“根号项”分别放在等号两边,两边平方后 他项放在方程的另一边,然后进行平方,这样求解比较简单. 思如考果: 含不两解解个只方“程根含,号你”有能的一判无断理个出方下程“列中根方还程有号的其根他”的“情项的况”无吗,?通理理常要方由经是程过什两时么次?平,方一,才般能把将原“方程根号项”放在方程的一边,把 他解他项只放 含项在有放方一程个在的“另根方一号程边”,的的然无后理另进方一行程平时边方,,一,这般然样将求“后解根比号进较项行简”单放平在. 方方程,的一这边,样把其求解比较简单. 解无理方程必须要把求得的x的值代入原方程检验. 再整理,这样可以简化解题过程.
冀教版数学八年级下册数学21.4 一次函数的应用课件(共24张PPT)

(2)超过30千克后,每千克需付 多少元? 0.2元
30
2.某手机的电板剩余电量y毫安是使用天数x的一次函数x和y
关系如图 : 此种手机的电板最大带电量是多少?
y/毫安
1 000毫安
x/天
小结
通过这节课的学习,你有什么收获? 1.知识方面:通过一次函数的图像获取相关的信息; 2.数学思维:①数形结合,函数与方程的思想
车每行驶100千米消耗2升汽油. (3)当y=1时,x=450,因此行驶了450千米后,摩托车将 自动报警.
上题中摩托车行至加油站加完油后,摩托车油箱的剩余油量y(升)和摩 托车行驶路程x(千米)之间 的关系变为图1:
( ,6)
图1
( ,2)
图1为加油后的图象 试问: ⑴加油站在多少千米处?
400千米
用了4 升,,因此摩托车每行驶100千米消耗 2 升汽油.
上题中摩托车行至加油站加完油后,摩托车油箱的剩余油量
y(升)和摩托车行驶路程x(千米)之间 的关系变为图1:
图1
原图
⑶若乙地与加油站之间还有250千米,要到达乙地所加的油是否够用?
答:够
理由:由图像上观察的:400千米处设加油站,到700米处油用
21.4 一次函数的应用
1.能根据实际问题中变量之间的关系, 确定一次函数关系式.
2.能将简单的实际问题转化为数学问题 (建立一次函数),从而解决实际问题.
一次函数图像可获得哪些信息?
1. 由一次函数的图像可确定k 和 b 的符号; 2.由一次函数的图像可估计函数的变化趋势; 3.可直接观察出x与y 的对应值; 4.由一次函数的图像与y 轴的交点的坐标可确定b值,
春八年级数学下册21.4无理方程1教案

整式方程
有理方程
分式方程
代数方程
无理方程
3、巩固练习1
1)已知下列关于 的方程:
其中无理方程是____________________(填序号).
2)思考与尝试
怎样解方程 ?
4、归纳方法
无理方程 有理方程
提问
解得有理方程的根 ,它们都是原方程的根吗?
讨论
方程 的根究竟是什么?怎样知道 是原方程的根,而 不是原方程的根?
重 点
只含一个或两个关于未知数的二次根式的无理方程的解法;对无理方程产生增根的理解.
难 点
只含一个或两个关于未知数的二次根式的无理方程的解法;对无理方程产生增根的理解.
教 学
准 备
学生活动形式
讨论,交流,总结,练习
教学过程
设计意图
课题引入:
1、解整式方程与分式方程、高次方程的解题思路是什么?
知识呈现:
无理方程
课 题
21.4(1)无理方程
设计
依据
(注:只在开始新章节教学课必填)
教材章节分析:
学生学情分析:
课 型
新授课
教
学
目
标
(1)理解无理方程的概念,会识别无理方程,知道有理方程及代数方程的概念.
(2)经历探索无理方程解法的过程,领会无理方程“有理化”的化归思想.
(3)知道解无理方程的一般步骤,知道解无理方程必须验根,并掌握验根的方法.
1、引入:用一根30cm长的细铁丝弯折成一个直角三角形,使它的一条直角边长为5cm,应该怎样弯折?
2.观察
思考题中的纳概念
1方程中含有根式,且被开方数是含有未知数的代数式,这样的方程叫做无理方程.
214 无理方程

21.4 无理方程(1)一、教学目标:(1)理解无理方程的概念,会识别无理方程,知道有理方程及代数方程的概念.(2)了解解无理方程的基本思想:无理方程有理方程;掌握简单无理方程的基本解法,懂得解无理方程必须验根,并掌握验根的方法.(3)学会归纳总结有关方程的知识系统.二、教学重点、难点:重点:经历解无理方程的过程,归纳、总结解无理方程的一般步骤,掌握简单无理方程的基本解法。
领会无理方程“有理化”的化归思想. 难点:解无理方程可能产生增根的原因.三、教学过程:(一)温故知新1、解分式方程的一般思路.2、有理方程的概念.(二)探索与发现1、问题:用一根30厘米长的细铁丝弯折成一个直角三角形,使它的一条直角边长为5厘米,应该怎样弯折?2、问题:观察比较所列方程,看看它们之间有什么区别和联系?(三)学习新知1、给出概念无理方程:方程中含有根式,且被开方数是含有未知数的代数式,这样的方程叫做无理方程.因为方程中含有根式,所以我们也把它叫做根式方程.初等代数方程:有理方程和无理方程统称为初等代数方程(简称代数方程).2、巩固概念判断:下列关于x 的方程中哪些是无理方程?21)6(12)3(11113)5(015)2(721)4(015)1(3222=++=+=+++=++=+-=++xx x x x x x x x a x x3、无理方程的解法(1)例1、解下列方程(1)223=+x(2)例2、解下列方程(1)x x =+43 (2)x x -=+43问题:①解无理方程为什么会产生增根?②怎样验根(3)归纳解简单无理方程的一般步骤.(四)巩固练习1、下面四个方程中,有一个根x=2的方程是( ) (A) 21+=+x x (B) 26=-x (C) x x =+2 (D) 012=++x x2、解方程(1) x x -=+2; (2) 1212-=-x x ;(3)632-=-x x ; (4)22-=-x ;(5) 22=-+x x ,(五)小结1、解决问题的需要2、概念;3、解无理方程的基本思想;4、解无理方程可能产生增根验根;(六)布置作业(1)写出本节课学习要点;(2)练习册 习题21.4(1)(3)解下列方程:045=--x。
上海初数---八年级-无理方程(1)
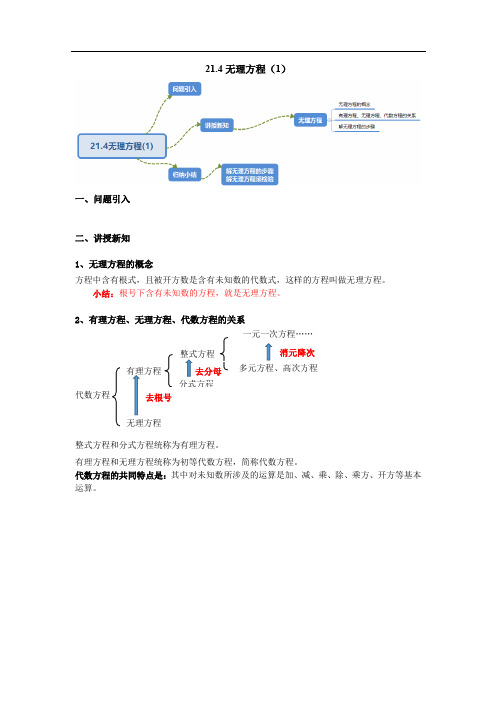
21.4无理方程(1)一、问题引入二、讲授新知1、无理方程的概念方程中含有根式,且被开方数是含有未知数的代数式,这样的方程叫做无理方程。
小结:根号下含有未知数的方程,就是无理方程。
2代数方程整式方程和分式方程统称为有理方程。
有理方程和无理方程统称为初等代数方程,简称代数方程。
代数方程的共同特点是:其中对未知数所涉及的运算是加、减、乘、除、乘方、开方等基本运算。
3、解无理方程的步骤解无理方程的基本思路:将“无理方程”通过“去根号”转化为“有理方程”,再进行求解(需要检验)。
无理方程检验的主要方法:将解有理方程的根直接代入原方程,检验两边是否相等即可。
课后思考:不计算,判断0122=++=x x x 是不是的根?(提示:可以从根式的意义和结果来判断) 小结:①当方程中只有一个含未知数的二次根式时,可先把方程变形,使这个二次根式单独在一边,然后方程两边同时平方,将这个方程转化为有理方程;②由于这去根号一步骤必需且可能产生增根,因此必须验根; ③对方程变形时,尽量找整数系数方程。
三、归纳小结1、代数方程的共同特点是:其中对未知数所涉及的运算是加、减、乘、除、乘方、开方等基本运算;2、解无理方程的基本思路:将“无理方程”通过“去根号”转化为“有理方程”,再进行求解;3、解无理方程,验根是必不可少的。
补充练习:1:下列方程是哪些是关于x 的无理方程?(1)49=;(2)26250-=; (3)1211x -=;(41=;(5)27-=;(6)21x -2:解下列方程:(1x ;(23x =.(3)10x =-;(4)()30x +=;3:解下列方程:(11=+;(2)5x =.补充练习答案:1:下列方程是哪些是关于x 的无理方程?(1)49=;(2)26250-=; (3)1211x -=;(41=;(5)27-=;(6)21x -【答案】(1)、(2)、(3)、(4)、(6)是无理方程. 2:解下列方程:(2x ;(23x =.(3)10x =-;(4)()30x +=;【答案】(1)3x =;(2)5x =.(3)20x =;(4)1x =.3:解下列方程:(11=+;(2)5x =.【答案】(1)x =2)4x =.。
