深圳市南山区数学期末统考试题 (优选.)
南山期末考试数学试卷答案

一、选择题(每题5分,共20分)1. 下列各数中,有理数是()A. √2B. πC. -3/4D. 0.1010010001…答案:C解析:有理数是可以表示为两个整数比的数,因此C选项-3/4是有理数。
2. 如果a < b,那么下列不等式中正确的是()A. a - 1 < b - 1B. a + 1 > b + 1C. a - 2 < b - 2D. a + 2 > b + 2答案:C解析:在不等式两边同时加上或减去相同的数,不等式的方向不变,因此C选项正确。
3. 下列各式中,完全平方公式是()A. (a + b)^2 = a^2 + 2ab + b^2B. (a - b)^2 = a^2 - 2ab + b^2C. (a + b)^2 = a^2 - 2ab + b^2D. (a - b)^2 = a^2 + 2ab - b^2答案:B解析:完全平方公式是(a - b)^2 = a^2 - 2ab + b^2,因此B选项正确。
4. 下列各数中,正数是()A. -5B. 0C. -3/2D. 4答案:D解析:正数是大于0的数,因此D选项4是正数。
5. 下列各函数中,一次函数是()A. y = 2x^2 + 3x - 1B. y = 3x + 4C. y = x^3 + 2D. y = √x答案:B解析:一次函数的形式是y = ax + b,其中a和b是常数,因此B选项y = 3x + 4是一次函数。
二、填空题(每题5分,共20分)6. 若x^2 - 5x + 6 = 0,则x的值为______。
答案:2或3解析:使用因式分解法,将x^2 - 5x + 6分解为(x - 2)(x - 3) = 0,得到x = 2或x = 3。
7. 若a^2 + b^2 = 25,且a > 0,b < 0,则a + b的值为______。
答案:5解析:由于a > 0,b < 0,a和b的绝对值相加等于5,因此a + b = 5。
2023-2024学年广东省深圳市南山区九年级(上)期末数学试卷及答案解析
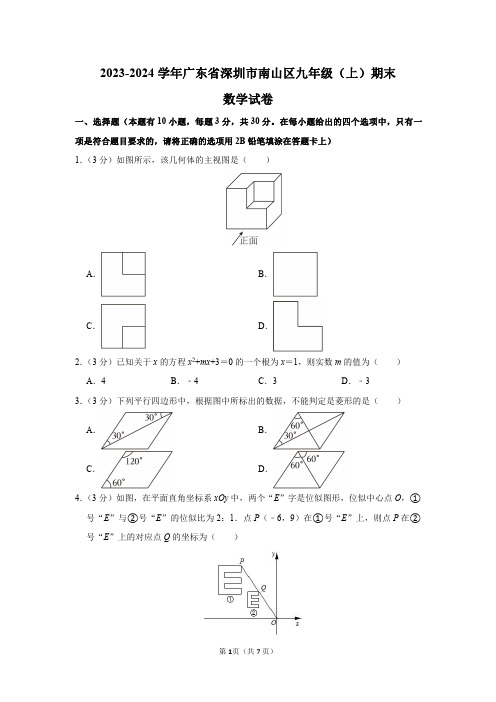
2023-2024学年广东省深圳市南山区九年级(上)期末数学试卷一、选择题(本题有10小题,每题3分,共30分。
在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确的选项用2B铅笔填涂在答题卡上)1.(3分)如图所示,该几何体的主视图是()A.B.C.D.2.(3分)已知关于x的方程x2+mx+3=0的一个根为x=1,则实数m的值为()A.4B.﹣4C.3D.﹣33.(3分)下列平行四边形中,根据图中所标出的数据,不能判定是菱形的是()A.B.C.D.4.(3分)如图,在平面直角坐标系xOy中,两个“E”字是位似图形,位似中心点O,①号“E”与②号“E”的位似比为2:1.点P(﹣6,9)在①号“E”上,则点P在②号“E”上的对应点Q的坐标为()A.(﹣3,)B.(﹣2,3)C.(﹣,3)D.(﹣3,2)5.(3分)近几年,二维码逐渐进入了人们的生活,成为广大民众生活中不可或缺的一部分.小刚将二维码打印在面积为20的正方形纸片上,如图,为了估计黑色阴影部分的面积,他在纸内随机掷点,经过大量重复实验,发现点落在黑色阴影的频率稳定在0.6左右,则据此估计此二维码中黑色阴影的面积为()A.8B.12C.0.4D.0.66.(3分)如图,嘉嘉在A时测得一棵4m高的树的影长DF为8m,若A时和B时两次日照的光线互相垂直,则B时的影长DE为()A.2m B.C.4m D.7.(3分)下面说法正确的是()A.两条直线被一组平行线所截,所得的线段成比例B.对于反比例函数,y随x的增大而减小C.关于x的方程ax2+b=0是一元二次方程D.顺次连接对角线相等的四边形各边中点所组成的图形是菱形8.(3分)近年来,由于新能源汽车的崛起,燃油汽车的销量出现了不同程度的下滑,经销商纷纷开展降价促销活动.某款燃油汽车今年3月份售价为23万元,5月份售价为16万元.设该款汽车这两月售价的月均下降率是x,则所列方程正确的是()A.16(1+x)2=23B.23(1﹣x)2=16C.16(1+2x)2=23D.23(1﹣2x)2=169.(3分)如图,在矩形ABCD中,以A为圆心,AD长为半径画圆弧,交BC于点E,以E 为圆心AE长为半径画圆弧与BC的延长线交于点F,连接AF分别与DE、DC交于点M、N,连接DF,下列结论中错误的是()A.四边形AEFD为菱形B.CN=CEC.△CFN∽△DAN D.△ABE≌△DCF10.(3分)某学习小组用绘图软件绘制出了函数如图所示的图象,根据你学习函数的经验,下列对a,b大小的判断,正确的是()A.a>0,b<0B.a>0,b>0C.a<0,b>0D.a<0,b<0二、填空题:(本大题共5小题,每小题3分,共15分)11.(3分)若,则=.12.(3分)大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”的美.如图,点P为AB的黄金分割点(AP>PB).如果BP的长度为2cm,那么AP的长度为_____cm.13.(3分)如图,在△ABC中,∠ABC=90°,∠A=60°,直尺的一边与BC重合,另一边分别交AB,AC于点D,E.点B,C,D,E处的读数分别为15,12,0,1,则直尺宽BD的长为.14.(3分)如图,在矩形OABC中,OA=12,OC=10,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=(x>0)的图象与BC边交于点E,若S△AEF=k 时,则k=.15.(3分)如图,△ABC为直角三角形,∠ACB=90°,AC=1,BC=3,D是AB边上的中点,将△ACB绕着点A逆时针旋转,使点C落在线段CD上的点E处,点B的对应点为F,边EF与边AB交于点G,则DG的长是.三、解答题:(本题共7小题,其中第16题6分,第17题6分,第18题8分,第19题8分,第20题8分,第21题9分,第20题10分,共55分)16.(6分)解下列方程:(1)(x﹣3)2=4x(x﹣3);(2)x2+8x﹣9=0.17.(6分)已知:▱ABCD的两邻边AB,AD的长是关于x的方程x2﹣mx+2m=0的两个实数根.(1)当m为何值时,▱ABCD是菱形?(2)若AB的长为3,求▱ABCD的周长.18.(8分)某校在九年级随机抽取了20名学生分成甲、乙两组,每组各10人,进行“网络安全”知识竞赛.把甲、乙两组的成绩进行整理分析(满分100分,竞赛得分用x表示:90≤x≤100为网络安全意识非常强,80≤x<90为网络安全意识比较强,x<80为网络安全意识一般).收集整理的数据制成了如下统计图表:平均数中位数众数甲组a8080乙组83b c根据以上信息回答下列问题:(1)填空:a=,b=,c=;(2)已知该校九年级有500人,估计九年级网络安全意识非常强的人数一共是多少?(3)现在准备从甲乙两组满分人数中抽取两名同学参加全区比赛,用树状图或者列表法求抽取的两名同学恰好一人来自甲组,另一人来自乙组的概率.19.(8分)如图,在正方形ABCD中,点E,F分别在AD,CD上,AF⊥BE,垂足为M.(1)求证:AE=DF;(2)若正方形ABCD的边长是8,,点N是BF的中点,求MN的长.20.(8分)园林部门计划在公园建一个如图(甲)所示的长方形花圃ABCD,花圃的一面靠墙(墙足够长),另外三边用木栏围成,BC=2AB,建成后所用木栏总长120米,在图(甲)总面积不变的情况下,在花圃内部设计了一个如图(乙)所示的正方形网红打卡点和两条宽度相等的小路,其中,小路的宽度是正方形网红打卡点边长的,其余部分种植花卉,花卉种植的面积为1728平方米.(1)求长方形ABCD花圃的长和宽;(2)求出网红打卡点的面积.21.(9分)【综合与实践】:北师大版九年级上册数学教材第122页第21题:“怎样把一块三角形的木板加工成一个面积最大的正方形桌面?”某小组同学对此展开了思考.=1.5m2,AB=【特例感知】:(1)若木板的形状是如图(甲)所示的直角三角形,S△ABC1.5m,根据“相似三角形对应的高的比等于相似比”可以求得此时正方形DEFG的边长是.【问题解决】:若木板是面积仍然为1.5m2的锐角三角形ABC,按照如图(乙)所示的方式加工,记所得的正方形DEFG的面积为S,如何求S的最大值呢?某学习小组做了如下思考:=ah,∴h=,由△BDE∽△BAC 设DE=x,AC=a,AC边上的高BH=h,则S△ABC得:,从而可以求得x=,若要内接正方形面积S最大,即就是求x的最大值.因为S=1.5为定值,因此只需要分母最小即可.(2)小组同学借鉴研究函数的经验,令y=a+h=a+(a>0).探索函数y=a+的图象和性质:①下表列出了y与a的几组对应值,其中m=;a…1234…y…129m43344…②在如图(丙)所示的平面直角坐标系中画出该函数的大致图象;③结合表格观察函数y=a+图象,以下说法正确的是.A.当a>1时,y随a的增大而增大.B.该函数的图象可能与坐标轴相交.C.该函数图象关于直线y=a对称.D.当该函数取最小值时,所对应的自变量a的取值范围在1~2之间.22.(10分)某数学学习小组学习完四边形后进行了如下探究,已知四边形EFGH为矩形,请你帮助他们解决下列问题:(1)【初步尝试】:他们将矩形EFGH的顶点E、G分别在如图(1)所示的▱ABCD的边AD、BC上,顶点F、H恰好落在▱ABCD的对角线BD上,求证:BF=DH;(2)【深入探究】:如图2,若▱ABCD为菱形,∠ABC=60°,若AE=ED,求的值;(3)【拓展延伸】:如图(3),若▱ABCD为矩形,AD=m,AB=n且AE=ED,请直接写出此时的值是(用含有m,n的代数式表示).2023-2024学年广东省深圳市南山区九年级(上)期末数学试卷参考答案与试题解析一、选择题(本题有10小题,每题3分,共30分。
南山区初一期末数学试卷

一、选择题(每题3分,共30分)1. 下列各数中,不是有理数的是()A. 3.14B. -5/7C. √4D. π2. 已知x=2,那么方程2x-3=5的解是()A. x=4B. x=2C. x=1D. x=03. 如果a+b=5,a-b=3,那么a²-b²的值是()A. 4B. 8C. 12D. 164. 下列函数中,是反比例函数的是()A. y=x+2B. y=2xC. y=x²D. y=2/x5. 在直角坐标系中,点A(-2,3)关于原点的对称点是()A.(-2,-3)B.(2,3)C.(2,-3)D.(-2,3)6. 下列各图中,是平行四边形的是()A. 图①B. 图②C. 图③D. 图④7. 在△ABC中,若∠A=60°,∠B=45°,则∠C的度数是()A. 60°B. 45°C. 75°D. 90°8. 下列各数中,绝对值最小的是()A. -3B. -2C. 0D. 29. 已知a=3,b=-4,那么|a+b|的值是()A. 7B. 1C. 5D. 310. 下列各数中,能被3整除的是()A. 24B. 25C. 26D. 27二、填空题(每题3分,共30分)11. 计算:(-5)²×(-2)=__________。
12. 简化表达式:2x+3x-5x=__________。
13. 如果m=5,那么3m-2=__________。
14. 计算下列分式的值:5/8+3/4=__________。
15. 简化下列根式:√(16/9)=__________。
16. 如果a=2,b=-3,那么a²+b²=__________。
17. 已知x=2,那么方程3x-4=5的解是x=__________。
18. 下列函数中,是正比例函数的是y=__________。
19. 在直角坐标系中,点B(3,-4)关于x轴的对称点是__________。
南山区数学七年级期末试卷

一、选择题(每题3分,共30分)1. 下列数中,既是正整数又是质数的是()A. 4B. 6C. 8D. 112. 若一个数的平方是4,那么这个数是()A. 2B. -2C. ±2D. 03. 下列方程中,正确的是()A. 2x + 3 = 7B. 3x - 5 = 0C. 5x = 10D. x + 2 = 3x4. 在等腰三角形ABC中,若AB = AC,则∠BAC是()A. 锐角B. 钝角C. 直角D. 无法确定5. 下列图形中,是轴对称图形的是()A. 正方形B. 等腰梯形C. 平行四边形D. 矩形6. 已知三角形ABC中,AB = 5,BC = 6,AC = 7,则该三角形是()A. 直角三角形B. 等腰三角形C. 等边三角形D. 钝角三角形7. 下列函数中,是反比例函数的是()A. y = 2x + 3B. y = 3/xC. y = x^2D. y = x^38. 下列式子中,正确的是()A. (a + b)^2 = a^2 + 2ab + b^2B. (a - b)^2 = a^2 - 2ab + b^2C.(a + b)^2 = a^2 - 2ab + b^2 D. (a - b)^2 = a^2 + 2ab - b^29. 在直角坐标系中,点P(2, -3)关于x轴的对称点是()A. (2, 3)B. (-2, 3)C. (2, -3)D. (-2, -3)10. 下列数据中,中位数是5的是()A. 1, 2, 3, 4, 5, 6, 7B. 1, 2, 3, 4, 5, 6, 8C. 1, 2, 3, 4, 5, 7,8 D. 1, 2, 3, 4, 5, 6, 9二、填空题(每题3分,共30分)11. 3的平方根是__________,它的立方根是__________。
12. 若a = 2,b = -3,则a^2 + b^2 = _________。
13. 等腰三角形的底边长是10,腰长是8,那么这个三角形的面积是_________。
七下期末数学试卷南山区

一、选择题(每题4分,共40分)1. 下列各数中,不是有理数的是()A. 3.14B. √2C. -5D. 1/22. 下列各组数中,成等差数列的是()A. 1, 3, 5, 7B. 2, 4, 8, 16C. 3, 6, 9, 12D. 1, 2, 4, 83. 已知一元二次方程x^2 - 4x + 3 = 0,则该方程的解为()A. x = 1 或 x = 3B. x = 2 或 x = 2C. x = 1 或 x = -3D. x = 2 或 x = -24. 下列函数中,为一次函数的是()A. y = 2x^2 + 1B. y = x^3 - 3x + 2C. y = 2x + 1D. y = 3x^2 + 2x + 15. 已知等腰三角形ABC中,AB = AC,且底边BC的中点为D,若AD = 5cm,则AB 的长度为()A. 5cmB. 10cmC. 15cmD. 20cm6. 在平面直角坐标系中,点P(-2,3)关于原点对称的点为()A.(2,-3)B.(-2,-3)C.(-2,3)D.(2,3)7. 下列关于圆的性质中,正确的是()A. 圆的直径是圆中最长的弦B. 圆内接四边形的对角互补C. 圆周角等于它所对的圆心角的一半D. 圆的半径等于圆心到圆上任意一点的距离8. 下列关于三角形中位线的说法中,正确的是()A. 三角形中位线平行于第三边B. 三角形中位线等于第三边的一半C. 三角形中位线的中点在第三边上D. 三角形中位线的中点在第三边的延长线上9. 已知正方形的边长为a,则其对角线的长度为()A. √2aB. √3aC. 2aD. a10. 下列关于函数图象的说法中,正确的是()A. 函数图象上的点一定满足函数关系式B. 函数图象上的点不一定满足函数关系式C. 函数图象上的点一定在函数关系式的定义域内D. 函数图象上的点不一定在函数关系式的定义域内二、填空题(每题4分,共40分)11. 若m + n = 5,m - n = 1,则m = __________,n = __________。
南山区数学六年级期末试卷

1. 下列各数中,既是质数又是合数的是()A. 2B. 9C. 15D. 172. 一个数的因数共有8个,这个数最小是()A. 16B. 18C. 20D. 243. 下列图形中,面积最大的是()A. 正方形B. 长方形C. 平行四边形D. 梯形4. 一个数的平方根是±2,这个数是()A. 4B. 9C. 16D. 255. 下列各数中,有理数是()A. √3B. √2C. πD. -36. 下列运算正确的是()A. (a+b)² = a² + b²B. (a-b)² = a² - b²C. (a+b)² = a² + 2ab + b²D. (a-b)² = a² - 2ab + b²7. 下列图形中,对称轴最多的是()A. 等腰三角形B. 正方形C. 矩形D. 等边三角形8. 下列各数中,正数是()A. -1B. 0C. 1D. -29. 下列图形中,周长最小的是()A. 正方形B. 长方形C. 平行四边形D. 梯形10. 下列运算正确的是()A. a² + b² = (a+b)²B. a² - b² = (a-b)²C. a² + 2ab + b² = (a+b)²D. a² - 2ab + b² = (a-b)²11. 2的平方根是_______,3的立方根是_______。
12. 下列各数中,质数有_______个。
13. 一个长方形的长是5cm,宽是3cm,它的周长是_______cm。
14. 下列图形中,轴对称图形有_______个。
15. 下列各数中,正数是_______。
16. 下列图形中,面积最大的是_______。
17. 下列各数中,有理数是_______。
南山区八下期末数学试卷

一、选择题(每题3分,共30分)1. 下列各数中,有理数是()A. √2B. πC. √-1D. 0.1010010001…2. 若a、b是方程2x^2-5x+3=0的两根,则a+b的值为()A. 1B. 2C. 3D. 53. 已知等差数列{an}的前n项和为Sn,若S5=20,S10=70,则公差d为()A. 1B. 2C. 3D. 44. 下列函数中,是反比例函数的是()A. y=x^2B. y=2xC. y=3/xD. y=2x+15. 在△ABC中,∠A=30°,∠B=45°,则∠C的度数为()A. 105°B. 120°C. 135°D. 150°6. 已知二次函数y=ax^2+bx+c的图象开口向上,且顶点坐标为(1,-2),则a的值为()A. 1B. 2C. -1D. -27. 下列各式中,正确的是()A. √(9^2) = 3B. (-3)^2 = 9C. √(-9) = 3iD. √(16/25) = 4/58. 若|a| > 2,则下列不等式中正确的是()A. a > 2B. a < 2C. a ≥ 2D. a ≤ 29. 已知函数y=2x-1,若x=3,则y的值为()A. 5B. 4C. 3D. 210. 在平面直角坐标系中,点A(2,3)关于原点的对称点为()A.(-2,-3)B.(2,-3)C.(-2,3)D.(3,-2)二、填空题(每题5分,共25分)11. 3的平方根是______,-5的立方根是______。
12. 若x^2-5x+6=0,则x的值为______。
13. 等差数列{an}的前5项和为25,公差为2,则第10项an=______。
14. 已知一次函数y=kx+b过点(2,3)和(-1,-1),则k=______,b=______。
15. 在△ABC中,若a=5,b=7,c=8,则△ABC的面积S=______。
南山区六年级期末数学试卷

一、选择题(每题3分,共30分)1. 下列数中,哪个数是质数?A. 28B. 37C. 50D. 642. 一个长方形的长是8厘米,宽是5厘米,它的周长是多少厘米?A. 26B. 27C. 30D. 323. 小华有一些苹果,他先吃了5个,然后又吃掉了剩下苹果的$\frac{1}{3}$,最后还剩下10个苹果。
请问小华原来有多少个苹果?A. 15B. 18C. 21D. 244. 下列图形中,哪个图形的面积是36平方厘米?A. 正方形B. 长方形C. 等腰三角形D. 平行四边形5. 小明骑自行车去图书馆,速度是每小时12千米,他用了2小时到达图书馆。
请问小明骑自行车的路程是多少千米?B. 26C. 28D. 306. 一个三位数的百位数字是2,十位数字比个位数字大3,这个数是:A. 256B. 265C. 276D. 2877. 小华从家出发,向北走了5千米,然后向东走了3千米,再向南走了2千米,最后向西走了1千米。
请问小华现在距离家有多远?A. 4千米B. 5千米C. 6千米D. 7千米8. 下列算式中,计算错误的是:A. 8 + 6 × 2 = 28B. 12 - 4 × 3 = 0C. 5 × 5 ÷ 5 = 5D. 7 × 6 ÷ 2 = 219. 一个数的十分位是4,百分位是7,这个数是:A. 0.47B. 0.74C. 4.0710. 下列图形中,哪个图形是轴对称图形?A. 矩形B. 正方形C. 等腰三角形D. 平行四边形二、填空题(每题3分,共30分)11. 0.25 + 0.75 = _______12. 36 ÷ 9 = _______13. 4 × 5 + 3× 2 = _______14. 7 - 3 × 2 = _______15. 100 ÷ 4 = _______16. 6 × 6 = _______17. 0.8 × 0.9 = _______18. 3.5 × 2 = _______19. 12 + 8 - 4 = _______20. 24 ÷ 3 × 2 = _______三、解答题(每题10分,共40分)21. 一辆汽车从A地出发,以每小时60千米的速度向B地行驶,行驶了2小时后,又以每小时80千米的速度继续行驶。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
wo最新文件---------------- 仅供参考--------------------已改成-----------word文本--------------------- 方便更改
rd
2016-2017学年南山区八年级(上)期末数学试卷
一、选择题(本题共12小题,每题3分,共36分)
1.下列各数中最小的是()
A.0 B.1 C.3
-D.π-
2.关于实数2,下列说法错误的是()
A.可以化成小数B.是无理数
C.是2的平方根D.它的值在0到1之间
3.在函数
x x
y
-
=
2中,自变量x的取值范围是()
A.x>2 B.x≤2且x≠0 C.x<2 D.x>2且x≠0 4.数据4,8,6,4,3的中位数是()
A.4 B.6 C.3 D.5
5.如图,阴影部分是一个长方形,它的面积是()A.32
cm B.42
cm C.52
cm D.62
cm
1cm
①②③④
第5题第6题
6.在以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a、b互相平行的是()
A.如图①,展开后测得∠1=∠2
B.如图②,展开后测得∠1=∠2且∠3=∠4
C.如图③,测得∠1=∠2
D.如图④,展开后再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD
7.某班为筹备元旦联欢晚会,在准备工作中,班长对全班同学爱吃什么水果作了民意调查,再决定最终买哪种水果,下面的调查数据中,他最关注的是()
A. 中位数
B. 平均数
C. 加权平均数
D. 众数
8.在△ABC中,∠A=∠B+∠C,∠B=2∠C-6°,则∠C的度数为()
A.90°B.58°C.54°D.32°
9.下列叙述错误的是()
A. 所有的命题都有条件和结论
B. 所有的命题都是定理
C. 所有的定理都是命题
D. 所有的公理都是真命题
10.关于一次函数b
=2(b为常数),下列说法正确的是()
-
x
y+
A. y随x的增大而增大
B. 当b=4时,直线与坐标轴围成的面积是4
C. 图象一定过第一、三象限
D. 与直线y=3-2x相交于第四象限内一点
11.如图,雷达探测器测得六个目标A,B,C,D,E,F出现按照规定的目标表示方法,目标E,F的位置表示为E(3,︒
210),按照
300),F(5,︒
此方法在表示目标A,B,D,E的位置时,其中表示不正确的是()A.A(4,︒
120) D.D(3,
30) B.B(2,︒
90) C.C(6,︒
240)
︒
第11题 第12题 12.如图,长方体的长为10 cm ,宽为5 cm ,高为20 cm .若一只蚂蚁沿着
长方体的表面从点A 爬到点B ,需要爬行的最短路径是( ) A .5520+ B .5 C .5510+ D .215
二、填空题(本题共4小题,每题3分,共12分)
13.实数-8的立方根是 .
14.如果用(7,8)表示七年级八班,那么八年级七班可表示成 .
15.计算:)35)(35(-+= ;7
1
7÷
= ;9±= .
16.不透明的布袋中装着三个小球,小球上标有-2,0,1三个数,这三个球除了标的数不同外,其余均相同.从布袋中任意摸出一个球,记下小球上所标之数后放回,……,这样一共摸了13次.若记下的13个数之和等于-4,平方和等于14,则在这13次摸球中,摸到球上所标之数是0的次数是 .
三、解答题(本大题有7题,其中17题8分,18题6分,19题8分,20题6
分,21题8分,22题8分,23题8分,共52分,把答案填在答题卷上) 17.解下列方程组:
(1)⎩⎨⎧-=-=-102304y x y x (2)⎪⎩⎪⎨⎧=-=-243143y x y
x
18.九年级甲、乙两名同学期末考试的成绩(单位:分)如下:
根据表格中的数据,回答下列问题:
(1)甲的总分为522分,则甲的平均成绩是 分,乙的总分为520
分, 的成绩好一些.
(2)经计算知2甲S =7.67,2乙S =5.89.你认为 不偏科;(填“甲”
或者“乙”)
(3)中招录取时,历史和体育科目的权重是0.3,请问谁的成绩更好一些?
O
C
B
A
19.小明和小华做游戏,游戏规则如下:
(1)每人每次抽取四张卡片,如果抽到白色卡片,那么加上..
卡片上的数或算式;如果抽到底板带点的卡片,那么减去..卡片上的数或算式. (2)比较两人所抽的4张卡片的计算结果,结果大者为胜者。
小明抽到的卡片如下: 小华抽到的卡片如下:
请你通过计算判断谁为胜者?
20.在八年级读书的杨洋听到学弟在讨论数学问题,请你帮杨洋的学弟
乙正确回答问题,并帮他证明.
学弟甲:用平面去截一个立方体,截面的形状可以是三角形吗?
18
8
4
32
2
1 20 4
53
3
312
2
7
学弟乙:肯定可以啊!
学弟甲:那截面的形状可以是直角三角形吗?
学弟乙:我觉得 (填“可以”或者“不可以”)
学弟甲:空口无凭,必须进行有根有据的证明!
21.“三等分一个任意角”是数学史上一个著名问题,今天人们已经知道,仅用圆规直尺是不可能做出的。
在探索中,有人曾利用过如图所示的图形,其中,ABCD是长
方形(AD∥CB),F是DA延长线上一点,G 是CF上一点,并
F E
G
D
C B
A
22.某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含
14吨),则每吨按政府补贴优惠价m 元收费;若每月用水量超过14吨,则超过部分每吨按市场价n 元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价和市场价分别是多少?
(2)设每月用水量为x 吨,应交水费为y 元,请写出y 与x 之间的函数关系式;
(3)小明家5月份用水26吨,则他家应交水费多少元?
23.如图,直线L :22
1+-=x y 与x 轴、y 轴分别交于A 、B 两点,在y 轴上有一点N (0,4),
动点M 从A 点以每秒1个单位的速度匀速沿x 轴向左移动. (1)点A 的坐标: ;点B 的坐标: ; (2)求△NOM 的面积S 与M 的移动时间t 之间的函数关系式; (3)在y 轴右边,当t 为何值时,△N OM ≌△AOB ,求出此时点M 的
坐标;
(4)在(3)的条件下,若点G 是线段ON 上一点,连结MG ,△MGN 沿MG 折叠,点
O
y
x
N
A
M
B
N恰好落在x轴上的点H处,求点G的坐标.
最新文件---------------- 仅供参考--------------------已改成-----------word文本--------------------- 方便更改
赠人玫瑰,手留余香。
