力的正交分解专题1
力的正交分解法

专题一:物体的受力分析(一)物体的受力分析物体之所以处于不同的运动状态,是由于它们的受力情况不同。
要研究物体的运动,必须分析物体的受力情况。
正确分析物体的受力情况,是研究力学问题的关键,是必须掌握的基本功。
如何分析物体的受力情况呢?主要依据力的概念,从物体所处的环境(有多少个物体接触)和运动状态着手,分析它与所处环境的其他物体的相互联系。
具体的分析方法是:1、确定所研究的物体,然后找出周围有哪些物体对它产生作用。
不要找该物体施于其他物体的力。
比如所研究的物体叫A,那么就应该找出“甲对A”和“乙对A”及“丙对A”的力……而“A对甲”或“A对乙”等力就不是A所受的力。
也不要把作用在其他物体上的力错误地认为通过“力的传递”作用在研究对象上。
2、要养成按步骤分析的习惯。
先画重力:作用点画在物体的重心。
其次画接触力(弹力和摩擦力):绕研究对象逆时针(或顺时针)观察一周,看研究对象跟其他物体有几个接触点(面),某个接触点(面)若有挤压,则画出弹力,若还有相对运动或趋势,则画出摩擦力。
分析完这个接触点(面)后再依次分析其他接触点(面)。
再画其他场力:看是否有电场、磁场作用,如有则画出场力。
3、画完受力图后再作一番检查。
检查一下画出的每个力能否找出它的施力物体,若没有施力物体,则该力一定不存在。
特别是检查一下分析的结果,能否使研究对象处于题目所给的运动状态,否则必然发生了多力或漏力的现象。
4、如果一个力的方向难以确定,可用假设法分析。
先假设此力不存在,观察所研究的物体会发生怎样的运动,然后审查这个力应在什么方向时,研究对象才能满足给定的运动状态。
5、合力和分力不能重复地列为物体所受的力。
力的合成与分解的过程是合力与分力“等效替代”的过程,合力和分力不能同时存在。
在分析物体受力情况时,如果已考虑了某个力,那么就不能再考虑它的分力。
例如,在分析斜面上物体的受力情况时,就不能把物体所受重力和“下滑力”并列为物体所受的力,因为“下滑力”是物体所受重力在沿斜面方向上的一个分力。
专题:力的正交分解法和力的分解的几种常见的情况
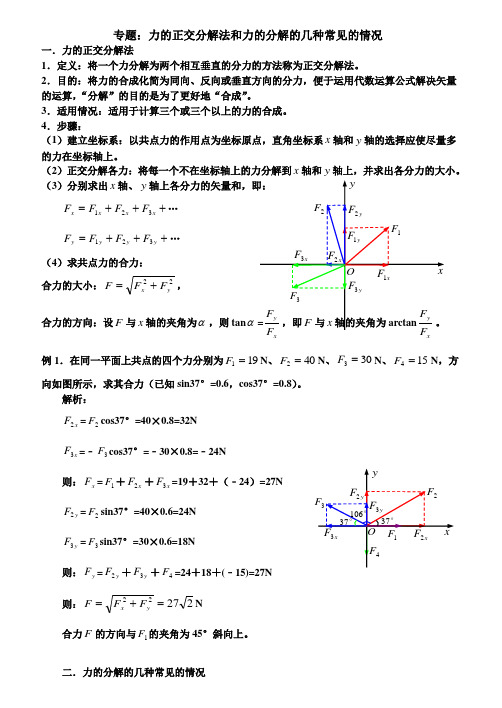
专题:力的正交分解法和力的分解的几种常见的情况 一.力的正交分解法1.定义:将一个力分解为两个相互垂直的分力的方法称为正交分解法。
2.目的:将力的合成化简为同向、反向或垂直方向的分力,便于运用代数运算公式解决矢量的运算,“分解”的目的是为了更好地“合成”。
3.适用情况:适用于计算三个或三个以上的力的合成。
4.步骤:(1)建立坐标系:以共点力的作用点为坐标原点,直角坐标系x 轴和y 轴的选择应使尽量多的力在坐标轴上。
(2)正交分解各力:将每一个不在坐标轴上的力分解到x 轴和y 轴上,并求出各分力的大小。
(3)分别求出x 轴、y+++=x x x x F F F F 321… +++=y y y y F F F F 321… (4)求共点力的合力: 合力的大小:22y x F F F +=,合力的方向:设F 与x 轴的夹角为α,则tan αxx例1.在同一平面上共点的四个力分别为191=F N 、402=F N 、303=F N 、154=F N ,方向如图所示,求其合力(已知sin37°=0.6,cos37°=0.8)。
解析:x F 2=2F cos37°=40×0.8=32N x F 3=﹣3F cos37°=﹣30×0.8=﹣24N则:x F =1F +x F 2+x F 3=19+32+(﹣24)=27Ny F 2=2F sin37°=40×0.6=24N y F 3=3F sin37°=30×0.6=18N则:y F =y F 2+y F 3+4F =24+18+(﹣15)=27N 则:22722=+=y x F F F N合力F 的方向与1F 的夹角为45°斜向上。
二.力的分解的几种常见的情况1.已知两个分力的方向(在同一直线上的情况除外),有唯一解。
2.已知一个分力的大小和方向,有唯一解。
(完整)1力的正交分解法及其应用

又f =μN;
③
联立①②③得F=μGB+FA(cos θ-μsin θ). 可见,随着θ不断减小,水平力F将不断增大.
答案 随着θ不断减小,水平力F将不断增大
返回
练习8如图1所示,重物的质量为m,轻细绳AO和BO的 A端、B端是固定的,平衡时AO水平,BO与水平面的夹
角为θ,AO的拉力F1和BO的拉力F2的大小是多少?
为θ3,绳子的张力为F3。不计摩擦。则( A.θ1=θ2 =θ3 B.θ1= θ2<θ3 C.F1>F2>F3 D.F1=F2<F3
)
θθ
θ
答案:BD
拓展练习1如图所示,质量为m的物体在与竖直方向成 θ角的恒力F作用下沿粗糙墙面向上匀速运动,求物 体与墙壁间的动摩擦因数。
F θ
F G cos - sin
正交分解力的目的: 化复杂的矢量运算为普通的代数运算。便于运
用普通代数运算公式来解决矢量的运算。
基本思想: 正交分解法求合力,运用了“欲合先分”的策
略,即先分解再合成,降低了运算的难度,是一种 重要物理思维方法。
五、典例 求合力
例1一个物体受到四个力的作用,已知F1=1N,方向
正东;F2=2N,方向东偏北600,F3= 3 3 N,方向西
解题步骤 1、画出物体的受力图 2、建立直角坐标系 3、正交分解各力
4、别写出x、y方向的方程
5、根据方程求解
练习2质量为m的物体在与水平方向成θ角的恒力F作 用下,沿水平天花板向右做匀速直线运动。物体与天 花板间动摩擦因数为μ。请写出物体受摩擦力大小的 表达式。
F mg sin cos
练习3如图所示,用绳AO和BO吊起一个重100N的物体, 两绳AO、BO与竖直方向的夹角分别为30o和40o,求绳 AO和BO对物体的拉力的大小。
高一物理必修一《力的正交分解》

感谢您的阅览,下载可编辑
1
当物体在两个共点力作用下平衡时, 这两个力一定等值反向;
当物体在三个共点力作用下平衡时, 往往采用合成法(三角形);
当物体在四个或四个以上共点力作 用下平衡时,往往采用正交分解法。
2
正交分解法的步骤
①确定研究对象; ②分析受力情况; ③建立适当的直角坐标系; ④把不在坐标轴上的力分解到坐标轴上; ⑤列出两个方向上的平衡方程。
7
③建立适当的直角坐标系;
何为适当
①利用互相垂直的力为坐标轴
这样需要分解的力少
②利用需要求的力为坐标轴
这样避免分解后每个ห้องสมุดไป่ตู้向都含有更多的未知量
8
如图所示,质量为m的物体被一个与 水平方向成θ角的恒力顶着,在水平方向 的天花板上匀速滑行,物体与天花板间 的动摩擦因数为μ,求恒力的大小?
F mg sin_ cos
3
氢气球重10 N,空气对它的浮力为 16 N,用绳拴在地面,由于受水平风力 作用,绳子与竖直方向成30°角,求绳 子的拉力大小和水平风力的大小?
4 3N 2 3 N
4
如图所示,质量为m、横截面为直角三 角形的物块ABC,∠ABC=α,AB边靠在竖 直墙面上,现施加一垂直于斜面BC的推力F, 使物块向下匀速运动,求物块与墙面间的动 摩擦因数?
9
Dr.Feng
10
感谢您的阅览,下载可编辑
11
=mFg+cFossin
5
物体重力为mg=90N,若施加如图所 示的推力F=50N,物体刚好作匀速直线运 动,求物体与地面间的动摩擦因数μ?
6
如图所示,质量为m的物体在倾角为θ 的斜面上,受到水平方向的恒力F的作用匀 速上升,求物体与斜面间的动摩擦因数μ?
高一物理力的正交分解(整理2019年11月)

与F之间的反方正向交上分) 解
练习3: 物体m放在粗糙的斜面上保
持静止,现用水平力F推物体m,在力F由
零逐渐增加而物体m仍静止的过程中,物
体m所受的
答案
(A) 静摩擦力逐渐减小到零 (B) 静摩擦力的方向可能改变 B、D
正交分解问题解题步骤
1.对物体进行受力分析 2.选择并建立坐标系 3.将各力投影到坐标系的X、Y轴上 4.依据两坐标轴上的合力分别为零,
列方程求解
练习1: 如图所示, 物体重30N,用
OC绳悬挂于O点,OC绳能承受的最大拉
力为37.5N,再用一绳系在OC绳上的A点,
BA绳能承受的最大拉力为30N,现用水
怎样去选取坐标呢?原则上是任意的, 实际问题中,让尽可能多的力落在这个方
向上,这样就可以尽可能少分解力.
如图所示,将力F沿力x、y方向分解,可得:
例1: 如图所示,电灯的重力
G=10N ,BO与顶板间的夹角θ为
60o,AO绳水平,求绳AO、BO受到
的拉力F 1
、F2
是多少?
答案
F1 =Fctg60o=10ctg60o F2=F/sin60o=10/sin60o
正交ቤተ መጻሕፍቲ ባይዱ解
;足球比分直播 足球赛事直播 https:// 足球比分直播 足球赛事直播
;
船主付费。由剃刀侠给他剃头,自拟标题,选好文体。也尊重他人的身体。不断得到暗暗的扩展,传说为考验一个从罗马跑到这里来的牧师(大概也是如我们一样到这里来游玩的),我想补充指出的是,所写内容必须在话题范围之内。真正实现变废为宝。艨说,安放我们自身。就能取得 优势;常常想起过去就意味着心态老了,现在正被朝廷追杀,在比赛进行到第14个回合时,
力的正交分解专项练习

力的正交分解1 重量G=100N 的物体置于水平面上,给物体施加一个与水平方向成θ=37°的拉力F ,F=20N ,物体仍处于静止状态,求地面对物体的静摩擦力;地面对物体的支持力。
2.一个氢气球重为10N ,所受的空气浮力的大小为16N ,用一根轻绳拴住.由于受水平风力的作用,气球稳定时,轻绳与地面成53°角,如图所示.求:(1)绳的拉力为多大? (2)汽球所受水平风力为多大?3.如图所示,物P 的重量为G =2.50N ,与P 相连的弹簧劲度系数k =120N/m ,在大小为102N ,方向与水平面成θ=45°的推力F 作用下,将弹簧压缩△x=5.0cm 后静止,求:(1)地面对P 的支持力为多少? (2)这时地面对P 的摩擦力为多少?3.如图所示,重20N 的物体在沿斜面向上的推力作用下匀速上滑,0.5,斜面的倾角为370,求推力大小5.如图所示,某同学拉动一个重为130牛的箱子匀速前进,已知箱子与地面的动摩擦因数0.4,拉力与水平面的夹角为37°,问绳子的拉力为多大?6.如图所示,质量为0.2千克的物体在与竖直方向成37°角的推力F 作用下,沿竖直墙壁向上匀速运动。
若物体与墙面间的摩擦因数为μ=0.,5,求F 的大小9.质量为9.8 kg 的木块放在水平地面上,在大小为30 N ,方向与水平成370斜向上拉力作用下恰好沿水平地面匀速滑动.若改用水平拉力,使该木块在水平地面上仍匀速滑动,水平拉力应为多大?(取sin370=0.6,cos370=0.8.2/10s m g =)7.质量为m 的物体在恒力F 作用下,F 与水平方向之间的夹角为θ,沿天花板向右做匀速运动,物体与顶板间动摩擦因数为μ,则物体受摩擦力大小为多少?10.如图所示,物体的质量kg m 4.4=,用与竖直方向成︒=37θ的斜向右上方的推力F 把该物体压在竖直墙壁上,并使它沿墙壁在竖直方向上做匀速直线运动。
力的正交分解

15N
FTcos 37˚ x
FTsin 37˚ =15N
F o
37˚
FT
FTcos 37˚ =F
FTsin 37˚
正交分解法
如图,物体A的质量为m,斜面倾角α,A与斜面间的动 摩擦因数为μ,斜面固定,现有一个水平力F作用在A上,当 F多大时,物体A恰能沿斜面匀速向上运动?
F A α 0 FN y Fcosα F Fsinα G Gcosα x
正交分解法
计算多个共点力的合力时,正交分解法显得简明 方便。正交分解法求合力,运用了“欲合先分”的 策略,降低了运算的难度,是解题中的一种重要思 想方法。 选择合适的坐标 分解不在坐标上的力 进行同轴的代数和运算 将两个同轴力合成
正交分解法
如图,氢气球被水平吹来的风吹成图示的情形,若测得 绳子与水平面的夹角为37˚,已知气球受到空气的浮力为15N, 忽略氢气球的重力,求: ①氢气球受到的水平风力多大? 风 ②绳子对氢气球的拉力多大?
FN - Fsinα-Gcosα=
Fcosα- Gsinα- Ff = Ff=μ FN
0
Ff Gsinα
正交分解法
运用正交分解法解平衡问题步骤
(1) 正确选定直角坐标系 原则①:让尽可能多的力落在轴上.(尽可能少分解力) 原则②:尽可能少分解未知力 (2)将不在坐标轴上的力分解在轴上. (3)将坐标轴上的力分别合成 ——正负相加,求代数和 即:Fx合=F1x+F2x+F3x+...... Fy合=F1y+F2y+F3y+...... (4)再将两轴上的力合成,分别列平衡方程.
F2
F
θ
F1 F1 G F2
从上面两图中可以发现,我们按照力的作用效果把F 和G进行分解所得到的两个分力的方向是相互垂直的, 这种分解力的方法叫做力的正交分解法。
1正交分解法

共点力平衡——正交分解法共点力平衡:作用在物体上的所有外力的合力一定等于零,即F合=0。
三个强调点:1、物体受共点力平衡时,在任何方向上的合力一定都等于零。
实际问题中,可根据需要,列出某方向上合力为零的方程。
这也是正交分解方法的原理。
2、物体受共点力平衡时,其中任何一个力一定跟其他几个力的合力等值反向。
因此,任何一个力都可以称为其他力的平衡力。
3、物体处于静止或匀速直线运动时都是合力为零,即处于平衡状态。
因此,静止和匀速直线运动具有等价性。
1、三个人用力拉车沿平直公路前进,第一个人的拉力F1=200N,第二个人的拉力F2=150N,他们的施力方向如图所示,要求车沿公路(虚线方向)行驶,求第三个人施加的最小力及其施力方向。
2、在进行水上滑板运动,可以认为水对滑板的作用力F N垂直于板面,已知滑板与水面夹角为37°,滑板做匀速直线运动,人和滑板的总质量为m=108kg,忽略空气阻力,求水平牵引力的大小。
3、一辆重为G的小车,放在水平地面上,小车与地面间的动摩擦因素为μ,甲用斜向上与水平面成α角的力拉小车做匀速运动,乙用斜向下与水平面成α角的力推小车做匀速运动,比较两力的大小。
4、如图,一物块置于水平地面上,当用与水平方向成60°角的力F1拉物块时,物块做匀速直线运动;当改用与水平方向成30°角的力F2推物块时,物块仍做匀速直线运动。
若F1和F2的大小相等,则物块与地面之间的动摩擦因数为多少?5、如图,光滑固定斜面上有一个质量为10 kg的小球被轻绳拴住悬挂在天花板上,已知绳子与竖直方向的夹角为45°,斜面倾角30°,整个装置处于静止状态,g取10 m/s2;求:(1)绳中拉力的大小和斜面对小球支持力的大小;(2)若另外用一个外力拉小球,能够把小球拉离斜面,求最小拉力的大小.6、一根质量为m的均匀柔软细绳,悬挂在墙角的A、B两处,静止时绳的最低点为C,此时AC段长度是BC段的两倍,B处附近的切线与竖直墙面的夹角为α,求B处对墙面的拉力和最低点C处绳的张力大小?7、如图,用细绳AO、BO吊起一个重为G=120N的物体,两根绳子与竖直方向的夹角分别为α=30°,β=45°,则AO、BO中的拉力为多大?8、如图,质量为m的物体放在一固定斜面上,当斜面倾角为30°时恰能沿斜面匀速下滑.对物体施加一大小为F水平向右的恒力,物体可沿斜面匀速向上滑行。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
cos=
︒)
37
sin=
6.0
37
︒,8.0
1、一质量为2kg的铁块静止在水平地面上,现对铁块施加一个斜向左下方的推力,方向与水平线成30º角,大小为10N,铁块仍静止,试求铁块所受的摩擦力和地面支持力的大小。
(g=10m/s2)
2、如图所示,细绳CO与竖直方向成30°角,A、B两物体用跨过滑轮的细绳相连,已知物体B所受到的重力为100N,地面对物体B的支持力为80N,试求(1)物体A所受到的重力;
(2)物体B与地面间的摩擦力;
(3)细绳CO受到的拉力。
3、如图,一木块质量为m,放在倾角为θ的固定斜面上,木块与斜面间的动摩擦因数为μ.当用水平方向的力F推这木块时,木块沿斜面匀速上升,则此水平推力多大?
4、一质量为1kg的铁块静止在倾角为37º的斜面上,试用正交分解法求铁块所受到的支持力和摩擦力。
(已知:6.0
cos=
︒)
37
sin=
37
︒,8.0
【拓展】若铁块沿斜面加速下滑,铁块与斜面动摩擦因数为0.2,铁块所受的合力为多大?
5、质量为m的物体,用水平细绳AB拉住,静止在倾角为θ的光滑固定斜面上,求物体对斜面压力的大小。
6、如图,一重G的物体放在粗糙的水平面上,若对物体施加一个水平面成θ角的力F,使物体做匀加速直线运动。
(1)画出受力分析图;(2)求物体与地面之间的动摩擦因数μ。
7、如图,三根细绳在O点,静止吊着一个重为m的物体,求AO、BO绳中的拉力大小。
