第五章 信号处理初步(1)
第5章信号处理初步

好在工程上不仅关心有无误差,而更重要的是了解误差的 具体数值,以及是否能以经济、有效的手段提取足够精确 的信息。
只要概念清楚,处理得当,就可以利用计算机有效地处理 测试信号,完成在模拟信号处理技术中难以完成的工作。
二、时域采样、混叠和采样定理
式中:x(nTs)x(t) tnTS
,N1
TS——采样间隔; N——序列长度,N=T/TS; fs——采样频率, fs =1/TS。
若采样间隔太小(采样频率高),则对定长的时间记录来说 其数字序列就很长,计算工作量迅速增大;如果数字序列 长度一定,则只能处理很短的时间历程,可能产生较大的 误差。 若采样间隔过大(采样频率低),则可能丢掉有用的信息。
采样——把连续时间信号变成离散时间序列的过程。 这一过程相当于在连续时间信号上“摘取”’许多离散时 刻上的信号瞬时值。 在数学处理上,可看作以等时距的单位脉冲序列(称其为 采样信号)去乘连续时间信号,各采样点上的瞬时值就变 成脉冲序列的强度。以后这些强度值将被量化而成为相应 的数值。
x(n)x(nTs) x(nfs),n0,1,2,
(f1+f2)/2=fs/2 这也就是称fs/2为折叠频率的由来。
不产生混叠的条件:
a)模拟信号x(t)为带限信号
b)
1 fs Ts 2 fh
奈魁斯特采样定理 通常fs=(3—4)fc
二、量化和量化误差
量化——用有限个允许值近似地代替精确值。
量化方法:截尾、舍入
截尾——将二进制数的多余位舍掉。
二、信号的自相关函数
对各态历经随机信号及功率信号可定义自相关函数Rx(τ)为
R x (
机械工程测试技术第五章信号处理初步

0
S( f ) 1/Ts
0
│X( f )*S( f )│
f
1/Ts t
-21Ts 0
1
1f
2Ts
Ts
窗函数
w(t) 1
0
Tt
x(t) s(t) w(t)
W(f )
▲
0
f
-1/T 1/T
│[X( f )*S( f )]*W( f )│
0
T
t
d(t)
10
1
f
2Ts
2Ts
D( f )
频域采样
1
-T
0
...
2 e
Dx
e 2 2
Dx 2
1 de
Dx
Dx 2 12
误差的标准差为: se =0.29Dx
4. 采样、混叠和采样定理
(1).信号采样和混叠 10 A
x1(t) x2(t)
x1(t ) Asin(2 10t ) 5
0
x2 (t ) A sin(2 50t ) -5 1 2 3 4 5 6 7 8 t
f
旁瓣
| X( f )|
正弦信号
A 2 的频谱
= =
t
将截断信号谱 |X-(Af )WR(f )|与原始信号谱 X正(f弦)相信比号较可xRR知(t)),它已不是原来的两条谱 线的,加而窗是两段++A振A 荡的连续谱. 原来集中 在 去了f1处,-的这TT能种量现被象0分0称--散A之到为两频TT个谱较能宽量的泄t频漏带。中
...
Tf t
1
0
1
f
2Ts
2Ts
D( f )
...
0
Df
机械工程测试技术第五章信号处理初步

4)Rx(τ)的取值范围
x 2x 2R x()x 2x 2
13
5)周期函数的自相关函数仍为同频率的周期函数, 其幅值与原周期信号的幅值有关,而丢失了原信 号的相位信息。
图5·14是四种典型信号的自相关函数,稍加对比就可以看到自 相关函数是区别信号类型的一个非常有效的手段。只要信号 中含有周期成分,其自相关函数在τ很大时都不衰减,并具有明 显的周期性。不包含周期成分的随机信号,当τ稍大时自相关 函数就将趋近于零。宽带随机噪声的自相关函数很快衰减到 零,窄带随机噪声的自相关函数则有较慢的衰减特性。
§5-3 功率谱分析及其应用
时域中的相关分析为在噪声背景下提取有用信息提供了途径。 功率谱分析则从频域提供相关技术所能提供的信息,它是研究平 稳随机过程的重要方法。
一、自功率谱密度函数
若τ→∞,Rx(τ)→0。(收敛,可积) 自相关函数Rx(τ)进行傅里叶变换Sx(f) 。
逆变换
Sx(f) Rx()ej2fd
s
1 2
m
v——音响通过管道的事传播速度。
18
由式(5-19)和式(5-25)所定义的相关函数只适用于各态历经 随机信号和功率信号。对于能量有限信号的相关函数,其中 的积分若除以趋于无限大的时间T后,无论时移τ为何值,其 结果都将趋于零。因此,对能量有限信号进行相关分析时, 应按下面定义来计算:
R x() x(t)x(t)dt Rxy () x(t)y(t)dt
§5-1 随机信号的幅值域分析
一、随机信号的基本概念
随机信号是不能用确定的数学关系式来描述的,不能预 测其未来任何瞬时值,任何一次观测值只代表在其变动 范围中可能产生的结果之一,但其值的变动服从统计规 律。
样本函数:对随机信号按时间历程所作的各次长时 间观测记录,记作xi(t)。 样本记录:样本函数在有限时间上的部分
(优选)第部分信号处理初步

x ( ) 0
4)自相关函数是偶函数
Rx
(
)
2 x
5)周期信号的自相关函数仍然是同频率的周期信号, 其幅值与原信号有关,但丢失了原信号的相位信息。
相关分析
相关分析
例 5-1 求正弦函数的自相关函数
x(t) x0 sin(t )
Rx ( )
x02 2
cos
0
自相关系数
x ( )
Rx ( )
2 x
2 x
周期信号
Rx
(
)
1 T0
T0 x(t )x(t )dt
0
相关分析
自相关函数有如下性质:
1)取值范围
2 x
2 x
Rx (
)
2 x
2 x
2)当 = 0 时,自相关函数具有最大值(=均方值)。
3)当 足够大或 →时,随机变量 x(t) 和 x(t+) 之
x(t)
0
频域解释 |X( f )|
t
0
f
0 t
0
f
0 t
0
f
采样定理
采样定理 为保证采样后信号能真实地保留原始
模拟信号信息,信号采样频率必须至少为原 信号中最高频率成分的2倍。这是采样的基 本法则,称为采样定理。
fs > 2 fh
采样定理
需注意,满足采样定理,只保证不发生频率混 叠,而不能保证此时的采样信号能真实地反映原 信号x(t)。工程实际中采样频率通常大于信号中最 高频率成分的3到5倍。
量化―把采样信号经过舍入变为只有有限个有效 数字的数,这一过程称为量化.
编码―将经过量化的值变为二进制数字的过程。
第五章信号处理初步资料

《机械工程测试技术》第五章数字信号处理初步主讲:王建军山东理工大学•机械工第五章信号处理初步●测试的目的:获取被测对象的状态和特征的信息。
但信号总是与噪声混杂在一起。
所以,有必要进行信号处理。
●信号处理的目的:➢1)分离信、噪,提高信噪比。
➢2)从信号中提取有用的特征信息。
➢3)修正测试系统的某些误差,如:传感器的线性误差、温度影响。
●信号分析:研究信号的构成和特征值。
●信号处理:信号经过必要的变换以获取所需信息的过程。
●信号处理分为两类:模拟信号处理和数字信号处理模拟信号处理:●实现模拟运算的电路,如模拟滤波器、乘法器、微分放大器等。
●模拟信号处理也可用于数字信号处理的前奏(如滤波、限幅、隔直、解调)及后续处理(如模拟显示、记录)。
数字信号处理:●用数字方法处理信号,可采用通用计算机,或专用的信号处理机实现。
●数字信号处理技术目前正处于迅速的发展阶段,如DSP芯片的开发与使用,势头很好。
第一节数字信号处理的基本步骤预处理A/D 转换数字信号处理器或计算机A/D 转换结果显示预处理x(t)y(t)物理信号x(t)传感器电信号信号调理电信号A/D 转换数字信号数字信号分析仪或计算机显示物理信号y(t)传感器电信号信号调理电信号A/D 转换数字信号☐1、信号的预处理:把信号变成适于数字处理的形式,减轻数字处理的困难。
●1)电压幅值调理,便于采样。
例如:12位A/D 转换器,参考电压为±5V ,其末位数字的当量电压为2.5mV 。
●2)必要的滤波,提高信噪比,虑去信号中的高频噪声。
●3)隔离信号中的直流分量(如果所测信号不允许有直流分量)。
●4)对调制信号进行预先解调。
预处理A/D 转换数字信号处理器或计算机A/D 转换结果显示预处理x(t)y(t)☐2、A/D 转换:●模拟信号经采样、量化并转化为二进制数的过程。
预处理A/D 转换数字信号处理器或计算机A/D 转换结果显示预处理x(t)y(t)☐3、数字信号处理器或计算机的作用●数字信号处理器或计算机的作用:对离散的信号进行处理,如去除奇异点、加权处理、进行温度和非线性的补偿,及数字滤波。
测试技术 第五章 信号处理初步

自相关函数是区别信号类型的一个非常有效的手段。 只要信号中含有周期成分,其自相关函数在τ很大时都不衰减,并具有明显 的周期性。而不包含周期成分的随机信号,当τ稍大时自相关函数就将趋近 于零。 于零
PDF 文件使用 "pdfFactory Pro" 试用版本创建
5.2.2 自相关函数 应用2:机械加工表面粗糙度的自相关分析
1 T R xy (τ ) = lim ∫0 x(t ) y (t + τ )dt T →∞T 1 T = ∫0 0 x0 sin(ωt + θ ) y 0 sin[ω (t + τ ) + θ − ϕ ]dt T0 1 ωt + θ = α sin α sin(α + ωτ − ϕ ) = − [cos(2α + ωτ − ϕ ) − cos(ϕ − ωτ )] 2 1 = x0 y 0 cos(ωτ − ϕ ) 结论:两个均值为零并具有相同频率的 2
第五章 信号处理初步
济南大学机械工程学院
5.1 信号处理概述
测试工作的目的:获取反映被测对象的状态和特征的信息。
但是有用的信号总是和各种噪声混杂在一起,很难识别,需要对其进 行必要的处理和分析、消除和修正系统误差。
信号处理的目的: 1)分离信号与噪声,提高信噪比; 2)从信号中提取有用的特征信号; 3)修正测试系统的某些误差,如线性误差等。
PDF 文件使用 "pdfFactory Pro" 试用版本创建
5.2.3 互相关函数 互相关函数
1 T (τ ) = lim ∫0 x(t ) y (t + τ ) dt R xy T → ∞T
R xy (τ ) → µ x µ y
《机械工程测试技术基础》课后试题及答案

《机械⼯程测试技术基础》课后试题及答案课后答案章节测试题第⼀章信号及其描述(⼀)填空题1、测试的基本任务是获取有⽤的信息,⽽信息总是蕴涵在某些物理量之中,并依靠它们来传输的。
这些物理量就是信号,其中⽬前应⽤最⼴泛的是电信号。
2、信号的时域描述,以时间(t )为独⽴变量;⽽信号的频域描述,以频率(f )为独⽴变量。
3、周期信号的频谱具有三个特点:离散性,谐波性,收敛性。
4、⾮周期信号包括准周期信号和瞬态⾮周期信号。
5、描述随机信号的时域特征参数有均值、均⽅值、⽅差。
6、对信号的双边谱⽽⾔,实频谱(幅频谱)总是偶对称,虚频谱(相频谱)总是奇对称。
(⼆)判断对错题(⽤√或×表⽰)1、各态历经随机过程⼀定是平稳随机过程。
(√ )2、信号的时域描述与频域描述包含相同的信息量。
( √ )3、⾮周期信号的频谱⼀定是连续的。
(╳)4、⾮周期信号幅频谱与周期信号幅值谱的量纲⼀样。
(╳)5、随机信号的频域描述为功率谱。
( √ )(三)简答和计算题1、求正弦信号t x t x ωsin )(0=的绝对均值µ|x|和均⽅根值x rms 。
2、求正弦信号)sin()(0?ω+=t x t x 的均值x µ,均⽅值2x ψ,和概率密度函数p(x)。
3、求指数函数)0,0()(≥>=-t a Ae t x at 的频谱。
4、求被截断的余弦函数≥<=T t T t tt x ||0||cos )(0ω的傅⽴叶变换。
5、求指数衰减振荡信号)0,0(sin )(0≥>=-t a t e t x at ω的频谱。
第⼆章测试装置的基本特性(⼀)填空题1、某⼀阶系统的频率响应函数为121)(+=ωωj j H ,输⼊信号2sin )(t t x =,则输出信号)(t y 的频率为=ω 1/2 ,幅值=y 2/1 ,相位=φ。
2、试求传递函数分别为5.05.35.1+s 和2224.141n n ns s ωωω++的两个环节串联后组成的系统的总灵敏度。
测试技术基础答案 第五章 信号处理初步
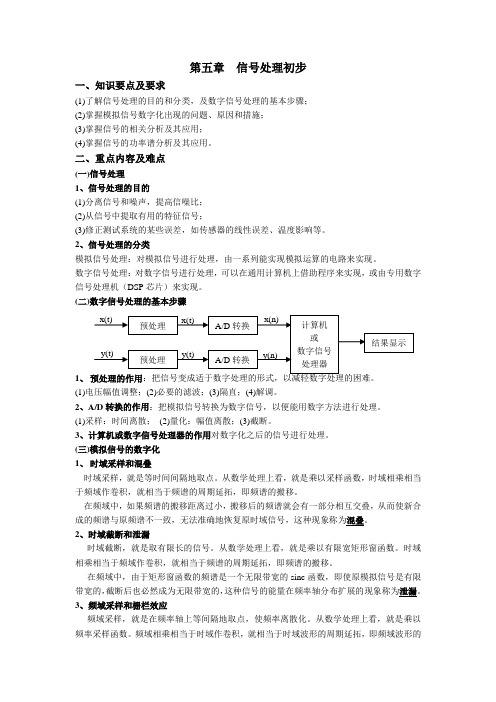
第五章信号处理初步一、知识要点及要求(1)了解信号处理的目的和分类,及数字信号处理的基本步骤;(2)掌握模拟信号数字化出现的问题、原因和措施;(3)掌握信号的相关分析及其应用;(4)掌握信号的功率谱分析及其应用。
二、重点内容及难点(一)信号处理1、信号处理的目的(1)分离信号和噪声,提高信噪比;(2)从信号中提取有用的特征信号;(3)修正测试系统的某些误差,如传感器的线性误差、温度影响等。
2、信号处理的分类模拟信号处理:对模拟信号进行处理,由一系列能实现模拟运算的电路来实现。
数字信号处理:对数字信号进行处理,可以在通用计算机上借助程序来实现,或由专用数字信号处理机(DSP芯片)来实现。
(二)数字信号处理的基本步骤1、(1)电压幅值调整;(2)必要的滤波;(3)隔直;(4)解调。
2、A/D转换的作用:把模拟信号转换为数字信号,以便能用数字方法进行处理。
(1)采样:时间离散;(2)量化:幅值离散;(3)截断。
3、计算机或数字信号处理器的作用对数字化之后的信号进行处理。
(三)模拟信号的数字化1、时域采样和混叠时域采样,就是等时间间隔地取点。
从数学处理上看,就是乘以采样函数,时域相乘相当于频域作卷积,就相当于频谱的周期延拓,即频谱的搬移。
在频域中,如果频谱的搬移距离过小,搬移后的频谱就会有一部分相互交叠,从而使新合成的频谱与原频谱不一致,无法准确地恢复原时域信号,这种现象称为混叠。
2、时域截断和泄漏时域截断,就是取有限长的信号。
从数学处理上看,就是乘以有限宽矩形窗函数。
时域相乘相当于频域作卷积,就相当于频谱的周期延拓,即频谱的搬移。
在频域中,由于矩形窗函数的频谱是一个无限带宽的sinc函数,即使原模拟信号是有限带宽的,截断后也必然成为无限带宽的,这种信号的能量在频率轴分布扩展的现象称为泄漏。
3、频域采样和栅栏效应频域采样,就是在频率轴上等间隔地取点,使频率离散化。
从数学处理上看,就是乘以频率采样函数。
频域相乘相当于时域作卷积,就相当于时域波形的周期延拓,即频域波形的搬移。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角窗
特点: 特点:主瓣较宽 (高T/2,宽 , 4/T),旁瓣则较 ),旁瓣则较 ), 低,不会出现负 值 分析窄带信号, 分析窄带信号, 且有较强的干扰 噪声时采用
汉宁窗
特点:主瓣较宽( ),分辨力较差 特点:主瓣较宽(高T/2,宽4/T),分辨力较差;旁瓣则较低 , ),分辨力较差;
倍程), (主瓣的2.4% ,-32dB,旁瓣的率减率为 主瓣的 ,旁瓣的率减率为60dB/10倍程),具有 倍程),具有 抑制泄漏的作用;分析窄带信号, 抑制泄漏的作用;分析窄带信号,且具有较强的干扰噪声时采 随即信号和非整周期截断周期函数。 用,如:随即信号和非整周期截断周期函数。
主要内容
• 数字信号处理的基本步骤 • 信号数字化出现的问题 • 相关分析及应用 • 功率谱分析及应用
数字信号处理的基本步骤
1)电压幅值调理,以适宜采样。 2)滤波,以提高信噪比。 3)隔离信号中的直流分量。 4)调制解调。
模拟信号经采 样、量化并转 化为二进制
信号数字化出现的问题
• 数字信号处理:模拟信号 数字信号
• 泄漏产生的原因:窗函数的频谱是无限带宽的。 泄漏产生的原因: • 减小泄漏的措施:采用合适的窗函数来对所截取 减小泄漏的措施
的时域信号进行加权处理。
余弦信号被矩形窗函数截断形成的泄漏
信号数字化出现的问题 —频域采样、时域周期延拓1
• 频域采样:是使频率离散化,在频率轴上等间距地 频域采样:
取点的过程。而从数学处理上看,则是用采样函数去 乘连续频谱。 • 依据 FT的卷积特性——频域相乘就等于时域做卷积 • 依据 依据δ函数的卷积特性——时域作卷积就等于时域波 形的周期延拓 • 频域离散化,无疑已将时域信号“改造”成周期信号 • 频域采样和时域采样相似,在频域中用脉冲序列乘信 号的频谱函数。
信号数字化出现的问题 —栅栏效应
• 定义:采样的实质就是摘取采样点上对应的函数值, 定义:采样的实质就是摘取采样点上对应的函数值,
其效果有如透过栅栏的缝观看外景一样, 其效果有如透过栅栏的缝观看外景一样,只有落在缝 隙 前的少数景象被看到,其余景象都被栅栏挡住, 前的少数景象被看到,其余景象都被栅栏挡住, 视为零。这种现象称为栅栏效应 栅栏效应。 视为零。这种现象称为栅栏效应。
注意: 注意:将原频谱X(f) 依次平移1/Ts至个 采样脉冲对应的频 域序列点上,然后 全部叠加而成
信号数字化出现的问题 —混叠2
• 混叠产生原因
– 采样频率fs太低 – 原模 →∞
• 对非有限带宽的模拟信号,在采样之前先通过模拟低 通滤波器滤去高频成分,使其成为带限信号。这种处 理称为抗混叠滤波预处理。 • 满足采样定理
fs > 2fh
信号数字化出现的问题 —采样定理
• 采样定理:为了不产生频率混叠,应使采样 频率大于带限信号的最高频率的2倍,即
fs > 2fh
提醒注意:在实际工作中, 提醒注意:在实际工作中, 考虑实际滤波器不可能有理 想的截止特性, 想的截止特性,在其截止频 率 fc 之后总有一定的过渡 带,通常取
指数窗
特点:主瓣很宽,无旁瓣,非对称窗,起抑 特点:主瓣很宽,无旁瓣,非对称窗, 制噪声的作用; 制噪声的作用; 在测量系统的脉冲响应时适宜采用
第五章 信号处理初步
郑惠萍 河北科技大学机械电子工程学院
绪论
分 信 噪 提 信 比 离 、 , 高 噪
信 处 号 理 的 目
提 有 的 征 取 用 特 修 测 系 的 些 差 正 试 统 某 误
模 拟 信 号 处 理 系 统
内 容 方 法 数 字 信 号 处 理 系 统
专 用 数 字 信 号 处 理 机 CAT
x(n) = x(nT ) = x(n fs ) s
n =0,12⋯ −1 , N
信号数字化出现的问题 —时域采样2 x(n) = x(nT ) = x(n fs ) n =0,12⋯ −1 , N s
样 隔 T →采 间 ; s
x(n s ) = x(t) t=nTs T
N →序 长 , =T T 列 度 N s fs →采 频 ,s =1 T 样 率 f s
采样和截断
采样是用一个等时距的周期脉冲序列(或采样函数) s(t)去乘原模拟信号x(t)。时距Ts称为采样间隔, 1/Ts=fs称为采样频率。
时域采样
时域截断
频域采样
注意:频域采样形成频域函数离散化,相应地把 其时域函数周期化了。
信号数字化出现的问题 —时域采样1
• 采样是把连续时间信号变成离散时间序列的过程,就 是等间距地取点。而从数学处理上看,则是用采样函 数去乘连续信号。 • 依据 FT的卷积特性 的卷积特性:时域相乘就等于频域做卷积 的卷积特性 • 依据δ函数的卷积特性 依据δ函数的卷积特性 函数的卷积特性:频域作卷积就等于频谱的周 期延拓 • 长度为T的连续时间信号x(t),从t=0点开始采样,得到 离散时间序列x(n)为
fs =(3~ 4) fc
信号数字化出现的问题 —量化和量化误差
• 定义:时域采样只是把连续信号的时间离散化了。 定义:
而对于幅值如果用二进制数码组来表示,就是离散信 号变成数字信号。这一过程称为量化。量化一般是由 A/D转换器来实现的。
• 量化误差 设A/D转换器的位数为b,允许的动态工 量化误差:
• 影响:时域采样和频域采样,都有相应的栅栏效应。 影响:时域采样和频域采样,都有相应的栅栏效应。
时域采样如满足采样定理要求 如满足采样定理要求, 不过 时域采样如满足采样定理要求,栅栏效应不会 有什么影响。 频域采样的栅栏效应则影响很大 的栅栏效应则影响很大, 有什么影响。而频域采样的栅栏效应则影响很大, 挡住” “挡住”或丢失的频率成分有可能是重要的或具有特 征的成分,以致于整个处理失去意义。 征的成分,以致于整个处理失去意义。
信号数字化出现的问题 —栅栏效应
• 采取措施
• 减小频率采样间隔 ,即提高频率分辨力,则栅栏效 减小频率采样间隔∆f,即提高频率分辨力, 应中被挡住的频率成分越少。但同时∆f=fs/N=1/T是 应中被挡住的频率成分越少。但同时 是 DFT算法固有的特征,在满足采样定理的情况下,这 算法固有的特征, 算法固有的特征 在满足采样定理的情况下, 往往加剧频率分辨力和计算工作量的矛盾。 往往加剧频率分辨力和计算工作量的矛盾。 • 对周期信号实行整周期截断。(是获得准确频谱的先 对周期信号实行整周期截断。 是获得准确频谱的先 决条件) 决条件
信号数字化出现的问题 —频域采样、时域周期延拓2
• 重要参数 频率分辨率) 重要参数(频率分辨率 频率分辨率
1 fs = →频 采 间 ; 率 样 隔 T N 1 fs N = Ts = → 依 D T的 有 征 N 序 的 谱 列 ( 据F 固 特 ,点 列 频 序 1 ∆ f T 仍 N ) 为点 ∆ = f
量化误差特点
• 量化误差将形成信号采样值上的随机噪 声 (1) 提高A/D转换的位数,既降低
1 概 密 为 率 度 ∆ x (2)实际上,和信号获取、处理的其 均 为 值 0 他误差相比,量化误差通常不大,所 ∆2 x 方 为 以一般可忽略其影响。 均 值 12 ∆2 x ∆ x 标 差 方 = 准 为 差 −0 = ≈0.29∆ x 12 2 3
x 作范围为D,则相邻量化电平之差 ∆ = D 2 (由于 实际上字长的第一位常用作符号位),每个量化电平 对应一个二进制数码。若采样点的电平落在两相邻量 化电平之间,就必须含入到相近的一个量化电平上。 改制与实际电平的差值称为量化误差。
(b− ) 1
ε(n) = x(n)实 −x(n)量 电 际 化 平
注意:采样间隔的选择是个重要的问题!
小 过
过
大
工作量会很大
丢失有用信息
信号数字化出现的问题 —时域采样3
由于采样频率过低造成的混叠现象
信号数字化出现的问题 —混叠1
• 定义:在频域中,如果平移距离过小,平移后的频
谱就会有一部分相互交叠,从而使新合成的频谱与原 频谱不一致,因而无法准确地恢复原时域信号,这种 现象称为混叠。
sinπfT =Tsin c(πfT) πfT
特点:主瓣最窄( )、旁瓣则较高 特点:主瓣最窄(高T,宽2/T)、旁瓣则较高(-13dB, , )、旁瓣则较高( 主瓣的20% ,旁瓣的率减率为 旁瓣的率减率为20dB/10倍频程 、泄漏最 倍频程)、 主瓣的 倍频程 在需要获得精确的频谱主峰所在频率, 大。在需要获得精确的频谱主峰所在频率,而幅值要求 不高时采用, 不高时采用,如:测量物体的自振频率
了量化误差,但A/D转换的位数选择应 视信号的具体情况和量化的精度要求 而定,位数增多后,成本显著增加, 转换速率下降。
信号数字化出现的问题 —截断、泄漏和窗函数
• 截断: 截断: • 泄漏:由于矩形窗函数的频谱是一个无限带宽的 泄漏
sinc函数。所以即使x(t)是带限信号,在截断后也仍 然成为无限带宽的信号,这种信号的能量在频率轴 分布扩展的现象称为泄漏。
常用的窗函数
• 作用 为了减少和抑制泄漏 作用:为了减少和抑制泄漏
最大旁瓣值与 主峰值之比 窗函数 评价标准 最大旁瓣的倍 频程衰减率 主瓣宽度
小的旁瓣 可以减少 泄漏
窄的主瓣 提高频率 分辨能力
矩形窗
1 ω t) = ( 0 t < T 2 T t > 2
W( f ) =T
