第一章导学案1、2
鲁教版九年级第一章反比例函数

九年级_____班姓名__________ 2018年_____月_____日第一章反比例函数“1.1 反比例函数”导学案学习目标:1 理解反比例函数的意义,能根据已知条件确定其表达式;2 积累从实际问题抽象出变量之间的关系并加以表示的经验.教学过程:一、自主学习1 回顾函数的概念:一般地,如果在某个______________中有两个__________,并且对于_____ ______________,变量y都有___________________________,那么我们就称________________。
其中_________________________。
2表示函数的方法有_________、__________________和____________________。
3若_______________________________________________________________________________________,则称y是x的一次函数。
特别地,当b = 0时,称y是x的_________________。
4 汽车从南京出发开往上海(全程约300km),全程所用时间t(h),随速度v(km/h)的变化而变化. (1)用含v的代数式表示t: ______________________(2)利用(1)的关系式完成下表:随着v的变化,t是如何变化的?(3)时间t是速度v的函数吗?为什么?5 某村有耕地346.2公顷,人口数量n逐年发生变化,那么该村人均占有耕地面积m(公顷/人)与全村人口数n之间有怎样的关系?m是n的函数吗?_____________________________6 实数a与b的积为-200,a与b之间的函数关系是_______________________二、新知探究1 交流上述问题的答案,观察列出的函数关系式,它们有什么共同特点?2 仿照一次函数的概念,给出反比例函数的概念,其中自变量x的取值范围是__________;3(1)已知y是x的反比例函数,当 x = 3时,y = -2 ,求y与x的函数关系式.(2)已知函数y=y1+y2,y1与x+1成正比例,y2与x成反比例,且当x =1时,y =0;当x =4时,y =9,求当x =-1时y的值。
卢氏县第二中学七年级数学上册第一章有理数1.2有理数1.2.1有理数导学案新版新人教版1

1.2.1 有理数1.掌握有理数的概念,会对有理数按一定标准进行分类,培养分类能力;2.了解分类的标准与集合的含义;3.体验分类是数学上常用的处理的问题的方法.重点:正确理解有理数的概念;难点:正确理解分类的标准和按照一定标准分类.一、温故知新通过上节课的学习,那么你能写出3个不同类的数吗?(4名学生板书)二、自主学习问题1:观察黑板上的12个数,我们将这4位同学所写的数做一下分类.该分为几类,又该怎样分呢?先分组讨论交流,再写出来分为__五__类,分别是:正数,0,负数,正分数,负分数 问题2:我们是否可以把上述数分为两类?如果可以,应分为哪两类?师生共同交流、归纳.三、引导归纳1.正整数,0,负整数统称为整数,整数和分数统称为有理数.2.正数集合与负数集合所有的正数组成正数集合,所有的负数组成负数集合.1.P6练习.(做在课本上)2.把下列各数填入它所属于的集合的圈内:15,-19,-5,215,-138,0.1,-5.32,-80,123,2.333.正整数集合 负整数集合正分数集合 负分数集合有理数分类⎩⎪⎨⎪⎧正有理数⎩⎪⎨⎪⎧正整数正分数零负有理数⎩⎪⎨⎪⎧负整数负分数 或者有理数⎩⎪⎨⎪⎧整数⎩⎪⎨⎪⎧正整数零负整数分数⎩⎪⎨⎪⎧正分数负分数到现在为止我们学过的大部分数都是有理数(圆周率除外),有理数可以按不同的标准进行分类,标准不同,分类的结果也不同.下列说法中不正确的是( C )A .-3.14既是负数、分数,也是有理数B .0既不是正数,也不是负数,但是整数C .-2000既是负数,也是整数,但不是有理数D .0是正数和负数的分界3.4 实际问题与一元一次方程第1课时实际问题与一元一次方程(1)知能演练提升能力提升1.一群学生在某电站建设工地进行社会实践活动,男生戴白色安全帽,女生戴红色安全帽.休息时他们坐在一起,大家发现了一个有趣的现象,每名男生看到白色与红色的安全帽一样多,而每名女生看到白色的安全帽是红色的2倍.根据这些信息,请你推测这群学生共有()A.3人B.4人C.7人D.8人2.某车间28名工人生产螺栓和螺母,每人每天平均生产螺栓12个或螺母18个.现有x名工人生产螺栓,其他工人生产螺母,恰好每天生产的螺栓和螺母按1∶2配套,为求x列出的方程是()A.12x=18(28-x)B.12x=2×18(28-x)C.2×18x=18(28-x)D.2×12x=18(28-x)3.一个两位数,个位数字与十位数字的和是9,如果将个位数字与十位数字对调后所得的新数比原数大9,那么原来的两位数为()A.54B.27C.72D.454.某工程,甲单独做需12天完成,乙单独做需8天完成.现由甲先做3天,乙再参加合作,求完成这项工程共用的时间.若设完成此项工程共用x天,则下列方程正确的是()A.=1B.=1C.=1D.=15.敌我两军相距14 km,敌军于1 h前以4 km/h的速度逃跑,现我军以7 km/h的速度沿敌军逃跑路线追击,几小时后可追上敌军?若设x h后可追上敌军,则可列方程为.6.一种牙膏出口处直径为5毫米,小明每次刷牙都挤出1厘米长的牙膏,这样一支牙膏可以用36次.该品牌牙膏推出新包装,只是将出口处直径改为6毫米,小明还是按习惯每次挤出1厘米的牙膏,这一支牙膏能用次.7.一水池装有甲、乙、丙三个水管,甲、乙是进水管,丙是出水管,单开甲管需要16分钟注满,单开乙管需要10分钟注满,单开丙管20分钟可将全池水放完.现在先开甲、乙两管4分钟后,接着关上甲管,开丙管,再过几分钟能将水池注满?设再经过x分钟能将水池注满,则根据题意,列方程得.8.红星服装厂生产某种型号的学生服装,已知每3 m布料可做上衣2件或裤子3条(1件上衣和1条裤子为一套),计划用600 m布料生产这批学生服装,应分别用多少布料生产上衣和裤子使其恰好配套?一共能生产多少套学生服装?9.某工厂安排600名工人生产A,B型机器共69台,已知7名工人能生产一台A型机器,10名工人能生产一台B型机器.(1)有多少工人分别生产A型机器和B型机器?(2)如果人数不变,那么能生产这两种机器共70台吗?创新应用★10.数学活动课上,李老师布置了这样一道题,“学校校办工厂需制作一块广告牌,请来2名工人师傅.已知师傅单独完成需3天,徒弟单独完成需6天,请你补充一个问题并解答.”(1)调皮的小明说:“让我试一试,”上去添了“两人合做需要几天完成?”请你就小明的补充进行解答;(2)小红说:“我也来试一试,”她添了“现由徒弟先做3天,再由两人合做,两人再需要合做几天完成?”请你就小红的补充进行解答.参考答案知能演练·提升能力提升1.C设男生有x人,则女生有(x-1)人.根据题意,得x=2(x-1-1),解得x=4.x-1=3.故这群学生共有7人.2.D因为螺栓和螺母按1∶2配套,所以螺栓的个数是螺母个数的一半,即相等关系为螺栓的个数×2=螺母的个数.3.D设原来两位数的个位上的数字为x,则十位上的数字为(9-x),由题意,得10x+(9-x)-[10(9-x)+x]=9,解得x=5,所以原来的两位数为45.4.D5.7x=4(x+1)+146.25设这一支牙膏能用x次,根据题意,得3.14××10×36=3.14××10·x,解得x=25.7.=1根据相等关系“甲、乙两管4分钟注入的水+乙管x分钟注入的水-丙管x分钟放出的水=1”,列方程得=1.8.解设用x m布生产上衣,则用(600-x)m布生产裤子.根据题意,得×2=×3,解得x=360.600-360=240(m).360÷3×2=240(套).答:用360 m布料生产上衣,240 m布料生产裤子,恰好配套,一共能生产240套学生服装.9.解(1)设生产A型机器的工人有x名,则生产B型机器的工人有(600-x)名.根据题意,得=69,解得x=210.600-210=390(名).答:生产A型机器和B型机器的工人分别有210名和390名.(2)设生产A型机器的工人有y名,则生产B型机器的工人有(600-y)名.根据题意,得=70.解得y=233.因为人数必须是非负整数,所以x的值不符合题意.答:如果人数不变,那么不能生产这两种机器共70台.创新应用10.解(1)设两人合做需要x天完成,列方程,得x=1,解得x=2.答:两人合做需要2天完成.(2)设两人再需要合做y天完成,列方程,得×3+y=1.解得y=1.答:两人再需要合做1天完成.一、新课导入1.课题导入:上节课我们学习了方程的解,你能说出4x=24,x+1=3这样简单方程的解吗?你能直接看出方程21132x x+--=1的解吗?若不能,那么应如何求出它的解呢?因为方程是含有未知数的等式,因此,我们就从等式的性质入手来解方程.(板书课题)2.三维目标:(1)知识与技能①了解等式的两条性质.②会用等式的性质解简单的(用等式的一条性质)一元一次方程.(2)过程与方法①渗透“化归”的思想.②培养学生观察、分析、概括及逻辑思维能力.(3)情感态度培养言必有据的思维能力和良好的思维品质.3.学习重、难点:重点:等式的性质.难点:等式的性质解方程.二、分层学习1.自学指导:(1)自学内容:教材第81页的内容.(2)自学时间:8分钟.(3)自学方法:注意从图中不同方向的两个箭头所示的天平中物体的变化,归纳出相应的等式的性质.(4)自学参考提纲:①在图3.1-1中,如果把左边天平左盘中的量用a表示,把右盘中的量用b表示,则由天平左右平衡可以得出a=b;如果把天平左右盘中变化的量用c表示. 由天平保持平衡,观察:从左边天平到右边天平,盘中的量是增加(填“增加”或“减少”)的,用字母a、b、c的式子表示为:如果a=b,那么a+c=b+c;类似地,反过来如果a=b,那么a-c=b-c.由此可得等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等.②在图3.1-2中,把左边天平左盘中的量用a表示,右盘中的量用b表示,由天平左右平衡,可以得出a=b;由左边天平到右边天平,用数学式子可表示为:如果a=b,那么3a=3b ;类似地,反过来有,如果a=b ,那么3a =3b .在上面结论中,如果把3换成字母c ,结论还成立吗?请你用文字语言和数学式子表述等式的性质2.等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.即如果a=b ,那么ac=bc;如果a=b (c ≠0),那么a c =bc . ③依据等式的性质判断下列变形是否正确.a.如果3a+2=b+2,那么3a=b.(√)b.如果x-2=y+3,那么x=y+5.(√)c.如果xy=1,那么x=1y.(√) d.如果ab=bc ,那么a=c.(×)2.自学:学生可结合自学指导进行自学.3.助学:(1)师助生:①明了学情:教师巡视课堂了解学生的自学情况和存在的问题.②差异指导:对学习有困难的学生进行点拨和指导.(2)生助生:小组同学们相互交流探讨,互助解决学习中的问题.4.强化:(1)等式的性质1及其数学式子表达.(2)等式的性质2及其数学式子表达.(3)研讨:某同学得出了一个错误的结论“-5=3”,你知道是怎么回事吗?原来他是这样得到的:已知-5a=3a ,两边同时除以a ,即5a a =3a a,∴-5=3.你知道他错在哪里吗? 解:a 值为0,而等式性质二是除以同一个不为0的数,结果才相等.1.自学指导:(1)自学内容:教材第82页的内容.(2)自学时间:8分钟.(3)自学要求:认真阅读课文例2中每个方程的求解过程,思考每一步变形的依据是什么?不清楚的地方相互交流研讨.(4)自学参考提纲:①解以x 为未知数的方程,就是把方程逐步转化为x=a(常数)的形式,其转化的依据是等式的性质.②解方程x+7=26.要把方程转化为x=a的形式,就必须消去等号左边的常数7,因此只有根据等式的性质1,方程两边同时减7.③解方程-5x=20.要把方程转化为x=a的形式,就必须把等号左边-5x的系数化为1,因此只有根据等式的性质2,方程两边同时除以-5.④解方程-13x-5=4.要把方程转化为x=a的形式,就既要把等号左边的常数项-5消去,又要把的系数化为1,因此,先要根据等式的性质1,方程两边同时加5,再根据等式性质2,方程两边同时除以-13.2.自学:学生可结合自学指导进行自学.3.助学:(1)师助生:①明了学情:教师巡视课堂充分了解学生的自学情况.②差异指导:对学习困难的学生进行点拨和指导.(2)生助生:小组内同学们相互交流、讨论,互助解决疑难问题.4.强化:①解方程时,方程的变形目标:逐步转化为x=a(常数)的形式.②解方程时方程的变形依据是等式的两个性质,并且通常都是把含有未知数的项放在等号的左边.③解方程要养成检验的习惯.④练习:利用等式的性质解下列方程并检验.a.x-5=6 c.5x+4=0 d.2-14x=3解:a.x=11; b.x=150; c.x=-45d.x=-4.三、评价1.学生自我评价:学生代表交流学习的收获和困惑.2.教师对学生的评价:(1)表现性评价:教师对学生在本节课的学习中的优异表现、获得的成效和存在的问题进行总结和点评.(2)纸笔评价:课堂评价检测.3.教师的自我评价(教学反思):本课时教学要重视学生思维的多角度培养,教师对教材中的实际问题要直观演示,指导学生观察图形,从实验中归纳结论,并用实验验证.对发现的结论用文字、数学语言分别表达出来,突出对等式性质的理解和应用.在解方程时,要求说明每一步变形的依据,解题后及时小结.扎实做到这些,可为后面教与学打下坚实基础.一、基础巩固1.(20分)下列说法错误的是(D)A.若x=3,则3=x.B.若x=y,y=z,则x=z.C.若ab=1,则a=1b. D.若2+a=b-3, 则4+2a=2b-3.2.(20分)如果mx=my,那么下列等式中不一定成立的是(D)A.mx+1=my+1B.mx-3=my-3C.-mx=-myD.x=y3.(20分)用等式的性质解下列方程.(1)x-4=29 (2)12x+2=6解:x=33 解:x=8(3)3x+1=4 (4)4x-2=2解:x=1解:x=1二、综合应用4.(10分)下列变形正确的是(A)5.(20分)利用等式的性质解下列方程并检验.(1)5-15x=-5 (2)512x-14=13解:x=50 解:x=1.4 三、拓展延伸6.(10分)一个两位数个位上的数是1,十位上的数是x,把1与x对调,新两位数比原两位数小18,试列出关于x的方程,并解这个方程.解:依题意可得:10x+1-(10+x)=18,9x-9=18,9x=27,x=3.。
导学案-第一章 声现象

第一章声现象一、声音是什么【课前预习】1、用手摸一摸家里正在发声的电视机的喇叭或音箱,你可以感觉到喇叭在_________。
2、声音是由物体的产生的。
我们把正在发声的物体叫做_________。
3、通过课本活动1.2,你可以得出,声音可以在_______、________、________中传播,但不能在_________中传播。
4、声音在空气中是以波动的形态传播的,我们把它叫做_________。
声音还具有能量,叫做_________。
5、通常情况下,声音在空气中的传播速度为____________,在水中传播要比空气中要______,在钢铁中传播比水中还要_________。
【课堂重点】〖学习过程〗一、活动1.1探究声音的产生:通过使一张报纸、一根橡皮筋、一杯水、一个笔帽发出声音,归纳物体发声与不发声时的不同,物体发声时的共同特征。
二、活动1.2声音能在固体、液体、气体中传播吗1.平时人们听到的声音是通过______传播的。
2.通过实验探究声音是否可以在固体、液体中传播。
3.实验探究真空是否能够传播声音。
①将正在发声的手机放在正在抽出空气的玻璃瓶内,声音会____________。
②通过推理,我们可知,声音______(能/不能)在真空中传播。
三、声音是一种波通过演示实验及观察水波知道声音也是波,叫声波。
四、声音传播的快慢(声速)阅读课本P10内容知道,通常声音在空气中传播速度_______m/s,声音在水中传播速度________m/s,声音在钢铁中传播速度________m/s。
阅读“生活物理社会”,了解声能。
〖要点归纳〗1、声音是由于物体_________产生的。
2、我们把___________的物体叫做声源。
固体、液体、气体都能发声,都可以作为声源。
3、声音可以在、、中传播。
但不能在______传播4、声音也是一种波,叫做_______,是一种疏、密相间的波。
5、声波能使物体振动,能粉碎小石头,这表明声具有能量,这种能量叫做________。
第一、二单元(导学案)一年级上册数学西师大版

第一单元导学案
学习目标
1.了解数学的基础概念;
2.理解数学的重要性;
3.能够使用适当的数学术语和符号表达数学思想。
学习内容
数学的基础概念
1.数的概念
2.数值的大小和比较
3.数线
数学的重要性
1.数学在生活中的应用
2.数学在其他学科中的应用
3.数学对人生的影响
数学术语和符号
1.数字、数位和数值
2.加减乘除基本符号
3.数学术语的使用
学习方法
1.培养对数学的兴趣;
2.注重实践操作,强调理论应用;
3.整体思维,将知识点联系起来;
4.多角度、多维度思考问题,提升思维能力。
学习评价
1.课堂表现;
2.作业完成情况;
3.考试成绩。
第二单元导学案
学习目标
1.理解数的分解和组合;
2.掌握常见的数学方法;
3.能够应用数字和数学知识解决问题。
学习内容
数的分解和组合
1.十以内数的分解和组合
2.二十以内数的分解和组合
3.数的分解和组合在实际生活中的应用常见数学方法
1.算式和计算法则
2.运算顺序
3.基本的计量单位
数字和数学知识的应用
1.数量的比较
2.数量的测量
3.数学知识在生活中的应用
学习方法
1.注重提高数学实际应用能力;
2.多进行数学思维训练;
3.培养逻辑思维能力。
学习评价
1.课堂表现;
2.作业完成情况;
3.考试成绩。
湖北省高中数学第一章计数原理1.2排列与组合1.2.3组合与组合数公式导学案新人教A版选修2-3教案

1.2.3 组合与组合数公式【学习目标】1.正确理解组合与组合数的概念;2.弄清组合与排列之间的关系;3.掌握组合数公式,能运用组合数公式进行计算.重点难点重点:组合的概念和组合数公式难点:组合的概念和组合数公式【使用说明与学法指导】预习教材P 21~ P 23,找出疑惑之处复习1:什么叫排列?排列的定义包括两个方面,分别是取元素和排顺序 . 复习2:排列数的定义:从个不同元素中,任取个元素的排列的个数叫做从n 个元素中取出m 元素的排列数,用符号表示复习3:排列数公式:m n A =(,,m n N m n *∈≤【问题导学】组合的概念:一般地,从 n 个不同元素中取出m (m n ≤个元素合成一组,叫做从n 个不同元素中取出m 个元素的一个组合.组合数的概念:从n 个不同元素中取出m (m n ≤个元素的所有不同组合的个数,叫做从n 个不同元素中取出m 个元素的组合数....用符号 m n C 表示. 组合数公式及性质:问题1:“abc”和“acb”是相同的排列还是相同的组合?问题2:我们知道,“排列”与“排列数”是两个不同的概念,那么“组合”与“组合数”是同一个概念吗?为什么?【合作探究】问题1:判断下列问题是组合还是排列,并求出相应的组合数或排列数.(1若已知集合{}1,2,3,4,5,6,7,则集合的子集中有3个元素的有多少个?(28人相互发一个电子邮件,共写了多少个邮件?(38人相互握手一次,共握了多少次手?(4在北京、上海、广州、成都四个民航站之间的直达航线上,有多少种不同的飞机票?有多少种不同的飞机票价?解析:(1与顺序无关,是组合问题.共有3735C=个.(2发电子邮件有先后之分,与顺序有关是排列问题,共有2856A=个.(3相互握手无顺序,是组合问题,共有2828C=次.(4飞机票与起点站、终点站有关,是排列问题,共有2412A=种.机票价格只与两站的距离有关,是组合问题,共有246C=种.新知:排列不仅与元素有关,而且与元素的排列顺序有关,组合只与元素有关,与顺序无关,要区分排列与组合,可以选择一个结果,交换这个结果中两个元素先后顺序,看是否对结果产生影响,若无新变化,则是组合问题.变式:判断下列问题是组合还是排列:(1把当日动物园的4张门票分给5个人,每人至多分一张,而且票必须分完,有多少种分配方法?(2从2,3,5,7,11这5个质数中,每次取2个数分别作为分子和分母构成一个分数,共能构成多少个不同的分数?(3从9名学生中选出4名参加一个联欢会,有多少种不同选法?问题2:(1计算4331073C C A -;(2证明11m m n n mC nC --=.解析:(14331073C C A -=43107C A -=1098776504321⨯⨯⨯=-⨯⨯=⨯⨯⨯ (2证明:左边=!(1!!(!(1!(!n n n m m n m m n m -==---(1!(1!(!n n m n m -==--11m n nC --==右边. 新知:组合数的两个公式的应用有所区别,一般地,公式m mn n m mA C A =常用于,n m 为具体自然数的题目,偏向于具体组合数的计算;公式m n C =!!(!n m n m -常用于,n m 为字母或含有字母的式子的题目,偏向于方程的求解或有关组合数的恒等式的证明.变式:(1求值:591n n n n C C --++(2求证:11m m n n m C C n m++=-. 解析:5509190n n n n n n -≤⎧⎪-≥⎪⎨-≤+⎪⎪-≥⎩,解得45n ≤≤.又n N +∈,所以4=5n n =或.当4n =时,原式1545=+=5C C .当5n =时同理得原式=16.问题3:计算:(19796959898982C C C ++; (25555555678910C C C C C C +++++. 解析:(1原式=9796969598989898((C C C C +++=979697399991001001009998161700321C C C C ⨯⨯=+====⨯⨯(2原式= 6555556678910(C C C C C C+++++=65555657789101111462C C C C C C C =++++==== 新知:(1当2n m >时,通常不直接计算m n C ,而改为计算n m n C -(2注意组合数两个性质的灵活应用(凑项、拆项、变用、逆用等.变式:计算:(1598781007C C C + ; (2012345555555C C C C C C +++++ (311n n n n C C -+. 解析:(1原式=5006.(2原式=0125552(C C C ++=32.(3原式=(1(11n n n n n n C C +---+ =111n n C C +=(1n n + 【深化提高】解方程:232551616x x x C C +++=.错解:∵232551616x x x C C +++=, ∴23255x x x ++=+,即2230x x --=,解得11x =-(舍去,23x =,∴原方程的解为3x =.错因:错解的原因有二:一是将组合数的方程转化为代数方程时不等价.事实上, +=,,,,;x y n n x y x y n C C n x n y x y N =⎧⎪=⇔≥≥⎨⎪∈⎩或二是最后得出的结果没有检验,出现根的取舍错误.正解:∵232551616x x x C C +++=, ∴23255x x x ++=+,或2(32+(55=16x x x +++,即2230x x --=或2890x x +-=∴1x =-或3x =或9x =-或1x =.经检验3x =,9x =-不合题意,舍去,故原方程的解为1x =-,或1x =.【学习评价】●自我评价你完成本节导学案的情况为( .A. 很好B. 较好C. 一般D. 较差●当堂检测A 组(你一定行:1.下列四个问题属于组合问题的是(CA.从4名志愿者中选出2人分别参加导游和翻译的工作.B.从0,1,2,3,4这5个数字中选出3个不同的数字,组成一个三位数.C.从全班同学中选出3名同学出席深圳世界大学生运动会开幕式.D. 从全班同学中选出3名同学分别担任班长、副班长和学习委员.2.若3212n nA C =,则n 等于( A A.8 B.5或6 C.3或4 D.4B 组(你坚信你能行:3. 5688C C +得值为(B A.36 B.84 C.88 D.5044.已知2110100x x C C +-=,则x = 1或3 .C 组(我对你很有吸引力哟:5. 已知456,,n n nC C C 成等差数列,求12n C 的值. 解析:由已知得5462n n nC C C =+,所以 !!!25!(5!4!(4!6!(6!n n n n n n =+--- 整理得221980n n -+=解得7n =或14n =,要求12nC 的值,故12n ≥,所以14n =,则 122141414139121C C ⨯===⨯.【小结与反思】用后觉得难度、容量都大了。
七年级数学上册 第一章 基本的几何图形 1.2《几何图形》导学案1(新版)青岛版

1.2 几何图形【学习目标】1、通过一个侧面为长方体实物中,抽象出线和点,认识长方体的棱,顶点,各个面。
2、通过''通过点动成线,线动成面,面动成体'的生活实例,感受点、线、面、体之间的关系。
3、能判断一个图形是否正方体的展开图,能根据展开图想象和制作正方体模型。
【学习重点】1、从现实生活中抽象出点、线、面等图形,培养学生的观察能力;掌握点、线、面、体之间的关系.2、能初步判断一个图形是不是立方体的展开图,会利用展开图制作立方体模型.【学习难点】进一步发展学生的几何直觉,体验空间图形和平面图形的相互转化,发展合情推理和空间观念。
【课前预习】预习任务一:认识几何图形1、完成教材第7-8页的“观察与思考”,将答案写在课本上。
2、分别举出生活中成“点、线、面”形象的例子:点:___________________________________________________________线:___________________________________________________________面:___________________________________________________________3、举出生活中的实例:点动成线:_____________________________________________________线动成面:_____________________________________________________面动成体:_____________________________________________________4、举例:平面图形:_____________________________________________________立体图形:_____________________________________________________预习任务二:认识正方体的表面展开图1、完成教材第9页的“实验与探究”,将答案写在课本上。
青岛版数学七年级上第一章导学案
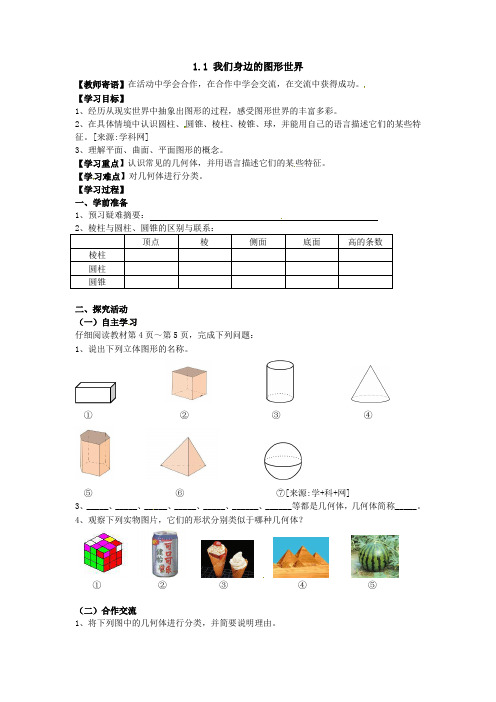
1.1 我们身边的图形世界【教师寄语】在活动中学会合作,在合作中学会交流,在交流中获得成功。
【学习目标】1、经历从现实世界中抽象出图形的过程,感受图形世界的丰富多彩。
2、在具体情境中认识圆柱、圆锥、棱柱、棱锥、球,并能用自己的语言描述它们的某些特征。
[来源:学科网]3、理解平面、曲面、平面图形的概念。
【学习重点】认识常见的几何体,并用语言描述它们的某些特征。
【学习难点】对几何体进行分类。
【学习过程】一、学前准备1、预习疑难摘要:2、棱柱与圆柱、圆锥的区别与联系:顶点棱侧面底面高的条数棱柱圆柱圆锥二、探究活动(一)自主学习仔细阅读教材第4页~第5页,完成下列问题:1、说出下列立体图形的名称。
①②③④⑤⑥⑦[来源:学+科+网]3、_____、_____、_____、_____、_____、______、______等都是几何体,几何体简称_____。
4、观察下列实物图片,它们的形状分别类似于哪种几何体?①②③④⑤(二)合作交流1、将下列图中的几何体进行分类,并简要说明理由。
①②③④⑤2、如图所示的各图中包含哪些简单的平面图形?①②③④3、在下图中的三幅图案中,你分别看到了哪些图形?它们是怎样组合而成的?三、巩固练习1、教材第5页练习1、2、3。
2、教材第7页练习1、2、3。
四、小结反思[来源:]这节课我学会了:;我的困惑:。
(1)(2)当堂测试1、写出如图所示图形的名称:①______;②______;③______;④______;⑤_____。
①②③④⑤2、下列几何体中不是多面体的是( )A、立方体B、长方体C、三棱锥D、圆柱3、下列几何体没有曲面的是()A、圆柱B、圆锥C、球D、棱柱4、下列图案是由哪些简单的几何图形组成的?5、请你用两个圆、两个三角形和两条线段组合几幅新奇、有趣的图形,并给出文字说明。
六、自我评价A B C D掌握知识的情况参与活动的积极性给自己一句鼓励的话1.2 点、线、面、体【教师寄语】相信自己,没错的!【学习目标】1、通过丰富的实例,认识点、线、面、体,初步感受点、线、面、体之间的关系。
高中化学必修一第一章第二节 离子反应导学案(人教版新教材)

第二节离子反应学习目标1.通过实验探究物质导电及原因,理解电解质导电能力强弱的本质原因。
2.理解电解质概念,能利用分类的方法判断物质属于电解质与非电解质。
3.理解电离概念和学会书写电离方程。
4.结合电离总结物质的性质,从电离角度解释一类物质的共同性质。
5.用实验证明离子反应的发生,理解离子反应的概念6.用“写”、“改(拆)”、“删”、“查”的方法书写离子方程7.离子反应发生的条件,离子反应的判断8.探究离子反应在分离、物质鉴定、离子共存等方面的应用初高衔接1.金属单质可以导电,酸、碱、盐的溶液可以导电,它们导电的原理是否相同呢?2.复分解反应发生的条件:生成沉淀、气体或者水,试分别写出不同类别物质发生的复分解反应方程(至少写3个不同的情况)知识点思维导图第1课时 电解质的电离知识点梳理一、电解质导电原理探析1.物质导电的原因: 。
2.化合物(以NaCl 为例)导电的原因。
结论:电解质能导电的状态为 。
二、电解质和非电解质 1.电解质:在 或 状态下能够导电的 。
如: 。
2.非电解质:在和状态下均不能导电的 。
如: 。
3.强电解质:在水溶液中能的电解质。
如:①强酸:HClO 4、H 2SO 4、HNO 3、HCl 、HBr 、HI 等②强碱:KOH 、NaOH 、Ba(OH)2、Ca(OH)2 等③绝大多数盐:NaCl 、KNO 3、BaSO 4、NaHSO 4、NaHCO 3、CH 3COONH 4 等 4.弱电解质:在水溶液中只能的电解质。
如:①弱酸(中强酸):H 2SO 3、H 3PO 4、HF 、CH 3COOH 、H 2CO 3、H 2S 、H 2SiO 3 等②弱碱:NH 3·H 2O 、Fe(OH)2、Fe(OH)3、Cu(OH)2、Zn(OH)2 等③水:H2O④少数盐:Pb(CH3COO)2等二、电离和电离方程1.电离概念:电解质在或解离成的离子的过程。
2.电离方程式的书写(1)强电解质完全电离,用表示,如:HCl ;(2)弱电解质部分电离,用表示,如:CH3COOH 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一节从生物圈到细胞
课型:新授课主备:李玮审核:王成富编号:1—101
班级学习小组姓名
【学习目标】
1.举例说出生命活动建立在细胞的基础之上。
2.举例说明生命系统的结构层次,并能区分生命系统的不同结构层次。
3.认同细胞是基本的生命系统。
【自主学习】
结论:。
2.生命系统的结构层次(从小到大):→→→→→→→→
最基本的生命系统是,最大的生命系统是。
【合作探究】
一、为什么说生命活动离不开细胞?
1、在你和父母之间,什么细胞充当了遗传物质的“桥梁”?胚胎发育与细胞的生命活动有什么关系?
2、HIV破坏淋巴细胞,导致艾滋病。
你还能举出特定细胞受损伤导致疾病的例子吗?
二、生命系统的结构层次有哪些?
1、所有生物都具有生命系统的的九大结构层次吗?举例说明。
2、一个分子或一个原子,也是一个系统吗?如果是,它们是不是生命系统?如果不是,请说明理由。
3、一个池塘中的所有鲤鱼、所有鱼、所有生物分别属于生命系统的哪个结构层次?
【课堂演练】
【例1】下列关于细胞与生命活动的叙述,错误的是 ( ) A.生命活动离不开细胞
B.病毒不具有细胞结构,所以它的生命活动与细胞无关
C.细胞是生物体结构和功能的基本单位
D.多细胞生物依赖高度分化的细胞密切协作,才能完成生命活动
【例2】下列组合,在生命系统的层次中依次属于种群、群落和生态系统的一组是 ( )
①一个池塘中的全部生物②一片草地上的全部昆虫
③某水库中的全部鲫鱼④一条河流
A.①②① B.③①④ C.①②③ D.②③④
【疑惑收集】通过本节课的学习,你还有哪些疑惑,请写在这里!
【评价检测】
A类(基础题)
1.生物体结构和功能的基本单位是()A.细胞B.组织C.分子 D.器官
2.下列生物中,没有细胞结构的是() A.大肠杆菌 B.HIV C.酵母菌 D.青霉菌
3.从生命系统的结构层次来分析,培养皿中的大肠杆菌菌落对应于下列哪一层次()A.个体B.种群C.群落 D.细胞
4.下列哪一项是一个生物群落()A.一座山上的所有蛇 B.一个城市的所有居民
C.一条河里的所有鱼D.一片森林的所有生物
5.地球上最基本的生命系统是()A.生态系统B.生物个体C.细胞 D.分子
6.最大的生态系统是()A.海洋生态系统B.森林生态系统C.草原生态系统D.生物圈
7.下列各项不属于生命系统的是 ( ) A.池塘中的一只青蛙
B.青蛙的表皮细胞
C.表皮细胞中的水和蛋白质分子
D.池塘中的水、阳光等因素以及在池塘中生活的青蛙等各种生物
8.一段朽木上面长满了苔藓、地衣,朽木凹处堆积的雨水中还生活着孑孓、水蚤等,树洞中还有老鼠、蜘蛛等,下列与这段朽木的“生命系统层次”水平相当的是 ( ) A.一块稻田里的全部昆虫 B.一个池塘中的全部鲤鱼
C.一片松林中的全部生物 D.一间充满生机的温室大棚
B类(拓展题)
9.在一个阳光明媚的小岛上,树木杂草茂盛,树上栖息着小益鸟和猫头鹰,地面上有田鼠、
青蛙和蛇,此外还有大量的昆虫、细菌和真菌等,从生命系统的结构层次分析回答:(1)该岛上全部的猫头鹰组成了。
(2)该岛上的一只田鼠属于。
(3)整个小岛组成一个。
(4)猫头鹰在繁殖季节繁殖了2只小猫头鹰,联系亲代和子代遗传物质的桥梁是。
(5)该岛上最基本的生命系统是。
第二节细胞的多样性和统一性
课型:新授课主备:李玮审核:王成富编号:1—102
班级学习小组姓名
【学习目标】
1、说出原核细胞和真核细胞的区别和联系。
2、分析细胞学说建立的过程。
3、认同细胞学说的建立是一个开拓、继承、修正和发展的过程,讨论技术进步在科学发展中的作用。
【自主学习】
1、回顾初中学过的动植物细胞的结构,观察图1—4和图1—5,完成下列填空。
细胞都有相似的结构,如、、,这反映了细胞的(统一性或多样性)。
但细菌、蓝藻细胞没有由包被的细胞核(称为拟核),这体现了细胞的性。
因此,科学家根据细胞内有无把细胞分成和。
2、阅读教材P9的文字,认识原核生物蓝藻和细菌
蓝藻常见种类有、、、等;蓝藻细胞内含有和,是能进行的自养生物;在淡水水域富营养化时会出现。
绝大多数细菌为营或的异养生物。
3、细胞学说的主要建立者是和,其要点为见教材P10。
细胞学说的意义:揭示了细胞性和生物体性。
【合作探究】
一、原核生物和真核生物的区别和联系
1、真核生物的细胞核与原核生物的拟核在结构和成分上有什么不同?
2、列表比较原核细胞和真核细胞的异同
3、以细胞结构为依据对生物进行分类,并举例。
(要求用概念图的形式呈现)
二、细胞学说的建立
阅读教材P10—11资料分析,完成下列问题:
1、细胞的发现者和命名者是谁?第一个观察到活细胞的科学家是谁?对细胞学说进行修正的科学家有哪些,他们的结论分别是什么?
2、从细胞学说的建立过程,你领悟到科学发现具有哪些特点?
【课堂演练】
【例1】下列四组生物中,细胞结构最相似的是()A.小麦和番茄 B.大肠杆菌和酵母菌
C.大豆和变形虫 D.灵芝和豌豆
【例2】下列细菌和蓝藻的叙述中,正确的是()A.都是自养生物 B.大小一样
C.都有DNA D.都有染色体
【例3】细胞学说的内容不包括()A.一切动植物都是由细胞发育而来,并由细胞及其代谢产物所构成
B.细胞是一个相对独立的单位,是具有生命的有机体
C.新细胞可以从老细胞中产生
D.细胞是一切生物结构和功能的基本单位
【疑惑收集】通过本节课的学习,你还有哪些疑惑,请写在这里!
【评价检测】
A类(基础题)
1、下列4种生物中,属于原核生物的是()
A、酵母菌;
B、乳酸菌;
C、草履虫;
D、水绵
2、发菜在生物学的分类上属于()
A、绿藻
B、蓝藻
C、细菌
D、植物
3、噬菌体和大肠杆菌的主要区别是()
A、无细胞壁
B、无核膜
C、无RNA
D、无细胞结构
4、病毒、蓝藻、和酵母菌都具有的物质或结构是()
A、细胞壁
B、细胞膜
C、线粒体
D、核酸
4、下列四组生物中,都属真核生物的一组是()
A、噬菌体和根霉
B、细菌和草履虫
C、蓝藻和酵母菌
D、衣藻和变形虫
5、细胞学说揭示了()
A、植物细胞和动物细胞的区别
B、生物体结构的统一性
C、细胞为什么能产生新的细胞
D、人们对细胞的认识是一个艰难曲折的过程
B类(拓展题)
6、下列说法正确的是()
(1)含细胞壁结构的细胞必定为植物细胞(2)蓝藻以群体形式存在,所以单个蓝藻不是一个个体(3)新细胞可以从老细胞中来(4)能进行自养的生物不一定是绿色植物
A、(1)(3)
B、(1)(4)
C、(3)(4)
D、(2)(4)
7、下图是几种生物的基本结构单位。
请根据图回答下面的问题。
(1)最有可能属于病毒的是,它在结构上不同于其他三种图示的显著特点是;病毒的生活及繁殖必须在内才能进行。
(2)图中属于原核细胞的是,它在结构上不同于真核细胞的最显著特点是,与真核细胞的统一性表现在。
(3)图中能进行光合作用的是〔〕,能完成此生理过程的物质基础是因为其内含有,因而它是一类营生活的生物。
(4)图展示了哺乳动物的平滑肌细胞,其遗传物质在存在方式上不同于其他三种图示的特点为。
