主成分分析报告报告材料实验报告材料
主成分分析报告

主成分分析报告第一点:主成分分析的定义与重要性主成分分析(Principal Component Analysis,PCA)是一种统计方法,它通过正交变换将一组可能相关的变量转换为一组线性不相关的变量,这组变量称为主成分。
这种方法在多变量数据分析中至关重要,尤其是在数据的降维和可视化方面。
在实际应用中,数据往往包含多个变量,这些变量可能存在一定的相关性。
这样的数据集很难直接进行分析和理解。
主成分分析通过提取数据中的主要特征,将原始的多维数据转化为少数几个互相独立的主成分,使得我们能够更加清晰地看到数据背后的结构和模式。
主成分分析的重要性体现在以下几个方面:1.降维:在数据集中存在大量变量时,通过PCA可以减少数据的维度,简化模型的复杂性,从而降低计算成本,并提高模型的预测速度。
2.去除相关性:PCA能够帮助我们识别和去除变量间的线性相关性,使得我们分析的是更加纯净的独立信息。
3.数据可视化:通过将多维数据映射到二维或三维空间中,PCA使得数据的可视化成为可能,有助于我们直观地理解数据的结构和模式。
4.特征提取:在机器学习中,PCA可以作为一种特征提取工具,提高模型的性能和泛化能力。
第二点:主成分分析的应用案例主成分分析在各个领域都有广泛的应用,下面列举几个典型的案例:1.图像处理:在图像处理领域,PCA被用于图像压缩和特征提取。
通过将图像转换到主成分空间,可以大幅度减少数据的存储空间,同时保留图像的主要信息。
2.金融市场分析:在金融领域,PCA可以用来分析股票或证券的价格动向,通过识别影响市场变化的主要因素,帮助投资者做出更明智的投资决策。
3.基因数据分析:在生物信息学领域,PCA被用于基因表达数据的分析。
通过识别和解释基因间的相关性,PCA有助于揭示生物过程中的关键基因和分子机制。
4.客户细分:在市场营销中,PCA可以用来分析客户的购买行为和偏好,通过识别不同客户群的主要特征,企业可以更有效地制定市场策略和个性化推荐。
《多元统计实验》主成分分析实验报告二

《多元统计实验》主成分分析实验报告三、实验结果分析6.5人均粮食产量x5,经济作物占农作物播种面积x6,耕地占土地面积比x7,果园与林地面积之比x8,灌溉田占1耕地面积比例x9等五个指标有较强的相关性, 人口密度x1,人均耕地面积x2,森林覆盖率x3,农民人均收入x4相关性也很强,再作主成分分析,求样本相关矩阵的特征值和主成分载荷。
λ11/2=2.158962,λ21/2=1.4455076,λ31/2 =1.0212708,λ41/2 =0.71233588,λ51/2 =0.5614001,λ61/2 =0.43887788,λ71/2 =0.33821497,λ81/2 =0.212900230,λ91/2=0.177406876。
确定主成分分析,前两个主成分的累积方差贡献率为75.01%,前三个主成分的累积方差贡献率为86.59%,按照累积方差贡献率大于80%的原则,主成分的个数取为3,前三个主成分分别为:Z*1=0.3432x*1-0.446x*3+0.376x*5+0.379x*6+0.432x*7+0.446x*9Z*2=0.368x*1-0.614x*2-0.61x*4-0.307x*5-0.1224x*6Z*3=-0.122x*6+0.246x*7-0.950x*8第一主成分在x*7,x*9两个指标上取值为正且载荷较大,可视为反映耕地占比和灌溉田占耕地面积比例的主成分,第二主成分在x*2和x*4这两个指标的取值为负,绝对值载荷最大,不能作为人均耕地和人均收入的主成分。
第三主成分,x*8这个指标取值为负且,载荷绝对值最大,不能反映果园与林地面积之比的主成分。
根据该图结果可以认为选取前两个指标作为主成分分析的选择是正确的。
将八个指标按前两个主成分进行分类:由结果可以得出森林覆盖率为一类,人口密度、果园与林地面积之比、耕地占土地面积比、灌溉田占耕地面积比为一类,经济作物占农作物播种面积比例、人均粮食产量、农民人均收入、人均耕地面积为一类。
产品成份分析报告

产品成份分析报告1. 概述本报告对产品成份进行了详细分析,包括成份的数量和比例,以及对各成份的功能和特性进行解释和评估。
该产品是一种化妆品,主要用于肌肤的护理和修复。
通过对成份的分析,可以更好地了解该产品的配方和功效。
2. 成份分析以下是该产品的主要成份以及它们的功能和特性:2.1 成份1•名称:成份1•含量:X%•功能:成份1具有XXX功能,可以XXX。
•特性:成份1具有XXX特性,可以XXX。
2.2 成份2•名称:成份2•含量:Y%•功能:成份2具有XXX功能,可以XXX。
•特性:成份2具有XXX特性,可以XXX。
2.3 成份3•名称:成份3•含量:Z%•功能:成份3具有XXX功能,可以XXX。
•特性:成份3具有XXX特性,可以XXX。
3. 成份比例分析根据成份的含量和比例,以下是对各成份的比例分析:•成份1占总成份的A%。
•成份2占总成份的B%。
•成份3占总成份的C%。
从比例分析结果来看,成份1在该产品中占比最大,其次是成份2和成份3。
这意味着成份1是该产品的主要成份,其功能和特性可能对产品的功效起着重要作用。
4. 功能评估根据对各成份功能的分析,以下是对产品的功能进行评估:•产品具有XXX功能,可以XXX。
•产品具有YYY功能,可以YYY。
•产品具有ZZZ功能,可以ZZZ。
从功能评估结果来看,该产品具有多种功能,能够满足不同肌肤问题的需求。
同时,不同成份的功能相互补充和协同作用,提高了产品的综合效果。
5. 安全性评估根据成份的特性和已知的安全性信息,以下是对产品的安全性进行评估:•成份1在常用浓度下已被证明是安全的。
•成份2在常用浓度下已被证明是安全的。
•成份3在常用浓度下已被证明是安全的。
综合评估结果显示,该产品的成份在常用浓度下具有良好的安全性,不会对用户造成不良影响。
6. 结论通过对产品成份的分析,我们得出以下结论:•该产品的成份包括成份1、成份2和成份3。
•成份1在该产品中含量最高,功能和特性对产品的功效有重要作用。
主成份分析报告(包含sas程序)
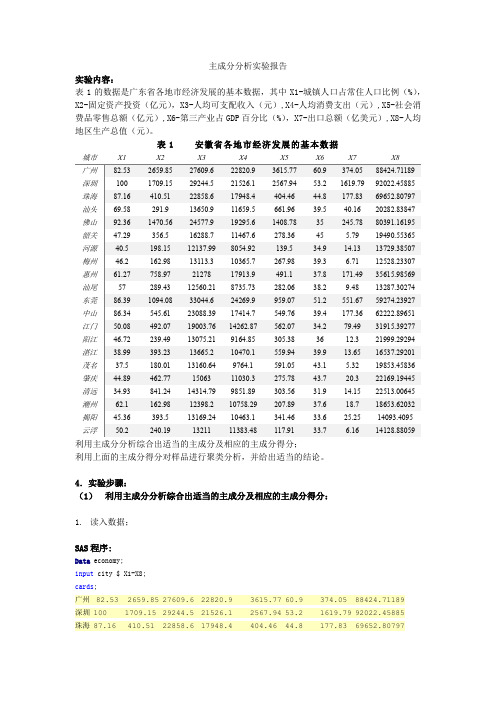
主成分分析实验报告实验内容:表1的数据是广东省各地市经济发展的基本数据,其中X1-城镇人口占常住人口比例(%),X2-固定资产投资(亿元),X3-人均可支配收入(元),X4-人均消费支出(元),X5-社会消费品零售总额(亿元),X6-第三产业占GDP百分比(%),X7-出口总额(亿美元),X8-人均地区生产总值(元)。
表1 安徽省各地市经济发展的基本数据城市X1X2X3X4X5X6X7X8广州82.532659.8527609.622820.93615.7760.9374.0588424.71189深圳1001709.1529244.521526.12567.9453.21619.7992022.45885珠海87.16410.5122858.617948.4404.4644.8177.8369652.80797汕头69.58291.913650.911659.5661.9639.540.1620282.83847佛山92.361470.5624577.919295.61408.7835245.7880391.16195韶关47.29356.516288.711467.6278.3645 5.7919490.55365河源40.5198.1512137.998054.92139.534.914.1313729.38507梅州46.2162.9813113.310365.7267.9839.3 6.7112528.23307惠州61.27758.972127817913.9491.137.8171.4935615.98569汕尾57289.4312560.218735.73282.0638.29.4813287.30274东莞86.391094.0833044.624269.9959.0751.2551.6759274.23927中山86.34545.6123088.3917414.7549.7639.4177.3662222.89651江门50.08492.0719003.7614262.87562.0734.279.4931915.39277阳江46.72239.4913075.219164.85305.383612.321999.29294湛江38.99393.2313665.210470.1559.9439.913.6516537.29201茂名37.5180.0113160.649764.1591.0543.1 5.3219853.45836肇庆44.89462.771506311030.3275.7843.720.322169.19445清远34.93841.2414314.799851.89303.5631.914.1522513.00645潮州62.1162.9812398.210758.29207.8937.618.718653.62032揭阳45.36393.513169.2410463.1341.4633.625.2514093.4095云浮50.2240.191321111383.48117.9133.7 6.1614128.88059利用主成分分析综合出适当的主成分及相应的主成分得分;利用上面的主成分得分对样品进行聚类分析,并给出适当的结论。
主成分分析实验报告

一、实验目的本次实验旨在通过主成分分析(PCA)方法,对给定的数据集进行降维处理,从而简化数据结构,提高数据可解释性,并分析主成分对原始数据的代表性。
二、实验背景在许多实际问题中,数据集往往包含大量的变量,这些变量之间可能存在高度相关性,导致数据分析困难。
主成分分析(PCA)是一种常用的降维技术,通过提取原始数据中的主要特征,将数据投影到低维空间,从而简化数据结构。
三、实验数据本次实验采用的数据集为某电商平台用户购买行为的调查数据,包含用户年龄、性别、收入、职业、购买商品种类、购买次数等10个变量。
四、实验步骤1. 数据预处理首先,对数据进行标准化处理,消除不同变量之间的量纲影响。
然后,进行缺失值处理,删除含有缺失值的样本。
2. 计算协方差矩阵计算标准化后的数据集的协方差矩阵,以了解变量之间的相关性。
3. 计算特征值和特征向量求解协方差矩阵的特征值和特征向量,特征值表示对应特征向量的方差,特征向量表示数据在对应特征方向上的分布。
4. 选择主成分根据特征值的大小,选择前几个特征值对应特征向量作为主成分,通常选择特征值大于1的主成分。
5. 构建主成分空间将选定的主成分进行线性组合,构建主成分空间。
6. 降维与可视化将原始数据投影到主成分空间,得到降维后的数据,并进行可视化分析。
五、实验结果与分析1. 主成分分析结果根据特征值大小,选取前三个主成分,其累计贡献率达到85%,说明这三个主成分能够较好地反映原始数据的信息。
2. 主成分空间可视化将原始数据投影到主成分空间,绘制散点图,可以看出用户在主成分空间中的分布情况。
3. 主成分解释根据主成分的系数,可以解释主成分所代表的原始数据特征。
例如,第一个主成分可能主要反映了用户的购买次数和购买商品种类,第二个主成分可能反映了用户的年龄和性别,第三个主成分可能反映了用户的收入和职业。
六、实验结论通过本次实验,我们成功运用主成分分析(PCA)方法对数据进行了降维处理,提高了数据可解释性,并揭示了数据在主成分空间中的分布规律。
主成分分析、因子分析实验报告--SPSS

主成分分析、因子分析实验报告--SPSS主成分分析、因子分析实验报告SPSS一、实验目的主成分分析(Principal Component Analysis,PCA)和因子分析(Factor Analysis,FA)是多元统计分析中常用的两种方法,旨在简化数据结构、提取主要信息和解释变量之间的关系。
本次实验的目的是通过使用 SPSS 软件对给定的数据集进行主成分分析和因子分析,深入理解这两种方法的原理和应用,并比较它们的结果和差异。
二、实验原理(一)主成分分析主成分分析是一种通过线性变换将多个相关变量转换为一组较少的不相关综合变量(即主成分)的方法。
这些主成分是原始变量的线性组合,且按照方差递减的顺序排列。
主成分分析的主要目标是在保留尽可能多的数据信息的前提下,减少变量的数量,从而简化数据分析和解释。
(二)因子分析因子分析则是一种探索潜在结构的方法,它假设观测变量是由少数几个不可观测的公共因子和特殊因子线性组合而成。
公共因子解释了变量之间的相关性,而特殊因子则代表了每个变量特有的部分。
因子分析的目的是找出这些公共因子,并估计它们对观测变量的影响程度。
三、实验数据本次实验使用了一份包含多个变量的数据集,这些变量涵盖了不同的领域和特征。
数据集中的变量包括具体变量 1、具体变量 2、具体变量 3等,共X个观测样本。
四、实验步骤(一)主成分分析1、打开 SPSS 软件,导入数据集。
2、选择“分析”>“降维”>“主成分分析”。
3、将需要分析的变量选入“变量”框。
4、在“抽取”选项中,选择主成分的提取方法,如基于特征值大于1 或指定提取的主成分个数。
5、点击“确定”,运行主成分分析。
(二)因子分析1、同样在 SPSS 中,选择“分析”>“降维”>“因子分析”。
2、选入变量。
3、在“描述”选项中,选择相关统计量,如 KMO 检验和巴特利特球形检验。
4、在“抽取”选项中,选择因子提取方法,如主成分法或主轴因子法。
主成分分析报告报告材料试验报告材料

主成分分析地信0901班陈任翔010******* 【实验目的及要求】掌握主成分分析与因子分析的思想和具体步骤。
掌握SPSS实现主成分分析与因子分析的具体操作。
【实验原理】1.主成分分析的主要目的是希望用较少的变量去解释原来资料中的大部分变异,将我们手中许多相关性很高的变量转化成彼此相互独立或不相关的变量。
通常是选出比原始变量个数少,能解释大部分资料中的变异的几个新变量,即所谓主成分,并用以解释资料的综合性指标。
由此可见,主成分分析实际上是一种降维方法。
2•因子分析研究相关矩阵或协方差矩阵的内部依赖关系,它将多个变量综合为少数几个因子,以再现原始变量与因子之间的相关关系。
【实验步骤】1.数据准备1)首先在Excel中打开“水样元素成分分析数据”,删除表名“水样元素成分分析数据”,保存数据。
2)在SPSS中打开保存好的Excel数据进行分析。
水样元素成分分析数据3 )数据格式转换。
2. 数据描述分析操作1) Descriptives 过程点击 Analyze 下的 Descriptive Statistics 选项,选择该选项下的Descriptives 选中待处理的变量(左侧的As…..Hg等);点击使变量 As…..Hg移至Variable(s)中;选中 Save standrdized values as variables点击 Options2)数据标准化实用标准文案Descriptive!: OptionsH«scendin4 ■««&:标准化处理后的结果ZAsppn ZCdppmZ'Crppm ZC^ppmZFbppmZZnptm ZHgppm ZPppm-.2984 28269 -.37883 1.70087 .26855 -.28112 1.43406 .32324 -.2933 29968 -.5393A -.01708 57821 -.29527-.30335 -.48108-.3705 -.30052 -.52820 -1.02804 70026 2991258292 7781T-.3601 -.29569-.37447-.22317 -.50634-.29341 -.36835 ■ 06352 -.0197 29443 .56016 1,94589 65025 --29394 .83326 -.20599 -.0301-.299783.02675-.45503 20357 *.29410*.54001 2. 82861 一.3474J6813 -.S4136 64tjJ2 2yblM92624 24ti35 -.3554 29705 -.30788 -.65727 -.48657 -.29421-.3833229241 -.2371 22483 -.39349 -.012962.111^4 25138 .48994 125563. 1472 3U7473 -.39270.797283. 17518 2. 1636059787 -.3998 -,28510.05519 .27484 .19989 -.28473 58292 .S8E01 -.429229989-.35901-,37895-.674S4-.29522-.5687594451wHinimwnMeanSid.Devi ationHg (ppm 】 12 02.71 .2353 .2330G Ft @pm) 12 59 33. 7& 8.651T 11 T9T94 Cu(ppm) 128 24.7 9.&80 7 7137 Cr (ppm) 12 1 03 91.0014.0375 25. 2K18 Cd (ppm )12 0&331.eo29.7383 的-39763As (ppm)12 2.33407.71 51.0242 113. 333S9 P 如jm)12 L869005 £393 48 £337.3716Zu (ppm)Vslid N Qistwise) 12121:.345360.04135. 6€5139ZA.13592.主成分分析选抒所耍的瑕 〜7 … Mean(均数) Std.deviation (标准差 Minimum (热小值)一 Maximum (最大值) rp?;j ih 列 means) 点丨丨「ContinueDisplay OrderVtrilist Alphkbttic?ant inutCaictl1) 点击Analyze 下的Data Reduction 选项,选择该选项下的Factor过程。
测食物成分实验报告单

测食物成分实验报告单实验目的:本实验旨在测定食物样品中的主要成分,包括蛋白质、脂肪、碳水化合物和灰分的含量,以了解食物的营养成分,并对不同食物样品进行比较。
实验步骤:1. 样品制备:a. 将不同食物样品取适量并粉碎成细粉。
b. 将每种食物样品(约1克)分别称量到已称重的干燥皿中。
2. 测定蛋白质含量:a. 将每个食物样品的干燥皿放入前置加热器中,并设置加热温度为高温模式,以去除食物中的水分。
b. 将加热后的样品放入称量皿中,并记录称量皿的重量(W1)。
c. 将样品放入烧杯中,加入适量的浓氢氧化钠溶液,并用玻璃棒搅拌均匀,使样品中的蛋白质与钠氢氧化物反应。
d. 使用标准稀硫酸溶液滴定反应液,直到出现红色终点。
e. 记录滴定过程中标准稀硫酸溶液的消耗量(V1)。
f. 重复以上步骤,得到平均滴定值。
g. 根据滴定值计算蛋白质含量的百分比:蛋白质含量(%)=(V1 × HCl标准溶液浓度 × 0.014 × 100)/样品的重量。
3. 测定脂肪含量:a. 将蛋白质测定中得到的样品放入清洗干净的玻璃烧杯中。
b. 在沸水中加热样品,使其中的脂肪溶解。
c. 将玻璃棒插入样品中,使其中的脂肪涂在玻璃棒上。
d. 将玻璃棒置于明火上燃烧,直至脂肪完全燃烧为止。
e. 记录燃烧前后玻璃棒的重量差(W2)。
f. 根据重量差计算脂肪含量的百分比:脂肪含量(%)=(W2 - W1)/样品的重量。
4. 测定碳水化合物含量:a. 将脂肪测定中得到的样品放入锥形瓶中。
b. 加入适量的浓硫酸溶液,使样品中的脂肪和蛋白质分解。
c. 放入水浴中加热2小时,使蛋白质和脂肪完全分解。
d. 将瓶中溶液冷却至室温,并用去离子水稀释。
e. 取适量稀释后的溶液,以过氧化氢溶液进行氧化反应。
f. 加入甲基橙指示剂,使反应终点由绿色变为橙色。
g. 使用标准碘溶液滴定反应液,直到反应液由橙色变为浅黄色。
h. 记录滴定过程中标准碘溶液的消耗量(V2)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
主成分分析
地信0901班陈任翔010******* 【实验目的及要求】
掌握主成分分析与因子分析的思想和具体步骤。
掌握SPSS实现主成分分析与因子分析的具体操作。
【实验原理】
1.主成分分析的主要目的是希望用较少的变量去解释原来资料中的大部分变异,将我们手中许多相关性很高的变量转化成彼此相互独立或不相关的变量。
通常是选出比原始变量个数少,能解释大部分资料中的变异的几个新变量,即所谓主成分,并用以解释资料的综合性指标。
由此可见,主成分分析实际上是一种降维方法。
2.因子分析研究相关矩阵或协方差矩阵的内部依赖关系,它将多个变量综合为少数几个因子,以再现原始变量与因子之间的相关关系。
【实验步骤】
1.数据准备
●1)首先在Excel中打开“水样元素成分分析数据”,删除表名“水样元素成分分析
数据”,保存数据。
●2)在SPSS中打开保存好的Excel数据进行分析。
2
Z-W-3-0
2 5.71 1.5416.0311.811.21169.90.13996
Z-W-4-0
2 2.380.1
3 5.58 2.90.8923.820.08185.8
●3)数据格式转换。
2.数据描述分析操作
1)Descriptives过程
点击Analyze下的Descriptive Statistics选项,选择该选项下的Descriptives
●选中待处理的变量(左侧的As…..Hg等);
●点击使变量As…..Hg 移至Variable(s)中;
●选中Save standrdized values as variables;
●点击Options
2)数据标准化
标准化处理后的结果
2.主成分分析
1)点击Analyze下的Data Reduction选项,选择该选项下的Factor过程。
选中待
处理的变量,移至Variables
2)点击Descriptives判断是否有进行因子分析的必要
Coefficients(计算相关系数矩阵)
Significance levels(显著水平)
KMO and Bartlett’s test of sphericity (对相关系数矩阵进行统计学检验) Inverse(倒数模式):求出相关矩阵的反矩阵;
Reproduced(重制的):显示重制相关矩阵,上三角形矩阵代表残差值,而主对角线及下三角形代表相关系数;
Determinant(行列式):求出前述相关矩阵的行列式值;
Anti-image(反映像):求出反映像的共同量及相关矩阵。
Univariate descriptive单变量描述统计量(输出被选中的各变量的均数与标准差)
Initial solution未转轴之统计量(显示因素分析未转轴前之共同性、特征值、变异数百分比及累积百分比)
3)点击Extraction :
●选择主成分分析方法
●输出未旋转的因子载荷矩阵
4)点击Rotation
5)点击Scores
●选中Save as variables (把因子得分作为新变量保存在数据文件中)
●选中Regression(回归因子得分)
●点击Continue
6)点击Options
●选中Exclude cases listwise(去除所有含缺失数据的样本、再进行分析)
●选中Sorted by size(载荷系数将按照数值大小排列,并构成矩阵)
●点击Continue
3.结果分析
●SPSS输出的第一个表格列出了标准化后数据的平均值(Mean)、标准差
(Std. Deviation)和分析用到的取值个数(N)
●系统输出的第2个表格是8个原始变量的相关矩阵与单尾显著性检验
(多个变量之间的相关系数较大,说明这些变量之间存在着较为显著的相关性,且其对应的Sig值普遍较小,根据分析,这些数据有进行因子分析的必要。
)
●KMO检验法和巴特利特球形检验法(KMO and Bartlett Test of Sphericity)的
检验结果
(Bartlett球形检验统计量的Sig<0.01,认为各变量之间存在着显著的相关性。
一般,KMO大于0.9时效果最佳,0.7以上可以接受,0.5以下不宜作因子分析。
但是相关矩阵和Bartlett球形检验统计量的效果都比较好,认为是可以作因子分析)
●SPSS输出的第四个表格“成分矩阵”是初始的未经旋转的因子载荷矩阵
(已选出了3个主因子,以替代原有的8个变量所含的信息)
●SPSS输出的第七个表格“旋转成分矩阵”是经过旋转(转轴法使得因素负荷量
易于解释)后的因子载荷矩阵。
(旋转后每个公因子上的载荷分配地更清晰,因子变量代表的变量相对集中,比未旋转时更容易解释各因子的意义。
载荷绝对值较大的因子与变量的关系更为密切,也更能代表这个变量
●第1公因子代表Cd、Zn、As、Pb这几个变量因素
●第2公因子代表Cr、P两个变量
●第3公因子代表Cu、Hg两个变量
●可以根据实际情况对第1公因子、第2公因子、第3公因子命名
●我们将第1公因子命名为镉类,第2公因子命名为铬类,第3公因子命名为铜类)
●SPSS输出的第八个表格“成分转换矩阵”是正交旋转后因素相关矩阵
●SPSS输出的第六个表格表示各因子变量的特征值与累积贡献率(表明m个主
成分综合原始变量的能力)
(由于前3个特征值累计贡献率达到91.798%,根据累计贡献率大于85%的原则,故
选取前三个特征值)
●SPSS输出的第五个表格表示变量的共同度(m个公共因子对第i个变量Xi的
方差贡献)
(As的共同度为0.974,可以理解为3个公共因子能够解释As的方差的97.4%;Pb的共同度为0.581,可以理解为3个公共因子能够解释As的方差的58.1%。
)
●回到Data View窗口的当前数据集,会看到文件中增加了3列FAC1_1(第1因
子得分)、FAC2_1(第2因子得分)和FAC3_1(第3因子得分)
(可以通过第1因子得分来了解镉类元素的分布情况,第2公因子来了解铬类元素的分布情况,第3公因子来了解铜类元素的分布情况。
样号为Z-W-2-02的样品Cd、Zn、As、Pb含量较高,样号为C-W-06-01的样品Cr、P含量较高,样号为C-W-01-02的样品重金属含量较高)
zF(综合得分)=46.048%* FAC1_1 + 24.085%* FAC2_1 + 21.665%* FAC3_1。
根据综合得分可以看出总体情况
【实验总结】
通过本次实验,了解SPSS软件的运行管理方式;熟悉各主要操作模块,窗口及其功能,相关的系统参数设置等。
基本掌握了应用SPSS软件Analyze菜单中的Data Reduction模块对数据进行主成分分析和因子分析,但是在操作过程和文字分析上还是有些生疏,有待进一步的熟练。
2011-11-4。
