主成分分析实验报告
主成分分析
主成分分析法实验报告一、实验名称：主成分分析二、实验目的：利用计算机实现主成分分析，完成综合评价。
三、实验原理：四、实验过程：（一）数据录入：将相关指标数据录入如下表（二）数据标准化：为避免不同量纲引起的大数吃小数问题，我们对相关数据进行标准化，结果如下：表1：标准化后的数据录入表表2：描述统计量表表1是标准化后的相关数据，表2给出了标准化过程中涉及到的均值、标准差等数值。
（三）分析表3：公因子方差表表3给出了该次分析从每个原始变量中提取的信息，表格下的表注表明，该次分析使用主成分分析完成的。
可以看出除百元销售收入实现利税信息损失较大外，主成分几乎包含了各个原始变量至少85%的信息。
表4：相关矩阵表4为各指标因素量化后的相关矩阵。
表5：解释的总方差表由输出结果表5可以看出，前两个主成分y1,y2的方差和占全部方差的的比例为84.7%。
我们就选取y1为第一主成分，y2为第二主成分，且这两个主成分的方差和占全部方差的84.7%，即基本上保留了原来的指标的信息，这样由原来的9个指标转化为2个新指标，起到了降维的作用。
表6：因子载荷矩阵因子载荷矩阵（表6）是主成分和变量间的因子负荷量，即相关系数，代表相关度。
并非主成分的系数；所以我们要通过该成分矩阵计算出主成分的系数，计算结果如表7：表7：主成分系数表7中，a1代表第一主成分与各变量间的因子负荷量，a2代表第二主成分与各变量间的因子负荷量；u1代表y1的系数，u2代表y2的相应系数。
由此可得到两个主成分y1、y2的线性组合。
（四）主成分得分及分类表8：主成分得分为了分析各样品在主成分所反映的经济意义方面的情况，还将标准化后的原始数据代入主成分表达式中计算出各样品的主成分得分，如表8，得到28个省的、直辖市、自治区的主成分的分。
将这28个样品在平面直角坐标系上描出来，进而得到样品分类，如下图所示：由上图可以看出，分布在第一象限的是上海、北京、天津、广西四个省区，这四个省区的经济效益在全国来说属于较好的，上海经济效益最好。
《多元统计实验》主成分分析实验报告二
《多元统计实验》主成分分析实验报告三、实验结果分析6.5人均粮食产量x5,经济作物占农作物播种面积x6,耕地占土地面积比x7,果园与林地面积之比x8,灌溉田占1耕地面积比例x9等五个指标有较强的相关性, 人口密度x1,人均耕地面积x2,森林覆盖率x3,农民人均收入x4相关性也很强，再作主成分分析，求样本相关矩阵的特征值和主成分载荷。
λ11/2=2.158962，λ21/2=1.4455076，λ31/2 =1.0212708，λ41/2 =0.71233588，λ51/2 =0.5614001，λ61/2 =0.43887788，λ71/2 =0.33821497，λ81/2 =0.212900230，λ91/2=0.177406876。
确定主成分分析，前两个主成分的累积方差贡献率为75.01%，前三个主成分的累积方差贡献率为86.59%，按照累积方差贡献率大于80%的原则，主成分的个数取为3，前三个主成分分别为：Z*1=0.3432x*1-0.446x*3+0.376x*5+0.379x*6+0.432x*7+0.446x*9Z*2=0.368x*1-0.614x*2-0.61x*4-0.307x*5-0.1224x*6Z*3=-0.122x*6+0.246x*7-0.950x*8第一主成分在x*7,x*9两个指标上取值为正且载荷较大，可视为反映耕地占比和灌溉田占耕地面积比例的主成分，第二主成分在x*2和x*4这两个指标的取值为负，绝对值载荷最大，不能作为人均耕地和人均收入的主成分。
第三主成分，x*8这个指标取值为负且，载荷绝对值最大，不能反映果园与林地面积之比的主成分。
根据该图结果可以认为选取前两个指标作为主成分分析的选择是正确的。
将八个指标按前两个主成分进行分类：由结果可以得出森林覆盖率为一类，人口密度、果园与林地面积之比、耕地占土地面积比、灌溉田占耕地面积比为一类，经济作物占农作物播种面积比例、人均粮食产量、农民人均收入、人均耕地面积为一类。
主成份分析报告(包含sas程序)
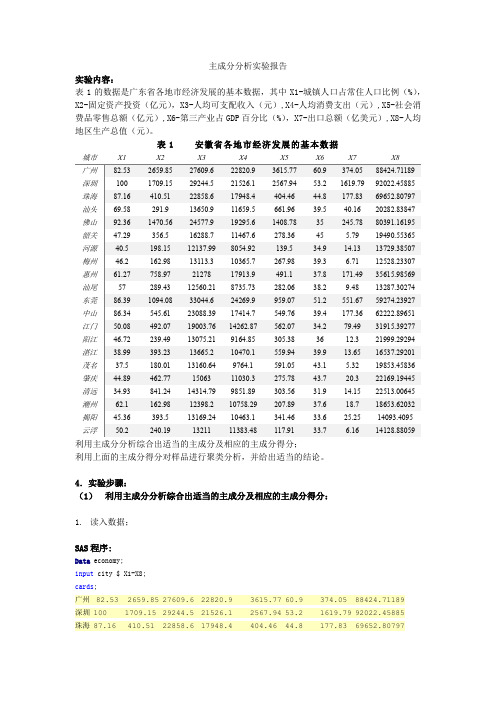
主成分分析实验报告实验内容：表1的数据是广东省各地市经济发展的基本数据，其中X1-城镇人口占常住人口比例（%），X2-固定资产投资（亿元），X3-人均可支配收入（元）,X4-人均消费支出（元）,X5-社会消费品零售总额（亿元）,X6-第三产业占GDP百分比（%），X7-出口总额（亿美元）,X8-人均地区生产总值（元）。
表1 安徽省各地市经济发展的基本数据城市X1X2X3X4X5X6X7X8广州82.532659.8527609.622820.93615.7760.9374.0588424.71189深圳1001709.1529244.521526.12567.9453.21619.7992022.45885珠海87.16410.5122858.617948.4404.4644.8177.8369652.80797汕头69.58291.913650.911659.5661.9639.540.1620282.83847佛山92.361470.5624577.919295.61408.7835245.7880391.16195韶关47.29356.516288.711467.6278.3645 5.7919490.55365河源40.5198.1512137.998054.92139.534.914.1313729.38507梅州46.2162.9813113.310365.7267.9839.3 6.7112528.23307惠州61.27758.972127817913.9491.137.8171.4935615.98569汕尾57289.4312560.218735.73282.0638.29.4813287.30274东莞86.391094.0833044.624269.9959.0751.2551.6759274.23927中山86.34545.6123088.3917414.7549.7639.4177.3662222.89651江门50.08492.0719003.7614262.87562.0734.279.4931915.39277阳江46.72239.4913075.219164.85305.383612.321999.29294湛江38.99393.2313665.210470.1559.9439.913.6516537.29201茂名37.5180.0113160.649764.1591.0543.1 5.3219853.45836肇庆44.89462.771506311030.3275.7843.720.322169.19445清远34.93841.2414314.799851.89303.5631.914.1522513.00645潮州62.1162.9812398.210758.29207.8937.618.718653.62032揭阳45.36393.513169.2410463.1341.4633.625.2514093.4095云浮50.2240.191321111383.48117.9133.7 6.1614128.88059利用主成分分析综合出适当的主成分及相应的主成分得分；利用上面的主成分得分对样品进行聚类分析，并给出适当的结论。
主成分分析实验报告
一、实验目的本次实验旨在通过主成分分析（PCA）方法，对给定的数据集进行降维处理，从而简化数据结构，提高数据可解释性，并分析主成分对原始数据的代表性。
二、实验背景在许多实际问题中，数据集往往包含大量的变量，这些变量之间可能存在高度相关性，导致数据分析困难。
主成分分析（PCA）是一种常用的降维技术，通过提取原始数据中的主要特征，将数据投影到低维空间，从而简化数据结构。
三、实验数据本次实验采用的数据集为某电商平台用户购买行为的调查数据，包含用户年龄、性别、收入、职业、购买商品种类、购买次数等10个变量。
四、实验步骤1. 数据预处理首先，对数据进行标准化处理，消除不同变量之间的量纲影响。
然后，进行缺失值处理，删除含有缺失值的样本。
2. 计算协方差矩阵计算标准化后的数据集的协方差矩阵，以了解变量之间的相关性。
3. 计算特征值和特征向量求解协方差矩阵的特征值和特征向量，特征值表示对应特征向量的方差，特征向量表示数据在对应特征方向上的分布。
4. 选择主成分根据特征值的大小，选择前几个特征值对应特征向量作为主成分，通常选择特征值大于1的主成分。
5. 构建主成分空间将选定的主成分进行线性组合，构建主成分空间。
6. 降维与可视化将原始数据投影到主成分空间，得到降维后的数据，并进行可视化分析。
五、实验结果与分析1. 主成分分析结果根据特征值大小，选取前三个主成分，其累计贡献率达到85%，说明这三个主成分能够较好地反映原始数据的信息。
2. 主成分空间可视化将原始数据投影到主成分空间，绘制散点图，可以看出用户在主成分空间中的分布情况。
3. 主成分解释根据主成分的系数，可以解释主成分所代表的原始数据特征。
例如，第一个主成分可能主要反映了用户的购买次数和购买商品种类，第二个主成分可能反映了用户的年龄和性别，第三个主成分可能反映了用户的收入和职业。
六、实验结论通过本次实验，我们成功运用主成分分析（PCA）方法对数据进行了降维处理，提高了数据可解释性，并揭示了数据在主成分空间中的分布规律。
主成分分析、因子分析实验报告--SPSS
主成分分析、因子分析实验报告--SPSS主成分分析、因子分析实验报告SPSS一、实验目的主成分分析（Principal Component Analysis，PCA）和因子分析（Factor Analysis，FA）是多元统计分析中常用的两种方法，旨在简化数据结构、提取主要信息和解释变量之间的关系。
本次实验的目的是通过使用 SPSS 软件对给定的数据集进行主成分分析和因子分析，深入理解这两种方法的原理和应用，并比较它们的结果和差异。
二、实验原理（一）主成分分析主成分分析是一种通过线性变换将多个相关变量转换为一组较少的不相关综合变量（即主成分）的方法。
这些主成分是原始变量的线性组合，且按照方差递减的顺序排列。
主成分分析的主要目标是在保留尽可能多的数据信息的前提下，减少变量的数量，从而简化数据分析和解释。
（二）因子分析因子分析则是一种探索潜在结构的方法，它假设观测变量是由少数几个不可观测的公共因子和特殊因子线性组合而成。
公共因子解释了变量之间的相关性，而特殊因子则代表了每个变量特有的部分。
因子分析的目的是找出这些公共因子，并估计它们对观测变量的影响程度。
三、实验数据本次实验使用了一份包含多个变量的数据集，这些变量涵盖了不同的领域和特征。
数据集中的变量包括具体变量 1、具体变量 2、具体变量 3等，共X个观测样本。
四、实验步骤（一）主成分分析1、打开 SPSS 软件，导入数据集。
2、选择“分析”＞“降维”＞“主成分分析”。
3、将需要分析的变量选入“变量”框。
4、在“抽取”选项中，选择主成分的提取方法，如基于特征值大于1 或指定提取的主成分个数。
5、点击“确定”，运行主成分分析。
（二）因子分析1、同样在 SPSS 中，选择“分析”＞“降维”＞“因子分析”。
2、选入变量。
3、在“描述”选项中，选择相关统计量，如 KMO 检验和巴特利特球形检验。
4、在“抽取”选项中，选择因子提取方法，如主成分法或主轴因子法。
实验报告8 主成分分析
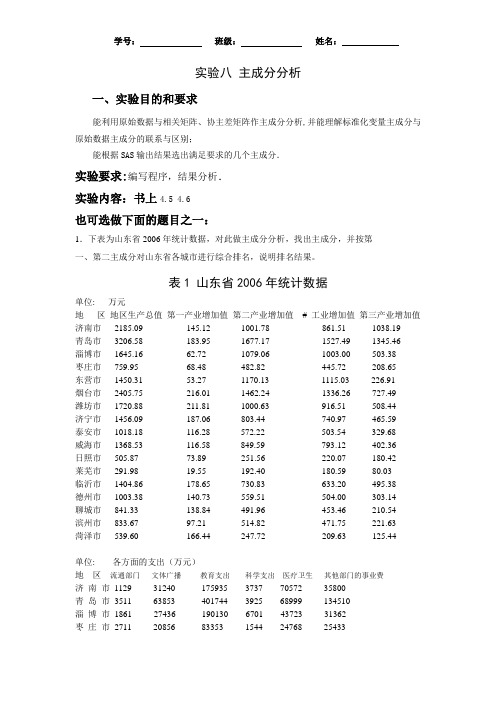
实验八主成分分析一、实验目的和要求能利用原始数据与相关矩阵、协主差矩阵作主成分分析,并能理解标准化变量主成分与原始数据主成分的联系与区别；能根据SAS输出结果选出满足要求的几个主成分．实验要求:编写程序，结果分析．实验内容：书上4.5 4.6也可选做下面的题目之一：1．下表为山东省2006年统计数据，对此做主成分分析，找出主成分，并按第一、第二主成分对山东省各城市进行综合排名，说明排名结果。
表1 山东省2006年统计数据单位: 万元地区地区生产总值第一产业增加值第二产业增加值# 工业增加值第三产业增加值济南市2185.09 145.12 1001.78 861.51 1038.19青岛市3206.58 183.95 1677.17 1527.49 1345.46淄博市1645.16 62.72 1079.06 1003.00 503.38枣庄市759.95 68.48 482.82 445.72 208.65东营市1450.31 53.27 1170.13 1115.03 226.91烟台市2405.75 216.01 1462.24 1336.26 727.49潍坊市1720.88 211.81 1000.63 916.51 508.44济宁市1456.09 187.06 803.44 740.97 465.59泰安市1018.18 116.28 572.22 503.54 329.68威海市1368.53 116.58 849.59 793.12 402.36日照市505.87 73.89 251.56 220.07 180.42莱芜市291.98 19.55 192.40 180.59 80.03临沂市1404.86 178.65 730.83 633.20 495.38德州市1003.38 140.73 559.51 504.00 303.14聊城市841.33 138.84 491.96 453.46 210.54滨州市833.67 97.21 514.82 471.75 221.63菏泽市539.60 166.44 247.72 209.63 125.44单位: 各方面的支出（万元）地区流通部门文体广播教育支出科学支出医疗卫生其他部门的事业费济南市1129 31240 175935 3737 70572 35800青岛市3511 63853 401744 3925 68999 134510淄博市1861 27436 190130 6701 43723 31362枣庄市2711 20856 83353 1544 24768 25433东营市1127 16566 114045 2016 23907 27969烟台市216 30788 220599 3634 49379 60217潍坊市977 36484 252298 2974 37211 43285济宁市2174 46338 204464 2858 43159 46694泰安市1382 19672 103466 2358 36980 24055威海市717 18468 120004 1266 29562 37796日照市70 10814 58024 1098 16571 15238莱芜市388 7588 49980 676 13010 10942临沂市4475 39946 194380 2777 51723 34332德州市1415 20080 100432 2777 31442 16555聊城市3677 26234 103399 2352 27636 13616滨州市759 17096 100284 1062 24930 19961菏泽市413 31410 125664 1152 33193 1617012-9 各市农林牧渔业总产值(2006年)单位:万元地区农林牧农业产值林业产值牧业产值渔业产值农林牧渔服务业产值渔业总产值济南市2477193 1479799 64385 848623 28902 55484青岛市3396096 1360755 23546 1076254 855131 80410淄博市1160195 766074 52589 294504 19835 27193枣庄市1278410 831435 32985 347404 30842 35744东营市1045593 477566 11371 264438 216534 75684烟台市3832237 1795414 45611 679950 1238827 72435潍坊市4230441 2392085 43644 1437142 240827 116743济宁市3680065 1993193 69607 1229986 267302 119977泰安市2062840 1236797 64195 622845 76841 62162威海市2186326 465164 6216 337948 1352551 24447日照市1286840 550601 36468 261814 398981 38976莱芜市353735 224665 21764 91013 5519 10774临沂市3233487 2016291 153830 908942 79723 74701德州市2661008 1562942 37421 844453 67174 149018聊城市2470609 1638065 34141 710461 45450 42492滨州市1803325 1076124 23910 424643 230605 48043菏泽市2983624 1993394 64882 802778 76574 459962．调查美国50个州7种犯罪率，得结果列于表35.2，其中给出的是美国50个州每100 000个人中七种犯罪的比率数据．这七种犯罪是：murder（杀人罪），rape（强奸罪），robbery （抢劫罪），assault（斗殴罪），burglary（夜盗罪），larceny（偷盗罪），auto（汽车犯罪），很难直接从这七个变量出发来评价各州的治安和犯罪情况，试作主成份分析．说明选几个主成分合适，找出几个主成分，并按照第一、第二主成分分别对50个周进行排名，并解释之。
实验：主成分分析
数理经济学分析方法实验报告2：主成分分析1.采用数据student.txt，对六个变量做协方差矩阵和相关系数矩阵。
我在做主成分分析之前对student.txt进行90%的随机抽样，然后根据抽样后的数据，利用spss计量分析软件对六个变量做协方差矩阵和相关系数矩阵如下。
（1）协方差矩阵（2）相关系数矩阵项间相关性矩阵VAR00001 VAR00002 VAR00003 VAR00004 VAR00005 VAR00006 VAR00001 1.000 .634 .623 -.606 -.491 -.502 VAR00002 .634 1.000 .537 -.432 -.337 -.365 VAR00003 .623 .537 1.000 -.442 -.338 -.366 VAR00004 -.606 -.432 -.442 1.000 .815 .829 VAR00005 -.491 -.337 -.338 .815 1.000 .806 VAR00006 -.502 -.365 -.366 .829 .806 1.0002.采用数据student.txt，先对六个变量做标准化，然后求协方差矩阵和相关系数矩阵。
观察步骤1和步骤2的结果，并做说明。
运用spss计量分析软件对六个变量做标准化后，得出协方差矩阵和相关系数矩阵如下。
（1）标准化后协方差矩阵（2）标准化后相关系数矩阵解释说明：步骤1是原始数据未经过标准化处理得到的协方差矩阵和相关系数矩阵，而步骤2是经过标准化处理后得到的协方差矩阵和相关系数矩阵。
从表格中，我们可以发现，标准化以后的协方差矩阵和相关系数矩阵对应相等，并且与未经标准化处理的相关系数矩阵对应相等，唯独与未经标准化处理的协方差矩阵对应不相等。
这表明在进行主成分分析时，一般采用相关系数矩阵进行分析，因为相关系数就是标准化以后的协方差，它可以消除量纲的影响，从而避免了由于量纲影响而导致的分析误差。
主成分分析实验报告
《系统工程》主成分分析实验报告
1500米.448 -.
81
-.274 -.788 .612 .577 -.267 -.404 -.124 1.000
a. 行列式 = 3.15E-005
KMO 和 Bartlett 的检验
取样足够度的 Kaiser-Meyer-Olkin 度量。
.780
Bartlett 的球形度检验近似卡方153.735
df 45
Sig. .000
由表可知：巴特利特球度检验统计量的观测值为153.735，相应的概率p值接近0，小于显著性水平(取0.05)，所以应拒绝原假设，认为相关系数矩阵与单位矩阵有显著差异。
同时，KMO值为0.780，可知原有变量可以进行因子分析。
3.旋转前的因子矩阵
（表四）
表四成份矩阵也即是因子载荷矩阵，根据该表可以写出因子分析模型：
110米栏=-0.948f1+0.017f2+0.020f3 跳远=0.918f1-0.062f2+0.074f3
旋转后的成分矩阵
采用最大方差法对成份矩阵(因子载荷矩阵)实施正交旋转以使因子具有命名解释性，指定按第一因子载荷降序的顺序输出旋转后的因子载荷矩阵如表六所示
（表六）。
主成分分析实验报告剖析
一、引言主成分分析（PCA）是一种常用的数据降维方法，通过对原始数据进行线性变换，将高维数据投影到低维空间，从而简化数据结构，提高计算效率。
本文通过对主成分分析实验的剖析，详细介绍了PCA的基本原理、实验步骤以及在实际应用中的注意事项。
二、实验背景随着数据量的不断增长，高维数据在各个领域变得越来越普遍。
高维数据不仅增加了计算难度，还可能导致信息过载，影响模型的性能。
因此，数据降维成为数据分析和机器学习中的关键步骤。
PCA作为一种有效的降维方法，在众多领域得到了广泛应用。
三、实验目的1. 理解主成分分析的基本原理；2. 掌握PCA的实验步骤；3. 分析PCA在实际应用中的优缺点；4. 提高数据降维的技能。
四、实验原理主成分分析的基本原理是将原始数据投影到新的坐标系中，该坐标系由主成分构成。
主成分是原始数据中方差最大的方向，可以看作是数据的主要特征。
通过选择合适的主成分，可以将高维数据降维到低维空间，同时保留大部分信息。
五、实验步骤1. 数据准备：选择一个高维数据集，例如鸢尾花数据集。
2. 数据标准化：将数据集中的每个特征缩放到均值为0、标准差为1的范围，以便消除不同特征之间的尺度差异。
3. 计算协方差矩阵：计算标准化数据集的协方差矩阵，以衡量不同特征之间的相关性。
4. 特征值分解：对协方差矩阵进行特征值分解，得到特征值和特征向量。
5. 选择主成分：根据特征值的大小选择前k个特征向量，这些向量对应的主成分代表数据的主要特征。
6. 数据投影：将原始数据投影到选择的主成分上，得到降维后的数据。
六、实验结果与分析1. 实验结果：通过实验，我们得到了降维后的数据集，并与原始数据集进行了比较。
结果表明，降维后的数据集保留了大部分原始数据的信息，同时降低了数据的维度。
2. 结果分析：实验结果表明，PCA在数据降维方面具有良好的效果。
然而，PCA也存在一些局限性，例如：（1）PCA假设数据服从正态分布，对于非正态分布的数据，PCA的效果可能不理想；（2）PCA降维后，部分信息可能丢失，尤其是在选择主成分时，需要权衡保留信息量和降低维度之间的关系；（3）PCA降维后的数据可能存在线性关系，导致模型难以捕捉数据中的非线性关系。
主成分分析和因子分析实验报告
主成分分析实验报告一、实验数据2013年，在国内外形势错综复杂的情况下，我国经济实现了平稳较快发展。
全年国内生产总值568845亿元，比上年增长7.7%。
其中第三产业增加值262204亿元，增长8.3%，其在国内生产总值中的占比达到了46.1%，首次超过第二产业。
经济的快速发展也带来了就业的持续增加，年末全国就业人员76977万人，其中城镇就业人员38240万人，全年城镇新增就业1310万人。
随着我国城镇化进程的不断加快，加之农业用地量的不断衰减，工业不断的转型升级，使得劳动力就业压力的缓解需要更多的依靠服务业的发展。
（一）指标选择根据指标选择的可行性、针对性、科学性等原则，选择13个指标来衡量服务业的发展水平，指标体系如表1所示：表1 服务业发展水平指标体系（二）指标数据本次实验采用的数据是我国31个省（市、自治区）2012年的数据，原数据均来自《2013中国统计年鉴》以及2013年各省（市、自治区）统计年鉴，不能直接获得的指标数据是通过对相关原始数据的换算求得。
原始数据如表2所示：表2（续）二、实验步骤本次实验是在SPSS中实现主成分分析，具体步骤如下：（一）数据标准化，单击主菜单“Analyze”(分析)展开下拉菜单，在下拉菜单中寻找“Descriptive Statistics”,在小菜单中寻找“Descriptives”(描述)，展开Descriptives对话框，将左面的矩形框中的变量X1、X2、 (X13)通过单击向右的箭头按钮，调入到右面的“Variables”(变量)框中。
选中Savestandardized values as variables(对变量进行标准化)复选框，点击OK按（二）单击主菜单“Analyze”(分析)展开下拉菜单，在下拉菜单中寻找“Data Reduction”弹出小菜单，在小菜单中寻找“Factor”(因子)，展开“Factor Analysis”(因子分析)主对话框。
主成分分析和因子分析实验报告
主成分分析和因子分析实验报告目录主成分分析和因子分析实验报告 (1)引言 (1)研究背景 (1)研究目的 (2)研究意义 (3)主成分分析 (4)主成分分析的概念 (4)主成分分析的原理 (5)主成分分析的步骤 (6)因子分析 (7)因子分析的概念 (7)因子分析的原理 (8)因子分析的步骤 (8)实验设计 (9)数据收集 (9)数据预处理 (11)主成分分析实验 (11)因子分析实验 (13)实验结果与分析 (14)主成分分析结果 (14)因子分析结果 (15)结果对比与讨论 (16)结论与展望 (17)实验结论 (17)实验不足与改进方向 (17)后续研究建议 (18)参考文献 (19)引言研究背景主成分分析（Principal Component Analysis，简称PCA）和因子分析（Factor Analysis，简称FA）是多元统计分析中常用的降维技术，广泛应用于数据挖掘、模式识别、图像处理、金融风险评估等领域。
这两种方法可以帮助我们从大量的变量中提取出最为重要的信息，简化数据集，减少冗余信息，同时保留原始数据的主要特征。
随着信息技术的迅速发展，数据的规模和复杂性不断增加，传统的统计分析方法已经无法满足对大规模数据的处理需求。
在这种背景下，主成分分析和因子分析成为了研究者们的关注焦点。
它们能够对高维数据进行降维处理，提取出最为重要的特征，从而更好地理解和解释数据。
主成分分析是一种无监督学习方法，通过线性变换将原始数据映射到一个新的坐标系中，使得新坐标系下的变量之间不相关。
这样做的好处是可以减少数据的维度，同时保留了原始数据的主要信息。
主成分分析的基本思想是找到能够最大程度解释数据方差的投影方向，即找到一组新的变量，使得它们之间的协方差为零。
这些新的变量被称为主成分，它们按照解释方差的大小排序，前几个主成分能够解释原始数据中大部分的方差。
因子分析是一种潜变量模型，它假设观测数据是由一组潜在因子和测量误差共同决定的。
主成分分析实验报告
项目名称实验4―主成分分析所属课程名称多元统计分析（英）项目类型综合性实验实验(实训)日期2012年 4 月15 日实验报告4主成分分析（综合性实验）(Principal component analysis)实验原理：主成分分析利用指标之间的相关性，将多个指标转化为少数几个综合指标，从而达到降维和数据结构简化的目的。
这些综合指标反映了原始指标的绝大部分信息，通常表示为原始指标的某种线性组合，且综合指标间不相关。
利用矩阵代数的知识可求解主成分。
实验题目：下表中给出了不同国家及地区的男子径赛记录：(t8a6)Country 100m(s) 200m(s)400m(s)800m(min)1500m(min)5000m(min)10,000m(min)Marathon(mins)Argentina 10.39 20.81 46.84 1.81 3.7 14.04 29.36 137.72 Australia 10.31 20.06 44.84 1.74 3.57 13.28 27.66 128.3 Austria 10.44 20.81 46.82 1.79 3.6 13.26 27.72 135.9 Belgium 10.34 20.68 45.04 1.73 3.6 13.22 27.45 129.95 Bermuda 10.28 20.58 45.91 1.8 3.75 14.68 30.55 146.62 Brazil 10.22 20.43 45.21 1.73 3.66 13.62 28.62 133.13 Burma 10.64 21.52 48.3 1.8 3.85 14.45 30.28 139.95Chile 10.34 20.8 46.2 1.79 3.71 13.61 29.3 134.03 China 10.51 21.04 47.3 1.81 3.73 13.9 29.13 133.53 Columbia 10.43 21.05 46.1 1.82 3.74 13.49 27.88 131.35 Cook Islands 12.18 23.2 52.94 2.02 4.24 16.7 35.38 164.7 Costa Rica 10.94 21.9 48.66 1.87 3.84 14.03 28.81 136.58 Czechoslovakia 10.35 20.65 45.64 1.76 3.58 13.42 28.19 134.32 Denmark 10.56 20.52 45.89 1.78 3.61 13.5 28.11 130.78 Dominican Republic 10.14 20.65 46.8 1.82 3.82 14.91 31.45 154.12 Finland 10.43 20.69 45.49 1.74 3.61 13.27 27.52 130.87 France 10.11 20.38 45.28 1.73 3.57 13.34 27.97 132.3 German (D.R.) 10.12 20.33 44.87 1.73 3.56 13.17 27.42 129.92 German (F.R.) 10.16 20.37 44.5 1.73 3.53 13.21 27.61 132.23 Great Brit.& N.Ireland 10.11 20.21 44.93 1.7 3.51 13.01 27.51 129.13 Greece 10.22 20.71 46.56 1.78 3.64 14.59 28.45 134.6 Guatemala 10.98 21.82 48.4 1.89 3.8 14.16 30.11 139.33 Hungary 10.26 20.62 46.02 1.77 3.62 13.49 28.44 132.58 India 10.6 21.42 45.73 1.76 3.73 13.77 28.81 131.98 Indonesia 10.59 21.49 47.8 1.84 3.92 14.73 30.79 148.83 Ireland 10.61 20.96 46.3 1.79 3.56 13.32 27.81 132.35 Israel 10.71 21 47.8 1.77 3.72 13.66 28.93 137.55Japan 10.34 20.81 45.86 1.79 3.64 13.41 27.72 128.63 Kenya 10.46 20.66 44.92 1.73 3.55 13.1 27.38 129.75 Korea 10.34 20.89 46.9 1.79 3.77 13.96 29.23 136.25 D.P.R Korea 10.91 21.94 47.3 1.85 3.77 14.13 29.67 130.87 Luxembourg 10.35 20.77 47.4 1.82 3.67 13.64 29.08 141.27 Malaysia 10.4 20.92 46.3 1.82 3.8 14.64 31.01 154.1 Mauritius 11.19 22.45 47.7 1.88 3.83 15.06 31.77 152.23 Mexico 10.42 21.3 46.1 1.8 3.65 13.46 27.95 129.2 Netherlands 10.52 20.95 45.1 1.74 3.62 13.36 27.61 129.02 New Zealand 10.51 20.88 46.1 1.74 3.54 13.21 27.7 128.98 Norway 10.55 21.16 46.71 1.76 3.62 13.34 27.69 131.48 Papua New Guinea 10.96 21.78 47.9 1.9 4.01 14.72 31.36 148.22 Philippines 10.78 21.64 46.24 1.81 3.83 14.74 30.64 145.27 Poland 10.16 20.24 45.36 1.76 3.6 13.29 27.89 131.58 Portugal 10.53 21.17 46.7 1.79 3.62 13.13 27.38 128.65 Rumania 10.41 20.98 45.87 1.76 3.64 13.25 27.67 132.5 Singapore 10.38 21.28 47.4 1.88 3.89 15.11 31.32 157.77 Spain 10.42 20.77 45.98 1.76 3.55 13.31 27.73 131.57 Sweden 10.25 20.61 45.63 1.77 3.61 13.29 27.94 130.63 Switzerland 10.37 20.46 45.78 1.78 3.55 13.22 27.91 131.2 Taipei 10.59 21.29 46.8 1.79 3.77 14.07 30.07 139.27Thailand 10.39 21.09 47.91 1.83 3.84 15.23 32.56 149.9 Turkey 10.71 21.43 47.6 1.79 3.67 13.56 28.58 131.5 USA 9.93 19.75 43.86 1.73 3.53 13.2 27.43 128.22 USSR 10.07 20 44.6 1.75 3.59 13.2 27.53 130.55 Western Samoa 10.82 21.86 49 2.02 4.24 16.28 34.71 161.83 （数据来源：1984年洛杉机奥运会IAAF/AFT径赛与田赛统计手册）实验要求：（1）试用Princomp过程求主成分；并对结果进行解释；（2）试用方差累积贡献率和Scree图确定主成分的个数；（3）计算各国第一主成分的得分并排名；（4）试对结果进行解。
主成分分析因子分析实验报告
主成分分析因子分析实验报告引言：方法：数据集：本次实验使用的数据集是关于一组学生的各项成绩数据，包括语文、数学、英语等科目的成绩。
数据集共有100个样本，每个样本包含5个特征。
主成分分析（PCA）：主成分分析的主要思想是通过线性变换将原始数据映射到一个新的坐标系中，使得数据在新的坐标系下的方差最大化。
这样可以使得数据在新的坐标系下尽可能地被压缩到一维或者二维空间中，从而实现降维的目的。
在本次实验中，我们将对数据集进行主成分分析，寻找数据中的主要结构。
因子分析（Factor Analysis）：因子分析的主要思想是假设观测数据是由一组潜在因子和测量误差组成的。
因子分析试图通过最大似然估计的方法找出最可能的潜在因子，并将观测数据映射到潜在因子的空间中。
在本次实验中，我们将使用因子分析探索数据集中的潜在因子结构。
结果：主成分分析（PCA）：通过主成分分析，我们发现数据集的前两个主成分可以解释约80%的数据方差。
这表明数据在二维空间下已经能够充分表示原始数据的特征。
同时，我们还可以观察到各个特征在主成分空间中的投影，从而了解不同特征之间的相关性。
因子分析（Factor Analysis）：通过因子分析，我们找到了数据集中的两个主要因子，分别是“数理化”因子和“语言能力”因子。
这两个因子可以代表数据中的大部分信息，与原始特征之间存在着较高的相关性。
因子分析帮助我们发现了数据中的潜在结构，并解释了数据之间的关系。
讨论：主成分分析和因子分析是两种常用的数据降维技术，能够通过线性变换和潜在因子的挖掘来发现数据的主要结构和潜在信息。
在本次实验中，我们使用这两种方法对一个学生成绩数据集进行了分析，发现了数据中的主要结构和隐藏因子。
通过主成分分析，我们找到了能够解释数据80%方差的主成分，并可视化了数据在主成分空间中的表现。
通过因子分析，我们发现了数据中的两个主要因子，并解释了数据中的潜在结构。
结论：主成分分析和因子分析是一种强大的数据分析工具，能够帮助我们更好地理解数据并发现数据中的潜在结构。
主成分分析实验报告
主成分分析实验报告主成分分析实验报告引言主成分分析（Principal Component Analysis, PCA）是一种常用的数据降维方法，可以将高维数据转化为低维数据，同时保留原始数据的主要信息。
本实验旨在通过主成分分析方法对一个实际数据集进行分析，探索数据的内在结构和特征。
实验设计我们选择了一个包含多个变量的数据集，该数据集包括了一些关于学生的信息，如年龄、身高、体重、成绩等。
我们的目标是通过主成分分析，找出这些变量之间的相关性，并将其转化为更少的几个主成分。
实验步骤1. 数据收集和预处理我们首先收集了一组学生的相关数据，并进行数据预处理。
对于缺失值，我们选择了删除或填补。
对于离群值，我们考虑了使用替代值或剔除的方法。
2. 数据标准化为了确保各个变量具有相同的尺度，我们对数据进行了标准化处理。
通过减去均值并除以标准差，我们使得每个变量的均值为0，标准差为1。
3. 计算协方差矩阵我们利用标准化后的数据计算协方差矩阵。
协方差矩阵反映了不同变量之间的线性关系。
4. 计算特征值和特征向量通过对协方差矩阵进行特征值分解，我们得到了一组特征值和对应的特征向量。
特征值表示了数据在对应特征向量方向上的方差。
5. 选择主成分我们按照特征值的大小，选择了最大的几个特征值对应的特征向量作为主成分。
这些主成分能够尽可能多地解释原始数据的方差。
6. 数据转化通过将原始数据与所选主成分进行线性组合，我们得到了转化后的数据。
这些转化后的数据具有更低的维度，但仍然保留了原始数据的主要信息。
实验结果通过主成分分析，我们得到了一组主成分，并计算了每个主成分对原始数据的解释方差比例。
我们发现，前几个主成分能够解释原始数据的大部分方差，而后面的主成分对方差的解释能力较弱。
讨论与结论主成分分析帮助我们发现了学生数据集中的一些内在结构和特征。
通过主成分分析，我们可以将原始数据转化为更少的几个主成分，从而降低了数据的维度，方便后续的数据分析和可视化。
实验报告一主成分分析
实验报告一主成分分析一、实验目的二、实验原理主成分分析的基本原理是寻找能够最大化数据方差的主轴方向，并以此来确定各个主成分的权重。
具体步骤如下：1.去除数据的均值，使数据集的中心为原点。
2.计算数据的协方差矩阵。
3.对协方差矩阵进行特征值分解，得到特征值和特征向量。
4.对特征值从大到小进行排序，选择前k个特征值对应的特征向量作为主成分。
5.将原始数据映射至选取的k个主成分构成的新坐标系中。
三、实验步骤2.对数据集进行预处理，包括去除缺失值、标准化处理等。
3.计算协方差矩阵。
4.对协方差矩阵进行特征值分解，并选择主成分。
5.将原始数据集映射至选取的主成分构成的新坐标系中。
6.可视化处理后的数据集，以便观察降维效果。
四、实验结果及分析经过主成分分析处理后，我们得到了降维后的数据集。
通过对比降维前后的数据，可以观察到数据在新坐标系中的分布情况。
如果降维后的数据集能够较好地保留原始数据的特征和结构，即数据点在新坐标系中的分布比较紧密，那么主成分分析的效果就较好。
五、实验结论通过实验，我们对主成分分析的原理和应用有了更深入的了解。
主成分分析可以有效地降低数据的维度，并保留原始数据的重要特征。
在实际应用中，主成分分析常用于多变量数据的预处理、降维和数据可视化等任务中，具有广泛的应用价值。
六、实验总结本次实验我们学习了主成分分析的基本原理和应用，并进行了实际操作。
实验结果表明主成分分析可以有效地降低数据的维度，保留了原始数据的重要特征，并成功地将数据映射到新的坐标系中。
通过本次实验的学习，我进一步掌握了主成分分析的方法和技巧，并了解了其在数据分析中的重要作用。
在实际应用中，我们可以根据需求选择适当的主成分数目，以达到最佳的降维效果和数据解释性。
主成分分析实验报告
应用多元统计分析实验报告主成分分析专业：数学与应用数学班级：09-01姓名：***学号：************应用多元统计分析实验报告实验2 主成分分析1.1 实验名称:主成分分析1.2 实验目的：通过本实验掌握使用SAS进行主成分分析1.3 实验内容：编程作主成分分析1.3.1 程序代码1）主成分分析程序代码proc princomp data=sasuser.exec76 out=prin;var x1-x7;proc sort;by prin1;proc print;id state;var prin1 prin2;proc sort;by prin2;proc print;id state ;var prin1 prin2;proc plot data=prin;plot prin2*prin1=state/haxis=-4.0to 6.0by 0.5vaxis=-3.5to 3.5by 0.5; run;1.3.2 实验结果描述统计量和相关矩阵还有相关矩阵的特征值的图表：相关矩阵的特征向量：由前两个最大的特征值对应的特征值向量可以写出第一和第二主成分：xx x x x x x *7*6*5*4*3*2*11295177.0357360.0440157.0396652.0396875.0431759.0300279.0yˆ++++++=xx x x x x x *7*6*5*4*3*2*12502421.04023190.0203341.0343528.00422475.0169435.0629174.0yˆ+++-+--=x x x x x x x *7*6*5*4*3*2*13568384.0539281.0209895.0069510.0495681.0244198.0178245.0yˆ+---+-=按第一主成分得分排序：按第二主成分分析排序：前两个主成分得分的散点图：．．1.4 实验体会经过几次的实验练习，发现对SAS明显熟练了许多，能对某些操作熟练掌握，看程序也能理解其中的意思了。
主成分分析因子分析实验报告
主成分分析因子分析实验报告实验目的：实验步骤：1.收集数据：我们选择了一个包含10个观测变量的数据集，其中包括身高、体重、年龄、血压等变量。
数据集总共有100个样本。
2.数据预处理：在进行主成分分析和因子分析之前，我们首先进行数据预处理，包括缺失值填充、异常值处理和数据标准化等。
通过这些步骤，我们可以确保数据的准确性和可靠性。
3. 主成分分析（PCA）：在进行PCA之前，我们需要确定主成分的数量。
我们使用Kaiser准则和累计方差解释比来确定主成分的个数。
接下来，我们使用PCA方法进行主成分分析，并计算每个主成分的贡献率和累计贡献率。
此外，我们还绘制了特征值图，以便更好地理解主成分的贡献。
4. 因子分析（FA）：在进行因子分析之前，我们需要确定因子的数量和旋转方法。
我们使用Bartlett球形检验和Kaiser-Meyer-Olkin （KMO）测度来确定因子的数量。
然后，我们使用最大方差旋转方法进行因子分析，以获得更清晰和可解释的因子结构。
我们计算每个因子的贡献率和累计贡献率，并通过因子载荷矩阵来解释因子和变量之间的关系。
5.结果分析：根据主成分和因子的贡献率和解释性，我们可以确定最重要的主成分和因子。
通过对主成分和因子的解释，我们可以深入了解变量之间的关联性和结构。
此外，我们还可以利用主成分和因子进行变量降维，以便更好地理解和解释数据。
实验结果：在主成分分析中，我们确定了3个主成分，其中第一个主成分的贡献率为35%，第二个主成分的贡献率为22%，第三个主成分的贡献率为16%。
累计贡献率达到73%，说明这3个主成分可以很好地解释观测变量之间的关系。
从特征值图中可以看出，前3个主成分的特征值明显大于其他主成分。
在因子分析中，我们确定了2个因子，并使用最大方差旋转方法进行了因子分析。
第一个因子解释了25%的方差，第二个因子解释了18%的方差。
因子载荷矩阵显示了变量和因子之间的关系，可以用来解释因子的含义。
数据分析实验报告8 主成分分析
实验八主成分分析一、实验目的和要求能利用原始数据与相关矩阵、协主差矩阵作主成分分析,并能理解标准化变量主成分与原始数据主成分的联系与区别；能根据SAS输出结果选出满足要求的几个主成分．实验要求:编写程序，结果分析．实验内容：书上4.5 4.64.5 data examp4_5;input id x1-x8;cards;1 8.35 23.53 7.51 8.62 17.42 10.00 1.04 11.212 9.25 23.75 6.61 9.19 17.77 10.48 1.72 10.513 8.19 30.50 4.72 9.78 16.28 7.60 2.52 10.324 7.73 29.20 5.42 9.43 19.29 8.49 2.52 10.005 9.42 27.93 8.20 8.14 16.17 9.42 1.55 9.766 9.16 27.98 9.01 9.32 15.99 9.10 1.82 11.357 10.06 28.64 10.52 10.05 16.18 8.39 1.96 10.818 9.09 28.12 7.40 9.62 17.26 11.12 2.49 12.659 9.41 28.20 5.77 10.80 16.36 11.56 1.53 12.1710 8.70 28.12 7.21 10.53 19.45 13.30 1.66 11.9611 6.93 29.85 4.54 9.49 16.62 10.65 1.88 13.6112 8.67 36.05 7.31 7.75 16.67 11.68 2.38 12.8813 9.98 37.69 7.01 8.94 16.15 11.08 0.83 11.6714 6.77 38.69 6.01 8.82 14.79 11.44 1.74 13.2315 8.14 37.75 9.61 8.49 13.15 9.76 1.28 11.2816 7.67 35.71 8.04 8.31 15.13 7.76 1.41 13.2517 7.90 39.77 8.49 12.94 19.27 11.05 2.04 13.2918 7.18 40.91 7.32 8.94 17.60 12.75 1.14 14.8019 8.82 33.70 7.59 10.98 18.82 14.73 1.78 10.1020 6.25 35.02 4.72 6.28 10.03 7.15 1.93 10.3921 10.60 52.41 7.70 9.98 12.53 11.70 2.31 14.6922 7.27 52.65 3.84 9.16 13.03 15.26 1.98 14.5723 13.45 55.85 5.50 7.45 9.55 9.52 2.21 16.3024 10.85 44.68 7.32 14.51 17.13 12.08 1.26 11.5725 7.21 45.79 7.66 10.36 16.56 12.86 2.25 11.6926 7.68 50.37 11.35 13.30 19.25 14.59 2.75 14.8727 7.78 48.44 8.00 20.51 22.12 15.73 1.15 16.6128 7.94 39.65 20.97 20.82 22.52 12.41 1.75 7.9029 8.28 64.34 8.00 22.22 20.06 15.12 0.72 22.8930 12.47 76.39 5.52 11.24 14.52 22.00 5.46 25.50;run;proc corr cov nosimple data=examp4_5;var x1-x8;run;proc princomp data=examp4_5 prefix=y out=bb;var x1-x8;run;proc plot data=bb;plot y2*y1 $ id='*';proc sort data=bb;by descending y1;run;proc print data=bb;var id y1 y2 x1-x8;run;输出结果：1、样本相关系数矩阵Correlation Matrixx1 x2 x3 x4 x5 x6 x7 x8x1 1.0000 0.3336 -.0545 -.0613 -.2894 0.1988 0.3487 0.3187x2 0.3336 1.0000 -.0229 0.3989 -.1563 0.7111 0.4136 0.8350x3 -.0545 -.0229 1.0000 0.5333 0.4968 0.0328 -.1391 -.2584x4 -.0613 0.3989 0.5333 1.0000 0.6984 0.4679 -.1713 0.3128x5 -.2894 -.1563 0.4968 0.6984 1.0000 0.2801 -.2083 -.0812x6 0.1988 0.7111 0.0328 0.4679 0.2801 1.0000 0.4168 0.7016x7 0.3487 0.4136 -.1391 -.1713 -.2083 0.4168 1.0000 0.3989x8 0.3187 0.8350 -.2584 0.3128 -.0812 0.7016 0.3989 1.00002、调用主成分分析的princomp过程，从相关系数矩阵出发进行主成分分析，输出集bb The PRINCOMP ProcedureObservations 30Variables 8Simple Statisticsx1 x2 x3 x4Mean 8.706666667 39.05600000 7.629000000 10.86566667 StD 1.614728190 12.43875828 3.052716540 3.89495579Simple Statisticsx5 x6 x7 x8Mean 16.58900000 11.62600000 1.902000000 13.06100000 StD 2.99785481 3.05810805 0.851576226 3.647070961）样本相关系数矩阵R的特征值、各主成分贡献率及累计贡献率Eigenvalues of the Correlation Matrix特征值∧*iλ Difference 贡献率% 累计贡献率%1 3.09628829 0.72906522 0.3870 0.38702 2.36722307 1.44723572 0.2959 0.6829已达68.29%3 0.91998735 0.21406199 0.1150 0.79794 0.70592536 0.20748303 0.0882 0.88625 0.49844233 0.26855403 0.0623 0.94856 0.22988831 0.09911254 0.0287 0.97727 0.13077577 0.07930623 0.0163 0.99368 0.05146954 0.0064 1.0000SAS 系统 14:09 Monday, October 22, 2001 22The PRINCOMP Procedure2）样本相关系数矩阵R特征值的正交化特征向量The SAS System 17:30 Tuesday, October 26, 2012 4The PRINCOMP ProcedureEigenvectorsy1 y2 y3 y4 y5 y6 y7 y8x1 0.249607 -.241238 0.693918 -.376770 0.502313 -.018418 -.036543 0.045052x2 0.519234 -.037607 -.071261 -.224871 -.424453 0.001760 -.282467 0.642950x3 -.018480 0.475439 0.577819 0.032379 -.510472 -.173344 0.381416 -.050854x4 0.254092 0.538081 -.021777 -.231066 0.010358 0.399113 -.471680 -.458432x5 0.021695 0.575449 -.048087 0.285368 0.516270 0.146109 0.159192 0.520977x6 0.492663 0.134676 -.145348 0.224222 0.177156 -.754966 -.081452 -.244442x7 0.317147 -.260682 0.286391 0.768116 -.090759 0.355165 -.130720 -.089297x8 0.509332 -.087081 -.271279 -.176990 0.026015 0.304720 0.708416 -.1808213）按第一主成分对各省份进行排序The SAS System 17:30 Tuesday, October 26, 2012 6 Obs id y1 y2 x1 x2 x3 x4 x5 x6 x7 x81 30 6.89591 -2.27833 12.47 76.39 5.52 11.24 14.52 22.00 5.46 25.502 29 3.24842 2.56095 8.28 64.34 8.00 22.22 20.06 15.12 0.72 22.893 27 1.79214 2.88809 7.78 48.44 8.00 20.51 22.12 15.73 1.15 16.614 26 1.51507 1.37353 7.68 50.37 11.35 13.30 19.25 14.59 2.75 14.875 23 1.40116 -3.17840 13.45 55.85 5.50 7.45 9.55 9.52 2.21 16.306 21 1.15390 -1.37420 10.60 52.41 7.70 9.98 12.53 11.70 2.31 14.697 22 1.05651 -1.23524 7.27 52.65 3.84 9.16 13.03 15.26 1.98 14.578 24 0.43543 0.47409 10.85 44.68 7.32 14.51 17.13 12.08 1.26 11.579 25 0.15329 0.11320 7.21 45.79 7.66 10.36 16.56 12.86 2.25 11.6910 17 0.04520 0.98056 7.90 39.77 8.49 12.94 19.27 11.05 2.04 13.2911 28 -0.13324 4.90844 7.94 39.65 20.97 20.82 22.52 12.41 1.75 7.9012 18 -0.13489 0.34363 7.18 40.91 7.32 8.94 17.60 12.75 1.14 14.8013 19 -0.14112 0.68197 8.82 33.70 7.59 10.98 18.82 14.73 1.78 10.1014 12 -0.17044 -0.58962 8.67 36.05 7.31 7.75 16.67 11.68 2.38 12.8815 8 -0.39220 -0.29562 9.09 28.12 7.40 9.62 17.26 11.12 2.49 12.6516 10 -0.43040 0.64570 8.70 28.12 7.21 10.53 19.45 13.30 1.66 11.9617 14 -0.51802 -0.55227 6.77 38.69 6.01 8.82 14.79 11.44 1.74 13.23 18 9 -0.61274 -0.28257 9.41 28.20 5.77 10.80 16.36 11.56 1.53 12.17 19 13 -0.66670 -0.29548 9.98 37.69 7.01 8.94 16.15 11.08 0.83 11.67 20 11 -0.81850 -0.42128 6.93 29.85 4.54 9.49 16.62 10.65 1.88 13.61 21 7 -1.11335 -0.01815 10.06 28.64 10.52 10.05 16.18 8.39 1.96 10.81 22 15 -1.11496 -0.44043 8.14 37.75 9.61 8.49 13.15 9.76 1.28 11.28 23 6 -1.18223 -0.19296 9.16 27.98 9.01 9.32 15.99 9.10 1.82 11.35 24 2 -1.25819 -0.13224 9.25 23.75 6.61 9.19 17.77 10.48 1.72 10.51 25 16 -1.25934 -0.42827 7.67 35.71 8.04 8.31 15.13 7.76 1.41 13.25 26 3 -1.29370 -0.86033 8.19 30.50 4.72 9.78 16.28 7.60 2.52 10.32 27 4 -1.32567 -0.10239 7.73 29.20 5.42 9.43 19.29 8.49 2.52 10.00 28 5 -1.48595 -0.35156 9.42 27.93 8.20 8.14 16.17 9.42 1.55 9.76 29 1 -1.68448 0.16743 8.35 23.53 7.51 8.62 17.42 10.00 1.04 11.21 30 20 -1.96091 -2.10827 6.25 35.02 4.72 6.28 10.03 7.15 1.93 10.3由输出结果可以看出：前两个主成分的累计贡献率已达68.29%，因此，取前两个主成分做进一步分析即可．给出了对应于∧*1λ和∧*2λ的正交单位化特征向量∧*1e 和∧*2e ，由此得到标准化指标的前两个样本主成分为11123456780249605092001840254100217049270317105093∧==+-+++++e x***********........Ty x x x x x x x x为8个指标加权平均，反映各省份在生活基本消费的消费水平能力的综合指标．*1y 值大，则各省份的生活水平越低，21123456780241200376047540538005754013470360700871∧==--++++-+e x***********........Ty x x x x x x x x反映各省份在生活消费品德消费能力综合指标，2*y 值大，则各省份的消费水平越高。
检测食品成分实验报告(3篇)
第1篇一、实验目的本次实验旨在通过化学分析和仪器分析方法，检测食品中的主要成分，包括蛋白质、脂肪、碳水化合物、矿物质、维生素等，以了解食品的营养成分和卫生状况。
二、实验原理1. 蛋白质：采用双缩脲法测定蛋白质含量，原理为蛋白质中的肽键与双缩脲试剂发生反应，生成紫色络合物，其颜色深浅与蛋白质含量成正比。
2. 脂肪：采用索氏抽提法测定脂肪含量，原理为脂肪不溶于水，可被有机溶剂抽提，通过称量抽提出的脂肪量来计算脂肪含量。
3. 碳水化合物：采用苯酚-硫酸法测定碳水化合物含量，原理为碳水化合物与苯酚在硫酸作用下生成蓝绿色化合物，其颜色深浅与碳水化合物含量成正比。
4. 矿物质：采用原子吸收光谱法测定矿物质含量，原理为样品中的矿物质元素在特定波长下吸收特定波长的光，通过测定吸光度来计算元素含量。
5. 维生素：采用高效液相色谱法测定维生素含量，原理为维生素具有特定的紫外吸收峰，通过测定样品的紫外吸收光谱来计算维生素含量。
三、实验材料1. 样品：面粉、牛奶、鸡蛋、水果等。
2. 试剂：双缩脲试剂、苯酚、硫酸、盐酸、氢氧化钠、三氯化铁、氯化钠、硝酸、高氯酸、原子吸收光谱标准溶液、维生素标准溶液等。
3. 仪器：分光光度计、索氏抽提器、电子天平、原子吸收光谱仪、高效液相色谱仪等。
四、实验步骤1. 蛋白质含量测定（1）称取样品0.5g，加入5mL双缩脲试剂，充分混合，室温放置10min。
（2）以试剂空白为参比，在540nm波长下测定吸光度。
（3）根据标准曲线计算蛋白质含量。
2. 脂肪含量测定（1）称取样品5g，加入50mL石油醚，在索氏抽提器中抽提6h。
（2）将抽提液转移至锥形瓶中，挥去石油醚，加入5mL盐酸，加热至近干。
（3）加入5mL氢氧化钠溶液，充分混合，加入5mL三氯化铁溶液，静置10min。
（4）以试剂空白为参比，在520nm波长下测定吸光度。
（5）根据标准曲线计算脂肪含量。
3. 碳水化合物含量测定（1）称取样品5g，加入10mL苯酚溶液，充分混合。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
主成分分析
地信0901班陈任翔010******* 【实验目的及要求】
掌握主成分分析与因子分析的思想和具体步骤。
掌握SPSS实现主成分分析与因子分析的具体操作。
【实验原理】
1.主成分分析的主要目的是希望用较少的变量去解释原来资料中的大部分变异，将我们手中许多相关性很高的变量转化成彼此相互独立或不相关的变量。
通常是选出比原始变量个数少，能解释大部分资料中的变异的几个新变量，即所谓主成分，并用以解释资料的综合性指标。
由此可见，主成分分析实际上是一种降维方法。
2.因子分析研究相关矩阵或协方差矩阵的内部依赖关系，它将多个变量综合为少数几个因子，以再现原始变量与因子之间的相关关系。
【实验步骤】
1.数据准备
●1）首先在Excel中打开“水样元素成分分析数据”，删除表名“水样元素成分分析数据”,
保存数据。
●3）数据格式转换。
2.数据描述分析操作
1）Descriptives过程
点击Analyze下的Descriptive Statistics选项，选择该选项下的Descriptives
●选中待处理的变量（左侧的As…..Hg等）；
●点击使变量As…..Hg 移至Variable(s)中；
●选中Save standrdized values as variables；
●点击Options
2）数据标准化
标准化处理后的结果
2.主成分分析
1）点击Analyze下的Data Reduction选项，选择该选项下的Factor过程。
选中待处理的变量，移至Variables
2）点击Descriptives判断是否有进行因子分析的必要
Coefficients(计算相关系数矩阵)
Significance levels(显著水平)
KMO and Bartlett’s test of sphericity (对相关系数矩阵进行统计学检验)
Inverse(倒数模式）：求出相关矩阵的反矩阵；
Reproduced(重制的):显示重制相关矩阵，上三角形矩阵代表残差值，而主对角线及下三角形代表相关系数；
Determinant(行列式)：求出前述相关矩阵的行列式值；
Anti-image(反映像)：求出反映像的共同量及相关矩阵。
Univariate descriptive单变量描述统计量(输出被选中的各变量的均数与标准差)
Initial solution未转轴之统计量（显示因素分析未转轴前之共同性、特征值、变异数百分比及累积百分比）
3）点击Extraction ：
●选择主成分分析方法
●输出未旋转的因子载荷矩阵
4）点击Rotation
5）点击Scores
●选中Save as variables (把因子得分作为新变量保存在数据文件中)
●选中Regression(回归因子得分)
●点击Continue
6）点击Options
●选中Exclude cases listwise(去除所有含缺失数据的样本、再进行分析)
●选中Sorted by size(载荷系数将按照数值大小排列，并构成矩阵)
●点击Continue
3．结果分析
●SPSS输出的第一个表格列出了标准化后数据的平均值（Mean）、标准差
（Std. Deviation）和分析用到的取值个数(N)
●系统输出的第2个表格是8个原始变量的相关矩阵与单尾显著性检验
（多个变量之间的相关系数较大，说明这些变量之间存在着较为显著的相关性，且其对应的Sig值普遍较小，根据分析，这些数据有进行因子分析的必要。
）
●KMO检验法和巴特利特球形检验法（KMO and Bartlett Test of Sphericity）的检验
结果
（Bartlett球形检验统计量的Sig<0.01，认为各变量之间存在着显著的相关性。
一般，KMO大于0.9时效果最佳，0.7以上可以接受，0.5以下不宜作因子分析。
但是相关矩阵和Bartlett球形检验统计量的效果都比较好，认为是可以作因子分析）
●SPSS输出的第四个表格“成分矩阵”是初始的未经旋转的因子载荷矩阵
（已选出了3个主因子,以替代原有的8个变量所含的信息）
●SPSS输出的第七个表格“旋转成分矩阵”是经过旋转（转轴法使得因素负荷量
易于解释）后的因子载荷矩阵。
（旋转后每个公因子上的载荷分配地更清晰，因子变量代表的变量相对集中，比未旋转时更容易解释各因子的意义。
载荷绝对值较大的因子与变量的关系更为密切，也更能代表这个变量
●第1公因子代表Cd、Zn、As、Pb这几个变量因素
●第2公因子代表Cr、P两个变量
●第3公因子代表Cu、Hg两个变量
●可以根据实际情况对第1公因子、第2公因子、第3公因子命名
●我们将第1公因子命名为镉类，第2公因子命名为铬类，第3公因子命名为铜类）
●SPSS输出的第八个表格“成分转换矩阵”是正交旋转后因素相关矩阵
●SPSS输出的第六个表格表示各因子变量的特征值与累积贡献率（表明m个主成
分综合原始变量的能力）
（由于前3个特征值累计贡献率达到91.798%，根据累计贡献率大于85%的原则，故选
取前三个特征值）
●SPSS输出的第五个表格表示变量的共同度（m个公共因子对第i个变量Xi的方
差贡献）
（As的共同度为0.974,可以理解为3个公共因子能够解释As的方差的97.4%;Pb的共同度为0.581,可以理解为3个公共因子能够解释As的方差的58.1%。
）
●回到Data View窗口的当前数据集，会看到文件中增加了3列FAC1_1(第1因子
得分)、FAC2_1(第2因子得分)和FAC3_1(第3因子得分)
（可以通过第1因子得分来了解镉类元素的分布情况，第2公因子来了解铬类元素的分布情况，第3公因子来了解铜类元素的分布情况。
样号为Z-W-2-02的样品Cd、Zn、As、Pb含量较高，样号为C-W-06-01的样品Cr、P含量较高，样号为C-W-01-02的样品重金属含量较高）
zF(综合得分)＝46.048%* FAC1_1 + 24.085%* FAC2_1 + 21.665%* FAC3_1。
根据综合得分可以看出总体情况
【实验总结】
通过本次实验，了解SPSS软件的运行管理方式；熟悉各主要操作模块，窗口及其功能，相关的系统参数设置等。
基本掌握了应用SPSS软件Analyze菜单中的Data Reduction模块对数据进行主成分分析和因子分析，但是在操作过程和文字分析上还是有些生疏，有待进一步的熟练。
2011-11-4。