2017届高考数学(理)一轮复习学案 53排列组合
【高优指导】2017高考数学一轮复习 第十一章 计数原理 11.2 排列与组合课件 理 北师大版

2.排列数与组合数的概念
名称 排列数 组合数
定义 从 n 个不同元素中取出 m(m≤n) 个元素的所有不同 排列的个数 组合的个数
-4-
3.排列数、组合数的公式及性质 (1)排列数公式:A������ ������ =n(n-1)(n-2)…(n-m+1)= (2)全排列:A������ ������ =n×(n-1)×(n-2)×…×2×1=n!. (3)组合数的计算公式:
考点1
考点2
考点3
知识方法
易错易混
2 种有C34 =561(种 ),
关闭
答案
-18考点1 考点2 考点3 知识方法 易错易混
思考:解决组合问题的一般思路是什么?常用方法有哪些? 解题心得:1.解组合问题的一般思路为:首先分清问题是不是组合 问题;其次要搞清是“分类”还是“分步”,一般是先整体分类,然后局 部分步,将复杂问题通过两个原理化归为简单问题. 2.含有附加条件的组合问题的常用方法有:通常用直接法或间接 法,应注意“至少”“最多”“恰好”等词的含义的理解,对于涉及“至 少”“至多”等词的组合问题,既可考虑反面情形间接求解,也可以分 类研究进行直接求解.
-7-
1 2 3 4 5
3.用数字1,2,3,4,5组成的无重复数字的四位偶数的个数为( A.8 B.24 C.48 D.120
)
关闭
3 1 3 先排个位有A1 种排法 , 再排前三位有 A 种排法 , 故共有 A 2 4 2 A 4 =48 种排 法.
关闭
C
解析 答案
-8-
1 2 3 4 5
4.(2015广东,理12)某高三毕业班有40人,同学之间两两彼此给对 方仅写一条毕业留言,那么全班共写了 条毕业留言.(用 数字作答)
高三数学一轮复习教学案:排列、组合、二项式定理 学案
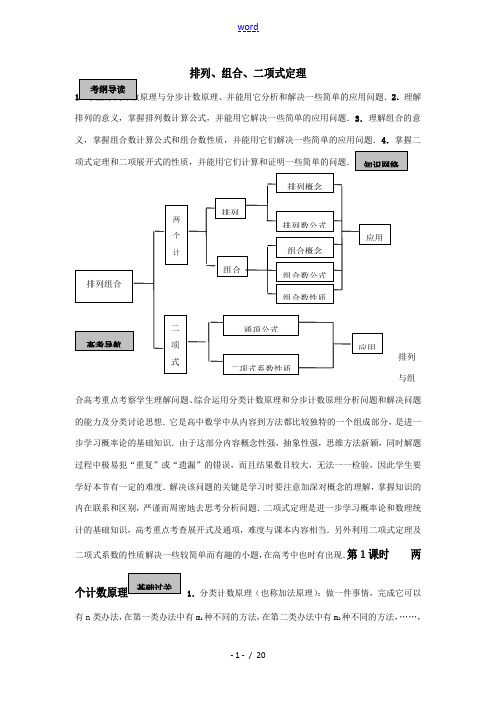
排列、组合、二项式定理2.理解排列的意义,掌握排列数计算公式,并能用它解决一些简单的应用问题.3.理解组合的意义,掌握组合数计算公式和组合数性质,并能用它们解决一些简单的应用问题.4.掌握二排列与组合高考重点考察学生理解问题、综合运用分类计数原理和分步计数原理分析问题和解决问题的能力及分类讨论思想.它是高中数学中从内容到方法都比较独特的一个组成部分,是进一步学习概率论的基础知识.由于这部分内容概念性强,抽象性强,思维方法新颖,同时解题过程中极易犯“重复”或“遗漏”的错误,而且结果数目较大,无法一一检验,因此学生要学好本节有一定的难度.解决该问题的关键是学习时要注意加深对概念的理解,掌握知识的内在联系和区别,严谨而周密地去思考分析问题.二项式定理是进一步学习概率论和数理统计的基础知识,高考重点考查展开式及通项,难度与课本内容相当.另外利用二项式定理及二项式系数的性质解决一些较简单而有趣的小题,在高考中也时有出现.第1课时两1.分类计数原理(也称加法原理):做一件事情,完成它可以有n类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,……,在第n 类办法中有m n 种不同的方法,那么完成这件事共有N =种不同的方法.2.分步计数原理(也称乘法原理):做一件事情,完成它需要分成n 个步骤,做第一步有m 1种不同的方法,做第二步有m 2种不同的方法,……,做n 步有m n 种不同的方法,那么完成这件事共有N =种不同的方法.3.解题方法:枚举法、插空法、隔板法.(2)、(3)班分别有学生48,50,52人(1) 从中选1人当学生代表的方法有多少种?(2) 从每班选1人组成演讲队的方法有多少种?(3) 从这150名学生中选4人参加学代会有多少种方法?(4) 从这150名学生中选4人参加数理化四个课外活动小组,共有多少种方法?解:(1)48+50+52=150种 (2)48×50×52=124800种 (3)4150C (4)4150A 变式训练1:在直角坐标x -o -y 平面上,平行直线x=n ,(n=0,1,2,3,4,5),y=n ,(n=0,1,2,3,4,5),组成的图形中,矩形共有( )A 、25个B 、36个C 、100个D 、225个解:在垂直于x 轴的6条直线中任意取2条,在垂直于y 轴的6条直线中任意取2条,这样的4条直线相交便得到一个矩形,所以根据分步记数原理知道:得到的矩形共有22515152626=⨯=⋅C C 个, 故选D 。
高中数学一轮复习:排列组合

高中数学一轮复习:排列组合一、单选题(共10题;共20分)1.某电视台连续播放5个不同的广告,其中有3个不同的商业广告和2个不同的奥运宣传广告,要求最后播放的必须是奥运宣传广告,且两个奥运宣传广告不能连续播放,则不同的播放方式有( )A. 120种B. 48种C. 36种D. 18种2.(2019高二下·蓝田期末)18×17×16×⋯×12×11等于()A. A188B. A189C. A1810D. A18113.(2018高二下·河北期中)老王和小王父子俩玩一种类似于古代印度的“梵塔游戏”;有3个柱子甲、乙、丙,在甲柱上现有4个盘子,最上面的两个盘子大小相同,从第二个盘子往下大小不等,大的在下,小的在上(如图),把这4个盘子从甲柱全部移到乙柱游戏即结束,在移动过程中每次只能移动一个盘子,甲、乙、丙柱都可以利用,且3个柱子上的盘子始终保持小的盘子不能放在大的盘子之下,设游戏结束需要移动的最少次数为n,则n=()A. 7B. 8C. 11D. 154.若C82x−1=C8x+3,则x的值为()A. 1或2B. 3或4C. 1或3D. 2或45.(2017高三上·长沙开学考)若二项式(x2+ a)7展开式的各项系数之和为﹣1,则含x2项的系数为x()A. 560B. ﹣560C. 280D. ﹣2806.(2018高二下·西安期末)《中国诗词大会》(第二季)亮点颇多,十场比赛每场都有一首特别设计的开场诗词在声光舞美的配合下,百人团齐声朗诵,别有韵味.若《将进酒》《山居秋暝》《望岳《送杜少府之任蜀州》和另确定的两首诗词排在后六场,且《将进酒》排在《望岳》的前面,《山居秋暝》与《送杜少府之任蜀州》不相邻且均不排在最后,则后六场的排法有()A. 288种B. 144种C. 720种D. 360种7.(2017高二下·桂林期末)在哈尔滨的中央大街的步行街同侧有6块广告牌,牌的底色可选用红、蓝两种颜色,若要求相邻两块牌的底色不都为蓝色,则不同的配色方案共有()A. 20B. 21C. 22D. 248.从1,3,5,7,9这5个奇数中选取3个数字,从2,4,6,8这4个偶数中选取2个数字,再将这5个数字组成没有重复数字的五位数,且奇数数字与偶数数字相间排列.这样的五位数的个数是( )A. 180B. 360C. 480D. 7209.(2019·台州模拟)已知 (x −1)5=a 0+a 1(x +1)+a 2(x +1)2+⋯+a 5(x +1)5 ,则 a 2= ( ) A. 20 B. −20 C. 80 D. −8010.(2018高二下·黑龙江月考)学校计划在全国中学生田径比赛期间,安排6位志愿者到4个比赛场地提供服务,要求甲、乙两个比赛场地各安排一个人,剩下两个比赛场地各安排两个人,其中的小李和小王不在一起,不同的安排方案共有( )A. 168种B. 156种C. 172种D. 180种二、填空题(共10题;共10分)11.(2019高二下·延边月考)3名男生,2名女生排成一排,女生不排两端,则有________种不同排法. 12.(2019高二下·牡丹江月考)从1,3,5,7四个数中选两个数字,从0,2,4三个数中选一个数字,组成没有重复数字的三位数,其中奇数的个数为________13.(2020·安阳模拟)(ax +1)(x −1)5 的展开式中, x 3 的系数是20,则 a = ________. 14.(2019高三上·沈阳月考)(1+2x )8(1 +y4 )4的展开式中x 2y 2的系数是________. 15.(2020高三上·泸县期末)(1+x)(1−x)5 的展开式中含 x 2 项的系数为________.16.(2020·江西模拟)已知 (x 2−1)2(x +1)96=a 0+a 1(x +1)+a 2(x +1)2+⋯+a 100(x +1)100 ,则 2a 1+22a 2+⋯+2100a 100= ________. 17.观察下列各式:C 10=40 C 30+C 31=41C 50+C 51+C 52=42C 70+C 71+C 72+C 73=43……照此规律,当n ∈N 时,C 2n−10+C 2n−11+C 2n−12+···+C 2n−1n−1=________ .18.(2020高三上·浦东期末)在 (x +√x )6 的二项展开式中,常数项的值为________19.(2020高三上·闵行期末)已知 (x 2−1)8=a 0+a 1x 2+a 2x 4+⋅⋅⋅+a 8x 16 ,则 a 3= ________ (结果用数字表示) 20.已知 (x 2√5x 3)5的展开式中的常数项为 T , f(x) 是以 T 为周期的偶函数,且当 x ∈[0,1] 时,f(x)=x ,若在区间 [-1,3] 内,函数 g(x)=f(x)-kx-k 有4个零点,则实数 k 的取值范围是________三、解答题(共30题;共360分)21.(2016高二上·衡水期中)10双互不相同的鞋子混装在一只口袋中,从中任意取出4只,试求各有多少种情况出现以下结果: (1)4只鞋子没有成双的; (2)4只恰好成两双;(3)4只鞋子中有2只成双,另2只不成双.22.(2015高二下·福州期中)已知 (√x −√x 3)n 的二项展开式中所有奇数项的系数之和为512, (1)求展开式的所有有理项(指数为整数).(2)求(1﹣x )3+(1﹣x )4+…+(1﹣x )n 展开式中x 2项的系数.23.(2016高二下·张家港期中)已知在( √x 3 ﹣ 2x 3)n 的展开式中,第6项为常数项. (1)求n ;(2)求含x 2项的系数; (3)求展开式中所有的有理项.24.(2019高二下·佛山月考)已知二项式 (2√x −1x )6 . (1)求展开式第4项的二项式系数. (2)求第4项.25.(2016高二下·鹤壁期末)已知f (x )=(2x ﹣3)n 展开式的二项式系数和为512,且(2x ﹣3)n =a 0+a 1(x ﹣1)+a 2(x ﹣1)2+…+a n (x ﹣1)n (1)求a 2的值;(2)求a 1+a 2+a 3+…+a n 的值.26.(2016高二下·姜堰期中)有4名男生,5名女生,全体排成一行. (1)其中甲不在中间也不在两端,有多少种排法? (2)男女生相间,有多少种排法?27.6男4女站成一排,求满足下列条件的排法各有多少种?(用式子表达)(1)男甲必排在首位; (2)男甲、男乙必排在正中间; (3)男甲不在首位,男乙不在末位; (4)男甲、男乙必排在一起; (5)4名女生排在一起; (6)任何两个女生都不得相邻; (7)男生甲、乙、丙顺序一定.28.(2018高二上·南通月考)已知函数 f(x)=(1+x)n ,n ∈N ∗ . (1)当 n =8 时,求展开式中系数的最大项;(2)化简 C n 02n−1+C n 12n−2+C n 22n−3+⋯+C n n 2−1 ;(3)定义: ∑a i n i=1=a 1+a 2+⋯+a n ,化简: ∑(i +1)C n i ni=1 .29.(2017·泰州模拟)已知恒等式(1+x+x 2)n =a 0+a 1x+a 2x 2+…+a 2n x 2n . (1)求a 1+a 2+a 3+…+a 2n 和a 2+2a 3+22a 4+…+22n ﹣2a 2n 的值;(2)当n≥6时,求证: A 22 a 2+2A 32a 3+…+22n ﹣2 A 2n 2 a 2n <49n ﹣2. 30.(2016高二下·泰州期中)在二项式(ax m +bx n )12(a >0,b >0,m 、n≠0)中有2m+n=0,如果它的展开式里最大系数项恰是常数项. (1)求它是第几项; (2)求 ab 的范围.31.(2016高二下·黄骅期中)用0,1,2,3,4,5这六个数字: (1)能组成多少个无重复数字的四位偶数?(2)能组成多少个无重复数字且为5的倍数的五位数?(3)能组成多少个无重复数字且比1325大的四位数?(以上各问均用数字作答) 32.(2016高二下·晋江期中)已知 (x 2-2x -3)10=a 0+a 1(x -1)+a 2(x -1)2+⋯+a 20(x -1)20 (1)求a 2的值(2)求a 1+a 3+a 5+…+a 19的值 (3)求a 0+a 2+a 4+…+a 20的值.33.由四个不同的数字1,2,4,x 组成无重复数字的三位数.(1)若x=5,其中能被5整除的共有多少个? (2)若x=9,其中能被3整除的共有多少个? (3)若x=0,其中的偶数共有多少个?(4)若所有这些三位数的各位数字之和是252,求x .34.(2016高二下·高密期末)已知(x+ 2√x )n 的展开式中的第二项和第三项的系数相等. (1)求n 的值;(2)求展开式中所有二项式系数的和; (3)求展开式中所有的有理项.35.(2016高二下·晋江期中)有4名男生,3名女生排成一排: (1)从中选出3人排成一排,有多少种排法?(2)若男生甲不站排头,女生乙不站在排尾,则有多少种不同的排法? (3)要求女生必须站在一起,则有多少种不同的排法? (4)若3名女生互不相邻,则有多少种不同的排法?36.(2016高二下·辽宁期中)现有0,1,2,3,4,5六个数字. (1)用所给数字能够组成多少个四位数?(2)用所给数字可以组成多少个没有重复数字的五位数?(3)用所给数字可以组成多少个没有重复数字且比3142大的数?(最后结果均用数字作答) 37.(2016高二下·福建期末)已知二项式( √x 3 ﹣ 1x )n 展开式中的各项系数的绝对值之和为128. (1)求展开式中系数最大的项; (2)求展开式中所有的有理项.38.(2016高二下·清流期中)若二项式 (√x +2√x4)n 的展开式中,前三项的系数成等差数列,求:(1)展开式中含x的项;(2)展开式中所有的有理项.39.(2016高二下·通榆期中)用0、1、2、3、4这五个数字,可以组成多少个满足下列条件的没有重复数字的五位数?(1)奇数;(2)比21034大的偶数.40.(2016高二下·南安期中)用数字0,1,2,3,4,5组成没有重复数字的四位数.(1)可以组成多少个不同的四位数?(2)若四位数的十位数字比个位数字和百位数字都大,则这样的四位数有多少个?(3)将(1)中的四位数按从小到大的顺序排成一数列,问第85项是什么?41.(2017高二上·湖北期末)已知(3x2+√x)n的展开式各项系数和为M,(3x2−√x)n+5的展开式各)2n的展开式项系数和为N,(x+1)n的展开式各项的系数和为P,且M+N﹣P=2016,试求(2x2−1x2中:(1)二项式系数最大的项;(2)系数的绝对值最大的项.42.(2017高二上·襄阳期末)设(x+2)n=a0+a1x+a2x2+…+a n x n(n∈N*,n≥2),且a0,a1,a2成等差数列.(1)求(x+2)n展开式的中间项;(2)求(x+2)n展开式所有含x奇次幂的系数和.43.(2016高二上·弋阳期中)某校高2010级数学培优学习小组有男生3人女生2人,这5人站成一排留影.(1)求其中的甲乙两人必须相邻的站法有多少种?(2)求其中的甲乙两人不相邻的站法有多少种?(3)求甲不站最左端且乙不站最右端的站法有多少种?44.(2016高二下·邯郸期中)从1到9这9个数字中任取3个偶数和3个奇数,组成无重复数字的六位数,(1)有多少个偶数?(2)若奇数排在一起且偶数排在一起,这样的六位数有多少个?(3)若三个偶数不能相邻,这样的六位数有多少个?(4)若三个偶数从左到右的排练顺序必须由大到小,这样的六位数有多少个?45.(2019高二下·涟水月考)请阅读:当x>1时,在等式1+x+x2+⋯+x n=1−x n的两边对x求1−x导,得1+2x+3x2+⋯+nx n−1=1−nx n−1+(n−1)x n,利用上述方法,试由等式(1+x)n=C n0+C n1x+(1−x)2⋯+C n n−1x n−1+C n n x n(x∈R,正整数n≥2).(1)证明: n[(1+x)n−1−1]=∑n k=2kC n k x k−1 ;(注: ∑ni=1a i =a 1+a 2+⋯+a n )(2)求 C 101+2C 102+3C 103+⋯+10C 1010 ; (3)求 12C 1001+32C 1003+52C 1005+⋯+992C 10099 . 46.(2016高二下·抚州期中)已知 (x 2√x )n 的展开式中第3项的系数与第5项的系数之比为 314 . (1)求n 的值;(2)求展开式中的常数项.47.(2015高二下·椒江期中)设m ,n ∈N ,f (x )=(1+x )m +(1+x )n .(1)当m=n=5时,若 f(x)=a 5(1−x)5+a 4(1−x)4+⋯+a 1(1−x)+a 0 ,求a 0+a 2+a 4的值; (2)f (x )展开式中x 的系数是9,当m ,n 变化时,求x 2系数的最小值.48.(2016高二下·三门峡期中)二项式 (√x 3x2)r 展开式中第五项的二项式系数是第三项系数的4倍.求: (1)n ;(2)展开式中的所有的有理项.49.(2017·南京模拟)设n ∈N * , n≥3,k ∈N * . (1)求值: ①kC n k ﹣nC n ﹣1k ﹣1; ② k 2C nk−n(n −1)C n−2k−2−nC n−1k−1 (k≥2); (2)化简:12C n 0+22C n 1+32C n 2+…+(k+1)2C n k +…+(n+1)2C n n . 50.(2019高二下·上海月考)(1)在 (ax−√x2)9 的二项展开式中 x 3 的系数为 94 ,求实数 a 的值;(2)若 (3x −1)7=a 7x 7+a 6x 6+⋅⋅⋅+a 1x +a 0 ,求 a 1+a 3+a 5+a 7 .答案解析部分一、单选题1.【答案】C2.【答案】A3.【答案】C4.【答案】D5.【答案】A6.【答案】B7.【答案】B8.【答案】D9.【答案】D10.【答案】B二、填空题11.【答案】3612.【答案】6013.【答案】−114.【答案】4215.【答案】516.【答案】017.【答案】4n−118.【答案】1519.【答案】-56]"20.【答案】"(0,14三、解答题21.【答案】(1)解:先从10双中取出4双,然后再从每双中取出一只,结果就是取出的4只鞋子,任何两只都不能配成1双,根据分布计数原理得:C104×2×2×2×2=3360,(2)解:4只恰好成两双,从10双中取出2双,故有C102=45,(3)解:先从10双中取出1双,再从9双中取出2双,然后再从每双中取出一只,结果就是4只鞋子中有2只成双,另2只不成双,根据分布计数原理得:C101×C92×2×2=1440.22.【答案】(1)解:C n0+C n2+…=2n﹣1=512=29∴n﹣1=9,n=10= (r=0,1,10)∵5﹣ Z ,∴r=0,6有理项为T 1=C 100x 5 , T 7=C 106x 4=210x 4(2)解:∵C n r +C n r ﹣1=C n+1r ,∴x 2项的系数为C 32+C 42+…+C 102=(C 43﹣C 33)+…+(C 113﹣C 103) =C 113﹣C 33=16423.【答案】 (1)解:根据题意,可得( √x 3 ﹣ 2√x3 )n 的展开式的通项为 T r+1=C n r (x 13)n -r (-12x -13)r = (-12)r C n r x 10-2r3,又由第6项为常数项,则当r=5时, n -2r 3=0 ,即 n -103=0,解可得n=10(2)解:由(1)可得,T r+1=(﹣ 12 )r C 10r x 10-2r3 , 令 10-2r3=2,可得r=2, 所以含x 2项的系数为 (-12)2C 102=454(3)解:由(1)可得,T r+1=(﹣ 12 )r C 10r x 10-2r3 , 若T r+1为有理项,则有 10-2r3∈Z ,且0≤r≤10, 分析可得当r=2,5,8时, 10-2r 3 为整数, 则展开式中的有理项分别为454x 2,-638,45256x -224.【答案】 (1)解:由已知得 (2√x −1x )6 的展开式的通项是T k+1=C 6k (2√x)6−k(−1x)k=C 6k 26−k(−1)k x 6−3k2(k =0,1,2,⋯,6)展开式第4项的二项式系数为 C 63=20 .(2)解:展开式的第4项为 T 4=−160x −32 .25.【答案】 (1)解:(1)由)=(2x ﹣3)n 展开式的二项式系数和为512,可得2n =512,∴n=9. ∵(2x ﹣3)9=[﹣1+2(x ﹣1)]9=a 0+a 1(x ﹣1)+a 2(x ﹣1)2+…+a 9(x ﹣1)9 ,∴a 2= C 92 •(﹣1)7•22=﹣144.(2)解:在(2x ﹣3)9=a 0+a 1(x ﹣1)+a 2(x ﹣1)2+…+a 9(x ﹣1)9中,令x=1,可得a 0=﹣1.再令x=2,可得a 0+a 1+a 2+a 3+…+a n =1, ∴a 1+a 2+a 3+…+a n =2.26.【答案】 (1)解:其中甲不在中间也不在两端,则甲6种选择,其余的任意排,故有6A 88=241920种排法(2)解:先排4名男生形成了5个空,把5名女生插入,故有A 44A 55=2880种排法 27.【答案】 解:(1)男甲必排在首位,则其他人任意排,故有A 99种,(2)男甲、男乙必排在正中间,则其他人任意排,故有A 22A 77种, (3)男甲不在首位,男乙不在末位,利用间接法,故有A 1010﹣2A 99+A 88种,(4)男甲、男乙必排在一起,利用捆绑法,把甲乙两人捆绑在一起看作一个复合元素和另外全排,故有A 22A 88种,(5)4名女生排在一起,利用捆绑法,把4名女生捆绑在一起看作一个复合元素和另外全排,故有A 44A 77种,(6)任何两个女生都不得相邻,利用插空法,故有A 66A 74种,(7)男生甲、乙、丙顺序一定,利用定序法,"A 1010A 33"=A 107种28.【答案】 (1)解: f(x)=(1+x)8 ∴ 系数最大的项即为二项式系数最大的项T 5=C 84x 4=70x 4(2)解: f(x)=(1+x)n =C n 0+C n 1x +C n 2x 2+⋯C n n−1x n−1+C n n x n ∴ 原式 =12(C n 02n +C n 12n−1+C n 22n−2+⋯+C n n 20)=12(1+2)n =3n 2(3)解: ∑(i +1)ni=1C n i =2C n 1+3C n 2+⋯nC n n−1+(n +1)C n n ① ∑(i +1)ni=1C n i =(n +1)C n n +nC n n−1+⋯3C n 2+2C n 1 ② 在①、②添加 C n 0 ,则得1+ ∑(i +1)n i=1C n i =C n 0+2C n 1+3C n 2+⋯nC n n−1+(n +1)C n n ③ 1+ ∑(i +1)n i=1C n i =(n +1)C n n +nC n n−1+⋯3C n 2+2C n 1+1C n0 ④ ③+④得:2(1+ ∑(i +1)ni=1C n i ) =(n +2)(C n 0+C n 1+C n 2+⋯+C n n−1+C n n )=(n +2)2n ∴ ∑(i +1)ni=1C ni= (n +2)2n−1−1 29.【答案】 (1)解:令x=0,则a 0=1.令x=1,则a 0+a 1+a 2+…+a 2n =3n , ∴a 1+a 2+…+a 2n =3n ﹣1. ∵(1+x+x 2)n =a 0+a 1x+a 2x 2+…+a 2n x 2n .∴两边对x 求导可得:n (1+x+x 2)n ﹣1=a 1+2a 2x+…+2na 2n x 2n ﹣1 . 令x=0,则n=a 1 ,由(1+x+x 2)n =a 0+a 1x+a 2x 2+…+a 2n x 2n .令x=2,则 14 ×7n = 14a 0 + 12a 1 +a 2+2a 3+…+22n ﹣2a 2n . ∴a 2+2a 3+…+22n ﹣2a 2n = 14×7n ﹣ 14 ﹣ 12n(2)证明:∵(1+x+x 2)n =a 0+a 1x+a 2x 2+…+a 2n x 2n .∴两边对x 求导可得:n (1+x+x 2)n ﹣1(1+2x )=a 1+2a 2x+…+2na 2n x 2n ﹣1 ,再一次求导可得:n[(n ﹣1)(1+2x )2+2](1+x+x 2)n ﹣2=2a 2+3×2a 3x+…+2n (2n ﹣1)a 2n x 2n ﹣2 ,A k 2 =k (k ﹣1), 令x=2可得: A 22 a 2+2A 32 a 3+…+22n ﹣2 A 2n 2 a 2n =n[25(n ﹣1)+2]×7n ﹣2, n≥6时,n[25(n ﹣1)+2]<7n ﹣2 ,∴ A 22 a 2+2A32a 3+…+22n ﹣2 A 2n 2 a 2n =n[25(n ﹣1)+2]×7n ﹣2<49n ﹣2 . 30.【答案】 (1)解:设T r+1=C 12r (ax m )12﹣r •(bx n )r =C 12r a 12﹣r b r x m (12﹣r )+nr 为常数项, 则有m (12﹣r )+nr=0,即m (12﹣r )﹣2mr=0,∴r=4,它是第5项(2)解:∵第5项又是系数最大的项,∴有 {c 124a 8b 4≥c 123a 9b 3①c 124a 8b 4≥c 125a 7b 5②由①得a 8b 4≥ 49 a 9b 3 ,∵a >0,b >0,∴ 94 b≥a ,即 ab ≤ 94 . 由②得 ab ≥ 85 , ∴ 85 ≤ ab ≤ 9431.【答案】 (1)解:符合要求的四位偶数可分为三类: 第一类:0在个位时有A 53个;第二类:2在个位时,首位从1,3,4,5中选定1个(有A 41种),十位和百位从余下的数字中选(有A 42种),于是有 A 41⋅A 42 个;第三类:4在个位时,与第二类同理,也有 A 41⋅A 42个.由分类加法计数原理知,共有四位偶数: A 53+A 41⋅A 42+A 41⋅A 42=156 个(2)解:符合要求的数可分为两类:个位数上的数字是0的五位数有A 54个;个位数上的数字是5的五位数有 A 41⋅A 43 个.故满足条件的五位数的个数共有 A 54+A 41⋅A 43=216 个(3)解:符合要求的比1325大的四位数可分为三类:第一类:形如2,3,4,5,共 A 41⋅A 53 个;第二类:形如14□□,15□□,共有A41⋅A42个;第三类:形如134□,135□,共有A21⋅A31个;由分类加法计数原理知,无重复数字且比1325大的四位数共有:A41⋅A53+A41⋅A42+A21⋅A31=270个.32.【答案】(1)解:令x﹣1=t,则已知条件即(x2﹣2x﹣3)10=[t2﹣4]10=a0+a1(t2-14)10=a0+a1t+a2t2+⋯+a20t20.可得a2=c109⋅(-4)9=-49×10(2)解:令t=1可得a0+a1+a2+⋯+a20=310;再令t=﹣1可得a0-a1+a2-a3⋯+a20=310,∴a1+a3+a5+…+a19=0(3)解:由(2)可得a0+a2+a4+…+a20=31033.【答案】解:(1)若x=5,则四个数字为1,2,4,5;又由要求的三位数能被5整除,则5必须在末尾,在1、2、4三个数字中任选2个,放在前2位,有A32=6种情况,即能被5整除的三位数共有6个;(2)若x=9,则四个数字为1,2,4,9;又由要求的三位数能被3整除,则这三个数字为1、2、9或2、4、9,取出的三个数字为1、2、9时,有A33=6种情况,取出的三个数字为2、4、9时,有A33=6种情况,则此时一共有6+6=12个能被3整除的三位数;(3)若x=0,则四个数字为1,2,4,0;又由要求的三位数是偶数,则这个三位数的末位数字为0或2或4,当末位是0时,在1、2、4三个数字中任选2个,放在前2位,有A32=6种情况,当末位是2或4时,有A21×A21×A21=8种情况,此时三位偶数一共有6+8=14个,(4)若x=0,可以组成C31×C31×C21=3×3×2=18个三位数,即1、2、4、0四个数字最多出现18次,则所有这些三位数的各位数字之和最大为(1+2+4)×18=126,不合题意,故x=0不成立;当x≠0时,可以组成无重复三位数共有C41×C31×C21=4×3×2=24种,共用了24×3=72个数字,则每个数字用了"724"=18次,则有252=18×(1+2+4+x),解可得x=7.34.【答案】(1)解:二项式(x+2√x)n展开式的通项公式为T r+1= C n r•x n﹣r• (2√x )r= C n r• (12)r• x n−32r,(r=0,1,2,…,n);根据展开式中的第二项和第三项的系数相等,得C n1• 12= C n2• (12)2,即12n= 14• n(n−1)2,解得n=5;(2)解:展开式中所有二项式系数的和为C 50 + C 51 + C 52 +…+ C 55 =25=32(3)解:二项式展开式的通项公式为T r+1= C 5r • (12)r • x 5−32r ,(r=0,1,2,…,5);当r=0,2,4时,对应项是有理项, 所以展开式中所有的有理项为T 1= C 50 • (12)0 •x 5=x 5 , T 3= C 52 • (12)2 •x 5﹣3= 52x 2 , T 5= C 54 • (12)4 x 5﹣6=516x35.【答案】 (1)解:由题意可得从中选出3人排成一排的方法种数为 A 73 =210 (2)解:间接法:总的方法种数共 A 77 =5040,去掉男生甲站排头,女生乙站在排尾共2 A 66 =1440,而其中重复的为男生甲站排头,同时女生乙站在排尾的 A 55 =120故总的方法种数为:5040﹣1440+120=3720(3)解:捆绑法:把3名女生看作1个元素与其它排列共 A 55 =120种, 再对3名女生作调整共 A 33 =6种,由分步计数原理可得共120×6=720(4)解:插空法:先排4名男生共 A 44 =24种,在把3名女生插到所产生的5个空位, 共 A 53 =60种,由分步计数原理可得共24×60=144036.【答案】 (1)解:能够组成四位数的个数为:5×6×6×6=1080(2)解:能组成没有重复数字的五位数的个数为: A 51⋅A 54 =600(3)解:比3142大的数包含四位数、五位数和六位数,其中:六位数有: C 51⋅A 55=5×5×4×3×2×1=600 ; 五位数有: A 51⋅A 54 =600;四位数有千位是4或5的,千位是3的,而千位是4或5的有 C 51⋅A 53=2×5×4×3=120 ;千位是3的分为百位是2、4、5的与百位是1的,百位是2、4、5的有 C 31⋅A 42=3×4×3=36 ,百位是1的分为十位是4和5两种情况,十位是5的有3种,十位是4的有1种, 所以共有600+600+120+36+3+1=1360.答:能组成四位数1080个;没有重复数字的五位数600个;比3142大的数1360个 37.【答案】 (1)解:二项式( √x 3 ﹣ 1x )n 展开式中的各项系数的绝对值之和为128, 即为各项二项式系数之和为128,即2n =128得n=7,则二项式( √x 3 ﹣ 1x )7展开式的通项为(﹣1)r C 7r x 7−4r3,∵C 73=C 74=35,∴当r=4时,展开式中系数最大, ∴展开式中系数最大的项为35x ﹣3 ,(2)解:当7−4r 3为整数时,即r=7,4,1∴展开式中所有的有理项(﹣1)7C 77x ﹣7=﹣x ﹣7 , 或35x ﹣3 , ﹣7x38.【答案】 (1)解:二项式的展开式的通项公式为: T r+1=C n r (√x)n -r (2√x4)r=C n r 12x 2n -3r4前三项的r=0,1,2得系数为 t 1=1,t 2=C n 1⋅12=12n ,t 3=C n 2⋅14=18n(n -1) 由已知: 2t 2=t 1+t 3,n =1+18n(n -1) 得n=8通项公式为 T r+1==C 8r 12rx 16-3r4令16﹣3r=4,得r=4,得 T 5=358x(2)解:当r=0,4,8时,依次得有理项 T 1=x 4,T 5=C 84124x =358x ,T 9=C 88128x -2=1256x 239.【答案】 (1)解:先排个位,再排首位,其它任意排,可组成奇数个数为 A 21A 31A 33=36 个奇数(2)解:①当末位数字是0时,首位数字可以为2或3或4,满足条件的数共有3×A 33=18个. ②当末位数字是2时,首位数字可以为3或4,满足条件的数共有2×A 33=12个.③当末位数字是4时,首位数字是3的有A 33=6个,首位数字是2时,有3个,共有9个. 综上知,比21034大的偶数共有18+12+9=39个40.【答案】 (1)解:用间接法,从6个数中,任取4个组成4位数,有A 64种情况,但其中包含0在首位的有A 53种情况, 依题意可得,有A 64﹣A 53=300个,(2)解:先选一个数排在首位,再选3个数,排在百,十,个位,其中十位数字比个位数字和百位数字都大,则选的3个数中最大的只能在十位,其它任意,故有A 51C 53A 22=100个,(3)解:千位是1的四位数有A 53=60个,千位是2,百位是0或1的四位数有2A42=24个,∴第85项是230141.【答案】(1)解:∵M+N﹣P=4n+2n+5﹣2n=(2n)2+31•2n=2016,∴(2n)2+31•2n﹣2016=0,∴(2n+63)(2n﹣32)=0,∴2n=32,∴n=5,∴的展开式的通项,的展开式共有11项,二项式系数最大的项为中间项第6项,其值为(2)解:第r+1项T r+1的系数的绝对值为,若第r+1项T r+1的系数的绝对值最大,则{ ,可得,又r∈N*,∴r=3,故系数的绝对值最大的项为42.【答案】(1)解:,∴,∵a0,a1,a2成等差数列,∴解得:n=8或n=1(舍去)∴(x+2)n展开式的中间项是(2)解:在(x+2)8=a0+a1x+a2x2+⋯+a8x8中,令x=1,则38=a0+a1+a2+a3+…+a7+a8令x=﹣1,则1=a0﹣a1+a2﹣a3+…﹣a7+a8两式相减得:∴43.【答案】(1)解:把甲乙捆绑成一个整体与其余3人当着4个人作全排列有A44种,且甲、乙的位置还可以互换 ∴不同站法有A 44•A 22=48种.(2)解:除甲乙两人外其余3人的排列数为A 33 , 而甲乙二人应插其余3人排好的空才不相邻; 且甲、乙位置可以互换.故有C 42A 22种排列方式. ∴不同站法有A 33•C 42A 22=72种.(3)解:优先考虑甲:若甲站最右端,则乙与其余三人可任意排,则此时的排法数为A 44种; 若甲不站最右端,则先从中间3个位置中选一个给甲, 再从除最右端的省余的3个位置给乙,其余的三个人任意排,则此时的排法数为C 31C 31A 33种; ∴不同站法有A 44+C 31C 31A 33=78种.44.【答案】 (1)解:先从4个偶数中选一个为偶数,在从剩下3个偶数选2个和从5个奇数中选3个,把这5个数全排,故有C 41C 32C 53A 55=14400种,(2)解:把所选的3个奇数,和3个偶数分别捆绑在一起,再全排,故有A 43A 53A 22=2880种, (3)解:把所选的三个偶数插入到所选的3个奇数所形成的4个空中,故有C 43A 53A 43=5760种, (4)解:所选的3个偶数共有6种顺序,其中三个偶数从左到右的排练顺序必须由大到小是其中一种,故有 16 C 43C 53A 66=4800种45.【答案】 (1)证明:由 (1+x)n =C n 0+C n 1x +⋯+C n n−1x n−1+C n n x n , 两边对 x 求导得 n(1+x)n−1=C n 1+2C n 2x +3C n 3x 2+⋯+nC n n x n−1 •, 所以 n[(1+x)n−1−1]=2C n 2+3C n 3x 2+⋯+nC n n x n−1=∑n k=2kC n k xk−1 .(2)解:在①式中,令 n =10,x =1 得C 101+2C 102+3C 103+⋯+10C 1010=10(1+1)10−1 =10⋅29=5120 .(3)解:将•式两边同乘以 x 得 nx(1+x)n−1=C n 1x +2C n 2x 2+3C n 3x 3+⋯+nC n n x n 两边对 x 求导得, n[(1+x)n−1+x(n −1)(1+x)n−2]=C n 1+22C n 2x +32C n 3x 2+⋯+n 2C n n x n−1 , 取 n =100 得, C 1001+22C 1002x +32C 1003x 2+⋯+1002C 100100x 99=100[(1+x)99+99x(1+x)98] =100(1+100x)(1+x)98 , 令 x =1 得, C 1001+22C 1002+32C 1003+⋯+1002C 100100=100×101×298 ,令 x =−1 得, C 1001−22C 1002+32C 1003+⋯−1002C 100100=0 ,两式相加得, 2(C 1001+32C 1003+52C 1005⋯+992C 10099)=25×101×2100 , 所以 12C 1001+32C 1003+52C 1005⋯+992C 10099=2525×299 . 46.【答案】 (1)解:由题设,得 c n 2(-1)2:c n 4(-1)4 = 314 ,则 n(n -1)2n(n -1)(n -2)(n -3)4⋅3⋅2= 314 ⇒ 4(n -2)(n -3)=114 ⇒n 2﹣5n ﹣50=0⇒n=10或n=﹣5(舍)(2)解: T r+1=c 10r(x 2)10−r (-1)r (√x)r = c 10x r 20-2r -12r(-1)r 当 20-2r -12r =0即当r=8时为常数项 T 9=c 108(-1)8r =c 102=4547.【答案】 (1)解:当m=n=5时,f (x )=2(1+x )5 , 令x=0时,f (0)=a 5+a 4+…+a 1+a 0=2, 令x=2时,f (0)=﹣a 5+a 4+…﹣a 1+a 0=2×35 , 相加可得:a 0+a 2+a 4= =244(2)解:由题意可得: ∁m 1+∁n 1=m+n=9. x 2系数= ∁m 2+∁n 2 =m 2−m+n 2−n2= == (m −92)2 +634.又m ,n ∈N ,∴m=4或5,其最小值为16. 即或时,x 2系数的最小值为1648.【答案】 (1)解:开式的通项为 T r+1=(−12)r C n r x4r−n3,据题意有C n 4=4× (−12)2 •C n 2 , , 解得n=6(2)解:展开式的通项为 T r+1=(−12)r C 6r x 4r−63= (−12)r C 6r x 4r−63−2 ,当r 是3的倍数时,为有理项, 所以r=0,3,6,T 1=x −2,T 4=−52x 2,T 7=x 66449.【答案】 (1)解: ① =② k 2C nk−n(n −1)C n−2k−2−nC n−1k−1 = k 2×n!k!(n−k)!−n(n −1)×(n−2)!(k−2)!(n−k)!= = .(2)解:方法一:由(1)可知当k≥2时 (k +1)2C n k =(k 2+2k +1)C n k =k 2C n k +2kC n k +C n k = [n(n −1)C n−2k−2+nC n−1k−1]+2nC n−1k−1+C n k =n(n −1)C n−2k−2+3nC n−1k−1+C nk . 故==(1+4n )+n (n ﹣1)2n ﹣2+3n (2n ﹣1﹣1)+(2n ﹣1﹣n )=2n ﹣2(n 2+5n+4).方法二:当n≥3时,由二项式定理,有 (1+x)n =1+C n 1x +C n 2x 2+⋯+C n k x k +⋯+C n n x n , 两边同乘以x ,得 (1+x)n x =x +C n 1x 2+C n 2x 3+⋯+C n k x k+1+⋯+C n n xn+1 , 两边对x 求导,得 (1+x)n +n(1+x)n−1=1+2C n 1x +3C n 2x 2+⋯+(k +1)C n k x k +⋯+(n +1)C n n x n ,两边再同乘以x ,得 (1+x)n x +n(1+x)n−1x 2=x +2C n 1x 2+3C n 2x 3+⋯+(k +1)C n k x k+1+⋯+(n +1)C n n x n+1 ,两边再对x 求导,得(1+x )n +n (1+x )n ﹣1x+n (n ﹣1)(1+x )n ﹣2x 2+2n (1+x )n ﹣1x= 1+22C n 1x +32C n 2x 2+⋯+(k +1)2C n k x k +⋯+(n +1)2C n n xn . 令x=1,得2n +n2n ﹣1+n (n ﹣1)2n ﹣2+2n2n ﹣1=,即=2n ﹣2(n 2+5n+4)50.【答案】 (1)解: (ax −√x2)9 的二项展开式通项为: T r+1=C 9r (a x )9−r (−√x2)r =√2)r a 9−r C 9r x 3r−182当3r−182=3 ,即 r =8 时, T 9=√2)8aC 98x 3=9a 16x 3又 x 3 的系数为 94 , ∴9a16=94 ,解得: a =4(2)解:令 x =1 得: a 7+a 6+a 5+a 4+a 3+a 2+a 1+a 0=27 ……① 令 x =−1 得: −a 7+a 6−a 5+a 4−a 3+a 2−a 1+a 0=−47 ……② ① − ②得: 2a 7+2a 5+2a 3+2a 1=27+47=16512 ∴a 1+a 3+a 5+a 7=8256。
福建省2017届高三数学理一轮复习专题突破训练:排列组合与二项式定理 含答案

福建省2017届高三数学理一轮复习专题突破训练排列组合与二项式定理一、二项式定理1、(2016年全国I 卷)5(2x 的展开式中,x3的系数是 。
(用数字填写答案)2、(2015年全国I 卷)25()xx y ++的展开式中,52x y 的系数为(A )10 (B)20 (C )30(D )603、(2014年全国I 卷)8()()x y x y -+的展开式中22x y 的系数为 .(用数字填写答案) 4、(福建省2016届高三4月质检)若()5112ax x x ⎛⎫++ ⎪⎝⎭展开式中的常数项为40-,则a =.5、(福州市2016届高三5月综合质量检测)512x x ⎛⎫++ ⎪⎝⎭的展开式中,2x 的系数为 (A )45 (B )60 (C )90(D)1206、(龙岩市2016届高三3月质量检查)8()()x y x y +-的展开式中,27x y 的系数为 .7、(南平市2016届高三3月质量检查) 已知正实数m ,若10201210()()()x a a m x a m x a m x =+-+-+⋅⋅⋅⋅⋅⋅+-101210()()()x a a m x a m x a m x =+-+-+⋅⋅⋅⋅⋅⋅+-,其中8a =180,则m 值为 (A )4 (B)2 (C )3 (D )6 8、(莆田市2016高中毕业班3月质量检测)若3*1()(N )ny x n xy+∈的展开式中存在常数项,则常数项为A .15B .20C .30D .1209、(泉州市2016届高三第二次(5月)质量检查)已知()52345012345ax b a a x a x a x a x a x +=+++++,若011,10a a ==,则2a 等于( )A .10B .20C .40D .8010、(泉州市2016届高中毕业班3月质量检查)()622--x x 的展开式中2x 的系数等于A 。
-48 B.48 C.234 D.43211、(三明市2016届普通高中毕业班5月质量检查)在23(2)x x --学科网的展开式中5x 的系数是(用数字作答).12、(厦门市2016届高三第一次质量检查(3月))已知()()611ax x -+展开式中2x 项的系数为21,则实数=aA 。
推荐重庆市第一中学2017高考数学一轮复习:知识专题研

排列、组合问题的解答策略第一节 特殊优先法例1乒乓球队的10名队员中有3名主力队员,派5名参加比赛,3名主力队员要安排在第一、三、五位置,其余7名队员选2名安排在第二、四位置,那么不同的出场安排共有 252 种例2 将标号为1,2,…,10的10个球放入标号为1,2,…,10的10个盒子内,每个盒内放一个球,则恰好有3个球的标号与其所在盒子的标号不一致的放入方法共有( 240 )种?例3)1名老师和4名学生排成一排照相留念,若老师不排在两端,则共有不同的排法 72 例4 从a 、b 、c 、d 、e ,5个元素中,取出4个放在四个不同的格子中,且元素b 不能放在第二个格子里,问共有 72 种不同的放法?(用数字作答)第二节 合理分类准确分步例1 (天津)从1,3,5,7中任取2个数字,从0,2,4,6,8中任取2个数字,组成没有重复数字的四位数,其中能被5整除的四位数共有 300 个。
(用数字作答)例2 某天某班的课程表要排入数学、语文、英语、物理、化学、体育六门课程,第一节不排体育,第六节不排数学,一共有 504 种不同的排法?(用数字作答)例3 有11名外语翻译人员,其中5名会英语,4名会日语,另外两名英、日语都精通,从中选出8人,组成两个翻译小组,其中4人翻译英语,另4人翻译日语,问共有 185 不同的选派方式? 例4 一个小组有10名同学,其中4女6男,现从中选出3名代表,其中至少有一名女生的选法有 ( 100 )种?例5 已知()y f x =是定义域{}|17,A x x x N =≤≤∈,值域为{}0,1B =的函数。
(1)试问:这样的函数()f x 共有多少个?126(2)若对于定义域中的4个不同元素,对应的函数值都是1,那么这样的函数()f x 共有多少个?35第三节 选排问题先选后排法例1 有5个男生和3个女生,从中选出5个担任5门代表,求符合下列条件的选法数。
(1)有女生但人数少于男生。
2017届高三数学人教版A版数学(理)高考一轮复习教案:5.5 数列的综合应用 Word版含答案

第五节数列的综合应用数列的综合应用能在具体的问题情境中,识别数列的等差关系或等比关系,抽象出数列的模型,并能用有关知识解决相应的问题.知识点数列的实际应用问题数列应用题常见模型(1)等差模型:如果增加(或减少)的量是一个固定量时,该模型是等差模型,增加(或减少)的量就是公差.(2)等比模型:如果后一个量与前一个量的比是一个固定的数时,该模型是等比模型,这个固定的数就是公比.(3)递推数列模型:如果题目中给出的前后两项之间的关系不固定,随项的变化而变化时,应考虑是a n与a n+1的递推关系,还是前n项和S n与S n+1之间的递推关系.必备方法解答数列应用题的步骤:(1)审题——仔细阅读材料,认真理解题意.(2)建模——将已知条件翻译成数学(数列)语言,将实际问题转化成数学问题,弄清该数列的结构和特征.(3)求解——求出该问题的数学解.(4)还原——将所求结果还原到原实际问题中.具体解题步骤用框图表示如下:[自测练习]1.有一种细菌和一种病毒,每个细菌在每秒钟杀死一个病毒的同时将自身分裂为2个,现在有一个这样的细菌和100个这样的病毒,问细菌将病毒全部杀死至少需要() A.6秒钟B.7秒钟C.8秒钟D.9秒钟解析:设至少需要n 秒钟,则1+21+22+…+2n -1≥100, ∴1-2n 1-2≥100,∴n ≥7. 答案:B2.一个凸多边形的内角成等差数列,其中最小的内角为2π3,公差为π36,则这个多边形的边数为________.解析:由于凸n 边形的内角和为(n -2)π, 故2π3n +n (n -1)2×π36=(n -2)π. 化简得n 2-25n +144=0.解得n =9或n =16(舍去). 答案:93.某住宅小区计划植树不少于100棵,若第一天植2棵,以后每天植树的棵数是前一天的2倍,则需要的最少天数n (n ∈N *)等于________.解析:每天植树的棵数构成以2为首项,2为公比的等比数列,其前n 项和S n =a 1(1-q n )1-q =2(1-2n )1-2=2n +1-2.由2n +1-2≥100,得2n +1≥102.由于26=64,27=128,则n +1≥7,即n ≥6.答案:6考点一 等差、等比数列的综合应用|在数列{a n }中,a 1=2,a 2=12,a 3=54,数列{a n +1-3a n }是等比数列.(1)求证:数列⎩⎨⎧⎭⎬⎫a n 3n -1是等差数列;(2)求数列{a n }的前n 项和S n .[解] (1)证明:∵a 1=2,a 2=12,a 3=54, ∴a 2-3a 1=6,a 3-3a 2=18. 又∵数列{a n +1-3a n }是等比数列,∴a n +1-3a n =6×3n -1=2×3n , ∴a n +13n -a n3n -1=2, ∴数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a n 3n -1是等差数列.(2)由(1)知数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a n 3n -1是等差数列,∴a n 3n -1=a 130+(n -1)×2=2n , ∴a n =2n ×3n -1.∵S n =2×1×30+2×2×31+…+2n ×3n -1, ∴3S n =2×1×3+2×2×32+…+2n ×3n .∴S n -3S n =2×1×30+2×1×3+…+2×1×3n -1-2n ×3n =2×1-3n1-3-2n ×3n=3n -1-2n ×3n , ∴S n =⎝⎛⎭⎫n -12×3n +12.等差数列、等比数列综合问题的解题策略(1)分析已知条件和求解目标,为最终解决问题设置中间问题,例如求和需要先求出通项、求通项需要先求出首项和公差(公比)等,确定解题的顺序.(2)注意细节:在等差数列与等比数列综合问题中,如果等比数列的公比不能确定,则要看其是否有等于1的可能,在数列的通项问题中第一项和后面的项能否用同一个公式表示等,这些细节对解题的影响也是巨大的.1.(2016·贵州七校联考)已知{a n }是等差数列,{b n }是等比数列,S n 为数列{a n }的前n 项和,a 1=b 1=1,且b 3S 3=36,b 2S 2=8(n ∈N *).(1)求a n 和b n ;(2)若a n <a n +1,求数列⎩⎨⎧⎭⎬⎫1a n a n +1的前n 项和T n .解:(1)由题意得⎩⎪⎨⎪⎧q 2(3+3d )=36,q (2+d )=8,解得⎩⎪⎨⎪⎧d =2q =2或⎩⎪⎨⎪⎧d =-23,q =6,∴⎩⎪⎨⎪⎧a n =2n -1,b n =2n -1,或⎩⎪⎨⎪⎧a n =13(5-2n ),b n =6n -1.(2)若a n <a n +1,由(1)知a n =2n -1,∴1a n a n +1=1(2n -1)(2n +1)=12⎝ ⎛⎭⎪⎫12n -1-12n +1, ∴T n =12⎝ ⎛⎭⎪⎫1-13+13-15+…+12n -1-12n +1 =n 2n +1.考点二 数列的实际应用问题|为了加强环保建设,提高社会效益和经济效益,长沙市计划用若干时间更换一万辆燃油型公交车,每更换一辆新车,则淘汰一辆旧车,替换车为电力型和混合动力型车.今年初投入了电力型公交车128辆,混合动力型公交车400辆;计划以后电力型车每年的投入量比上一年增加50%,混合动力型车每年比上一年多投入a 辆.(1)求经过n 年,该市被更换的公交车总数S (n ); (2)若该市计划7年内完成全部更换,求a 的最小值.[解] (1)设a n ,b n 分别为第n 年投入的电力型公交车、混合动力型公交车的数量. 依题意,得{a n }是首项为128,公比为1+50%=32的等比数列,{b n }是首项为400,公差为a 的等差数列.所以{a n }的前n 项和S n=128×⎣⎡⎦⎤1-⎝⎛⎭⎫32n1-32=256⎣⎡⎦⎤⎝⎛⎭⎫32n-1,{b n}的前n项和T n=400n+n(n-1)2a.所以经过n年,该市被更换的公交车总数为S(n)=S n+T n=256⎣⎡⎦⎤⎝⎛⎭⎫32n-1+400n+n(n-1)2a.(2)若计划7年内完成全部更换,则S(7)≥10 000,所以256⎣⎡⎦⎤⎝⎛⎭⎫327-1+400×7+7×62a≥10 000,即21a≥3 082,所以a≥1461621.又a∈N*,所以a的最小值为147.解决数列应用题一个注意点解决数列应用问题,要明确问题属于哪一种类型,即明确是等差数列问题还是等比数列问题,要求a n还是S n,特别是要弄清项数.2.某工业城市按照“十二五”(2011年至2015年)期间本地区主要污染物排放总量控制要求,进行减排治污.现以降低SO2的年排放量为例,原计划“十二五”期间每年的排放量都比上一年减少0.3万吨,已知该城市2011年SO2的年排放量约为9.3万吨.(1)按原计划,“十二五”期间该城市共排放SO2约多少万吨?(2)该城市为响应“十八大”提出的建设“美丽中国”的号召,决定加大减排力度.在2012年刚好按原计划完成减排任务的条件下,自2013年起,SO2的年排放量每年比上一年减少的百分率为p,为使2020年这一年SO2的年排放量控制在6万吨以内,求p的取值范围.⎝⎛⎭⎪⎫参考数据:823≈0.9505,923≈0.955 9解:(1)设“十二五”期间,该城市共排放SO2约y万吨,依题意,2011年至2015年SO2的年排放量构成首项为9.3,公差为-0.3的等差数列,所以y =5×9.3+5×(5-1)2×(-0.3)=43.5(万吨).所以按原计划“十二五”期间该城市共排放SO 2约43.5万吨. (2)由已知得,2012年的SO 2年排放量为9.3-0.3=9(万吨),所以2012年至2020年SO 2的年排放量构成首项为9,公比为1-p 的等比数列. 由题意得9×(1-p )8<6,由于0<p <1, 所以1-p <823,所以1-p <0.950 5,解得p >4.95%.所以SO 2的年排放量每年减少的百分率p 的取值范围为(4.95%,1).考点三 数列与不等式的综合问题|(2015·高考浙江卷)已知数列{a n }满足a 1=12且a n +1=a n -a 2n (n ∈N *). (1)证明:1≤a na n +1≤2(n ∈N *);(2)设数列{a 2n }的前n 项和为S n ,证明:12(n +2)≤S n n ≤12(n +1)(n ∈N *). [证明] (1)由题意得a n +1-a n =-a 2n ≤0,即a n +1≤a n , 故a n ≤12.由a n =(1-a n -1)a n -1得a n =(1-a n -1)(1-a n -2)…(1-a 1)a 1>0. 由0<a n ≤12得a n a n +1=a n a n -a 2n =11-a n ∈[1,2],即1≤a na n +1≤2. (2)由题意得a 2n =a n -a n +1, 所以S n =a 1-a n +1.① 由1a n +1-1a n =a n a n +1和1≤a n a n +1≤2得1≤1a n +1-1a n ≤2,所以n≤1a n +1-1a 1≤2n ,因此12(n +1)≤a n +1≤1n +2(n ∈N *).②由①②得12(n +2)≤S n n ≤12(n +1)(n ∈N *).数列与不等式相结合问题的处理方法解决数列与不等式的综合问题时,如果是证明题要灵活选择不等式的证明方法,如比较法、综合法、分析法、放缩法等;如果是解不等式问题要使用不等式的各种不同解法,如列表法、因式分解法等.3.(2016·云南一检)在数列{a n }中,a 1=35,a n +1=2-1a n ,设b n =1a n -1,数列{b n }的前n项和是S n .(1)证明数列{b n }是等差数列,并求S n ; (2)比较a n 与S n +7的大小.解:(1)∵b n =1a n -1,a n +1=2-1a n ,∴b n +1=1a n +1-1=1a n -1+1=b n +1,∴b n +1-b n =1,∴数列{b n }是公差为1的等差数列. 由a 1=35,b n =1a n -1得b 1=-52,∴S n =-5n 2+n (n -1)2=n 22-3n .(2)由(1)知:b n =-52+n -1=n -72.由b n =1a n -1得a n =1+1b n =1+1n -72.∴a n -S n -7=-n 22+3n -6+1n -72.∵当n ≥4时,y =-n 22+3n -6是减函数,y =1n -72也是减函数,∴当n ≥4时,a n -S n -7≤a 4-S 4-7=0.又∵a 1-S 1-7=-3910<0,a 2-S 2-7=-83<0,a 3-S 3-7=-72<0,∴∀n ∈N *,a n -S n -7≤0, ∴a n ≤S n +7.6.数列的综合应用的答题模板【典例】 (12分)(2015·高考四川卷)设数列{a n }(n =1,2,3,…)的前n 项和S n 满足S n =2a n -a 1,且a 1,a 2+1,a 3成等差数列.(1)求数列{a n }的通项公式;(2)记数列⎩⎨⎧⎭⎬⎫1a n 的前n 项和为T n ,求使得|T n -1|<11 000成立的n 的最小值.[思路点拨] 由S n =2a n -a 1,得a 2=2a 1,a 3=4a 1,再通过a 1,a 2+1,a 3成等差数列确定首项a 1=2是解决(1)的切入点;由(1)知⎩⎨⎧⎭⎬⎫1a n 是首项为12,公比为12的等比数列,所以T n =1-12n ,然后解不等式即可. [规范解答] (1)由已知S n =2a n -a 1,有 a n =S n -S n -1=2a n -2a n -1(n ≥2), 即a n =2a n -1(n ≥2).所以a =2. 从而a 2=2a 1,a 3=2a 2=4a 1.(2分)又因为a 1,a 2+1,a 3成等差数列,即a 1+a 3=2(a 2+1). 所以a 1+4a 1=2(2a 1+1),解得a 1=2.所以,数列{a n }是首项为2,公比为2的等比数列. 故a n =2n .(6分) (2)由(1)得1a n =12n .所以T n =12+122+…+12n =12⎣⎡⎦⎤1-⎝⎛⎭⎫12n 1-12=1-12n .(8分)由|T n -1|<11 000,得⎪⎪⎪⎪1-12n -1<11000,即2n >1 000.因为29=512<1 000<1 024=210, 所以n ≥10.(10分) 于是,使|T n -1|<11 000成立的n 的最小值为10.(12分) [模板形成][跟踪练习] (2015·湖北七市联考)数列{a n }是公比为12的等比数列,且1-a 2是a 1与1+a 3的等比中项,前n 项和为S n ;数列{b n }是等差数列,b 1=8,其前n 项和T n 满足T n =nλ·b n+1(λ为常数,且λ≠1).(1)求数列{a n }的通项公式及λ的值; (2)比较1T 1+1T 2+1T 3+…+1T n 与12S n 的大小.解:(1)由题意得(1-a 2)2=a 1(a 3+1), 即⎝⎛⎭⎫1-12a 12=a 1⎝⎛⎭⎫14a 1+1, 解得a 1=12,∴a n =⎝⎛⎭⎫12n . 设{b n }的公差为d ,又⎩⎪⎨⎪⎧ T 1=λb 2,T 2=2λb 3,即⎩⎪⎨⎪⎧8=λ(8+d ),16+d =2λ(8+2d ),解得⎩⎪⎨⎪⎧λ=12,d =8或⎩⎪⎨⎪⎧λ=1,d =0(舍),∴λ=12.(2)由(1)知S n =1-⎝⎛⎭⎫12n, ∴12S n =12-⎝⎛⎭⎫12n +1≥14,①又T n =4n 2+4n ,1T n =14n (n +1)=14⎝ ⎛⎭⎪⎫1n -1n +1, ∴1T 1+1T 2+…+1T n=14⎣⎢⎡⎦⎥⎤⎝⎛⎭⎫1-12+⎝⎛⎭⎫12-13+…+⎝ ⎛⎭⎪⎫1n -1n +1 =14⎝ ⎛⎭⎪⎫1-1n +1<14,②由①②可知1T 1+1T 2+…+1T n <12S n .A 组 考点能力演练1.(2015·杭州二模)在正项等比数列{a n }中,22为a 4与a 14的等比中项,则2a 7+a 11的最小值为( )A .16B .8C .6D .4解析:因为{a n }是正项等比数列,且22为a 4与a 14的等比中项,所以a 4a 14=8=a 7a 11,则2a 7+a 11=2a 7+8a 7≥22a 7·8a 7=8,当且仅当a 7=2时,等号成立,所以2a 7+a 11的最小值为8,故选择B.答案:B2.(2016·宝鸡质检)《莱因德纸草书》是世界上最古老的数学著作之一,书中有一道这样的题目:把100个面包分给5个人,使每个人所得成等差数列,且使较大的三份之和的17是较小的两份之和,问最小的一份为( )A.53B.103C.56D.116解析:由100个面包分给5个人,每个人所得成等差数列,可知中间一人得20块面包,设较大的两份为20+d,20+2d ,较小的两份为20-d,20-2d ,由已知条件可得17(20+20+d+20+2d )=20-d +20-2d ,解得d =556,∴最小的一份为20-2d =20-2×556=53,故选A.答案:A3.(2016·豫南十校联考)设f (x )是定义在R 上的恒不为零的函数,且对任意的x ,y ∈R ,都有f (x )·f (y )=f (x +y ).若a 1=12,a n =f (n )(n ∈N *),则数列{a n }的前n 项和S n 的取值范围是( )A.⎣⎡⎭⎫12,2B.⎣⎡⎦⎤12,2C.⎣⎡⎭⎫12,1D.⎣⎡⎦⎤12,1解析:在f (x )·f (y )=f (x +y )中令x =n ,y =1,得f (n +1)=f (n )f (1),又a 1=12,a n =f (n )(n ∈N *),则a n +1=12a n ,所以数列{a n }是首项和公比都是12的等比数列,其前n 项和S n =12×⎝⎛⎭⎫1-12n 1-12=1-12n ∈⎣⎡⎭⎫12,1,故选择C. 答案:C4.已知在等差数列{a n }中,a 1>0,d >0,前n 项和为S n ,等比数列{b n }满足b 1=a 1,b 4=a 4,前n 项和为T n ,则( )A .S 4>T 4B .S 4<T 4C .S 4=T 4D .S 4≤T 4解析:法一:设等比数列{b n }的公比为q ,则由题意可得q >1,数列{b n }单调递增,又S 4-T 4=a 2+a 3-(b 2+b 3)=a 1+a 4-a 1q -a 4q =a 1(1-q )+a 4⎝⎛⎭⎫1-1q =q -1q (a 4-a 1q )=q -1q(b 4-b 2)>0,所以S 4>T 4.法二:不妨取a n =7n -4,则等比数列{b n }的公比q =3a 4a 1=2,所以S 4=54,T 4=b 1(1-q 4)1-q=45,显然S 4>T 4,选A.答案:A5.正项等比数列{a n }满足:a 3=a 2+2a 1,若存在a m ,a n ,使得a m ·a n =16a 21,m ,n ∈N *,则1m +9n的最小值为( ) A .2 B .16 C.114 D.32解析:设数列{a n }的公比为q ,a 3=a 2+2a 1⇒q 2=q +2⇒q =2,∴a n =a 1·2n -1,a m ·a n =16a 21⇒a 21·2m +n -2=16a 21⇒m +n =6,∵m ,n ∈N *,∴(m ,n )可取的数值组合为(1,5),(2,4),(3,3),(4,2),(5,1),计算可得,当m =2,n =4时,1m +9n 取最小值114. 答案:C6.(2016·兰州双基)等差数列{a n }的公差为2,若a 2,a 4,a 8成等比数列,则{a n }的前n 项和S n =________.解析:由题意,得(a 1+3×2)2=(a 1+2)(a 1+7×2),解得a 1=2,所以S n =2n +n (n -1)2×2=n 2+n .答案:n 2+n7.(2015·高考湖南卷)设S n 为等比数列{a n }的前n 项和.若a 1=1,且3S 1,2S 2,S 3成等差数列,则a n =________.解析:由3S 1,2S 2,S 3成等差数列,得4S 2=3S 1+S 3,即3S 2-3S 1=S 3-S 2,则3a 2=a 3,得公比q =3,所以a n =a 1q n -1=3n -1.答案:3n -18.从盛满2升纯酒精的容器里倒出1升纯酒精,然后填满水,再倒出1升混合溶液后又用水填满,以此继续下去,则至少应倒________次后才能使纯酒精体积与总溶液的体积之比低于10%.解析:设倒n 次后纯酒精与总溶液的体积比为a n ,则a n =⎝⎛⎭⎫12n ,由题意知⎝⎛⎭⎫12n <10%, ∴n ≥4.答案:49.已知f (x )=2sin π2x ,集合M ={x ||f (x )|=2,x >0},把M 中的元素从小到大依次排成一列,得到数列{a n },n ∈N *.(1)求数列{a n }的通项公式;(2)记b n =1a 2n +1,设数列{b n }的前n 项和为T n ,求证:T n <14. 解:(1)∵|f (x )|=2,∴π2x =k π+π2,k ∈Z ,x =2k +1,k ∈Z . 又∵x >0,∴a n =2n -1(n ∈N *).(2)∵b n =1a 2n +1=1(2n +1)2=14n 2+4n +1<14n 2+4n =14⎝ ⎛⎭⎪⎫1n -1n +1,∴T n =b 1+b 2+…+b n <14⎝ ⎛⎭⎪⎫1-12+12-13+…+1n -1n +1=14-14(n +1)<14, ∴T n <14得证. 10.已知数列{a n }的前n 项和为S n ,且满足a 1=12,a n =-2S n ·S n -1(n ≥2). (1)求数列{a n }的通项公式a n ;(2)求证:S 21+S 22+…+S 2n ≤12-14n. 解:(1)∵a n =-2S n ·S n -1(n ≥2),∴S n -S n -1=-2S n ·S n -1.两边同除以S n ·S n -1,得1S n -1S n -1=2(n ≥2), ∴数列⎩⎨⎧⎭⎬⎫1S n 是以1S 1=1a 1=2为首项,以d =2为公差的等差数列, ∴1S n =1S 1+(n -1)·d =2+2(n -1)=2n , ∴S n =12n. 将S n =12n代入a n =-2S n ·S n -1, 得a n =⎩⎪⎨⎪⎧ 12, (n =1),12n -2n 2, (n ≥2).(2)证明:∵S 2n =14n 2<14n (n -1)=14⎝ ⎛⎭⎪⎫1n -1-1n (n ≥2), S 21=14, ∴当n ≥2时,S 21+S 22+…+S 2n=14+14×2×2+…+14·n ·n<14+14⎝⎛⎭⎫1-12+…+14⎝ ⎛⎭⎪⎫1n -1-1n=12-14n; 当n =1时,S 21=14=12-14×1. 综上,S 21+S 22+…+S 2n ≤12-14n. B 组 高考题型专练1.(2015·高考浙江卷)已知数列{a n }和{b n }满足a 1=2,b 1=1,a n +1=2a n (n ∈N *),b 1+12b 2+13b 3+ (1)b n =b n +1-1(n ∈N *). (1)求a n 与b n ;(2)记数列{a n b n }的前n 项和为T n ,求T n . 解:(1)由a 1=2,a n +1=2a n ,得a n =2n (n ∈N *). 由题意知:当n =1时,b 1=b 2-1,故b 2=2.当n ≥2时,1n b n =b n +1-b n ,整理得b n +1n +1=b n n, 所以b n =n (n ∈N *).(2)由(1)知a n b n =n ·2n ,因此,T n =2+2×22+3×23+…+n ·2n , 2T n =22+2×23+3×24+…+n ·2n +1, 所以T n -2T n =2+22+23+…+2n -n ·2n +1. 故T n =(n -1)2n +1+2(n ∈N *).2.(2015·高考安徽卷)设n ∈N *,x n 是曲线y =x 2n +2+1在点(1,2)处的切线与x 轴交点的横坐标.(1)求数列{x n }的通项公式;(2)记T n =x 21x 23…x 22n -1,证明:T n ≥14n. 解:(1)y ′=(x 2n +2+1)′=(2n +2)x 2n +1,曲线y =x 2n +2+1在点(1,2)处的切线斜率为2n +2,从而切线方程为y -2=(2n +2)(x -1).令y =0,解得切线与x 轴交点的横坐标x n =1-1n +1=n n +1. 所以数列{x n }的通项公式x n =n n +1. (2)证明:由题设和(1)中的计算结果知T n =x 21x 23…x 22n -1=⎝⎛⎭⎫122⎝⎛⎭⎫342…⎝ ⎛⎭⎪⎫2n -12n 2. 当n =1时,T 1=14. 当n ≥2时,因为x 22n -1=⎝ ⎛⎭⎪⎫2n -12n 2=(2n -1)2(2n )2>(2n -1)2-1(2n )2=2n -22n =n -1n , 所以T n >⎝⎛⎭⎫122×12×23×…×n -1n =14n. 综上可得对任意的n ∈N *,均有T n ≥14n. 3.(2014·高考新课标全国卷Ⅱ)已知数列{a n }满足a 1=1,a n +1=3a n +1.(1)证明:⎩⎨⎧⎭⎬⎫a n +12是等比数列,并求{a n }的通项公式; (2)证明:1a 1+1a 2+…+1a n <32. 证明:(1)由a n +1=3a n +1得a n +1+12=3⎝⎛⎭⎫a n +12. 又a 1+12=32, 所以⎩⎨⎧⎭⎬⎫a n +12是首项为32,公比为3的等比数列. 所以a n +12=3n 2, 因此{a n }的通项公式为a n =3n -12. (2)由(1)知1a n =23n -1. 因为当n ≥1时,3n -1≥2×3n -1,所以13n -1≤12×3n -1.于是1a 1+1a 2+…+1a n ≤1+13+…+13n -1 =32⎝⎛⎭⎫1-13n <32. 所以1a 1+1a 2+…+1a n <32.。
2017届一轮复习北师大版 排列、组合 课件

叫做从n个不同元素中取出m个元素的排列数,用 Am n 表示.
(3)排列数公式: =① Am n
n(n-1)…(n-m+1)
.
(4)全排列:n个不同元素全部取出的排列,叫做n个不同元素的一个全排 列, =n· (n-1)· (n-2)· …· 3· 2· 1=n!.于是排列数公式写成阶乘形式为 = Am An n n
1.分类加法计数原理、分步乘法计数原理
(1)完成一件事有几类办法,各类办法相互独立,每类办法中又有多种不同 的办法,则完成这件事的不同方法数是各类不同方法种数的和,这就是分
类加法计数原理.
(2)完成一件事,需要分成几个步骤,每一步的完成有多种不同的方法,则
完成这件事的不同方法数是各种不同的方法种数的乘积,这就是分步乘
2 3 A3 A A + · 3 3 3 =48种;若C排在第4,5,6位时,其排法数与排在第3,2,1位相同,故
共有排法2×(120+72+48)=480种.
(3)记5件产品为A、B、C、D、E,A、B相邻视为一个元素,先与D、E排
3 1 列,有 3 种方法;再将C插入,仅有3个空位可选,故共有 =2×6×3= A2 A2 2 A3 2 A3 C 3
c
种(用
2 ①有一个人获得两张有奖奖券,另外还有一个人获得一张有奖奖券,有 C3
A2 4 =36种获奖情况.
②有三个人各获得一张有奖奖券,有 =24种获奖情况. A3 4
故不同的获奖情况有36+24=60种.
1-2 (2013福建,5,5分)满足a,b∈{-1,0,1,2},且关于x的方程ax2+2x+b=0有
2017高考数学一轮复习排列组合答题技巧

2017高考数学一轮复习排列组合答题技巧
1.掌握分类计数原理与分步计数原理,并能用它们分析和解决一些简单的应用问题。
2.理解排列的意义,掌握排列数计算公式,并能用它解决一些简单的应用问题。
3.理解组合的意义,掌握组合数计算公式和组合数的性质,并能用它们解决一些简单的应用问题。
4.掌握二项式定理和二项展开式的性质,并能用它们计算和证明一些简单的问题。
5.了解随机事件的发生存在着规律性和随机事件概率的意义。
6.了解等可能性事件的概率的意义,会用排列组合的基本公式计算一些等可能性事件的概率。
7.了解互斥事件、相互独立事件的意义,会用互斥事件的概率加法公式与相互独立事件的概率乘法公式计算一些事件的概率。
8.会计算事件在n次独立重复试验中恰好发生k次的概率
2017高考数学一轮复习排列组合答题技巧就为大家分享到这里,更多精彩内容请关注高考数学答题技巧栏目。
精心整理,仅供学习参考。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
排列组合考纲要求1.理解分类加法计数原理和分步乘法计数原理.2.理解排列、组合的概念,并能用排列组合解决简单的实际问题.基础知识梳理1.分类加法计数原理做一件事,完成它有n 类办法,在第一类办法中有种不同的方法,在第二类办法中有种不同的方法在第n 类办法中有种不同的方法.那么完成这件事共有_____________________________种不同的方法。
2. 分步乘法计数原理做一件事,完成它需要分成n 个步骤,做第一个步骤有种不同的方法,做第二个步骤有种不同的方法做第n 个步骤有种不同的方法.那么完成这件事共有_____________________________种不同的方法。
3.排列(1)排列定义:从个不同元素中,任取()个元素(这里的被取元素各不相同)按照排成一列,叫做从个不同元素中取出个元素的一个排列....两个排列相同的条件:①;②.排列数定义: 从个不同元素中,任取()个元素的所有排列的叫做从个元素中取出个元素的排列数,用符号表示.(2)排列数公式: ==n·(n-1)…(n-m+1); (3)全排列: =n!.(4)记住下列几个阶乘数:1!=1,2!=2,3!=6,4!=24,5!=120,6!=720.4.组合(1)组合的定义:一般地,从n 个不同元素中取出m (m ≤n )个元素________,叫做从n 个不同元素中取出m 个元素的一个组合.组合与排列的不同是:取出的元素. 1m 2m ......n m 1m 2m n m n m m n ≤n m n m m n ≤n m A m n A m n )!(!m n n -A m n组合数的定义:从n 个不同元素中取出m (m ≤n )个元素的所有组合的个数,叫做从n 个不同元素中取出m 个元素的组合数,用符号 表示.(2)组合数公式: == (3)组合数的性质①;②;③; ④,即.预习自测 1.把5张座位编号为1,2,3,4,5的电影票发给3个人,每人至少1张,最多分2张,且这两张票具有连续的编号,那么不同的分法种数是( )A .360B .60C .54D .182.某学校周五安排有语文、数学、英语、物理、化学、体育六节课,要求体育不排在第一节课,数学不排在第四节课,则这天课表的不同排法种数为( )A .600B .288C .480D .5043.我们把各位数字之和为6的四位数称为“六合数”(如2013是“六合数”),则“六合数”中首位为2的“六合数”共有( )A .18个B .15个C .12个D .9个4. 2013年第12届全国运动会在沈阳举行,某校4名大学生申请当A,B,C 三个比赛项目的志愿者,组委会接受了他们的申请,每个比赛项目至少分配一人,每人只能服务一个比赛项目,若甲要求不去服务A 比赛项目,则不同的安排方案共有( )A .20种B .24种C .30种D .36种5.航空母舰“辽宁舰”将进行一次编队配置科学实验,要求2艘攻击型核潜艇一前一后,2艘驱逐舰和2艘护卫舰分列左、右,同侧不能都是同种舰艇,则舰艇分配方案的方法数为_______.6.两个正整数的公因数只有1的两个数,叫做互质数,例如:2与7互质,3与4互质,在2,3,4,5,6,7的任一排列中使相邻两数都互质的不同排列方式共有_______种(用数字作答).C m n)!(!!m n m n -()()()11.121n n n m m m -⋅⋅⋅-+⨯-⨯⋅⋅⋅⨯⨯C C m n m n n-=r n r n r n C C C 11+-=+01C C 2n n n n n C ++⋅⋅⋅+= ⋅⋅⋅01n n n n n C -C ++(-1)C =0⋅⋅⋅⋅⋅⋅02413n-1n n n n n C +C +C +=C +C +=2典型例题考点1 排列、组合的概念及排列数、组合数、公式、性质【典例1】(1)已知20,则n=. (2)若,则=. 考点2 排列的应用题【典例2】.六人按下列要求站一横排,分别有多少种不同的站法?(1)甲不站两端; (2)甲乙必须相邻(3)甲乙不相邻 (4)甲乙之间间隔两人(5)甲乙站在两端 (6)甲不站左端,乙不站右端【变式1】一场晚会有5个歌唱节目和3个舞蹈节目,要求排出一个节目单.(1) 若前4个节目中要有舞蹈节目,则有多少种排法?(2)若3个舞蹈节目互不相邻,则有多少种排法?考点3 组合问题【典例3】7名男生和5名女生中选取5人,分别求符合下列条件的选法总数有多少种?(1)A,B 必须当选; (2)A,B 必不当选;(3)A,B 不全当选; (4)至少有两名女生当选.(5)选取3名男生和2名女生分别担任班长、体育委员等5种不同的工作,但体育委员必须由男生担任,班长必须由女生担任.【变式2】有4个不同的球,4个不同的盒子,把球全部放入盒内.(1)共有多少种放法?()12533C 4C 15A n n n n n n n -+++=++567117-C C 10C m m m =8C m(2)恰有一个盒子不放球,有多少种放法?考点4 排列组合的综合问题【典例4】从1,3,5,7,9五个数字中选两个,从0,2,4,6,8五个数字中选三个,能组成多少个无重复数字的五位数?【变式3】(1)6本不同的书分成三组,分别是1本、2本、3本,共有_______________________种分法;(2)6本不同的书分成三组,每组2本,共有_______________________________种分法;(3)6本不同的书分成三组,分别是1本、1本、4本,共有____________________种分法;(4)7本不同的书,分给甲、乙、丙三个人,依次得3、2、2本,有_______________种分法。
当堂检测1.某班同学准备参加学校在寒假里组织的“社区服务”、“进敬老院”、“参观工厂”、“民俗调查”、“环保宣传”五个项目的社会实践活动,每天只安排一项活动,并要求在周一至周五内完成.其中“参观工厂”与“环保宣讲”两项活动必须安排在相邻两天,“民俗调查”活动不能安排在周一.则不同的安排方法种数是()A.48 B.24 C.36 D.642 .如图所示,使电路接通,开关不同的开闭方式有()()A.11种B.20种C.21种D.12种3 .从六个数字中任取两个奇数和两个偶数,组成没有重复数字的四位奇数,有多少种取法()A.B.C.D.4 .某单位安排2013年春节期间7天假期的值班情况,7个员工每人各值一天. 已知某员工甲必须排在前两天,员工乙不能排在第一天,员工丙必须排在最后一天,则不同的值班顺序有()A.120种B.216种C.720种D.540种5.某车队准备从甲、乙等7辆车中选派4辆参加救援物资的运输工作,并按出发顺序前后排成一队,要求甲、乙至少有一辆参加,且若甲、乙同时参加,则它们出发时不能相邻,那么不同排法种数为( )A .360B .520C .600D .720A 组全员必做题1.用0,1,…,9十个数字,可以组成有重复数字的三位数的个数为( )A .243B .252C .261D .2792.从这五个数中,每次取出两个不同的数分别记为,共可得到的不同值的个数是( )A .B .C .D .3.从4名男同学和6名女同学中随机选取3人参加某社团活动,选出的3人中男女同学都有的概率为________(结果用数值表示).4.将六个字母排成一排,且均在的同侧,则不同的排法共有________种(用数字作答)5.从名骨科、名脑外科和名内科医生中选派人组成一个抗震救灾医疗小组,则骨科、脑外科和内科医生都至少有人的选派方法种数是___________(用数字作答)6.将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是_________.7.个人排成一行,其中甲、乙两人不相邻的不同排法共有____________种.(用数字作答)B 组提高选做题1.若一系列函数的解析式相同,值域相同但定义域不同,则称这些函数为“孪生函数”,那么函数解析式为,值域为{3,19}的“孪生函数”共有( )个( )A .7B .8C .9D .10 1,3,5,7,9,a b lg lg a b -9101820FE D C B A ,,,,,B A ,C 345516122+=x y2.用1,2,3,4,5,6组成数字不重复的六位数,满足1不在左右两端,2,4,6三个偶数中,有且只有两个偶数相邻,则这样的六位数的个数为 ( )A .B .C .D .3.用8个数字可以组成不同的四位数个数是 ( )A .168B .180C .204D .4564 .从6人中选4人分别到北京、哈尔滨、广州、成都四个城市游览,要求每个城市有一人游览,每人只游览一个城市,且在这6人中甲、乙不去哈尔滨游览,则不同的选择方案共有( ) A .300种 B .240种 C .144种 D .96种5 .某学习小组共有位同学,毕业之前互赠一份纪念品,任意两位同学之间最多交换一次,已知这位同学之间共进行了次交换,其中一人收到份纪念品,另外位同学收到的纪念品的数量最少是个,最多是个,则=( )A .B .C .D .6.将四个相同的红球和四个相同的黑球排成一排,然后从左至右依次给它们赋以编号l,2,…,8.则红球的编号之和小于黑球编号之和的排法有______种.7.某高三学生希望报名参加某6所高校中的3所学校的自主招生考试,由于其中2所学校的考试时间相同,因此该学生不能同时报考这2所学校,该学生不同的报考方法种数是_____种(用数字作答)参考答案预习自测1.D2.D3.B4.B5.32 4322882161441,1,2,2,3,3,4,455824m n m n 5678典型例题【典例1】(1)2.(2)28【例2】(1)480;(2)240;(3)480;(4)144;(5)48;(6)504【变式1】(1)37440;(2)14400【典例3】(1)120;(2)252;(3)672;(4)596;(5)12600【变式2】(1)256;(2)144【典例4】10560【变式3】(1).60 (2).15(3).15 (4).210 当堂检测1.C2.C3.B4.B5.CA 组全员必做题1.B2 .C3.4.4805.6.967.480B 组提高选做题1.C2.B 3.C4 .B 5.C 455907.16。
