CS2 试题解答 第三单元 图像
PhotoshopCS2平面设计:绘制图像与处理图像(1)

(3)选中“云图”图像画布窗口。在“云图”图像内用鼠标拖 曳,即可将“气球”图像以基准点为中心复制到“云图”图像 中。如果在复制中多次重新拖曳鼠标,也不会重新复制图像, 而是继续前面的复制工作,直到整幅完毕,如图6-1-14左图所示 。
修复画笔工具 的选项栏如图6-1-18所示,其中各选项的作用 如下。
图6-1-18 修复画笔工具的选项栏
6.1 图章和修复工具组
(1)“源”栏:它有两个单选项。选择“取样”单选项后,需 要先取样,再复制;选择“图案”单选项后,不需要取样,复 制的是选择的图案。选择“图案”单选项后,其右边的图案选 择下拉列表框会变为有效,单击它的黑色箭头按钮可以调出图 案调板,用来选择图案。
图6-2-26 海绵工具的选项栏
图6-2-27 海绵工具加工后的图像
6.3 橡皮擦工具组
【相关知识】橡皮擦工具组
工具箱内的橡皮擦工具组有三个工具,如 图6-3-5所示。它们的作用如下。
图6-3-5 橡皮擦工具组
1.橡皮擦工具 单击按下“橡皮擦工具”按钮 后,它的选项栏如图6-3-6所示。 利用它可以设置橡皮的画笔模式、画笔形状和不透明度等。
操作提示:打开的两幅图像应具有相同的彩色模式。
(1)单击按下工具箱内的“仿制图章工具”按钮 ,在其选项栏 内进行画笔、模式、不透明度等设置,如图6-1-2所示。选择 “对齐”复选框的目的是复制一幅图像。
6.1 图章和修复工具组
(1)单击按下工具箱内的“仿制图章工具”按钮 ,在其选项 栏内进行画笔、模式、不透明度等设置,如图6-1-2所示。选择 “对齐”复选框的目的是复制一幅图像。
湘教版八年级下册数学第3章 图形与坐标含答案(考试突破)

湘教版八年级下册数学第3章图形与坐标含答案一、单选题(共15题,共计45分)1、在平面直角坐标系中,等腰直角三角形的两个锐角顶点坐标为(2,3),(0,﹣1),则它的直角顶点坐标为()A.(3,0)B.(﹣1,2)C.(1,1)D.(3,0),(﹣1,2)2、△DEF(三角形)是由△ABC平移得到的,点A(﹣1,﹣4)的对应点为D (1,﹣1),则点B(1,1)的对应点E,点C(﹣1,4)的对应点F的坐标分别为()A.(2,2),(3,4)B.(3,4),(1,7)C.(﹣2,2),(1,7)D.(3,4),(2,﹣2)3、在平面直角坐标系中,点(1,﹣m2﹣1)一定在()A.第一象限B.第二象限C.第三象限D.第四象限4、已知M(2,2).规定“把点M先作关于x轴对称,再向左平移1个单位”为一次变换.那么连续经过2018次变换后,点M的坐标变为().A.(-2016,2)B.(-2016,-2)C.(-2017,-2)D.(-2017,2)5、在平面直角坐标系中,将点绕原点O逆时针旋转180°,得到的对应点的坐标是()A. B. C. D.6、点M(2,-3)关于原点对称的点N的坐标是: ( )A.(-2,-3)B.(-2, 3)C.(2, 3)D.(-3, 2)7、点A(﹣3,﹣4)到原点的距离为()A.3B.4C.5D.78、若点 P(a,a-2)在第四象限,则a的取值范围是()A.-2<a<0B.0<a<2C.a>2D.a<09、如图,△ABC三个顶点的坐标分别为A(2,2),B(4,2),C(6,4),以原点O为位似中心,将△ABC缩小为原来的一半,则线段AC的中点P变换后在第一象限对应点的坐标为( )A.(3,2)B.(-3,-2)或(3,2)C.(2,- )D.(2,)10、如图所示是围棋棋盘中的一部分,放置在某个平面直角坐标系中,白棋②的坐标是(﹣3,﹣1),白棋④的坐标是(﹣2,﹣5),则黑棋①的坐标是()A.(﹣3,﹣5)B.(0,0)C.(1,﹣4)D.(2,﹣2)11、如图,在平面直角坐标系中,点A的坐标是,点A关于直线的对称点为B,若抛物线与线段恰有一个公共点,则a 的取值范围是()A. B. C. D.12、若点P(3a+5,-6a-2)在第四象限,且到两坐标轴的距离相等,则a的值为( )A.-1B.C.1D.213、直角坐标系中,点P(x,y)在第二象限,且P 到x 轴、y 轴距离分别为3,7,则P 点坐标为()A.(-3,7)B.(-7,3)C.(3,7)D.(7,3)14、如图,在平面直角坐标系中,点A(1,),点B(2,0),P为线段OB上一点,过点P作PQ∥OA,交AB于点Q,连接AP,则△APQ面积最大值为()A. B. C. D.15、如图,在平面直角坐标系xOy中,已知点A( ,0),B(1,1).若平移点A到点C,使以点O,A,C,B为顶点的四边形是菱形,则正确的平移方法是( )A.向左平移1个单位,再向下平移1个单位B.向左平移(2 -1个单位,再向上平移1个单位C.向右平移个单位,再向上平移1个单位 D.向右平移1个单位,再向上平移1个单位二、填空题(共10题,共计30分)16、若点到两坐标轴的距离相等,则该点的坐标为________.17、如图,已知A1(1,0),A2(1,﹣1),A3(﹣1,﹣1),A4(﹣1,1),A 5(2,1),…,则点A2010的坐标是________.18、点到轴的距离是________.19、已知点A(2,1),线段AB∥y轴,且AB=3,则B点坐标________.20、在平面直角坐标系中,抛物线y=x2的图象如图所示.已知A点坐标为(1,1),过点A作AA1∥x轴交抛物线于点A1,过点A1作A1A2∥OA交抛物线于点A2,过点A2作A2A3∥x轴交抛物线于点A3,过点A3作A3A4∥OA交抛物线于点A4……,依次进行下去,则点A2019的坐标为________.21、通过平移把点A(2,﹣3)移到点A′(4,﹣2),按同样的平移方式可将点B(﹣3,1)移到点B′,则点B′的坐标是________.22、已知抛物线y=x2+(m+1)x﹣m﹣2(m>0)与x轴交于A、B两点,与y轴交于点C,不论m取何正数,经过A、B、C三点的⊙P恒过y轴上的一个定点,则该定点的坐标是________.23、在平面直角坐标系中,将点A(2,﹣3)向右平移3个单位后得到点B,则点B的坐标为________.24、点M(﹣2,1)关于x轴对称的点N的坐标________,直线MN与x轴的位置关系是________.25、长春高新第二实验学校在设计图上记大门的坐标为,旗杆的坐标为,则食堂的坐标为________.三、解答题(共5题,共计25分)26、如图,直线AB交x轴于点B,交y轴于点A(0,4),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=6,连接DA,∠DAC=90°,AD:AB=1:2.(1)求点D的坐标;(2)求经过O、D、B三点的抛物线的函数关系式.27、如图,正方形ABCD关于x轴、y轴均成轴对称,若这个正方形的面积为16,请分别写出点A、B、C、D的坐标.28、建立平面直角坐标系,依次描出点A(-2,0),B(0,-3),C(-3,-5),连接AB、BC、CA.求△ABC的面积.29、如下图所示,从2街4巷到4街2巷,走最短的路线,共有几种走法?30、在平面直角坐标系中,点A(0,a)、B(b,0)且a>|b|.(1)若a、b满足a2+b2﹣4a﹣2b+5=0.①求a、b的值;②如图1,在①的条件下,将点B在x轴上平移,且b满足:0<b<2;在第一,并写出解答过象限内以AB为斜边作等腰Rt△ABC,请用b表示S四边形AOBC程.(2)若将线段AB沿x轴向正方向移动a个单位得到线段DE(D对应A,E对应B)连接DO,作EF⊥DO于F,连接AF、BF.①如图2,判断AF与BF的关系并说明理由;②若BF=OA﹣OB,求∠OAF的度数(直接写出结果).参考答案一、单选题(共15题,共计45分)1、D2、B3、D4、A5、B6、B7、C8、B9、D10、C11、C12、C13、B14、B15、D二、填空题(共10题,共计30分)16、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、29、30、。
新人教版高中数学必修第二册第三单元《立体几何初步》测试(答案解析)
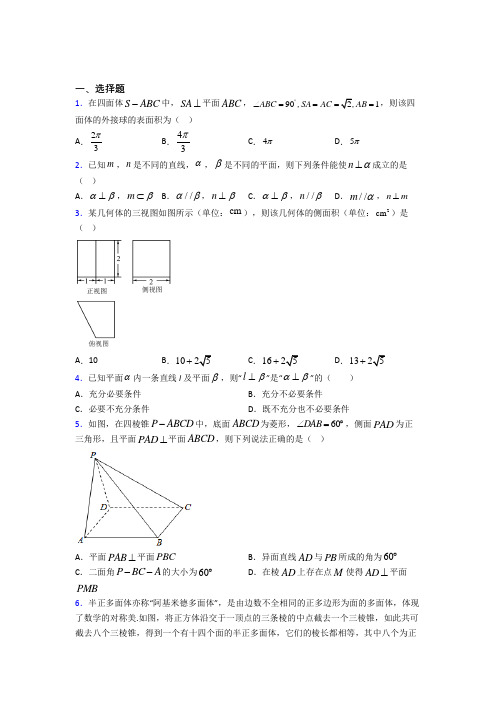
一、选择题1.在四面体S ABC -中,SA ⊥平面ABC ,9021ABC SA AC AB ︒∠====,,,则该四面体的外接球的表面积为( )A .23πB .43πC .4πD .5π2.已知m ,n 是不同的直线,α,β是不同的平面,则下列条件能使n α⊥成立的是( )A .αβ⊥,m β⊂B .//αβ,n β⊥C .αβ⊥,//n βD .//m α,n m ⊥ 3.某几何体的三视图如图所示(单位:cm ),则该几何体的侧面积(单位:2cm )是( )A .10B .1025+C .1625+D .1325+ 4.已知平面α内一条直线l 及平面β,则“l β⊥”是“αβ⊥”的( ) A .充分必要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件5.如图,在四棱锥P ABCD -中,底面ABCD 为菱形,60DAB ∠=︒,侧面PAD 为正三角形,且平面PAD ⊥平面ABCD ,则下列说法正确的是( )A .平面PAB ⊥平面PBCB .异面直线AD 与PB 所成的角为60︒C .二面角P BC A --的大小为60︒D .在棱AD 上存在点M 使得AD ⊥平面PMB6.半正多面体亦称“阿基米德多面体”,是由边数不全相同的正多边形为面的多面体,体现了数学的对称美.如图,将正方体沿交于一顶点的三条棱的中点截去一个三棱锥,如此共可截去八个三棱锥,得到一个有十四个面的半正多面体,它们的棱长都相等,其中八个为正三角形,六个为正方形,称这样的半正多面体为二十四等边体.一个二十四等边体的各个顶点都在同一个球面上,若该球的表面积为16π,则该二十四等边体的表面积为( )A .1243+B .1863+C .2483+D .36123+ 7.边长为2的正方形ABCD 沿对角线AC 折叠使得ACD 垂直于底面ABC ,则点C 到平面ABD 的距离为( )A .263B .23C .22D .6 8.如图,在长方体ABCD ﹣A 1B 1C 1D 1中,AA 1=8,AB =3,AD =8,点M 是棱AD 的中点,点N 是棱AA 1的中点,P 是侧面四边形ADD 1A 1内一动点(含边界),若C 1P ∥平面CM N ,则线段C 1P 长度的取值范围是( )A .17,5⎤⎦B .[4,5]C .[3,5]D .17⎡⎣9.如图,正方体1111ABCD A B C D -的棱长为2,点O 为底面ABCD 的中心,点P 在侧面11BB C C 的边界及其内部运动.若1D O OP ⊥,则11D C P △面积的最大值为( )A .25B .455C .5D .25 10.如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm ,底面周长为10cm ,在容器内壁离容器底部3cm 的点B 处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm 的点A 处,则蚂蚁吃到饭粒需爬行的最短路径是( )A .13cmB .61cmC 61cmD .234cm11.αβ、是两个不同的平面,mn 、是平面α及β之外的两条不同直线,给出四个论断:①m n ⊥;②αβ⊥;③n β⊥;④.m α⊥以其中三个论断作为条件,余下一个作为结论,其中正确命题的个数是( ) A .1个 B .2个 C .3个 D .4个 12.已知m 为一条直线,,αβ为两个不同的平面,则下列说法正确的是( ) A .若//,//m ααβ,则//m βB .若,,m αβα⊥⊥则//m βC .若,//,m ααβ⊥则m β⊥D .若//,,m ααβ⊥则m β⊥ 13.长方体1111ABCD A B C D -的8个顶点都在球O 的表面上,E 为AB 的中点,3CE =,53cos ACE ∠=11ABB A 为正方形,则球O 的直径为( ) A .4 B 51C .451D .4或5 14.用一个平行于圆锥底面的平面截这个圆锥,截得的圆台上、下底面的面积之比为1:16,截去的圆锥的母线长是3cm ,则圆台的母线长是( )A .9cmB .10cmC .12cmD .15cm二、解答题15.如图,已知三棱柱111ABC A B C -的侧面11BCC B 为矩形,2AB AC ==,2BC =,D ,E 分别为BC 、11B C 的中点,过BC 作平面α分别交11A B 、1A E 、11A C 于点M 、F 、N .(1)求证:平面BCNM ⊥平面1AA ED .(2)若Q 为线段AD 上一点,3AD AQ =,1//A Q 平面BCNM ,则当1A Q 为何值时直线BM 与平面1AA ED 所成角的正弦值为13(请说明理由). 16.如图,已知AB 是圆O 的直径,2AB =,C 是圆O 上一点,且AC BC =,6PA =,22=PC ,10PB =.(1)求证:平面PBC⊥平面PAC;-的体积.(2)求三棱锥P ABC⊥,D是棱AB的中点,且17.如图,在三棱锥V-ABC中,VC⊥底面ABC,AC BCAC BC VC==.(1)证明:平面VAB⊥平面VCD;(2)若22AC=,且棱AB上有一点E,使得线VD与平面VCE所成角的正弦值为15,试确定点E的位置,并求三棱锥C-VDE的体积.15-中,底面ABCD是边长为2的正方形,18.在四棱锥P ABCD∠==∠=,E为PD的中点.90,,60ADP PD AD PDC(1)证明:CE⊥平面PAD.-外接球的体积.(2)求三棱锥E ABC19.如图所示,在四面体ABCD中,点P,Q,R分别为棱BC,BD,AD的中点,AB=,3⊥,2AB BDPR=,22CD=.CD平面PQR;(1)证明://(2)证明:平面ABD⊥平面BCD.20.如图,三棱柱111ABC A B C -的所有棱长都相等,平面11AA C C ⊥平面ABC ,160AAC ∠=︒,点D 为线段AC 的中点,点E 在线段AB 上.(1)求证:平面1A DE ⊥平面ABC ;(2)若2AB =,求点C 到平面1ABC 的距离.21.如图,在四棱锥P ABCD -中,ABCD 为菱形,PA ⊥平面ABCD ,连接AC ,BD 交于点O ,6AC =,8BD =,E 是棱PC 上的动点,连接DE .(1)求证:平面BDE ⊥平面PAC ;(2)当BED 面积的最小值是6时,求此时点E 到底面ABCD 的距离.22.如图,在三棱锥D -ABC 中,已知△BCD 是正三角形,AB ⊥平面BCD ,AB =BC =a ,E 为BC 中点,F 在棱AC 上,且AF =3FC .(1)求三棱锥D -ABC 的体积;(2)求证:AC ⊥平面DEF ;(3)若M 为DB 中点,N 在棱AC 上,且3,8CN CA =求证:MN //平面DEF .23.如图,在三棱锥P ABC -中,1PA PC ==,AB BC =,60APC ∠=︒,90ABC ∠=︒,AC PB =.(1)证明:AC PB ⊥;(2)求三棱锥A PBC -的体积.24.如图,在四棱锥P ABCD -中,底面ABCD 为平行四边形,2AB =,1AD =,60DAB ∠=︒,PD BD =,且PD ⊥平面ABCD .(1)证明:平面PBC ⊥平面PBD ;(2)若Q 为PC 的中点,求三棱锥D PBQ -的体积.25.如图,在四棱锥P ABCD -中,底面ABCD 为菱形,PA ⊥平面ABCD ,E 为PD 上的动点.(1)确定E 的位置,使//PB 平面AEC ;(2)设1==PA AB ,3PC =,根据(1)的结论,求点E 到平面PAC 的距离. 26.如图,四棱锥P ABCD -中,底面ABCD 是菱形,,60,PA PD BAD E =∠=是AD 的中点,点Q 在侧棱PC 上.(1)求证:AD ⊥平面PBE ;(2)若Q 是PC 的中点,求证://PA 平面BDQ ;(3)若2P BCDE Q ABCD V V --=,试求CP CQ的值.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】根据题目条件先确定出外接球的球心,得出外接球半径,然后计算表面积.【详解】因为SA ⊥平面ABC ,BC ⊂平面ABC ,所以SA ⊥BC ,又90ABC ∠=,SA AB A ⋂=,且AB平面SAB ,SA ⊂平面SAB , 所以BC ⊥平面ABC ,所以BC SB ⊥. 因为21SA AC AB ===,,所以2SC =,3SB =1BC =,根据该几何体的特点可知,该四面体的外接球球心位于SC 的中点, 则外接球半径112R SC ==, 故该四面体的外接球的表面积为244R ππ=.故选:C.,【点睛】本题考查棱锥的外接球问题,难度一般,根据几何条件确定出球心是关键. 2.B解析:B【分析】n α⊥必有n 平行α的垂线,或者n 垂直α的平行平面,依次判定选项即可.【详解】解:αβ⊥,m β⊂,不能说明n 与α的关系,A 错误;//αβ,n β⊥能够推出n α⊥,正确;αβ⊥,//n β可以得到n 与平面α平行、相交,所以不正确.//m α,n m ⊥则n 与平面α可能平行,所以不正确.故选:B .【点睛】本题考查直线与平面垂直的判定,考查空间想象能力,是基础题.3.B解析:B【分析】由三视图可知,该几何体的直观图为直四棱柱1111ABCD A B C D -,由矩形的面积公式得出该几何体的侧面积.【详解】由三视图可知,该几何体的直观图为直四棱柱1111ABCD A B C D -,如下图所示11AD A D ===∴该几何体的侧面积为122222210⨯+⨯+⨯=+故选:B【点睛】本题主要考查了由三视图计算几何体的侧面积,属于中档题.4.B解析:B【分析】根据面面垂直和线面垂直的定义,结合充分条件和必要条件的定义进行判断即可.【详解】解:由面面垂直的定义知,当“l ⊥β”时,“α⊥β”成立,当αβ⊥时,l β⊥不一定成立,即“l β⊥”是“αβ⊥”的充分不必要条件,故选:B .【点睛】本题考查命题充分性和必要性的判断,涉及线面垂直和面面垂直的判定,属基础题. 5.D解析:D【分析】根据线面垂直,异面直线所成角的大小以及二面角的求解方法分别进行判断即可.【详解】解:对于D ,取AD 的中点M ,连PM ,BM ,侧面PAD 为正三角形, PM AD ∴⊥,又底面ABCD 是60DAB ∠=︒的菱形,∴三角形ABD 是等边三角形,AD BM ∴⊥,PM BM M =,PM ⊂平面PBM ,BM ⊂平面PBMAD ∴⊥平面PBM ,故D 正确,对于B ,AD ⊥平面PBM ,AD PB ∴⊥,即异面直线AD 与PB 所成的角为90︒,故B 错误,对于C ,底面ABCD 为菱形,60DAB ∠=︒,平面PAD ⊥平面ABCD , AD ⊥平面PBM ,//AD BC ,BC PB ∴⊥,BC BM ⊥,”则PBM ∠是二面角P BC A --的平面角,设1AB =,则BM =PM =, 在直角三角形PBM 中,tan 1PM PBM BM ∠==,即45PBM ∠=︒,故二面角P BC A --的大小为45︒,故C 错误,对于A ,AD ⊥平面PBM ,//AD BC ,所以BC ⊥平面PBM ,BC ⊂平面PBC , 所以面PBC ⊥平面PBM ,显然平面PAB 与平面PBC 不垂直,故A 错误;故选:D .【点睛】本题主要考查空间直线和平面位置关系以及二面角的求解,根据相应的判断和证明方法是解决本题的关键.综合性较强,属于中档题.6.C解析:C【分析】通过二十四等边体的外接球表面积求得半径,进而计算出二十四等边体的边长,进而计算出二十四等边体的表面积.【详解】由于二十四等边体的外接球表面积为16π,设其半径为r ,则2416r π=π,解得2r .设O 为球心,依题意可知四边形,,,A B C D 分别为正方体侧棱的中点,所以ABCD 正方形,由于2OA OB OC OD ====,所以四边形ABCD 是正方形,2222AB OA OB =+=.所以二十四等边体的边长为2.所以二十四等边体的边长的表面积为122622sin 823π⨯⨯+⨯⨯⨯⨯ 2483=+.故选:C【点睛】本小题主要考查几何体外接球有关计算,考查空间想象能力,属于中档题.7.A解析:A【分析】取AC 的中点O ,连接DO 和BO ,由等腰三角形的性质得出DO AC ⊥,可求出DO 和BO 的长,再由平面ACD ⊥平面ABC ,根据面面垂直的性质可得DO ⊥平面ABC ,进而得到DO OB ⊥,利用勾股定理即可求出BD ,最后利用等体积法得出C ABD D ABC V V --=,进而求出点C 到平面ABD 的距离.【详解】解:取AC 的中点O ,连接DO 和BO ,则DO AC ⊥,BO AC ⊥,由于四边形ABCD 是边长为2的正方形,2AD CD AB BC ∴====,则AC ==DO BO ===由题知,平面ACD ⊥平面ABC ,且交线为AC ,而DO ⊂平面ACD ,则DO ⊥平面ABC ,又BO ⊂平面ABC ,所以DO BO ⊥,∴在Rt BOD 中,2BD ==,∴ABD △是等边三角形,则122sin 6032ABD S =⨯⨯⨯=△, 则在Rt ABC 中,12222ABC S =⨯⨯=, 设点C 到平面ABD 的距离为d , 则C ABD D ABC V V --=,即1133ABD ABC S d S DO ⋅=⋅△△,即:11233=⨯d =,即点C 到平面ABD 的距离为3. 故选:A.【点睛】本题考查利用等体积法求点到面的距离,还涉及面面垂直的性质和棱锥的体积公式,考查推理证明和运算能力.8.A解析:A【分析】取A 1D 1中点E ,取DD 1中点F ,连接EF 、C 1E 、C 1F ,则平面CM N ∥平面C 1EF ,推导出P ∈线段EF ,当P 与EF 的中点O 重合时,线段C 1P 长度取最小值PO ,当P 与点E 或点F 重合时,线段C 1P 长度取最大值PE 或PF ,由此能求出线段C 1P 长度的取值范围.【详解】解:取A 1D 1中点E ,取DD 1中点F ,连接EF 、C 1E 、C 1F ,则//,EF MN EF ⊄面MNC ,MN ⊂面MNC ,所以//EF 面MNC ,同理1//EC 面MNC ,又1EFEC E =, 则平面MNC ∥平面C 1EF ,∵P 是侧面四边形内一动点(含边界),C 1P ∥平面MNC ,∴P ∈线段EF ,∵在长方体ABCD ﹣A 1B 1C 1D 1中,AA 1=8,AB =3,AD =8, 则2211345C E C F ==+=,所以1EC F ∆为等腰三角形,∴当P 与EF 的中点O 重合时,线段C 1P 长度取最小值PO ,当P 与点E 或点F 重合时,线段C 1P 长度取最大值PE 或PF ,∴1max 115C P C E C F ===,22442EF =+= ()222min 111252217C P C O C E EO ==-=-=.∴线段C 1P 长度的取值范围是17,5⎤⎦.故选:A .【点睛】本题考查线段的取值范围的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力与运算求解能力,属于中档题.9.C解析:C【分析】取1BB 的中点F ,由题意结合正方体的几何特征及平面几何的知识可得1OD OC ⊥,1OD OF ⊥,由线面垂直的判定与性质可得1OD CF ⊥,进而可得点P 的轨迹为线段CF ,找到1C P 的最大值即可得解.【详解】取1BB 的中点F ,连接OF 、1D F 、CF 、1C F ,连接DO 、BO 、OC 、11D B 、1D C ,如图:因为正方体1111ABCD A B C D -的棱长为2,所以11B F BF ==,2DO BO OC ===11122D B DC ==1BB ⊥平面ABCD ,1BB ⊥平面1111D C B A ,11C D ⊥平面11BB C C , 所以22116OD OD DD =+=223OF OB BF =+=2211113D F D B B F =+=,所以22211OD OF D F +=,22211OD OC D C +=,所以1OD OC ⊥,1OD OF ⊥,由OC OF O =可得1OD ⊥平面OCF ,所以1OD CF ⊥,所以点P 的轨迹为线段CF ,又221111152C F B C B F C C =+=>=,所以11D C P △面积的最大值1111125522S C F D C =⋅=⨯⨯=. 故选:C.【点睛】本题考查了正方体几何特征的应用,考查了线面垂直的判定与性质,关键是找到点P 的轨迹,属于中档题.10.A解析:A【分析】如图所示:图像为圆柱的侧面展开图,A 关于EF 的对称点为'A ,则AE BE +的最小值为'A B ,计算得到答案.【详解】如图所示:图像为圆柱的侧面展开图,A 关于EF 的对称点为'A ,则AE BE +的最小值为'A B ,易知5BC =,'12A C =,故'13A B =.故选:A .【点睛】本题考查了立体几何中的最短距离问题,意在考查学生的计算能力和空间想象能力. 11.B解析:B【分析】分别以①②③④作为结论,另外三个作条件,根据线面垂直和面面垂直的判定定理依次判断真假.【详解】若m n ⊥,αβ⊥,n β⊥,则m 与α可能平行可能相交,即①②③不能推出④; 同理①②④不能推出③;若m n ⊥,n β⊥,m α⊥,两个平面的垂线互相垂直则这两个平面垂直,则αβ⊥,即①③④能够推出②;若αβ⊥,n β⊥,m α⊥,两个平面互相垂直,则这两个平面的垂线互相垂直,即m n ⊥,所以②③④能够推出①.所以一共两个命题正确.故选:B【点睛】此题考查空间直线与平面位置关系的辨析,根据选择的条件推出结论,关键在于熟练掌握空间垂直关系的判定和证明.12.C解析:C【分析】利用线面平行、面面平行、线面垂直、面面垂直的判定定理和性质定理进行逐项判断即可.【详解】对于选项A: 若//,//m ααβ,则//m β或m β⊂,故选项A 错误;对于选项B: 若,,m αβα⊥⊥则//m β或m β⊂,故选项B 错误;对于选项C: 若,//,m ααβ⊥由面面平行的性质和线面垂直的判定知m β⊥成立, 故选项C 正确;对于选项D: 若//,,m ααβ⊥则//m β或m β⊂或m 与β相交,故选项D 错误; 故选:C【点睛】本题考查利用线面平行、面面平行、线面垂直、面面垂直的判定定理和性质定理,判断空间中直线与平面的位置关系;考查学生的逻辑思维能力和空间想象能力;属于中档题、常考题型.13.C解析:C【分析】设2AB x =,则AE x =,BC =,由余弦定理可得22939239x x =++-⨯,求出x ,即可求出球O 的直径. 【详解】 根据题意,长方体内接于球O 内,则球的直径为长方体的体对角线,如图作出长方体1111ABCD A B C D -:设2AB x =,则AE x =,29BC x =-,由余弦定理可得:222539392393x x x =++-⨯+,∴1x =6, ∴2AB =,22BC =O 4484++=; 或26AB =3BC =,球O 2424351++=故选:C .【点睛】本题考查球的直径的计算方法,考查余弦定理,考查计算能力和分析能力,属于常考题. 14.A解析:A【分析】计算得到12:1:4r r =,根据相似得到3134l =+,计算得到答案. 【详解】圆台上、下底面的面积之比为1:16,则12:1:4r r =.设圆台母线长为l ,根据相似得到:3134l =+,故9l =. 故选:A .【点睛】本题考查了圆台的母线长,意在考查学生的计算能力和空间想象能力. 二、解答题15.(1)证明见解析(2)1223AQ =,理由见解析 【分析】(1)先根据直线与平面垂直的判定定理证明BC ⊥平面1AA ED ,再根据平面与平面垂直的判定定理证明平面BCNM ⊥平面1AA ED ;(2)连DF ,可推得1A Q 与DF 平行且相等,在线段BD 上取点H ,使BH FM ==23,连FH ,可推得HFD ∠为直线BM 与平面1AA ED 所成角,利用正弦值可求得DF 的值,即可得1A Q 的值.【详解】(1)因为AB AC =,BD DC =,所以BC AD ⊥,又D ,E 分别为BC 、11B C 的中点,所以1//DE BB ,因为侧面11BCC B 为矩形,所以1BC BB ⊥,所以BC DE ⊥,又AD DE D ⋂=,所以BC ⊥平面1AA ED ,因为BC ⊂平面BCNM ,所以平面BCNM ⊥平面1AA ED .(2)因为2AB AC ==,2BC =,所以222AB AC BC +=,所以AB AC ⊥,又D 为BC 的中点,112AD BC ==,因为3AD AQ =,所以13AQ =,23QD =, 连接DF ,因为1//AQ 平面BCNM ,平面1A ADE 平面BCNM DF =, 所以1//A Q DF ,因为1A A 与1B B 平行且相等,1B B 与DE 平行且相等,所以1A A 与DE 平行且相等, 所以四边形1A ADE 为平行边形,所以1A F 与QD 平行且相等,所以四边形1A QDF 为平行四边形,所以1A Q 与DF 平行且相等,因为123A F QD ==,所以13EF =,所以2233FM BD ==, 在线段BD 上取点H ,使BH FM ==23,则21133DH =-=,连FH ,则四边形FMBH 为平行四边形,所以FH 与BM 平行且相等,因为BD ⊥平面1AA ED ,所以HFD ∠为直线BM 与平面1AA ED 所成角,所以1sin 3HFD ∠=,即13DH HF =,所以31HF DH ==,所以3DF ===,所以13A Q DF ==. 【点睛】 关键点点睛:(1)证明面面垂直的关键是找到线面垂直,利用直线与平面垂直的判定定理可证BC ⊥平面1AA ED ;(2)解题关键是找到直线BM 与平面1AA ED 所成角,通过计算可知,在线段BD 上取点H ,使BH FM ==23,连FH ,则HFD ∠为直线BM 与平面1AA ED 所成角.16.(1)证明见解析;(2)3. 【分析】(1)根据已知条件证明BC ⊥平面PAC ,再根据面面垂直的判定定理证明出平面PBC ⊥平面PAC ;(2)由(1)的分析可知:BC ⊥平面PAC ,由此得到三棱锥P ABC -的体积计算公式为13PAC S BC ⋅⋅,结合线段BC 的长度以及PAC S 求解出结果.【详解】(1)因为AB 是圆O 的直径,所以BC AC ⊥.在Rt ABC 中,2AB =,AC BC =,所以AC BC ==因为在PCB 中,PB ==PC BC =222PB PC BC =+,所以BC PC ⊥. 又PC AC C ⋂=,所以BC ⊥平面PAC . 因为BC ⊂平面PBC ,所以平面PBC ⊥平面PAC .(2)由(1)知BC ⊥平面PAC ,所以BC 是三棱锥 B PAC -的高.在 PAC 中,AC =PA ==PC222268AC PA PC ∴+=+==,即PAC △是直角三角形.1122PAC S AC PA ∴=⋅==.11333P ABC B PAC PAC V V S BC --∴==⋅⋅==. 【点睛】关键点点睛:解答本题的第二问的关键是通过变换三棱锥的顶点位置,使三棱锥能较容易得到对应的高和底面积,从而求解出体积.17.(1)证明见解析;(2)点E 位于线段AD 的中点或线段BD 的中点;3. 【分析】(1)易得CD AB ⊥,再根据VC ⊥底面ABC ,得到 VC AB ⊥,进而AB ⊥平面VCD ,再利用面面垂直的判定定理证明.(2)过点D 在平面ABC 内作DF CE ⊥于F ,DF ⊥平面VCE ,则DVF ∠就是直线VD 与平面VCE 所成的角,在Rt VFD 中,由15sin DF DVF VD ∠==,求得DF ,然后在Rt DCE 中,求出1DE =,然后由三棱锥C-VDE 的体积为13CDE V S VC =⋅⋅求解. 【详解】(1)因为AC BC =,D 是AB 的中点,所以CD AB ⊥.又VC ⊥底面ABC ,AB 平面ABC ,所以VC AB ⊥,而VC CD C ⋂=,所以AB ⊥平面VCD .又AB 平面VAB ,所以平面VAB ⊥平面VCD .(2)过点D 在平面ABC 内作DF CE ⊥于F ,则由题意知DF ⊥平面VCE .,连接VF ,于是DVF ∠就是直线VD 与平面VCE 所成的角.在Rt VFD 中,1515DF VD =. 又因为3VD =55DF =. 在Rt DCE 中,1DE =.故知点E 位于线段AD 的中点或线段BD 的中点,三棱锥C-VDE 的体积为1112221223323CDE S VC ⋅⋅=⨯⨯⨯⨯=. 【点睛】方法点睛:(1)证明平面和平面垂直的方法:①面面垂直的定义;②面面垂直的判定定理(a ⊥β,a ⊂α⇒α⊥β).(2)已知两平面垂直时,一般要用性质定理进行转化,在一个平面内作交线的垂线,转化为线面垂直,然后进一步转化为线线垂直.18.(1)证明见解析;(282π【分析】(1)由已知条件知AD ⊥面DPC ,即有AD CE ⊥,由PDC △为等边三角形有CE DP ⊥,结合线面垂直的判定有CE ⊥平面PAD .(2)由勾股定理可证AEC 为直角三角形,且ABC 为等腰直角三角形,即可知AC 的中点O 为外接球的球心,进而得到半径求球的体积. 【详解】(1)由90ADP ∠=知:AD DP ⊥,底面ABCD 是正方形有AD DC ⊥,又DP DC D =,∴AD ⊥面DPC ,而CE ⊂面DPC ,即AD CE ⊥,∵PD AD DC ==,60PDC ∠=,∴PDC △为等边三角形,E 为PD 的中点,故CE DP ⊥, ∵DP AD D ⋂=, ∴CE ⊥平面PAD .(2)由(1)知:ABC 为等腰直角三角形且2AB BC == ,有22AC =, 在AEC 中3,5CE AE ==,即222AC CE AE =+,故AE CE ⊥,∴由上知:ABC 、AEC 都是以AC 为斜边的直角三角形,由直角三角形斜边中点O 到三顶点距离相等知:OE OC OA OB ===,即O 为三棱锥E ABC -外接球的球心, ∴外接球的半径为22AC=, 所以三棱锥E ABC -外接球的体积为3482(2)3V ππ=⨯=. 【点睛】 关键点点睛:(1)由90°及正方形有线面垂直:AD ⊥面DPC ,再由等边三角形的性质和线面垂直的判定证明CE ⊥平面PAD ;(2)由勾股定理说明AEC 是以AC 为斜边的直角三角形,同样ABC 也是AC 为斜边的直角三角形,即可确定三棱锥E ABC -外接球的球心,进而求体积. 19.(1)证明见解析;(2)证明见解析. 【分析】(1)推导出//PQ DC ,由此能证明//CD 平面PQR .(2)推导//RQ AB ,//PQ CD ,且12RQ AB =,12PQ CD =,从而RQ BD ⊥,PQ RQ ⊥,进而RQ ⊥平面BCD ,由此能证明平面ABD ⊥平面BCD .【详解】 证明:(1)点P ,Q 分别为棱BC ,BD 的中点,//PQ DC ∴,PQ ⊂平面PQR ,CD ⊂/平面PQR ,//CD ∴平面PQR .(2)点P ,Q ,R 分别为棱BC ,BD ,AD 的中点,//RQ AB ∴,//PQ CD ,且12RQ AB =,12PQ CD =, AB BD ⊥,RQ BD ∴⊥,2AB =,3PR =,22CD =.112RQ AB ∴==,122PQ CD ==, 222PQ QR PR ∴+=,PQ RQ ∴⊥, BD PQ Q ⋂=,RQ ∴⊥平面BCD , RQ ⊂平面ABD ,∴平面ABD ⊥平面BCD .【点睛】思路点睛:证明线面平行、面面垂直的常见思路:(1)证明线面平行的思路:通过三角形中位线或者证明平行四边形说明线线平行或者证明面面平行;(2)证明面面垂直的思路:证明线面垂直结合面面垂直的判定定理完成证明. 20.(1)证明见解析;(2)23913【分析】(1)根据题意可得1A D AC ⊥,由面面垂直的性质定理可得1A D ⊥平面ABC ,再由面面垂直的判定定理即可证明.(2)过点1C 作1C F AC ⊥的延长线于点F ,连接BF ,利用等体积法11113C ABC A ABC ABC V V S AD --∴==⋅△,即可求出点C 到平面1ABC 的距离.【详解】(1)证明:1AA AC =,160AAC ∠=︒, 1ACA ∴△是等边三角形,D 为线段AC 的中点, 1A D AC ∴⊥,平面11AA C C ⊥平面ABC ,平面11AAC C平面ABC AC =,1A D ∴⊥平面ABC , 1A D ⊂平面1A DE , ∴平面1A DE ⊥平面ABC ;(2)解:过点1C 作1C F AC ⊥的延长线于点F ,连接BF ,可得1C F ⊥平面ABC ,且13C F =11113C ABC A ABC ABC V V S A D --∴==⋅△113223132=⨯⨯⨯=, 在1ABC 中,2AB =,()2222113323C F AF AC +=+==21122221BF C F BD DF C F BC +=++===22212cos 20ABC +-∠∠==1sin ABC ∴∠=122202ABC S ∴=⨯=△.记点C 到平面1ABC 的距离为h ,则113ABC S h ⋅⋅=△,解得13h =,即点C 到平面1ABC 【点睛】关键点点睛:本题考查了面面垂直的证明、求点到面的距离,解题的关键“等体积法”解题方法的应用,考查了计算能力.21.(1)证明见解析;(2)4. 【分析】(1)根据线面垂直的判定定理可证得BD ⊥平面PAC ,再由面面垂直的判定定理可得证.(2)由(1)知BD ⊥平面PAC ,根据三角形的面积公式求得()min 32OE =,作//EH PA 交AC 于H ,可得EH ⊥平面ABCD ,从而求得点E 到底面ABCD 的距离. 【详解】(1)证明:∵四边形ABCD 是菱形,∴AC BD ⊥.PA ⊥平面ABCD ,BD ⊂平面ABCD ,∴PA BD ⊥.又PA AC A =,∴BD ⊥平面PAC ,又BD ⊂平面BDE ,∴平面BDE ⊥平面PAC .(2)解:如图(1),连接OE ,由(1)知BD ⊥平面PAC ,OE ⊂平面PAC .BD OE ∴⊥.∵8BD =,由()min 162BDE S BD OE =⋅⋅=△,得()min 32OE =,∵当OE PC ⊥时,OE 取到最小值32,此时2CE ===. 作//EH PA 交AC 于H ,∵PA ⊥平面ABCD ,∴EH ⊥平面ABCD ,如图(2),由33OE CE EH OC ⋅==,得点E 到底面ABCD 的距离33.【点睛】本题考查线面垂直的判定和面面垂直的判定定理,以及求点到面的距离,关键在于逐一满足判定定理所需的条件,在求点到面的距离时,可以采用几何法,由题目的条件直接过已知点作出面的垂线,运用求解三角形的知识,求点到面的距离,属于中档题. 22.(133a ;(2)证明见解析;(3)证明见解析. 【分析】(1)根据三棱锥的体积公式计算;(2)证明AC 与EF 和DF 垂直,然后可得线面垂直;(3)连接CM 交DE 于点H ,证明//MN FH 即可得线面平行. 【详解】(1)由题意234BCD S a =△,231133·33412D ABC A DBC DBCV V SAB a a a --===⨯⨯=; (2)由AB ⊥平面BCD ,得,AB BC AB BD ⊥⊥,AB BC a ==,则2AC AD a ==,如图,在ADC 中,取CD 中点G ,连接AG ,则AG DC ⊥, ∵3AF FC =,∴24CF a=,又12CG a =, ∴CF CDCG CA =,C ∠公用,∴CDF ∽CAG ,∴90CFD CGA ∠=∠=︒,即AC DF ⊥,取AC 中点K ,连接BK ,则BK AC ⊥, 又由3AF FC =得12CF CK =,而12CE CB =,∴//EF BK ,∴EF AC ⊥,EF DF F =,∴AC ⊥平面DEF ;(3)连接CM 交DE 于点H ,∵,M E 分别是,BD BC 中点,∴H 是DBC △的重心,23CH CM =,又38CN AC =,14CF AC =,∴23CF CN =,即CF CH CN CM =, ∴//HF MN ,HF ⊂平面DEF ,MN ⊄平面DEF ,∴//MN 平面DEF .【点睛】关键点点睛:本题考查求棱锥的体积,考查证明线在垂直与线面平行,掌握线面平行与垂直的判定定理是解题关键.证明时定理的条件缺一不可,一般都需一一证明列举出来,才能得出相应的结论. 23.(1)证明见解析,(23【分析】(1)取AC 的中点O ,连接,PO BO ,可得,PO AC BO AC ⊥⊥,再由线面垂直的判定定理可得AC ⊥平面POB ,从而可证得AC PB ⊥;(2)求解三角形证明PO OB ⊥,可得PO ⊥平面ABC ,利用等体积法求得结果 【详解】(1)证明:取AC 的中点O ,连接,PO BO , 因为1PA PC ==,AB BC =, 所以,PO AC BO AC ⊥⊥,因为PO OB O =,所以AC ⊥平面POB , 因为PB 在平面POB 内,所以AC PB ⊥,(2)解:在PAC △中,因为1PA PC ==,60APC ∠=︒, 所以32PO =,1AC =, 在ABC 中,因为AB BC =,90ABC ∠=︒,所以12BO =, 在PBO 中,由于3PO =,12BO =,1AC PB ==,所以222PO BO PB +=,所以PO OB ⊥, 因为 ,PO AC BOAC O ⊥=,所以PO ⊥平面ABC ,所以111331322224A PBC P ABC V V --==⨯⨯⨯⨯=【点睛】此题的两个等腰三角形有相同的底,所以利用等腰三角形“三线合一”的性质可证得线线垂直,再利用了线面垂直的判定和性质,由于三棱锥A PBC -的体积不易求解,所以利用等体积法求三棱锥A PBC -的体积,此题考查数学转化思想 24.(1)证明见解析;(2)14【分析】(1)由余弦定理可得23BD =,证得AD BD ⊥,则BC BD ⊥由PD ⊥底面ABCD ,BC ⊂平面ABCD ,证得PD BC ⊥,得证.(2)Q 为PC 的中点,利用等积法12D PBQ D BCQ Q BCD P BCD V V V V ----=== ,即可求出结果. 【详解】(1) 在ABD △中,由余弦定理得2222cos 3BD BA AD BA AD DAB =+-⋅∠=, ∵222AD BD AB +=,∴AD BD ⊥,∵//AD BC ,∴BC BD ⊥.又∵PD ⊥底面ABCD ,BC ⊂平面ABCD ∴PD BC ⊥.∵PD BD D ⋂=,∴BC ⊥平面PBD .(2)因为Q 为PC 的中点,所以三棱锥D PBQ -的体积A PBQ V -, 与三棱锥D QBC -的体积相等,即1111313232412D PBQ D BCQ Q BCD P BCD V V V V ----=⨯⨯====. 所以三棱锥A PBQ -的体积14D PBQ V -=.【点睛】本题主要考查了线面垂直的证明,在含有长度时需要解三角形来证垂直,并且不要忘记线面垂直的性质运用,在求三棱锥的体积时注意等体积法的使用 25.(1)E 为PD 的中点;(2)24.【分析】(1)E 为PD 的中点,连接BD 交AC 于点O ,连接OE ,则//OE PB ,故而//PB 平面AEC ;(2)点E 到平面PAC 距离等于点D 到平面PAC 距离的12倍,由1122E PAC D PAC P ACD V V V ---==可得答案.【详解】(1)E 为PD 的中点.证明:连接BD ,使AC 交BD 于点O ,取PD 的中点为E ,连接EO , ∵O ,E 分别为BD ,PD 的中点, ∴//OE PB .又OE ⊂平面AEC ,PB ⊄平面AEC , ∴//PB 平面AEC . (2)222AC PC PA =-=,∴222AB BC AC +=,∴AB BC ⊥,即菱形ABCD 为正方形.又点E 到平面PAC 距离等于点D 到平面PAC 距离的12倍, 设点E 到平面PAC 的距离为h , ∴1122E PAC D PAC P ACD V V V ---==, 111111211132322h ⎛⎫⎛⎫⨯⨯⨯⋅=⨯⨯⨯⨯⨯ ⎪ ⎪⎝⎭⎝⎭解得24h =. 【点睛】本题考查了线面平行的判定,等体积法求棱锥的高,属于基础题. 26.(1)证明见解析;(2)证明见解析;(3)83. 【分析】(1)由线面垂直判定定理,要证线面垂直,需证AD 垂直平面PBE 内两条相交直线,由,E 是AD 的中点,易得AD 垂直于,再由底面是菱形,得三角形为正三角形,所以AD垂直于PA,(2)由线面平行判定定理,要证线面平行,需证PC平行于平面内一条直线,根据1h是的中点,联想到取AC中点O所以OQ为△PAC中位线.所以OQ // PA注意在写定理条件时,不能省,要全面.例如,线面垂直判定定理中有五个条件,线线垂直两个,相交一个,线在面内两个;线面平行判定定理中有三个条件,平行一个,线在面内一个,线在面外一个,(3)研究体积问题关键在于确定高,由于两个底面共面,所以求的值就转化为求对应高的长度比.【详解】(1)因为E是AD的中点,PA=PD,所以AD⊥PE.因为底面ABCD是菱形,∠BAD=,所以AB=BD,又因为E是AD的中点,所以AD⊥BE.因为PE∩BE=E,所以AD⊥平面PBE.(2)连接AC交BD于点O,连结OQ.因为O是AC中点,Q是PC的中点,所以OQ为△PAC中位线.所以OQ//PA.因为PA 平面BDQ,OQ平面BDQ.所以PA//平面BDQ.(3)设四棱锥P-BCDE,Q-ABCD的高分别为2h,1h,所以V P-BCDE=13S BCDE2h,V Q-ABCD=13S ABCD1h.因为V P-BCDE=2V Q-ABCD,且底面积S BCDE=S ABCD.所以,因为,所以.。
计算机图形图像处理(Photoshop CS2中级)中级_试题汇编
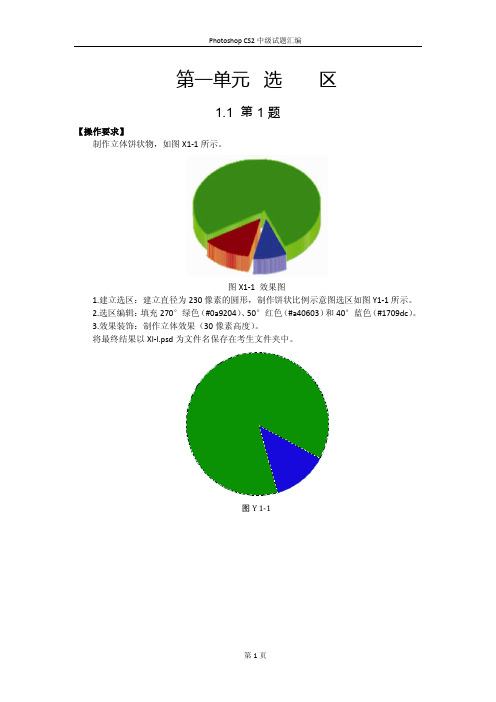
第一单元选区1.1 第1题【操作要求】制作立体饼状物,如图X1-1所示。
图X1-1 效果图1.建立选区:建立直径为230像素的圆形,制作饼状比例示意图选区如图Y1-1所示。
2.选区编辑:填充270°绿色(#0a9204)、50°红色(#a40603)和40°蓝色(#1709dc)。
3.效果装饰:制作立体效果(30像素高度)。
将最终结果以Xl-l.psd为文件名保存在考生文件夹中。
图Y 1-1【操作要求】合成窗外风景效果,如图X1-2所示。
图X1-2 效果图1.建立选区:打开C:\2007PS\Unit1\window.jpg和green.jpg素材文件,如图所示。
2.选区编辑:把风景图像合成到窗口。
3.效果装饰:调整透过窗口看到两棵大树的位置。
将最终结果以X1-2.psd为文件名保存在考生文件夹中。
【操作要求】制作连体字,如图X1-3所示。
图1-3 效果图1.建立选区:输入130像素、宋体、斜体字符“2(#340fea)、0(#74ebef)、0(#86e32e)、0(#ecec00)”并做立体化处理,如图Y1-3所示。
2.选区编辑:制作相互嵌套的连环字符。
3.效果装饰:添加红色(#d7042f)前景。
将最终结果以X1-3.psd为文件名保存在考生文件夹中。
图Y1-3【操作要求】制作三色谱,如图X1-4所示。
图X1-4效果图1.建立选区:制作直径为85像素的红色(#f60400)、绿色(#08fb01)和蓝色(#0100fe)三个圆形,如图Y1-4所示。
2.选区编辑:将红蓝圆形选区交集填充为洋红色(f7004fe)、将红绿圆形相交处填充为黄色(#feff01)、将绿蓝圆形相交处填充为青色(#09fbff),将红绿蓝三圆相交处填充为白色(#ffffff)。
3.效果装饰:调整圆形交集大小等比,并且调整圆形至圆心处位置。
将最终结果以X1-4. psd为文件名保存在考生文件夹中。
CS2--案例实操笔记资料

CS2 实操笔录选区 =X1-绘画=X2-图像=X3-画图=X4-图层=X5-滤镜=X6-网页=X7-应用=X8-X1-1 练习题图(饼状切三角)1.快捷键 Ctrl+N= 新建,宽度300 像素,高度300 像素,分辨率为200, RGB 颜色,背景为白色的文件。
2.新建图层3.快捷键 Ctrl+R= 标尺(单位设置:编写 --- 首选项 --- 单位与标尺,把标尺改为像素,宽度与高度改为厘米)4. 点椭圆选框工具,将“款式”点为“固定大小”宽度设230PX ,高度 230PX5. 点椭圆选框工具,鼠标放在标尺中心,当十字都变为红色时,按Ctrl+ Shift ,点鼠标左键,画出固定大小的圆6. 点前风景,颜色,绿色( #0a9204),填补前风景 Alt + 删除 .7. 点矩形选框工具,选中右下角四分之一处,按删除键, Ctrl+D8.按 Ctrl ,选中缩略图, Ctrl+J= 复制选区图层,按二下,生成两个图层9. 按 Ctrl ,选中第二个图层缩略图,填补前风景红色(#a40603),将第一个图层眼睛去掉,显示出红色10. 撤消选区 Ctrl+D , Ctrl+T ,设置旋转度数为 -50,按回车。
11. 将图层 2 的眼睛去掉,按 Ctrl ,选中第三个图层缩略图,填补前风景蓝色(#1709dc) Ctrl+T ,设置旋转度数为40,按回车。
把上两个图层的眼睛都显示。
12.点中最顶的图层, Ctrl+E ,点两下,归并为一个图层。
13.点魔棒,选中图层, Ctrl+T ,设置旋转度数为 60,回车14. Ctrl+T ,点下中点,把图层压扁。
撤消选区Ctrl+D15. 点魔棒,选红色选区,用挪动工具,把红选区合适拉出。
16. 点魔棒,选蓝色选区,用挪动工具,把蓝选区合适拉出。
17.归并所有图层,再挪动复制18. 点魔棒,选中整个图层,用挪动工具,Alt +向上箭头,撤消选区Ctrl+D19. ctrl+H,隐蔽标尺线20.保留:命名为 X1-1.psd 。
(全优)湘教版八年级下册数学第3章 图形与坐标含答案

湘教版八年级下册数学第3章图形与坐标含答案一、单选题(共15题,共计45分)1、如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(﹣1,0),B(﹣2,3),C(﹣3,1).将△ABC沿y轴翻折得到△A′B′C′,则点B′的坐标为()A.(2,1)B.(2,3)C.(4,1)D.(0,2)2、在平面直角坐标系中,点A的坐标是(3,a),点B的坐标是(b,-1),若点A与点B关于原点O对称,则ab=( )A.3B.2C.-6D.-33、在平面直角坐标系中,点为,连接并把线段绕原点逆时针旋转90°,所得到的对应点的坐标为()A. B. C. D.4、在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,………按这样的规律进行下去,第2012个正方形的面积为()A. B. C. D.5、如果p(a-3,a+1)在第二象限,那么a的取值范围是A.a>-1B.a<3C.-3<a<3D.-1<a<36、若,则点P(x,y)一定在A.x轴上.B.y轴上.C.坐标轴上.D.原点.7、如图,正方形OABC对角线交点为D,过D的直线分别交AB,OC于E,F,已知点E关于y轴的对称点坐标为(﹣,2),则图中阴影部分的面积是()A.1B.2C.3D.48、平面直角坐标系中,点A的坐标为(4,3),将线段OA绕原点O顺时针旋转90°得到OA',则点A'的坐标是A.(-4,3)B.(-3,4)C.(3,4)D.(4,-3)9、如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,3),M是第三象限内上一点,∠BMO=120°,则⊙C的半径长为()A.6B.5C.3D.310、在平面直角坐标系中,点关于轴对称的点的坐标是()A. B. C. D.11、在平面直角坐标系中,将点P(-2,3)沿X轴方向向右平移3个单位得到点Q,则点Q的坐标是()A.(-2,6)B.(-2,0)C.(-5,3 )D.(1,3)12、点P(a , b)关于x轴的对称点为P'(1,-6),则a , b的值分别为( )A.-1,6B.-1,-6C.1,-6D.1,613、点P(-3,5)所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限14、点C在x轴的下方,y轴的右侧,距离x轴3个单位长度,距离y轴5个单位长度,则点C的坐标为().A.(-3,5)B.(3,-5)C.(5,-3)D.(-5,3)15、如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交X轴于点M,交Y轴于点N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(3a-1,b),则a与b的数量关系为()A. B. C. D.二、填空题(共10题,共计30分)16、如图,在直角坐标系中,点A,B的坐标分别为(1,4)和(3,0),点C 是y轴上的一个动点,且A,B,C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是________.17、如图,在平面直角坐标系xOy中,点A1, A2, A3,…,An在x轴的正半轴上,且OA1=2,OA2=2OA1, OA3=2OA2,…,OAn=2OAn﹣1,点B1, B2,B 3,…,Bn在第一象限的角平分线l上,且A1B1, A2B2,…,AnBn都与射线l垂直,则B1的坐标是________,B3的坐标是________,Bn的坐标是________.18、如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向不断地移动,每次移动1个单位长度,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…,那么点A2 019的坐标为________.19、在平面直角坐标系中,点A(0,-4)到x轴的距离为________.20、在平面直角坐标系xOy中,已知直线l:y=x,作A1(1,0)关于y=x 的对称点B1,将点B1向右水平平移2个单位得到点A2;再作A2关于y=x的对称点B2,将点B2向右水平平移2个单位得到点A3;….请继续操作并探究:点A3的坐标是________,点B2014的坐标是________.21、在平面直角坐标系xOy中,已知A(0,1),B(1,0),C(3,1),若以A、B、C、D为顶点的四边形是平行四边形,则点D的坐标是________.22、把点P(1,1)向右平移3个单位长度,再向上平移2个单位长度后的坐标为________.23、如图,在平面直角坐标系中,将点P(-4,2)绕原点顺时针旋转90°,则其对应点Q的坐标为________.24、若A(1,2),B(3,﹣3),C(x,y)三点可以确定一个圆,则x、y需要满足的条件是________.25、如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B的坐标分别为(-3,0),(2,0),点D在y轴上,则点C的坐标是________.三、解答题(共5题,共计25分)26、已知点A 和点B 关于轴对称,求的值.27、多多和爸爸、妈妈周末到动物园游玩,回到家后,她利用平面直角坐标系画出了动物园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴、y 轴.只知道马场的坐标为(﹣1,﹣2),你能帮她建立平面直角坐标系并求出其他各景点的坐标?(图中每个小正方形的边长为1 )28、已知四边形AOCD是放置在平面直角坐标系内的梯形,其中O是坐标原点,点A,C,D的坐标分别为(0,8),(5,0),(3,8).若点P在梯形内,且△PAD的面积等于△POC的面积,△PAO的面积等于△PCD的面积. 求点P的坐标.29、在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如图所示.(1)填写下列各点的坐标:A4(,),A8(,),A12(,);(2)写出点A4n的坐标(n是正整数)(,);(3)指出蚂蚁从点A2014到点A2015的移动方向为.30、如图的方格中有25个汉字,如四1表示“天”,请沿着以下路径去寻找你的礼物:(1)一1→三2→二4→四3→五1(2)五3→二1→二3→一5→三4(3)四5→四1→一2→三3→五2.参考答案一、单选题(共15题,共计45分)1、B2、D3、D4、D5、D6、C7、B8、C9、C10、C11、D12、D13、B14、C15、A二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)26、29、30、。
PhotoshopCS2工具与绘图

3)选择工具箱中的 (渐变工具),渐变类型
选择
(线性渐变),然后在图像工作区
中从上往下进行拖拉,结果如图3-21所示。
4)选择工具栏中的 选择画笔模式为
(历史记录画笔工具), ,然后在图像上拖动鼠标,
结果如图3-22所示
2)在“画笔名称”对话框 中输入画笔名称,如图36所示。
3)对新建的画笔进行参数 设置。
自定义特殊画笔的方法:
1)打开一幅图像,并建立选区。 2)执行菜单中的“编辑” →“定义画笔
预设”命令,在弹出的“画笔名称”对 话框输入画笔名称。 3)此时,在画笔面板中出现一新画笔。可 对其进行画笔设置绘制图像。
3.1.2 铅笔工具
(铅笔工具):常用来画一些棱角突 出的线条。使用方法和画笔工具类似,只 不过 (铅笔工具)工具栏中的画笔都是 硬边的,如图3-18所示。
3.1.2 铅笔工具
铅笔工具有一个特有的“自动抹掉”复选框。 作用:此项被选中后,铅笔工具可实现擦除的 功能。即在与前景色颜色相同的图像区域中绘 图时,会自动擦除前景色而填入背景色。
图3-13为不同间距值的比较。
角度:设置画笔角度。 变化范围为-180~180。
圆度:用于控制椭圆形 画笔长轴和短轴的比例 。变化范围为0~100。
3)除了设置上述参数外, 还可以设置画笔的纹理 效果、“动态形状”、 “散布”、“双重画笔” 等效果。
4. 保存、载入、删除和复位画笔
(1)保存画笔 为方便以后使用,可将整个画笔面板
4. 保存、载入、删除和复位画笔
(3)删除画笔 方法:在画笔面板中选择画笔,单击右键, 从弹出的快捷菜单中选择“删除画笔”命令。 或者将要删除的画笔拖到 (删除画笔)按 钮上即可。
高新技术考试photoshopCS2试题解答第二单元绘画

第二单元绘画2.1第1题解答(1)打开C:\2007PS\Unit2\wood.jpg素材图,如图2-1-1所示,提取色彩'便川 1 大的褐色硬笔刷,在轮廓范用内尝试笔刷的色彩。
(2)分别使用不同方向的笔刷进•步描绘格个木板表面和断面,如图厶1・2丿办小。
图2-1-1尝试色彩图2-1-2描绘整个木板(3)使用一些较小的笔刷放大图像细部,勾画木板的边缘,细致描绘木板边缘破裂部分,形成陈旧木板效果。
用较明亮的色彩表现灯光效果,用较暗的笔刷表现阴暗区域,如图2-1-3所示。
(4)使用较小的笔刷在小范围内描绘更形木板的裂纹结构,勾忸木纹直线纹理,注意图2-1-3破裂部分图2亠4明暗变化(5)继续使用-些散射效果、尖头、不规则粗糙笔刷添加纹理效果,建立•个新图层,使用30%透明度,进一步绘制木板的明亮及阴暗区域增强立体效果,如图2」・5所示。
(6)做-些覆盖工作,在--个新图层上使用40%透明度自然较长笔刷’描绘一•些尖锐的笔触,如图2-1-6所示。
第:单・元绘刚图2-1-5立体效果图2・1・6细致纹理(7)将最终结果以X2-l.psd为文件名保存在考生文件夹中。
2.2第2题解答(1)打开C:\2007PS\Unit2\girl.jpg 素材图•如图2-2-1 所示。
(2)新建一个2cmX2cm的小文件,选择铅笔工具用黑色点儿2 •般设定笔头大小为1〜3像素之间比较适合,如图2-2-2所示。
图2-2-1素材图图222设理笔刷(3)执行“编轿” > “定义画笔”命令,左义画笔,依照同样方法再定义儿个不同大小、不同方向的画笔.如图2・2・3所示。
(4)使用画笔工具,启用“喷枪模式为“正片叠底流屋为56%,选择稍大点的定义笔刷,将画笔间距设置为1%,卜面画笔依照此设置。
用黑色在头发暗部刷儿F. •般靠发根的地方比较暗,如图2-2-4所示。
2-2-4幽发根图2-2-3定义刚笔—乡"图形图像处理(Photoshop平台)PhoioshopCS2试题解逬 --------------- --------(5)再选择淡点的颜色,换个稍小的笔刷,画出发梢,如图2・2・5所示,第•遍墓本冗成后,再用“模糊”工具在发梢处涂抹。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、打开house1.jpg素材图。
执行“图像”->“模式”-> “RGB彩色”命令,把当前灰度模式文件转换为RGB彩色模式。
2、用“多边形套索”工具选择蓝天部分,执行“图像”->“调整”-> “色相/饱和度”命令。
选择“着色”,设置色相:220;饱和度:50;明度:0。
原来灰色的天空变成蔚蓝色。
3、用“魔棒工具”选择图像最下部的植物(注意设置魔棒工具的选项:选区的加减,容差,连续等),执行“图像”->“调整”-> “色相/饱和度”命令。
选择“着色”,设置色相:130;饱和度:25;明度:0。
原来灰色的植物变成绿色。
4、用“魔棒工具”选择图像中部的墙体,执行“图像”->“调整”-> “色相/饱和度”命令。
选择“着色”,设置色相:40;饱和度:45;明度:0。
原来灰色的墙面变成浅黄色。
4、用“魔棒工具”选择图像中部的墙体,执行“图像”->“调整”-> “色相/饱和度”命令。
选择“着色”,设置色相:40;饱和度:45;明度:0。
原来灰色的墙面变成浅黄色。
4、用“魔棒工具”和“套索工具”选择图像墙上的木头,执行“图像”->“调整”-> “色相/饱和度”命令。
选择“着色”,设置色相:30;饱和度:25;明度:0。
原来黑色的木头变成暗红色。
1、打开car1.jpg素材图2、用磁性套索工具选择跑车的蓝色油漆部分。
3、新建“图层1”,填充为红色。
4、设置图层的混合模式为“颜色”,填充部分只是更换了颜色,继承了原有的饱和度和明暗区域等。
3.31、打开shi.jpg素材图,打开“图像”->“画布大小”,选择“相对”,向左,宽度为218,高度为0。
得到加宽2倍画布尺寸。
2、复制柿子图像到一个新图层。
3、在新图层中,选择整个柿子图形,再设置选区运输为减法,用磁性套索功能根据选择柿子叶柄处。
保证叶柄不被选中。
4、执行“图像”->“调整”-> “替换颜色”命令,用吸管工具点取绿色区域,颜色容差设为120,色相为-79,饱和度为70,明度为0。
得到红色效果。
5、取消选区,绿色柿子变为红色柿子。
1、打开Cloud.jpg素材图。
2、执行“图像”->“调整”-> “反相”命令,将图像的颜色反相。
3、执行“图像”->“调整”-> “替色阶”命令,设置如下输入色阶:0 0.2 255;输出色阶:0 2554、执行“图像”->“调整”-> “色相/饱和度”命令,选择“着色”,设置如下色相:236;饱和度:53;明度:-1出现蓝色闪光效果。
3.51、打开“blood.jpg”文件。
2、执行“图像”->“调整”-> “色相/饱和度”命令,不选择“着色”,设置如下:色相:;饱和度:+100;明度:+83、复制背景层,将复制的图层混合模式设为“叠加”。
1、打开crosse.jpg素材图2、使用魔棒工具选择填空背景。
3、设置前景色为(#321FF7),背景色为(#FFB98E),使用线性渐变,设置从前景色到背景色状态,在图像选区内从上至下拖拉,填充渐变色。
4、可以使用“图像”->“调整”-> “亮度/对比度”命令,亮度为0,对比度为+20,增加对比度。
5、执行“选择”->“方向”命令,反转选区,选择街道与路灯等物体。
6、“图像”->“调整”-> “去色”命令。
7、选择铅笔,设置画笔大小为1~2像素,前景色为白色,在图像的背景填空随机点些两点作为星空。
3.71、新建大小为240*160像素的文件,前景色为黑色,背景色为白色,填充黑色。
2、执行“滤镜”->“素描”-> “绘图笔”命令,参数设置:线条长度为15、明/暗平衡为40、描边方向为垂直。
3、执行“图像”->“图像大小”-> 命令,参数设置:图像高度为1像素,宽度不变。
4、由于图像存在灰度等级,为了只保留黑白二色。
执行“图像”->“调整”-> “亮度/对比度”命令,参数设置:对比度为+100,亮度为0.5、全部选择黑白色条,执行“编辑”-> “定义图案”命令,定义图案。
再新建大小为240*160像素的文件,执行“编辑”->“填充”命令,用定义图案进行填充。
3.81、打开tower.jpg素材图2、执行“图像”->“调整”-> “色相/饱和度”命令,选择“着色”,参数设置为:色相为0,饱和度为60,明度为0.3、使用多边形套索工具建立顶部选区。
4、删除选区。
3.91、打开flower.jpg素材图。
2、执行“图像”->“调整”-> “曲线”命令,调整曲线为图像加亮,加亮的同时压制图片的暗部,增强影调的对比,为配合高光与暗部的调整将中间调适当上调。
3、执行“图像”->“调整”-> “可选颜色”命令,控制每种颜色的黑色成分,分别对图片的3个主要色彩进行混合,也就是花瓣的红色,花蕊的黄色和叶子的绿色。
4、执行“图像”->“调整”-> “曲线”命令,选择“设置黑场”吸管工具,在花朵背景处单击,使背景模糊,花朵更加鲜艳锐化。
3.101、打开dog.jpg素材图。
2、执行“滤镜”->“消失点”命令。
选择“创建平面工具”,在图像中单击4个点,在图像中定义透视平面。
Photoshop将以蓝色显示网格。
3、使用矩形选框工具框选透视平面,按Alt键,拖动选区覆盖到刷子上。
在对话框顶部选择“修复”选项,选区就会无缝过渡复制到周围环境中,并且保持透视效果。
4、用同样的方法复制地板并去掉绳子。
5、应用“消失点”命令。
3.111、打开flower1.jpg素材图。
并将背景图层进行复制2、在背景图层上,执行“图像”->“调整”-> “去色”命令。
再执行“图像”->“调整”-> “色阶”命令,参数设置:输入色阶为15 1.00 200;输出色阶为0 255。
以此增加黑白对比。
3、执行“图像”->“调整”-> “反相”命令。
执行“图像”->“调整”-> “高斯模糊”命令,半径设置为1像素。
再执行“滤镜”->“画笔描边”-> “喷溅”命令,喷色半径为2,平滑度为1。
4、新建图层1,设置图层混合模式为颜色,用红色画笔涂抹荷花。
3.121、打开water.jpg素材图。
2、执行“图像”->“调整”-> “曲线”命令,参数设置为:输入109,输出1413、执行“图像”->“调整”-> “色彩平衡”命令,参数设置为:暗调色阶为0 0 100;中间调色阶为-100 0 0;高光色阶为0 30 1004、执行“图像”->“画布大小”命令。
宽度450像素不变,高度改为600像素,空白处填充深蓝色。
5、描白色边框12像素,添加阴影和文字“海景“。
3.131、打开cat.jpg素材。
2、在图层面板中单击“创建新的填充或调整图层“按钮,选择”照片滤镜“命令,参数设置:滤镜为冷却滤镜(82),浓度为70%,保留亮度。
3、将图层合并,使用多边形套索工具,选择猫的五官区域,按CTRL+J键将选区新建为“图层1”。
4、指背景图层上,执行“图像”->“调整”-> “色阶”命令,选择“设置白场”吸管工具,在小猫毛发位置单击取样。
5、将“图层1”图层混合模式改为“柔光”,执行“图像”->“调整”-> “色相/饱和度”命令,参数设置为:色相为-8,饱和度为33,明度为0,。
6、选择“橡皮擦工具”,使用合适笔触及不透明度,将“图层1”小猫五官取样多余部分擦除。
3.141、打开photo.jpg素材图。
2、执行“滤镜”-> “消失点”命令,使用“创建平面工具”,在图像中单击4个点定义“栏杆”区域。
如果透视正确,photoshop将显示蓝色网格,如果是黄色或红色框线说明透视平面不够正确,需要调整。
3、设置好透视网格后,选择图章工具,在蓝色网格内,按ALT键单击取得源图像,松开ALT键,在人物图像上单击,按照透视角度复制图像,无缝过渡复制融合到周围环境中。
3.151、打开tree.jpg素材图。
2.复制背景图层,重新命名为“树”,执行“图像”->“调整”-> “阈值”命令,阈值色阶为117。
用魔棒工具选取背景白色,全部清除。
3、选择背景图层,在图层面板上,单击“创建新的填充或调整图层”按钮,建立“渐变层填充”图层,在渐变填充编辑器中,设置前景色为#fa01bd,背景色为#f9d706的线性渐变。
4、如果树的边缘有白边,执行“图层”->“修边”-> “去除白边”命令。
3.161、打开leaf.jpg素材图,复制图层。
2、执行“图像”->“调整”-> “阈值”命令,阈值色阶设置为128。
3、用橡皮擦工具将多余的建筑擦去,用魔棒工具选取白色背景,全部清除。
4、选择背景图层,在图层面板上,单击“创建新的填充或调整图层”按钮,建立“渐变层填充”图层,在渐变填充编辑器中,设置前景色为#fcad51,背景色为#fc6a05的线性渐变。
5、如果树的边缘有白边,执行“图层”->“修边”-> “去除白边”命令。
6、装饰飞鸟、夕阳,添加文字“SAFARI SKIES”.3.171、打开house.jpg图像,转换为RGB模式。
2、将屋顶调整为红褐色:使用魔棒工具,配合shift键,选择图片中屋顶区域,执行“选择”->“羽化”羽化,设置2像素。
执行“图像”->“调整”-> “色彩平衡”命令,设置中间调,色阶为39 -19 -44。
3、将树木调整为绿色:用魔棒工具选择图中树木,按CTRL+B ,进行“色彩平衡”命令,给树木添加绿色。
4、将门窗调整为桔红色:用多边形套索工具将门窗选中,按CTRL+B,进行“色彩平衡”,设置阴影,色阶为12 0 0。
5、将天空调整为蓝色:用魔棒工具将天空区域选中,按CTRL+B,进行“色彩平衡”,将选区调整为蓝色。
6、执行“图像”->“调整”-> “色相/饱和度”命令,设置:色相为0,饱和度为15,明度为0。
增加图像的亮度。
3.181、打开woman.jpg人物图像。
2、使用“仿制图章工具”、“修复画笔工具”和“橡皮擦工具”将眉毛进行细化处理。
3、使用“修复画笔工具”抹平眼袋和眼角皱纹。
4、使用“污点修复工具”或“修复画笔工具”修复脸部瑕疵部位。
5、使用“画笔工具”或“减淡工具”亮白化牙齿处理。
5、使用“仿制图章工具”,复制头发遮盖耳朵。
3.191、打开skin.jpg人物脸部图像。
2、选择“污点修复工具”或“修复画笔工具”,设置画笔:直径为20px,硬度为0%,间距为25%,角度为0度,圆度为100%,大小为钢笔压力。
