匀变速直线运动规律推论1
匀变速直线运动公式推论推导及规律总结
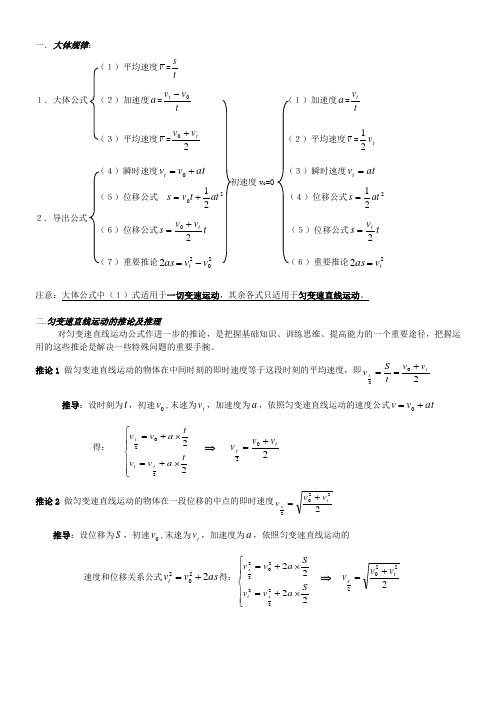
一.大体规律:v =ts 1.大体公式a =t v v t 0-a =tvtv =20t v v + v =t v 21at v v t +=0 at v t =021at t v s +=221at s = t v v s t 20+= t vs t 2= 2022v v as t -= 22t v as =注意:大体公式中(1)式适用于一切变速运动,其余各式只适用于匀变速直线运动。
二.匀变速直线运动的推论及推理对匀变速直线运动公式作进一步的推论,是把握基础知识、训练思维、提高能力的一个重要途径,把握运用的这些推论是解决一些特殊问题的重要手腕。
推论1 做匀变速直线运动的物体在中间时刻的即时速度等于这段时刻的平均速度,即202tt v v t S v +==推导:设时刻为t ,初速0v ,末速为t v ,加速度为a ,依照匀变速直线运动的速度公式at v v +=0得: ⎪⎪⎩⎪⎪⎨⎧⨯+=⨯+=22202t a v v t a v v t t t ⇒ 202t t v v v += 推论2 做匀变速直线运动的物体在一段位移的中点的即时速度22202t s v v v +=推导:设位移为S ,初速0v ,末速为t v ,加速度为a ,依照匀变速直线运动的速度和位移关系公式as v v t 2202+=得:⎪⎪⎩⎪⎪⎨⎧⨯+=⨯+=22222222022S a v v S a v v s t s⇒ 22202t s v v v +=推论3 做匀变速直线运动的物体,若是在持续相等的时刻距离t 内的位移别离为1S 、2S 、 3S ……n S ,加速度为a ,那么=-=-=∆2312S S S S S……21at S S n n =-=-推导:设开始的速度是0v通过第一个时刻t 后的速度为at v v +=01,这一段时刻内的位移为20121at t v S +=, 通过第二个时刻t 后的速度为at v v +=022,这段时刻内的位移为202122321at t v at t v S +=+=通过第三个时刻t 后的速度为at v v +=023,这段时刻内的位移为202232521at t v at t v S +=+=…………………通过第n 个时刻t 后的速度为at nv v n +=0,这段时刻内的位移为202121221at n t v at t v S n n -+=+=- 则=-=-=∆2312S S S S S……21at S S n n =-=-点拨:只若是匀加速或匀减速运动,相邻的持续的相同的时刻内的位移之差,是一个与加速度a 与时刻“有关的恒量”.这也提供了一种加速度的测量的方式: 即2t Sa ∆=,只要测出相邻的相同时刻内的位移之差S ∆和t ,就容易测出加速度a 。
高一物理匀变速直线运动规律推论

匀变速直线运动推论公式:
1、任意两个连续相等时间间隔T内,位移之差 是常数,即△x=x2-x1=aT2。
拓展:△xMN=xM-xN=(M-N)aT2
的色泽和质感。蘑菇王子:“哇!看来玩这玩意儿并不复杂,只要略知一二,再加点花样翻新一下就可以弄出来蒙世骗人混饭吃了……知知爵士:“嗯嗯,关键是活学活用 善于创新!本人搞装潢的专业可是经过著名领袖亲传的.”蘑菇王子:“哈哈,学知识就需要你这种的革新态度!”知知爵士:“嗯嗯,谢谢学长鼓励,我真的感到无比自
例2、已知一物体做匀变速直线运动,加速度为 a,试证明在任意一段时间t内的平均速度等于该 段时间中点t/2时刻的瞬时速度。
证明:设物体在匀变速直线运动中,任意一段
时间t的初速度为v0,位t的为时t时移位间为移内vxxxv0t12a2t 中间时刻t/2的速度 联上得v间的均度2t立两内平速为以式v0vtv01212aatt
分别是x1和x2。
由运动学知识:
x1v0T12a2x2v1T12a2Tv10aTT
两个连续相等的时间T内的位移之差:
x x2 x1 (v1 v0 )T aT 2 因为T是个恒量,小车加速度也是恒量,因此 △x也是个恒量。
即:只要物体做匀变速直线运动,它在任意两 个连续相等的时间内的位移之差等于一个 .
匀变速直线运动 规律推论
1、速度公式: v=v0+at
2、位移 公式:
xv0t12a2t
3、位移 与速度关
v2v022ax
4、平均 速度:
v系12:(v0v)xt
例1、证明:物体做匀变速直线运动,在任意两 个连续相等的时间内的位移之差等于一个常数。
证明:设加速度为a,经过任意一点A的速度为
v0,从A点开始经两个连续相等的时间T的位移
高一物理匀变速直线运动规律推论

2
两个连续相等的时间T内的位移之差:
x x2 x1 (v1 v0 )T aT 2
因为T是个恒量,小车加速度也是恒量,因此 △x也是个恒量。 即:只要物体做匀变速直线运动,它在任意两 个连续相等的时间内的位移之差等于一个常数.
匀变速直线运动推论公式:
1、任意两个连续相等时间间隔T内,位移之差 是常数,即△x=x2-x1=aT2。 拓展:△xMN=xM-xN=(M-N)aT2
思考:物体拉动的条件?
(拉力大于最大静摩擦力) 说明:最大静摩擦力大于滑动摩擦力
思考:1只有静止的物体才受到静摩擦力的作用? 2静摩擦力一定是阻力?
二 滑动摩擦力 1定义:两个接触的物体,当一个物体在另一个物 体表面滑动的时候,会受到另一个物体阻碍它滑动 的力
2产生条件:①接触面粗糙②接触并挤压③ 发生相对滑动 3作用点:接触面间
支持力与压力属于弹力
4、绳的弹力:
A A
B
总结:绳的弹力方向总是 沿着绳并指向绳的收缩方向。 绳的弹力处处相等
拉力属于弹力
三、弹力有无判断
方法:撤去支撑物法
FN
假设法+共点力平衡法
FN
F
F
FN FN G FN FN G FNLeabharlann F不平衡G
不平衡
不平衡
四、弹力的大小
弹力的大小与物体 的形变有关,形变越大, 弹力越大,形变消失, 弹力随着消失
探究:探究静摩擦力的变化
器材:木块,砝码一盒,弹簧测力计,木板。
实验结论:静摩擦力随拉力的增大而增大,当拉力 达到某一数值时木块开始移动,拉力突然减小。
补充:静摩擦力是个聪明的力,不但大小随外力而 变化,方向也随外力方向变化而变,且有最大值。 6最大静摩擦力:(在数值上等于物体刚刚开始运动时的拉力) 静摩擦力的范围: 0<F≤Fmax
匀变速直线运动的规律(推论

速度和物体的加速度。 则物体在斜面上和水平面上有位移之比?
突然发现正前方有一辆自行车以4 m/s的速度做同方向的匀速直线运动,汽车立即关闭油门,做加速度大小为 的匀减速直线运动,汽 车恰好不碰上自行车。
突然发现正前方有一辆自行车以4 m/s的速度做同方向的匀速直线运动,汽车立即关闭油门,做加速度大小为 的匀减速直线运动,汽
求: 车恰好不碰上自行车。
4 m m,求物体的加速度a和相邻各1s始末的瞬时速度v 1 、 v 2 、v 3 2、判断匀变速直线运动的方法:
(1)钢球运动的加速度; (1) v= v0+at 速度均匀变化或 (加速度不变)
(3)照片上D球离C 球的距离. 2、初速度为零的匀变速直线运动,第一个 T s,第二个 T s,第三个 T s内的位移之比
(1) v= v0+at 速度均匀变化或 (加速度不变) 4、中间时刻、中间位置的瞬时速度
v-t图像解题和追及相遇问题
例1、物体由静止开始做匀加速直线运动, 当速度达到10m/s时,立即改做匀减速直 到停下,物体共运动20s,则物体的位移 为多少?
车恰好不碰上自行车。
思考:如果上题改为自行车、汽车同一地点同向运动,其它条件不变,什么时候相遇?什么时候相距最远?为多少?
(1) v= v0+at 速度均匀变化或 (加速度不变)
例3、一质点做匀减速运动,走过36 m后 停止,若将这位移分为三段,而且通过 每段的时间相等,试求第一段的长度。
作业:(要求:至少两种以上
s放下一颗使之做匀加速直线运动,在连续放下 4、中间时刻、中间位置的瞬时速度
匀变速直线运动公式及推论

x1:x2:x3::xn = 1 ::::n … 2 3 …
③第1 个T 内、第2 个T 内、第3 个T 内、… 、第n 个T 内, 位移之比为
xⅠ xⅡ: x Ⅲ: : x n = 1::: : 2 n − 1 ) : … 3 5 … (
④ 从静止开始通过连续相等的位移所用的时间之比为
1: 2 − 1): 3 − ( (
匀 变 速 直 线 运 动 公 式 及 推 论
v = v 0 + at 1 x = v0t + at 2 2 2 v − v 0 = 2 ax v v
t 22Biblioteka v0 + v = = v 2 = v
2 0
x 2
+ v 2
2
三个重要推论
• 推论 :加速度为a的匀变速直线运动在相 推论1:加速度为 的匀变速直线运动在相 邻的等时间T内的位移差都相等 内的位移差都相等, 邻的等时间 内的位移差都相等,即aT2。 • 推论2:某过程中间时刻的瞬时速度大小等 推论 : 于该过程的平均速度大小, 平均速度大小 于该过程的平均速度大小,即 v = v中时 =
2 ): : n − … (
n − 1)
s v 0 + vt = t 2
• 推论三: 推论三:
初速度为零 初速度为零的匀加速直线运动 1T秒末 2T秒末 3T秒末 秒末、 秒末、 秒末、 、nT秒末 秒末, ①1T秒末、2T秒末、3T秒末、…、nT秒末,速度之比 为
v1:v2:v3::vn = 1 2:…:n … :3 :
nT秒内 秒内, ②1T秒内、2T秒内、3T秒内、… 、nT秒内,位移之比 1T秒内、2T秒内、3T秒内、 秒内 秒内 秒内 2 2 2 2 为
匀变速直线运动规律常见推论及推理过程

匀变速直线运动规律常见推论及推理过程本文对匀变速直线运动的常见推论、以及相关推理过程进行归纳总结,结合相关示意图将推理过程详细呈现给读者,适合高一学生学习参考。
匀变速直线运动基本公式如下: at v v +=02021at t v x +=()t v v x +=021ax v v 2202=-常用推论: 一.适用于任意匀变速直线运动的推论1. 某段匀变速直线运动中间时刻瞬时速度与该过程的平均速度相等,且都等于初、末速度和的一半,即:()v v t x v v t +===02212. 任意匀变速直线运动相邻相等时间间隔内的位移之差都相等,都等于2aT ,即:212312aT x x x x x x x n n =-==-=-=∆-拓展结论:x m −x n =(m −n)aT 23. 某段匀变速直线运动中间位置的瞬时速度:22202v v v x +=二. 仅适用于初速度为零的匀加速直线运动的推论1. 从开始运动起,前1个T 末、前2个T 末、前3个T 末……前n 个T 末的瞬时速度之比为:n v v v v n ::3:2:1::::321 =;2. 从开始运动起,前1个T 内、前2个T 内、前3个T 内……前n 个T 内的位移之比为:2222321::3:2:1::::n x x x x n =;3. 从开始运动起,第1个T 内、第2个T 内、第3个T 内……第n 个T 内的位移之比为:x Ⅰ:x Ⅱ:x Ⅲ: … :x N =1:3:5: … : (2n-1);4. 从开始运动起,前1个x 末、前2个x 末、前3个x 末……前n 个x 末的瞬时速度之比为:n v v v v n ::3:2:1::::321 =;5. 从开始运动起,第1个x 内、第2个x 内、第3个x 内……第n 个x 内所用时间之比为)1(::)23(:)12(:1::::321----=n n t t t t n 。
匀变速直线运动规律推论及其应用

匀变速直线运动规律:
推论1:物体做匀变速直线运动,两 个连续相等的时间T内的位移之差:定 值为aT2。
小试牛刀:有一物体做匀加速直线运动,第一 个2秒内通过的位移为12m,第二个2秒内通过 的位移为24m,求该质点的加速度。
答案:3m/s2 试题拓展:有一物体做匀加速直线运动,第一 个2秒内通过的位移为12m,第三个2秒内通过 的位移为24m,求该质点的加速度和初速度。 拓展:△xMN=xM-xN=(M-N)aT2
• 推论3:做匀变速直线运动的物体,某 段位移的中间位置的瞬时速度等于初、 末速度的方均根
例:做匀加速直线运动的列车出站时,车头经过站 台时的速度为1m/s,车尾经过站台时的速度为 7m/s,则车身的中部经过站台的速度为( )
A、3.5m/s
C、5.0m/s
B、4.0m/s
D、5.5m/s 答案:C
多学一些
• • 初速度为零的匀加速直线运动的规律(设T为等分时间间隔) (1)1T内、2T内、3T内……位移之比x1∶x2∶x3…=
12∶22∶32 … .
•
•
(2)1 T末、2T末、3T末……速度之比v1∶v2∶v3…= 1∶2∶3 …
.
(3) 第 一 个 T 内 、 第 二 个 T 内 、 第 三 个 T 内 …… 的 位 移 之 比 为
SⅠ∶SⅡ∶SⅢ…= 1∶3∶5 …
•
.
(4)从静止开始通过连续相等的位移所用时间之比为t1∶t2∶t3…
•
=______________________
练习:1、一石块从楼房阳台边缘向下做自由落 体运动, 到达地面, 把它在空中运动的时间分为相 等的三段, 如果它在第一段时间内的位移是1.2m, 那么它在第三段时间内的位移是( C )
必修一物理匀变速直线运动的推论及推理过程

匀变速直线运动常用公式(附匀变速直线运动的推论及推理过程)一、 基本公式速度公式at v vt+=0当00=v 时,atvt=位移公式2021at t v s+=221at s =二、 几个常用的推论1.位移推导公式222v vast-=,t v v st2+=2.平均速度v 、中间时刻的瞬时速度2/t v 、中间位置的瞬时速度2/s v 为:/22tt v vx v v t+===,2222/t s v v v +=3.做匀变速直线运动的物体,在各个连续相等的时间T 内的位移分别是s 1、s 2、s 3…s n ,则Δs =s 2-s 1=s 3-s 2=…=s n -s n-1=aT 22.4.V 0=0的匀加速直线运动中的几个常用的比例公式(1)等分运动时间,以T 为单位时间.为单位时间. ①1T 末,2T 末,末,33T 末…,末…,n n T 末的速度之比末的速度之比v 1:v 2:v 3:…:v n =1=1::2:3…:…:n n②1T 内、内、22T 内、内、33T 内…内…n n T 内通过的位移之比内通过的位移之比s 1:s 2:s 3:…:s n=1=1::4:9…:…:n n 2③第1个T 内、第2个T 内、第3个T 内…、第n 个T 内通过的位移之比内通过的位移之比s Ⅰ:s Ⅱ:s Ⅲ:…:s N =1=1::3:5…:(…:(2n 2n 2n——1)④第1个T 内、第2个T 内、第3个T 内…、第n 个T 内的平均速度之比内的平均速度之比v Ⅰ:v Ⅱ:v Ⅲ:…:v N =1=1::3:5…:(…:(2n 2n 2n——1) (2)等分位移,以x 为位移单位.为位移单位. ①通过1x 、2x 2x、、3x …、…、n n x 所需时间之比所需时间之比 t 1:t 2:t 3:…:t n =1=1::3:2…:n②通过第1个x 、第2个x 、第3个x 、…第n 个x 所需时间之比所需时间之比t Ⅰ:t Ⅱ:t Ⅲ:…:t N =1=1:::23:12--…:1--n n③1x 末,末,22x 末,末,33x 末…,末…,n n x 末的速度之比末的速度之比v 1:v 2:v 3:…:v n =1=1::3:2…:n对匀变速直线运动公式作进一步的推论,是掌握基础知识、训练思维、提高能力的一个重要途径,掌握运用的这些推论是解决一些特殊问题的重要手段。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
通过第二段相同位移所以时间
• 推证:由x=1/2*at2 得
2x t1 = a
2 * 2x 2x 2x t2 = − = ( 2 − 1) a a a
3* 2 x 2 * 2x 2x ( 3 − 2) t3 = − = a a a
t1:t2:t3:........:tn =1 2−):( 3− 2 :( 1 ):......:( n− n− ) 1
补充:纸带问题的分析方法
• “位移差法”判断运动情况,设时间间隔 相等的相邻两点之间的位移分别是 x1,x2,x3….. 1.若x2-x1=x3-x2=….=Xn-Xn-1=0,则匀速直 线运动 2.若x2-x1=x3-x2=….=Xn-Xn-1≠0,则匀变速 直线运动
• “逐差法”求加速度 根据Xn+3-Xn=3T2 X4-X1=X5-X2=X6-X3=3aT2
1、任意两个连续相等时间间隔T内,位移之差 、任意两个连续相等时间间隔 内 是常数, 是常数,即△x=x2-x1=aT2。
拓展:△xMN=xM-xN=(M-N)aT2 拓展 △
进一步推论可得: 进一步推论可得:
a≡
∆X
T
2
≡ X
n +1
−
2
X
n
T
≡ X
n +2
−
2T
2
X
n
≡ X
n +3
−
3T
2
X
n
推论二: 推论二:已知一物体做匀变速直线运 动,加速度为a,试证明在任意一段 加速度为 , 时间t内的平均速度等于该段时间中点 时间 内的平均速度等于该段时间中点 内的平均速度 t/2时刻的瞬时速度。 时刻的瞬时速度。 时刻的瞬时速度
证明:设物体在匀变速直线运动中, 证明:设物体在匀变速直线运动中,任意一段 时间t的初速度为 的初速度为v 位移为x 时间 的初速度为 0,位移为
1 2 t时间内的位移为 x = v0t + at 时间内的位移为 2
1 联立以上两式得 v = v0 + at 2 1 中间时刻t/2的速度 中间时刻 的速度 v t = v0 + at 2 2
练习2:某市规定, 练习 :某市规定,车辆在市区内行驶不得超 过40km/h,有一辆汽车遇到情况紧急刹车后, ,有一辆汽车遇到情况紧急刹车后, 经时间t=1.5s停止,量得路面刹车的痕迹长为 停止, 经时间 停止 x=9m,问该车是否违章?(刹车后汽车做匀 ?(刹车后汽车做匀 ,问该车是否违章?( 减速运动) 减速运动) a= - 8m/s2 v0=12m/s=43.2km/h
推论一: 推论一: 物体做匀变速直线运动, 物体做匀变速直线运动,在任 意两个连续相等的时间 连续相等的时间内的位 意两个连续相等的时间内的位 移之差等于一个常数。 移之差等于一个常数。 △X=aT2
证明:设加速度为 ,经过任意一点A的速度为 证明:设加速度为a,经过任意一点 的速度为 点开始经两个连续相等的时间T的位移 v0,从A点开始经两个连续相等的时间 的位移 点开始经两个连续相等的时间 分别是x 分别是 1和x2。
联立以上两式得
x t时间内的平均速度为 v = 时间内的平均速度为 t
v = vt / 2
推论三: 某段位移内中间位置的瞬时速 度 V 与这段位移的初末速度 V0与Vt的关系
x 2
推证:由速度——位移公式得:
(1)
(2)
由(1)式得
(3)
匀变速直线运动推论公式: 匀变速直线运动推论公式:
1、任意两个连续相等时间间隔T内,位移之差 、任意两个连续相等时间间隔 内 是常数, 是常数,即△x=x2-x1=aT2。 拓展:△ 拓展 △xMN=xM-xN=(M-N)aT2 2、在一段时间内,中间时刻的瞬时速度等于这 、在一段时间内,中间时刻的瞬时速度等于这 瞬时速度 段时间内的平均速度 段时间内的平均速度 v = 1 (v + v) = v
(2)第一个 内、第二个 内、第三个 第一个Ts内 第二个Ts内 第三个Ts 第一个 内….位移之比 位移之比 X1:X2:X3...Xn=1:3:5:….(2n-1) :
(2)第一个 内、第二个 内、第三个 第一个Ts内 第二个Ts内 第三个Ts 第一个 内….位移之比 位移之比 X1:X2:X3...Xn=1:3:2 X 1 = aT 2
得
X
− X1= 2
3
1 1 3 2 a (2T ) 2 − aT = aT 2 2 2 2
X
−
X
1 1 5 2 2 2 = a (3T ) − a (2T ) = aT 2 2 2 2
所以
X1:X2:X3...Xn=1:3:5:….(2n-1) :
t/2
2
0
3、某段位移内中间位置的瞬时速度与这段位移 的初末速度的关系为
填空: 填空:
1.物体的初速度为2m/s,加速度为2m/s2, 1.物体的初速度为2m/s,加速度为2m/s 当它的速度增加到6m/s时,所通过的位 当它的速度增加到6m/s时,所通过的位 移是 _m. 2.物体的初速度为2m/s,用4s的时间速度 2.物体的初速度为2m/s,用4s的时间速度 增加到6m/s,那么该物体在这段时间内 增加到6m/s,那么该物体在这段时间内 发生的位移为 _m.
补充:初速度为0的匀加速直线运 补充:初速度为 的匀加速直线运 动的几个比例式
设以t=0开始计时,以T为时间单 位
(1)1Ts末、2Ts末、3Ts末…的速度之比 V1:V2:V3:…Vn=1:2:3:…..n 由速度V=at V1=aT,V2=2aT,V3=3aT,….Vn=naT V1:V2:V3:…Vn=1:2:3:…..n
练习1:一小球从静止开始做匀加速直线运动, 练习 :一小球从静止开始做匀加速直线运动, 在第15s内的位移比前 内的位移多0.2m,求 内的位移比前1s内的位移多 在第 内的位移比前 内的位移多 , 小球运动的加速度和前15s内的平均速度 内的平均速度。 小球运动的加速度和前 内的平均速度。 a=0.2m/s2 v=1.5m/s
(3)前1Ts内、前2Ts内、前3Ts内… 前 内 内 内 位移之比 X1:X2:X3...Xn=1:4;9;….:n2 ;
•由公式 由公式X=1/2*at2 由公式
• (4)通过连续相等时间的位移 ) 所用的时间之比
t1:t2:t3:........:tn =1 2−):( 3− 2 :( 1 ):......:( n− n− ) 1
因为T是个恒量,小车加速度也是恒量, 因为T是个恒量,小车加速度也是恒量,因此 也是个恒量。 △x也是个恒量。
只要物体做匀变速直线运动, 即:只要物体做匀变速直线运动,它在任 只要物体做匀变速直线运动 意两个连续相等的时间内的位移之差等 于一个常数 常数. 于一个常数
匀变速直线运动推论公式: 匀变速直线运动推论公式:
匀变速直线运动 规律推论
匀变速直线运动规律: 匀变速直线运动规律:
1、速度公式: v=v0+at 、速度公式: =
1 2 2、位移公式: x = v0t + at 、位移公式: 2 2 2 3、位移与速度关系:v − v0 = 2ax 、位移与速度关系:
x 1 4、平均速度: v = (v0 + v) = 、平均速度: 2 t
1 2 1 2 x1 = v0T + aT x2 = v1T + aT v1 = v0 + aT 2 2
由运动学知识: 由运动学知识: 两个连续相等的时间 内的位移之差 两个连续相等的时间T内的位移之差: 连续相等的时间 内的位移之差:
∆x = x2 − x1 = (v1 − v0 )T = aT
2
