新教材高一数学第一册4.3 4.3.2 对数的运算
4.3.2对数的运算(1) 教案 高一上学期数学人教A版(2019)必修第一册
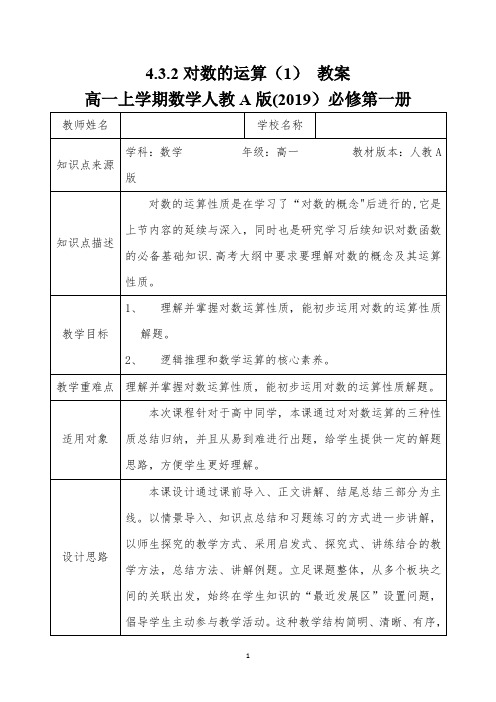
4.3.2对数的运算(1)教案高一上学期数学人教A版(2019)必修第一册()log log log .a a a MN M N =+故这也是对数运算的第一个性质.概念可能过于抽象,我们下面一起看个实例1. 请根据上面的公式化简一下lg9和lg27lg9=lg (3×3),根据上面讲的对数运算法则lg(3×3)是不是可以写作lg3+lg3?所以lg9=lg (3×3)=lg3+lg3=2lg3那lg27呢。
推导方法和上面是一样的,我把步骤列出来,请同学自行思考一下.lg27=lg (9×3)=2lg3+lg3=3lg39是3的2次方,lg9=2lg3,27是3的三次方,lg27=3lg3,你有没有发现什么规律?这就是对数的另一个运算性质.接下来我们将两个运算性质结合起来求解下题2、log 2(25×47)该式子的真数为25×47我们把真数相乘的对数变成对数相加的真数得log 225+log 247,其中很容易得出log 225=547可以看做(22)7=214,故log 247=log 2214=14得,log 225+log 247=5+14=19两个真数相乘的对数结果等于两个真数的对数和,那两个真数相除的对数呢?按照指数运算性质,应该等于两个真数的对数差.公式如下这里留个课后思考:请课后把上面的两个对数运算性质自己推导一下。
综上所述,对数运算具有如下性质:0,1,0,0,1log ()log log 2log log log 3log log .a a a a a a n a a a a M N MN M N M M N NM n M >≠>>=+=-=如果且那么();();()下面我们将三个运算公式结合,来解这道进阶题目3、lg14-2lg 73+lg7-lg18 和上题一样,我们可以先把一些真数相乘的对数变成对数相加的真数,不过这里面还有真数相除的对数,比方说lg 73,可以看做lg7-lg3, 故2lg 73=2(lg7-lg3)①,lg14也可以看成lg2+lg7②,lg18=lg2+2lg3③把①②③带入式中,lg2+lg7-2(lg7-lg3)+lg7-(lg2+2lg3),将式中项相互抵消,最后结果为0.。
4.3.2对数的运算第2课时换底公式课件高一上学期数学人教A版【05】

(2)已知 2x=3y=5z,且1x+1y+1z=1,求 x,y,z.
令2x=3y=5z=k(k>0),所以x=log2k,y=log3k,z=log5k, 所以1x=logk2,1y=logk3,1z=logk5, 由1x+1y+1z=1,得 logk2+logk3+logk5=logk30=1,所以 k=30, 所以x=log230=1+log215,y=log330=1+log310,z=log530=1+log56.
对数
第 四
对数的运算
章
第2课时 对数换底公式
1.掌握换底公式及其推论.
学习目标
2.能熟练运用对数的运算性质进行化简求值.
探索新知
数学史上,人们经过大量的努力,制作了 常用对数表和自然对数表,通过查表就能求出 任意正数的常用对数和自然对数。现在,利用 计算工具,也可以直接求出任意正数的常用对 数和自然对数。这样,如果能将其他底的对数 转换为以10或以e为底的对数,就能方便地求 出这些对数。
例题巩固
例3
求值:log2
3
log 3
4
log 4
5
log5
2.
解:原式= lg 3 lg 4 lg 5 lg 2 =1.
lg 2 lg 3 lg 4 lg 5
思考:logab
log b
c
logc
a
?
你还能得出其
他结论吗?
解析:类比例3,可知ห้องสมุดไป่ตู้
logab
log b
c
logc
a
1.
同理可知:logab
练习巩固
3. (1)设 3a=4b=36,求2+1的值; ab
(2)已知 2x=3y=5z,且1x+1y+1z=1,求 x,y,z.
4.3.2 对数的运算 课件(共13张PPT) 高一数学人教A版(2019)必修第一册

新课讲授
课堂总结
例1 求下列各式的值. (1)lg5 100;
(2)原式 (lg 2 lg 2)( lg 3 lg 3)
lg 3 lg 9 lg 4 lg 8
(lg 2 lg 2 )( lg 3 lg 3 ) lg 3 2 lg 3 2 lg 2 3lg 2
3lg 2 5lg 3 5 2 lg 3 6 lg 2 4
学习目标
新课讲授
课堂总结
总结归纳
1.在化简带有对数的表达式时,若对数的底不同,需利用换底公式;
2.常用的公式有:
log a
b logb
a
1,logan
bm
m n
loga
b,
loga
b
1 logb
a
等.
学习目标
新课讲授
课堂总结
练一练
已知log189=a,18b=5,试用a,b表示log3645.
解:∵log189=a,18b=5,
(2)log2(47 25)
解:(1) lg5
1
100 lg1005
1 lg100 2 ;
5
5
(2) log2(47 25) log2 47 log2 25 7 log2 4 5log2 2 7log2 22 5 725
19
学习目标
新课讲授
课堂总结
例2 用 ln x, ln y, ln z 表示 ln x2 y 3z
4.3.2 对数的运算
学习目标
4.3.2对数的运算教学设计-2024-2025学年高一上学期数学人教A版(2019)必修第一册

- 提交预习成果:学生将预习成果(如笔记、思维导图、问题等)提交至在线平台或老师处。
教学方法/手段/资源:
- 自主学习法:学生自主阅读和思考,培养自主学习能力。
- 信息技术手段:利用在线平台、微信群等,实现预习资源的共享和监控。
- 反馈作业情况:及时批改作业,给予学生反馈和指导。
学生活动:
- 完成作业:学生认真完成老师布置的课后作业,巩固学习效果。
- 拓展学习:学生利用老师提供的拓展资源,进行进一步的学习和思考。
- 反思总结:学生对自己的学习过程和成果进行反思和总结,提出改进建议。
教学方法/手段/资源:
- 自主学习法:引导学生自主完成作业和拓展学习。
教学方法/手段/资源:
- 讲授法:通过详细讲解,帮助学生理解对数的定义、性质和运算法则。
- 实践活动法:设计小组讨论,让学生在实践中掌握对数的运算技能。
- 合作学习法:通过小组讨论等活动,培养学生的团队合作意识和沟通能力。
作用与目的:
- 帮助学生深入理解对数的定义、性质和运算法则,掌握对数的运算技能。
- 提供一些拓展性的题目,鼓励学生进行深入研究和探索,如对数函数的图像分析、对数运算的数学证明等。
作业反馈:
- 及时批改学生的作业,给出明确的评分和评价。
- 在批改过程中,注意指出学生作业中的错误和不足之处,并提供改进建议。
- 对于学生作业中的亮点和优秀表现,给予肯定和鼓励。
- 通过面对面的交流或书面反馈,将作业批改结果告诉学生,并与他们讨论改进的方法。
- 数学教科书和配套练习册,作为教学的主要材料。
- 计算器,用于辅助计算和对数的运算练习。
4.3.2对数的运算法则课件(第一课时)-2024-2025学年高一上学期数学湘教版(2019)必修

和 =
= ( ∈ ,a > 0, a ≠ 1)
= 称作为对数运算的基础。
巩固练习
例一、设 = = = 用A、B、C表示
2
3
解:
3
3
若 = 不一定有 = ,需要保证, ≠
若 = 也不一定有M=N;
反例: = (−)
但 ≠ −
课堂小结
在学习完对数的基本运算法则后我们一定要掌握:
(1) = + (2) = ( ∈ )
= − Βιβλιοθήκη = + − = + − ;
= − = + −
= + −
巩固练习
50
5
1
(2) 10 12.5 − 10 + 10
8
2
解:
−
= =
− = ÷
÷ =
. − + = . ÷ ×
−
= + −
[方法二] = − = × −
= + −
= + − −
= + − − = + −
现在假设
= = 则 = =
4.3.2对数的运算法则(1)课件高一上学期数学

方法归纳 选择适当的对数运算法则求值,注意掌握一些对数的性质:loga1= 0,logaa=1,alogaN=N(a>0且a≠1,N>0).
lg 27+lg 8-3lg 10 lg 1.2
方法归纳
1.对于同底的对数的化简,常用方法是: (1)“收”,将同底的两对数的和(差)收成积(商)的对数; (2)“拆”,将积(商)的对数拆成对数的和(差). 2.对数式的化简、求值一般是正用或逆用公式,要养成正用、逆用、 变形应用公式的习惯,lg2+lg5=1在计算对数值时会经常用到,同时 注意各部分变形要化到最简形式.
第1课时 对数的运算法则(1)
新知初探 课前预习
题型探究 课堂解透
新知初探 课前预习
最新课程标准 1. 理解对数运算性质.
2.知道用换底公式能将一般对数转化成自然对数或常用对数.
学科核心素养
1. 会推导对数运算性质并进行化学运算)
答案:A
答案:B
3.若10a=5,10b=2,则a+b等于( ) A.-1 B.0 C.1 D.2
答案:C
解析:由已知得a=lg 5,b=lg 2, 故a+b=lg 5+lg 2=lg 10=1,故选C.
1
解析:(1)原式=(lg 5)2+lg 2(lg 5+lg 10) =(lg 5)2+lg 2×lg 5+lg 2 =lg 5(lg 5+lg 2)+lg 2=lg 5+lg 2=1.
log320
0.826 6
方法归纳
先将条件或结论适当变形,再准确应用对数运算公式及有关性质解 题.
B
B 4
2
答案:4
易错警示
易错原因
本题易错地方是忽视对数的限 制条件,尤其x-2y>0这一条 件,得出错误答案1或4.
4.3.2 对数的运算-2020-2021学年高一数学新教材配套课件(人教A版必修第一册)

b logb
c logc
a
ln ln
b a
ln ln
c b
ln ln
a c
1
(2)
log am
bn
ln bn ln am
n ln b m ln a
n m log a b
例4 计算下列各式的值:
(1) log8 9 log27 37
log27 16 (2) log3 4
解:(1)原式
ln 9 ln 32 ln 8 ln 27
答案:2
课堂小结
1.记牢 2 个知识点 (1)对数的运算性质;(2)换底公式. 2.掌握 2 种方法 (1)利用对数的运算性质,可以把乘、除、乘方运算转化为加、减、乘 的运算,加快计算速度. (2)利用结论 logab·logba=1,loganbm=mnlogab 化简求值更方便.
课堂作业 作业:完成对应练习
[解析]
由题意,得lg4·lg8·lgm=lgm=1, lg3 lg4 lg8 lg3 2
∴lgm=1lg3,即 lgm=lg31,
2
2
∴m= 3.
跟踪训练4
(1)
求证:log a
b
1 log b
a
(2) 求值:log9 27
解:(1)证明:loga
b
ln b ln a
1 ln a
1 logb
a
ln b
3 (3)loga
yxz2=13logayxz2=13(logax-loga(yz2))=13(logax-logay
-2logaz).
题型二 对数换底公式应用
例3 证明下列等式:
(1)log a b logb c logc a 1
高一数学必修第一册2019(A版)_4.3.2_对数的运算_练习(解析版)

第四章 指数函数与对数函数 4.3.2 对数的运算一、选择题1.(2019全国高一课时)若a >0,a≠1,x >0,y >0,x >y ,下列式子中正确的个数是( ) ①log a x·log a y =log a (x +y);②log a x -log a y =log a (x -y); ③log axy=log a x÷log a y; ④log a (xy)=log a x·log a y. A.0 B.1 C.2 D.3 【答案】A【解析】由对数的运算性质,得到logax•logay≠loga (x+y );log log log xx y y a a a-= ;log a (xy )=log a x+log a y . 故选A2.(2019全国高一课时练)lg8+3lg5的值为( ) A.-3 B.-1C.1D.3【答案】D 【解析】383585212510003lg lg lg lg lg lg lg ==+==++,故选D 。
3.(2019甘肃武威十八中高一课时练)已知lg2=0.301,lg3=0.477 ,则lg12= ( ) A.0.778 B.1.079C.0.301D.0.477【答案】B【解析】因为lg12lg3lg 4lg32lg 20.47720.301 1.079.=+=+=+⨯=所以选B. 4.(2019全国高一课时) 若log 34·log 8m =log 416,则m 等于( ) A.3 B.9 C.18 D.27 【答案】D【解析】原式可化为log 8m =432log ,lg 2lg 43lg 2lg 3m = ,即lg m =6lg 2lg 32lg 2⋅, lg m =lg 27,m =27.故选D. 5.(2017·全国高一课时练习)设,则f[f(2)]的值为A.0B.1C.2D.3 【答案】C【解析】f(2)=log 3(22−1)=log 33=1,则f[f(2)]=2. 6.(2017·全国高一课时练习)已知,,,,则下列等式一定成立的是A. B. C.D.【答案】B 【解析】因为,,所以,.又,所以,则.二、填空题7.(2019·全国高一课时练)地震的震级R 与地震释放的能量E 的关系为R =23(lg E -11.4).2011年3月11日,日本东海岸发生了9.级特大地震,2008年中国汶川的地震级别为8.0级,那么2011年地震的能量是2008年地震能量的__________倍. 【答案】【解析】设震级9.0级、8.0级地震释放的能量分别为21E E 、,则212983lgE lgE ()-=-,即3222113102E E lg E E ,=∴== . 那么2011年地震的能量是2008年地震能量的8.(2019全国高一课时练)方程lg x +lg (x -1)=1-lg 5的根是________. 【答案】2【解析】方程变形为lg [x (x -1)]=lg 2,所以x (x -1)=2,解得x =2或x =-1.经检验x =-1不合题意,舍去,所以原方程的根为x =2. 9.(2017·全国高一课时练习)若,则【答案】【解析】,从而,故选D .10.(2017·北京市第二中学分校高一课时练习)设函数()(0a f x log x a >=且1)a ≠,若()122?0128f x x x ⋯=,则222122012()()()f x f x f x +++的值等于________.【答案】16【解析】由()1220128f x x x ⋯=,得()1220128a log x x x ⋯=. 因为()()()222222122012122012a a a f x f x f x log x log x log x +++=+++12201222?2a a a log x log x log x =+++()1220122?a a a log x log x log x =+++()1220122?2816a log x x x =⋯=⨯=故答案为16.三、解答题11.(2019·全国高一课时练习)化简:(1)23lg 3lg 955lg81lg 27++-; (2)(lg5)2+lg2lg50+2211+log 52. 【答案】(1)115(2)1+ 【解析】 (1)原式===.(2)原式=(lg5)2+lg2(lg5+1)+21·2log 52=lg5·(lg5+lg2)+lg2+2=1+2.12.(2019·全国高一课时练习)若a 、b 是方程2lg 2 x -lg x 4+1=0的两个实根,求lg(ab )·lg lg lg lg b a a b ⎛⎫+ ⎪⎝⎭的值. 【答案】12【解析】原方程可化为2lg 2x -4lg x +1=0,设t =lg x ,则原方程化为2t 2-4t +1=0,∴t 1+t 2=2,t 1t 2=. 由已知a ,b 是原方程的两个根,则t 1=lg a ,t 2=lg b ,即lg a +lg b =2,lg a ·lg b =,lg(ab )·lg lg lg lg b a a b ⎛⎫+⎪⎝⎭==(lg a +lgb )·()2lg lg 2lg lg lg lg a b a ba b+-=2×=12.故lg(ab )·lg lg lg lg b a a b ⎛⎫+⎪⎝⎭=12.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10 lg =2lg
18 110.8=2llgg11..88=12.
解
题型二 换底公式的应用
例 2 已知 log189=a,18b=5,求 log3645(用 a,b 表示). [解] 因为 18b=5,所以 b=log185. 所以 log3645=lloogg11883465=lloogg118825××198 =lloogg118825++lloogg1188198=1+a+logb182=1+al+ogb18198
-2lg 2+lg 7+12lg 5
=12lg 2+12lg 5=12(lg 2+lg 5)
=12lg 10=12.
(2)原式=2lg 5+2lg 2+lg 5(2lg 2+lg 5)+(lg 2)2=2lg 10+(lg 5+lg 2)2
=2+(lg 10)2=2+1=3.
(3)原式=12lg
2+lg 9-lg lg 1.8
2.做一做
(1)计算 log69+log64=( )
A.log62
B.2
C.log63
D.3
(2)计算 log550-log52=( )
A.log548
B.2
C.log5100
4
(3)计算 log2781=____3____.
D.3
(4)lloogg2293的值为____2____.
答案
2
PART TWO
3
PART THREE
随堂水平达标
1.计算 log84+log82 等于( A.log86 C.6
) B.8 D.1
解析 log84+log82=log8(4×2)=log88=1.
解析 答案
2.计算 log92×log43=( )
A.4
B.2
C.12
D.14
解析 log92×log43=llgg 29×llgg 34=2llgg23×2llgg32=14.
n ③logambn= 04 __m__lo_g_a_b__ (a>0,b>0,且均不为 1,m≠0).
1.判一判(正确的打“√”,错误的打“×”) (1)loga(MN)=logaM+logaN.( × ) (2)loga(27-16)=loga27-loga16.( × ) (3)llooggaa186=loga2.( × ) (4)log2(-2)3=3log2(-2).( × )
解析 答案
3.设 10a=2,lg 3=b,则 log26=( )
A.ba
a+b B. a
C.ab
D.a+b
解析
∵10a=2,∴lg
2=a.∴log26=llgg
26=lg
2+lg lg 2
3 a+b =a.
解析 答案
本课结束
x-1=x2-3,
x+ 3>0, 故x- 3>0,
x-1>0.
解得 x=2.
(2)由 3x=4y=36,可得 x=log336,y=log436.
所以2x+1y=log2336+log1436=
2 1
+
1 1
=2log363+log364=log369+
log363 log364
log364=log3ຫໍສະໝຸດ (9×4)=1. 解析核心素养形成
题型一 对数运算性质的应用
例 1 计算下列各式的值:
(1)12lg 3429-43lg 8+lg 245;
(2)lg 52+23lg 8+lg 5×lg 20+(lg 2)2;
lg 2+lg 3-lg 10
(3)
lg 1.8
.
[解] (1)原式=12(5lg 2-2lg 7)-43×32lg 2+12(2lg 7+lg 5)=52lg 2-lg 7
第四章 指数函数与对数函数
4.3 对数 4.3.2 对数的运算
1
PART ONE
核心概念掌握
知识点一 对数运算性质 如果 a>0 且 a≠1,M>0,N>0,那么 (1)loga(MN)= 01 __l_o_g_aM__+__l_o_g_aN____; (2)logaMN= 02 ___lo_g_a_M__-__lo_g_a_N___; (3)logaMn= 03 _____n_l_o_g_aM_______ (n∈R).
a+b a+b =2-log189=2-a.
解
题型三 对数运算的综合与实际应用
例3 设 3x=4y=36,则2x+1y=______1__.
答案 见解析 答案
[解析] (1)由 log3(x+ 3)+log3(x- 3)=log3[(x+ 3)(x- 3)]=log3(x2 -3),可得 log3(x-1)=log3(x2-3),
知识点二 换底公式 (1)对数的换底公式:01 __lo_g_a_b_=__lloo_gg_cc_ab_(_a_>_0_,且___a_≠__1_;b_>_0_;_c_>_0_,且___c_≠__1_)___. (2)三个较为常用的推论 ① 02 ____lo_g_a_b_·_lo_g_b_c_·l_o_g_ca_=__1_(_a_>_0_,__b_>_0_,__c_>_0_,__且__均__不__为___1_)_____; ② 03 _l_o_g_ab_=__l_o_g1_b_a_(a_>_0__,__b_>_0_,__且__均__不__为__1_)_;
