高等数学课件 中值定理和导数的应用
合集下载
第四章中值定理与导数的应用(全)

e e e( x 1) e x e
x
于是
e e x.
x
例2
证明 当x 0时,
x l n1 x x 1 x
证 设 f x ln1 x , 在[0, x]上应用拉格朗日中值定理
f x f 0 f x 0, 0 x
, 使得f () f () 0
证 则F(x)在[0,1]上 构造函数:令F(x)=xf(x), 满足罗尔中值定理的条件,于是在开区间(0,1) 内至少存在一点 ,使得
f () f () 0
二、拉格朗日中值定理 (Lagrange):
若f x 在 a, b 上连续,在a, b内可导,
f ( x 0 x ) f ( x 0 ) 0 x
C
从而当x 0时
f ( x 0 x ) f ( x 0 ) 0 x
x
0
根据函数f ( x)在x0可导的条件,再由极限 的保号性,便得到
f ( x 0 x ) f ( x 0 ) f ( x0 ) f ( x0 ) lim 0 x 0 x
即 5 使得f 0. , , 2 6 6
5
例2、不求导数,判断函数 f ( x ) ( x 1)( x 2)( x 3)的导数有几个 实根,以及其所在范围 。
解 显然,f (1) f (2) f (3) 0.
且f ( x)在[1,2]和[2,3]上满足罗尔定理条件。
则至少有一点 ,
a b,使得
f 0
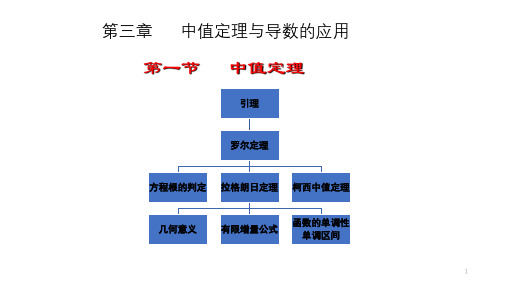
几何意义
几何上,若f x 满足罗尔定理, 则此曲线上至少存在一 点C, 过该点的切线平行于x轴如图.
高等数学 第3章 第一节 中值定理
6 6
(函数
即
6
,
y
5
6
ln sin x
是 y
是初等函数, 且当
x
6
ln sin x 定义域内的一部分;
,
5
6
时,cossixn
y'
sin x
x
0,
cot x.)
且ln s in
lnsin 5
ln 1 .
6
62
令 y' cos x cot x 0, sin x
得 x , 5 .
F(b) F(a)
( x) 满足罗尔定理的全部条件,且:
'(x) f '(x) f (b) f (a) F '(x)
F(b) F(a)
Y F , f Fb, f b
C•
•B
由罗尔定理,至少存在一点 ∈(a,b) ,
即:
使
f
'( )
'( ) 0,
f (b) f (a) F '( ) 0
即 1、 2、 3都是方程 f 'x 0 的根。 注意到 f ' x 0 为三次方程, 它最多有三个根。
我们已经找到它的三个实根
1、 2、 3 ,
所以这三个根就是方程
f 'x 0 的全部根。
14
例3 证明当x 0时, x ln1 x x
1 x
证 设f x ln1 x, 显然,函数 f x 在 0, x 上满足
f (b) f (a)
O a
bx
结论等价于: f f b f a
ba
或: f f b f a 0
ba
AB的方程为:
(函数
即
6
,
y
5
6
ln sin x
是 y
是初等函数, 且当
x
6
ln sin x 定义域内的一部分;
,
5
6
时,cossixn
y'
sin x
x
0,
cot x.)
且ln s in
lnsin 5
ln 1 .
6
62
令 y' cos x cot x 0, sin x
得 x , 5 .
F(b) F(a)
( x) 满足罗尔定理的全部条件,且:
'(x) f '(x) f (b) f (a) F '(x)
F(b) F(a)
Y F , f Fb, f b
C•
•B
由罗尔定理,至少存在一点 ∈(a,b) ,
即:
使
f
'( )
'( ) 0,
f (b) f (a) F '( ) 0
即 1、 2、 3都是方程 f 'x 0 的根。 注意到 f ' x 0 为三次方程, 它最多有三个根。
我们已经找到它的三个实根
1、 2、 3 ,
所以这三个根就是方程
f 'x 0 的全部根。
14
例3 证明当x 0时, x ln1 x x
1 x
证 设f x ln1 x, 显然,函数 f x 在 0, x 上满足
f (b) f (a)
O a
bx
结论等价于: f f b f a
ba
或: f f b f a 0
ba
AB的方程为:
第三章中值定理与导数的应用课件
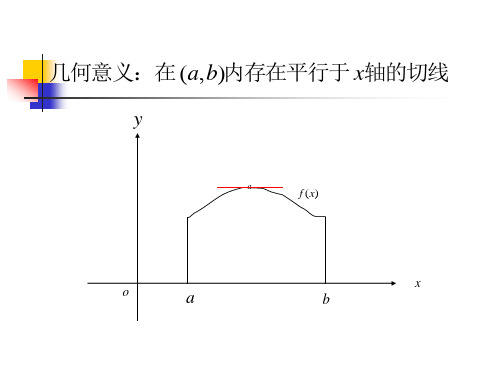
那么在(a,b)内至少有一点 使等式
f (b) f (a) f ' ( ) 成立 F (b) F (a) F ' ( )
例1:验证罗尔定理对函数y ln sin x在区间
[
6
,
5
6
]的正确性
解:y ln sin x在[ , 5 ]上连续
66
y ln sin x在( , 5 )上可导
66
lim 2 cos3x 3 1 x0 3 cos2x 2
例6:求
lim
x
xn ex
(n 0, 0)
解:lim xn lim n xn1 lim n (n 1) xn2
e e x x x
x x
2 ex
lim n! 0
x n ex
例7:求 lim x sin x
且f ( ) ln 1 f (5 )
6
2
6
又
y'
c os x
ctgx
令
0
x
(
, 5 )sin x源自2 662罗尔定理正确
例2:证明arctgx arcctgx
2
证 : (arctgx arcctgx)' 1 1 0 1 x2 1 x2
arctgx arcctgx c
取x 1 c c
若f (x)是一般的函数,且它存在直到n 1 阶的导数,那么
n
f (x)
f (k) (a) (xa)k ?
k 0 k!
泰勒(Taylor)中值定理
泰勒(Taylor)中值定理 如果函数 f ( x)在含有 x0 的某个开区间(a, b)内具有直到(n 1)阶的导数,则
当 x在(a, b)内时, f ( x)可以表示为( x x0 )的一个
f (b) f (a) f ' ( ) 成立 F (b) F (a) F ' ( )
例1:验证罗尔定理对函数y ln sin x在区间
[
6
,
5
6
]的正确性
解:y ln sin x在[ , 5 ]上连续
66
y ln sin x在( , 5 )上可导
66
lim 2 cos3x 3 1 x0 3 cos2x 2
例6:求
lim
x
xn ex
(n 0, 0)
解:lim xn lim n xn1 lim n (n 1) xn2
e e x x x
x x
2 ex
lim n! 0
x n ex
例7:求 lim x sin x
且f ( ) ln 1 f (5 )
6
2
6
又
y'
c os x
ctgx
令
0
x
(
, 5 )sin x源自2 662罗尔定理正确
例2:证明arctgx arcctgx
2
证 : (arctgx arcctgx)' 1 1 0 1 x2 1 x2
arctgx arcctgx c
取x 1 c c
若f (x)是一般的函数,且它存在直到n 1 阶的导数,那么
n
f (x)
f (k) (a) (xa)k ?
k 0 k!
泰勒(Taylor)中值定理
泰勒(Taylor)中值定理 如果函数 f ( x)在含有 x0 的某个开区间(a, b)内具有直到(n 1)阶的导数,则
当 x在(a, b)内时, f ( x)可以表示为( x x0 )的一个
中值定理与导数的应用(高等数学)省名师优质课赛课获奖课件市赛课一等奖课件
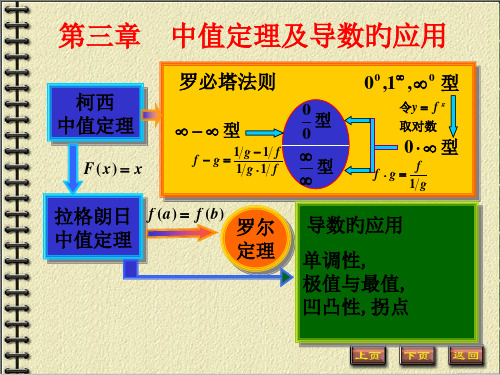
函数旳极大值与极小值统称为极值,使函数取得 极值旳点称为极值点.
定义 使导数为零的点(即方程f ( x) 0的实根)叫 做函数f ( x)的驻点.
定理(必要条件) 设 f ( x) 在点x0 处具有导数,且 在 x0处取得极值,那末必定 f '( x0 ) 0.
注意:可导函数 f ( x) 的极值点必定是它的驻 点, 但函数的驻点却不一定 是极值点.
2、罗必塔法则
(1). 0 型及 型未定式 0
定义 这种在一定条件下经过分子分母分别求导再 求极限来拟定未定式旳值旳措施称为罗必塔法则.
(2). 0 , , 00,1 , 0型未定式
关键:将其他类型未定式化为罗必塔法则可处理 旳类型 ( 0 ), ( ) .
0
定理 设(1)当x 0时,函数 f ( x) 及 F ( x) 都趋于零; (2) 在 a 点的某领域内(点 a 本身可以除外 ), f ( x) 及 F ( x) 都存在且 F ( x) 0; (3) lim f ( x) 存在(或为无穷大);
(2) 在开区间 ( a , b ) 内可导
(3)在开区间 ( a , b ) 内F(x) 0
至少存在一点
(a,b) , 使
f (b) f (a) F (b) F (a)
f ( ) . F( )
注意:若令F(x)=x,则柯西中值定理变为拉氏中值 定理,即拉
0
原式
lim
x
1
1
x 1 x2
2
lim
x
1
x
2
x
2
1.
例8
求
lim
x0
tan x x2 tan
x x
.
解
定义 使导数为零的点(即方程f ( x) 0的实根)叫 做函数f ( x)的驻点.
定理(必要条件) 设 f ( x) 在点x0 处具有导数,且 在 x0处取得极值,那末必定 f '( x0 ) 0.
注意:可导函数 f ( x) 的极值点必定是它的驻 点, 但函数的驻点却不一定 是极值点.
2、罗必塔法则
(1). 0 型及 型未定式 0
定义 这种在一定条件下经过分子分母分别求导再 求极限来拟定未定式旳值旳措施称为罗必塔法则.
(2). 0 , , 00,1 , 0型未定式
关键:将其他类型未定式化为罗必塔法则可处理 旳类型 ( 0 ), ( ) .
0
定理 设(1)当x 0时,函数 f ( x) 及 F ( x) 都趋于零; (2) 在 a 点的某领域内(点 a 本身可以除外 ), f ( x) 及 F ( x) 都存在且 F ( x) 0; (3) lim f ( x) 存在(或为无穷大);
(2) 在开区间 ( a , b ) 内可导
(3)在开区间 ( a , b ) 内F(x) 0
至少存在一点
(a,b) , 使
f (b) f (a) F (b) F (a)
f ( ) . F( )
注意:若令F(x)=x,则柯西中值定理变为拉氏中值 定理,即拉
0
原式
lim
x
1
1
x 1 x2
2
lim
x
1
x
2
x
2
1.
例8
求
lim
x0
tan x x2 tan
x x
.
解
微分中值定理与导数应用.ppt

拉格朗日中值公式又称有限增量公式. 拉格朗日中值定理又称有限增量定理.
定理 如果函数 f (x) 在区间 I 上的导数恒为零, 那末 f (x) 在区间 I 上是一个常数.
第一节 中值定理
例2 证明 arcsin x arccos x (1 x 1). 2
证 设 f ( x) arcsin x arccos x, x [1,1]
f (b) F (b)
f (a) F (a)
f '( F '(
). )
第一节 中值定理
证: 作辅助函数
( x) f ( x) f (a) f (b) f (a) [F ( x) F (a)]. F(b) F(a)
( x) 满足罗尔定理的条件, 则在(a, b)内至少存在一点,使得 () 0.
弦AB方程为 y f (a) f (b) f (a) ( x a).
ba 曲线 f ( x) 减去弦 AB,
所得曲线a, b两端点的函数值相等.
第一节 中值定理
作辅助函数
F ( x) f ( x) [ f (a) f (b) f (a) ( x a)]. ba
F( x) 满足罗尔定理的条件, 则在(a, b)内至少存在一点,使得 F () 0. 即 f () f (b) f (a) 0
y f (x)
2 b x
第一节 中值定理
第一节 中值定理
二、拉格朗日(Lagrange)中值定理
拉格朗日(Lagrange)中值定理 如果函数 f(x)满足
(1)在闭区间[a, b]上连续; (2)在开区间(a, b) 内可导; 那么在(a, b)内至少有一点(a b) ,使得
f (b) f (a) f ' ()(b a) .
定理 如果函数 f (x) 在区间 I 上的导数恒为零, 那末 f (x) 在区间 I 上是一个常数.
第一节 中值定理
例2 证明 arcsin x arccos x (1 x 1). 2
证 设 f ( x) arcsin x arccos x, x [1,1]
f (b) F (b)
f (a) F (a)
f '( F '(
). )
第一节 中值定理
证: 作辅助函数
( x) f ( x) f (a) f (b) f (a) [F ( x) F (a)]. F(b) F(a)
( x) 满足罗尔定理的条件, 则在(a, b)内至少存在一点,使得 () 0.
弦AB方程为 y f (a) f (b) f (a) ( x a).
ba 曲线 f ( x) 减去弦 AB,
所得曲线a, b两端点的函数值相等.
第一节 中值定理
作辅助函数
F ( x) f ( x) [ f (a) f (b) f (a) ( x a)]. ba
F( x) 满足罗尔定理的条件, 则在(a, b)内至少存在一点,使得 F () 0. 即 f () f (b) f (a) 0
y f (x)
2 b x
第一节 中值定理
第一节 中值定理
二、拉格朗日(Lagrange)中值定理
拉格朗日(Lagrange)中值定理 如果函数 f(x)满足
(1)在闭区间[a, b]上连续; (2)在开区间(a, b) 内可导; 那么在(a, b)内至少有一点(a b) ,使得
f (b) f (a) f ' ()(b a) .
高等数学 微分中值定理与导数的应用

f (b) f (a) f ' ()(b a) 成立.
注意 : 与罗尔定理相比条件中去掉了 f (a) f (b). 结论亦可写成 f (b) f (a) f (). ba
f (b) f (a) f ( )
ba
y 几何解释:
在曲线弧 AB 上至少有
一点 C ,在该点处的切
A
C
y f (x)
有一点(a b),使等式
f (a) F (a)
f (b) F (b)
f F
' () 成立. ' ()
Cauchy定理又称为广义微分中值定理
结构图
特例
推广
Rolle定理
Lagrange定理
Cauchy定理
拉格朗日中值定理又称微分中值定理.
第二节 洛必达法则
一、0 型及 型未定式解法: 洛必达法则 0
且除去两个端点外处 o a 处有不垂直于横轴的
1
2 b x
切线,在曲线弧AB上至少有一点C ,在该点处的
切线是水平的.
注① Rolle定理有三个条件:闭区间连续;开区间可导
区间端点处的函数值相等; 这三个条件只是充分条件,而非必要条件
如:y=x2在[-1,2]上满足(1),(2),不满足(3) 却在(-1,2)内有一点 x=0 使
第三章 微分中值定理与导数的应用
§3. 1 微分中值定理
一、罗尔(Rolle)定理
定理(Rolle) 若函数f ( x ) 满足 (1)在闭区间[a,b]上连续 (2)在开区间(a,b)内可导 (3)在区间端点处的函数值相等f(a)=f(b)
则在(a,b)内至少存在一点 , (a,b)使得函数 f ( x)在该点的导数为零,即 f ( ) 0
注意 : 与罗尔定理相比条件中去掉了 f (a) f (b). 结论亦可写成 f (b) f (a) f (). ba
f (b) f (a) f ( )
ba
y 几何解释:
在曲线弧 AB 上至少有
一点 C ,在该点处的切
A
C
y f (x)
有一点(a b),使等式
f (a) F (a)
f (b) F (b)
f F
' () 成立. ' ()
Cauchy定理又称为广义微分中值定理
结构图
特例
推广
Rolle定理
Lagrange定理
Cauchy定理
拉格朗日中值定理又称微分中值定理.
第二节 洛必达法则
一、0 型及 型未定式解法: 洛必达法则 0
且除去两个端点外处 o a 处有不垂直于横轴的
1
2 b x
切线,在曲线弧AB上至少有一点C ,在该点处的
切线是水平的.
注① Rolle定理有三个条件:闭区间连续;开区间可导
区间端点处的函数值相等; 这三个条件只是充分条件,而非必要条件
如:y=x2在[-1,2]上满足(1),(2),不满足(3) 却在(-1,2)内有一点 x=0 使
第三章 微分中值定理与导数的应用
§3. 1 微分中值定理
一、罗尔(Rolle)定理
定理(Rolle) 若函数f ( x ) 满足 (1)在闭区间[a,b]上连续 (2)在开区间(a,b)内可导 (3)在区间端点处的函数值相等f(a)=f(b)
则在(a,b)内至少存在一点 , (a,b)使得函数 f ( x)在该点的导数为零,即 f ( ) 0
高等数学》课件4.微分中值定理与导数的应用

思考题
1. 将拉格朗日中值定理中的条件 f (x) “在 闭区间[a,b]上连续”换为“在开区(a,b) 内连续” 后,定理是否还成立?试举例(只需画图)说明.
2. 罗尔(Rolle)中值定理是微分中值定理中一 个最基本的定理.仔细阅读下面给出的罗尔中值定理 的条件与结论,并回答所列问题.
罗尔(Rolle)中值定理 若 f (x)满足如下 3 条: (1) 在闭区间[a,b]上连续; (2) 在开区间(a,b)内可导; (3) 在 区 间 [a,b] 端 点 出 的 函 数 值 相 等 , 即
例1
求
lim
x1
x3 x3 x
3x 2
x
2
. 1
解
lim
x 1
x3 x3 x
3x 2
x
2
1
=
lim
x 1
3x2 3x2
3 2x
1
= lim 6x = 6 = 3 .
x1 6x 2
4
2
例 2 求lim1 cos x . xπ tan x
解 lim1 cos x = lim sin x = 0.
推 论 2 如 果 对 (a,b) 内 任 意 x , 均 有 f (x) g(x),则在(a,b) 内 f (x)与 g(x)之间只差一个 常数,即 f (x) g(x) C (C 为常数).
证 令F (x) f (x) g(x),则F(x) 0,由推论 1 知 , F(x) 在 (a,b) 内 为 一 常 数 C , 即 f (x) g(x) C, x (a,b),证毕.
f (a) f (b),则在开区间(a,b) 内至少存在一点 ,使 得 f ( ) 0.
需回答的问题: (1) 罗尔中值定理与拉格朗日中值定理的联系与
高等数学-中值定理与导数的应用省名师优质课赛课获奖课件市赛课一等奖课件

仍属
0 0
型, 且
f
( x) ,
F ( x) 满足定
理1条件, 则
lim f (x) lim f (x) lim f (x)
F ( x)
F ( x)
F ( x)
例1.
求Leabharlann x3 3x 2lim
x1
x3
x2
x
1
.
0型 0
解: 原式 lim 3x2 3 x1 3x2 2x 1
lim 6x 3 x1 6x 2 2
(1) 在区间 [a , b] 上连续
(2) 在区间 (a , b) 内可导
y
y f (x)
o
a
bx
(3) f ( a ) = f ( b )
在( a , b ) 内至少存在一点 , 使 f ( ) 0.
证:因 f (x) 在[a , b]上连续,故在[ a , b ]上取得最大值
M 和最小值 m .
因为
1
1 1 x
故 ln(1 x) ln x x (x 0). 1 x
例6. 证明不等式 x ln(1 x) x (x 0). 1 x
证: 设 f (t) ln(1 t) , 则 f (t) 在[0, x]上满足拉格朗日
中值定理条件, 所以应有
f (x) f (0) f ( )(x 0), 0 x
x0
x
sin x3
x
.
0型 0
解:
原式 lim x0
1 cos x 3x2
lim sin x x0 6x
1 6
例5.
求lim x0
ln(1 x2
x)
.
1
解: 原式 lim 1 x x0 2x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
也可写成 y f ( x 0 x ) x (0 1). 增量 y的精确表达式 .
拉格朗日中值公式又称有限增量公式. 拉格朗日中值定理又称有限增量定理.
微分中值定理
推论 如果函数 f ( x ) 在区间 I 上的导数恒为零 , 那末 f ( x ) 在区间 I 上是一个常数 .
五、证明下列不等式: 1、 arctan a arctan b a b ; 2、当x 1时 , e x ex . 六、证明方程 x 5 x 1 0 只有一个正根 .
七、设函数 y f ( x ) 在 x 0 的某邻域内且有 n 阶导数, 且 f (0) f (0) f ( n 1) ( 0) 试用柯西中值定理 f ( x ) f ( n ) (x ) 证明: n , ( 0 1). n! x 八、设 f ( x ) 在[ a , b ]内上连续,在( a , b )内可导,若 0 a b ,则在( a , b )内存在一点 ,使 af (b ) bf (a ) [ f ( ) f ( )](a b ) ] .
f ( x )在[0, x ]上满足拉氏定理的条件 ,
f ( x ) f (0) f ( )( x 0), (0 x ) 1 f ( 0 ) 0, f ( x ) , 由上式得 ln(1 x ) x , 1 x 1 1 1 又0 x 1, 1 1 1 x 1 x 1 x x x x, 即 ln(1 x ) x . 1 x 1 1 x
(a , b) 内至少有一点(a b ),使等式
f (b ) f (a ) f ' ( )(b a ) 成立.
注意 : 与罗尔定理相比条件中 去掉了 f ( a ) f (b ).
f (b) f (a ) 结论亦可写成 f ( ). ba
几何解释:
在曲线弧 AB 上至少有 一点 C , 在该点处的切 线平行于弦 AB .
一、罗尔(Rolle)定理
罗尔(Rolle)定理 如果函数 f ( x )在闭区间 [a , b] ( 2) ( 3) 上连续,在开区间 (a , b) 内可导,且在区间端点的函数 值相等,即 f (a ) f (b ),那末在 (a , b ) 内至少有一点 (a b ),使得函数 f ( x )在该点的导数等于零,
例2
证明 arcsin x arccos x ( 1 x 1). 2
1 1 x
2
证 设 f ( x ) arcsin x arccos x , x [1,1]
f ( x) C ,
x [ 1,1]
但 f ( x ) 5( x 4 1) 0, ( x ( 0,1)) 矛盾, 为唯一实根 .
二、拉格朗日(Lagrange)中值定理
拉格朗日(Lagrange)中值定理 如果函数 f(x)在 闭区间[a , b]上连续,在开区间(a , b ) 内可导,那末在
( 2) (1)
f (a ) f (b ),
最值不可能同时在端点 取得 . 设 M f ( a ), 则在 (a , b ) 内至少存在一点 使 f ( ) M .
f ( x ) f ( ),
f ( x ) f ( ) 0,
f ( x ) f ( ) 若 x 0, 则有 0; x f ( x ) f ( ) 0; 若 x 0, 则有 x f ( x ) f ( ) f ( ) lim 0; x 0 x f ( x ) f ( ) f ( ) lim 0; x 0 x
o
F (a ) F ( 1 ) F ( x )
x
f (b) f (a ) ( x ) f ( x ) f ( a ) [ F ( x ) F (a )]. F (b) F (a ) ( x ) 满足罗尔定理的条件 ,
证 作辅助函数
则在( a , b )内至少存在一点 , 使得 ( ) 0.
则在( a , b )内至少存在一点 , 使得 ( ) 0.
即 f ( ) f (b) f (a ) F ( ) 0, F (b) F (a )
f ( b ) f ( a ) f ( ) . F ( b ) F ( a ) F ( )
三、柯西(Cauchy)中值定理
柯西(Cauchy)中值定理 如果函数 f ( x ) 及 F ( x ) 在闭区间[a , b]上连续,在开区间(a , b) 内可导,且 F ' ( x ) 在(a , b ) 内每一点处均不为零,那末在(a , b ) 内至少 有一点(a b),使等式
又 f ( 0) arcsin 0 arccos 0 0 , 2 2 即C . 2 arcsin x arccos x . 2
x ln(1 x ) x . 例3 证明当 x 0时, 1 x 证 设 f ( x ) ln(1 x ),
y
C
M N
y f ( x)
B D
A
o a
1
x
2 b
x
证 分析: 条件中与罗尔定理相差 f (a ) f (b ).
f (b) f (a ) 弦AB方程为 y f (a ) ( x a ). ba 曲线 f ( x ) 减去弦 AB ,
所得曲线 a , b两端点的函数值相等 .
当 F ( x) x,
F ( b ) F (a ) b a , F ( x ) 1,
f (b) f (a ) f ( ). ba
f ( b ) f ( a ) f ( ) F ( b ) F ( a ) F ( )
例4 设函数 f ( x )在[0,1]上连续 , 在(0,1)内可导, 证明 :
f (a ) f (b) f ' ( ) ' 成立. F (a ) F (b) F ( )
几何解释:
在曲线弧 AB上至少有 一点C ( F ( ), f ( )), 在 该点处的切线平行于 弦AB .
y
C
X F ( x) Y f ( x) M B
A
N
D
F ( 2 )F ( b )
' f 即 () 0
(1)
例如, f ( x ) x 2 2 x 3 ( x 3)( x 1).
在[1,3]上连续 ,
f ( x ) 2( x 1),
在( 1,3)上可导,
且 f ( 1) f ( 3) 0,
f ( ) 0.
取 1, (1 ( 1,3))
或 f (b ) f (a ) f ( )(b a ).
拉格朗日中值公式
注意:拉氏公式精确地表达了函数在一个区间上的 增量与函数在这区间内某点处的导数之间的关系.
设 f ( x )在 在(a , b )内可导, x 0 , x 0 x (a , b ), 则有
f ( x 0 x ) f ( x 0 ) f ( x 0 x ) x (0 1).
几何解释:
在曲线弧 AB上至少有一 点C , 在该点处的切线是 水平的.
y
C
y f ( x)
o a
1
2
b
x
证 f ( x ) 在 [a , b] 连续 , 必有最大值 M 和最小值 m .
(1) 若 M m . 则 f ( x) M . 都有 f ( ) 0. 由此得 f ( x ) 0. (a , b ), ( 2) 若 M m .
且 f (0) 1, f (1) 3.
x 0 ( 0,1), 使 f ( x 0 ) 0. 即为方程的小于1的正实根. 设另有 x1 (0,1), x1 x 0 , 使 f ( x1 ) 0.
f ( x ) 在 x0 , x1 之间满足罗尔定理的条 件, 至少存在一个 (在 x0 , x1 之间), 使得 f ( ) 0.
f ( )存在,
f ( ) f ( ).
只有 f ( ) 0.
注意:若罗尔定理的三个条件中有一个不满足,其 结论可能不成立. 例如, y x , x [ 2,2];
在[2,2]上除f (0)不存在外, 满足罗尔定理的 一切条件 , 但在内找不到一点能使 f ( x ) 0.
x [a , b ]
且 ab 0
不满足在开区间内可微的条件; 以上两个都可说明问题.
练习题
一、 填空题: 1、 函数 f ( x ) x 4 在区间[1,2]上满足拉格朗日中值 定理,则ξ=_______. 2、 设 f ( x ) ( x 1)( x 2)( x 3)( x 4) , 方 程 f ( x ) 0 有____________个根,它们分别在区间 _____________上. 3、 罗 尔 定 理 与 拉 格 朗 日 定 理 之 间 的 关 系 是 _________________. 4、 微分中值定理精确地表达函数在一个区间上的 _______与函数在这区间内某点处的_______之间 的关系. 5、 如果函数 f ( x ) 在区间 I 上的导数__________,那 么 f ( x ) 在区间 I 上是一个常数.
在(0,1)内至少存在一点 , 有
f (1) f (0) f ( ) 1 0 2
即 f ( ) 2[ f (1) f (0)].
四、小结
罗尔定理、拉格朗日中值定理及柯西中值定理 之间的关系;
Rolle f (a ) f (b ) Lagrange 定理 中值定理
拉格朗日中值公式又称有限增量公式. 拉格朗日中值定理又称有限增量定理.
微分中值定理
推论 如果函数 f ( x ) 在区间 I 上的导数恒为零 , 那末 f ( x ) 在区间 I 上是一个常数 .
五、证明下列不等式: 1、 arctan a arctan b a b ; 2、当x 1时 , e x ex . 六、证明方程 x 5 x 1 0 只有一个正根 .
七、设函数 y f ( x ) 在 x 0 的某邻域内且有 n 阶导数, 且 f (0) f (0) f ( n 1) ( 0) 试用柯西中值定理 f ( x ) f ( n ) (x ) 证明: n , ( 0 1). n! x 八、设 f ( x ) 在[ a , b ]内上连续,在( a , b )内可导,若 0 a b ,则在( a , b )内存在一点 ,使 af (b ) bf (a ) [ f ( ) f ( )](a b ) ] .
f ( x )在[0, x ]上满足拉氏定理的条件 ,
f ( x ) f (0) f ( )( x 0), (0 x ) 1 f ( 0 ) 0, f ( x ) , 由上式得 ln(1 x ) x , 1 x 1 1 1 又0 x 1, 1 1 1 x 1 x 1 x x x x, 即 ln(1 x ) x . 1 x 1 1 x
(a , b) 内至少有一点(a b ),使等式
f (b ) f (a ) f ' ( )(b a ) 成立.
注意 : 与罗尔定理相比条件中 去掉了 f ( a ) f (b ).
f (b) f (a ) 结论亦可写成 f ( ). ba
几何解释:
在曲线弧 AB 上至少有 一点 C , 在该点处的切 线平行于弦 AB .
一、罗尔(Rolle)定理
罗尔(Rolle)定理 如果函数 f ( x )在闭区间 [a , b] ( 2) ( 3) 上连续,在开区间 (a , b) 内可导,且在区间端点的函数 值相等,即 f (a ) f (b ),那末在 (a , b ) 内至少有一点 (a b ),使得函数 f ( x )在该点的导数等于零,
例2
证明 arcsin x arccos x ( 1 x 1). 2
1 1 x
2
证 设 f ( x ) arcsin x arccos x , x [1,1]
f ( x) C ,
x [ 1,1]
但 f ( x ) 5( x 4 1) 0, ( x ( 0,1)) 矛盾, 为唯一实根 .
二、拉格朗日(Lagrange)中值定理
拉格朗日(Lagrange)中值定理 如果函数 f(x)在 闭区间[a , b]上连续,在开区间(a , b ) 内可导,那末在
( 2) (1)
f (a ) f (b ),
最值不可能同时在端点 取得 . 设 M f ( a ), 则在 (a , b ) 内至少存在一点 使 f ( ) M .
f ( x ) f ( ),
f ( x ) f ( ) 0,
f ( x ) f ( ) 若 x 0, 则有 0; x f ( x ) f ( ) 0; 若 x 0, 则有 x f ( x ) f ( ) f ( ) lim 0; x 0 x f ( x ) f ( ) f ( ) lim 0; x 0 x
o
F (a ) F ( 1 ) F ( x )
x
f (b) f (a ) ( x ) f ( x ) f ( a ) [ F ( x ) F (a )]. F (b) F (a ) ( x ) 满足罗尔定理的条件 ,
证 作辅助函数
则在( a , b )内至少存在一点 , 使得 ( ) 0.
则在( a , b )内至少存在一点 , 使得 ( ) 0.
即 f ( ) f (b) f (a ) F ( ) 0, F (b) F (a )
f ( b ) f ( a ) f ( ) . F ( b ) F ( a ) F ( )
三、柯西(Cauchy)中值定理
柯西(Cauchy)中值定理 如果函数 f ( x ) 及 F ( x ) 在闭区间[a , b]上连续,在开区间(a , b) 内可导,且 F ' ( x ) 在(a , b ) 内每一点处均不为零,那末在(a , b ) 内至少 有一点(a b),使等式
又 f ( 0) arcsin 0 arccos 0 0 , 2 2 即C . 2 arcsin x arccos x . 2
x ln(1 x ) x . 例3 证明当 x 0时, 1 x 证 设 f ( x ) ln(1 x ),
y
C
M N
y f ( x)
B D
A
o a
1
x
2 b
x
证 分析: 条件中与罗尔定理相差 f (a ) f (b ).
f (b) f (a ) 弦AB方程为 y f (a ) ( x a ). ba 曲线 f ( x ) 减去弦 AB ,
所得曲线 a , b两端点的函数值相等 .
当 F ( x) x,
F ( b ) F (a ) b a , F ( x ) 1,
f (b) f (a ) f ( ). ba
f ( b ) f ( a ) f ( ) F ( b ) F ( a ) F ( )
例4 设函数 f ( x )在[0,1]上连续 , 在(0,1)内可导, 证明 :
f (a ) f (b) f ' ( ) ' 成立. F (a ) F (b) F ( )
几何解释:
在曲线弧 AB上至少有 一点C ( F ( ), f ( )), 在 该点处的切线平行于 弦AB .
y
C
X F ( x) Y f ( x) M B
A
N
D
F ( 2 )F ( b )
' f 即 () 0
(1)
例如, f ( x ) x 2 2 x 3 ( x 3)( x 1).
在[1,3]上连续 ,
f ( x ) 2( x 1),
在( 1,3)上可导,
且 f ( 1) f ( 3) 0,
f ( ) 0.
取 1, (1 ( 1,3))
或 f (b ) f (a ) f ( )(b a ).
拉格朗日中值公式
注意:拉氏公式精确地表达了函数在一个区间上的 增量与函数在这区间内某点处的导数之间的关系.
设 f ( x )在 在(a , b )内可导, x 0 , x 0 x (a , b ), 则有
f ( x 0 x ) f ( x 0 ) f ( x 0 x ) x (0 1).
几何解释:
在曲线弧 AB上至少有一 点C , 在该点处的切线是 水平的.
y
C
y f ( x)
o a
1
2
b
x
证 f ( x ) 在 [a , b] 连续 , 必有最大值 M 和最小值 m .
(1) 若 M m . 则 f ( x) M . 都有 f ( ) 0. 由此得 f ( x ) 0. (a , b ), ( 2) 若 M m .
且 f (0) 1, f (1) 3.
x 0 ( 0,1), 使 f ( x 0 ) 0. 即为方程的小于1的正实根. 设另有 x1 (0,1), x1 x 0 , 使 f ( x1 ) 0.
f ( x ) 在 x0 , x1 之间满足罗尔定理的条 件, 至少存在一个 (在 x0 , x1 之间), 使得 f ( ) 0.
f ( )存在,
f ( ) f ( ).
只有 f ( ) 0.
注意:若罗尔定理的三个条件中有一个不满足,其 结论可能不成立. 例如, y x , x [ 2,2];
在[2,2]上除f (0)不存在外, 满足罗尔定理的 一切条件 , 但在内找不到一点能使 f ( x ) 0.
x [a , b ]
且 ab 0
不满足在开区间内可微的条件; 以上两个都可说明问题.
练习题
一、 填空题: 1、 函数 f ( x ) x 4 在区间[1,2]上满足拉格朗日中值 定理,则ξ=_______. 2、 设 f ( x ) ( x 1)( x 2)( x 3)( x 4) , 方 程 f ( x ) 0 有____________个根,它们分别在区间 _____________上. 3、 罗 尔 定 理 与 拉 格 朗 日 定 理 之 间 的 关 系 是 _________________. 4、 微分中值定理精确地表达函数在一个区间上的 _______与函数在这区间内某点处的_______之间 的关系. 5、 如果函数 f ( x ) 在区间 I 上的导数__________,那 么 f ( x ) 在区间 I 上是一个常数.
在(0,1)内至少存在一点 , 有
f (1) f (0) f ( ) 1 0 2
即 f ( ) 2[ f (1) f (0)].
四、小结
罗尔定理、拉格朗日中值定理及柯西中值定理 之间的关系;
Rolle f (a ) f (b ) Lagrange 定理 中值定理
