学生用：初中数学二次函数存在性问题总复习试题及解答

合集下载

二次函数存在性问题专题复习(全面典型含答案)

中考数学专题复习——存在性问题存在性问题是指判断满足某种条件的事物是否存在的问题，这类问题的知识覆盖面较广，综合性较强，题意构思非常精巧，解题方法灵活，对学生分析问题和解决问题的能力要求较高，是近几年来包括深圳在内各地中考的“热点”。

这类题目解法的一般思路是：假设存在→推理论证→得出结论。

若能导出合理的结果，就做出“存在”的判断，导出矛盾，就做出不存在的判断。

以下为几种典型的二次函数中出现的存在性问题，讲解后希望各位考生在以后的考试中如果遇到此类型时能够很顺畅的把过程写下来。

一、二次函数中相似三角形的存在性问题1.（2011枣庄10分）如图，在平面直角坐标系xoy 中，把抛物线2y x =向左平移1个单位，再向下平移4个单位，得到抛物线2()y x h k =-+.所得抛物线与x 轴交于A ，B 两点（点A 在点B 的左边），与y 轴交于点C ，顶点为D. （1）写出h k 、的值；（2）判断△ACD 的形状，并说明理由；（3）在线段AC 上是否存在点M ，使△AOM ∽△ABC ？若存在，求出点M 的坐标；若不存在，说明理由.2.（2011临沂13分）如图，已知抛物线经过A （﹣2，0），B （﹣3，3）及原点O ，顶点为C ．（1）求抛物线的解析式；（2）若点D 在抛物线上，点E 在抛物线的对称轴上，且A 、O 、D 、E 为顶点的四边形是平行四边形，求点D 的坐标；（3）P 是抛物线上的第一象限内的动点，过点P 作PM ⊥x 轴，垂足为M ，是否存在点P ，使得以P 、M 、A 为顶点的三角形△BOC 相似？若存在，求出点P 的坐标；若不存在，请说明理由．二、二次函数中面积的存在性问题3. （2011日照10分）如图，抛物线()20y ax bx a >=+与双曲线ky x=相交于点A ，B ．已知点B 的坐标为（－2，－2），点A 在第一象限内，且tan ∠AOX 错误!未找到引用源。

中考数学二次函数存在性问题与参考答案

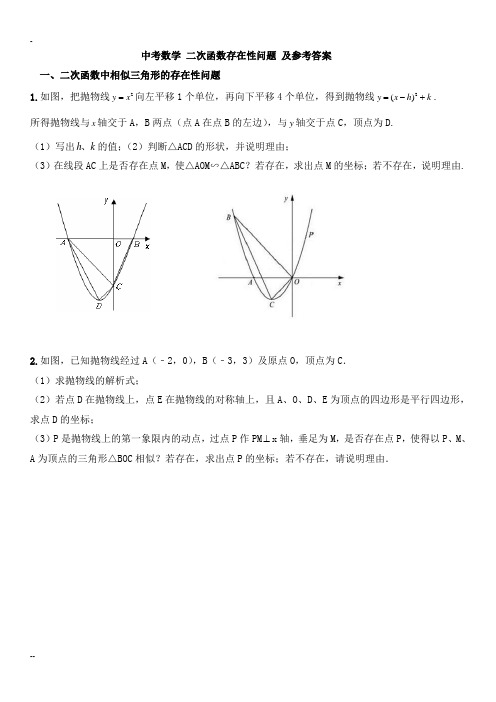
中考数学二次函数存在性问题及参考答案一、二次函数中相似三角形的存在性问题1.如图，把抛物线2=向左平移1个单位，再向下平移4个单位，得到抛物线2y x=-+.y x h k()所得抛物线与x轴交于A，B两点（点A在点B的左边），与y轴交于点C，顶点为D.（1）写出h k、的值；（2）判断△ACD的形状，并说明理由；（3）在线段AC上是否存在点M，使△AOM∽△ABC？若存在，求出点M的坐标；若不存在，说明理由.2.如图，已知抛物线经过A（﹣2，0），B（﹣3，3）及原点O，顶点为C．（1）求抛物线的解析式；（2）若点D在抛物线上，点E在抛物线的对称轴上，且A、O、D、E为顶点的四边形是平行四边形，求点D的坐标；（3）P是抛物线上的第一象限内的动点，过点P作PM⊥x轴，垂足为M，是否存在点P，使得以P、M、A为顶点的三角形△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．二、二次函数中面积的存在性问题3.如图，抛物线()20y ax bx a >=+与双曲线ky x=相交于点A ，B ．已知点B 的坐标为（－2，－2），点A 在第一象限内，且tan ∠AOX ＝4．过点A 作直线AC ∥x 轴，交抛物线于另一点C ．（1）求双曲线和抛物线的解析式；（2）计算△ABC 的面积；（3）在抛物线上是否存在点D ，使△ABD 的面积等于△ABC 的面积．若存在，请你写出点D 的坐标；若不存在，请你说明理由．4.如图，抛物线y ＝ax 2＋c （a ＞0）经过梯形ABCD 的四个顶点，梯形的底AD 在x 轴上，其中A （－2,0），B （－1, －3）．（1）求抛物线的解析式；（3分）（2）点M 为y 轴上任意一点，当点M 到A 、B 两点的距离之和为最小时，求此时点M 的坐标；（2分）（3）在第（2）问的结论下，抛物线上的点P 使S △PAD ＝4S △ABM 成立，求点P 的坐标．（4分） (4)在抛物线的BD 段上是否存在点Q 使三角形BDQ 的面积最大，若有，求出点Q 的坐标，若没有，请说明理由。

中考数学总复习《二次函数中的相似三角形存在性问题》专题训练-附答案

中考数学总复习《二次函数中的相似三角形存在性问题》专题训练-附答案学校:___________班级：___________姓名：___________考号：___________1．如图，在平面直角坐标系xOy 中，直线AB 的函数表达式为2(0y ax a a =-≠，a 为常数），点A 、B 分别在y 轴和x 轴上，且2OA OB =，点A 关于x 轴的对称点为C ，点B 关于y 轴的对称点为D ，以点C 为顶点的抛物线经过点D ．(1)求点,A B 的坐标；(2)求抛物线的解析式；(3)在（2）中拋物线的对称轴上有一点P ，且以点D O P 、、为顶点的三角形与AOB 相似，求出所有满足条件的点P 的坐标．2．已知在平面直角坐标系中，抛物线212y x bx c =-++与x 轴相交于点A ，B ，与y 轴相交于点C ，直线4y x =+经过A ，C 两点(1)求抛物线的表达式；(2)如果点P ，Q 在抛物线上，并与对称轴对称，（P 点在对称轴左边），且2PQ AO =，求P ，Q 的坐标；(3)动点M 在直线4y x =+上，且ABC 与COM 相似，求点M 的坐标．3．已知：抛物线2:3L y x bx =+-交x 轴于(),3,0A B 两点，交y 轴于C ．(1)求抛物线的解析式；(2)如图1，点D 在第四象限的抛物线上，DE BC ⊥于点E ，若12DE BE =，求点D 的坐标； (3)如图2，抛物线L 经过平移后得到抛物线21:4H y x =-，直线OP 交抛物线的其中一个点为P ，直线PQ 与抛物线有且只有一个交点P ，且与y 轴不平行，⊥OQ OP 交PQ 于点Q ，求点Q 的纵坐标．4．如图，抛物线22y ax x c =++与x 轴交于1,0A ，B 两点，与y 轴交于点G ，抛物线的对称轴为直线=1x -，交x 轴于点E ，交抛物线于点F ，连接BC ．(1)求抛物线的解析式．(2)如图，点P 是线段BC 上一动点，过点P 作PD x ⊥轴，交抛物线于点D ，问当动点P 运动到什么位置时，四边形CEBD 的面积最大？求出四边形CEBD 的最大面积及此时P 点的坐标．(3)坐标轴上是否存在点G ，使得以A ，C ，G 为顶点的三角形与BCF △相似？若存在，请求出点G 的坐标；若不存在，请说明理由．5．如图，抛物线22y ax bx =-+-经过A （4，0），B （1，0）两点．(1)求出抛物线的解析式；(2)P 是抛物线在第一象限上的一动点，过P 作PM x ⊥轴，垂足为M ，是否存在P 点，使得以A ，P ，M 为顶点的三角形与OAC 相似？若存在，请求出符合条件的点P 的坐标；若不存在，请说明理由；(3)若抛物线上有一点Q （点Q 不与点B 重合），使得点Q 与点B 到直线AC 的距离相等，请直接写出点Q 坐标．6．如图，已知二次函数的图象与x 轴交于1,0A 和()3,0B -两点，与y 轴交于点()0,3C -，直线2y x m =-+经过点A ，且与y 轴交于点D ，与抛物线交于点E ．(1)求抛物线的解析式；(2)如图1，点M 在AE 下方的抛物线上运动，求AME △的面积最大值；(3)如图2，在y 轴上是否存在点P ，使得以D 、E 、P 为顶点的三角形与AOD △相似，若存在，求出点P 的坐标；若不存在，试说明理由．7．如图1，平面直角坐标系中，抛物线2y ax bx c =++交x 轴于1,0A ，()3,0B -两点，交y 轴于点()0,3C ，点M 是线段OB 上一个动点，过点M 作x 轴的垂线，交直线BC 于点F ，交抛物线于点E ．(1)求抛物线的解析式； (2)当BCE 面积最大时，求M 点的坐标；(3)如图2，是否存在以点C 、E 、F 为顶点的三角形与ABC 相似，若存在，求点M 的坐标；若不存在，请说明理由．8．如图①，抛物线2y x bx c =-++与x 轴交于两点A ，()4,0B （点A 位于点B 的左侧），与y 轴交于点()0,4C ，拋物线的对称轴l 与x 轴交于点N ，长为2的线段PQ （点P 位于点Q 的上方）在x 轴上方的抛物线对称轴上运动．(1)求抛物线的关系式；(2)在线段PQ 运动过程中，当PC PA +的值最小时，求此时点P 的坐标；(3)如图①过点P 作PM y ⊥轴于点M ，当CPM △和QBN 相似时，求点Q 的坐标．9．如图，已知抛物线2y ax bx c =++与x 轴交于A 、()3,0B 两点，与y 轴交于点C ，顶点为()2,1D -，直线l 是抛物线的对称轴．(1)求抛物线的函数表达式；(2)点M 是直线l 上的动点，当以点M 、B 、D 为顶点的三角形与ABC 相似时，求点M 的坐标． 10．如图，抛物线23y ax bx =++经过点于()1,0A -，()3,0B 两点，与y 轴交于点C ，连接AC ．(1)求抛物线的解析式；(2)如图①，若点E 是第二象限内抛物线上的一点，直线AE 与BC 相交于点F ，连接CE ，BE ，若BCE 的面积3，求点E 的横坐标；(3)如图①，点D 与点C 关于抛物线的对称轴对称，直线AD 交y 轴于点G ，点P 在平面内，以点B ，C ，P 为顶点的三角形与ACG 相似且∠=∠CBP CAG 时，请直接写出符合条件的点P 的坐标．11．如图，顶点为D 的抛物线2y x bx c =-++与x 轴交于A ，B 两点（点A 在点B 的左侧），与y 轴交于点C ，直线3y x =-+经过点B ，C ．(1)求抛物线的解析式；(2)连接AC ，CD ，BD ．求证：ACO DBC ∽△△；(3)点P 为抛物线对称轴上的一个动点，点M 是平面直角坐标系内一点，当以点A ，C ，M ，P 为顶点的四边形是菱形时，请直接写出点P 的坐标．12．已知抛物线2y x bx c =++与x 轴交于()()1030A B ，、，两点，且与y 轴的公共点为点C ，设该抛物线的顶点为D ．(1)求抛物线的表达式，并求出顶点D 的坐标；(2)若点P 为抛物线上一点，且满足PB PC =，求点P 的横坐标；(3)连接CD BC ，，点E 为线段BC 上一点，过点E 作EF CD ⊥交CD 于点F ，若12=DF CF ，求点E 的坐标． 13．如图，在平面直角坐标系xOy 中，抛物线213442y x x =-++与两坐标轴分别相交于A B C ，，三点．(1)求证：90ACB ∠=︒；(2)点D 是第一象限内抛物线上的动点，过点D 作x 轴的垂线交BC 于点E ，交x 轴于点F ．①求255DE BE +的最大值； ①点G 是AC 的中点，若以点C D E ，，为顶点的三角形与AOG 相似，求点D 的坐标．14．如图，抛物线2134y x x =-++与x 轴交于A ，B 两点（点A 在点B 的左侧），与y 轴交于点C ，顶点为D ，抛物线的对称轴与x 轴交于点E ，连接AC ，BD ．(1)求点A ，B ，C ，D 的坐标；(2)点F 为抛物线对称轴上的动点，且BEF △与AOC 相似，请直接写出符合条件的点F 的坐标；(3)点P 为抛物线上的动点，是否存在这样的点P ，使BDP △是直角三角形？若存在，请求出点P 的坐标；若不存在，请说明理由．15．如图，已知A （﹣2，0）、B （3，0），抛物线y ＝ax 2＋bx ＋4经过A 、B 两点，交y 轴于点C ．点P 是第一象限内抛物线上的一动点，点P 的横坐标为m ．过点P 作PM ①x 轴，垂足为点M ，PM 交BC 于点Q ．过点P 作PN ①BC ，垂足为点N ．(1)直接写出抛物线的函数关系式；(2)请用含m 的代数式表示线段PN 的长；(3)连接PC ，在第一象限的抛物线上是否存在点P ，使得①BCO ＋2①PCN ＝90°？若存在，请求出m 的值；若不存在，请说明理由；(4)连接AQ ，若△ACQ 为等腰三角形，请直接写出m 的值．参考答案：1．(1)()0,4A ()2,0B(2)抛物线的解析式为24y x =-(3)满足条件的点P 的坐标为()0,4或()0,4-或()0,1或()0,1-2．(1)2142y x x =--+(2)775,,3,22P Q ⎛⎫⎛⎫---- ⎪ ⎪⎝⎭⎝⎭ (3)84,33⎛⎫- ⎪⎝⎭或()3,1-3．(1)抛物线解析式为223y x x =--(2)()2,3D -(3)12Q y =-4．(1)223y x x =+-(2)当32m =-，四边形CEBD 的面积最大，最大面积为518，此时点P 的坐标为33,22⎛⎫-- ⎪⎝⎭(3)存在，点G 的坐标为()()10,0,0,,9,03⎛⎫- ⎪⎝⎭5．(1)抛物线的解析式为215222y x x =-+- (2)存在，符合条件的点P 的坐标为（2，1）(3)点Q 的坐标为（3，1）或75(27,)22+-或75(27,)22---6．(1)223y x x =+-；(2)27；(3)存在，点P 的坐标为()0,12或290,2⎛⎫ ⎪⎝⎭．7．(1)223y x x =--+；(2)3,02M ⎛⎫- ⎪⎝⎭； (3)存在， 3,02M ⎛⎫- ⎪⎝⎭或5,03M ⎛⎫- ⎪⎝⎭．8．(1)234y x x =-++(2)35,22P ⎛⎫ ⎪⎝⎭(3)Q 的坐标是35,24⎛⎫ ⎪⎝⎭或3,52⎛⎫ ⎪⎝⎭或3219,22⎛⎫+ ⎪ ⎪⎝⎭9．(1)243y x x =-+(2)点M 的坐标是()2,2或12,3⎛⎫- ⎪⎝⎭．10．(1)223y x x =-++(2)3172- (3)()16,3-P 263,55⎛⎫ ⎪⎝⎭P ()30,9P 4129,55⎛⎫ ⎪⎝⎭P11．(1)223y x x =-++(3)()11，或()16，或()16-，或()10，12．(1)243y x x =-+ ()21-，(2)51351322⎛⎫-- ⎪⎝⎭，或51351322⎛⎫++ ⎪⎝⎭， (3)207,99⎛⎫ ⎪⎝⎭13．(2)①9；①(4,6)D 或25(3,)4D ．14．(1)()()2,0,6,0A B - ()0,3C ()2,4D (2)()2,6或()2,6-或82,3⎛⎫ ⎪⎝⎭或82,3⎛⎫- ⎪⎝⎭； (3)()2,0-或()6,12--15．(1)222433y x x =-++(2)22655PN m m =-+(3)存在 74 (4)65或125。

中考数学总复习《二次函数中的面积问题存在性问题》专题训练-附答案

中考数学总复习《二次函数中的面积问题存在性问题》专题训练-附答案学校:___________班级：___________姓名：___________考号：___________1．如图，在平面直角坐标系中，二次函数()230y ax bx a =++≠的图象与x 轴交于()3,0A ，()1,0B -两点，与y 轴交于点C ．(1)求抛物线的函数解析式；(2)P 是直线AC 上方的抛物线上一动点，当ACP △的面积最大时，求点P 的坐标．2．综合与探究：如图，在平面直角坐标系中，二次函数228y x x =--的图像与x 轴交于A ，B 两点，点A 在点B 的左侧，与y 轴交于点C ，点P 是直线BC 下方抛物线上的一个动点．(1)求点A ，B ，C 的坐标；(2)连接PO 和PC ，并将POC △沿y 轴对折，得到四边形POP C '．是否存在点P ，使四边形POP C '为菱形？若存在，求出此时点P 的坐标；若不存在，请说明理由；(3)当点P 运动到什么位置时，四边形ABPC 的面积最大？求出此时点P 的坐标和四边形ABPC 的最大面积． 3．如图，抛物线2y x bx c =-++过点(1,0)A -和(3,0)B ，与y 轴交于点C ．(1)求抛物线的解析式；(2)点P 为抛物线对称轴上一动点，当PCB 是以BC 为底边的等腰三角形时，求P 的坐标；(3)在（2）条件下，是否存在点M 为抛物线上的点，使得2BCM BCP S S =△△？若存在，求出点M 的横坐标；若不存在，请说明理由．4．综合与实践如图，在平面直角坐标系中，直线4y x =-+与两坐标轴分别交于B 、C 两点，抛物线2(1)y x m x m =-+-+经过B 、C 两点与x 轴的另一个交点为A ．(1)求m 的值(2)直接写出点A 的坐标(3)已知点D 在第一象限的抛物线上，过点D 作DE OC ∥交直线BC 于点E ，点E 的坐标为()2,2，点F 在第二象限的抛物线上，且5FDE S =△，求点F 到直线DE 的距离(4)在（3）的条件下，在坐标平面内是否存在点P ，使以A 、D 、E 、P 为顶点的四边形是平行四边形？若存在，请直接写出点P 的坐标，若不存在，请说明理由5．如图，二次函数2y x bx c =-++的图象经过坐标原点，与x 轴交于点()2,0A -．(1)求此二次函数的解析式及点顶点B 的坐标；(2)在抛物线上否存在点P ，使1AOP S =？若存在，请求出点P 的坐标；如果不存在，请说明理由． 6．在平面直角坐标系xOy 中，抛物线22y ax ax c =-+（0a >，a 、c 为常实数）交x 轴于A 、B 两点，与y 轴交于C 点．(1)如图1，若(1,0),(2,3)A D --在此抛物线上，求出这个抛物线解析式；(2)如图2，在（1）的条件下，M 为（1）中抛物线第四象限一动点，连CM 、BM ，求能使四边形ABMC 面积最大时的M 点坐标；并求出四边形ABMC 的最大面积．(3)将抛物线平移到以坐标原点O 为顶点的位置，P 为坐标系y 轴正半轴上一点，E 、F 为平移后的抛物线上两点，E 始终在F 点左边，连AE 、AF 、EF ，若E 、F 点横坐标分别为m 、，则当PEF 为等腰直角三角形，且90EPF ∠=︒时，求m 、n 间的数量关系．7．如图，抛物线2y x bx c =++与x 轴交于()1,0A -，()3,0B 两点．(1)求该抛物线的解析式；(2)连接BC ，点P 是直线BC 下方抛物线上的动点，当点P 在该抛物线上什么位置时，PBC 面积最大，最大值为多少，并求出此时P 点的坐标；(3)设点D 是该抛物线的对称轴上的一点，在抛物线上是否存在点Q ，使得以B 、C 、D 、Q 为顶点的四边形是平行四边形，若存在，求出Q 点的坐标；若不存在，请说明理由．8．如图，有长为30m 的篱笆，一面利用墙（墙的最大可用长度为10m ），围成中间隔有一道篱笆（平行于AB ）的矩形花圃．设花圃的一边AB 为m x ，面积为2m y ．(1)求y 与x 的函数关系式；(2)如果要围成面积为263m 的花圃，AB 的长是多少？(3)当x 取何值时，y 有最大值？并求出最大值．9．如图，抛物线2y ax =与直线y bx c =+的两个交点分别为()2,4A -和()1,1B ．(1)求a ，b ，c 的值；(2)连接,AO BO ，求ABO 的面积；(3)点P 在y 轴上，且ABP 的面积是ABO 面积的2倍，求点P 的坐标．10．如图，直线1y x =+与抛物线245y x x =-+交于A ，B 两点，点P 是y 轴上的一个动点．(1)求A 、B 两点坐标．(2)当PAB 的周长达最小时，求P 点坐标和PAB 的面积．11．如图，抛物线23y x bx c =-++交x 轴于点()1,0A -和B ，交y 轴于点()0,33C ，顶点为D ．(1)求抛物线的表达式；(2)若点E 在第一象限内对称右侧的抛物线上，四边形ODEB 的面积为73，求点E 的坐标；12．如图，在平面直角坐标系xOy 中，抛物线2y ax bx c =++与x 轴交于点()30A -,和点()10B ,，顶点为D ．直线l 与抛物线交于B ，C 两点，其中点C 的坐标为()2,3--．(1)求抛物线和直线l 的解析式；(2)直线l 与抛物线的对称轴交于点E ，P 为线段BC 上一动点（点P 不与点B ，C 重合），过点P 作PF ∥DE 交抛物线于点F ，设点P 的横坐标为t ．①当t 为何值时，四边形PEDF 是平行四边形；①设BCF 的面积为S ，当t 为何值时，S 最大？最大值是多少？13．如图，直线l ：33y x =--与x 轴、y 轴分别相交于A ，B 两点，与抛物线224y ax ax a =++-交于点B ．(1)求该抛物线的解析式；(2)已知点M 是抛物线上的一个动点，并且点M 在第三象限内，连接AM 、BM ，设点M 的横坐标为m ，四边形OAMB 的面积为S ，求S 与m 的函数表达式，并求出S 的最大值；(3)若点C 在直线AB 上，抛物线上是否存在点D 使得以O ，B ，C ，D 为顶点的四边形是平行四边形．若存在，请直接写出点D 的坐标．14．如图，抛物线2y ax 2x c =++经过点()3,0A -和点()1,0B ，与y 轴交于点C ，点P 在直线AC 下方的抛物线上，过点P 作PQ y ∥轴交AC 于点Q ，连接PA ，PC ，BC ，设点P 的横坐标为m ．(1)求抛物线的解析式及点C 的坐标；(2)求线段PQ 长度的最大值；(3)当APC 的面积大于BOC 的面积时，求m 的取值范围．15．如图，已知二次函数232y ax x c =++的图象与y 轴交于点()0,4A ，与x 轴交于点B 、C ，点C 坐标为(8,0)．连接AB 、AC ．(1)请直接写出二次函数的232y ax x c =++表达式； (2)若点N 在线段BC 上运动（不与点B 、C 重合），连接AN ．①当以点A 、N 、C 为顶点的三角形是等腰三角形时，请求出此时点N 的坐标； ①过点N 作NM AC ∥，交AB 于点M ，求AMN 面积的取值范围．参考答案：1．(1)223y x x =-++(2)31524P ⎛⎫ ⎪⎝⎭，2．(1)(2,0)-，(4,0)和(0,8)-(2)存在 (15,4)+-(3)(2,8)-，323．(1)223y x x =-++(2)()1,1P(3)M 点横坐标为3172+或3172-或1或24．(1)4(2)()1,0A -(3)52 (4)存在，()11,4P -或()21,4P --或()35,8P5．(1)22y x x =-- ()1,1B -(2)()()()1,1211,21,1,------，6．(1)2=23y x x --(2)315,24M ⎛⎫- ⎪⎝⎭，四边形ABMC 面积行最大值，为758 (3)0m n +=或1n m a-=7．(1)抛物线的解析式为2=23y x x --(2)当t ＝32时，PBC 的面积最大，最大值为278，此时点P 的坐标为315,24⎛⎫- ⎪⎝⎭ (3)存在，满足条件的点()4,5Q 或()2,5- ()2,3-．8．(1)2330y x x =-+(2)7m(3)当20m 3x =时面积最大，最大面积为2200m 39．(1)1a = 1,2b c =-=(2)3(3)()0,2-或()0,610．(1)点A 的坐标为()1,2，点B 的坐标为()4,5； (2)点P 的坐标为130,5⎛⎫ ⎪⎝⎭，PAB 的面积为125．11．(1)232333y x x =-++(2)()2,33E12．(1)223y x x =+- 1y x =-；(2)①0=t ；①12t =-，最大值是278．13．(1)该抛物线的解析式为223y x x =+-(2)S 有最大值，当52m =-时，S 的最大值是378(3)53715337,22⎛⎫-+- ⎪ ⎪⎝⎭ 53715337,22⎛⎫--+ ⎪ ⎪⎝⎭ 5133313,22⎛⎫-+- ⎪ ⎪⎝⎭ 5133313,22⎛⎫--+ ⎪ ⎪⎝⎭14．(1)抛物线的解析式为223y x x =+- ()0,3C -(2)PQ 长度的最大值是94(3)352--<m <352-+15．(1)213442y x x =-++(2)①()3,0或()845,0-；①05AMN S <≤△。

中考数学二次函数存在性问题及参考答案

(完整版)二次函数中的存在性问题(答案)

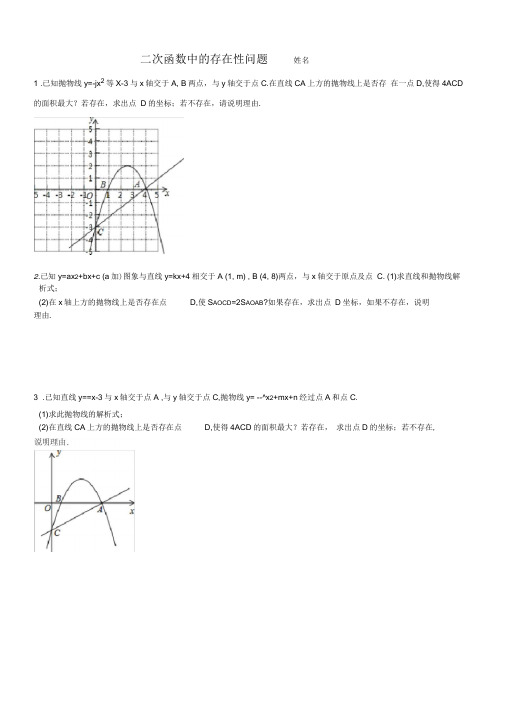
二次函数中的存在性问题姓名1 .已知抛物线y=-jx2等X-3与x轴交于A, B两点，与y轴交于点C.在直线CA上方的抛物线上是否存在一点D,使得4ACD 的面积最大？若存在，求出点D的坐标；若不存在，请说明理由.2.已知y=ax2+bx+c (a加)图象与直线y=kx+4相交于A (1, m) , B (4, 8)两点，与x轴交于原点及点C. (1)求直线和抛物线解析式；(2)在x轴上方的抛物线上是否存在点D,使S AOCD=2S AOAB?如果存在，求出点D坐标，如果不存在，说明理由.3 .已知直线y==x-3与x轴交于点A ,与y轴交于点C,抛物线y= --^x2+mx+n经过点A和点C.(1)求此抛物线的解析式；(2)在直线CA上方的抛物线上是否存在点D,使得4ACD的面积最大？若存在，求出点D的坐标；若不存在,4 .在平面直角坐标系xOy中，抛物线y= - x2+bx+c与x轴交于A、B两点(点A在点B的左侧)，过点A的直线y=kx+1交抛物线于点 C (2, 3).(1)求直线AC及抛物线的解析式；(2)若直线y=kx+1与抛物线的对称轴交于点E,以点E为中心将直线y=kx+1顺时针旋转90彳导到直线1,设直线1与y轴的交点为P,求△ APE的面积；(3)若G为抛物线上一点，是否存在x轴上的点F,使以B、E、F、G为顶点的四边形为平行四边形？若存在，直接写出点F的坐标；若不存在，请说明理由.5 .如图，在平面直角坐标系中，抛物线广2交x轴于A, B两点(A 在B的左侧)，交y轴于点C.(1)求直线BC的解析式；(2)求抛物线的顶点及对称轴；(3)若点Q是抛物线对称轴上的一动点，说明理由；(4)若点P是直线BC上方的一个动点, 的面积；若不存在，说明理由.线段AQ+CQ是否存在最小值？若存在,△ PBC的面积是否存在最大值？若存在,求出点Q的坐标；若不存在,求出点P的坐标及此时4PBC1 .已知抛物线y=—:\2+匪x ― 3与x轴交于A , B两点，2 .与y轴交于点C.在直线CA上方的抛物线上是否存在3 . 一点D,使得4ACD的面积最大？若存在，求出点D4 .的坐标；若不存在，请说明理由.牛目, 解：对于抛物线y= - -x2+—x - 3,4 4令y=0 ,得到--x2+i^x- 3=0, [4 4解得：x=1或x=4 ,B (1, 0), A (4, 0),令x=0,得至ij y= - 3,即 C (0, - 3), 设直线AC解析式为y=kx+b ,将A与C坐标代入得：]业上0 , 1b=-3解得：k=工，b= - 3,4・•・直线AC解析式为y=Wx-3,4设平行于直线AC,且与抛物线只有一个交点的直线方程为y/x+m,4此时直线与抛物线交于点D,使得4ACD的面积最大，与二次函数解析式联立消去y得：-总x2+"x - 3=^x+m ,4 4 4整理得：3x2- 12x+4m+12=0 ,A=144 - 12 (4m+12) =0,解得：m=0,，此时直线万程为y=^x,点D坐标为(2,―).4 42. (2008?宁波校级自主招生)已知y=ax2+bx+c (a沟)图象与直线y=kx+4相交于A (1, m), B (4, 8)两点, 与x轴交于原点及点 C.(1)求直线和抛物线解析式；(2)在x轴上方的抛物线上是否存在点D,使S AOCD=2S AOAB?如果存在，求出点D坐标，如果不存在，说明理由.解答：解：(1) 丁直线y=kx+4 过 A (1, m), B (4, 8)两点,金-Iy= - x2+6x；(2)存在.设D点纵坐标为h (h>0),由O (0, 0), A (1, 5), B (4, 8),可知S AOAB=6,把O、A、B三点坐标代入抛物线解析式，得c=0S A OCD =2S AOAB =12, —>6><h=12,解得 h=4, 2由-x 2+6x=4 ,得 x=3 父 5,•••D (3+、闻 4)或(3-V5, 4).3. (2014春？昌平区期末)已知直线 y=Cx-3与x 轴交于点A,与y 轴交于点4点A 和点C.(1)求此抛物线的解析式；(2)在直线CA 上方的抛物线上是否存在点 D,使得4ACD 的面积最大？若存在，求出点 D 的坐标；若不存在，说明理由.—3得y= - 3,则C 点坐标为(0, — 3), -3=0,解得x=4 ,则A 点坐标为(4, 0),把 A (4, 0), C (0, - 3)代入 y=--？x 2+mx+n 得4k=-7,即 y=—x+b ,4 412x+4b+12=0 ,.・・△=122-4MX (4b+12) =0,解得 b=0, 3x 2 - 12x+12=0 ,解得 x 1=x 2=2, 把 x=2 , b=0 代入 y=—x+b 得 y=—,4 2D 点坐标为(2, -1).4. (2010?孝感模拟)在平面直角坐标系 xOy 中，抛物线y= - x 2+bx+c 与x 轴交于A 、B 两点(点A 在点B 的左侧)，过点A 的直线y=kx+1交抛物线于点 C (2, 3).(1)求直线AC 及抛物线的解析式； (2)若直线y=kx+1与抛物线的对称轴交于点 E,以点E 为中心将直线y=kx+1顺时针旋转90彳导到直线1,设直线l 与y 轴的交点为P,求△ APE 的面积；解答:解得15n= - 3所以二次函数解析式为 y=- ±x 2+¥x - 3;4 4(2)存在.过D 点作直线AC 的平行线y=kx+b ,当直线y=kx+b 与抛物线只有一个公共点时，点大，此时4ACD 的面积最大， D 到AC 的距离最直线AC 的解析式为y3 「x — 3,4由直线y=—x+b 和抛物线y=-x - 3组成方程组得y=-/+b厂「¥苧一3,消去y 得至iJ 3x 2-解：(1)把x=0代入把 y=0 代入 y=-^x —3 4经过(3)若G 为抛物线上一点，是否存在 x 轴上的点F,使以B 、E 、F 、G 为顶点的四边形为平行四边形？若存在, 直接写出点F 的坐标；若不存在，请说明理由. 解答：解：(1) 丁点C (2, 3)在直线y=kx+1上,，2k+1=3 .解得k=1.直线AC 的解析式为y=x+1 . •・•点A 在x 轴上，A (T, 0).,「抛物线 y= -x 2+bx+c 过点 A 、C,I - 4f2b+c=3解得抛物线的解析式为 y= - x 2+2x+3 . (2)由 y= - x 2+2x+3= - (x-1)2+4, 可得抛物线的对称轴为 x=1, B (3, 0). • . E (1, 2).根据题意，知点 A 旋转到点B 处，直线l 过点B 、E. 设直线l 的解析式为y=mx+n . 将B 、E 的坐标代入y=mx+n 中，联立可得m= - 1, n=3. 直线l 的解析式为y= - x+3. P (0, 3).过点E 作ED^x 轴于点D.••• S APA E=S APAB - S AEAB =±AB ?PO -4AB?ED=± MX (3-2) =2.2 2 2(3)存在，点F 的坐标分别为(3-死，0), (3+,万，0), (- 1-右，0) (- 1+/6, 0).在B 的左侧)，交y 轴于点C.(1)求直线BC 的解析式； (2)求抛物线的顶点及对称轴；5. (2013秋?红安县校级月考)如图，在平面直角坐标系中，抛物线 y=+4工十2交x 轴于A , B 两点(A考点：二次函数综合题. 专题：压轴题.分析：(1)令y=0,解关于x 的一元二次方程求出点 B 的坐标，令x=0求出点C 的坐标，设直线 BC 的解析式为y=kx+b ,然后利用待定系数法求一次函数解析式解答即可；(2)把二次函数解析式整理成顶点式形式，然后写出顶点坐标与对称轴即可；(3)根据轴对称确定最短路线问题，直线 BC 与对称轴的交点即为使线段 AQ+CQ 最小的点Q,然后利用直线解析式求解即可；(4)过点P 作PD// y 轴与BC 相交于点D,根据抛物线解析式与直线BC 的解析式表示出 PD,再根据S APBC =S APCD +S APBD 列式整理，然后利用二次函数最值问题解答. 解答：解：(1)令 y=0,贝u― -^x 2+4x+2=0 ,3 3整理得，x 2 - 2x - 3=0 , 解得 x i = - 1, x 2=3,所以，点B 的坐标为(3, 0), 令 x=0 ,则 y=2,所以，点C 的坐标为(0, 2),设直线BC 的解析式为y=kx+b ,则｛:"仁。

二次函数综合(存在性、动点、面积)含答案超级好用

2
Bx
C
（3）由（1）得 D 0，1 m 2 2 ，设存在实数 m，使得△BOD 为等腰三角形，∵△BOD 为直角三角形
2

且∠BOD=900，∴只能有 OD=OB，∴ 1 m2 2 m 2 ， 2
当 m+2>0 时，解得 m=4 或 m= -2（舍去）当 m+2<0 时，解得 m=0（舍去）或 m= -2（舍去）当 m+2=0 时，即 m= -2 时，B、O、D 三点重合（不合题意，舍去），综上所述：存在实数 m=4，使得△BOD 为等腰三角形. 点评：此题考查抛物性质，巧妙设抛物线解析式，还考了三角形垂直性质和抛物线的平移，最后探究存在性问题．
（3）在 x 轴下方的抛物线上是否存在一点 D，使四边形 ABDC 的面积最大？若存在，请求出点 D 的坐标；若不存在，请说明理由；
2
学如逆水行舟，不进则退
学如逆水行舟，不进则退
（4）在抛物线 y x2 2x k 上求点 Q，使△BCQ 是以 BC 为直角边的直角三角形．
（1）
（2）
2．如图，已知抛物线 C1： y a x 2 2 5 的顶点为 P，与 x 轴相交于 A、B 两点（点 A 在点 B 的左
边），点 B 的横坐标是 1．
（1）求P点坐标及a的值；（4分）
（2）如图（1），抛物线 C2 与抛物线 C1 关于 x 轴对称，将抛物线 C2 向右平移，平移后的抛物线记为 C3，C3 的顶点为 M，当点 P、M 关于点 B 成中心对称时，求 C3 的解析式；（4 分）
（3）如图（2），点 Q 是 x 轴正半轴上一点，将抛物线 C1 绕点 Q 旋转 180°后得到抛物线 C4．抛物线 C4 的顶点为 N，与 x 轴相交于 E、F 两点（点 E 在点 F 的左边），当以点 P、N、F 为顶点的三角形是直角三角形时，求点 Q 的坐标．（5 分）

二次函数的存在性问题(Word版解析+答案)

中考压轴题解析二次函数的存在性问题【典例分析】【考点1】二次函数与相似三角形问题【例1】已知抛物线23y ax bx =++与x 轴分别交于(3,0)A -，(1,0)B 两点，与y 轴交于点C ．（1）求抛物线的表达式及顶点D 的坐标；（2）点F 是线段AD 上一个动点． ①如图1，设AF k AD =，当k 为何值时，2CF AD =1. ②如图2，以A ，F ，O 为顶点的三角形是否与ABC ∆相似？若相似，求出点F 的坐标；若不相似，请说明理由．【变式1-1】如图，抛物线2y 2ax x c =++经过(1,0)A -，B 两点，且与y 轴交于点(0,3)C ，抛物线与直线1y x =--交于A ，E 两点．（1）求抛物线的解析式；（2）坐标轴上是否存在一点Q ，使得AQE ∆是以AE 为底边的等腰三角形？若存在，请直接写出点Q 的坐标；若不存在，说明理由．（3）P 点在x 轴上且位于点B 的左侧，若以P ，B ，C 为顶点的三角形与ABE ∆相似，求点P 的坐标．【变式1-2】如图，已知抛物线1(2)()y x x m m=-+-(m ＞0)与x 轴相交于点A ，B ，与y 轴相交于点C ，且点A 在点B 的左侧.（1）若抛物线过点（2，2），求抛物线的解析式；（2）在（1）的条件下，抛物线的对称轴上是否存在一点H ，使AH+CH 的值最小，若存在，求出点H 的坐标；若不存在，请说明理由；（3）在第四象限内，抛物线上是否存在点M ，使得以点A ，B ，M 为顶点的三角形与△ACB 相似？若存在，求出m 的值；若不存在，请说明理由.【考点2】二次函数与直角三角形问题【例2】如图，抛物线()20y ax bx c a =++≠的顶点坐标为()2,1-，图象与y 轴交于点()0,3C ，与x 轴交于A 、B 两点．()1求抛物线的解析式；()2设抛物线对称轴与直线BC 交于点D ，连接AC 、AD ，求ACD 的面积；()3点E 为直线BC 上的任意一点，过点E 作x 轴的垂线与抛物线交于点F ，问是否存在点E 使DEF 为直角三角形？若存在，求出点E 坐标，若不存在，请说明理由．【变式2-1】如图，经过x 轴上(10)(30)A B -，，，两点的抛物线2(1)4y m x m =--（0m <）交y 轴于点C ，设抛物线的顶点为D ，若以DB 为直径的⊙G 经过点C ，求解下列问题：，的坐标；（1）用含m的代数式表示出C D（2）求抛物线的解析式；△为直角三角形？如能，求出Q点的坐标，若不能，请说明理（3）能否在抛物线上找到一点Q，使BDQ由。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

专题三：二次函数存在性问题
1．（10广东深圳）如图，抛物线y＝ax2＋c（a＞0）经过梯形ABCD的四个顶点，梯形的底AD在x轴上，其中A（－2,0），B（－1, －3）．
(1）求抛物线的解析式；
(2）点M为y轴上任意一点，当点M到A、B两点的距离之和为最小时，求此时点M的坐标；
(3）在第（2）问的结论下，抛物线上的点P使S△P AD＝4S△ABM成立，求点P的坐标．
图2
2． (10北京）在平面直角坐标系xOy 中，抛物线y = -
4
1-m x 2+45m
x +m 2-3m +2
与x 轴的交点分别为原点O 和点A ，点B (2，n )在这条抛物线上。

(1) 求点B 的坐标；
(2) 点P 在线段OA 上，从O 点出发向点运动，过P 点作x 轴的垂线，与直线OB 交于点E 。

延长PE 到点D 。

使得ED =PE 。

以PD 为斜边在PD 右侧作等腰直角三角形PCD (当P 点运动时，C 点、D 点也随之运动)
当等腰直角三角形PCD 的顶点C 落在此抛物线上时，求
OP 的长；
若P 点从O 点出发向A 点作匀速运动，速度为每秒1个单位，同时线段OA 上另一点Q 从A 点出发向O 点作匀速运动，速度为每秒2个单位(当Q 点到达O 点时停止运动，P 点也同时停止运动)。

过Q 点作x 轴的垂线，与直线AB 交于点F 。

延长QF 到点M ，使得FM =QF ，以QM 为斜边，在QM 的左侧作等腰直角三角形QMN (当Q 点运动时，M 点，N 点也随之运动)。

若P 点运动到t 秒时，两个等腰直角三角形分别有一条直角边恰好落在同一条直线上，求此刻t 的值。

3．
4．（10贵州遵义）如图，已知抛物线)0(2≠++=a c bx ax y 的顶点坐
标为Q ()1,2-，且与y 轴交于点C ()3,0，与x 轴交于A 、B 两
点（点A 在点B 的右侧），点P 是该抛物线上一动点，从点C 沿抛物线向点A 运动（点P 与A 不重合），过点P 作PD ∥y 轴，交AC 于点D ．
(1)求该抛物线的函数关系式；
(2)当△ADP 是直角三角形时，求点P 的坐标；
(3)在问题(2)的结论下，若点E 在x 轴上，点F 在抛物线上，问是否存在以A 、P 、E 、F 为顶点的平行四边形？若存在，求点F 的坐标；若不存在，请说明理由．
5．（10湖北黄冈）已知抛物线2
(0)y ax bx c a =++≠顶点为C （1，1）且过原点O.过抛物
线上一点P （x ，y ）向直线5
4
y =作垂线，垂足为M ，连FM （如图）. (1）求字母a ，b ，c 的值；
(2）在直线x ＝1上有一点3(1,)4
F ，求以PM 为底边的等腰三角形PFM 的P 点的坐标，并
证明此时△PFM 为正三角形；
6．（10辽宁丹东）如图，平面直角坐标系中有一直角梯形OMNH ，点H 的坐标为（－8，0），点N 的坐标为（－6，－4）．
(1）画出直角梯形OMNH 绕点O 旋转180°的图形OABC ，并写出顶点A ，B ，C 的坐标（点M 的对应点为A ，点N 的对应点为B ，点H 的对应点为C ）； (2）求出过A ，B ，C 三点的抛物线的表达式；
(3）截取CE =OF =AG =m ，且E ，F ，G 分别在线段CO ，OA ，AB 上，求四边形．．．BEFG 的面积S 与m 之间的函数关系式，并写出自变量m 的取值范围；面积S 是否存在最小值?若存在，请求出这个最小值；若不存在，请说明理由；
(4）在（3）的情况下，四边形BEFG 是否存在邻边相等的情况，若存在，请直接．．
写出此时m 的值，并指出相等的邻边；若不存在，说明理由．．
7．已知：函数y =ax 2+x +1的图象与x 轴只有一个公共点． (1）求这个函数关系式； (2）如图所示，设二次．．函数y =ax 2+x +1图象的顶点为B ，与y 轴的交点为A ，P 为图象上的一点，若以线段PB 为直径的圆与直线AB 相切于点B ，求P 点的坐标；
(3）在(2)中，若圆与x 轴另一交点关于直线PB 的对称点为M ，试探索点M 是否在抛物
线y =ax 2+x +1上，若在抛物线上，求出M 点的坐标；若不在，请说明理由．
O M
N H
A C
E F
D
B
↑
→ －8
(－6，－4)
x y
8．（10重庆潼南）如图, 已知抛物线c bx x y ++=
2
2
1与y 轴相交于C ，与x 轴相交于A 、B ，点A 的坐标为（2，0），点C 的坐标为（0，-1）. (1）求抛物线的解析式；
(2）点E 是线段AC 上一动点，过点E 作DE ⊥x 轴于点D ，连结DC ，当△DCE 的面积
最大时，求点D 的坐标；
(3）在直线BC 上是否存在一点P ，使△ACP 为等腰三角形，若存在，求点P 的坐标，
若不存在，说明理由.
9． (10山东临沂）如图，二次函数y = -x 2+ax +b 的图像与x 轴交于A (-
2
1
，0)、 B (2，0)两点，且与y 轴交于点C ；
(1) 求该拋物线的解析式，并判断△ABC 的形状；
(2) 在x 轴上方的拋物线上有一点D ，且以A 、C 、D 、B 四
点为顶点的四边形是等腰梯形，请直接写出D 点的坐标；
(3) 在此拋物线上是否存在点P ，使得以A 、C 、B 、P 四点
为顶点的四边形是直角梯形？若存在，求出P
10．（10山东潍坊）如图所示，抛物线与x 轴交于点()()1030A B -，、，两点，与y 轴交于点()03.C -，以AB 为直径作M ⊙，过抛物线上一点P 作M ⊙的切线PD ，切点为D ，并与M ⊙的切线AE 相交于点E ，连结DM 并延长交M ⊙于点N ，连结.AN AD 、 (1）求抛物线所对应的函数关系式及抛物线的顶点坐标；
(2）若四边形EAMD 的面积为求直线PD 的函数关系式；
(3）抛物线上是否存在点P ，使得四边形EAMD 的面积等于DAN △的面积？若存在，求出点P 的坐标；若不存在，说明理由.
11．(10山东省淄博)已知直角坐标系中有一点A （－4，3），点B 在x 轴上，△AOB 是等腰三角形．
(1）求满足条件的所有点B 的坐标；
(2）求过O 、A 、B 三点且开口向下的抛物线的函数表达式（只需求出满足条件的一条即可）；
(3）在（2）中求出的抛物线上存在点P ，使得以O ，A ，B ，P 四点为顶点的四边形是梯形，求满足条件的所有点P 的坐标及相应梯形的面积．
12． (10广西河池）
如图，在直角梯形OABC 中，CB ∥OA ，90OAB ∠=
，点O 为坐标原点，点A 在x 轴的正半轴上，对角线OB ，AC 相交于点M ，4OA AB ==，2OA CB =． (1）线段OB 的长为，点C 的坐标为； (2）求△OCM 的面积；
(3）求过O ，A ，C 三点的抛物线的解析式； (4）若点E 在（3）的抛物线的对称轴上，点F 为该抛物线上的点，且以A ，O ，F ，E 四点为顶点的四边形
为平行四边形，求点F 的坐标．
13．（10广西桂林）如图，过A（8，0）、B（0
，两点的直线与直线x
y3
=交于点C．平
行于y轴的直线l从原点O出发，以每秒1个单位长度的速度沿x轴向右平移，到C点
时停止；l分别交线段BC、OC于点D、E，以DE为边向左侧作等边△DEF，设△DEF 与△BCO重叠部分的面积为S（平方单位），直线l的运动时间为t（秒）．
(1）直接写出C点坐标和t的取值范围；
(2）求S与t的函数关系式；
(3）设直线l与x轴交于点P，是否存在这样的点P，使得以P、O、F为顶点的三角形为等腰三角形，若存在，请直接写出点P的坐标；若不存在，请说明理由．
备用图1。