安徽省2001-2012年中考数学试题分类解析专题3:方程(组)和不等式(组)
【中考12年】安徽省2001-2012年中考数学试题分类解析 专题1 实数

2001-2012年某某省中考数学试题分类解析汇编专题1:实数一、选择题1. (2001某某省4分)-3+3= ▲ 。
【答案】0。
【考点】有理数的加法。
【分析】根据有理数的运算法则计算:因为-3与3互为相反数,所以-3+3=0。
2.(2001某某省4分)-2的平方是▲ 。
【答案】4。
【考点】有理数的乘方、【分析】-2的平方表示2个-2的乘积,(-2)2=(-2)×(-2)=4。
3. (2002某某省4分)4的平分根是▲ .【答案】±2。
【考点】平方根。
【分析】根据平方根的定义,求数a的平方根,也就是求一个数x,使得x2=a,则x就是a的一个平方根:∵(±2)2=4,∴4的平方根是±2。
4. (2002某某省4分)有资料表明,被资称为“地球之肺”的森林正以每年15000000公顷的速度从地球上消失,每年森林的消失量用科学记数法表示应有▲ 公顷.【答案】1.5×107。
【考点】科学记数法。
【分析】根据科学记数法的定义,科学记数法的表示形式为a×10n,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值。
在确定n的值时,看该数是大于或等于1还是小于1。
当该数大于或等于1时,n为它的整数位数减1;当该数小于1时,-n为它第一个有效数字前0的个数(含小数点前的1个0)。
15 000 000一共8位,从而15 000 000=1.5×107。
5. (2003某某省4分)冬季某天我国三个城市的最高气温分别是-10℃、1℃、-7℃,把它们从高到低排列正确的是【】A :-10℃、-7℃、1℃ B:-7℃、-10℃、1℃ C :1℃ 、-7℃、-10℃ D:1℃ 、-10℃、-7℃ 【答案】C 。
【考点】有理数大小比较。
【分析】根据有理数大小的比较规则可知正数>负数,在两个负数中绝对值大的反而小。
因此,∵1>-7>-10,∴从高到低排列正确的是1℃,-7℃,-10℃。
浙江省杭州市2001-2012年中考数学试题分类解析 专题3 方程(组)和不等式(组)

[中考12年]杭州市2001-2012年中考数学试题分类解析专题3:方程(组)和不等式(组)一、选择题1. (2001年浙江杭州3分)方程()()222x 13x 140+-+-=的实数根有【 】.A .1个B .2个C .3个D .4个2. (2002年浙江杭州3分)已知2是关于x 的方程23x 2a 02-=的一个解,则2a 1-的值是【 】. (A )3(B )4(C )5(D )63. (2002年浙江杭州3分)不等式组2x 1x 30≤⎧⎨+>⎩的解在数轴上可表示为【 】.(A ) (B )(C ) (D )【答案】A 。
不等式组的解集在数轴上表示的方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个。
在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示。
因此,不等式组2x 1x 30≤⎧⎨+>⎩的解在数轴上可表示为A 。
故选A 。
4. (2003年浙江杭州3分)设1x ,2x 是关于x 的方程2x px q 0++=的两根,1x 1+,2x 1+是关于x 的方程2x qx p 0++=的两根,则p ,q 的值分别等于【 】(A )1,-3 (B )1,3 (C )-1,-3 (D )-1,3【分析】∵1x ,2x 是关于x 的方程2x px q 0++=的两根,∴1212x x p x x q +=-⋅=,。
又∵1x 1+,2x 1+是关于x 的方程2x qx p 0++=的两根,∴()()1212x 1x 1q x 1x 1p +++=-++=,,即121212x x q 2x x x x p 1+=--⋅++=-,。
将1212x x p x x q +=-⋅=,代入,得()p=q 2q p p 1-=--⎧⎪⎨+-=-⎪⎩,解得p 1q 3=-⎧⎨=-⎩。
中考数学试题分类分析汇编专题3:方程(组)和不定式(组)

中考数学试题分类分析汇编(12专题) 专题3:方程(组)和不定式(组)一.选择题1. (2001年福建福州4分)随着计算机技术的迅猛发展,电脑价格不断降低。
某品牌电脑按原售价降低m 元后,又降价20%,现售价为n 元,那么该电脑的原售价为【 】 A. 4(n m )5+元B. 5(n m )4+元 C. (5m n)+元D. (5n m)+元【答案】B 。
【考点】一元一次方程的应用。
【分析】设电脑的原售价为x 元,则()()x m 120%n --=,∴x=5n m 4+。
故选B 。
2. (2003年福建福州4分)不等式组2x 4x 30≥⎧⎨+>⎩的解集是【 】(A ) x>-3 (B )x≥2 (C )-3<x≤2 (D ) x<-3 【答案】B 。
【考点】解一元一次不等式组。
【分析】解一元一次不等式组,先求出不等式组中每一个不等式的解集,再利用口诀求出这些解集的公共部分:同大取大,同小取小,大小小大中间找,大大小小解不了(无解)。
因此,2x 4x 2x 2x 30x 2≥≥⎧⎧⇒⇒≥⎨⎨+>>-⎩⎩。
故选B 。
3.(2003年福建福州4分)已知α、β满足α+β=5,且αβ=6,则以α、β为两根的一元二次方程是【 】(A )2x 5x 60++= (B )2x 5x 60-+= (C )2x 5x 60--= (D )2x 5x 60+-=【答案】B 。
【考点】一元二次方程根与系数的关系。
【分析】∵所求一元二次方程的两根是α、β,且α、β满足α+β=5、αβ=6,∴这个方程的系数应满足两根之和是b 5a-=,两根之积是c 6a =。
当二次项系数a=1时,一次项系数b=-5,常数项c=6。
故选B 。
4. (2005年福建福州大纲卷3分)如图,射线OC 的端点O 在直线AB 上,∠AOC 的度数比∠BOC 的2倍多10度.设∠AOC 和∠BOC 的度数分别为x ,y ,则下列正确的方程组为【 】A 、x+y=180x=y+10⎧⎨⎩错误!未找到引用源。
12年安徽省中考数学解答题全解

2012年安徽省初中毕业学业考试数学试题解析三、(本大题共2小题,每小题8分,满分16分)15. (2012安徽,15,8分)计算:)2()1)(3(-+-+a a a a15. 解析:根据整式的乘法法则,多项式乘多项式时,用其中一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加;单项式乘多项式,可以按照乘法分配率进行.最后再根据合并同类项法则进行整式加减运算.解:原式=a 2-a+3a -3+a 2-2a =2a 2-3 16. (2012安徽,16,8分)解方程:1222+=-x x x16. 解析:根据一元二次方程方程的几种解法,本题不能直接开平方,也不可用因式分解法.先将方程整理一下,可以考虑用配方法或公式法.解:原方程化为:x 2-4x=1配方,得x 2-4x+4=1+4 整理,得(x -2)2=5∴x -2=5±,即521+=x ,522-=x .四、(本大题共2小题,每小题8分,满分16分)17. (2012安徽,17,8分)在由m ×n (m ×n >1)个小正方形组成的矩形网格中,研究它的一条对角线所穿过的小正方形个数f ,(1)当m 、n 互质(m 、n 除1外无其他公因数)时,观察下列图形并完成下表:猜想:当m 、n 互质时,在m ×n 的矩形网格中,一条对角线所穿过的小正方形的个数f 与m 、n 的关系式是______________________________(不需要证明); 解:(2)当m 、n 不互质时,请画图验证你猜想的关系式是否依然成立, 17:解析:(1)通过题中所给网格图形,先计算出2×5,3×4,对角线所穿过的小正方形个数f ,再对照表中数值归纳f 与m 、n 的关系式.(2)根据题意,画出当m 、n 不互质时,结论不成立的反例即可. 解:(1)如表:mnm n +f1 2 3 2 1 3 4 3 2 3 5 4 2 4 7 3 5 7m nm n + ff=m+n-1(2)当m、n不互质时,上述结论不成立,如图2×42×418. (2012安徽,18,8分)如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.(1)画出一个格点△A1B1C1,并使它与△ABC全等且A与A1是对应点;(2)画出点B关于直线AC的对称点D,并指出AD可以看作由AB绕A点经过怎样的旋转而得到的.解:18.解析:(1)考查全等变化,可以通过平移、旋转、轴对称等来完成;(2)先作出图形,因为要回答旋转角度,利用方格纸算出AB、AD、BD的长度,再计算角度.解:(1)答案不唯一,如图,平移即可1 2 3 21 3 4 32 3 5 42 4 7 63 5 7 6(2)作图如上,∵AB=10,AD=10,BD=52∴AB 2+AD 2=BD 2新课标 一网∴△ABD 是直角三角形,AD 可以看作由AB 绕A 点逆时针旋转90°得到的.点评:图形变换有两种,全等变换和相似变换,掌握每种变换的概念、性质是作图的基础,一般难度不大.五、(本大题共2小题,每小题10分,满分20分)19. (2012安徽,19,10分)如图,在△ABC 中,∠A=30°,∠B=45°,AC=32,求AB 的长,解:19. 解析:本题在一个三角形中已知两个角和一边,求三角形的边.不是直角三角形,要利用三角函数必须构筑直角三角形,过点C 作CD ⊥AB 于D,利用构造的两个直角三角形来解答. 解:过点C 作CD ⊥AB 于D,在Rt △ACD 中,∠A=30°,AC=32 ∴CD=AC ×sinA=32×0.5=3,AD=AC ×cosA=32×23=3, 在Rt △BCD 中,∠B=45°,则BD=CD=3, ∴AB=AD+BD=3+3点评:解直角三角形中,除了直角外,还知道两个元素(至少有一个是边),就能求出其余的边和角. 一般三角形中,知道三个元素(至少有一个是边),就能求出其余的边和角. 这时将三角形转化为直角三角形时,注意尽量不要破坏所给条件.20. (2012安徽,20,10分)九(1)班同学为了解2011年某小区家庭月均用水情况,随45°30°C BA 第19题图 频数(户)机调查了该小区部分家庭,并将调查数据进行如下整理, 月均用水量x (t) 频数(户) 频率05x <≤ 6 0.12 510x <≤ 0.24 1015x <≤ 16 0.32 1520x <≤ 10 0.20 2025x <≤ 4 2530x <≤ 2 0.04 请解答以下问题:(1)把上面的频数分布表和频数分布直方图补充完整;(2)若该小区用水量不超过15t 的家庭占被调查家庭总数的百分比; 解:(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t 的家庭大约有多少户? 解:20. 本题考查了数据的统计中的频数分布表和不完整的频数分布直方图.所有的频数和就是样本容量,所有频率和等于1,且有n数据总数频数频率=,(1)数据总数5012.06===频率频数 ,50×0.24=12,4÷50=0.08, (2)用水量不超过15吨是前三组,(0.12+0.24+0.32)×100﹪=68﹪(3)用样本来估计总体,根据抽取的样本超过20吨的家庭数,来估计该小区的情况.. 解:(1)统计中的频数分布表和不完整的频数分布直方图,补充如下 (2)用水量不超过15吨是前三组,(0.12+0.24+0.32)×100﹪=68﹪ (3)1000×(0.04+0.08)=120(户)六、(本题满分12分)21. (2012安徽,21,12分)甲、乙两家商场进行促销活动,甲商场采用“慢200减100”的促销方式,即购买商品的总金额满200元但不足400元,少付100元;满400元但不足600元,少付200元;……,乙商场按顾客购买商品的总金额打6折促销。
中考2001年安徽省中考数学试卷(含答案)

2001年安徽中考数学一、填空题(本题满分40分,共10小题,每小题4分)1、–3+3= 。
2、–2的平方是 。
3、将1+--n m mn 分解因式的结果是 。
4、如图4,长方体中,与棱AA /平行的面是 。
图45、某音像社对外出租光盘的收费方法是:每张光盘在租出后的头两天每天收0.8元,以后每天收0.5元,那么一张光盘在租出的第n 天(n 是大于2的自然数)应收租金 。
6、如图6,要把角钢(1)弯成1200的钢架(2),则在角钢(1)上截去的缺口是 度。
图67、方程组⎩⎨⎧--=+=3212x x y x y 的解是 。
8、恩格尔系数表示家庭日常饮食开支占家庭经济总收入的比例,它反映了居民家庭的实际生活水平,各种类型家庭的恩格尔系数如下表所示:则用含n 的不等式表示小康家庭屡的恩格尔系数为 。
第9题图 9、如图9,已知AC=BD ,要使得△ABC ≌△DCB ,只需增加的一个条件是 。
10、⊙O 1、⊙O 2和⊙O 3是三个半径为1的等圆,且圆心在同一条直线上。
若⊙O 2分别与⊙O 1、⊙O 3相交,⊙O 1与⊙O 3不相交,则⊙O 1与⊙O 3的圆心距d 的取值范围是 。
二、选择题(本大题共8小题;每小题4分,共32分)11、下列运算正确的…………………………………………………………………………………( )(A )()22a a -= (B )()33a a -= (C )||22a a -=- (D )||33a a =2212、今年第一季度我国增值税、消费税比上年同期增收3.07×l010元,也就是………………( )(A )30.7亿元 (B )307亿元 (C )3.07亿元 (D )3070万元13、近年来国内生产总值年增长率的变化情况如图,从图上看,下列结论中不正确的是……( )(A )1995一1999年,国内生产总值的年增长率逐年减小 (B )2000年国内生产总值的年增长率开始回升 (C )这7年中,每年的国内生产总值不断增长 (D )这7年中,每年的国内生产总值有增有减第18题图14、解方程526311322=+-+-+x x x x 时,设132-+=x x y ,则原方程可化为……………………………( ) (A )026552=-+y y (B )02652=-+y y (C )02652=--y y (D )052652=+-y y 15、关于x 的一元二次方程01232=-+-k x x 有两个不相等的实数根,则k 的取值范围是…( )(A )34<k (B )34<k 且1≠k (C )34≤k (D )34>k 16、P 是Rt △ABC 的斜边BC 上异于B 、C 的一点,过点P 作直线截△ABC ,使截得的三角形与△ABC 相似。
2002012年安徽中考数学试题分类解析汇编12专题

2001-2012年安徽省中考数学试题分类解析汇编(12专题)专题7:统计与概率1.选择题1. (2002安徽省4分)2001年中国人民银行统计司就城镇居民对物价水平满意程度进行了抽样调查,结果如右图,据此,可估计2001年城镇居民对物价水平表示认可的约占▲%.【答案】85.9。
【考点】扇形统计图,用样本估计总体。
【分析】从图中抽样调查的结果可以看出能够认可的人数约占30.2%+55.7%=85.9%,于是可以估计2009年城镇居民中对物价水平表示认可的约占85.9%。
2. (2002安徽省4分)某电视台综艺节目接到热线电话3000个,现要从中抽取“幸运观众”10名,张华同学打通了一次热线电话,那么他成为“幸运观众”的概率为▲_.【答案】1 300。
【考点】概率。
【分析】根据概率的求法,找准两点:①全部等可能情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率。
因此,∵共有热线电话3000个,从中抽取“幸运观众”10名,,∴张华同学打通了一次热线电话,成为“幸运观众”的概率为1013000300。
3. (2005安徽省大纲4分)某市社会调查队对城区内一个社区居民的家庭经济状况进行调查.调查的结果是,该社区共有500户,高收入、中等收入和低收入家庭分别有125户、280户和95户.已知该市有100万户家庭,下列表述正确的是【】A、该市高收入家庭约25万户B、该市中等收入家庭约56万户C、该市低收入家庭约19万户D、因城市社区家庭经济状况较好,所以不能据此数据估计全市所有家庭经济状况【答案】D。
【考点】抽样调查的可靠性。
【分析】抽样调查的样本的选取要有代表性和科学性。
因城市社区家庭经济状况较好,抽取的样本不具有代表性,所以不能据此数据估计全市所有家庭经济状况。
故选D。
4. (2005安徽省大纲4分)下图是某地区用水量与人口数情况统计图.日平均用水量为400万吨的那一年,人口数大约是【】A、180万B、200万C、300万D、400万【答案】A。
2001-2012年安徽省中考数学试题分类解析汇
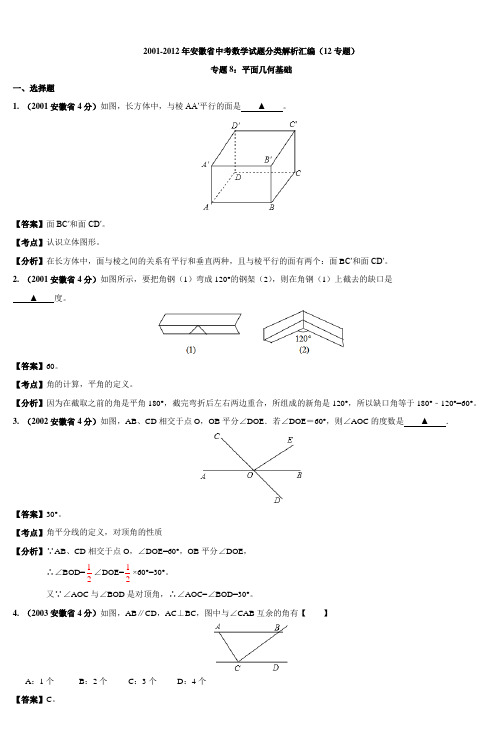
2001-2012年安徽省中考数学试题分类解析汇编(12专题)专题8:平面几何基础一、选择题1. (2001安徽省4分)如图,长方体中,与棱AA′平行的面是▲ 。
【答案】面BC′和面CD′。
【考点】认识立体图形。
【分析】在长方体中,面与棱之间的关系有平行和垂直两种,且与棱平行的面有两个:面B C′和面CD′。
2. (2001安徽省4分)如图所示,要把角钢(1)弯成120°的钢架(2),则在角钢(1)上截去的缺口是▲ 度。
【答案】60。
【考点】角的计算,平角的定义。
【分析】因为在截取之前的角是平角180°,截完弯折后左右两边重合,所组成的新角是120°,所以缺口角等于180°﹣120°=60°。
3. (2002安徽省4分)如图,AB、CD相交于点O,OB平分∠DOE.若∠DOE=60°,则∠AOC的度数是▲ .【答案】30°。
【考点】角平分线的定义,对顶角的性质【分析】∵AB、CD相交于点O,∠DOE=60°,OB平分∠DOE,∴∠BOD=12∠DOE=12×60°=30°。
又∵∠AOC与∠BOD是对顶角,∴∠AOC=∠BOD=30°。
4. (2003安徽省4分)如图,AB∥CD,AC⊥BC,图中与∠CAB互余的角有【】A:1个B:2个C:3个D:4个【答案】C。
【考点】平行线的性质,余角和补角,对顶角的性质,直角三角形两锐角的关系。
【分析】∵AB∥CD,∴∠ABC=∠BCD。
设∠ABC的对顶角为∠1(如图),则∠ABC=∠1。
又∵AC⊥BC,∴∠ACB=90°。
∴∠CAB+∠ABC=∠CAB+∠BCD=∠CAB+∠1=90°。
∴与∠CAB互余的角为∠ABC,∠BCD,∠1。
故选C。
12的是【】5. (2005安徽省课标4分)下列图中能够说明∠>∠A.B.C.D.【答案】D。
安徽省2001-2019年中考数学试题分类解析专题3:方程(组)和不等式(组)

2001-2019年安徽省中考数学试题分类解析汇编(12专题)专题3:方程(组)和不等式(组)一、选择题1. 2001安徽省4分)方程组2y x 1y x 2x 3=+⎧⎨=--⎩ 的解是 ▲ 。
【答案】x 1y 0=-⎧⎨=⎩或x 4y 5=⎧⎨=⎩。
【考点】解高次方程。
【分析】2y x 1 1y x 2x 3 2=+⎧⎪⎨=--⎪⎩()(), 由(2)得:y=(x -3)(x +1)…(3),把(1)代入(3)得:(x +1)(x -3-1)=0,解得x=-1或x=4。
∴相应的y=0或y=5。
∴原方程组的解为x 1y 0=-⎧⎨=⎩或x 4y 5=⎧⎨=⎩。
2. (2001安徽省4分)恩格尔系数表示家庭日常饮食开支占家庭经济总收入的比例,它反映了居民家庭的实际生活水平,各种类型家庭的恩格尔系数如下表所示:则用含n 的不等式表示小康家庭的恩格尔系数为 ▲ 。
【答案】40%≤n≤49%。
【考点】一元一次不等式的应用。
【分析】用含n 的不等式表示小康家庭的恩格尔系数,只要找出小康家庭所在的系数,令n 处在该范围内即可:依题意得不等式:40%≤n≤49%。
3. (2002安徽省4分)在解方程(x 2-1)2-2x 2-1=0时,通过换元并整理得方程y 2-2y -3=0,则y = ▲ .【答案】y =x 2-1。
【考点】换元法解高次方程。
【分析】对(x2-1)2-2x2-1=0进行变形整理为(x2-1)2-2(x2-1)-3=0,、所以令y=x2-1,即可得方程y2-2y-3=0。
4. (2002安徽省4分)某校去年对实验器材的投资为2万元,预计今明两年的投资总额为8万元,若设该校这两年在实验器材投资上的平均增长率为x,则可列方程:▲ .【答案】20(1+x)2=8。
【考点】由实际问题抽象出一元二次方程(增长率问题)。
【分析】设该校这两年购买的实验器材的投资年平均增长率为x,今年的投资金额为:2(1+x),则明年的投资金额为2(1+x) (1+x) =20(1+x)2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2001-2012年安徽省中考数学试题分类解析汇编(12专题)专题3:方程(组)和不等式(组)锦元数学工作室 编辑一、选择题1. 2001安徽省4分)方程组2y x 1y x 2x 3=+⎧⎨=--⎩的解是 ▲ 。
【答案】x 1y 0=-⎧⎨=⎩或x 4y 5=⎧⎨=⎩。
【考点】解高次方程。
【分析】2y x 1 1y x 2x 3 2=+⎧⎪⎨=--⎪⎩()(), 由(2)得:y=(x -3)(x +1)…(3),把(1)代入(3)得:(x +1)(x -3-1)=0,解得x=-1或x=4。
∴相应的y=0或y=5。
∴原方程组的解为x 1y 0=-⎧⎨=⎩或x 4y 5=⎧⎨=⎩。
2. (2001安徽省4分)恩格尔系数表示家庭日常饮食开支占家庭经济总收入的比例,它反映了居民家庭的实际生活水平,各种类型家庭的恩格尔系数如下表所示:则用含n 的不等式表示小康家庭的恩格尔系数为 ▲ 。
【答案】40%≤n≤49%。
【考点】一元一次不等式的应用。
【分析】用含n 的不等式表示小康家庭的恩格尔系数,只要找出小康家庭所在的系数,令n 处在该范围内即可:依题意得不等式:40%≤n≤49%。
3. (2002安徽省4分)在解方程(x 2-1)2-2x 2-1=0时,通过换元并整理得方程y 2-2y -3=0,则y = ▲ .【答案】y=x2-1。
【考点】换元法解高次方程。
【分析】对(x2-1)2-2x2-1=0进行变形整理为(x2-1)2-2(x2-1)-3=0,、所以令y=x2-1,即可得方程y2-2y-3=0。
4. (2002安徽省4分)某校去年对实验器材的投资为2万元,预计今明两年的投资总额为8万元,若设该校这两年在实验器材投资上的平均增长率为x,则可列方程:▲ .【答案】20(1+x)2=8。
【考点】由实际问题抽象出一元二次方程(增长率问题)。
【分析】设该校这两年购买的实验器材的投资年平均增长率为x,今年的投资金额为:2(1+x),则明年的投资金额为2(1+x) (1+x) =20(1+x)2。
据此列出方程:20(1+x)2=8。
5. (2003安徽省4分)党的十六大提出全面建设小康社会,加快推进社会主义现代化,力争国民生产总值到2020年比2000年翻两番。
在本世纪的头二十年(2001年~2020年),要实现这一目标,以十年为单位计算,设每个十年的国民生产总值的增长率都是x,那么x 满足的方程为【】A:(1+x)2=2 B:(1+x)2=4 C:1+2x=2 D:(1+x)+2(1+x)=4【答案】B。
【考点】由实际问题抽象出一元二次方程(增长率问题)。
【分析】设每个十年的国民生产总值的增长率都是x,2000年生产总值为1,则2020年的国民生产总值为22=4。
依题意得,2010年的国民生产总值:(1+x),则明则2020年的国民生产总值为 (1+x) (1+x) = (1+x)2。
据此列出方程: (1+x)2=4。
故选B。
6. (2004安徽省4分)方程x2—3x+1=0根的情况是【】.(A)有两个不相等的实数根 (B)有两个相等的实数根(C)没有实数根 (D)只有一个实数根【答案】A。
【考点】一元二次方程根的判别式。
【分析】判断一元二次方程的根的情况,只要看根的判别式△=b2-4ac的值的符号即可:∵△=4+12=16>0,∴方程有两个不相等的实数根。
故本题选A。
7. (2004安徽省4分)如图,扇子的圆心角为x°,余下扇形的圆心角为y°,x与y的比通常按黄金比来设计,这样的扇子外形较美观.若取黄金比为0.6,则x为【】.(A)216 (B)135 (C)120 (D)108【答案】B 。
【考点】二元一次方程组的应用(几何问题)。
周角的概念。
【分析】根据题意得:x 0.6y x y 360=⎧⎨+=︒⎩,解得:x=135°。
故选B 。
8. (2005安徽省课标4分)根据下图所示,对a 、b 、c 三种物体的重量判断不正确的是【 】A .a <cB .a <bC .a >cD .b <c【答案】C 。
【考点】一元一次不等式的应用。
【分析】找出不等关系列式求解:.由第一图可知:3a=2b ,b >a ;由第二图可知:3b=2c ,c >b ,故a <b <c ,∴A、B 、D 选项都正确,C 选项错误。
故选C 。
9. (2005安徽省课标4分)方程x(x 3)x 3+=+的解是【 】A. x 1=B. 12x 0x 3==-,C. 12x 1x 3==, D. 12x 1x 3==-, 【答案】B 。
【考点】因式分解法解一元二次方程。
【分析】原方程变形为:x (x +3)-(x +3)=0,∴(x +3)(x -1)=0。
∴12x 1x 3==-,。
故选B 。
10. (2006安徽省课标4分)方程120x 2x 1-=--的根是【 】 A .-3 B .0 C .2 D .3【答案】D 。
【考点】解分式方程。
【分析】方程两边都乘最简公分母(x -2)(x -1),得x -1-2(x -2)=0,解得x=3。
检验:当x=3时,(x -2)(x -1)≠0。
∴x=3是原方程的解。
故选D 。
11. (2008安徽省4分)分式方程x 1x 12=+的解是【 】 A. x=1 B. x=-1 C. x=2 D. x=-2【答案】A 。
【考点】解分式方程。
【分析】观察式子可得最简公分母为2(x +1),方程两边同乘最简公分母,转化为整式方程求解,结果要检验:方程两边乘2(x +1),得:2x=x +1,解得x=1。
将x=1代入2(x +1)=4≠0。
∴方程的解为x=1。
故选A 。
12. (2009安徽省4分)甲志愿者计划用若干个工作日完成社区的某项工作,从第三个工作日起,乙志愿者加盟此项工作,且甲、乙两人工效相同,结果提前3天完成任务,则甲志愿者计划完成此项工作的天数是【 】A .8 B.7 C .6 D .5【答案】A 。
【考点】分式方程的应用(工程问题)。
【分析】根据题意,设甲志愿者计划完成此项工作的天数是x 天,则甲、乙的工效都是1x 。
根据结果提前3天完成任务,知:整个过程中,甲做了(x -3)天,乙做了(x -5)天.再根据甲、乙做的工作量等于1,列方程求解: 根据题意,得x 3x 51x x--+=,解得x=8。
经检验x=8是方程的解。
∴甲志愿者计划完成此项工作的天数是8天。
故选A 。
13. (2009安徽省4分)某市2008年国内生产总值(GDP )比2007年增长了12%,由于受到国际金融危机的影响,预计今年比2008年增长7%,若这两年GDP 年平均增长率为x%,则x%满足的关系是【 】A .12%7%x%+=B .(112%)(17%)2(1x%)++=+C .12%7%2x%+=D .2(112%)(17%)(1x%)++=+ 【答案】D 。
【考点】由实际问题抽象出一元二次方程(增长率问题)。
【分析】设2007年的国内生产总值为1,∵2008年国内生产总值(GDP )比2007年增长了12%,∴2008年的国内生产总值为1+12%。
∵2009年比2008年增长7%,∴2009年的国内生产总值为(1+12%)(1+7%)。
∵这两年GDP 年平均增长率为x%,∴2009年的国内生产总值也可表示为:(1+x )2。
∴可列方程为:2(112%)(17%)(1x%)++=+。
故选D 。
14. (2011安徽省4分)一元二次方程x(x -2)=2-x 的根是【 】A .-1B .2C .1和2D .-1和2【答案】D 。
【考点】一元二次方程的根。
【分析】解出一元二次方程,直接得出结果。
二、填空题 1. (2001安徽省4分)解方程 22x 3x 126x 1x 35+-+=-+时,设2x 3y x 1+=-,则原方程可化为【 】 A .5y25y 260+-= B .25y y 260+-= C .25y y 260--=D .25y 26y 50-+=【答案】D 。
【考点】换元法解分式方程。
【分析】如果设2x 3y x 1+=-那么2x 11x 3y -=+,原方程可化为126y y 5+=,去分母,可以把分式方程转化为整式方程:25y 26y 50-+=。
故选D 。
2. (2012安徽省4分)关于x 的一元二次方程23x 2x k 10-+-=有两个实根,则k 的取值范围是【 】A .k <43 B .k <43且k≠1 C.k≤43 D .k >43【答案】C 。
【考点】一元二次方程根的判别式。
【分析】根据一元二次方程的根的判别式,建立关于k 的不等式,求出k 的取值范围:∵a=3,b=-2,c=k -1且方程有两个实数根,∴△=b 2-4ac=4-3×4(k -1)=16-12k≥0,∴k≤43。
故选C 。
3. (2002安徽省4分)据报载,我省人均耕地已从1951年的2.93亩减少到1999年的1.02亩,平均每年约减少0.04亩.若不采取措施,继续按此速度减下去,若干年后我省将无地可耕.无地可耕的情况最早会发生在【 】A . 2022年B .2023年C .2024年D .2025年【答案】D 。
【考点】一元一次方程的应用(增长率问题)。
【分析】设x 年后无耕地可耕,可得等式0.04x=1.02,解得x≈26年。
∴1999+26=2025。
故选D 。
4. (2003安徽省4分)用“84”消毒液配制药液,对白色衣物进行消毒,要求按1:200的比例进行稀释。
现要配制此种药液4020克,则需“84”消毒液 ▲ 克。
【答案】20。
【考点】一元一次方程的应用(溶液问题)。
【分析】设需“84”消毒液x 克,则根据等量关系:药:药液=1:(1+200)=1:201,据此列方程:x :4020=1:201,解得x=20。
5. (2005安徽省大纲4分)某射击运动爱好者在一次比赛中共射击10次,前6次射击共中53环(环数均是整数),如果他想取得不低于89环的成绩,第7次射击不能少于 ▲ 环.【答案】6。
【考点】一元一次不等式的应用。
【分析】设后4次射击中x 环,已知前6次射击共中53环,总成绩不低于89环,故53+x≥89,解得,x≥36。
假设最后3枪打最大值,则第7枪不得低于36﹣10×3=6环。
6. (2006安徽省大纲5分)不等式:x 221x >--()的解集是 ▲ 。
【答案】4x 3>。
【考点】解一元一次不等式。
【分析】将不等式右边的式子整理成2-2x ,然后整理将含有x 的式子放在式子左边,数字放右边,最后除以x 的系数:4x 221x x 222x x+2x 2+23x 4x 3>>>>>--⇒--⇒⇒⇒()。
