2010年中考数学试题分类汇编——圆的基本概念性质
中考数学试题分类汇编-圆的基本概念性质.doc

2010年中考数学试题分类汇编——圆的基本概念性质(2010哈尔滨)1.如图,AB 是⊙O 的弦,半径OA =2,∠AOB =120°,则弦AB 的长是( ).B (A )22 (B )32 (C )5 (D )53 (2010珠海)2.如图,⊙O 的半径等于1,弦AB 和半径OC 互相平分于点M.求扇形OACB 的面积(结果保留π)解:∵弦AB 和半径OC 互相平分 ∴OC ⊥ABOM=MC=21OC=21OA 在Rt △OAM 中,sinA=21=OA OM ∴∠A=30°又∵OA=OB ∴∠B=∠A=30° ∴∠AOB=120° ∴S 扇形=33601120ππ=⋅⋅(2010珠海)3.如图,△ABC 内接于⊙O ,AB =6,AC =4,D 是AB 边上一点,P 是优弧BAC的中点,连结PA 、PB 、PC 、PD.(1)当BD 的长度为多少时,△PAD 是以AD 为底边的等腰三角形?并证明; (2)若cos ∠PCB=55,求PA 的长. 解:(1)当BD =AC =4时,△PAD 是以AD 为底边的等腰三角形 ∵P 是优弧BAC 的中点 ∴弧PB =弧PC ∴PB =PC∵BD =AC =4 ∠PBD=∠PCA ∴△PBD ≌△PCA∴PA=PD 即△PAD 是以AD 为底边的等腰三角形(2)由(1)可知,当BD =4时,PD =PA ,AD =AB-BD =6-4=2 过点P 作PE ⊥AD 于E ,则AE =21AD=1 ∵∠PCB=∠PAD ∴cos ∠PAD=cos ∠PCB=55=PA AE ∴PA=5(1) (2010红河自治州)如图2,已知BD 是⊙O 的直径,⊙O 的弦AC ⊥BD 于点E ,若∠AOD=60°,则∠DBC( A ) A.30° B.40°C.50°D.60°(2010年镇江市)11.如图,AB 是⊙O 的直径,弦CD ⊥AB ,垂足为E ,若AB=10,CD=8,则线段OE 的长为 3 .(2010年镇江市)26.推理证明(本小题满分7分)如图,已知△ABC 中,AB=BC ,以AB 为直径的⊙O 交AC 于点D ,过D 作DE ⊥BC ,垂足为E ,连结OE ,CD=3,∠ACB=30°.(1)求证:DE 是⊙O 的切线; (2)分别求AB ,OE 的长;(3)填空:如果以点E 为圆心,r 为半径的圆上总存在不同的两点到点O 的距离为1,则r 的取值范围为 .(1)∵AB 是直径,∴∠ADB=90° (1分),)2(.//,.,BC DE BC OD BO AO CD AD BC AB ⊥∴==∴= 分又又 ∴OD ⊥DE ,∴DE 是⊙O 的切线. (3分) (2)在 30,3,=∠=∆ACB CD CBD Rt 中,.2,223330cos =∴===∴AB CDBC(4分))6(.27)23(1,)5(.2332121,30,3,2222分中在分中在=+=+=∆=⨯==∴=∠=∆OE OD OE ODE Rt CD DE ACB CD CDE Rt(3).127127+<<-r (7分)(2010遵义市)如图,△ABC 内接于⊙O,∠C=40,则∠ABO= ▲ 度.答案:50、(2010台州市)如图,⊙O 的直径CD ⊥AB ,∠AOC =50°,则∠CDB 大小为 (▲)A .25°B .30°C .40°D .50° 答案:A(玉溪市2010)11. 如图6,在半径为10的⊙O 中,OC 垂直弦AB 于点D ,AB =16,则CD 的长是 4 .(2010年兰州)4.有下列四个命题:①直径是弦;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.其中正确的有 A .4个 B .3个 C . 2个 D . 1个 答案 B2010年兰州)7. 将量角器按如图所示的方式放置在三角形纸板上,使点C 在半圆上.点A 、B 的读数分别为86°、30°,则∠ACB 的大小为A .15︒B .28︒C .29︒D .34︒A BCO D 图6 (第5题)ABOCDA第7题图 答案 B(2010年无锡)15.如图,AB 是O 的直径,点D 在O 上∠AOD=130°,BC ∥OD 交O于C,则∠A= ▲ . 错误!未指定书签。
2010年中考数学试题分类汇编(150套)专题二 实数的运算

1.(2010某某某某)20100的值是 A .2010 B .0 C .1 D .-1【答案】C2.(2010某某威海)计算()201020092211-⨯⎪⎭⎫ ⎝⎛-的结果是 A .-2 B .-1 C .2D .3【答案】B3.(2010某某)计算 | -1-(-35) |-| -611-67| 之值为何? (A) -37 (B) -31 (C) 34 (D)311。
【答案】A4.(2010某某)计算106⨯(102)3÷104之值为何?(A) 108 (B) 109 (C) 1010 (D) 1012。
【答案】A5.(2010某某)下列四个选项中的数列,哪一个不是等差数列? (A) 5,5,5,5,5 (B) 1,4,9,16,25(C)5,25,35,45,55 (D) 1,22,33,44,55。
【答案】D6.(2010某某)图(五)数在线的A 、B 、C 三点所表示的数分别为 a 、b 、c 。
根据图中各点位置,判断下列各式何者 正确? (A) (a -1)(b -1)>0 (B) (b -1)(c -1)>0 (C) (a +1)(b +1)<0 (D) (b +1)(c +1)<0 。
【答案】D7.(2010某某某某)计算 (– 1)2 + (– 1)3 =A.– 2B. – 1C. 0D. 2 【答案】C8.(2010 某某义乌)28 cm 接近于( ▲ )A .珠穆朗玛峰的高度B .三层楼的高度C .姚明的身高D .一X 纸的厚度A B CO a bc 0 -11图(五)9.(2010 某某德化)2-的3倍是() A 、6- B 、1 C 、6 D 、5- 【答案】A10.(2010 某某某某)某市2009年元旦的最高气温为2℃,最低气温为-8℃,那么这天的最高气温比最低气温高( )A .-10℃B .-6℃C .6℃D .10℃ 【答案】D11.(2010 东某某)下列各式中,运算正确的是()A =B .=C .632a a a ÷=D .325()a a =【答案】A12.(2010某某某某)计算()21-的值等于 (A )-1 (B )1 (C )-2 (D )2 【答案】B13.(2010 某某)计算3×(-2) 的结果是A .5B .-5C .6D .-6【答案】D14.(2010 某某)下列计算中,正确的是A .020=B .2a a a =+C 3±D .623)(a a =【答案】D15.(2010 某某省某某)下列计算正确的是(A)020=(B)331-=-3==【答案】C16.(2010某某宿迁)3)2(-等于A .-6B .6C .-8D .8 【答案】C17.(2010 某某莱芜)如图,数轴上A 、B 两点分别对应实数a 、b ,则下列结论正确的是A .0>abB .0>-b aC .0>+b aD .0||||>-b a【答案】D18.(2010某某) 计算 -2- 6的结果是( )A .-8B . 8C . -4D . 4 【答案】A19.(2010年某某某某)有一人患了流感,经过两轮传染后共有100人患了流感,那么每轮传染中,平均一个人传染的人数为() A .8人 B .9人 C .10人 D .11人【答案】B.20.(2010某某某某)()()2012321-+-+⎪⎭⎫ ⎝⎛--π的值为( )A .-1B .-3C . 1D . 0【答案】C21.(2010 某某某某)3x 表示( )(A )3x (B )x x x ++ (C )x x x ⋅⋅ (D )3x + 【答案】C22.(2010某某荆州)温度从-2°C 上升3°C 后是A .1°CB . -1°C C .3°CD .5°C 【答案】A1 0 -1 a b B A (第5题图)23.(2010某某荆州)下面计算中正确的是 A .532=+ B .()111=--C . ()2010201055=- D . x 32x •=x 6【答案】C24.(2010某某荆州)在电子显微镜下测得一个圆球体细胞的直径是5×105-cm.,3102⨯个这样的细胞排成的细胞链的长是A .cm 210- B .cm 110- C .cm 310- D .cm 410- 【答案】B25.(2010某某省某某)下列运算正确的是 A .263-=- B .24±=C .532a a a =⋅D .3252a a a+= 【答案】C26.(2010某某某某)观察下列各式:()1121230123⨯=⨯⨯-⨯⨯ ()1232341233⨯=⨯⨯-⨯⨯()1343452343⨯=⨯⨯-⨯⨯……计算:3×(1×2+2×3+3×4+…+99×100)=A .97×98×99B .98×99×100C .99×100×101D .100×101×102 【答案】C27.(2010某某某某)下列运算结果等于1的是() A .)3()3(-+-B .)3()3(---C .)3(3-⨯-D .)3()3(-÷-【答案】D28.(2010某某某某)如图,数轴上A 、B 两点对应的实数分别为,a b ,则下列结论不正确的是()A 、0a b +>B 、0ab <C 、0a b -<D 、0a b ->【答案】D29.(2010某某红河哈尼族彝族自治州)下列计算正确的是A .(-1)-1=1 B.(-3)20=1 D.(-2)6÷(-2)3=(-2)2 【答案】C30.(2010某某某某)下列计算正确的是( )A .a 2·a 3=a 6B .6÷2=3C .(21)-2=-2 D . (-a 3)2=-a 6 【答案】B31. (2010某某随州)下列运算正确的是( )A .1331-÷= B 2a a = C .3.14 3.14ππ-=- D .326211()24a b a b =【答案】D32. (2010某某某某)计算(-2)×3的结果是( )(A)-6 (B)6 (C)-5 (D)5 【答案】A33. (2010某某某某)某年某某市一月份的平均气温为-18℃,三月份的平均气温为2℃,则三月份的平均气温比一月份的平均气温高( )(A )16℃(B )20℃(C )-16℃(D ).-20℃【答案】B34. (2010 某某某某)如果□,1)23(=-⨯则□内应填的实数是 ( )A .23-B .32-C .23 D .32 【答案】B35. (2010某某襄樊)某市2010年元旦这天的最高气温是8℃,最低气温是-2℃,则这天的最高气温比最低气温高( ) A .10℃B .-10℃C .6℃D .-6℃【答案】A36. (2010 某某某某)2010)1(-的值是( )A .1B .—1C .2010D .—2010【答案】A37.(2010 某某某某)下列结论中不能由0=+b a 得到的是(A )ab a -=2(B )b a =(C )0=a ,0=b (D )22b a = 【答案】C38.(2010 某某某某)如图所示的运算程序中,若开始输入的x 值为48,我们发现第一次输出的结果为24,第二次输出的结果为12,…,则第2010次输出的结果为(A )6 (B )3 (C )200623(D )10033231003⨯+【答案】B39.(2010某某某某)的结果是)(计算12010)21(1:.1--- A. 1 B. -1 C.0 D. 2【答案】B40.(2010 某某)()=-21( )A .1B .-1C .2D .-2【答案】A41.(2010 某某荷泽)2010年元月19日,某某省气象局预报我市元月20日的最高气温是4℃,最低气温是-6℃,那么我市元月20日的最大温差是(第11题)A .10℃B .6℃C .4℃D .2℃【答案】A42.(2010某某某某)计算)3(21-⨯--的结果等于A.5B.5-C.7D.7-【答案】A43.(2010某某某某)用0,1,2,3,4,5,6,7,8这9个数字组成若干个一位数或两位数(每个数字都只用一次),然后把所得的数相加,它们的和不可能是( ) A .36 B .117 C .115 D .153 【答案】44.(2010某某某某)观察下列算式,用你所发现的规律得出20102的末位数字是( )21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,… A .2 B .4 C .6 D .8 【答案】B45.(2010某某某某)冰箱冷冻室的温度为-6℃,此时房屋内的温度为20℃,则房屋内的温度比冰箱冷冻室的温度高( )。
中考数学试题分类圆的有关性质
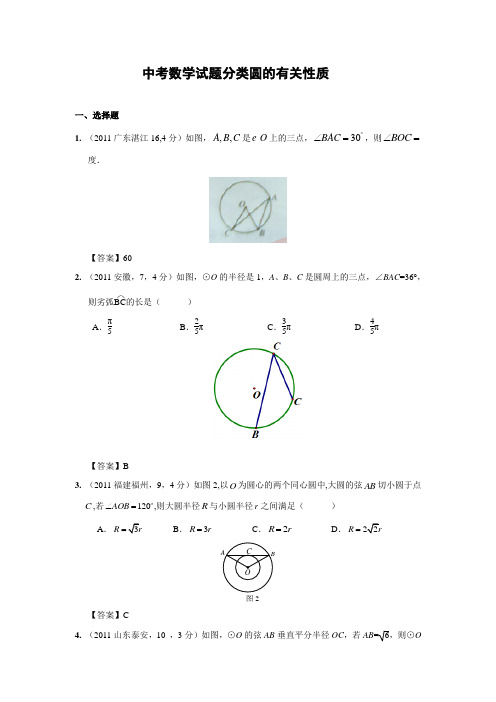
中考数学试题分类圆的有关性质一、选择题1. (2011广东湛江16,4分)如图,,,A B C 是O 上的三点,30BAC ︒∠=,则BOC ∠= 度.【答案】602. (2011安徽,7,4分)如图,⊙O 的半径是1,A 、B 、C 是圆周上的三点,∠BAC =36°,则劣弧 ⌒BC 的长是( ) A .π5B .25πC .35πD .45π【答案】B3. (2011福建福州,9,4分)如图2,以O 为圆心的两个同心圆中,大圆的弦AB 切小圆于点C ,若120AOB ∠= ,则大圆半径R 与小圆半径r 之间满足( )A.R = B .3R r =C .2R r =D.R =【答案】C4. (2011山东泰安,10 ,3分)如图,⊙O 的弦AB 垂直平分半径OC ,若AB =6,则⊙O图2的半径为()A. 2B.2 2C.22D.62【答案】A5. (2011四川南充市,9,3分)在圆柱形油槽内装有一些油。
截面如图,油面宽AB 为6分米,如果再注入一些油 后,油面AB 上升1分米,油面宽变为8分米,圆柱形油槽直径MN 为( )(A )6分米 (B )8分米 (C )10分米 (D )12分米 【答案】C6. (2011浙江衢州,1,3分)一个圆形人工湖如图所示,弦AB 是湖上的一座桥,已知桥AB 长100m ,测得圆周角45ACB ∠=︒,则这个人工湖的直径AD 为( )A.B.C.D.【答案】B7. (2011浙江绍兴,4,4分)如图,AB O 为的直径,点C 在O 上,若16C ∠=︒,则BOC ∠的度数是( )A.74︒B. 48︒C. 32︒D. 16︒【答案】C8. (2011浙江绍兴,6,4分)一条排水管的截面如图所示.已知排水管的截面圆半径10OB ,截面圆圆心O 到水面的距离OC 是6,则水面宽AB 是( )A.16B.10C.8D.6【答案】A9. (2011浙江省,5,3分)如图,小华同学设计了一个圆直径的测量器,标有刻度的尺子OA 、OB 在O 点钉在一起,并使它们保持垂直,在测直径时,把O 点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为( ) A. 12个单位 B. 10个单位 C.4个单位 D. 15个单位【答案】B10.(2011四川重庆,6,4分)如图,⊙O 是△A BC 的外接圆,∠OCB =40°则∠A 的度数等于( )A . 60°B . 50°C . 40°D . 30°【答案】B11.(2011浙江省嘉兴,6,4分)如图,半径为10的⊙O中,弦AB的长为16,则这条弦的弦心距为()(A)6 (B)8 (C)10 (D)12【答案】A12.(2011台湾台北,16)如图(六),BD为圆O的直径,直线ED为圆O的切线,A、C两点在圆上,AC平分∠BAD且交BD于F点。
2010年中考数学真题分类汇编专题十六

2010年中考数学真题分类汇编专题十六·一次函数的应用一、选择题:本大题共12个小题.每小题4分;共48分.1.的绝对值是()A.B.C.D.2.如图,,点在的延长线上,若,则的度数为()A.B.C.D.3.点关于原点对称的点的坐标是()A.B.C.D.4.同时抛掷两枚均匀的硬币,则两枚硬币正面都向上的概率是()A. B. C. D. 15.不等式组的解集用数轴表示为()6.若分式的值为,则的值为(A)A.B.C.D.或7.与如图所示的三视图对应的几何体是( )8.如图,与的边分别相交于两点,且.若,则AC等于().A. 1B.C.D. 29.如图,矩形OABC的边OA在x轴上,O与原点重合,OA=1,OC=2,点D的坐标为(2,0),则直线BD的函数表达式为()A. B. C. D.10.如图,已知AD是△ABC的外接圆的直径,AD =13 cm,,则AC的长等于()A.5 cm B.6 cmC.10 cm D.12 c m11.在如图所示的5×5方格中,每个小方格都是边长为1的正方形,△ABC是格点三角形(即顶点恰好是正方形的顶点),则与△ABC有一条公共边且全等的所有格点三角形的个数是()A. 1B. 2C. 3D. 412.已知二次函数的图象如图所示,有下列5个结论:①;②;③;④;⑤,(的实数)其中正确的结论有()A. 2个B. 3个C. 4个D. 5二、填空题:本大题共5个小题.每小题3分;共15分.13.分解因式: 2x2-18= .14.已知反比例函数的图象在第二、四象限,则取值范围是__________.15.用扇形统计图反映地球上陆地与海洋所占的比例时,“陆地”部分对应的圆心角是.宇宙中一块陨石落在地球上,落在陆地的概率是_________16.若,则下列函数①,②,③,④中,的值随的值增大而增大的函数是_______________(填上序号即可)17.如图,已知,点在边上,四边形是矩形.请你只用无刻度的直尺在图中画出的平分线(请保留画图痕迹).三、解答题:7个小题,57分.18.(本小题满分7分)(1)化简(2 )解方程:.19.(7分)(1)如图,在一次龙卷风中,一棵大树在离地面若干米处折断倒下,B为折断处最高点,树顶A落在离树根C的12米处,测得∠BAC=300,求BC的长。
中考复习——圆的有关概念及性质

圆的有关概念及性质复习【课标要求】:1.理解圆的定义和圆的有关概念;2.理解圆心角、弧、弦、弦心距之间的关系,并能运用它们之间的关系解决有关问题;3.掌握垂径定理及其应用【复习目标】:1.知道圆、弧、弦、圆心角、圆周角等基本概念;认识圆的对称性;了解圆锥的侧面展开图是扇形。
2.能用垂径定理,圆心角、弧、弦之间关系定理,圆周角定理及推论,等进行简单的运算和推理;会通过作图的方法理解确定圆的条件。
3.会用折叠、旋转、圆的对称性及分类讨论的思想方法探索图形的有关性质,能将有关弦长、半径的实际计算问题转化成解直角三角形问题解决。
【知识梳理】:考点导航1.与圆有关的概念(1)圆的定义_________________________________图形叫做圆.(2)弦:连结圆上___________的线段叫做弦.(3)直径:___________的弦叫做直径.(4)弧:圆上任意两点间的部分叫做___________.(5)优弧:___________叫做优弧.(6)劣弧:___________叫做劣弧.(7)同心圆:圆心相同、半径不相等的圆的叫做同心圆.(8)等圆:___________叫做等圆.(9)等弧:在同圆或等圆中,___________的弧叫做等弧.2.过三点的圆(1)经过___________三点不能作圆.(2)不在同一直线上的三点确定___________个圆.3.垂径定理及推论(1)垂径定理垂直于弦的直径___________,并且___________.(2)推论平分弦(不是直径)的直线___________,并且___________.弦的垂直平分线____________________________________________________.平分弦所对的一条弧的直径,______________________________________.4.圆心角、弧、弦、弦心距之间的关系在同圆或等圆中,相等的圆心角所对的弧___________,所对的弦___________,所对的弦的弦心距___________.5.圆周角定理及推论(1)定理:在___________或___________中,同弧或等弧所对的圆周角___________,都等于这条弧所对___________的一半.(2)推论:___________(或___________)所对的圆周角是___________,90°的圆周角所对的弦是___________.6.圆内接四边形圆内接四边形的对角___________,一个外角等于它的___________.考点点拨1.注意相关概念的区分(1)弧与半圆:半圆是弧,但弧不一定是半圆.(2)弦与直径:直径是弦,但弦不一定是直径,直径是圆中最长的弦.(3)等弧与长度相等的弧:等弧的长度一定相等,但长度相等的弧不一定是等弧.(4)等圆和同心圆:等圆是半径相等圆心不同的圆,而同心圆是半径不等圆心相同的圆.2.常用的辅助线(1)作半径,利用同圆的半径相等;(2)作弦心距,利用垂径定理进行计算或推理,或利用圆心角、弧、弦、弦心距之间的关系进行证明;(3)作半径和弦心距,构造直角三角形进行计算;(4)构造直径所对的圆周角——直角;(5)构造同弧或等弧所对的圆周角;(6)遇到三角形的外心常连结外心和三角形各顶点.3.分类讨论解“圆”题,防止漏解如:一条弦所对的圆周角有两种,所以在同圆或等圆中,等弦所对的圆周角相等或互补.圆内两条平行弦与圆心的位置关系有两种等.【考题研究】考点 1 圆的概念和性质例1 下列命题中,假命题是( )A .两条弧的长度相等,它们是等弧B .等弧所对的圆周角相等C .直径所对的圆周角是直角D .一条弧所对的圆心角等于它所对的圆周角的两倍意图:本题是考查圆的基本概念和性质,要结合图形深刻理解和熟练记忆.考点 2 圆的弦、半径、弦心距的计算例2 如图1-9-1,以O 为圆心的两个同心圆中,大圆的弦AB 是小圆的切线,若大圆半径为10 cm ,小圆半径为6 cm ,则弦AB 的长为___________.意图:在一个圆中,若已知圆的半径为r ,弦长为a ,这条弦的弦心距为d ,则有等式r 2=d 2+2a 2⎛⎫ ⎪⎝⎭成立,知道这三个量中的任意两个,就可以求出另外一个.考点 3 圆心角、弧、弦之间的关系例3 (2011·河南)如图1-9-3所示,边长为1的小正方形构成的网格中,半径为1的⊙O 的圆心O 在格点上,则∠AED 的正切值等于___________.意图:相同弧所对的周围角相等.考点 4 圆心角与圆周角的关系及应用例4 (2011·芜湖)如图1-9-5,已知点E是圆O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED的度数为___________.意图:本题主要考查秀点,一是在同圆或等圆中,等弧所对圆心角相等,二是同弧所对圆周角等于圆心解的一半.【中考链接】1.(2011浙江绍兴,4,4分)如图,AB为圆O的直径,点C在圆O上,若16∠=︒,C则B O C∠的度数是()A.74︒B. 48︒C. 32︒D. 16︒2.(2011浙江绍兴,6,4分)一条排水管的截面如图所示.已知排水管的截面圆半径10O B=,截面圆圆心O到水面的距离O C是6,则水面宽AB是()A.16B.10C.8D.63.(2011四川凉山州,9,4分)如图,100上,且点C不与A、∠= ,点C在OAOBB重合,则A C B∠的度数为()A.50 B.80 或50 C.130 D.50 或1304.(2011湖北荆州,12,4分)如图,⊙O是△ABC的外接圆,CD是直径,∠B=40°,则∠ACD的度数是.5.(2011浙江杭州,14,4)如图,点A,B,C,D都在⊙O上,的度数等于84°,CA 是∠OCD的平分线,则∠ABD十∠CAO= °6. (2011四川乐山6,3分)如图(3),CD是⊙O的弦,直径AB过CD的中点M,若∠BOC=40°,则∠ABD=( )A.40°B.60°C.70°D.80°7. (2011江西,21,8分)如图,已知⊙O的半径为2,弦BC的长为,点A为弦BC 所对优弧上任意一点(B,C两点除外)。
河北省中考数学复习 圆 第29讲 圆的基本性质试题(含解析)-人教版初中九年级全册数学试题

第29讲 圆的基本性质1. (2012,某某)如图,CD 是⊙O 的直径,AB 是弦(不是直径),AB ⊥CD 于点E ,则下列结论正确的是(D)第1题图A. AE >BEB. 弧AD =弧BCC. ∠D =12∠AEC D. △ADE ∽△CBE 【解析】 ∵CD 是⊙O 的直径,AB 是弦(不是直径),AB ⊥CD 于点E ,∴AE =BE ,弧AC =弧BC .∴A ,B 两选项错误.∵∠AEC 不是圆心角,∴∠D ≠12∠AE C. ∴C 选项错误.∵∠AED =∠CEB =90°,∠DAE =∠BCE ,∴△ADE ∽△CBE .∴D 选项正确.2. (2015,某某)如图,AC ,BE 是⊙O 的直径,弦AD 与BE 相交于点F .下列三角形中,外心不是点O 的是(B)第2题图A. △ABEB. △ACFC. △ABDD. △ADE【解析】 只有△ACF 的三个顶点不都在⊙O 上,故外心不是点O 的是△ACF .3. (2016,某某)如图所示的为4×4的网格图,A ,B ,C ,D ,O 均在格点上,点O 是(B)第3题图A. △ACD 的外心B. △ABC 的外心C. △ACD 的内心D. △ABC 的内心【解析】 由网格图,知点O 是边AC ,BC 的垂直平分线的交点.根据三角形外心的定义,知点O 是 △ABC 的外心.圆的有关概念例1 下列语句正确的是(D)A. 长度相等的两条弧是等弧B. 平分弦的直径垂直于弦C. 相等的圆心角所对的弧相等D. 经过圆心的每一条直线都是圆的对称轴【解析】 能完全重合的两条弧是等弧,所以A 选项错误.平分弦(不是直径)的直径垂直于弦,所以B 选项错误.在同圆或等圆中,相等的圆心角所对的弧相等,所以C 选项错误.经过圆心的每一条直线都是圆的对称轴,所以D 选项正确.针对训练1 如图,半圆O 是一个量角器,△AOB 为一纸片,AB 交半圆于点D ,OB 交半圆于点C .若点C ,D ,A 在量角器上对应的读数分别为45°,70°,160°,则∠B 的度数为(A)训练1题图A. 20°B. 30°C. 45°D. 60°【解析】 如答图,连接OD ,则∠DOC =70°-45°=25°,∠AOD =160°-70°= 90°.∵OD =OA ,∴∠ADO =∠A =45°.∵∠ADO =∠B +∠DOB ,∴∠B =45°-25°= 20°.训练1答图针对训练2 如图,点P 在线段AB 上,PA =PB =PC =PD .当∠BPC =60°时,∠BDC 的度数为(B)训练2题图A. 15°B. 30°C. 25°D. 60°【解析】 ∵PA =PB =PC =PD ,∴点A ,B ,C ,D 在以点P 为圆心,PB 的长为半径的圆上.∴∠BDC =12∠BPC =12×60°=30°.确定圆的条件例2 (2010,某某)如图,在5×5的正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是(B)例2题图A. 点PB. 点QC. 点RD. 点M【解析】如答图,连接BC,作AB和BC的垂直平分线,它们相交于点Q,则点Q即为圆心.例2答图针对训练3 在平面直角坐标系中,点A的坐标是(-1,0),点B的坐标是(3,0),在y 轴的正半轴上取一点C,使A,B,C三点确定一个圆,且使AB为圆的直径,则点C的坐标是(A)A. (0,3)B. (3,0)C. (0,2)D. (2,0)【解析】如答图,连接AC,CB.根据题意可证得△AOC∽△COB,∴OCOA=OBOC,即OC2=OA·OB.∴OC2OC= 3.故点C的坐标为(0,3).训练3答图针对训练4 如图,在矩形ABCD中,E为AB的中点,有一圆过C,D,E三点,且此圆分别与AD,BC相交于P,Q两点.甲、乙两人想找到此圆的圆心O,其作法如下:甲:连接DE,EC,作∠DEC的平分线EM,作DE的垂直平分线,交EM于点O,则点O即为所求.乙:连接PC,QD,两线段交于一点O,则点O即为所求.对于甲、乙两人的作法,下列判断正确的是(A)训练4题图A. 两人皆正确B. 两人皆错误C. 甲正确,乙错误D. 甲错误,乙正确【解析】 对于甲,易知ED =EC ,∴△DEC 为等腰三角形.进而易知EM 为CD 的垂直平分线.∴点O 为两垂直平分线的交点,即点O 为△CDE 的外心.∴点O 为此圆的圆心.对于乙,∵∠ADC =90°,∠DCB =90°,∴PC ,QD 为此圆的直径.∴PC 与QD 的交点O 为此圆的圆心.因此甲、乙两人皆正确.圆的基本性质例3 (2018,某某裕华区模拟)如图,在半径为5的⊙O 中,弦AB =6,C 是优弧AB 上一点(不与点A ,B 重合),则cos C 的值为(D)例3题图A. 43B. 34C. 35D. 45【解析】 如答图,作直径AD ,连接BD .∵AD 为直径,∴∠ABD =90°.在Rt △ABD 中,∵AD =10,AB =6,∴BD =102-62=8.∴cos D =BD AD =810=45.∵∠C =∠D ,∴cos C =45.例3答图针对训练5 (2018,某某模拟)如图,在半径为5的⊙A 中,弦BC ,ED 所对的圆心角分别是∠BAC ,∠EAD .若DE =6,∠BAC +∠EAD =180°,则弦BC 的长是(A)训练5题图A. 8B. 10C. 11D. 12【解析】 如答图,作直径CF ,连接BF ,则∠FBC =90°.∵∠BAC +∠EAD =180°,∠BAC +∠BAF =180°,∴∠DAE =∠BAF .∴弧DE =弧BF .∴BF =DE =6.∴BC =CF 2-BF 2=8.训练5答图 针对训练6 (2018,某某)已知⊙O 的半径为10,圆心O 到弦AB 的距离为5,则弦AB 所对的圆周角的度数为(D)A. 30°B. 60°C. 30°或150°D. 60°或120°【解析】 如答图.在Rt △OAD 中,∵OA =10,OD =5,∴cos ∠AOD =OD AO =12.∴∠AOD =60°.同理可得∠BOD =60°.∴∠AOB =∠AOD +∠BOD =60°+60°=120°.∴弦AB 所对的圆周角的度数是60°或120°.训练6答图垂径定理例4 (2018,某某,导学号5892921)已知⊙O 的直径CD =10 cm ,AB 是⊙O 的弦,AB ⊥CD ,垂足为M ,且AB =8 cm ,则AC 的长为(C)A. 2 5 cmB. 4 5 cmC. 2 5 cm 或4 5 cmD. 2 3 cm 或4 3 cm【解析】 如答图,连接AC ,AO .∵⊙O 的直径CD =10 cm ,AB ⊥CD ,AB =8 cm ,∴AM =12AB =12×8=4(cm),OD =OC =5 cm.当点C 的位置如答图①所示时,∵OA =5 cm ,AM = 4 cm ,CD ⊥AB ,∴OM =OA 2-AM 2=52-42=3(cm).∴CM =OC +OM =5+3=8(cm).∴AC =AM 2+CM 2=42+82=45(cm).当点C 的位置如答图②所示时,同理可得OM =3 cm.∵OC =5 cm ,∴MC =5-3=2(cm).∴在Rt △AMC 中,AC =AM 2+MC 2=42+22= 25(cm).综上所述,AC 的长为2 5 cm 或4 5 cm.例4答图针对训练7 (2018,某某)如图,AB 是⊙O 的直径,弦CD ⊥AB 于点E ,OC =5 cm ,CD =8 cm ,则AE 的长为(A)训练7题图A. 8 cmB. 5 cmC. 3 cmD. 2 cm【解析】 ∵CD ⊥AB ,CD =8 cm ,∴CE =12CD =4 cm.在Rt △OCE 中,OC =5 cm ,CE =4 cm ,∴OE =OC 2-CE 2=3 cm.∴AE =AO +OE =5+3=8(cm).一、 选择题1. (2018,聊城)如图,在⊙O 中,弦BC 与半径OA 相交于点D ,连接AB ,OC . 若∠A =60°,∠ADC =85°,则∠C 的度数是(D)第1题图A. 25°° C. 30° D. 35°【解析】 ∵∠A =60°,∠ADC =85°,∴∠B =85°-60°=25°,∠CDO =95°. ∴∠AOC =2∠B =50°.∴∠C =180°-95°-50°=35°.2. (2018,威海)如图,⊙O 的半径为5,AB 为弦,C 为弧AB 的中点.若∠ABC =30°,则弦AB 的长为(D)第2题图A. 12B. 5C. 532D. 53 【解析】 如答图,连接OA ,OC ,OC 与AB 相交于点E .∵∠ABC =30°,∴∠AOC = 60°.由AB 为弦,C 为弧AB 的中点,易知OC ⊥AB ,AE =BE .在Rt △OAE 中,AE =OA · sin ∠AOC =5×32=532,∴AB =2AE =5 3.第2题答图3. (2018,某某)如图,⊙A 过点O (0,0),C (3,0),D (0,1),B 是x 轴下方⊙A 上的一点,连接BO ,BD ,则∠OBD 的度数是(B)第3题图A. 15°B. 30°C. 45°D. 60°【解析】 如答图,连接DC .∵C (3,0),D (0,1),∴∠DOC =90°,OD =1,OC = 3.∴∠DCO =30°.∴∠OBD =∠DCO =30°.第3题答图4. (2018,某某)如图,BC 是⊙O 的直径,A 是⊙O 上的一点,∠OAC =32°,则∠B 的度数是(A)第4题图A. 58°B. 60°C. 64°D. 68°【解析】 ∵OA =OC ,∴∠C =∠OAC =32°.∵BC 是直径,∴∠CAB =90°.∴∠B = 90°-32°=58°.5. (2018,贵港)如图,点A ,B ,C 均在⊙O 上.若∠A =66°,则∠OCB 的度数是(A)第5题图A. 24°B. 28°C. 33°D. 48°【解析】 ∵∠A =66°,∴∠COB =132°.∵CO =BO ,∴∠OCB =∠OBC =12×(180°-132°)=24°.6. (2018,某某)如图,AB 为⊙O 的直径,CD 是⊙O 的弦,∠ADC =35°,则∠CAB 的度数为(C)第6题图A. 35°B. 45°C. 55°D. 65°【解析】 由圆周角定理,得∠ABC =∠ADC =35°.∵AB 为⊙O 的直径,∴∠ACB =90°.∴∠CAB =90°-∠ABC =55°.7. (2018,某某)如图,AB 是半圆的直径,O 为圆心,C 是半圆上的点,D 是弧AC 上的点.若∠BOC =40°,则∠D 的度数为(B)第7题图A. 100°B. 110°C. 120°D. 130°【解析】 ∵∠BOC =40°,∴∠AOC =180°-40°=140°.∴∠D =12×(360°-140°)=110°.8. (2018,某某)如图,点A ,B ,C ,D 在⊙O 上,∠AOC =140°,B 是弧AC 的中点,则∠D 的度数是(D)第8题图A. 70°B. 55°° D. 35°【解析】 如答图,连接OB .∵B 是弧AC 的中点,∴∠AOB =12∠AOC =70°.由圆周角定理,得∠D =12∠AOB =35°.第8题答图9. (2018,滨州)已知半径为5的⊙O 是△ABC 的外接圆.若∠ABC =25°,则劣弧AC 的长为(C)A. 25π36B. 125π36C. 25π18D. 5π36【解析】 如答图,连接AO ,CO .∵∠ABC =25°,∴∠AOC =50°.∴劣弧AC 的长为50π·5180=25π18.第9题答图10. (2018,某某)如图,AC 是⊙O 的直径,弦BD ⊥AO 于点E ,连接BC ,过点O 作OF ⊥BC 于点F .若BD =8 cm ,AE =2 cm ,则OF 的长是(D)第10题图A. 3 cmB. 6 cmC. 2.5 cmD. 5 cm【解析】 如答图,连接OB .∵AC 是⊙O 的直径,弦BD ⊥AO ,BD =8,∴BE =DE =4.∵AE =2,∴在Rt △OEB 中,OE 2+BE 2=OB 2,即OE 2+42=(OE +2)2.解得OE =3.∴OB =3+2=5.∴EC Rt △EBC 中,BC =BE 2+EC 2=42+82=4 5.∵OF ⊥BC ,∴∠OFC =∠CEB =90°.∵∠C =∠C ,∴△OFC ∽△BEC .∴OF BE =OC BC ,即OF 4=545.解得OF = 5.所以OF 的长是 5 cm.第10题答图二、 填空题11. (2018,某某)在同圆中,已知弧AB 所对的圆心角是100°,则弧AB 所对的圆周角是50°.【解析】 由圆周角定理,得弧AB 所对的圆周角为50°.12. (2018,某某模拟)如图,截面为圆形的油槽内放入一些油.若圆的直径为150 cm ,油的深度DC 为30 cm ,则油面宽度AB 是120cm.第12题图【解析】 ∵OC ⊥AB ,∴AD =BD =12AB .∵OC =OB =12×150=75(cm),∴OD =OC -CD =75-30=45(cm).在Rt △OBD 中,BD =OB 2-OD 2=752-452=60(cm),∴AB =2BD =120 cm.13. (2018,某某)如图,方格纸上每个小正方形的边长均为1个单位长度,点O ,A ,B ,C 在格点(两条网格线的交点叫格点)上,以点O 为原点建立直角坐标系,则过A ,B ,C 三点的圆的圆心坐标为(-1,-2).第13题图【解析】 如答图,连接AB ,CB ,作AB ,CB 的垂直平分线,相交于点D .所以点D 是过A ,B ,C 三点的圆的圆心.所以点D 的坐标为(-1,-2).第13题答图14. (2018,某某)如图,量角器的0度刻度线为AB ,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点C ,直尺另一边交量角器于点A ,D ,量得AD =10 cm ,点D 在量角器上的读数为60°,则该直尺的宽度为( 533)cm.第14题图【解析】 如答图,连接OC ,OD ,OC 与AD 相交于点E .∵直尺一边与量角器相切于点C ,∴OC ⊥AD .∵AD =10,∠DOB =60°,∴∠DAO =30°.∴OE =533,OA =1033.∴CE =OC -OE =OA -OE =533.即该直尺的宽度是533cm.第14题答图三、 解答题15. (2018,枣庄)如图,在Rt △ACB 中,∠C =90°,AC =3 cm ,BC =4 cm ,以BC 为直径作⊙O 交AB 于点D .(1)求线段AD 的长;(2)E 是线段AC 上的一点,当点E 在什么位置时,直线ED 与⊙O 相切?请说明理由.第15题图【思路分析】 (1)由勾股定理易求得AB 的长.可连接CD ,知CD ⊥AB ,易知Rt △ADC ∽Rt △ACB ,可得关于AC ,AD ,AB 的比例关系式,即可求出AD 的长.(2)当ED 与⊙O 相切时,由切线长定理知EC =ED ,则∠ECD =∠EDC .连接OD ,证OD ⊥DE 即可.解:(1)如答图,连接CD . 在Rt △ACB 中,∵AC =3 cm ,BC =4 cm ,∠ACB =90°, ∴AB =5 cm. ∵BC 为直径,∴∠ADC =∠BDC =90°. ∵∠A =∠A ,∠ADC =∠ACB , ∴Rt △ADC ∽Rt △ACB . ∴AC AB =AD AC. ∴AD =AC 2AB =325=95(cm).(2)当E是AC的中点时,直线ED与⊙O相切.理由:如答图,连接OD.∵DE是Rt△ADC的中线,∴ED=EC.∴∠EDC=∠ECD.∵OC=OD,∴∠ODC=∠OCD.∴∠EDO=∠EDC+∠ODC=∠ECD+∠OCD=∠ACB=90°.∴ED⊥OD.∴直线ED与⊙O相切.第15题答图16. (2018,某某,导学号5892921)如图,在△ABC中,AB=AC,以AB为直径的半圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.(1)求证:四边形ABFC是菱形;(2)若AD=7,BE=2,求半圆形和菱形ABFC的面积.第16题图【思路分析】 (1)根据对角线相互平分的四边形是平行四边形,证明四边形ABFC是平行四边形,再根据邻边相等的平行四边形是菱形即可证明.(2)连接BD.利用勾股定理构建方程即可解决问题.(1)证明:∵AB是直径,∴∠AEB=90°.∴AE⊥BC.∵AB =AC , ∴BE =CE . ∵AE =EF ,∴四边形ABFC 是平行四边形. ∵AC =AB ,∴四边形ABFC 是菱形. (2)解:如答图,连接BD . ∵AB 是直径,∴∠ADB =∠BDC =90°. ∴AB 2-AD 2=CB 2-CD 2. ∴(7+CD )2-72=(2+2)2-CD 2. 解得CD =1.∴AB =AC =AD +CD =7+1=8. ∴BD =82-72=15. ∴S 半圆形=12π·42=8π,S 菱形ABFC =AC ·BD =815.第16题答图1. (2018,襄阳)如图,点A ,B ,C ,D 都在半径为2的⊙O 上.若OA ⊥BC ,∠CDA = 30°,则弦BC 的长为(D)第1题图A. 4B. 2 2C. 3D. 23【解析】 如答图.∵OA ⊥BC ,∴CH =BH ,弧AB =弧AC .∴∠AOB =2∠CDA =60°.∴BH =OB ·sin ∠AOB = 3.∴BC =2BH =2 3.第1题答图2. (2018,某某)如图,AB 是⊙O 的直径,C 是半径OA 的中点,过点C 作DE ⊥AB ,交⊙O 于D ,E 两点,过点D 作直径DF ,连接AF ,则∠DFA =30°.第2题图【解析】 ∵C 是半径OA 的中点,∴OC =12OD .∵DE ⊥AB ,∴∠CDO =30°.∴∠DOA =60°.∴∠DFA =30°.3. (2018,某某,导学号5892921)如图,D 是△ABC 的边BC 上一点,连接AD ,作△ABD 的外接圆,将△ADC 沿直线AD 折叠,点C 的对应点E 落在弧BD 上.(1)求证:AE =AB ;(2)若∠CAB =90°,cos ∠ADB =13,BE =2,求BC 的长.第3题图【思路分析】 (1)由折叠得出∠AED =∠ACD ,AE =AC ,结合∠ABD =∠AED 知∠ABD =∠ACD ,从而得出AB =AC ,据此得证.(2)过点A 作AH ⊥BE 于点H ,由AB =AE 且BE =2知BH =EH =1.根据∠ABE =∠AEB =∠ADB 知cos ∠ABE =cos ∠ADB =BH AB =13,据此得AC =AB =3,利用勾股定理可得答案.(1)证明:由折叠的性质,知△ADE ≌△ADC . ∴∠AED =∠ACD ,AE =AC . ∵∠ABD =∠AED , ∴∠ABD =∠ACD . ∴AB =AC . ∴AE =AB .(2)解:如答图,过点A 作AH ⊥BE 于点H . ∵AB =AE ,BE =2, ∴BH =EH =1.∵∠ABE =∠AEB =∠ADB , ∴cos ∠ABE =cos ∠ADB =13.∴BH AB =13. ∴AB =3.∵∠CAB =90°,AC =AB =3, ∴BC =3 2.第3题答图。
2023年中考数学复习第一部分考点梳理第六章圆第1节圆的基本概念与性质

十年真题精选
十年真题精选
教材知识网络
重难考点突破
-3-
6.1 圆的基本概念与性质
2.(2021·安徽第20题)如图,圆O中两条互相垂直的弦AB,CD交
于点E.
(1)M是CD的中点,OM=3,CD=12,求圆O的半径长;
(2)点F在CD上,且CE=EF,求证:AF⊥BD.
十年真题精选
十年真题精选
教材知识网络
在Rt△AOD中,∵AD= AB=3,∠OAD=41.3°,
∴OD=AD·tan
41.3°≈3×0.88=2.64,OA=
.°
≈
=
.
4,
∴CD=CO+OD=OA+OD=6.64米.
答:运行轨道的最高点C到弦AB所在直线的距离约为6.64米.
十年真题精选
十年真题精选
教材知识网络
6.1
圆的基本概念与性质
6.1 圆的基本概念与性质
十年真题精选
十年真题精选(学用见P113~114)
命题点1垂径定理及其推论[10年7考]
1.(2022·安徽第7题)已知☉O的半径为7,AB是☉O的弦,点P在
弦AB上.若PA=4,PB=6,则OP=(
A.
B.4
C.
D.5
)D
十年真题精选
重难考点突破
-4-
6.1 圆的基本概念与性质
解:(1)如图,连接OC,OD.
因为M是CD的中点,且CD=12,
所以CM=DM=6,且OM⊥DM.
在Rt△OMD中,由勾股定理,得OD= + = +
=3 ,
所以圆O的半径长为3 .
十年真题精选
十年真题精选
中考数学分类汇编 知识点30 圆的基本性质

一、选择题7.(2019·嘉兴)如图,已知⊙O上三点A,B,C,半径OC=1,∠ABC=30°,切线P A交OC延长线于点P,则P A的长为()A.2 B.C.D.【答案】B【解析】连接OA,因为∠ ABC=30°,所以∠AOC=60°,又因为PA为切线,所以∠OAP=90°,因为OC=1,所以.3.(2019·杭州)如图,P为⊙O外一点,PA、PB分别切⊙O于A、B两点,若PA=3,则PB= ()A.2 B.3 C.4 D.5【答案】B【解析】因为P A和PB与⊙O相切,根据切线长定理,可知:P A=PB=3,故选B.12.(2019·烟台)如图,AB是Oe的直径,直线DE与Oe相切于点C,过点A,B分别作AD DE⊥,BE DE⊥,垂足为点D,E,连接AC,BC.若AD=3CE=,则»AC的长为().A.3B.3C.2D.3【答案】D【解题过程】连接OC,因为AD DE⊥,BE DE⊥,所以90ADC CEB∠=∠=︒所以90DAC ACD∠+∠=︒因为AB是Oe的直径,所以90ACB∠=︒,所以90BCE ACD∠+∠=︒,所以BCE DAC∠=∠,在△ADC与△CED,因为90ADC CEB∠=∠=︒,BCE DAC∠=∠所以△ADC∽△CED,所以BC CEAC AD===在Rt△ACB中,sin BCBACAC∠==所以60BAC∠=︒,OD EBA第12题答图又因为OA OC=,所以△AOC是等边三角形,所以60ACO∠=︒,因为直线DE与Oe相切于点C,所以OC DE⊥,因为AD DE⊥,OC DE⊥,所以AD//OC,所以60DAC ACO∠=∠=︒,所以9030ACD DAC∠=︒-∠=︒,所以2AC AD==,所以△AOC是等边三角形,所以OA AC==,60AOC∠=︒,所以»AC的长为601803π⨯⨯=.12.(2019·威海)如图,⊙P与x轴交与点A(—5,0),B(1,0),与y轴的正半轴交于点C,若∠ACB=60°,则点C的纵坐标为A.B.. .2【答案】D【解题过程】连接PA、PB、PC,过点P分别作PF⊥AB,PE⊥OC,垂足为F,E.由题意可知:四边形PFOE为矩形,∴PE=OF,PF=OE.∵∠ACB=60°,∴∠APB=120°.∵P A=PB,∴∠P AB=∠PBA=30°.∵PF⊥AB,∴AF=BF=3.∴PE=OF=2.cos30°=AFAP,∴PFAP=∴OEPC=在RT△PEC中,CE==∴OC=CE+EO=+2.5.(2019·青岛)如圈,结段AB经过⊙O的圆心,AC BD分别与⊙O相切于点D.若AC= BD = 4,∠A=45°,则圆弧CD的长度为A.πB. 2πC D.4π【答案】B【解析】连接CO,DO,因为AC,BD分别与⊙O相切于C,D,所以∠ACO=∠DBO=90°, 所以∠AOC=∠A=45°, 所以CO=AC=4,因为AC=BD,CO=DO,所以△ACO≌△BDO,所以∠DOB=π⨯=2∠AOC=45°,所以∠DOC=180°-∠DOB-∠AOC=180°-45°-45°=90°,»CD=904180π,故选B.9.(2019·益阳)如图,PA、PB为圆O的切线,切点分别为A、B,PO交AB 于点C,PO的延长线交圆O于点D,下列结论不一定成立的是()A. PA=PBB.∠BPD=∠APDC.AB⊥PDD.AB平分PD第9题图【答案】D【解析】∵PA、PB为圆O的切线,切点分别为A、B,PO交AB于点C,PO 的延长线交圆O于点D,∴PA=PB,∠BPD=∠APD,故A、B正确;∵PA=PB,∠BPD=∠APD,∴PD⊥AB,PD平分AB,但AB不一定平分PD,故C正确,D错误.7.(2019·黄冈)如图,一条公路的转弯处是一段圆弧(»AB),点O是这段弧所在圆的圆心,AB=40m,点C是»AB的中点,点D是AB的中点,且CD=10m.则这段弯路所在圆的半径为()A.25mB.24mC.30mD.60m【答案】A【解析】连接OD,由垂径定理可知O,C,D在同一条直线上,OC⊥AB,设半径为r,则OC=OA=r,AD=20,OD=OA-CD=r-10,在Rt△ADO,由勾股定理知:r2=202+(r-10)2,解得r=25.9.(2019·陇南)如图,点A,B,S在圆上,若弦AB的长度等于圆半径的倍,则∠ASB的度数是()A .22.5°B .30°C .45°D .60°【答案】C【解析】作AB 的垂直平分线,交圆与点C ,D ,设圆心为O ,CD 与AB 交于点E ,∵AB=OA ,∴AE=2,∴2sin 2OE AOE OA OA ∠===,∴∠AOE=45°,∴∠AOB=90°, ∴∠ASB=45°, 故选:C .1.(2019·滨州)如图,AB 为⊙O 的直径,C ,D 为⊙O 上两点,若∠BCD =40°,则∠ABD 的大小为( )A .60°B .50°C .40°D .20°【答案】B【解析】如图,连接AD,∵AB为⊙O的直径,∴∠ADB=90°.∵∠A和∠BCD 都是弧BD所对的圆周角,∴∠A=∠BCD=40°,∴∠ABD=90°-40°=50°.故选B.2. (2019·聊城)如图,BC是半圆O的直径,D,E是»BC上两点,连接BD,CE并延长交于点A,连接OD,OE,如果∠A=70°,那么∠DOE的度数为A.35°B.38°C.40°D.42°【答案】C【解析】∵∠A=70°,∴∠B+∠C=110°,∴∠BOE+∠COD=220°,∴∠DOE =∠BOE+∠COD-180°=40°,故选C.3.(2019·潍坊)如图,四边形ABCD内接于⊙O,AB为直径,AD=CD.过点D作DE⊥AB于点E.连接AC交DE于点F.若sin∠CAB=3,DF=5,则BC5的长为()A .8B .10C .12D .16 【答案】C 【解析】连接BD .∵AD =CD ,∴∠DAC =∠ACD .∵AB 为直径,∴∠ADB =∠ACB =90°.∴∠DAB +∠ABD =90°. ∵DE ⊥AB ,∴∠DAB +∠ADE =90°.∴∠ADE =∠ABD . ∵∠ABD =∠ACD ,∴∠DAC =∠ADE .∴AF =DF =5. 在Rt △AEF 中,sin ∠CAB =35EF AF = ∴EF =3,AE =4.∴DE =3+5=8.由DE 2=AE ▪EB ,得228164DE BE AE ===. ∴AB =16+4=20.在Rt △ABC 中,sin ∠CAB =35BC AB = ∴BC =12.4. (2019·凉山)下列命题:①直线外一点到这条直线的垂线段,叫做点到直线的距离;②两点之间线段最短;③相等的圆心角所对的弧相等;④平分弦的直径垂直于弦.其中,真命题的个数(▲)A.1 B.2 C.3 D.4【答案】A【解析】直线外一点到这条直线的垂线段的长度,叫做点到直线的距离;两点之间线段最短;在同圆或等圆中,相等的圆心角所对的弧相等;平分弦(不是直径)的直径垂直于弦,所以只有①是对的,故选A.5.(2019·眉山)如图,⊙O的直径AB垂直于弦CD.垂足是点E,∠CAO=22.5°,OC=6,则CD的长为B.C.6 D.12A.【答案】A【解析】∵∠A=22.5°,∴∠COE=45°,∵⊙O的直径AB垂直于弦CD,OC=6,OC=CD=2CE=∴∠CEO=90°,∵∠COE=45°,∴D.6.(2019·衢州)一块圆形宣传标志牌如图所示,点A,B,C在⊙O上,CD垂直平分AB于点D.现测得AB=8dm,DC=2dm,则圆形标志牌的半径为(A)A.6dmB.5dmC.4dmD.3dm【答案】B【解析】连接OD,OB,则O,C,D三点在一条直线上,因为CD垂直平分AB,AB=8dm,所以BD=4dm,OD=(r-2)dm,由勾股定理得42+(r-2)2=r2,r=5dm,故选B.7.(2019·泰安) 如图,△ABC是e O的内接三角形,∠A=119°,过点C的圆的切线交BO于点P,则∠P的度数为A.32 °B.31°C.29°D.61°【答案】A【解析】连接CO,CF,∵∠A=119°,∴∠BFC=61°,∴∠BOC=122°,∴∠COP =58°,∵CP与圆相切于点C,∴OC⊥CP,∴在Rt△OCP中,∠P=90°-∠COP=32°,故选A.8.9.10.11.二、填空题7.(2019·嘉兴)如图,已知⊙O上三点A,B,C,半径OC=1,∠ABC=30°,切线P A交OC延长线于点P,则P A的长为()A.2 B.C.D.【答案】B【解析】连接OA,因为∠ ABC=30°,所以∠AOC=60°,又因为PA为切线,所以∠OAP=90°,因为OC=1,所以.3.(2019·杭州)如图,P为⊙O外一点,PA、PB分别切⊙O于A、B两点,若PA=3,则PB= ()A.2 B.3 C.4 D.5【答案】B【解析】因为P A 和PB 与⊙O 相切,根据切线长定理,可知: P A =PB=3,故选B .12.(2019·烟台)如图,AB 是O e 的直径,直线DE 与O e 相切于点C ,过点A ,B 分别作AD DE ⊥,BE DE ⊥,垂足为点D ,E ,连接AC ,BC.若AD =3CE =,则»AC 的长为( ). A.3B.3C.2D.3【答案】D【解题过程】连接OC ,因为AD DE ⊥,BE DE ⊥,所以90ADC CEB ∠=∠=︒ 所以90DAC ACD ∠+∠=︒ODEBA 第12题答图因为AB 是O e 的直径,所以90ACB ∠=︒, 所以90BCE ACD ∠+∠=︒, 所以BCE DAC ∠=∠, 在△ADC 与△CED ,因为90ADC CEB ∠=∠=︒,BCE DAC ∠=∠ 所以△ADC ∽△CED ,所以BC CE AC AD ===在Rt △ACB 中,sin BCBAC AC∠== 所以60BAC ∠=︒, 又因为OA OC =,所以△AOC 是等边三角形, 所以60ACO ∠=︒,因为直线DE 与 O e 相切于点C , 所以OC DE ⊥,因为AD DE ⊥,OC DE ⊥, 所以AD//OC ,所以60DAC ACO ∠=∠=︒, 所以9030ACD DAC ∠=︒-∠=︒,所以2AC AD ==, 所以△AOC 是等边三角形,所以OA AC ==,60AOC ∠=︒,所以»AC=.12.(2019·威海)如图,⊙P 与x 轴交与点A (—5,0),B (1,0),与y 轴的正半轴交于点C ,若∠ACB =60°,则点C 的纵坐标为B.B.. .2 【答案】D【解题过程】连接PA 、PB 、PC ,过点P 分别作PF ⊥AB ,PE ⊥OC ,垂足为F,E.由题意可知:四边形PFOE 为矩形, ∴PE =OF ,PF =OE . ∵∠ACB =60°, ∴∠APB =120°. ∵P A =PB ,∴∠P AB=∠PBA=30°.∵PF⊥AB,∴AF=BF=3.∴PE=OF=2.,cos30°=AFAPAP=∴PF∴OE PC=在RT△PEC中,CE==∴OC=CE+EO=+2.5.(2019·青岛)如圈,结段AB经过⊙O的圆心,AC BD分别与⊙O相切于点D.若AC= BD = 4,∠A=45°,则圆弧CD的长度为A.πB. 2πC D.4π【答案】B【解析】连接CO,DO,因为AC,BD分别与⊙O相切于C,D,所以∠ACO=∠DBO=90°, 所以∠AOC=∠A=45°, 所以CO=AC=4,因为AC=BD,CO=DO,所以△ACO≌△BDO,所以∠DOB=π⨯=2∠AOC=45°,所以∠DOC=180°-∠DOB-∠AOC=180°-45°-45°=90°,»CD=904180π,故选B.16.(2019·娄底)如图(9),C、D两点在以AB为直径的圆上,AB=2,∠ACD=30°,则AD=_____________.【答案】1.【解析】如图,图9-1,连结AD,∵由AB为⊙O的直径,∴∠ADB=90°,又∵在⊙O中有∠ACD=30°,∴∠B=∠ACD=30°,∴112122AD AB==⨯=.17.(2019·衡阳)已知圆的半径是6,则圆内接正三角形的边长是.【答案】63【解析】如图,作OD⊥BC于D,∵OB=6,∠OBD=30,∴BD=12BC=33,∴BC=63,故答案为63.13.(2019·安徽)如图,△ABC 内接于⊙O ,∠CAB=30°,∠CBA=45°,CD ⊥AB 于点D ,若⊙O 的半径为2,则CD 的长为 .【答案】2【解析】本题考查了三角形的外接圆与外心,圆周角定理,等腰直角三角形的性质,正确的作出辅助线是解题的关键.连接CO 并延长交⊙O 于E ,连接BE ,于是得到∠E=∠A=30°,∠EBC=90°,解直角三角形即可得到结论.连接CO 并延长交⊙O 于E ,连接BE ,则∠E=∠A=30°,∠EBC=90°,∵⊙O 的半径为2,∴CE=4,∴BC=21CE=2,∵CD ⊥AB ,∠CBA=45°,∴CD=22BC=2,故答案为2.16.(2019·株洲)如图所示,AB 为⊙O 的直径,点C 在⊙O 上,且OC ⊥AB ,过点C 的弦CD 与线段OB 相交于点E ,满足∠AEC =65°,连接AD ,则∠BAD =度.A第16题【答案】20°【解析】如图,连接DO,因为CO⊥AB,所以∠COB=90°,∵∠AEC=65°,∴∠C=25°,∵OD=OC,∴∠ODC=∠C=25°,△DCO中,∠DOC=130°,∴∠DOB=40°,∴2∠BAD=∠DOB,∴∠BAD=20°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图2EDCB Ao(2010哈尔滨)1.如图,AB 是⊙O 的弦,半径OA =2,∠AOB =120°,则弦AB 的长是( ).B(A )22 (B )32 (C )5 (D )53 (2010珠海)2.如图,⊙O 的半径等于1,弦AB 和半径OC 互相平分于点M.求扇形OACB的面积(结果保留π)解:∵弦AB 和半径OC 互相平分∴OC ⊥ABOM=MC=21OC=21OA 在Rt △OAM 中,sinA=21=OA OM ∴∠A=30°又∵OA=OB ∴∠B=∠A=30° ∴∠AOB=120° ∴S 扇形=33601120ππ=⋅⋅(2010珠海)3.如图,△ABC 内接于⊙O ,AB =6,AC =4,D 是AB 边上一点,P 是优弧BAC 的中点,连结PA 、PB 、PC 、PD.(1)当BD 的长度为多少时,△PAD 是以AD 为底边的等腰三角形?并证明; (2)若cos ∠PCB=55,求PA 的长. 解:(1)当BD =AC =4时,△PAD 是以AD 为底边的等腰三角形 ∵P 是优弧BAC 的中点 ∴弧PB =弧PC ∴PB =PC∵BD =AC =4 ∠PBD=∠PCA ∴△PBD ≌△PCA∴PA=PD 即△PAD 是以AD 为底边的等腰三角形(2)由(1)可知,当BD =4时,PD =PA ,AD =AB-BD =6-4=2过点P 作PE ⊥AD 于E ,则AE =21AD=1 ∵∠PCB=∠PAD ∴cos ∠PAD=cos ∠PCB=55=PA AE ∴PA=51. (2010红河自治州)如图2,已知BD 是⊙O 的直径,⊙O 的弦AC ⊥BD 于点E ,若∠AOD=60°,则∠DBC的度数为 ( A ) A.30° B.40°C.50°D.60°(2010年镇江市)11.如图,AB 是⊙O 的直径,弦CD ⊥AB ,垂足为E ,若AB=10,CD=8,则线段OE的长为 3 .(2010年镇江市)26.推理证明(本小题满分7分)如图,已知△ABC 中,AB=BC ,以AB 为直径的⊙O 交AC 于点D ,过D 作DE ⊥BC ,垂足为E ,连结OE ,CD=3,∠ACB=30°.(1)求证:DE 是⊙O 的切线; (2)分别求AB ,OE 的长;(3)填空:如果以点E 为圆心,r 为半径的圆上总存在不同的两点到点O 的距离为1,则r 的取值范围为 .(1)∵AB 是直径,∴∠ADB=90° (1分),)2(.//,.,BC DE BC OD BO AO CD AD BC AB ⊥∴==∴= 分又又 ∴OD ⊥DE ,∴DE 是⊙O 的切线. (3分) (2)在 30,3,=∠=∆ACB CD CBD Rt 中,.2,223330cos =∴===∴AB CDBC(4分))6(.27)23(1,)5(.2332121,30,3,2222分中在分中在=+=+=∆=⨯==∴=∠=∆OE OD OE ODE Rt CD DE ACB CD CDE Rt(3).127127+<<-r (7分)(2010遵义市)如图,△ABC 内接于⊙O,∠C=40,则∠ABO= ▲ 度.答案:50、(2010台州市)如图,⊙O 的直径CD ⊥AB ,∠AOC =50°,则∠CDB 大小为 (▲)A .25°B .30°C .40°D .50° 答案:A(玉溪市2010)11. 如图6,在半径为10的⊙O 中,OC 垂直弦AB 于点D ,AB =16,则CD 的长是 4 .(2010年兰州)4.有下列四个命题:①直径是弦;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.其中正确的有 A .4个 B .3个 C . 2个 D . 1个 答案 B2010年兰州)7. 将量角器按如图所示的方式放置在三角形纸板上,使点C 在半圆上.点A 、B 的读数分别为86°、30°,则∠ACB 的大小为A .15︒B .28︒C .29︒D .34︒第7题图 答案 B(2010年无锡)15.如图,AB 是O 的直径,点D 在O 上∠AOD=130°,BC ∥OD 交O 于C,则∠A= ▲ .A BCO D 图6 (第5题)ABOCDABO · C第16题(2010年兰州)22.(本题满分6分)小明家的房前有一块矩形的空地,空地上有三棵树A 、B 、C ,小明想建一个圆形花坛,使三棵树都在花坛的边上.(1)(本小题满分4分)请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹).(2)(本小题满分2分))若△ABC 中AB=8米,AC=6米,∠BAC=90,试求小明家圆形花坛的面积.第22题图答案(本题满分6分)(1)(本小题满分4分)用尺规作出两边的垂直平分线 …………………2分 作出圆 …………………………3分 ⊙O 即为所求做的花园的位置.(图略) ……………………………4分 (2)(本小题满分2分) 解:∵∠BAC=90,AB=8米,AC=6米, ∴BC=10米∴ △ABC 外接圆的半径为5米 ……………………………………5分 ∴小明家圆形花坛的面积为25 平方米 . …………………………… 6分(2010年连云港)16.如图,点A 、B 、C 在⊙O 上,AB ∥CD ,∠B =22°,则∠A =________°. 答案 44(2010宁波市)24.如图,AB 是⊙O 的直径,弦DE 垂直平分半径OA ,C 为垂足,弦DF 与半径OB 相交于点P ,连结EF 、EO ,若DE =23,∠DPA =45°.(1)求⊙O 的半径;(2)求图中阴影部分的面积.(第15题)OC BDA6. (2010年金华)如图,△ABC 内接于⊙O ,∠A =40°,则∠BOC 的度数为( ▲ )DA . 20°B . 40°C . 60°21.(2010年金华)(本题8分)如图,AB 是⊙O 的直径,C 是的中点,CE ⊥AB 于 E ,BD 交CE 于点F .(1)求证:CF ﹦BF ;(2)若CD ﹦6, AC ﹦8,则⊙O 的半径为 ▲ ,CE 的长是 ▲ .解:(1) 证明:∵AB 是⊙O 的直径,∴∠ACB ﹦90° 又∵CE ⊥AB , ∴∠CEB ﹦90° ∴∠2﹦90°-∠A ﹦∠1(第6题图)ACBO ACBD(第21题图)EF O 12又∵C 是弧BD 的中点,∴∠1﹦∠A ∴∠1﹦∠2,∴ CF ﹦BF ﹒ …………………4分 (2) ⊙O 的半径为5 , CE 的长是524﹒ ………4分(各2分)8.(2010年长沙)如图,在⊙O 中,OA =AB ,OC ⊥AB ,则下列结论错误的是 D A .弦AB 的长等于圆内接正六边形的边长 B .弦AC 的长等于圆内接正十二边形的边长 C .AC BC = D .∠BAC =30°24.(2010年长沙)已知:AB 是⊙O 的弦,D 是AB 的中点,过B 作AB 的垂线交AD 的延长线于C .(1)求证:AD =DC ;(2)过D 作⊙O 的切线交BC 于E ,若DE =EC ,求sin C .证明:连BD ∵BD AD =∴∠A =∠ABD ∴AD =BD …………………2分 ∵∠A +∠C =90°,∠DBA +∠DBC =90°∴∠C =∠DBC ∴BD =DC∴AD =DC ………………………………………………………4分 (2)连接OD ∵DE 为⊙O 切线 ∴OD ⊥DE …………………………5分 ∵BD AD =,OD 过圆心 ∴OD ⊥AB又∵AB ⊥BC ∴四边形FBED 为矩形∴DE ⊥BC ……………………6分 ∵BD 为Rt △ABC 斜边上的中线∴BD =DC ∴BE =EC =DE∴∠C =45° …………………………………………………7分 ∴sin ∠C =22………………………………………………………………8分 BOA C O A C B第8题图B ECD A O OADB EC 第24题图(2010年湖南郴州市)7.如图,AB 是O 的直径,CD 为弦,CD AB ⊥于E , 则下列结论中不成立...的是 A.A D ∠=∠ B.CE DE = C.90ACB ∠= D.CE BD = 答案D(2010湖北省荆门市)16.在⊙O 中直径为4,弦AB =23,点C 是圆上不同于A 、B 的点,那么∠ACB 度数为___▲___. 答案60°或120°(2010年毕节)20.如图,AB 为⊙O 的弦,⊙O 的半径为5,OC ⊥AB 于点D ,交⊙O 于点C ,且CD =l ,则弦AB 的长是 .20.64.(10重庆潼南县)如图,已知AB 为⊙O 的直径,点C 在⊙O 上,∠C=15°,则∠BOC 的度数为( )BA .15°B . 30°C . 45°D .60°20.(10湖南怀化)如图6,已知直线AB 是⊙O 的切线,A 为切点,OB 交⊙O 于点C ,点D 在⊙O 上,且∠OBA=40°,则∠ADC=______.25(2010陕西省)9.如图,点A 、B 、P 在⊙O 上,点P 为动点,ABCO题图4Ay要是△ABP 为等腰三角形,则所有符合条件的点P 有(D ) A 1个 B 2个 C 3个 D 4个(2010陕西省)14、如图是一条水铺设的直径为2米的通水管道横截面,其水面宽1.6米, 则这条管道中此时最深为 0.4 米(2010年天津市)(7)如图,⊙O 中,弦AB 、CD 相交于点P , 若30A ∠=︒,70APD ∠=︒,则B ∠等于(C )(A )30︒ (B )35︒ (C )40︒ (D )50︒1.(2010宁德)如图,在⊙O 中,∠ACB =34°,则∠AOB 的度数是( ).D A.17° B.34° C.56° D.68°2.(2010黄冈)如图,⊙O 中,MAN 的度数为320°,则圆周角∠MAN =____________.20°1.(2010山东济南)如图所示,△ABC 的三个顶点的坐标分别为A (-1,3)、B (-2,-2)、C (4,-2),则△ABC 外接圆半径的长度为 .第5题图AOCB 第(7)题BCA DPO答案13(2010年常州)16.如图,AB 是⊙O 的直径,弦DC 与AB 相交于点E ,若∠ACD=60°,∠ADC=50°,则∠ABD= ,∠CEB= .16.60°,100°.(2010株洲市)21.(本题满分8分)如图,AB 是O e 的直径,C 为圆周上一点,30ABC ∠=︒,O e 过点B 的切线与CO 的延长线交于点D . 求证:(1)CAB BOD ∠=∠;(2)ABC ∆≌ODB ∆.21.(1)∵AB 是O 的直径,∴90ACB ∠=︒,由30ABC ∠=︒,∴60CAB ∠=︒又OB OC =,∴30OCB OBC ∠=∠=︒∴60BOD ∠=︒,∴CAB BOD ∠=∠.…… 4分 (2)在Rt ABC ∆中,30ABC ∠=︒,得12AC AB =,又12OB AB =,∴AC OB =.由BD 切O 于点B ,得90OBD ∠=︒. 在ABC ∆和ODB ∆中,CAB BODACB OBD AC OB ∠=∠∠=∠⎧=⎪⎨⎪⎩∴ABC ∆≌ ODB ∆ …… 8分(2010河北省)6.如图3,在5×5正方形网格中,一条圆弧经 过A ,B ,C 三点, 那么这条圆弧所在圆的圆心是A .点PB .点QC .点RD .点M(2010年安徽)13. 如图,△ABC 内接于⊙O ,AC 是⊙O 的直径,∠ACB =500,点D 是BAC 上一点,则∠D =____︒40__M RQ 图3A BCP DCBOA1、(2010山东烟台)如图,△ ABC 内接于⊙O ,D 为线段AB 的中点,延长OD 交⊙O 于点E ,连接AE ,BE ,则下列五个结论①AB ⊥DE,②AE=BE,③OD=DE,④∠AEO=∠C,⑤,正确结论的个数是A 、2B 、3C 、4D 、5答案:B2.(2010山东青岛市)如图,点A 、B 、C 在⊙O 上,若∠BAC = 24°,则∠BOC= °. 答案:48(2010·浙江温州)20.(本题8分)如图,在正方形ABCD 中,AB=4,0为对角线BD 的中点,分别以OB ,OD 为直径作⊙O 1,⊙02. 。
