CMOS模拟电路设计问题解答
专升本CMOS模拟集成电路分析与设计试卷答案

专升本CMOS模拟集成电路分析与设计试卷答案专升本《CMOS模拟集成电路分析与设计》一、(共75题,共150分)1. Gordon Moore在1965年预言:每个芯片上晶体管的数目将每()个月翻一番(2分)A.12B.18C.20D.24.标准答案:B2. MOS 管的小信号输出电阻是由MOS管的()效应产生的。
(2分)A.体B.衬偏C.沟长调制D.亚阈值导通.标准答案:C3. 在CMOS模拟集成电路设计中,我们一般让MOS管工作在()区。
(2分)A.亚阈值区B.深三极管区C.三极管区D.饱和区.标准答案:D4. MOS管一旦出现()现象,此时的MOS管将进入饱和区。
(2分)A.夹断B.反型C.导电D.耗尽.标准答案:A5. ()表征了MOS器件的灵敏度。
(2分)A.B.C.D..标准答案:C6. Cascode放大器中两个相同的NMOS管具有不相同的()。
(2分)A.B.C.D..标准答案:B7. 基本差分对电路中对共模增益影响最显著的因素是()。
(2分)A.尾电流源的小信号输出阻抗为有限值B.负载不匹配C.输入MOS不匹配D.电路制造中的误差.标准答案:C8. 下列电路不能能使用半边电路法计算差模增益()。
(2分)A.二极管负载差分放大器B.电流源负载差分放大器C.有源电流镜差分放大器D.Cascode负载Casocde差分放大器.标准答案:C9. 镜像电流源一般要求相同的()。
(2分)A.制造工艺B.器件宽长比C.器件宽度WD.器件长度L.标准答案:D10. 某一恒流源电流镜如图所示。
忽略M3的体效应。
要使和严格相等,应取为()。
(2分)A.B.C.D..标准答案:A11. 选择题:下列结构中密勒效应最大的是()。
(2分)A.共源级放大器B.源级跟随器C.共栅级放大器D.共源共栅级放大器.标准答案:A12. 下图中,其中电压放大器的增益为-A,假定该放大器为理想放大器。
请计算该电路的等效输入电阻为()。
拉扎维模拟CMOS集成电路设计第二章作业答案详解完整版中文

IX
1 2
nCOX
W L
[2 0.2(VX
1) (VX
1)
2
]
1 2
nCOX
W L
(1.4 VX )(VX
1)
gm
nCOX
W L
VDS
nCOX
W L
(Vx
1)
Copyright for zhouqn
③ 当VX≥1.2V时,MOS管工作在饱和区
IX
+
IX
1 2
nCOX
IX
1 2
PCox
W L
(0.1)2
gm
PCox
W L
(0.1)
+ 1.9V
-
② 当1.8V<VX≤1.9V时,MOS管工作在线性区
IX
1 2
PCox
W L
[2 (0.1) (VX
1.9) (VX
1.9)2 ]
gm
PCox
W L
(VX
1.9)
Copyright for zhouqn
第二章 作业答案
Copyright for zhouqn
2.1、W/L=50/0.5,假设|VDS|=3V,当|VGS|从0上升到 3V时,画出NFET和PFET的漏电流VGS变化曲线
解:
a) NMOS管: 假设阈值电压VTH=0.7V,不考虑亚 阈值导电
① 当VGS<0.7V时,NMOS管工作在截止区,则ID=0 ② 当VGS>0.7V时, NMOS管工作在饱和区,NMOS管
0 8.854 1012 F / m sio2 3.9
CMOS模拟集成电路设计习题参考答案Chap12

代入相关参数得到等效电阻: Ron, eq Ron1 || Ron 2 时间常数 Ron1 || Ron 2 C H 30.3 ps 。
由公式: 1 10
3
3 exp
t
t ln
3 242.6 ps 0.001
12.9 答案:假设沟道电荷全部注入到采样电容上,则:
VGS 6 , 7
2 I DS 6 , 7 W n C ox L eff 6 , 7
VTHN
350 10
4
2 50 10 6 5 50 6 .9 10 15 10 12 9 0 .34
0 .7
CMOS 模拟集成电路设计习题参考答案
By: 沈亚丁(769094724@) 2012 年 2 月 26 日
第 12 章 开关电容电路
12.3 答案:由题可知,运放是理想的。由虚短虚断,故 B 点为虚地,时间常数: Ron C1 。 在电路稳定时,开关消耗的能量等于电容 C1 存储的能量: 12.8 答案: Leff L 2 LD
Ron2
1 W V VTHP pCox L in eff 2 1 2 5 60 6.9 fF 100cm 2.2 2 vs 9 um 0.5 2 0.08 67.2
55.1 67.2 30.3 。 55.1 67.2
1 2 C1Vino 。 2
Ron1
1
W VDD Vin VTHN L eff 1 1 2 5 20 6.9 fF 350cm 2.3 2 vs 9 um 0.5 2 0.08 55.1
模拟cmos集成电路设计课后题

模拟CMOS集成电路设计课后题在现代电子科学领域中,模拟CMOS集成电路设计是一门重要的课程,它涉及到电子工程中的基本原理和技术,对从事电子电路设计和集成电路制造的专业人员来说,具有非常重要的意义。
而课后题作为知识的巩固和扩展,对于深入理解和掌握这门课程也至关重要。
接下来,我将针对模拟CMOS集成电路设计课后题进行深度和广度兼具的全面评估,并据此撰写一篇有价值的文章。
一、基本概念解释1. 什么是模拟CMOS集成电路设计?模拟CMOS集成电路设计即使用CMOS工艺制作的模拟电路。
它在数字电路的基础上加入了模拟电路。
2. 课后题的重要性课后题是对课堂所学知识的巩固和拓展,通过解答课后题可以帮助学生更深入地理解和掌握课程内容,提高解决问题的能力。
二、课后题解析1. 请列举一些模拟CMOS集成电路设计的常见应用?模拟CMOS集成电路设计常见的应用包括放大电路、滤波电路、比较器、运算放大器等。
2. 什么是CMOS工艺?CMOS是指互补型金属氧化物半导体技术,它是当今集成电路工艺的主流之一。
CMOS工艺具有低功耗、高集成度和良好的抗干扰能力等特点。
3. 请解释CMOS集成电路的工作原理。
CMOS集成电路由N型金属氧化物半导体场效应晶体管和P型金属氧化物半导体场效应晶体管组成。
当输入电压改变时,两个晶体管的导通状态都会随之改变,从而实现信号的放大和处理。
4. 请说明模拟CMOS集成电路设计中需要考虑的主要因素?在模拟CMOS集成电路设计中,需要考虑的主要因素包括功耗、速度、噪声、线性度、稳定性等。
5. 如何进行模拟CMOS集成电路的性能指标评估?模拟CMOS集成电路的性能指标评估包括静态指标和动态指标两部分,静态指标包括增益、带宽、输入输出阻抗等;动态指标包括上升时间、下降时间、过冲、欠冲等。
三、个人观点和总结从我个人的观点来看,模拟CMOS集成电路设计是电子工程领域中非常重要的一门课程,通过课后题的解答可以更好地理解和掌握课程中的知识点,培养自己的问题解决能力。
拉扎维模拟CMOS集成电路设计第三章作业答案详解完整版教程解析

拉扎维模拟CMOS集成电路设计第三章作业答案详解完整版教程解析1. 引言在拉扎维模拟CMOS集成电路设计第三章的作业中,涉及了多个内容,包括放大电路、反馈放大电路、功率放大电路等。
本文将对这些内容进行详细的解析和讲解,并给出相应的答案。
2. 放大电路放大电路是电子电路中非常常见且重要的一种电路结构。
在本章的作业中,我们需要设计一个放大电路,并回答一些相关问题。
2.1 放大电路设计根据作业要求,我们需要设计一个放大电路,输入信号为正弦波,放大倍数为10倍。
我们可以选择使用CMOS集成电路来实现这个放大电路。
首先,我们需要根据放大倍数和输入信号的幅度来确定CMOS放大电路的电路参数。
在设计过程中,我们需要考虑一些关键因素,包括电流源、负反馈电阻等。
其次,我们可以选择合适的电路拓扑结构,例如共源共栅放大电路、共源共漏放大电路等。
根据实际情况,我们可以选择合适的电路结构。
最后,我们需要进行电路参数的计算和电路的仿真。
通过计算和仿真,我们可以得到放大电路的性能指标,例如增益、截止频率等。
2.2 放大电路问题解答在作业中,还需要回答一些问题,例如输入电阻、输出电阻、频率响应等。
针对这些问题,我们需要根据放大电路的拓扑结构和电路参数做相应的计算和分析。
例如,输入电阻可以通过计算输入端的电流和电压之比得到;输出电阻可以通过计算输出端的电流和电压之比得到;频率响应可以通过对放大电路进行交流分析得到。
总的来说,放大电路的设计和问题解答需要综合考虑多个因素,包括电路参数、电路结构、输入信号的幅度、负载等。
需要进行一系列的计算和仿真,以得到满足要求的电路性能。
3. 反馈放大电路反馈放大电路是一种常见的电路结构,它可以通过引入反馈回路来改善电路性能,例如增益稳定性、线性度等。
在作业中,我们需要设计一个反馈放大电路,并回答一些相关问题。
3.1 反馈放大电路设计根据作业要求,我们需要设计一个反馈放大电路,输入信号为正弦波,放大倍数为20倍。
模拟cmos集成电路设计课后题

模拟cmos集成电路设计课后题CMOS(Complementary Metal-Oxide-Semiconductor)集成电路设计是现代电子技术的关键领域之一。
该领域涉及到各种基本电路以及整个系统的设计与优化。
本文将模拟一篇CMOS集成电路设计的课后题,其中包括对基本电路的设计以及系统级优化的考察。
第一部分:基本电路设计(2000字左右)1. 设计一个2输入与门的CMOS电路。
给出电路图,并写出相应的布尔表达式。
2. 为了减小功耗并提高响应速度,经常需要将电路设计为动态逻辑电路。
请设计一个动态逻辑的非门电路,给出电路图,并写出相应的时钟脉冲控制信号。
第二部分:CMOS集成电路设计(2000字左右)3. 设计一个3输入与门的CMOS电路,并对其功耗进行优化。
4. 设计一个4位二进制全加器的CMOS电路,并考虑功耗和面积的优化。
第三部分:系统级优化(2000字左右)5. 将两个2输入与门和一个2输入或门组合成一个3输入与门。
请给出详细的设计流程和最终的电路图。
6. 设计一个8位互补码加法器的CMOS电路,并考虑功耗、面积和延迟的优化。
第一部分:基本电路设计1. 设计一个2输入与门的CMOS电路。
给出电路图,并写出相应的布尔表达式。
CMOS与门的基本电路由PMOS管和NMOS管组成。
在输入A和B分别接入与门电路的两个输入端,而输出则连接到NMOS管和PMOS管接口的并联电路的输出端。
当A和B同时为高电平时,输出才为高电平。
其布尔表达式可以写为:Z = A * B。
2. 为了减小功耗并提高响应速度,经常需要将电路设计为动态逻辑电路。
请设计一个动态逻辑的非门电路,给出电路图,并写出相应的时钟脉冲控制信号。
动态非门电路的设计可以采用PMOS管串联的结构。
当输入S 为高电平时,NMOS管导通,输出结果为0;当输入S为低电平时,PMOS管导通,输出结果为1。
其时钟脉冲控制信号可以表示为:NAND(A, A)。
CMOS模拟集成电路设计复习题一复习进程

1.解释什么是体效应? 在初步分析MOSFET的时候我们假设衬底 和源级是接到地的。而实际上当VB<VS 时,器件仍能正常工作,但是随着VSB的 增加,阈值电压VTH会随之增加,这种
体电位(相对于源)的ຫໍສະໝຸດ 化影响阈值电压的效应称为体效应,也称为“背栅效 应”2.解释什么是沟道长度调制效应? 当沟道发生夹断后,如果VDS继续增大 ,有效沟道长度L'会随之减小,导致漏源 电流 Id的大小略有上升。这一效应成为 “沟道……”
4. 图(a)是什么结构?图(b)忽略了沟道调制效应和体效应。 如果体效应不能忽略,请画出Vin和Vout的关系曲线,并作 出解释。
5. 图中MOS管的作用是什么?应该工作在什么工作区?
即NMOS开关不能传递最高电位,仅对低电位是比较理想的开关 相对的,PMOS开关不能传递最低电位,仅对高电位是比较理想的开关
6. 计算电路的小信号增益
7. 画出下图的小信号等效电路,推导Rin的表达式
8.
此课件下载可自行编辑修改,仅供参考! 感谢您的支持,我们努力做得更好!谢谢
CMOS模拟集成电路设计复习 题一
2. 画出一个典型P阱CMOS工艺反向器的垂直剖面示意图, 要求器件的各个端口正确连接输入、输出、电源电位和地 电位
3. 什么是MOSFET小信号跨导,给出饱和区MOSFET小信 号跨导的三种表达形式
4. 什么是 MOSFET的亚阈区,指出亚阈区的电流与栅源 电压的关系
模拟CMOS集成电路复习题库及解答
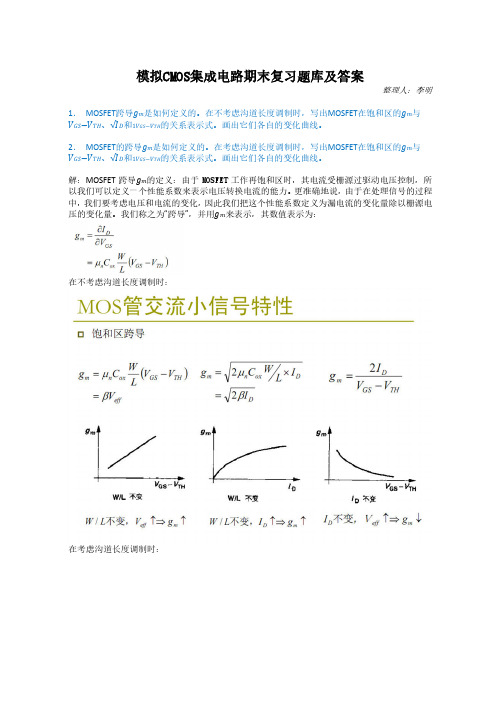
模拟CMOS集成电路期末复习题库及答案整理人:李明1.MOSFET跨导g m是如何定义的。
在不考虑沟道长度调制时,写出MOSFET在饱和区的g m与V GS−V TH、√I D和1V GS−V TH的关系表示式。
画出它们各自的变化曲线。
2.MOSFET的跨导g m是如何定义的。
在考虑沟道长度调制时,写出MOSFET在饱和区的g m与V GS−V TH、√I D和1V GS−V TH的关系表示式。
画出它们各自的变化曲线。
解:MOSFET跨导g m的定义:由于MOSFET工作再饱和区时,其电流受栅源过驱动电压控制,所以我们可以定义一个性能系数来表示电压转换电流的能力。
更准确地说,由于在处理信号的过程中,我们要考虑电压和电流的变化,因此我们把这个性能系数定义为漏电流的变化量除以栅源电压的变化量。
我们称之为“跨导”,并用g m来表示,其数值表示为:在不考虑沟道长度调制时:在考虑沟道长度调制时:3.画出考虑体效应和沟道长度调制效应后的MOSFET小信号等效电路。
写出r o和g mb的定义,并由此定义推出r o和g mb表示式。
解:4.画出由NMOS和PMOS二极管作负载的MOSFET共源级电路图。
对其中NMOS二极管负载共源级电路,推出忽略沟道长度调制效应后的增益表示式,分析说明器件尺寸和偏置电流对增益的影响。
对PMOS二极管负载的共源级电路,对其增益表示式作出与上同样的分析。
5.画出MOS共源共栅级电路的电路图和其对应的小信号等效电路图。
并推出此共源共栅级电路的电压增益和输出电阻表示式。
解:6.画出带源极负反馈电阻的以电阻作负载的MOS共源级电路的电路图和其对应的小信号等效电路图。
写出此电路的等效跨导定义式,并由此推出在不考虑沟道长度调制和体效应情况下的小信号电压增益表示式。
画出其漏电流和跨导随V in的变化曲线图。
7.画出带源极负反馈电阻的以电阻作负载的MOS共源级电路的电路图和其对应的小信号等效电路图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Solutions – Day 11.) (a.) The length and widths of M1 is 2µm and 10µm and of M2 is 2µm and 20µm.Therefore,C gd 1 = 220×10−12·10x10-6C gd 1 = 2.2fF C gd 2 = 220 × 10−12·20x10-6C gd 1 = 4.4fFNext, we must find the area and perimeter of each drain.AD1 = 60µm 2 & PD1 = 32µmAD2 = 120µm 2 & PD1 = 52µm C bd 1 = CJ·AD1 1+ 2.5V 2|φF |MJ + CJSW·PD11+ 2.5V 2|φF |MJSW = 770x10-6·60x10-12 1+ 2.5V 0.80.5 + 380x10-12·32x10-6 1+ 2.5V 0.80.38 C bd 1 = 22.75fF + 7.10fF =29.84fFC bd 2 = CJ·AD2 1+ 2.5V 2|φF |MJ + CJSW·PD2 1+ 2.5V 2|φF |MJSW = 560x10-6·120x10-12 1+ 2.5V 0.70.5 + 350x10-12·52x10-61+ 2.5V 0.70.35 C bd 2 =31.43fF +10.69fF =42.12fF(b.) Assume that the equivalent bulk resistance for the sources is found by the area defined by the rectangle between the edge of the polysilicon and the closest edge of the contacts. This assumption ignores the fact that current at the edges of the rectangle will not be the same as that in the middle. For M1, this rectangle is 2µm by 10µm and for M2 this rectangle is 2µm by 20µm. Therefore,R S 1 ≈ 35Ω/sq.x(2µm/10µm) + 4Ω/2 = 7Ω + 2Ω = 9 ΩandR S 2 ≈ 80Ω/sq.x(2µm/20µm) + 4Ω/4 = 8Ω + 1Ω = 9Ω2.) A simple first-order filter shown is to be built with a polysilicon resistor and a MOS capacitor. The polysilicon resistor has a sheet resistance of 50Ω/sq. ± 30% and is 5µmwide. The MOS capacitor is 2fF/µm 2 ± 10%. The -3dBfrequency of the lowpass filter is 1MHz. (a.) Choose the size of the resistor (the number of squares, N ) to minimize the total area of the filter including both the resistor and the capacitor.Find the area of the resistor and the capacitor in µm 2 and their values. (b.) Using the worst-case tolerance of the resistor and capacitor, find the maximum and minimum -3dB frequencies.Solution (a.)Value of R = 50Ω/sq.x N sq. = 50N ΩValue of C = 2fF/µm 2x A C µm 2 = 2A C fF Area of C = A CArea of R = A R = 25µm 2x N = 25N µm 2Total Area = A T = (25N + A C ) µm 2We know that the RC product is given asRC = 12πx106 = (50N )(2A C x10-15) = NA C x10-13∴ A C =12πx10-7NThus,A T = 25N +12πx10-7N →dA T dN = 25 - 12πx10-7N 2 = 0∴ N⇒A R = 252x25µm 2 = 6308µm 2 and A C =6308µm 2Also, R poly = R = 252x50 Ω = 12.6k Ω and C MOS = 6308µm 2 x2fF/µm 2 = 12.6pF (b.)Maximum -3dB frequency = 12π(0.7)(12.6k Ω)(0.9)(12.6pF) = 1.6MHzMinimum -3dB frequency = 12π(1.3)(12.6k Ω)(1.1)(12.6pF)= 0.7MHzR v inSolutions – Day 21.) A transmission gate is shown. If V DD = 2V, what is the highest possible large signal ON resistance of the transmissiongate. Ignore the bulk effects and assume that v DS ≈ 0V.SolutionR NMOS = 1K N (W 1/L 1)(V GS1-V TN ) = 106110(2-V AB-0.7)= 106110(1.3-VAB )⇒ G NMOS = 110(1.3-V AB )µSR PMOS = 1K P (W 2/L 2)(V SG2-|V TP |) = 10650(V AB -0.7) ⇒ G PMOS = 50(V AB -0.7)µSFirst, plot the sum of the conductances to graphically locate the minimum value of switchconductance.0.20.40.60.8 1.01.82.00V ABD2S1We note that the minimum value of switch conductance occurs at V AB = 1.3V. This corresponds to 30µS. Inverting this value gives the maximum switch resistance which is 33.3k Ω.Therefore, the maximum ON resistance occurs at 1.3V and is 33.3k Ω.R ON (max) = 33.3k Ω at V AB = 1.3V2.) (a.) If all W/Ls are 100µm/1µm, find the value of V GG that will give a minimum value of V MIN .(b.) Find the small signal values of R in , R out , and i out /i in .Solution :(a.) V GG = V GS 4 + V DS 1(sat) = V TN + 2·V DS (sat)V MIN = 2(0.135) = 0.27V(b.) R out ≈ g m4r ds 4r ds2 and i out /i in ≈ 1 Small signal model for R in calculation:v in = (i in - g m 3v gs 3)r ds 3 + (i in - g m 1v gs 1)r ds 1v gs 1 = v in and v gs 3 = -v s 3 = -(i in -g m 1v gs 1)r ds 1= -(i in -g m 1v in )r ds 1∴ v in = [i in r ds 3 + g m 3r ds 1r ds 3 - g m 1g m 3r ds 1r ds 3] + [i in r ds 1 - g m 1r ds 1v in ]or v in [1 + g m 1g m 3r ds 1r ds 3 + g m 1r ds 1] = i in [r ds 1 + r ds 3 + g m 3r ds 3]∴R in = v i n iin = r ds 1 + r ds 3 + r g m 3r ds 31 + g m 1g m 3r ds 1r ds 3 + g m 1r ds 1 ≈ 1g m 1g m 1g m 4, r ds 1 = r ds 2 = r ds 3 = r ds 4 = 0.25M Ω.∴ R i n ≈ 1gm 1= 11.48mS = 674ΩR out ≈ 250k Ω(1.48mS)250k Ω = 92.5M Ωand i outi in= 1Day 3 - SolutionsProblem 1A MOS cascode amplifier is shown below.Assume all transistors are saturated and the K N ’ =110µA/V 2, V T = 0.7V, and λN = 0.04V -1. The value of V GG 1 gives a dc bias current in both transistors of 100µA. (a.) Find the value of V GG 2 which gives a minimum output voltage (same as V MIN (out) for current sinks). What isthe value of miminum output voltage? (b.) Find the small-signal output resistance, R out . (c.) Find the small-signal voltage gain, v out /v in .Solution (a.) V ON∴ V GS = V ON + V T = 0.4264+0.7 = 1.1264V ⇒ V GG 2 = 2V O N +V T = 1.553VAlso V MIN = 2V ON = 2·0.4264 = 0.8528V (b.) R out = 20k Ω||g m 2r ds g mr ds = 1100µA·0.04 = 0.25M Ω∴ R out = 20k Ω||29.3M Ω ≈ 20k Ω(c.) The small signal voltage gain can be expressed asv outv in= -g m R out = -(469µS)(0.02M Ω) = -9.38V/Vv outV GG 2Problem 2A push-pull follower is shown which uses an NPN BJT and a p-channel MOSFET. In this problem, ignore the bulk effect, the channel length modulation, and the Early voltage. The parameters for the NPN BJT are βF = 100,I s = 10fA and V t = 25.9mV. The model parameters for the PMOS are K P ’ = 50µA/V 2 and V TP = -0.7V. (a.)Find the value of the dc batteries, V 1 and V 2, which will cause 100µA to flow in Q1 and M2 when the dc value of v IN = 0VDC. (b.) Find the small-signal input resistance,output resistance (not including R L ) and voltage gain when the dc value of v IN = 0VDC.Solution(a.) V 1= V BE 1 = V t ln i C I s = 0.0259ln100µA 10fA = 0.5964V → V 1=0.5964VV 2= V SG 2V TP → V 2=0.9V (b.) Small-signal model (simplified):g m 1 = I C 1V t = 100µA25.9mV = 3.86mSr π1 = 1+βFg m 1= 26.159k Ωg m 2R in :in π1in in + g m 1v π+ g m 2 v gs 2)R L = r π1i in + (i in + g m1r π1i in + g m 2 r π1i in )R LR in = v ini in= r π1 + R L + g m 1r π1R L + g m 2 r π1R L = r π1 + R L (1+βF ) + g m 2 r π1R L∴ R in = 26.159k Ω + 101·100Ω + 1·26.159k Ω ·0.1 = 38.875k Ω R in = 38.875k Ω R out : R out = 1gm 1 || 1g m 2= 13.86mS+1mS = 205.8Ω R out = 205.8Ωv out v in : v out v in = v out i in i in v in = R L (1+βF )+g m 2r π1R L r π1+R L (1+βF )+g m 2r π1RL= 12.71638.875 = 0.3271v outv in = 0.3271V/V=Ωv INDay 4 - SolutionsProblem 1A two-stage, BiCMOS op amp is shown.For the PMOS transistors, the modelparameters are K P ’=50µA/V 2, V TP = -0.7V and λP = 0.05V -1. For the NPN BJTs, the model parameters are βF = 100, V CE (sat) =0.2V, V A = 25V, V t = 26mV, I s = 10fA andn =1. (a.) Identify which input is positiveand which input is negative. (b.) Find the numerical values of differential voltage gain magnitude, |A v (0)|, GB (in Hertz), the slew rate, SR , and the location of the RHP zero.(c.) Find the numerical value of the maximum and minimum input commonmode voltages.Solution(a.) The plus and minus signs on the schematic show which input is positive and negative.(b.) The differential voltage gain, A v (0), is given as A v (0) = g m 1g ds 2+g o 4+g π6 ·g m 6g ds 7+g o 6g m 1 = g m 2r ds 2 =1λP I D = 2025µA= 0.8M Ω, r o 4 = V A I C = 25V 25µA = 1M Ω, g m 6 = I C V t = 100µA 26mV = 3846µS r π6 = βFg m 6 = 26k Ω,r ds 7 = 1λP I D= 20100µA = 0.2M Ω and r o 6 = V A I C = 25V100µA = 0.25M Ω∴|A v (0)| = [158.1(0.8||1||0.026)][3846(0.2||0.25)]= 3.888·427.36 =1,659.6V/V GB = g m 1C c = 158.1µS5pF = 31.62x106 rads/sec → GB = 5.0325MHzSR = 50µA 5pF = 10V/µsRHP zero = g m 6C c = 3.846mS5pF = 769.24x10 6 r ads/sec . (122MHz)(c.) The maximum input common mode voltage is given as v icm + = V CC -V DS5(sat) - V SG 1∴v icm + =0.0367V v icm - = -1.5 + V BE 3 - V T 1 = -1.5 + V t ln25µA 10fA - 0.7 = -2.2 + 0.5626 =-1.6374V50S01E2P1Problem2A CMOS circuit used as an output buffer for an OTA is shown. Find the value of the small signal output resistance, R out ,and from this value estimate the -3dB bandwidth if a 50pF capacitor is attached to the output. What is the maximum and minimum output voltage if a 1k Ω resistor is attached to the output? What is thequiescent power dissipation of this circuit? Use the following model parameters: K N ’=110µA/V 2, K P ’ =50µA/V 2, V TN = -V TP = 0.7V, λN =0.04V -1 and λP = 0.05V -1.Solution Use feedback concepts to calculate the output resistance, R out .R out = R o1-LGwhere R o is the output resistance with the feedback open and LG is the loop gain.R o = 1g ds 6+g ds 7 = 1(λN +λP )I 6 = 1060.09·500= 22.22k ΩThe loop gain is,LG = v out ’v out = - 12 g m 2g m 6g m 4 + g m 1g m 9g m 7 Rog m 1 = g m 2g m 3 = g m 4g m 6g m 7∴LG = v out ’v out= - 12-331.67·2236223.6 + -331.67·3316.7331.67 = -73.68V/V R out = R o 1-LG = 22.22k Ω1+73.68 = 294.5 Ωf -3dB = 12π·R out ·50pF = 12π·294.5·50pF= 10.81MHzTo get the maximum swing, we must check two limits. First, the saturation voltages of M6and M7.V ds 6and V ds 7Second, the maximum current available to the 1k Ω resistor is ±1mA which means that theoutput swing can only be ±1V. Therefore, maximum/minimum output = ±1V .P diss = 6V(650µA) = 3.9mWSS S01E2S3Day 5 - SolutionsProblem 1A comparator consists of an amplifier cascaded with a latch as shown below. The amplifier has a voltage gain of 10V/V and f -3dB = 100MHz and the latch has a time constant of 10ns.The maximum and minimum voltage swings of the amplifier and latch are V OH and V OL .When should the latch be enabled after the application of a step input to the amplifier of 0.05(V OH -V OL ) to get minimum overall propagation time delay? What is the value of the minimum propagation time delay? It may useful to recall that the propagation time delay ofthe latch is given as t p = τL lnV OH -V OL 2vil where v il is the latch input (∆V i of the text).v inSolutionThe solution is based on the figure shown.We note that,v oa (t ) = 10[1-e -ω-3dB t ]0.05(V OH -V OL ).If we define the input voltage to the latch as,v il = x ·(V OH -V OL )then we can solve for t 1 and t 2 as follows:x ·(V OH -V OL ) = 10[1-e -ω-3dB t 1]0.05(V OH -V OL ) → x = 0.5[1-e -ω-3dB t 1]This gives,t 1 = 1ω-3dB ln11-2x From the propagation time delay of the latch we get,t 2 = τL lnV OH -V OL 2v il = τL ln12x∴t p = t 1 + t 2 = 1ω-3dB ln 11-2x + τL ln12x → dt p dx = 0 gives x = π1+2π= 0.4313t 1 = 10ns 2π ln (1+2π) = 1.592ns·1.9856 = 3.16ns and t 2 = 10ns ln1+2π2π =1.477ns ∴t p = t 1 + t 2 = 3.16ns+1.477ns =4.637ns V OHV OLx (V OH -VProblem 2A 4-bit, binary-weighted, resistor DAC is shown. (a.) Assume that GB = ∞ and find the minimum differential gain,A vd (0), required for the DAC to have an INL of ±0.5LSB . (b.) If the differential gain is very large, find the conversion time of this DAC if GB = 1MHz.Solution(a.) First we need to find v out (ideal)and v out (actual) for the worst case condition which is when all switches are closed (closed loop gain is highest). v out (ideal) = -R EQR V REFandv out (actual) = -AR R +R EQ 1+ AR EQ R +R EQ V REF where R EQ = R 12 + 14 + 18 + 116 = 32R30 Now, v out (actual) - v out (ideal) ≤ V REF32 ⇒-ARR +R EQ 1+ AR EQ R +R EQV REF + R EQ R V REF ≤ V REF32 Which simplifies to,32RR EQ –1 ≤ AR EQ R +R EQ⇒A ≥ R +R EQ R EQ32RR EQ -1 A ≥15R +16R 16R 32R 32R 30 -1 = 311629 = 56.2V/V(b.) In this case, v out (ideal) = -3032V REF and v out (actual) = -3032 [1- e -t ωH ]V REF where ωH = GB·R EQ R +R EQ= 2πx10+6(32/30)1+ (32/30) = (32/31)πx10+6 rads/sec.Now, v out (actual) - v out (ideal) ≤ V REF 32 ⇒ -3032 [1- e -T ωH ]V REF + 3032V REF ≤ V REF 32which becomes,30 e -ωH T = 1⇒T = 1ωH ln (30) = 3132π ln (30) µs∴T = 1.0488µsV REF。
