偏微分上机报告三
偏微分方程数值解第三次上机实验报告
偏微分方程数值解法第三次上机实验报告一、实验题目:用线性元求解下列问题的数值解:2,1,1(x,1)u(x,1)0,1x 1(1,y)1,u (1,y)0,11xx u x y u u y =--<<⎧⎪-==-<<⎨⎪-==-<<⎩ (精确到小数点后四位)二、实验过程:利用PDEToolbox 工具箱求解该偏微分方程。
分析:方程是Possion 方程形式c u au f -+=,其中c=-1,a=0,f=-2; 第一个边界条件是Dirichlet 条件,第二个边界条件是Neumann 条件。
1.在MA TLAB 命令窗口键入pdetool 并运行,打开PDEToolbox 界面;2.在Options 菜单下选择Grid 命令,显示网格,能更容易确定所绘图形的大小;3.绘出区域,选择Boundary 的Boundary Mode ,双击每个边界,设置边界相应的参数值;4.选择PDE 菜单中PDE Mode 命令,进入PDE 模式。
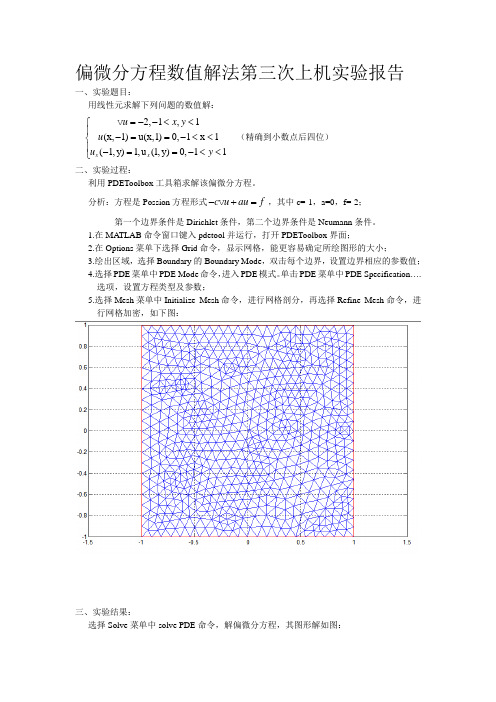
单击PDE 菜单中PDE Specification ….选项,设置方程类型及参数;5.选择Mesh 菜单中Initialize Mesh 命令,进行网格剖分,再选择Refine Mesh 命令,进行网格加密,如下图:三、实验结果:选择Solve 菜单中solve PDE 命令,解偏微分方程,其图形解如图:图1 图形解图2 三维图形解图3 解的等值线图和矢量场图选择Mesh菜单中的Export Mesh,得到结点xy坐标;选择Solve菜单中的Export Solution…,得到每个节点处的值,输出u,即解的数值。
四、实验总结:通过本次试验,掌握了利用Matlab中的PDE求解工具得到PDE的解的方法,并对偏微分方程的形式有了更多的掌握。
孙志忠北京理工大学偏微分方程数值解上机作业

偏微分方程数值解大作业目录第一题 (3)第二题 (7)第三题 (16)第四题 (20)第五题 (26)第六题(附加题1) (39)第七题(附加题2) (45)第八题(附加题3) (51)第一题习题13.(1)解曲线图图1 (2)误差曲线图图2(3)表格表1 部分点处精确解和取不同步长时所得的数值解表2 取不同步长时部分结点处数值解的误差的绝对值和数值解的最大误差(4)MATLAB源代码M=64;a=0;b=pi/2;h=(b-a)/M;x=[a+h:h:b-h];u=zeros(M-1,M-1);u(1,1)=(2/h^2)+(x(1)-1/2)^2;u(1,2)=-(1/h^2);u(M-1,M-1)=(2/h^2)+(x(M-1)-1/2)^2;u(M-1,M-2)=-(1/h^2);for i=2:M-2u(i,i-1)=-(1/h^2);u(i,i)=(2/h^2)+(x(i)-1/2)^2;u(i,i+1)=-(1/h^2);endf=zeros(M-1,1)f(1)=(x(1).*x(1)-x(1)+5/4).*sin(x(1));f(M-1)=(x(M-1).*x(M-1)-x(M-1)+5/4).*sin(x(M-1))+1/h^2; for j=2:M-2f(j)=(x(j).*x(j)-x(j)+5/4).*sin(x(j));endy=inv(u)*f; true=sin(x); plot(x,y'-true)第二题习题二(P67 第3题)(1)h=1/4, τ=1/4精确解数值解误差(2)h=1/8, τ=1/8精确解数值解误差(3)h=1/16, τ=1/16精确解数值解误差(4)h=1/32, τ=1/32精确解数值解误差(5)h=1/64, τ=1/64精确解精确解误差(6)表格(7)Matlab代码function[p,e,u,x,y,k]=fivepoint(h,m,n,kmax,ep)%五点差分法和G-S迭代法解椭圆型方程%kmax为最大迭代次数;%m,n分别为x,y方向的网格数;%ep为精度;%u为差分解,p为精确解,e为误差;%例如在命令行窗口输入[p,e,u,x,y,k]=fivepoint(1/64,64,64,10000,1e-10);%代表步长为1/64,精度为10^(-10),最大迭代次数为10000的五点差分格式syms temp;u=zeros(n+1,m+1);x=0+(0:m)*h;y=0+(0:n)*h;for(j=1:n+1)u(j,1)=sin(y(j))+cos(y(j));u(j,m+1)=exp(1)*(sin(y(j))+cos(y(j)));endfor(i=1:m+1)u(1,i)=exp(x(i));u(n+1,i)=exp(x(i))*(sin(1)+cos(1));endt=zeros(n-1,m-1);for(k=1:kmax)for(j=2:n)for(i=2:m)temp=(u(j,i+1)+u(j,i-1)+u(j+1,i)+u(j-1,i))/4; t(j,i)=(temp-u(j,i))*(temp-u(j,i));u(j,i)=temp;endendt(j,i)=sqrt(t(j,i));if(k>kmax)break;endif(max(max(t))<ep)break;endendfor(j=1:n+1)for(i=1:m+1)p(j,i)=(sin(y(j))+cos(y(j)))*exp(x(i));e(j,i)=abs(u(j,i)-p(j,i));endend代码使用说明:在命令行窗口输入[p,e,u,x,y,k]=fivepoint(1/64,64,64,10000,1e-10);代表步长为1/64,精度为10^(-10),最大迭代次数为10000的五点差分格式surf(x,y,p)可作出近似解曲线surf(x,y,u)可作出精确解曲线surf(x,y,e)可作出误差曲线注意精度不要选取的太低,否则随着步长减小误差反而增大。
偏微分方程数值解上机

偏微分方程数值解上机实习数值求解二维扩散方程的初边值问题2222(,,0)sin sin 2(0,,)(1,,)1(,0,)(,1,)1u u ut x yu x y x y u y t u y t u x t u x t ππ⎧∂∂∂=+⎪∂∂∂⎪⎪=⎨⎪==⎪⎪==⎩(0,1,0)(0,1)(01,0)(01,0)x y t x y y t x t <<><<<<≥<<≥ 古典显式格式:1,,1,,1,,1,,12222n nn n nn n nj l j lj l j l j lj l j l j l u u u u u u u u hhτ++-+---+-+=+将原格式化为:12,1,1,,1,1,(14),/n nnn nnj l j l j l j l j l j l u u u u u u h λλλλλλτ++-+-=++++-=其中 附源程序:%-------------------------------------------运用古典显式差分格式求解二维扩散方程的初边值问题; function gdxs(ti,h,t)%-------------------------------------------ti:时间步长; %-------------------------------------------h:空间步长; k=t/ti;m=1/h+1;r=ti/h^2; %------------------------------ r 为网格比; w=ones(m,m); u=ones(m,m); for i=2:m-1for j=2:m-1u(i,j)=sin(pi*(i-1)*h)*sin(2*pi*h*(j-1)); end end ticfor l=1:kfor i=2:m-1for j=2:m-1w(i,j)=r*u(i-1,j)+r*u(i,j-1)+r*u(i+1,j)+r*u(i,j+1)+(1-4*r)*u(i,j); end end u=w; end toc t=toc umesh(u)交替方向隐式格式(P-R 格式):11112222,,1,,1,,1,,122111111112222,,1,,1,,1,,122222222n n n n n n n n j l j l j l j l j l j l j l j l n n n n n n n n j l j l j l j l j l j l j l j l u u u u u u u u h hu u u u u u u u h h ττ+++++-+-+++++++++-+-⎧--+-+⎪=+⎪⎪⎪⎨⎪--+-+⎪=+⎪⎪⎩ 将原差分格式化为:1112221,,1,,1,,12111111222,1,,11,,1,/n n n n n n j l j l j l j l j l j l n n n n n n j l j l j l j l j l j lu u u u u u h u u u u u u λλλλλλλτλλλλλλ++++-+-+++++++-+-⎧-+-=++⎪=⎨⎪-+-=++⎩(2+2)(2-2),其中(2+2)(2-2) 121,,112,22,1,2,222222222222222222n nl j nn j l n j m n m lu u u u u u λλλλλλλλλλλλλλλλλλλλλλλλλλλ+++⎛⎫⎪⎛⎫-+--⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪-+-- ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪-+--⎝⎭⎝⎭⎝⎭ ⎪ ⎪⎝⎭-+-⎛-+--+-⎝1211,,1112,22,11,2,222222n n l j n n j l n j m n m lu u uu u u λλλλλλλλλ++++++⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎛⎫⎪ ⎪⎛⎫⎪-⎫⎛⎫ ⎪ ⎪⎪ ⎪ ⎪- ⎪ ⎪⎪ ⎪ ⎪⎪ ⎪⎪ ⎪⎪= ⎪⎪⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪-⎭⎝⎭⎝⎭ ⎪⎪ ⎪⎝⎭⎩代入边界条件,转化为三对角矩阵122,,212,33,1,121,2222222220022222222n nl j n n j l n j m n m lu u u u u u λλλλλλλλλλλλλλλλλλλ++-+-⎛⎫⎪⎛⎫+--⎛⎫⎛⎫⎛⎫⎪ ⎪⎪ ⎪⎪-+-- ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪=+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪⎪ ⎪ ⎪-+-⎝⎭⎝⎭⎝⎭⎝⎭ ⎪ ⎪⎝⎭+--+1212,,2112,33,11,121,2222220022222n n l j n n j l n j m n m lu uu u u u λλλλλλλλλλλλλ+++++-+-⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎛⎫⎪⎪⎛⎫⎪-⎛⎫⎛⎫⎛⎫ ⎪ ⎪⎪ ⎪ ⎪-- ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎪ ⎪=+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪-+-⎝⎭⎝⎭⎝⎭⎝⎭ ⎪ ⎪⎝⎭⎩⎪⎪⎪⎪⎪⎪⎪附追赶法源程序:%-------------------------------------------追赶法求解三对角方程组;function x=zg(a,b,c,d)%--------------------------------------------a:方程组系数矩阵A的下对角元素;%--------------------------------------------b:方程组系数矩阵A的主对角元素;%--------------------------------------------c:方程组系数矩阵A的上对角元素;%--------------------------------------------d:追赶法所求方程的右端向量;%--------------------------------------------l:系数矩阵A所分解成的下三角阵L中的下对角元素了l(i); %--------------------------------------------u:系数矩阵A所分解成的下三角阵U中的主对角元素了u(i); n=length(b);u(1)=b(1);y(1)=d(1);for i=1:n-1 %--------------------------追赶法求解之追过程求解Ly=d;l(i)=a(i)/u(i);u(i+1)=b(i+1)-l(i)*c(i);y(i+1)=d(i+1)-l(i)*y(i);endx(n)=y(n)/u(n); %------------------------追赶法求解之赶过程求解Uz=y;for j=n-1:-1:1if u(j)==0break;elsex(j)=(y(j)-c(j)*x(j+1))/u(j);endend%-----------------------------------------------运用P-R差分格式求解二维扩散方程的初边值问题; function pr(ti,h,t)%-------------------------------------------ti:时间步长h:空间步长;k=t/ti+1;m=1/h+1;r=ti/h^2; %------------------------------ r为网格比;w=ones(m,m);u=ones(m,m); %------------------------输入初始值v=ones(m,m);for i=2:m-1for j=2:m-1u(i,j)=sin(pi*(i-1)*h)*sin(2*pi*h*(j-1));endend%------------------------输入用P-R差分格式求解的三对角矩阵b=ones(1,m-2)*(2+2*r);a=-r*ones(1,m-3);c=-r*ones(1,m-3);A=zeros(m-2,m-2); for i=1:m-2A(i,i)=2-2*r; endfor i=1:m-3 A(i,i+1)=r; A(i+1,i)=r; endp=zeros(m-2,1); p(1)=2*r; p(m-2)=2*r; ticfor l=1:kfor i=2:m-1d1=A*u(i,2:m-1)'+p; d1=d1';w(2:m-1,i)=zg(a,b,c,d1); %-------------------------调用追赶法求解 d2=A*w(2:m-1,i)+p;v(i,2:m-1)=zg(a,b,c,d2); %-------------------------调用追赶法求解 end u=v'; end toc t=toc umesh(0:0.1:1,0:0.1:1,u)局部一维格式:11112222,,1,,1,1,,1,22111111112222,,,1,,1,1,,1222211()2222211()222n n n n n n n n j l j lj l j l j l j l j l j l n n n n n n n n j l j l j l j l j l j l j l j l u u u u u u u u h hu u u u u u u u h hττ+++++-+-+++++++++-+-⎧--+-+⎪=+⎪⎪⎪⎨⎪--+-+⎪=+⎪⎪⎩ 将原格式化为:1112221,,1,1,,1,2111111222,1,,1,1,,1(22)(22),/(22)(22)n n n n n n j l j l j l j l j l j l n n n n n n j l j l j l j l j l j l u u u u u u h u u u u u u λλλλλλλτλλλλλλ++++-+-+++++++-+-⎧-++-=+-+⎪=⎨⎪-++-=+-+⎩其中121,1,122,2,1,2,222222222222222222n nl l nn l l n m l n m lu u u u u u λλλλλλλλλλλλλλλλλλλλλλλλλλλ+++⎛⎫⎪⎛⎫-+--⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪-+-- ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪-+--⎝⎭⎝⎭⎝⎭ ⎪ ⎪⎝⎭-+-⎛-+--+-⎝121,1,1112,2,211,2,222222n n j j n n j j n j m n j mu u uu u u λλλλλλλλλ++++++⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎛⎫⎪ ⎪⎛⎫⎪-⎫⎛⎫ ⎪ ⎪⎪ ⎪ ⎪- ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪⎪= ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪-⎭⎝⎭⎝⎭ ⎪⎪ ⎪⎝⎭⎩代入边界条件,转化为三对角矩阵122,1,122,3,1,21,222222220022222222n nl l nn l l n m l n m lu u u u u u λλλλλλλλλλλλλλλλλλλλλλ+++-⎛⎫⎪⎛⎫+--⎛⎫⎛⎫⎛⎫ ⎪ ⎪⎪ ⎪ ⎪-+-- ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪=+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪⎪ ⎪ ⎪-+-⎝⎭⎝⎭⎝⎭⎝⎭ ⎪ ⎪⎝⎭+--+121,1,2112,3,211,12,2222002222n n j j n n j j n j m n j mu uuu u u λλλλλλλλλλλλλλ+++++-+⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎛⎫⎪⎪⎛⎫⎪-⎛⎫⎛⎫⎛⎫ ⎪ ⎪⎪⎪ ⎪ ⎪-- ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪⎪ ⎪=+ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪-+-⎝⎭⎝⎭⎝⎭⎝⎭ ⎪ ⎪⎝⎭⎩⎪⎪⎪附源程序:%------------------------------------------运用局部一维格式求解二维扩散方程的初边值问题;function god(ti,hi,t) %------------------------------------------------ti 为时间步长 , hi 为空间步长; m=1/hi;n=t/ti;g=ti/(hi^2); %--------------------------------- g 为网格比 u=ones(m+1,m+1); %------------------------输入初始值 for i=2:m for j=2:mu(i,j)=sin(pi*(i-1)*hi)*sin(2*pi*(j-1)*hi); end enda(1:m-2)=-0.5*g;b(1:m-1)=1+g;c(1:m-2)=-0.5*g; %------------------------输入用局部一维差分格式求解的三对角矩阵 B=zeros(m-1,m+1);for i=1:m-1B(i,i)=0.5*g;B(i,i+1)=1-g;B(i,i+2)=0.5*g;endf=zeros(m-1,1);f(1,1)=0.5*g;f(m-1,1)=0.5*g;w=ones(m+1,m+1);for i=1:nfor j=2:md=B*u(:,j)+f;%-------------------------调用追赶法求解x=zg(a,b,c,d);w(2:m,j)=x';endfor j=2:me=B*w(j,:)'+f;x=zg(a,b,c,e); %-------------------------调用追赶法求解u(j,2:m)=x;endendumesh(u)古典显式在t=1时运行结果:gdxs(0.0025,0.1,1)所用时间t=01.00000 000000 000 1.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.00000 000000 000 0.999999999707990.999999999445260.999999999235500.999999999102410.999999999055020.999999999102400.999999999235500.999999999445260.999999999707991.000000000000001.00000 000000 000 0.999999999445260.999999998943480.999999998547660.999999998290520.999999998204810.999999998290520.999999998547660.999999998943480.999999999445261.000000000000001.00000 000000 000 0.999999999235500.999999998547660.999999997998510.999999997650070.999999997526020.999999997650070.999999997998510.999999998547660.999999999235501.000000000000001.00000 000000 000 0.999999999102400.999999998290520.999999997650070.999999997234010.999999997095320.999999997234010.999999997650070.999999998290520.999999999102401.000000000000001.00000 000000 000 0.999999999055020.999999998204810.999999997526020.999999997095320.999999996941990.999999997095320.999999997526020.999999998204810.999999999055021.00000000000000000000 000 9999102409998290529997650079997234019997095329997234019997650079998290529999102400000000001.00000 000000 000 0.999999999235500.999999998547660.999999997998510.999999997650070.999999997526020.999999997650070.999999997998510.999999998547660.999999999235501.000000000000001.00000 000000 000 0.999999999445260.999999998943480.999999998547660.999999998290520.999999998204810.999999998290520.999999998547660.999999998943480.999999999445261.000000000000001.00000 000000 000 0.999999999707990.999999999445260.999999999235500.999999999102400.999999999055020.999999999102400.999999999235500.999999999445260.999999999707991.000000000000001.00000 000000 000 1.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.00000000000000P-R 格式t=1时运行结果:pr(0.0025,0.1,1)所用时间t=0.360000000000001.00000 000000 000 1.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.00000 000000 000 0.999999999544420.999999999133430.999999998807270.999999998597870.999999998525710.999999998597870.999999998807270.999999999133430.999999999544421.000000000000001.00000 000000 000 0.999999999133430.999999998351690.999999997731300.999999997332980.999999997195730.999999997332980.999999997731300.999999998351690.999999999133431.000000000000001.00000 000000 000 0.999999998807270.999999997731300.999999996877400.999999996329170.999999996140260.999999996329170.999999996877400.999999997731300.999999998807271.000000000000001.00000 000000 000 0.999999998597870.999999997332980.999999996329170.999999995684680.999999995462600.999999995684680.999999996329170.999999997332980.999999998597871.000000000000001.00000 000000 000 0.999999998525710.999999997195730.999999996140260.999999995462600.999999995229100.999999995462600.999999996140260.999999997195730.999999998525711.000000000000001.00000 000000 000 0.999999998597870.999999997332980.999999996329170.999999995684680.999999995462600.999999995684680.999999996329170.999999997332980.999999998597871.000000000000001.00000 000000 000 0.999999998807270.999999997731300.999999996877400.999999996329170.999999996140260.999999996329170.999999996877400.999999997731300.999999998807271.000000000000001.00000 000000 000 0.999999999133430.999999998351690.999999997731300.999999997332980.999999997195730.999999997332980.999999997731300.999999998351690.999999999133431.00000000000000000000 000 9999544429999133439998807279998597879998525719998597879998807279999133439999544420000000001.00000 000000 000 1.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.00000000000000局部一维格式t=1时的运行结果:god(0.0025,0.1,1)所用时间t= 0.390000000000001.00000 000000 000 1.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.00000 000000 000 0.999999999521570.999999999089960.999999998747440.999999998527530.999999998451750.999999998527530.999999998747440.999999999089960.999999999521571.000000000000001.00000 000000 000 0.999999999089960.999999998269010.999999997617490.999999997199200.999999997055060.999999997199200.999999997617490.999999998269010.999999999089961.000000000000001.00000 000000 000 0.999999998747440.999999997617490.999999996720760.999999996145030.999999995946640.999999996145030.999999996720760.999999997617500.999999998747441.000000000000001.00000 000000 000 0.999999998527530.999999997199200.999999996145030.999999995468210.999999995234990.999999995468210.999999996145030.999999997199200.999999998527531.000000000000001.00000 000000 000 0.999999998451750.999999997055060.999999995946640.999999995234990.999999994989770.999999995234990.999999995946640.999999997055060.999999998451751.000000000000001.00000 000000 000 0.999999998527530.999999997199200.999999996145030.999999995468210.999999995234990.999999995468210.999999996145030.999999997199200.999999998527531.000000000000001.00000 000000 000 0.999999998747440.999999997617490.999999996720760.999999996145030.999999995946640.999999996145030.999999996720760.999999997617500.999999998747441.000000000000001.00000 000000 000 0.999999999089960.999999998269010.999999997617490.999999997199200.999999997055060.999999997199200.999999997617500.999999998269010.999999999089961.000000000000001.00000 000000 000 0.999999999521570.999999999089960.999999998747440.999999998527530.999999998451750.999999998527530.999999998747440.999999999089960.999999999521571.000000000000001.00000 000000 000 1.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.000000000000001.00000000000000结论:由上面的表格数据可知:古典显式格式的计算速度最快,且当1/4λ≤时,才是稳定的,局部一维格式的计算速度最慢,但是它是无条件稳定的,P-R格式的速度居中,也是无条件稳定的。
偏微分方程报告范文

偏微分方程报告范文偏微分方程是研究多变量函数的微分方程,其中函数的未知量既依赖于自变量,又依赖于多个自变量。
偏微分方程在物理学、工程学和经济学等领域中有着广泛的应用。
本报告将介绍偏微分方程的基本概念、求解方法和应用领域。
一、偏微分方程的基本概念偏微分方程是由未知函数的偏导数和自变量构成的方程。
常见的偏微分方程包括波动方程、传热方程和扩散方程等。
偏微分方程根据阶数可分为一阶和二阶偏微分方程。
一阶偏微分方程中只涉及到未知函数的一阶偏导数,一般可以通过变量分离的方法求解。
二阶偏微分方程中涉及到未知函数的二阶偏导数,求解方法一般包括分离变量法、特征线法和变换法等。
二、偏微分方程的求解方法1.分离变量法:假设未知函数可以表示为两个只依赖于单个自变量的函数的乘积形式,然后将该形式代入到偏微分方程中,再将方程两边关于不同的自变量求积分,从而得到方程的通解。
2.特征线法:通过特征线曲线的方法将偏微分方程转化为常微分方程。
先找出特征线曲线,然后在特征线上引入新的变量,使得偏微分方程变为常微分方程,进而求解。
3.变换法:通过适当的变量变换,将原偏微分方程转化为一个更容易求解的形式。
常用的变换方法有坐标变换、函数变换和变量替换等。
三、偏微分方程的应用领域1.物理学:偏微分方程在物理学中有着广泛的应用。
例如,波动方程可以描述声波、光波和电磁波等在介质中的传播;传热方程可以描述热传导过程;薛定谔方程和波恩-奥本海默方程可以描述量子力学中的粒子行为等。
2.工程学:偏微分方程在工程学中被广泛应用于流体力学、结构力学和电磁场等领域。
例如,纳维-斯托克斯方程用于描述流体的运动;弹性方程用于描述结构的变形和应力分布等。
3.经济学:偏微分方程在经济学中应用较多,尤其是在金融学中。
例如,布莱克-斯科尔斯方程用于定价期权;黑-舒尔斯方程用于描述衍生品的定价和风险管理等。
通过对偏微分方程的研究和求解,可以更好地理解自然界的现象和规律,并为解决实际问题提供数学模型和解决方法。
偏微分方程数值及matlab实验报告

偏微分方程数值实验报告八实验题目:利用有限差分法求解.0)1(,0)1(),()()(==-=+''-u u x f x u x u 真解为)1()(22x e x u x -=-实现算法:对于两点边值问题,)(,)(,,d 22βα==∈=-b u a u l x f dxu(1)其中),(b a l =f b a ),(<为],[b a l =上的连续函数,βα,为给定常数.其相应的有限差分法的算法如下:1.对求解区域做网格剖分,得到计算网格.在这里我们对区间l 均匀剖分n 段,每个剖分单元的剖分步长记为nab h -=.2.对微分方程中的各阶导数进行差分离散,得到差分方程.运用的离散方法有:方法一:用待定系数和泰勒展开进行离散)()()()(d )(d 111122++--++≈i i i i i i i i x u x u x u x x u ααα方法二:利用差商逼近导数21122)()(2)()(d )(d h x u x u x u x x u i i i i i -++-≈(2)将(2)带入(1)可以得到)()()()(2)(211u R x f h x u x u x u i i i i i +=+---+,其中)(u R i 为无穷小量,这时我们丢弃)(u R i ,则有在i x 处满足的计算公式:1,...,1)()()(2)(211-==+---+n i x f hx u x u x u i i i i ,(3)3.根据边界条件,进行边界处理.由(1)可得βα==n u u ,0(4)称(3)(4)为逼近(1)的差分方程,并称相应的数值解向量1-n U 为差分解,i u 为)(i x u 的近似值.4.最后求解线性代数方程组,得到数值解向量1-n U .实验题目:用Lax-Wendroff 格式求解方程:.4sin 1),1(],1,0[,2sin 1)0,(,0),1,0(,02t t u x x x u t x u u x t ππ+=∈+=>∈=- (1) (精确解).2(2sin 1t x u ++=π) 数值边值条件分别为: (a )).(20101n 0nn nu u hu u -+=+τ (b ).1n 0nu u =(c ).02-12111n 0=++++n n u u u请将计算结果与精确解进行比较。
偏微分运算

偏微分运算【实用版】目录1.偏微分运算的定义和概念2.偏微分运算的基本运算法则3.偏微分运算在物理学和工程学中的应用正文偏微分运算是数学中的一个重要分支,它主要研究多元函数在某一点处的局部性质。
偏微分运算主要包括偏导数、梯度、散度、旋度等概念。
在物理学、工程学等领域,偏微分运算有着广泛的应用。
一、偏微分运算的定义和概念偏微分运算是多元函数微分学的基础。
偏导数是指多元函数在某一点处的局部性质,它是函数在这一点的切线斜率。
偏导数的定义为:设函数f(x,y) 在点 (x0,y0) 处可微,如果存在极限二、偏微分运算的基本运算法则偏微分运算有许多基本运算法则,主要包括以下几个方面:1.偏导数的线性性:如果两个函数在某点处都可微,那么它们的和也在该点处可微,其偏导数等于两个函数偏导数的和。
2.偏导数的求和:如果一个函数在某点处可微,那么它在该点处的常数函数的偏导数为 0。
3.偏导数的乘积:如果两个函数在某点处都可微,那么它们的乘积也在该点处可微,其偏导数等于两个函数偏导数的乘积。
三、偏微分运算在物理学和工程学中的应用偏微分运算在物理学和工程学中有广泛的应用,主要包括以下几个方面:1.在物理学中,偏微分运算主要用于研究场的性质,如电场、磁场、重力场等。
通过求解偏微分方程,可以得到场的强度、方向、梯度等信息。
2.在工程学中,偏微分运算主要用于优化设计、计算物理量等。
例如,在计算机图形学中,偏微分运算可以用来求解光线与物体的交点,从而实现光线追踪渲染。
总结:偏微分运算是数学中的一个重要分支,它研究多元函数在某一点处的局部性质。
偏微分运算在物理学和工程学中有广泛的应用,主要包括求解偏微分方程、优化设计等。
偏微分方程(PDE)期末报告

K=黏性或熱傳導 假設為常數
T T T 2 2 x y
2 2 2 2 2 T T 2 v T U 2 V 2 x y
有限差分近似及其符號表示
一個偏微分方程的有限差分近似由我們所 關心的區間上的網格所構成,採取矩形網 格結構,其間距為常量。
T v T k 2T t 2 2 T T T T T U V k 2 2 t x y y x 在空間交點ij處做離散 Tij 2 2 U 2 xTij V 2 yTij k x Tij y Tij t
偏微分方程的有限差分方法:介紹
謝謝大家~
偏微分方程(PDE)期末報告
-有限差分法簡單介紹
學生:李宗諺 B97520016 河工3A 指導教授:陳正宗 終身特聘教授
傳導-擴散方程
T 2 v T k T T T x , y , t t
v v x, y, t U x, y, t i V x, y, t j
Tijn 1 Tijn t
1 1 + 2 即可求解 2
運算元
Tijn T ix, jy, nt
一些常用的有限差分運算元:
1 2 xTij Ti 1 j Ti 1 j 中心差分 2x 1 xTij Tij Ti 1 j 向後差分 x 1 x Tij Ti 1 j Tij 向前差分 x 1 2 x Tij 2 Ti 1 j 2Tij Ti 1 j x
Tij t
U 2 xTij V 2 yTij k T T
2 x ij
2 y ij
由前向歐拉法可得 1 n 1 n Tij Tij 2 n n k x2Tijn y Tij U ij 2 xTijn Vijn 2 yTijn t 由後向歐拉法可得 2 Tijn1 Tijn 2 n 1 n 1 k x2Tijn1 y Tij U ij 2 xTijn1 Vijn1 2 yTijn1 t 再將求得的運算元代入
偏微分方程解的几道算例(差分、有限元)-含matlab程序(1)

A(i-1,i)=-r; A(i,i-1)=-r; end end u=zeros(N+1,M+1); u(N+1,:)=u1; for k=1:N b=u(N+2-k,2:M)+0.02; u(N+1-k,2:M)=inv(A)*b';%求解迭代方程组 end uT=u(1,:);%0.25时刻的解 %精确解与数值解画图 x1=[0,x,1]; plot(x1,uT,'o') hold u_xt = exp (-pi*pi*T)*sin (pi*x1) + x1.*(1 - x1); plot (x1, u_xt, ' r') e=u_xt-uT; 六点格式 function [e]=six(dx,dt,T) %用六点对称格式求解,dx为x方向步长,dt为t方向步长 % e为误差 M=1/dx; N=T/dt; %得到第一层的值 u1=zeros(1,M+1); x=[1:M-1]*dx; u1([2:M])= sin(pi*x)+x.*(1 - x); %网比 r=dt/dx/dx;r2=2+2*r;r3=2-2*r; %构造三对角矩阵A for i=1:M-1 A(i,i)=r2;
0.0070 0.0027
-0.0097 -0.0037
-0.0013 -0.0005
0.0082 0.0000
-0.0114 0.0000
-0.0015 0.0000
0.0087 -0.0120
-0.0016
注:这里的"误差"=精确解-数值解. 2.精确解与数值解结果图像对比
“向前差分格式”:
