【名校课堂】2016年九年级数学上册 小专题四 二次函数的图象与字母系数之间的关系 (新版)新人教版
人教版数学九年级上册 二次函数的图象与各项字母系数之间的关系

y
●
-2 -1 o 1 2
x
-1
a-b+c的值 ●
是正数
0
1
x
a-b+c的值 是负数
a
开口方向向上a>0 向下a<o
b c 2a+b
2a-b b2-4ac a+b+c a-b+c
对称轴与y轴比较 左侧ab同号 右侧ab异号 与y轴交点:交于上半轴c>o,下半轴c<0,交于原点c=0
- b 与1比较,等于1,大于1,小于1
数b的关系
x
b 2a
y
对称轴在y 轴的左侧
x
b 2a
0
0
x
x
b 2a
1b 2a
0
对称轴在y轴的左侧, a和b的符号相同
2.二次函数图象的对称轴的位置和二次项系数a、一次项系
数b的关系
y
x
b 2a
对称轴在y 轴的右侧
x
b 2a
0
0
x
x
b 2a
1b 2a
0
对称轴在y轴的右侧, a和b的符号相异
2a
- b 与-1比较,等于-1,大于-1,小于-1 2a 与x轴交点个数
令x=1,y=a+b+c,看纵坐标是在y轴的正半轴 上(>0)还是在负半轴上(<0)
令x=-1,y=a-b+c,看纵坐标
4a+2b+c 4a-2b+c
令x=2,y=4a+2b+c,看纵坐标 令x=-2,y=4a-2b+c,看纵坐标
23
能力提升
1.已知:二次函数y=ax2+bx+c的图象如图所示,
【名校课堂】2016年九年级数学上册-小专题四-二次函数的图象与字母系数之间的关系-(新版)新人教版

二次函数的图象与字母系数之间的关系抛物线y=ax2+bx+c的图象与字母系数a,b,c之间的关系:(1)当a>0时,开口______,当a<0时,开口______;(2)若对称轴在y轴的左边,则a,b______,若对称轴在y轴的右边,则a,b______;(3)若抛物线与y轴的正半轴相交,则c______0,若抛物线与y轴的负半轴相交,则c______0,若抛物线经过原点,则c______0;(4)当x=1时,y=ax2+bx+c=________;当x=-1时,y=ax2+bx+c=________;当x=2时,y=ax2+bx+c=__________;当x=-2时,y=ax2+bx+c=__________;…;(5)当对称轴x=1时,x=-b2a=______,所以-b=______,此时2a+b=______;当对称轴x=-1时,x=-b2a=______,所以b=______,此时2a-b=______;判断2a+b大于或者等于0,看对称轴与______的大小关系;判断2a-b大于或者等于0,看对称轴与______的大小关系;(6)b2-4ac>0二次函数与横轴________交点;b2-4ac=0二次函数与横轴________交点;b2-4ac<0二次函数与横轴______交点.1.(龙岩中考)若二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列选项正确的是( )A.a>0 B.c>0C.ac>0 D.bc<02.(深圳中考)二次函数y=ax2+bx+c的图象如图所示,给出以下结论:①a>0;②b>0;③c<0;④b2-4ac>0,其中所有正确结论的序号是( )A.②④ B.①③ C.③④ D.①②③3.(兰州中考)二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中错误的是( ) A.abc<0 B.2a+b=0C.b2-4ac>0 D.a-b+c>04.(滨州中考)如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(-1,0).则下面的四个结论:①2a+b=0;②4a-2b+c<0;③ac>0;④当y <0时,x<-1或x>2.其中正确的个数是( )A.1个 B.2个C.3个 D.4个5.(陕西中考)二次函数y =ax 2+bx +c(a≠0)的图象如图所示,则下列结论中正确的是( )A .c>-1B .b>0C .2a +b≠0D .9a +c>3b6.(恩施中考)如图是二次函数y =ax 2+bx +c 图象的一部分,图象过点(-3,0),对称轴为直线x =-1,给出四个结论:①b 2>4ac ;②2a+b =0;③a+b +c <0;④若点B(-52,y 1)、C(-12,y 2)为函数图象上的两点,则y 1<y 2,其中正确的是( )A .②④B .①④C .①③D .②③7.(达州中考)如图是二次函数y =ax 2+bx +c 的图象的一部分,对称轴是直线x =1.①b 2>4ac ;②4a-2b+c <0;③不等式ax 2+bx +c >0的解集是x≥3.5;④若(-2,y 1),(5,y 2)是抛物线上的两点,则y 1<y 2.上述4个判断中,正确的是( )A .①②B .①④C .①③④D .②③④8.(潍坊中考)已知二次函数y =ax 2+bx +c +2的图象如图所示,顶点为(-1,0),下列结论:①abc<0;②b 2-4ac =0;③a>2;④4a-2b +c >0.其中正确结论的个数是( )A .1B .2C .3D .49.(遵义中考)已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图,其中正确的是( )10.(咸宁中考)如图是二次函数y=ax2+bx+c的图象,下列结论:①二次三项式ax2+bx+c的最大值为4;②4a+2b+c<0;③一元二次方程ax2+bx+c=1的两根之和为-1;④使y≤3成立的x的取值范围是x≥0.其中正确的个数有( )A.1个 B.2个 C.3个 D.4个11.(扬州中考)如图,抛物线y=ax2+bx+c(a>0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(4,0)在该抛物线上,则4a-2b+c的值为________.12.已知关于x的二次函数y=ax2+bx+c(a>0)的图象经过点C(0,1),且与x轴交于不同的两点A,B,点A的坐标是(1,0).(1)求c的值;(2)求a的取值范围.13.如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2).(1)求m的值和抛物线的解析式;(2)求不等式x 2+bx +c>x +m 的解集(直接写出答案);(3)若M(a ,y 1),N(a +1,y 2)两点都在抛物线y =x 2+bx +c 上,试比较y 1与y 2的大小.参考答案向上 向下 同号 异号 > < = a +b +c a -b +c 4a +2b +c 4a -2b +c 1 2a 0 -1 2a 0 1 -1 有两个 有一个 无2.A3.D4.B5.D6.B7.B8.B9.D 10.B12.(1)c =1.(2)由图象过C(0,1),A(1,0),得a +b +1=0,∴b 2-4ac >0,可得(-a -1)2-4a >0,即(a -1)2>0,故a≠1.又∵a>0,∴a 的取值范围是a >0且a≠1.13.(1)∵直线y =x +m 经过点A(1,0),∴0=1+m.∴m=-1.∵抛物线y =x 2+bx +c 经过点A(1,0),B(3,2),∴⎩⎪⎨⎪⎧0=1+b +c ,2=9+3b +c.解得⎩⎪⎨⎪⎧b =-3,c =2.∴抛物线的解析式为y =x 2-3x +2. (2)x>3或x<1.(3)∵M(a,y 1),N(a +1,y 2)两点都在函数y =x 2-3x +2的图象上,∴y 1=a 2-3a +2,y 2=(a +1)2-3(a +1)+2=a 22-y 1=(a 2-a)-(a 2-3a +2)=2a -2.∴当2a -2<0,即a<1时,y 1>y 2;当2a -2=0,即a =1时,y 1=y 2;当2a -2>0,即a>1时,y 1<y 2.。
2016年秋期人教版九年级数学上册名校课堂练习22.3.1二次函数与图形面积.doc

第1课时 二次函数与图形面积基础题知识点 二次函数与平面面积1.(六盘水中考)如图,假设篱笆(虚线部分)的长度为16 m ,则所围成矩形ABCD 的最大面积是( )A .60 m 2B .63 m 2C .64 m 2D .66 m 22.(咸宁中考)用一根长为40 cm 的绳子围成一个面积为a cm 2的长方形,那么a 的值不可能为( )A .20B .40C .100D .1203.用长8 m 的铝合金条制成使窗户的透光面积最大的矩形窗框(如图),那么这个窗户的最大透光面积是( )A.6425 m 2B.43m 2 C.83m 2 D .4 m 24.(玉林、防城港中考)如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止,设小三角形移动的距离为x ,两个三角形重叠面积为y ,则y 关于x 的函数图象是( )5.如图,利用一面墙(墙的长度不超过45 m),用80 m长的篱笆围一个矩形场地.当AD=________时,矩形场地的面积最大,最大值为________.6.如图,在△ABC中,∠B=90°,AB=8 cm,BC=6 cm,点P从点A开始沿AB向B 点以2 cm/s的速度移动,点Q从点B开始沿BC向C点以1 cm/s的速度移动,如果P,Q 分别从A,B同时出发,当△PBQ的面积为最大时,运动时间t为________s.7.将一根长为20 cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,则这两个正方形面积之和的最小值是________ cm2.8.已知直角三角形两条直角边的和等于20,两条直角边各为多少时,这个直角三角形的面积最大?最大值是多少?9.(滨州中考)某高中学校为高一新生设计的学生单人桌的抽屉部分是长方体形,抽屉底面周长为180 cm,高为20 cm.请通过计算说明,当底面的宽x为何值时,抽屉的体积y最大?最大为多少?(材质及其厚度等暂忽略不计)中档题10.(潍坊中考)如图,有一块边长为6 cm 的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( ) A. 3 cm 2 B.323 cm 2 C.92 3 cm 2 D.2723 cm 211.(荆州中考)如图,正方形ABCD 的边长为3 cm ,动点P 从B 点出发以3 cm/s 的速度沿着边BC -CD -DA 运动,到达A 点停止运动;另一动点Q 同时从B 点出发以1 cm/s 的速度沿着边BA 向A 点运动,到达A 点停止运动.设P 点运动时间为x(s),△BPQ 的面积为y(cm 2),则y 关于x 的函数图象是( )12.手工课上,小明准备做一个形状是菱形的风筝,这个菱形的两条对角线长度之和恰好为60 cm ,菱形的面积S(单位:cm 2)随其中一条对角线的长x(单位:cm)的变化而变化.(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围);(2)当x是多少时,菱形风筝面积S最大?最大面积是多少?13.(淮安中考)用长为32米的篱笆围一个矩形养鸡场,设围成的矩形一边长为x米,面积为y平方米.(1)求y关于x的函数关系式;(2)当x为何值时,围成的养鸡场面积为60平方米?(3)能否围成面积为70平方米的养鸡场?如果能,请求出其边长;如果不能,请说明理由.综合题14.(朝阳中考)如图,正方形ABCD 的边长为2 cm ,△PMN 是一块直角三角板(∠N =30°),PM >2 cm ,PM 与BC 均在直线l 上,开始时M 点与B 点重合,将三角板向右平行移动,直至M 点与C 点重合为止.设BM =x cm ,三角板与正方形重叠部分的面积为y cm 2.下列结论:①当0≤x≤233时,y 与x 之间的函数关系式为y =32x 2; ②当233<x ≤2时,y 与x 之间的函数关系式为y =2x -233; ③当MN 经过AB 的中点时,y =123 cm 2; ④存在x 的值,使y =12S 正方形ABCD (S 正方形ABCD 表示正方形ABCD 的面积). 其中正确的是________(写出所有正确结论的序号).参考答案基础题1.C2.D3.C4.B5.20 m 800 m 26.27.2528.设直角三角形的一直角边长为x ,则另一直角边长为(20-x),其面积为y ,则y =12x(20-x)=-12x 2+10x =-12(x -10)2+50.当x =10时,面积y 值取最大,y 最大=50. 9.根据题意,得y =20x(1802-x).整理得y =-20x 2+1 800x =-20(x 2-90x +2 025)+40 500=-20(x -45)2+40 500.∵-20<0,∴当x =45时,函数有最大值,y 最大值=40 500.即当底面的宽为45 cm 时,抽屉的体积最大,最大为40 500 cm 3.中档题10.C 11.C12.(1)S =-12x 2+30x. (2)∵S =-12x 2+30x =-12(x -30)2+450,且a =-12<0,∴当x =30时,S 有最大值,最大值为450.即当x 为30 cm 时,菱形风筝的面积最大,最大面积是450 cm 2.13.(1)y =x(16-x)=-x 2+16x(0<x<16).(2)当y =60时,-x 2+16x =60,解得x 1=10,x 2=6.∴当x =10或6时,围成的养鸡场的面积为60平方米.(3)当y =70时,-x 2+16x =70,整理得x 2-16x +70=0.∵Δ=256-280=-24<0,∴此方程无实数根.∴不能围成面积为70平方米的养鸡场.综合题14.①②④。
专题:二次函数的图象与字母系数的关系

专题:二次函数y =ax 2+bx +c (a ≠0)的图象与字母系数的关系二次函数y =ax 2+bx +c (a ≠0)系数符号的确定:⑴a 由抛物线开口方向确定:开口方向向上,则a >0;否则a <0.⑵b 由对称轴和a 的符号确定:由对称轴公式x = -2ba判断符号(左同右异). ⑶c 由抛物线与y 轴的交点确定:交点在y 轴正半轴,则c >0;否则c <0.⑷b 2-4ac 的符号由抛物线与x 轴交点的个数确定:2个交点,b 2-4ac >0;1个交点,b 2-4ac =0;没有交点,b 2-4ac <0. ⑸当x =1时,y =a +b +c ,当x =-1时,y =a -b +c .故由点(1, a +b +c ) 所在的象限,可判断a +b +c 的符号;由点(-1, a -b +c ) 所在的象限,可判断a -b +c 的符号.同理,当x =2时,可确定4a +2b +c 的符号,当x =-2时,可确定4a -2b +c 的符号……⑹由对称轴x = -2b a 与x =±1的位置关系,可确定2a ±b 的符号.当x = -2b a =1时,b = -2a ,即2a +b =0;当x = -2ba=-1时,b = 2a ,即2a -b =0.例1.抛物线y =ax 2+bx +c 图象如图所示,则下列式子中正确的个数为( )①a <0;②b <0;③c >0;④a +b +c >0;⑤ 4a -2b +c <0;⑥2a +b >0;⑦b 2-4ac >0;⑧4a +c <0C .5D .6c 的图象如图所示,给出下列结论:①2a +b >0;②b >a >c ;③若-1<m <n <1,则m +n <-ba;④3|a |+|c |<2|b |.其中正确的结论是 (写出你认为正确的所有结论序号).例3.二次函数y =ax 2+bx +c (a ≠0)的图象如图所示,与y 轴相交点C ,与x 轴负半轴相交点A ,且OA =OC ,下列5个结论:①abc >0;②b <a +c ;③4a +2b +c >0;④2a +b =0;⑤c +1a= -2,其中正确的结论有 .(请填序号)强化训练1.如图为二次函数y =ax 2+bx +c (a ≠0)的图象,则下列说法:①a >0②2a +b =0 ③a +b +c >0 ④当-1<x <3时,y >0,其中正确的个数为( )A .1 B .2 C .3 D .42.已知二次函数y =ax 2+bx +c +2的图象如图所示,顶点为(-1,0),下列结论:①abc <0;②b 2-4ac =0;③a >2;④4a -2b +c >0.其中正确结论的个数是( )A .1 B .2 C .3 D .43.已知二次函数y =ax 2+bx +c 的图象如图所示,则下列结论:①c =2;②b 2-4ac >0;③2a +b =0;④a -b +c <0.其中正确的为( )A .①②③ B .①②④ C .①② D .③④4.如图是二次函数y =ax 2+bx +c =(a ≠0)图象的一部分,对称轴是直线x =-2.关于下列结论:①ab <0;②b 2-4ac >0;③9a -3b +c <0;④b -4a =0;⑤方程ax 2+bx =0的两个根为x 1=0,x 2=-4,其中正确的结论有( ) A .①③④ B .②④⑤ C .①②⑤ D .②③⑤5.已知二次函数y =ax 2+bx +c (a ≠0)的图象如图所示,有下列5个结论:①abc >0;②b <a +c ;③4a +2b +c >0;④2c <3b ;⑤a +b >m (am +b )(m ≠1的实数).其中正确的结论有( ) A .2个 B .3个 C .4个 D .5个6.如图,抛物线y =ax 2+bx +c (a ≠0)过点(1,0)和点(0,-2),且顶点在第三象限,设P =a -b +c ,则P 的取值范围是( )A .-4<P <0 B .-4<P <-2 C .-2<P <0 D .-1<P <07.已知二次函数y =ax 2+bx +c 的图象与x 轴交于点(-2,0)、(x 1,0),且1<x 1<2,与y 轴的正半轴的交点在(0,2)的下方.下列结论:①4a -2b +c =0;②a -b +c <0;③2a +c >0;④2a -b +1>0.其中正确结论的个数是( )个.A .4个B .3个C .2个D .1个8.如图,已知二次函数y =ax 2+bx +c (a ≠0)的图象与x 轴交于点A (-1,0),对称轴为直线x =1,与y 轴的交点B 在(0,2)和(0,3)之间(包括这两点),下列结论:①当x >3时,y <0;②3a +b <0;③-1≤a ≤-23;④4ac -b 2>8a ;其中正确的结论是( )A .①③④ B .①②③ C .①②④ D .①②③④9. 如图,二次函数y =ax 2+bx +c (a ≠0)的图象经过点(1,2)且与x 轴交点的横坐标分别为x 1,x 2,其中-1<x 1<0,1<x 2<2,下列结论:4a +2b +c <0,2a +b <0,b 2+8a >4ac ,a <-1,其中结论正确的有( ) A .1个B .2个C .3个D .4个10.抛物线y =ax 2+bx +c (a ≠0)满足条件:(1)4a -b =0;(2)a -b +c >0;(3)与x 轴有两个交点,且两交点间的距离小于2.以下有四个结论:①a <0;②c >0;③a +b +c <0;④4c <a <3c,其中所有正确结论的序号是 .有已知二次函数y=ax2+bx+c的图象与x轴交于点(-2,0),(x1,0),且1<x1<2,与y轴正半轴的交点在(0,2)的下方,下列结论:①a<b<0;②2a+c>0;③4a+c<0;④2a-b+1>0.其中正确的结论是.(填写序号)。
2016年秋期人教版九年级数学上册名校课堂练习22.1.4.2用待定系数法求二次函数的解析式.doc

第2课时用待定系数法求二次函数的解析式基础题知识点1利用"三点式〞求二次函数解析式1.已知二次函数y=-错误!x2+bx+c的图象经过A<2,0>,B<0,-6>两点,则这个二次函数的解析式为______________________.2.若二次函数y=ax2+bx+c的x与y的部分对应值如下表:则此二次函数的解析式为____________________.3.已知二次函数y=ax2+bx+c,当x=0时,y=1;当x=-1时,y=6;当x=1时,y=0.求这个二次函数的解析式.4.如图,抛物线y=x2+bx+c与x轴交于A,B两点.<1>求该抛物线的解析式;<2>求该抛物线的对称轴以与顶点坐标.知识点2利用"顶点式〞求二次函数解析式5.已知某二次函数的图象如图所示,则这个二次函数的解析式为<>A.y=2<x+1>2+8B.y=18<x+1>2-8C.y=错误!<x-1>2+8D.y=2<x-1>2-86.已知抛物线的顶点坐标为<4,-1>,与y轴交于点<0,3>,求这条抛物线的解析式.知识点3利用"交点式〞求二次函数解析式7.如图所示,抛物线的函数表达式是<>A.y=错误!x2-x+4B.y=-错误!x2-x+4C.y=错误!x2+x+4D.y=-错误!x2+x+48.已知一个二次函数的图象与x轴的两个交点的坐标分别为<-1,0>和<2,0>,与y轴的交点坐标为<0,-2>,则该二次函数的解析式为_______________.9.已知二次函数经过点A<2,4>,B<-1,0>,且在x轴上截得的线段长为2,求该函数的解析式.中档题10.抛物线的图象如图所示,根据图象可知,抛物线的解析式可能是<>A.y=x2-x-2B.y=-错误!x2-错误!x+2C.y=-错误!x2-错误!x+1D.y=-x2+x+211.二次函数y=-x2+bx+c的图象的最高点是<-1,-3>,则b,c的值分别是<> A.b=2,c=4 B.b=2,c=-4C.b=-2,c=4 D.b=-2,c=-412.<##一模>二次函数的图象如图所示,则其解析式为________________.13.已知抛物线y=ax2+bx+c<a≠0>的对称轴为x=1,且抛物线经过A<-1,0>,B<0,-3>两点,则这条抛物线所对应的函数关系式为________________.14.<##中考>设抛物线y=ax2+bx+c<a≠0>过A<0,2>,B<4,3>,C三点,其中点C在直线x=2上,且点C到抛物线的对称轴的距离等于1,则抛物线的函数解析式为___________________________________.15.<##中考>如图,已知抛物线的顶点为A<1,4>,抛物线与y轴交于点B<0,3>,与x轴交于C,D 两点.点P是x轴上的一个动点.<1>求此抛物线的解析式;<2>当PA+PB的值最小时,求点P的坐标.16.<##中考>已知抛物线y=ax2+bx+c与x轴交于点A<1,0>,B<3,0>,且过点C<0,-3>.<1>求抛物线的解析式和顶点坐标;<2>请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=-x上,并写出平移后抛物线的解析式.综合题17.<##中考>设函数y=<x-1>[<k-1>x+<k-3>]<k是常数>.<1>当k取1和2时的函数y1和y2的图象如图所示,请你在同一直角坐标系中画出当k 取0时函数的图象;<2>根据图象,写出你发现的一条结论;<3>将函数y2的图象向左平移4个单位,再向下平移2个单位,得到函数y3的图象,求函数y3的最小值.参考答案基础题1.y=-错误!x2+4x-62.y=-2x2-12x-133.由题意,得错误!解得错误!∴二次函数的解析式为y=2x2-3x+1.4.<1>∵抛物线y=x2+bx+c与x轴交于A<-1,0>,B<3,0>两点,∴错误!解得错误!∴二次函数解析式是y=x2-2x-3.<2>∵y=x2-2x-3=<x-1>2-4,∴抛物线的对称轴为x=1,顶点坐标为<1,-4>.5.D6.依题意,设y=a<x-h>2+k.将顶点坐标<4,-1>和与y轴交点<0,3>代入,得3=a<0-4>2-1.解得a=错误!.∴这条抛物线的解析式为y=错误!<x-4>2-1.7.D8.y=x2-x-29.∵B<-1,0>且在x轴上截得的线段长为2,∴与x轴的另一个交点坐标为<1,0>或<-3,0>.设该函数解析式为y=a<x-x1><x-x2>,把A<2,4>,B<-1,0>,<1,0>代入得a<2+1><2-1>=4,解得a=错误!.所以y=错误!<x+1><x-1>.同理,把A<2,4>,B<-1,0>,<-3,0>代入,可以求得y=错误!<x+1><x+3>.∴函数的解析式为y=错误!<x+1><x-1>或y=错误!<x+1><x+3>.中档题10.D11.D12.y=-x2+2x+313.y=x2-2x-314.y=错误!x2-错误!x+2或y=-错误! x2+错误!x+215.<1>∵抛物线顶点坐标为<1,4>,∴设y=a<x-1>2+4.∵抛物线过点B<0,3>,∴3=a<0-1>2+4,解得a=-1.∴抛物线的解析式为y=-<x-1>2+4,即y=-x2+2x+3.<2>作点B关于x轴的对称点E<0,-3>,连接AE交x轴于点P.设AE解析式为y=kx+b,则错误!解得错误!∴y AE=7x-3.∵当y=0时,x=错误!,∴点P的坐标为<错误!,0>.16.<1>∵A<1,0>,B<3,0>,∴设抛物线解析式为y=a<x-1><x-3>.∵抛物线过<0,-3>,∴-3=a<-1>×<-3>.解得a=-1.∴y=-<x-1><x-3>=-x2+4x-3.∵y=-x2+4x-3=-<x-2>2+1,∴顶点坐标为<2,1>.<2>答案不唯一,如:先向左平移2个单位,再向下平移1个单位,得到的抛物线的解析式为y=-x2,平移后抛物线的顶点为<0,0>落在直线y=-x上.综合题17.<1>当k=0时,y=-<x-1><x+3>,所画函数图象图略.<2>①三个图象都过点<1,0>和点<-1,4>;②图象总交x轴于点<1,0>;③k取0和2时的函数图象关于点<0,2>中心对称;④函数y=<x-1>[<k-1>x+<x-3>]的图象都经过点<1,0>和点<-1,4>;等等.<其他正确结论也行><3>将函数y2=<x-1>2的图象向左平移4个单位,再向下平移2个单位,得到函数y3=<x+3>2-2,∴当x=-3时,函数y3取最小值,等于-2.。
小专题(四) 二次函数图象信息题归类

小专题(四) 二次函数图象信息题归类小专题(四)二次函数图象信息题归类抛物线y=ax2+bx+c的图象与字母系数a,b,c 之间的关系:(1)当a>0时,开口向上;当a<0时,开口向下.(2)若对称轴在y轴的左侧,则a,b同号;若对称轴在y轴的右侧,则a,b异号.(3)若抛物线与y轴的正半轴相交,则c>0;若抛物线与y轴的负半轴相交,则c<0;若抛物线经过原点,则c=0.(4)当x=1时,y=ax2+bx+c=a+b+c;当x=-1时,y=ax2+bx+c=a-b+c;当x=2时,y=ax2+bx+c=4a+2b+c;当x=-2时,y=ax2+bx+c=4a-2b+c,…(5)当对称轴x=1时,2a+b=0;当对称轴x=-1时,2a-b=0;判断2a+b大于或者等于0,看对称轴与1的大小关系;判断2a-b大于或者等于0,看对称轴与-1的大小关系.(6)当b2-4ac>0时,抛物线与横轴有两个交点;当b2-4ac=0时,抛物线与横轴有一个交点;当b2-4ac<0时,抛物线与横轴没有交点.A.b≥5B.b≥1或b≤-14C.b≥2D.1≤b≤25.二次函数y=ax2+bx+c的图象如图所示,则下列解析式不正确的是(C)A.a<0B.abc>0C.a+b+c>0D.b2-4ac>06.如图,二次函数y=ax2+bx+c=0(a≠0)的图象与x轴正半轴相交于A,B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:①abc>0;②9a+3b+c<0;③-1<c<0;④关于x的方.其中正确的结程ax2+bx+c=0(a≠0)有一个根为-1a论有(C)A.1个B.2个C.3个D.4个7.(恩施中考)抛物线y1=ax2+bx+c与直线y2=mx+n的图象如图所示,下列判断中:①abc<0;②a+b+c>0;③5a-c=0;④当x<12或x>6时,y 1>y 2,其中正确的个数为(C )A.1B.2C.3D.4 类型3 利用二次函数图象求二次函数解析式8.如图,一个二次函数的图象经过A ,B ,C 三点,点A的坐标是(-1,0),点C 的坐标是(0,5),且OA ∶OB=1∶4,则这个二次函数的解析式是 y=-54x 2+154x+5 . 类型4 利用二次函数图象求一元二次方程的根9.(苏州中考)已知二次函数y=x 2-3x+m (m 为常数)的图象与x 轴的一个交点为(1,0),则关于x 的一元二次方程x 2-3x+m=0的两实数根是(B )A.x 1=1,x 2=-1B.x 1=1,x 2=2C.x 1=1,x 2=0D.x 1=1,x 2=310.若二次函数y=ax2+bx+c(a<0)的图象如图所示,且关于x的方程ax2+bx+c=k有两个不相等的实根,则常数k的取值范围是(D)A.0<k<4B.-3<k<1C.k<-3或k>1D.k<4类型5利用二次函数图象解不等式11.二次函数y=x2-x-2的图象如图所示,则不等式x2-x-2<0的解集是(C)A.x<-1B.x>2C.-1<x<2D.x<-1或x>212.如图,二次函数y1=ax2+bx+c与一次函数y2=kx 的图象交于点A和原点O,点A的横坐标为-4,点A和点B关于抛物线的对称轴对称,点B的横坐标为1,则满足0<y1<y2的x的取值范围是(A)A. -4<x<-3B.-4<x<0C.-3<x<0D.-4<x<113.如图是二次函数y=-x2+2x+4的图象,使y≤1成立的x的取值范围是x≤-1或x≥3.14.如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(-1,0)及点B.(1)求二次函数与一次函数的解析式;(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围.解:(1)二次函数的解析式为y=(x+2)2-1=x2+4x+3,一次函数的解析式为y=-x-1.(2)x≤-4或x≥-1.。
九年级数学上册第22章二次函数方法专题二次函数的图象与字母系数之间的关系及图象信息题习题名师公开课省
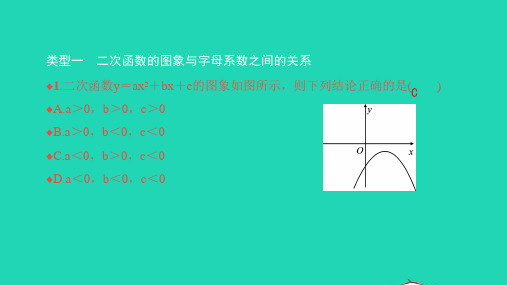
a1>a2>a3>a4
17.(课本P41习题T8改编)如图,点P,Q分别是正方形ABCD中边CD和AD的中点.动点E从点A向点B运动,到点B时停止运动;同时,动点F从点P出发,沿P→D→Q运动,点E,F的运动速度相同.设点E的运动路程为x,△AEF的面积为y,若y与x的大致函数图象如图所示,则△AEF的最大面积为________.
(0,2),且顶点在第一象限,设M=4a+2b+c,则M的取值范
围是 .
-6<M<6
类型二 根据函数性质判断函数图象
9.已知函数y=-x2+bx+c,其中b>0,c<0,此函数的图象可以是( )A. B. C. D.
了解面对逆境,远比如何接受顺境重要得多一般的伟人总是让身边的人感到渺小昨天是张退票的支票积极人格的完善是本,财富的确立是末昨晚多几分钟的准备每一发奋努力的背,必有加倍的赏赐要及时把握梦想,因为梦想一死10、一个人的梦想也许不值钱,但一个人的努力很值钱。11、在真实的生命里,每桩伟业都由信心开始,并由信心跨出第一步。
D
10.函数y=ax2+ax+a(a≠0)的图象可能是下列图象中的( )
A. B. C. D.
C
11.(2019·葫芦岛)二次函数y=ax2+bx的图象如图所示,则一次函数y=ax+b的图象大致是( )
A. B.C. D.
D
A.1个 B.2个 C.3个 D.4个
C
7.(2019·天水)二次函数y=ax2+bx+c的图象如图所示,若M=4a+2b,N=a-b,则M,N的大小关系为M________N.(填“>”“=”或“<”)
<
8.(2019·广元)如图,抛物线y=ax2+bx+c(a≠0)过点(-1,0),
小专题(四) 二次函数的图象与字母系数之间的关系

【思路点拨】 ①由对称轴与y轴的位置关系,可得出ab的符号,再 结合图象与y轴交点的位置,可得出c的符号,即可判断abc的符号;
②由图象与x轴交点的情况,可判断b2-4ac的符号; ③令x=-3,看函数值的符号,即可判断9a-3b+c与0的大小关系; ④比较两点与对称轴的距离,结合图象的开口方向,可得出结论; ⑤由对称轴位置可得a与b的等量关系,再由图象经过点(1,0),得 关于a,b,c的一个等量关系,进而转化得到a与c的等量关系,分别将b,c 用含a的式子代入5a-2b+c中,结合a的符号即可判断.
0),B(5,0),下列说法正确的是( D )
A.c<0
B.b2-4ac<0
C.a-b+c<0
D.图象的对称轴是直线x=3
3.(2019·益阳)已知二次函数y=ax2+bx+c的图象如图所示,下列结 论:①ac<0;②b-2a<0;③b2-4ac<0;④a-b+c<0.其中正确的是
(A) A.①② B.①④ C.②③ D.②④
2(m<0),下
个交点;③当x<-
1 3
,y随x的增大而增大;④二次函数图象顶点的纵坐标
大于等于6,其中正确的是(C ) A.①②③
B.①③④
C.①②④
D.②③④
6.(2019·西安三模)抛物线y=ax2+bx+c(a≠0)的图象如图所示,抛物 线经过点(-1,0),则下列说法:①abc<0;②2a-b=0;③b2>4ac;④ 3a+c=0;⑤a+b>am2+bm(m为一切实数),其中正确的有(C )
数学 九年级 下册
第二章 二次函数 小专题(四) 二次函数的图象与字母系数之间
的关系
【例】 抛物线y=ax2+bx+c的对称轴为直线x=-1,部分图象如图 所示,下列判断:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数的图象与字母系数之间的关系
抛物线y=ax2+bx+c的图象与字母系数a,b,c之间的关系:
(1)当a>0时,开口______,当a<0时,开口______;
(2)若对称轴在y轴的左边,则a,b______,若对称轴在y轴的右边,则a,b______;
(3)若抛物线与y轴的正半轴相交,则c______0,若抛物线与y轴的负半轴相交,则c______0,若抛物线经过原点,则c______0;
(4)当x=1时,y=ax2+bx+c=________;当x=-1时,y=ax2+bx+c=________;当x=2时,y=ax2+bx+c =__________;当x=-2时,y=ax2+bx+c=__________;…;
(5)当对称轴x=1时,x=-
b
2a
=______,所以-b=______,此时2a+b=______;当对称轴x=-1时,x=-
b
2a
=______,所以b=______,此时2a-b=______;判断2a+b大于或者等于0,看对称轴与______的大小关系;判断2a-b大于或者等于0,看对称轴与______的大小关系;
(6)b2-4ac>0 二次函数与横轴________交点;b2-4ac=0 二次函数与横轴________交点;b2-4ac<0 二次函数与横轴______交点.
1.(龙岩中考)若二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列选项正确的是( )
A.a>0 B.c>0
C.ac>0 D.bc<0
2.(深圳中考)二次函数y=ax2+bx+c的图象如图所示,给出以下结论:①a>0;②b>0;③c<0;④b2-4ac>0,其中所有正确结论的序号是( )
A.②④ B.①③ C.③④ D.①②③
3.(兰州中考)二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中错误的是( ) A.abc<0 B.2a+b=0
C.b2-4ac>0 D.a-b+c>0
4.(滨州中考)如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于C点,且对称轴为x =1,点B坐标为(-1,0).则下面的四个结论:①2a+b=0;②4a-2b+c<0;③ac>0;④当y<0时,x<-1或x>2.其中正确的个数是( )
A.1个 B.2个
C.3个 D.4个
5.(陕西中考)二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
A.c>-1 B.b>0
C .2a +b≠0
D .9a +c>3b
6.(恩施中考)如图是二次函数y =ax 2
+bx +c 图象的一部分,图象过点(-3,0),对称轴为直线x =-1,给出四
个结论:①b 2>4ac ;②2a+b =0;③a+b +c <0;④若点B(-52,y 1)、C(-12
,y 2)为函数图象上的两点,则y 1<y 2,其中正确的是( )
A .②④
B .①④
C .①③
D .②③
7.(达州中考)如图是二次函数y =ax 2+bx +c 的图象的一部分,对称轴是直线x =1.①b 2>4ac ;②4a-2b +c <0;
③不等式ax 2+bx +c >0的解集是x≥3.5;④若(-2,y 1),(5,y 2)是抛物线上的两点,则y 1<y 2.上述4个判断中,
正确的是( )
A .①②
B .①④
C .①③④
D .②③④
8.(潍坊中考)已知二次函数y =ax 2+bx +c +2的图象如图所示,顶点为(-1,0),下列结论:①abc<0;②b 2
-4ac =0;③a>2;④4a-2b +c >0.其中正确结论的个数是( )
A .1
B .2
C .3
D .4
9.(遵义中考)已知抛物线y =ax 2+bx 和直线y =ax +b 在同一坐标系内的图象如图,其中正确的是( )
10.(咸宁中考)如图是二次函数y =ax 2+bx +c 的图象,下列结论:①二次三项式ax 2
+bx +c 的最大值为4;②4a
+2b +c<0;③一元二次方程ax 2+bx +c =1的两根之和为-1;④使y≤3成立的x 的取值范围是x≥0.其中正确的
个数有( )
A .1个
B .2个
C .3个
D .4个
抛物线上,则4a-2b+c的值为________.
12.已知关于x的二次函数y=ax2+bx+c(a>0)的图象经过点C(0,1),且与x轴交于不同的两点A,B,点A的坐
标是(1,0).
(1)求c的值;
(2)求a的取值范围.
13.如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2).
(1)求m的值和抛物线的解析式;
(2)求不等式x2+bx+c>x+m的解集(直接写出答案);
(3)若M(a,y1),N(a+1,y2)两点都在抛物线y=x2+bx+c上,试比较y1与y2的大小.
参考答案
向上 向下 同号 异号 > < = a +b +c a -b +c 4a +2b +c 4a -2b +c 1 2a 0 -1 2a 0 1 -1 有两个 有一个 无 1.C 2.A 3.D 4.B 5.D 6.B 7.B 8.B 9.D 10.B 11.0
12.(1)c =1.
(2)由图象过C(0,1),A(1,0),得a +b +1=0,∴b =-a -1.由b 2-4ac >0,可得(-a -1)2-4a >0,即(a -1)
2>0,故a≠1.又∵a>0,∴a 的取值范围是a >0且a≠1.
13.(1)∵直线y =x +m 经过点A(1,0),∴0=1+m.∴m=-1.∵抛物线y =x 2+bx +c 经过点A(1,0),B(3,2),
∴⎩⎪⎨⎪⎧0=1+b +c ,2=9+3b +c.解得⎩⎪⎨⎪⎧b =-3,c =2.
∴抛物线的解析式为y =x 2-3x +2. (2)x>3或x<1.
(3)∵M(a,y 1),N(a +1,y 2)两点都在函数y =x 2-3x +2的图象上,∴y 1=a 2-3a +2,y 2=(a +1)2-3(a +1)+2=
a 2-a.y 2-y 1=(a 2-a)-(a 2-3a +2)=2a -2.∴当2a -2<0,即a<1时,y 1>y 2;当2a -2=0,即a =1时,y 1=y 2;当2a -2>0,即a>1时,y 1<y 2.。
