初中数学北师大版九年级下学期 第三章 3.8 圆内接正多边形E卷
83九年级下册第三章第八节圆内接正多边形课后作业
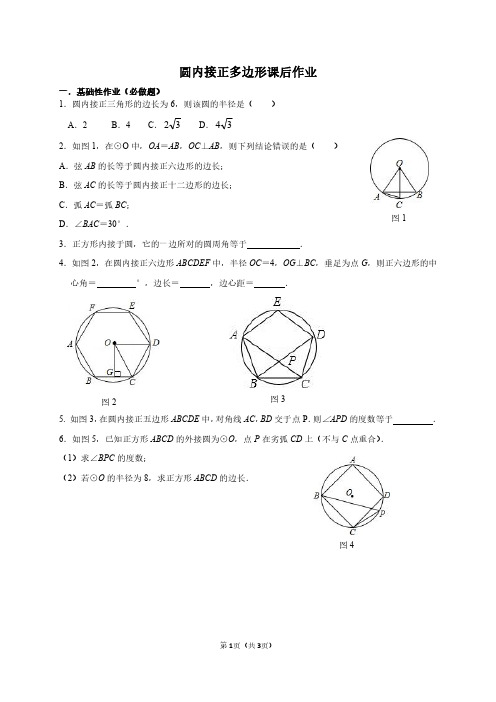
圆内接正多边形课后作业一.基础性作业(必做题)1.圆内接正三角形的边长为6,则该圆的半径是()A .2B .4C .32D .342.如图1,在⊙O 中,OA =AB ,OC ⊥AB ,则下列结论错误的是()A .弦AB 的长等于圆内接正六边形的边长;B .弦AC 的长等于圆内接正十二边形的边长;C .弧AC =弧BC ;D .∠BAC =30°.3.正方形内接于圆,它的一边所对的圆周角等于.4.如图2,在圆内接正六边形ABCDEF 中,半径OC =4,OG ⊥BC ,垂足为点G ,则正六边形的中心角=°,边长=,边心距=.5.如图3,在圆内接正五边形ABCDE 中,对角线AC ,BD 交于点P .则∠APD 的度数等于.6.如图5,已知正方形ABCD 的外接圆为⊙O ,点P 在劣弧CD 上(不与C 点重合).(1)求∠BPC 的度数;(2)若⊙O 的半径为8,求正方形ABCD 的边长.图1图2图4图3二、拓展性作业(选做题)1.如图5,请用直尺和圆规确定已知圆的圆心,并作出此圆的内接正六边形ABCDEF ;(保留作图痕迹,不写作法)2.我国魏晋时期的数学家刘徽首创“割圆术”,利用圆的内接正多边形来确定圆周率.若设⊙O 的半径为R ,圆内接正n 边形的边长、面积分别为a n ,S n ,圆内接正2n 边形边长、面积分别为a 2n ,S 2n .刘徽用以下公式求出a 2n 和S 2n .22222))21(()21(n n n a R R a a --+=,R na n 21S n 2=.如图6,若⊙O 的半径为1,则⊙O 的内接正八边形AEBFCGDH 的面积为.图5图63.【探索发现】小迪同学在学习圆的内接正多边形时,发现:如图7,若P是圆内接正三角形ABC 的外接圆的弧BC上任一点,则∠APB=60°,在PA上截取PM=PC.连接MC,可证明△MCP 是(填“等腰”“等边”或“直角”)三角形,从而得到PC=MC,再进一步证明△PBC ≌,得到PB=MA,可证得:PB+PC=PA.【拓展应用】小迪同学对以上推理进行类比研究,发现:如图8,若P是圆内接正四边形ABCD 的外接圆的弧BC上任一点,则∠APB=∠APD=°,分别过点B、D作BM⊥AP于M、DN⊥AP于N.【猜想证明】分别过点B,D作BM⊥AP于M,DN⊥AP于N.请写出PB、PD与PA之间的数量关系,并说明理由.图7图8。
北师版九下数学8 圆内接正多边形

顶点都在同一个圆上的正多边形叫做圆内接 正多边形. 这个圆叫做该正多边形的外接圆.
怎样由圆得到多边形呢?
定义:把一个圆分成 n 等分(n ≥ 3),
依次连结各分点,所得的多边形是这个圆 的内接正多边形.
正多边形有关的概念
E
D
.半径R
F中心角O 边心距r
C
A
B
例 如图,在圆内接正六边形ABCDEF中, 半径OC=4,OG⊥BC,垂足为G,求这个正六 边形的中心角、边长和边心距.
E
D
F
O
C
A
B
你能利用尺规作一个已知圆的内接正四边形
吗?你是怎么做的? D
A
O
C
B
随堂演练
1.下列说法中正确的是( C ) A.各边都相等的多边形是正多边形 B.正多边形既是轴对称图形,又是中心对称图形 C.各边都相等的圆内接多边形是正多边形 D.各角都相等的圆内接多边形是正多边形
2.如图,点 O 是正六边形的对称中心,如果用
EAOD来自GBC
解:连接 OD.
∵ 六边形 ABCDEF 为正六边形, E
∴ COD 360 60.
6
A
∴ △COD 为等边三角形.
O
∴ CD = OC = 4 .
G B
D C
在Rt△COG 中,OC = 4,
∴ OG OC2 CG2 42 22 2 3.
∴ 正六边形 ABCDEF 的中心角为60°, 边长为 4,边心距为2 3 .
利用尺规作一个已知圆的内接正六边形.
方法一:
由于正六边形的中心角为60°,因此它的边 长就是其外接圆的半径 R . 所以,在半径为 R 的 圆上,依次截取等于 R 的弦,就可以六等分圆, 进而作出圆内接正六边形.
圆内接正多边形练习北师大版九年级数学下册
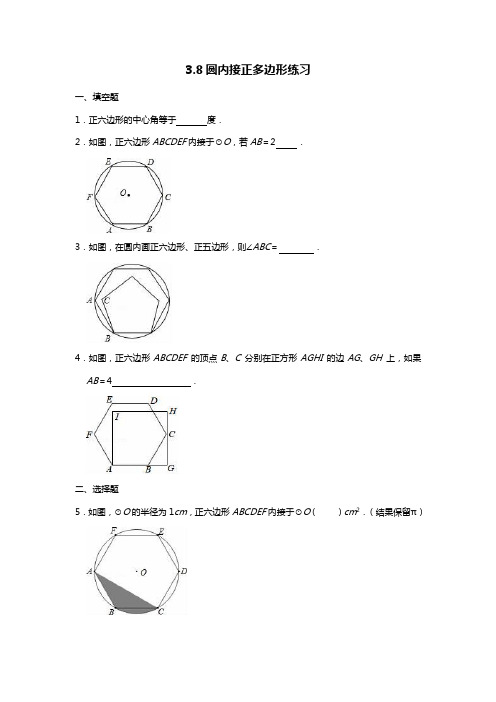
3.8圆内接正多边形练习一、填空题1.正六边形的中心角等于度.2.如图,正六边形ABCDEF内接于⊙O,若AB=2 .3.如图,在圆内画正六边形、正五边形,则∠ABC=.4.如图,正六边形ABCDEF的顶点B、C分别在正方形AGHI的边AG、GH上,如果AB=4 .二、选择题5.如图,⊙O的半径为1cm,正六边形ABCDEF内接于⊙O()cm2.(结果保留π)A.B.C.D.6.如图,正六边形ABCDEF是半径为2的圆的内接六边形,则图中阴影部分的面积是()A.B.C.D.7.已知等边三角形的内切圆半径,外接圆半径和高的比是()A.1:2:B.2:3:4 C.1::2 D.1:2:3 8.如图,正方形ABCD和正△AEF都内接于⊙O,EF与BC、CD分别相交于点G、H,则()A.B.C.D.29.蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,则△ABC是直角三角形的个数有()A.4个B.6个C.8个D.10个10.先作半径为的第一个圆的外切正六边形,接着作上述外切正六边形的外接圆,…,则按以上规律作出的第8个外切正六边形的边长为()A.B.C.D.11.如图,有一圆内接正八边形ABCDEFGH,若△ADE的面积为10()A.40 B.50 C.60 D.80 12.如图,正六边形的顶点在矩形的各条边上,若阴影部分的面积为3()A.B.6 C.9 D.12 13.如图,正六边形ABCDEF内接于⊙O,若直线PA与⊙O相切于点A()A.30°B.40°C.45°D.60°14.正方形的边长为2,则正方形外接圆的半径是()A.1 B.C.D.2 15.如图,正八边形ABCDEFGH内接于⊙O,则∠ADB的度数为()A.45°B.25°C.22.5°D.20°16.如图,正五边形ABCDE的边长为2,连接AC、AD、BE,连接DF,给出下列结论:①∠FDG=18°;③(S四边形CDEF)2=9+2;④DF2﹣DG2=7﹣2.其中结论正确的个数是()A.1 B.2 C.3 D.4三、解答题17.如图,正三角形ABC内接于⊙O,若AB=cm,求⊙O的半径.18.如图是由边长为2的六个等边三角形组成的正六边形,建立适当的直角坐标系,写出正六边形各顶点的坐标.19.如图,⊙O的周长等于8πcm,正六边形ABCDEF内接于⊙O.(1)求圆心O到AF的距离;(2)求正六边形ABCDEF的面积.20.如图正方形ABCD内接于⊙O,E为CD任意一点,连接DE、AE.(1)求∠AED的度数.(2)如图2,过点B作BF∥DE交⊙O于点F,连接AF,AF=1,AE=4,求DE的长度.21.如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,求⊙O的面积.。
3.8 圆内接正多边形课后练习2020-2021学年 北师大版九年级下册数学

第三章圆8.圆内接正多边形课后练习2020-2021学年下学期九年级下册初中数学北师大版一、单选题(共12题)⌢上,则∠P的度数为()1.如图,正方形ABCD内接于⊙O,点P在ABA. 30°B. 45°C. 60°D. 90°2.⊙O是一个正n边形的外接圆,若⊙O的半径与这个正n多边形的边长相等,则n的值为()A. 3B. 4C. 5D. 63.已知圆内接正六边形的半径为2,则该内接正六边形的边心距为()A. 2B. 1C. √3D. √324.如图,五边形ABCDE是⊙O的内接正五边形,AF是⊙O的直径,则∠BDF的度数是()A. 18°B. 36°C. 54°D. 72°5.如图,四边形ABCD为⊙O的内接正四边形,△AEF为⊙O的内接正三角形,若DF恰好是同圆的一个内接正n边形的一边,则n的值为()A. 8B. 10C. 12D. 156.正多边形的内切圆与外接圆的半径之比为√2,则这个正多边形为()2A. 正十二边形B. 正六边形C. 正四边形D. 正三角形7.一个圆的内接正六边形与内接正方形的边长之比为()A. 3:2B. 1:√3C. 1:√2D. √2:√38.正方形外接圆的半径为4,则其内切圆的半径为()A. 2 √2B. √2C. 1D. √229.已知正六边形ABCDEF内接于⊙O,若⊙O的直径为2,则该正六边形的周长是()A. 12B. 6√3C. 6D. 3√310.半径为a的圆的内接正六边形的边心距是()A. a2B. √2a2C. √3a2D. a11.半径为R的圆内接正三角形的面积是()A. √32R2 B. πR2 C. 3√32R2 D. 3√34R212.如图,在圆内接正六边形ABCDEF中,BF,BD分别交AC于点G,H.若该圆的半径为15cm,则线段GH 的长为()A. √5cmB. 5 √3cmC. 3 √5cmD. 10 √3cm二、填空题(共6题)13.如图,正五边形ABCDE内接于⊙O,点F在弧CD上,则∠BFE的度数为________14.如图,正方形ABCD和正六边形AEFCGH均内接于⊙O,连接HD;若线段HD恰好是⊙O 的一个内接正n边形的一条边,则n=________.15.若圆内接正方形的边心距为3,则这个圆内接正三角形的边长为________.16.数学家刘徽首创割圆术,用圆内接正多边形的面积去无限逼近圆面积并以此求出圆周率.如图,正六边形ABCDEF的边长为2,现随机向该图形内掷一枚小针,则针尖落在阴影区域的概率为________.17.如图,正六边形ABCDEF内接于⊙O,若AB=3cm,则⊙O的半径为________.18.我国古代数学家刘徽创造的“割圆术”,利用了圆内接正多边形和外切正多边形的面积或周长,无限逼近圆来近似估计圆的面积或周长,从而估算出π的范围.如图1,用圆内接正方形和外切正方形周长可得2 √2<r<4,那么利用图2中的圆内接正六边形和外切正六边形周长可进一步将π的范围缩小到________(结果保留根号)三、综合题(共4题)19.如图,已知圆O内接正六边形ABCDEF的边长为6cm,求这个正六边形的边心距n,面积S .20.如图,ABCDE是⊙O的内接正五边形.求证:AE∥BD.21.试比较图中两个几何图形的异同,请分别写出它们的两个相同点和两个不同点。
北师大版九年级数学下册 3.8 圆内接正多边形 单元测试题(无答案)

3.8 圆内接正多边形单元测试题(满分120分;时间:120分钟)真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!题号一二三总分得分一、选择题(本题共计10 小题,每题3 分,共计30分,)1. 正六边形的边心距是√3,则它的边长是()A.1B.2C.2√3D.3√32. 两个边数相同的正多边形周长的比不等于()A.边长的比B.半径的比C.边心距的比D.面积的比3. 正三角形内切圆半径与外接圆半径及高线之比为()A.1:2:3B.2:3:4C.1:√2:√3D.1:√3:24. 半径相等的圆的内接正三角形和正方形,正三角形与正方形的边长之比为()A.1:√2B.√3:√2C.3:2D.1:25. 正六边形的外接圆半径为1,则它的内切圆半径为()A.√3B.√32C.12D.16. 两圆半径之比为2:3,小圆外切正六边形与大圆内接正六边形面积之比为()A.2:3B.4:9C.16:27D.4:3√37. 下列说法错误的是()A.正多边形每个内角都相等B.正多边形都是轴对称图形C.正多边形都是中心对称图形D.正多边形的中心到各边的距离相等8. 既有外接圆,又有内切圆的四边形一定是()A.矩形B.菱形C.正方形D.等腰梯形9. 一个边长为1的正方形的边心距和中心角分别是()A.1 2;90∘B.12;45∘C.√2;90∘D.√2;45∘10. 有一个长为12cm的正六边形,若要剪一张圆形纸片完全盖住这个圆形,则这个圆形纸片的半径最小是()A.10cmB.12cmC.14cmD.16cm二、填空题(本题共计10 小题,每题3 分,共计30分,)11. 正多边形的边长为2,中心到边的距离为√3,则这个正多边形的边数为________.12. 已知正方形ABCD的边长为1,对角线AC,BD交于点O,E为AB的中点,DE与AC交于点M,CE交BD于点N,则四边形OMEN的内切圆的半径等于________.13. 周长相同的正三角形、正方形、正六边形的面积分别为S1、S2、S3,则其三者的大小关系为:________.14. 正六边形的半径为2cm,那么这个正六边形的周长为________cm.15. 圆内接正方形的边长为1,则该圆内接正三角形的边长为________.16. 正三角形与它的内切圆及外接圆的三者面积之比为________.17. 正n边形的边长与半径的夹角为75∘,那么n=________.18. 如图,在正九边形ABCDEFGHI中,若AB+AC=3,则对角线AE=________.19. 如图,正方形ABCD内接于⊙O,如果圆的半径为6,那么这个正方形的边长为________.20. 已知⊙O过正方形ABCD顶点A、B,且与CD相切,若正方形边长为2,则圆的半径为________.三、解答题(本题共计6 小题,共计60分,)21. 已知边长为1的正七边形ABCDEFG中,对角线AD,BG的长分别为a,b(a≠b),求证:(a+b)2(a−b)=ab2.22. 如图,一个正多边形的半径为√2,边心距为1,求该正多边形的中心角、边长、内角、周长和面积.23. 如图,已知⊙O是边长为2的等边三角形ABC的外接圆,求⊙O的半径.24. 如图,等边三角形ABC的外接圆⊙O的半径为R,求等边三角形ABC的边长,边心距、周长和面积.25. 如图,两个同心圆的圆心为O,正六边形ABCDEF的顶点在大圆上,六条边分别与小圆相切,大圆的半径OA、OB分别与小圆相交于点G、H,正六边形的边长为2a.(1)求AB^与GH^的弧长之差;(2)求阴影部分的面积.26. 某课题学习在探讨一团周长为4a的线圈时,发现了如下两个命题:命题1:如图①,当线圈做成正三角形ABC时,能被半径为a的圆形纸片完全盖住.命题2:如图②,当线圈做成正方形ABCD时,能被半径为a的圆形纸片完全盖住.请你继续探究下列几个问题:(1)如图③,当线圈做成正五边形ABCDE时,请说明能被半径为a的圆形纸片完全盖住;(2)如图④,当线圈做成平行四边形ABCD时,能否被半径为a的圆形纸片完全盖住请说明理由;(3)如图⑤,当线圈做成任意形状的图形时,是否还能被半径为a的圆形纸片完全盖住?若能盖住,请通过计算说明;若不能盖住,请你说明理由.。
九年级数学下册知识讲义-3圆内接正多边形(附练习及答案)-北师大版

一、考点突破1. 了解圆内接正多边形的有关概念。
2. 理解并掌握正多边形半径和边长、边心距、中心角之间的关系。
3. 会应用正多边形和圆的有关知识画正多边形。
二、重难点提示重点:圆内接正多边形的定义及相关性质。
难点:正多边形半径、中心角、弦心距、边长之间的关系。
考点精讲 1. 圆内接正多边形的有关概念 ① 顶点都在同一个圆上的正多边形叫做圆内接正多边形。
这个圆叫做该正多边形的外接圆。
② 正多边形的中心、半径、边心距、中心角正多边形的外接圆的圆心叫做这个正多边形的中心;正多边形的外接圆的半径叫做这个正多边形的半径;正多边形的中心到正多边形一边的距离叫做这个正多边形的边心距;正多边形的每一边所对的外接圆的圆心角叫做这个正多边形的中心角。
如图:五边形ABCDE 是⊙O 的内接正五边形, 圆心O 叫做这个正五边形的中心; OA 是这个正五边形的半径; OM 是这个正五边形的边心距。
AOB 叫做这个正五边形的中心角。
A E【要点诠释】① 只要把一个圆分成相等的一些弧,就可以做出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆。
② 求正n 边形中心角的常用方法:正n 边形有n 条边,每条边对应一个中心角,所以正n 边形的中心角为。
(正n 边形中心角度数与正n 边形的一个外角相等)2. 特殊的圆内接正多边形的半径、弦心距、边长之间的关系① 正三角形——在中进行:;② 正四边形——在中进行,;③ 正六边形——在中进行,。
D E OC OB O D B A CA A B【规律总结】正多边形的外接圆半径R 与边长a 、边心距r 之间的关系:R 2=r 2+(a )2,连接正n 边形的半径,弦心距,把正n 边形的有关计算转化为直角三角形中的问题。
典例精讲例题1 (义乌市)一张圆心角为45°的扇形纸板和圆形纸板按如下图所示方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是( )A. 5:4B. 5:2C.:2D.:思路分析:先画出图形,分别求出扇形和圆的半径,再根据面积公式求出面积,最后求出比值即可。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 1 页 共 5 页
初中数学北师大版九年级下学期 第三章 3.8 圆内接正多边形E卷
姓名:________ 班级:________ 成绩:________
一、 单选题 (共4题;共8分)
1. (2分) (2016九上·达拉特旗期末) 已知正方形的边长为a,其内切圆的半径为r,
外接圆的半径为R,则r:R:a=( )
A . 1:1:
B . 1: :2
C . 1: :1
D . :2:4
2. (2分) 圆内接正六边形的周长为24,则该圆的内接正三角形的周长为( )
A . 12
B . 6
C . 12
D . 6
3. (2分) (2019·天山模拟) 如图,已知边长为2的正三角形ABC顶点A的坐标为
(0,6),BC的中点D在y轴上,且在点A下方,点E是边长为2、中心在原点的正六边形
的一个顶点,把这个正六边形绕中心旋转一周,在此过程中DE的最小值为( )
第 2 页 共 5 页
A . 3
B . 4﹣
C . 4
D . 6﹣2
4. (2分) 如图,正六边形ABCDEF,连结AC,求作点P,Q使它们成为AC的三等分
点,下列作法正确的是( )
①取AB,BC的中点M,N,再分别以A,C为圆心,以AM,CN的长为半径画弧,交AC
于点P,Q
②连结 BF,BD,分别交AC于点P,Q
③连结BE交AC于点H,分别取AH,CH的中点P,Q
④作AB,BC的中垂线分别交AC于点P,Q.
A . ①②
B . ②③
第 3 页 共 5 页
C . ②④
D . ③④
二、 填空题 (共4题;共4分)
5. (1分) (2019·青岛) 如图,五边形 ABCDE 是⊙O 的内接正五边形, AF 是⊙O 的
直径,则∠ BDF 的度数是________°
6. (1分) (2019九上·台安月考) 已知正六边形的外接圆的半径是 ,则正六边形
的周长是________.
7. (1分) (2019九下·温州竞赛) 如图,正六边形ABCDEF的边长为1,以点A为圆
心,AB的长为半径,作扇形ABF,则图中阴影部分的面积为 ________(结果保留根号和 ).
8. (1分) (2018·余姚模拟) 如图,在平面直角坐标系中,正六边形ABCDEF的对称
中心与原点O重合, 点A在x轴上,点B在反比例函数 位于第一象限的图象上,
则正六边形ABCDEF的边长为________;
第 4 页 共 5 页
三、 解答题 (共1题;共5分)
9. (5分) 如图,已知正五边形ABCDE,AF∥CD交DB的延长线于点F,交DE的延长
线于点G.
(1)写出图中所有的等腰三角形;
(2)求证:∠G=2∠F.
四、 作图题 (共1题;共5分)
10. (5分) (2016·西安模拟) 用尺规作圆内接正三角形.
第 5 页 共 5 页
参考答案
一、 单选题 (共4题;共8分)
1、答案:略
2、答案:略
3、答案:略
4、答案:略
二、 填空题 (共4题;共4分)
5、答案:略
6、答案:略
7、答案:略
8、答案:略
三、 解答题 (共1题;共5分)
9、答案:略
四、 作图题 (共1题;共5分)
10、答案:略
