数值分析第五版欧拉法与改进欧拉法对比
常微分方程数值解法-欧拉法、改进欧拉法与四阶龙格库塔法常微分方程数值解法

y( xn1)
y( xn
Байду номын сангаас
h)
y(xn )
hy'( xn )
h2 2!
y''( )
进一步: 令
h2 y( xn ) hy'( xn ) 2! y''( xn )
常微分方 yn1 y( xn1 ) , yn y( xn )
程数值解
法-欧拉法 yn1 yn hf ( xn , yn ) h2
、改进欧 y( xn1 ) yn1
2
max y''( x)
a xb
拉法和四
三、Euler方法
已 知 初 值 问 题 的 一 般 形式 为:
dy
dx
f (x, y)
a xb
(1)
y( x0 ) y0
常微分方 用差商近似导数 程数值解 问题转化为
yn1 yn dy
h
dx
法-欧拉法 yn1 yn hf ( xn , yn )
法-欧 y(拉0) 法1
、改进欧
拉法和四
四、几何意义
由 x0 , y0 出发取解曲线 y yx 的切线(存在!),则斜率
dy
f x0, y0
dx x y
,
0
0
常微分方 由于 f x0, y0 及 x0, y0 已知,必有切线方程。
由点斜式写出切程线方数程:值解
法、-改欧进拉欧法 ddxy y y0 x x0
常微分方 程数值解 能用解析方法求出精确解的微分方程为数不多,
而且有的方程即使有解析解,也可能由于解的表达
法-欧拉法 式非常复杂而不易计算,因此有必要研究微分方程
Euler法与改进Euler法知识讲解

yn1 yn dy h dx
常用方法
(2) 用数值积分近似积分
dy xn1
xn1
dx f ( x, y)dx (n 0,1, )
xn dx
xn
即
y( xn1) y( xn )
xn1 f ( x, y( x))dx
xn
进一步: 令 yn1 y( xn1) , yn y( xn )
xn x0 nh, n 0,1,2 .
二、建立数值解法的常用方法
建立微分方程数值解法,首先要将微分方程离散化.
一般采用以下几种方法: (1) 用差商近似导数
dy
y xn1 yxn
xn1 xn
f xn , y(xn )
dx x y , n n
进一步 : 令 yn1 y(xn1) , yn y(xn )
y0 ( x x0 ) f ( x0 , y0 )
dx x y , 0 0
几何意义
等步长为h,则 x1 x0 h,可由切线算出y1 : y1 y0 hf(x0 , y0)
逐步计算出y
y( x)
在
xn
点
1
的
值
:
yn1 yn hf(xn , yn) n 0,1,2,
注意:这是“折线法”而非“切线法” y 除第一个点是曲线切线外,其他点不是!
能用解析方法求出精确解的微分方程为数不多, 而且有的方程即使有解析解,也可能由于解的表达 式非常复杂而不易计算,因此有必要研究微分方程 的数值解法
常微分方程数值解法
重点 研究一阶常微分方程的初值问题的数值解
其一般形式为:
dy
dx
f (x, y)
y( x0 ) y0
a xb
数值分析笔记

2
βk +1 ( x=)
(x
−
)
xk +1
Hale Waihona Puke x − xk xk +1 − xk
2
插值多项式: H3 (x) = ykαk (x) + yk+1αk+1(x) + mk βk (x) + mk+1βk+1(x)
3、三次样条
三、数值积分
∫ 1、梯形公式: I ( f ) = b f (x)dx ≈ b − a [ f (a) + f (b)] 代数精确度为 1
xi−1)(x − xi+1)(x − xn ) xi−1)(xi − xi+1)(xi − xn )
ωn+1(x) =(x − x0 )(x − x1)(x − xn )
li
(x)
=
(x
ωn +1 ( x) − xi )ωn′+1(x)
4)插值余项与误差估计
插值余项: Rn (x=)
f (x) − Ln (x=)
b
− ε
a
−1
计算器:
log2
x
=
ln ln
x 2
方程 f (x) = 0 改为等价形式 x = g(x) ,若 x* = g(x*) ,称 x* 为 g(x) 的一个不动点,
此时 x* 也是 f (x) = 0 的一个根。 ⇒ xk+1 = g(xk ) , g(x) 为迭代函数。
全局收敛:从任何初始值出发都收敛
k
=0,1,
2,
(k
表示迭代次数)
2、判断迭代法收敛:
①迭代阵
常微分方程的数值解法(欧拉法、改进欧拉法、泰勒方法和龙格库塔法)
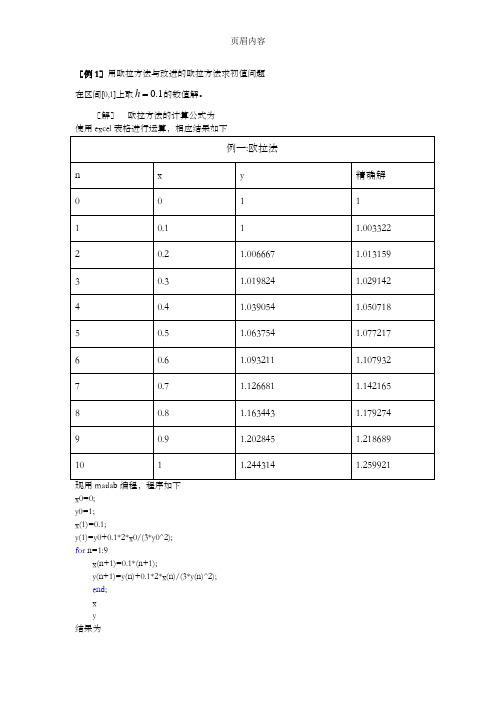
[例1]用欧拉方法与改进的欧拉方法求初值问题h 的数值解。
在区间[0,1]上取0.1[解]欧拉方法的计算公式为x0=0;y0=1;x(1)=0.1;y(1)=y0+0.1*2*x0/(3*y0^2);for n=1:9x(n+1)=0.1*(n+1);y(n+1)=y(n)+0.1*2*x(n)/(3*y(n)^2);end;xy结果为x =Columns 1 through 80.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Columns 9 through 100.9000 1.0000y =Columns 1 through 81.0000 1.0067 1.0198 1.0391 1.0638 1.0932 1.1267 1.1634 Columns 9 through 101.2028 1.2443改进的欧拉方法其计算公式为本题的精确解为()y x=x0=0;y0=1;ya(1)=y0+0.1*2*x0/(3*y0^2);y(1)=y0+0.05*(2*x0/(3*y0^2)+2*x0/(3*ya^2));for n=1:9x(n+1)=0.1*(n+1);ya(n+1)=ya(n)+0.1*2*x(n)/(3*ya(n)^2);y(n+1)=y(n)+0.05*(2*x(n)/(3*y(n)^2)+2*x(n+1)/(3*ya(n+1)^2));end;xy结果为x =Columns 1 through 80.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Columns 9 through 100.9000 1.0000y =Columns 1 through 81.0000 1.0099 1.0261 1.0479 1.0748 1.1059 1.1407 1.1783 Columns 9 through 101.2183 1.2600[例2]用泰勒方法解x=0.1, 0.2, …, 1.0处的数值解,并与精确解进行比较。
数值分析第五版_李庆扬

数值分析第五版_李庆扬数值分析第五版_李庆扬一、课程基本信息课程中文名称:数值分析课程英文名称:Numerical Analysis课程类别:专业基础课开课学期:秋适用专业:信息与计算科学;应用数学总学时:86学时(其中理论课56学时,上机实习30学时)总学分:5(理论课3学分;上机实习2学分)预修课程(编号):数学分析,高等代数,常微分方程课程简介:本课程是大学本科信息与计算科学和应用数学专业的一门基础课,也是工科研究生的必修课。
本课程的主要内容是研究各种数学问题的数值计算方法的设计、计算误差分析以及有关理论和具体实现的一门数学课程。
是应用数学的重要分支之一。
建议教材:《计算方法》(二版)(邓建中、刘之行),西安,西安交通大学出版社,2001 参考书:[1]数值分析学习指导,关治编,出版社:清华大学出版社,出版时间:2008年;[2]数值分析,何汉林,梅家斌,科学出版社,2007年;[3]《数值计算引论》白峰杉高等教育出版社 2005年[4]《数值分析》(第五版)李庆扬易大义等清华大学出版社2008年[5]Numerical Analysis,R.Kress,世界图书出版公司20036、数值分析学习辅导习题解析,李宏、徐长发编,华中科技大学出版社,2001年。
二、理论课程教育目标通过本课程的教学使学生能了解现代科学计算中常用的数值计算方法及其基本理论,系统掌握数值分析的基本概念和分析问题、解决问题的基本方法,为运用数值分析的理论知识并为掌握更复杂的现代计算方法打好。
三、理论教学内容与要求(含学时)第一章:计算方法的一般概念(4学时)本章教学内容:理解计算方法的意义、研究内容与方法,理解并掌握误差的概念(包括误差的来源、绝对误差、相对误差),掌握有效数字及舍入误差对计算的影响。
第二章:解线性方程组的直接法(8学时)本章教学内容:1、高斯消去法;选主元的高斯消去法;2、矩阵的LR分解;解三对角方程组的追赶法;解方程组的平方根法;矩阵的求逆;3、方程组的数;病态方程组的判断。
数值分析第5版

数值分析第5版简介数值分析是研究利用计算机进行数值计算的一门学科。
它包括了近似计算、数值解法、误差分析等内容,广泛应用于科学计算、工程计算以及其他领域。
《数值分析第5版》是数值分析领域的经典教材,由Richard L. Burden和J. Douglas Faires共同撰写。
内容概述本教材共分为12个章节,从基础概念开始,逐步介绍各种数值计算方法和技术。
以下是每个章节的简要介绍。
第1章:导论本章介绍了数值分析的基本概念和应用领域。
阐述了数值计算的重要性,并介绍了课程所涉及的主要内容和学习方法。
第2章:误差分析本章讲解了数值计算中的误差类型和误差分析方法。
包括绝对误差和相对误差的定义与计算、舍入误差、截断误差等。
第3章:插值与多项式逼近本章介绍了数值计算中的插值和多项式逼近方法。
包括拉格朗日插值、牛顿插值、三次样条插值等。
讲解了这些方法的原理和实现过程。
第4章:数值积分与数值微分本章讲解了数值计算中的数值积分和数值微分方法。
包括梯形法则、辛普森法则、数值微分的定义和计算过程。
第5章:非线性方程的数值解本章介绍了求解非线性方程的数值解法。
包括二分法、牛顿法、割线法等。
讲解了这些方法的原理和应用。
第6章:线性代数方程组的数值解法本章讲解了求解线性代数方程组的数值解法。
包括高斯消元法、LU分解法、迭代法等。
详细讲解了这些方法的原理和计算过程。
第7章:矩阵特征值问题本章介绍了求解矩阵特征值问题的数值解法。
包括幂法、反幂法、QR方法等。
讲解了这些方法的原理和实现过程。
第8章:常微分方程的数值解本章介绍了求解常微分方程的数值解法。
包括欧拉法、龙格-库塔法、多步法等。
讲解了这些方法的原理和应用。
第9章:偏微分方程的数值解本章讲解了求解偏微分方程的数值解法。
包括有限差分法、有限元法等。
详细讲解了这些方法的原理和实现过程。
第10章:函数逼近与数据拟合本章介绍了函数逼近和数据拟合的方法。
包括最小二乘法、曲线拟合等。
Euler法与改进Euler法PPT课件

yp
yn
0.1( yn
2 xn yn
)
yq
yn
0.1( y p
2( xn 0.1) ) yp
yn1
1 2
(
yp
yq )
七、 龙格 - 库塔法 /* Runge-Kutta Method */ 建立高精度的单步递推格式。
单步递推法的基本思想是从 ( xi , yi ) 点出发,以某一 斜率沿直线达到 ( xi+1 , yi+1 ) 点。欧拉法及其各种变
一、引 言
许多实际问题的数学模型是微分方程或微分方 程的定解问题,如物体运动,电路震荡,化学反映及 生物群体的变化等.
能用解析方法求出精确解的微分方程为数不多, 而且有的方程即使有解析解,也可能由于解的表达 式非常复杂而不易计算,因此有必要研究微分方程 的数值解法
常微分方程数值解法
重点 研究一阶常微分方程的初值问题的数值解
y(x) 在 xn 处展开:
y(xn
h)
y(xn ) hy(xn )
h2 2
y(xn )
取一次Taylor多项式近似函数,得
y(xn1) y(xn h)
y(xn ) hy(xn )
h2 2
y( )
y(xn )
hf
(xn ,
y(xn ))
1 2
h2
y( )
yn
hf
(xn ,
yn )
形所能达到的最高精度为2阶。
考察改进的欧拉法,可以将其改写为:
斜率
yi 1
yi
h
1 2
K1
1 2
K
2
一定取K1 K2 的平均值吗?
K1 f ( xi , yi )
欧拉法的若干基本概念

高阶偏微分方程的求解
总结词
对于高阶偏微分方程,欧拉法可以通过迭代的方式逐 步逼近解,但可能收敛速度较慢且精度较低。
详细描述
对于高阶偏微分方程,如 (u_{tt} = f(x, y, u, u_x, u_y, u_z, u_{xx}, u_{xy}, u_{xz}, u_{yy}, u_{yz}, u_{zz})),可 以通过泰勒级数展开等方式将其转化为多个一阶偏微分 方程,然后对每个一阶偏微分方程应用欧拉法进行求解。 但需要注意的是,由于欧拉法的精度和收敛速度限制, 对于高阶偏微分方程,可能需要采用其他数值方法如有 限元法、谱方法等来提高精度和收敛速度。
欧拉法的应用领域
物理模拟
欧拉法可用于求解物理现象的数学模 型,如流体动力学、电磁学和热传导
等。
工程设计
在工程设计中,欧拉法可用于模拟和 分析复杂系统的行为,如机械系统、
控制系统和航空航天系统等。
金融建模
欧拉法也可用于金融领域,如股票价 格模拟、期权定价和风险评估等。
02
欧拉法的基本原理
离散化思想
一阶偏微分方程的求解
总结词
欧拉法也可以用于求解一阶偏微分方程,通过将偏微分方程转化为多个一维常微分方程, 然后分别用欧拉法求解。
详细描述
对于形如 (u_t = f(x, y, u, u_x, u_y, u_z)) 的一阶偏微分方程,可以通过有限差分法等 手段将其转化为多个一维常微分方程,然后对每个一维常微分方程应用欧拉法进行求解。
研究欧拉法在处理高阶微分方程 和其他复杂问题中的应用,以扩 大其应用范围。
05
欧拉法的应用实例
一维常微分方程的求解
要点一
总结词
欧拉法在求解一维常微分方程时,通过选取离散的时间点 ,将微分方程转化为差分方程,然后通过迭代求解。
