现代雷达信号检测及处理
雷达系统中的信号处理技术
雷达系统中的信号处理技术摘要本文介绍了雷达系统及雷达系统信号处理的主要内容，着重介绍与分析了雷达系统信号处理的正交采样、脉冲压缩、MTD和恒虚警检测几种现代雷达技术，雷达系统通过脉冲压缩解决解决雷达作用距离和距离分辨力之间的矛盾，通过MTD来探测动目标，通过恒虚警〔CFAR〕来实现整个系统对目标的检测。
关键词雷达系统正交采样脉冲压缩MTD 恒虚警检测1雷达系统概述雷达是Radar〔Radio Detection And Ranging〕的音译词，意为“无线电检测和测距”，即利用无线电波来检测目标并测定目标的位置，这也是雷达设备在最初阶段的功能。
雷达的任务就是测量目标的距离、方位和仰角，还包括目标的速度，以及从目标回波中获取更多有关目标的信息。
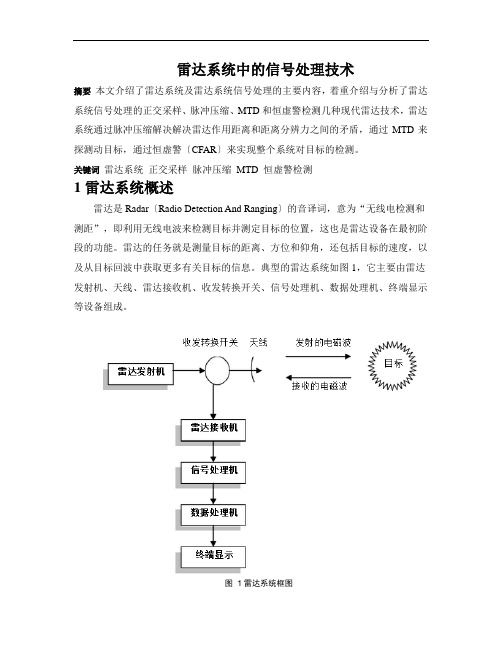
典型的雷达系统如图1，它主要由雷达发射机、天线、雷达接收机、收发转换开关、信号处理机、数据处理机、终端显示等设备组成。
图1雷达系统框图随着现代电子技术的不断发展，特别是数字信号处理技术、超大规模集成数字电路技术、电脑技术和通信技术的告诉发展，现代雷达信号处理技术正在向着算法更先进、更快速、处理容量更大和算法硬件化方向飞速发展，可以对目标回波与各种干扰、噪声的混叠信号进行有效的加工处理，最大程度低剔除无用信号，而且在一定的条件下，保证以最大发现概率发现目标和提取目标的有用信息。
雷达发射机产生符合要求的雷达波形，然后经馈线和收发开关由发射天线辐射出去，遇到目标后，电磁波一部分反射，经接收天线和收发开关由雷达接收机接收，然后对雷达回波信号依次进行信号处理、数据处理，就可以获知目标的相关信息。
雷达信号处理的流程如下：图 2 雷达信号处理流程2雷达信号处理的主要内容雷达信号处理是雷达系统的主要组成部分。
信号处理消除不需要的杂波，通过所需要的目标信号，并提取目标信息。
内容包括雷达信号处理的几个主要部分：正交采样、脉冲压缩、MTD和恒虚警检测。
正交采样是信号处理的第一步，担负着为后续处理提供高质量数据的任务。
现代雷达系统分析与设计(陈伯孝)第8章
(8.1.9)
17
代入式(8.1.7)，得到总错误概率与联合概率分布密度函数 的关系为
(8.1.10)
18
观察空间的划分应保证总错误概率Pe最小，即后面的积分 值最大。因此，满足
(8.1.11) 的所有点均划在D1范围，判为有信号；而将其它的点，即 满足
的所有点划在D0范围，判为无信号。
4
图8.1 雷达信号检测模型
5
雷达的检测过程可以用门限检测来描述，即将接收机的接 收信号经信号处理后的输出信号(本书中称为检测前输入信号) 与某个门限电平进行比较。如果检测前输入信号的包络超过了 某一预置门限，就认为有目标(信号)。雷达信号检测属于二元 检测问题，即要么有目标，要么无目标。当接收机只有噪声输 入时，为H0假设；当输入包括信号加噪声时，为H1假设，即：
0(只有噪声)，式(8.2.9)变成Rayleigh概率密度函数，
(8.2.11)
当
很大时，式(8.2.9)变成均值为A、方差为
的Gaussian概率密度函数，
(8.2.12)
30
对式(8.2.8)中的r积分得到随机变量j的pdf
其中
(8.2.13)
(8.2.14)
31
为标准正态分布函数，在大多数数学手册中可以查达接收信号进行正交双路匹配滤波、平方律检波和判 决的简化框图如图8.5所示。假设雷达接收机的输入信号由目 标回波信号s(t)和均值为零、方差为σ 2n的加性高斯白噪声 n(t)组成，且噪声与信号不相关。
23
图8.5 平方律检波器和门限判决器的简化框图
24
匹配滤波器的输出信号可以表示为
当只有噪声(A＝0)时，f(j)简化为{0，2π}区间的均匀分布
现代雷达信号处理的技术发展趋势
现代雷达信号处理的技术发展趋势1. 引言1.1 现代雷达信号处理的技术发展趋势随着科技的不断进步和发展，现代雷达信号处理技术也在不断地进行创新和改进。
雷达信号处理是指对雷达接收到的信号进行采集、处理、分析和识别的过程，其发展趋势主要体现在以下几个方面：数字信号处理技术在雷达中的应用得到了广泛的推广和应用。
随着数字化技术的发展，数字信号处理已经成为了现代雷达信号处理的重要手段，能够更加精准、高效地处理雷达信号，提高雷达系统的性能和可靠性。
基于人工智能的雷达信号处理技术逐渐兴起。
人工智能技术的快速发展使得雷达系统具有了更强的自主学习和适应能力，可以自动分析和处理雷达信号，提高了雷达系统的智能化水平。
多功能雷达系统的发展也成为了当前的一大趋势。
多功能雷达系统可以实现多种功能的集成，如搜索、跟踪、目标识别等，提高了雷达系统的综合性能和效率。
小型化、集成化和高性能化也是现代雷达信号处理技术的发展方向。
随着技术的进步，雷达系统已经实现了小型化和集成化，同时也在不断提升雷达系统的性能，以满足不同应用场景的需求。
高精度、高分辨率雷达信号处理技术的研究也逐渐受到重视。
高精度、高分辨率的雷达系统可以更准确地探测和识别目标，提高了雷达系统的监测和探测能力。
现代雷达信号处理技术的发展已经进入了数字化、智能化、多功能化、小型化和高性能化的阶段。
未来的发展方向将更加趋向于人工智能技术的应用、高精度、高分辨率雷达信号处理技术的研究以及雷达系统整体性能的进一步提升。
随着技术的不断发展和完善，相信雷达信号处理技术将会在未来取得更加显著的进步和突破。
2. 正文2.1 数字信号处理技术在雷达中的应用数字信号处理技术在雷达中的应用是现代雷达信号处理领域的重要发展趋势之一。
随着数字技术的飞速发展，传统的模拟信号处理逐渐被数字信号处理所取代。
数字信号处理技术在雷达中的应用主要体现在以下几个方面：数字信号处理技术可以实现雷达系统的数字化。
传统的雷达系统通常采用模拟信号处理方式，存在信号失真、干扰难以抑制等问题。
雷达信号处理中的算法研究
雷达信号处理中的算法研究
雷达是一种能够通过发射电磁波并接收其反射信号来探测目标的装置。
现代雷达系统不仅可以实现目标探测，还可以实现地形测绘，目标辨识，雷达干扰等多种功能。
在实际使用中，雷达信号会受到众多因素影响，如天气条件，目标状态等等，这就需要对雷达信号进行处理提高其质量。
雷达信号处理的几种算法
目前，常见的雷达信号处理算法主要包括：滤波、谱分析、匹配滤波等。
滤波：滤波是一种对信号进行降噪的方法，与此同时，滤波也可以处理由噪声引起的抖动等现象。
可以通过滤波器去除掉某些频率范围（低通滤波）或某些特定频率（带阻滤波）的信号。
谱分析：在雷达信号处理中，利用频谱分析可以完成从复杂的多普勒信号中提取目标的距离、速度、加速度等信息。
而频谱分析常用的方法则有快速傅里叶变换（FFT）和傅里叶积分变换（FTT）。
匹配滤波：匹配滤波是一种基于信号统计特征的算法，可以去除掉其他信号，提高对目标信号的识别。
雷达信号处理的应用
基于雷达信号处理的技术，可以实现一些实用的应用：
目标跟踪：雷达信号处理可以检测目标状态，识别目标信号并实现目标跟踪。
智能交通：通过雷达信号处理，可以测量速度和距离，用于监控交通状态，改变交通灯时间，提高交通效率。
军事用途：雷达信号处理可用于实现空中目标探测、火器控制等任务。
总结
雷达信号处理算法对于基于雷达技术的应用程序非常关键，有利于提高信号质量，提高目标探测的精度和效率。
随着技术的不断发展，信号处理算法将继续优化，为各种雷达类应用提供更完善的解决方案。
雷达信号与数据处理整理多媒体
雷达信号与数据处理整理多媒体雷达信号与数据处理是雷达系统中非常重要的一环。
雷达系统通过发射电磁波并接收回波来探测目标的位置和特征。
这些回波信号经过一系列的处理和整理才能被有效地利用。
雷达信号的处理涉及到一系列的步骤，其中最关键的就是波形处理。
波形处理通常包括目标检测、参数估计和目标识别等步骤。
目标检测通过比较接收到的信号强度和背景噪声的水平来确定是否存在目标。
参数估计则通过分析回波信号的特征来估计目标的距离、速度、方位角等参数。
目标识别则是根据目标的一些特征来对其进行分类和识别。
在波形处理之后，还需要对信号进行成像处理。
雷达信号经过成像处理可以获得目标的空间分布图像，从而更直观地观测目标。
成像处理通常包括距离像、速度像和方位角像等。
距离像用来表示目标与雷达的距离关系，速度像用来表示目标的运动状态，方位角像用来表示目标的方向。
除了信号处理外，雷达数据的整理也是非常重要的一步。
雷达系统通常会产生大量的数据，这些数据包含了丰富的信息，但同时也会存在大量的冗余和噪声。
数据整理主要包括数据去噪、数据压缩和数据融合等步骤。
数据去噪通过消除噪声信号来提高数据质量。
数据压缩则是将数据进行编码压缩，以减少数据量和传输带宽。
数据融合则是将多个雷达的数据进行融合，以提高目标探测和跟踪的精度。
整理后的数据可以被用于目标检测、目标跟踪和目标识别等应用。
在目标检测中，可以通过分析数据来确定目标是否存在，并给出目标的位置和特征等信息。
在目标跟踪中，可以通过分析数据的变化趋势来预测目标的位置和运动轨迹。
在目标识别中，可以通过分析数据的特征来对目标进行分类和识别。
综上所述，雷达信号与数据处理是雷达系统中非常重要的一环。
它们通过一系列的处理和整理步骤，将原始的雷达信号和数据转化为可用于目标探测、跟踪和识别的信息。
这些处理和整理步骤的优化和改进对于提高雷达系统性能和应用效果具有重要意义。
雷达信号与数据处理在现代雷达系统中起着至关重要的作用。
雷达探测系统的信号处理与故障诊断
雷达探测系统的信号处理与故障诊断雷达是一种基于电磁波的远程探测与测距装置，广泛应用于军事、航空、天文学等领域。
雷达系统的核心是信号处理，它负责接收、分析和处理从目标反射回来的信号，以实现目标的检测、跟踪和识别。
然而，在雷达系统的长期使用过程中，故障也是不可避免的。
这篇文章将探讨雷达探测系统的信号处理与故障诊断的重要性以及一些常见故障的诊断方法。
在雷达系统中，信号处理负责对接收到的回波信号进行处理和解析，提取目标的信息。
这包括对信号进行滤波、放大、解调和解算等一系列处理步骤。
信号处理的质量直接影响到雷达的性能和精度。
一般来说，信号处理应具备以下几个方面的要求。
首先，信号处理应具备高灵敏度和低噪声特性。
雷达系统的灵敏度决定了系统对小目标的检测能力，而噪声则会对目标信号的提取造成干扰，影响测距和测速的准确性。
因此，信号处理中的滤波和放大环节至关重要，能够有效提升信号与噪声的比值，从而增强系统的灵敏度。
其次，信号处理应具备高动态范围和抗干扰性。
在雷达工作中，目标的距离、速度和方位可能会因目标的变化而发生突变。
为了适应这种变化，信号处理需要具备较大的动态范围，能够有效地处理强信号和弱信号。
同时，雷达系统工作环境中通常存在各种干扰源，如天线旁瓷砖或飞行器机身的多路径反射，这些噪声会模糊目标信号的特征。
因此，信号处理需要具备抗干扰的能力，能够有效抑制噪声，提高目标信号的清晰度。
此外，信号处理还应具备高实时性和较低的功耗。
雷达系统通常需要实时处理海量的数据，并能够在极短的时间内提供准确的结果。
因此，信号处理的算法和硬件设计应尽量简洁高效，以实现低延迟和高速度的实时处理。
另外，随着节能环保意识的增强，雷达系统的功耗也应尽量降低，以减少能源消耗和环境污染。
当雷达系统出现故障时，快速准确地诊断问题并及时修复，对于恢复系统的正常工作至关重要。
常见的雷达系统故障包括信号处理器出现故障、天线驱动电路故障等。
针对这些故障，可以采用以下几种常见的故障诊断方法。
现代雷达信号处理
基于人工智能的雷达信号处理技术利用机器学习、深度学习等算法对雷达回波数据进行处理，自动提取目标特征， 实现高精度的目标检测、跟踪和识别。通过训练神经网络模型，可以快速处理大量数据，提高雷达系统的实时性 能。
基于量子计算的雷达信号处理技术
总结词
利用量子计算的优势对雷达信号进行优化处理，提高数据处理速度和计算精度。
雷达目标识别技术是利用雷达回波信息对目标进行分类和 识别的技术，是现代雷达系统的重要应用之一。
通过提取和分析目标的形状、尺寸、速度等特征信息，结 合人工智能和模式识别算法，实现对目标的自动分类和识 别，提高雷达的应用价值。
03 雷达信号处理的应用
军事应用
01
02
03
目标检测与跟踪
雷达信号处理在军事领域 中广泛应用于目标检测与 跟踪，如导弹制导、火控 系统等。
感谢您的观看
基于生物启发的雷达信号处理技术从生物感知机制中获得 灵感，创新雷达信号处理方法。例如，仿生雷达系统借鉴 昆虫的复眼结构和感知机制，通过阵列天线和信号处理算 法实现高分辨率和高灵敏度的目标感知。此外，基于生物 神经网络的雷达信号处理方法也正在研究和发展中，以提 高雷达系统的感知能力和适应性。
THANKS FOR WATCHING
解决方案
采用高速数字信号处理器、并行处理技术和高效的算法设 计，以提高雷达的数据处理速度和动态范围。
高精度测距和测速问题
总结词
高精度测距和测速是现代雷达信号处理的另一个关键问题。
详细描述
随着雷达应用范围的扩大，对测距和测速精度的要求也越来越高。如何提高测距和测速的精度是现代雷达信号处理面 临的挑战之一。
现代雷达信号处理
目录
• 雷达信号处理概述 • 现代雷达信号处理技术 • 雷达信号处理的应用 • 现代雷达信号处理面临的挑战和解决方案 • 新一代雷达信号处理技术展望
现代先进的雷达技术原理
现代先进的雷达技术原理
现代先进的雷达技术原理主要包括以下几个方面：
1. 雷达波束形成：利用天线阵列（如相控阵）或天线微电机系统，通过控制单个天线元件的相位和幅度，形成一个聚焦的波束，以实现精确瞄准和定位。
这可以提高雷达的目标检测性能，减少对干扰源的敏感性。
2. 多普勒频移处理：利用多普勒效应，通过测量目标反射回来的雷达波的频率变化，可以获取目标的速度信息。
这样的处理可以区分静止目标和运动目标，并进一步提高雷达的目标检测和跟踪能力。
3. 雷达信号处理：利用数字信号处理技术，对雷达返回的信号进行处理和分析。
这可以提取目标的特征信息，如目标的速度、距离、方位角和俯仰角等，以用于目标识别和跟踪。
4. 雷达脉冲压缩：通过发射短脉冲，并使用压缩滤波器对反射回来的信号进行处理，可以提高雷达的距离分辨率。
这意味着雷达可以在非常短的时间内区分非常接近的目标。
5. 基于目标特性的信号处理：利用现代信号处理技术，如极化处理和频谱分析，可以提取目标的形状、材料特性和运动模式等信息。
这有助于进一步识别目标并提高目标检测和跟踪能力。
6. 雷达网络和数据融合：现代雷达系统通常具有网络化和多源数据融合的能力，可以与其他雷达系统和传感器进行通信和数据交换。
这可以提高雷达探测和跟踪的准确性和鲁棒性，以适应更复杂的作战环境。
总体而言，现代先进的雷达技术依靠先进的信号处理、天线技术和网络化能力，实现了更高的目标检测和跟踪性能，提高了作战能力和对威胁的感知能力。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
现代雷达信号检测报告现代雷达信号匹配滤波器报告一 报告的目的1.学习匹配滤波器原理并加深理解2.初步掌握匹配滤波器的实现方法3.不同信噪比情况下实现匹配滤波器检测二 报告的原理匹配滤波器是白噪声下对已知信号的最优线性处理器，下面从实信号的角度来说明匹配滤波器的形式。
一个观测信号)(t r 是信号与干扰之和，或是单纯的干扰)(t n ，即⎩⎨⎧+=)()()()(0t n t n t u a t r (1)匹配滤波器是白噪声下对已知信号的最优线性处理器，对线性处理采用最大信噪比准则。
以)(t h 代表线性系统的脉冲响应，当输入为(1)所示时，根据线性系统理论，滤波器的输出为⎰∞+=-=0)()()()()(t t x d h t r t y ϕτττ (2)其中⎰∞-=00)()()(τττd h t u a t x ， ⎰∞-=0)()()(τττϕd h t n t (3)在任意时刻，输出噪声成分的平均功率正比于[]⎰⎰∞∞=⎥⎦⎤⎢⎣⎡-=020202|)(|2)()(|)(|τττττϕd h N d h t n E t E (4)另一方面，假定滤波器输出的信号成分在0t t =时刻形成了一个峰值，输出信号成分的峰值功率正比于20220)()()(⎰∞-=τττd h t u a t x (5)滤波器的输出信噪比用ρ表示，则[]⎰⎰∞∞-==20202220|)(|2)()(|)(|)(τττττϕρd h N d h t u a t E t x (6)寻求)(τh 使得ρ达到最大，可以用Schwartz 不等式的方法来求解.根据Schwartz 不等式，有⎰⎰⎰∞∞∞-≤-0202020|)(||)(|)()(τττττττd h d t u d h t u (7)且等号只在)()()(0*τττ-==t cu h h m (8)时成立。
由式(1)可知匹配滤波器的脉冲响应由待匹配的信号唯一确定，并且是该信号的共轭镜像。
在0=t t 时刻，输出信噪比SNR 达到最大。
在频域方面，设信号的频谱为，根据傅里叶变换性质可知，匹配滤波器的频率特性为(9)由式(9)可知除去复常数c 和线性相位因子之外，匹配滤波器的频率特性恰好是输入信号频谱的复共轭。
式(2)可以写出如下形式：(10)(11)匹配滤波器的幅频特性与输入信号的幅频特性一致，相频特性与信号的相位谱互补。
匹配滤波器的作用之一是：对输入信号中较强的频率成分给予较大的加权，对较弱的频率成分给予较小的加权，这显然是从具有均匀功率谱的白噪声中过滤出信号的一种最有效的加权方式；式(11)说明不管输入信号有怎样复杂的非线性相位谱，经过匹配滤波器之后，这种非线性相位都被补偿掉了，输出信号仅保留保留线性相位谱。
这意味着输出信号的各个频率分量在时刻达到同相位，同相相加形成输出信号的峰值，其他时刻做不到同相相加，输出低于峰值。
匹配滤波器的传输特性,当然还可用它的冲激响应来表示，这时有：（12）由此可见，匹配滤波器的冲激响应便是信号的镜像信号在时间上再平移。
当信号表示为复信号时，匹配滤波器的冲击响应为信号的共轭镜像在时间上平移。
三报告内容与结果3.1 线性调频（LFM）信号脉冲压缩雷达最常见的调制信号是线性调频（Linear Frequency Modulation）信号,接收时采用匹配滤波器（Matched Filter）压缩脉冲。
根据匹配滤波器原理，信号为零中频线性调频信号，其脉冲信号采用线性调频信号，其带宽B为20KHz；脉冲宽度T为10ms；采样频率fs为50KHz。
仿真结果如下：图1 LFM信号的时域波形和幅频特性3.2 无噪声时LFM脉冲的匹配滤波根据匹配滤波器原理，对匹配滤波器进行仿真，无噪声时，仿真结果如下：图2 匹配滤波器的时域输出匹配滤波器输出最大值为第601点，采样间隔=0.02ms ，信号持续时间是-5ms 到5ms ，第601点对应的时间为601*-=7ms ，即在信号结束那一时刻取得最大值。
对延迟时间的要求为，大于等于信号持续时间。
3.3 有噪声时LFM 脉冲的匹配滤波 当信噪比SNR=10dB 时，结果如下。
时间/s幅度幅度归一化/d B图3 信号时域波形 图4 匹配滤波器时域输出有噪声时，匹配滤波前时域波形受噪声影响，检测性能降低，匹配滤波后信号能量聚集，信噪比43.2dB 。
当SNR=0dB 时，结果如下。
时间/s幅度幅度归一化/d B图5 信号时域波形 图6 匹配滤波器时域输出信噪比SNR=0dB 时，匹配滤波前信号完全淹没在噪声中，检测不出信号，匹配滤波后输出信噪比33.8dB 。
3.4 现代雷达利用匹配滤波器测距设回波信号为，当回波信号通过匹配滤波器时，在时刻达到最大值，根据峰值对应的时刻求出回波信号的延时，，其中为信号持续时间，通过目标回波延时测距，目标距离。
3.4.1 雷达单目标回波仿真一个目标回波信号，无噪声，结果如下。
时间/s幅度时间/s幅度归一化/d B图7 匹配滤波输出由图7可知匹配滤波器输出峰值对应的时刻=0.022s ，则信号延时=0.002s ，对应的目标距离Rtar==300km 。
3.4.2 雷达多目标回波仿真两个目标回波信号，一个信噪比为-10dB ，一个信噪比为0dB 。
结果如图8所示。
两个峰值点对应的时间分别为=0.022s ，=0.0226s ，目标延时分别为=0.002s ，=0.0026s ，对应的目标距离分别为Rtar1=300km ，Rtar2=390km 。
经过匹配滤波器后两目标分离开来，能分别测得各自的时间延时和距离，原本无法分辨的两个目标，在匹配滤波后能分辨开来。
00.0050.010.0150.020.0250.030.0350.04-70-60-50-40-30-20-10时间/s幅度归一化/d B图8 匹配滤波输出3.5 现代雷达利用匹配滤波器进行DECHIRP 参数估计三次相位函数(Cubic Phase Function —CPF) 是一种检测和估计单分量二次调频信号参数的方法。
由于其计算复杂度低，而且估计精度在信噪比较高时接近Cramer-Rao 界，因此是一种很好的信号处理方法。
本节针对多分量LFM 信号的情况，提出了基于CPF 进行信号检测与参数估计的方法，过程如下：考虑如下单分量LFM 信号模型()()()2t t j t j be be t s βαφ+== (13)其中()t φ为信号相位，b 为幅度，α为初始频率，β为调频率。
其CPF 定义为()()()⎰+∞--+=02,ττττd et s t s u t CP ju (14)将式(13)代入式(14)可以得到()()()⎰+∞-+=022222,ττββαd e e b u t CP u j t t j (15)()u t CP ,的能量集中在直线β2=u 上，所以可通过谱峰检测获得调频率β的估计。
在估计出调频率β后，初始频率α可以通过解线性调频(dechirp)技术将原信号解调为正弦信号，通过傅里叶变换得到其估值，同时也可以得到幅度b 的估计。
图9 初始信号的时域和频域图本实验设的是两个线性调频信号的叠加，故不是规则的LFM时频图。
图10 LFM信号CPF三维分布图处出现峰值。
两个信由图10可以看出，在三维时频图中通过匹配滤波在延时号，故沿着时间轴有两个峰值。
图11 LFM信号DECHIRP图经过匹配滤波之后，进行DECHIRP操作，并进行谱峰搜索，此处再次用的匹配滤波器，它们在各自的初始频率714Hz和1330Hz处输出得到相应峰值。
四结论与讨论现代雷达匹配滤波器的输出最大信噪比已经指出，信号的能量越大输出的信噪比就会越大，所以要获得更高的信噪比只能通过加大信号能量的方式来完成，只要信号能量强于噪声功率谱密度，那么在再强的噪声背景下也是能够将信号检测出来的。
但是如果信号能量低于了噪声功率谱密度，那么信号就不容易检测了。
实验中的仿真结果也说明了这一点。
所以对于固定时刻观测而言，信号的匹配检测能力只与信号的能量有关，而与信号形式无关。
当观测时间内存在多个信号时，不同的信号形式具有不同的输出，当信号之间时差满足一定关系时可以从匹配输出上对其进行区分，不同信号形式对应的时差不同，当然这已经是分辨率的问题了。
可以知道，分辨率问题和信号的形式有着密切关系。
实际上从匹配输出的结果图上来看，一般为了检测的需要会设定一定的门限，以决定是否有信号的存在，当匹配输出具有更宽的等效时宽时，应该会具有更大的发现概率，因为对于最大信噪比时刻，发现概率都一样，但对于非最大输出信噪比的时刻，时宽越宽，对信号的检测概率就会越大。
所以从发现概率上来看，简单脉冲的匹配输出的信号检测概率会大于线性调频信号的检测概率。
这说明当从一段时间上观察时，信号形式对于信号检测还是有一定影响的。
匹配滤波器冲激函数与信号复共轭的时间翻转线性相关；当匹配滤波器的输入是匹配的信号加白噪声时，输出相应的峰值与信号的能量成线性关系。
经过匹配滤波器后信号输出信噪比最大，能从噪声中检测信号，仿真结果与理论分析相符。
利用匹配滤波器进行测距，目标回波通过匹配滤波器后，能量聚集，找出输出峰值点对应的时刻即可求出目标回波的延时，进而得到目标的距离。
线性调频信号通过匹配滤波器后，相当于对原信号进行脉冲压缩，原目标回波无法分辨的目标，匹配滤波后能分辨出原本两个目标，提高分辨力。
五附录%%==============现代雷达信号匹配滤波器报告==========%%----即在白噪声的环境下检测，当信号通过匹配滤波器后输出端信噪比最大。
%%---- Edit by sody_zhang, HIT, JAN, 2010%% LFM signalclose allclear allclc%% set parametersc=3e8;B=10e3;T=20e-3;K=B/T;fs=20e3;%% echost=-T/2:1/fs:T/2;N=length(t);s0=exp(1i*pi*K*t.^2);SNR=-10;s1=s0+sqrt(0.5*10^(-SNR/10))*(randn(1,N)+1i*randn(1,N));Rtar1=300e3;tao1=2*Rtar1/c;sr=exp(1i*pi*K*(t-tao1).^2).*(abs(t-tao1)<=T/2)+sqrt(0.5*10^(-SNR/10))*(randn(1,N)+1i*randn(1,N) );%%% 两个目标% Rtar2=390e3;% tao2=2*Rtar2/c;% sr=sr+3.16*exp(1i*pi*K*(t-tao2).^2).*(abs(t-tao2)<=T/2);%%%%% matched filter Time domainh=conj(s0);MF=conv(sr,h);%% frequency domainNfft=2*N;win=hamming(N).';S0=fftshift(fft(s0,Nfft));S1=fftshift(fft(sr,Nfft));w=-pi:pi/N:pi-pi/N;f=-fs/2:fs/Nfft:fs/2-fs/Nfft;H=conj(S0).*exp(-1i*2*pi*f*T);MF_f=H.*S1;MFoutput=ifft(MF_f);MFoutputmax=max(abs(MFoutput));MFoutput_db=20*log10(abs(MFoutput)/MFoutputmax);figure,plot(unwrap(angle(MF_f)))ylabel('相位')figure,plot(MFoutput_db)%% result% f=-fs/2:fs/Nfft:fs/2-fs/Nfft;% figure,plot(t,real(s1))% xlabel('时间/s')% ylabel('幅度')% figure,plot(f,abs(S0))% xlabel('频率/Hz')% ylabel('幅度')% figure,plot(real(h))NMF=length(MF);t_output=(0:NMF-1)/fs;MFmax=max(abs(MF));MF_db=20*log10(abs(MF)/MFmax);% figure,plot(t_output,abs(MF))% xlabel('时间/s')% ylabel('幅度')% figure,plot(t_output,MF_db)% xlabel('时间/s')% ylabel('幅度归一化/dB')%%==============匹配滤波器实验报告==========%%----即在白噪声的环境下检测，利用匹配滤波器进行DECHIRP参数估计。