§9势垒贯穿
量子力学——谐振子、势垒贯穿

量子隧道效应
量子力学中散射问题通常当作 定态问题处理
一维散射的核心问题是透射率 和反射率的计算
E
有限深方势阱
• 方势阱存在束缚 态,也存在散射态
E U0 散射态
U0
E U0
束缚态
E
U ( ) U0
势垒问题
E>0, U ( ) 0
粒子能量大于无穷远势能
没有束缚态(可以出现在无穷远)
A-振幅; 0 初始相位
量子谐振子的例子
• 电磁场量子运动可以借助于谐振子模型(量子光 学课程) • 微观粒子在平衡位置附近的微小振动可以近似当 作谐振子(统计物理部分) • U 1 2U
U ( x ) U(0)+ x x
x=0
2 x 2 U x
x 2 ....
x=0
n2
线 性 谐 振 子 位 置 概 率 密 度
x
n=11 时的概率密度分布
11
2
n 11
x
(经典力学最 1 远点)临界点
2
m x 0 E x 0
2 2
2E 2 m
经典粒子不能出现在E < U 区,量子粒子则 可以!
U( x )
基态E0
0
0
2
x
E0 U“经典禁区” ( )
d 2 2 E 2 2 2 2 2 x 0. 2 dx
无量纲化变换: x x ,
2E
得到
d 2 2 ( ) ( ) 0. 2 d
无量纲化的定态方程
d 2 2 ( ) ( ) 0. 2 d
取U(0)=0;因平衡位置 1 2U U ( x) 2 x 2
S(五章3讲)势垒贯穿

令
k2 ik3
1 2
Ⅰ
Ⅱ
Ⅲ
2 其中 k3 2 (U 0 E )
是实数
在(6)和(7)式中,把 k2换为 ik3, 得:
透射系数:
T
2 4k12 k3 2 , 2 2 2 2 2 (k1 k3 ) sh k3a 4k1 k3
反射系数:
2 2 (k12 k3 ) sh2 k3a R 2 2 2 2 (k1 k3 ) sh2 k3a 4k12k3
宾尼
罗赫尔
鲁斯卡
例1:
U(x)
U0
I 0 II
作业1: 作业2: 作业3:已知核的势能曲线如图,计算α 粒子的透射系数
1.
2.电子通过单一势垒时,透射系数一般很小,但是 在通过双势垒时,却可以出现透射系数为100%的情况,
称为共振隧穿,试研究这种情况并给出共振隧穿发生的条件
附录1:了解纳米与分子电子学
ik1a
可得透射波振幅 C 与入射波振幅 A 间的关系
4k1k 2 e C A 2 ik2 a 2 ik2 a (k1 k 2 ) e (k1 k 2 ) e
(4)
以及反射波振幅A '与入射波振幅A间的关系
2i(k k ) sin ak2 A A 2 ik2 a (k1 k 2 ) e (k1 k 2 ) e
(x a )
由左向右的透射波
因Ⅲ区无由右向左传播 的平面波,故 C 0
定系数:
由 波 函 数 的 连 续 性 条 件
I Aeik1x A eik1x III C eik1x
( x 0) (x a )
(1) (2) (3)
隧穿效应

同理得反射系数:
2 2 2 J R | A |2 ( k1 k2 ) si n2 k2a R 2 2 2 2 2 2 JI | A| ( k1 k2 ) si n2 k2a 4k1 k2
由以上二式显然有 D+R=1,说明入射粒子一部分贯穿势 垒到 x > a 的III区,另一部分则被势垒反射回来。
A
2i (k 12 k 22 ) sin k 2 a (k1 k 2 ) e
2 ik2 a
(k1 k 2 ) e
2 ik2 a
A
于是透射系数为:
2 J D | C |2 4k12 k2 D 2 2 2 2 2 JI | A| ( k1 k2 ) sin2 k2a 4k12 k2
§9 势垒贯穿
(一)引言 (二)方程求解 (三)讨论
(四入射被势垒散射的 一维运动问题。典型势垒是方势垒, 其定义如下:
V0 V ( x) 0
0 xa x 0, xa
E
I 0 V(x) V0 II a III
现在的问题是已知粒子以 能量 E 沿 x 正向入射。
透射系数 则变为:
因为
k1 k3
即势垒既宽又高,于是 :e k3a e k3a , 则 sinh 2 ( k 3a )
(e
1 2
k 3a
2 k 3a e k3a ) 1 e 4
2
2 4k12 k3 4 D 2 k3 2 2 k 3a 2 2 1 2 k 3a 2 1 k1 (k1 k3 ) 4 e 4k12 k3 [ 4 4 k3 k1 ] e
ik2 Be ik2a ik2 Be ik2a ik1Ce ik1a
第4:量子力学应用谐振子,势垒贯穿

d2 ∞ ψ −ξ 2 ∞ = 0 ψ 2 dξ
其解为: exp[± /2], 其解为:ψ∞ = exp[±ξ2/2],
dψ∞ d ±ξ 2 / 2 验证: e 验证: = dξ dξ
= ±ξe
±ξ 2 / 2
= ±ξψ∞
dψ∞ = ±ξψ∞ dξ
d2 ∞ d ψ [±ξψ∞ ] = 2 dξ dξ
dψ∞ = ± ∞ ±ξ ψ dξ
ξ2 >> ± 1
= [ξ 2 ± 1] ∞ ≈ ξ 2ψ∞ ψ
所以: exp[± /2], 所以:ψ∞ = exp[±ξ2/2], 波函数有限性条件当ξ→± 波函数有限性条件当ξ→±∞ 时,ψ=0 ξ→
ψ∞ = e
−ξ 2 / 2
d 2ψ ψ ψ 为了使方程 2 +[λ −ξ 2 ] ( x) = 0 的波函数 dξ 在无穷远处有 ∞ = e ψ
则 Schrödinger Schr dinger 方程可写为 :
h2 d 2 1 2 2 + [E − mω x ] ( x) = 0 ψ 2 2 2m dx
d2 2m 1 2 2 ψ 或: 2 + 2 [E − mω x ] ( x) = 0 h 2 dx
ψ(ξ ) = u(ξ )e
−ξ 2 / 2
式中 u = ∑ akξ k
k=0
为此考察相邻两项之比: 为此考察相邻两项之比:
2k + 1− λ 2 ak+2ξ k+2 ξ = k akξ (k + 1)(k + 2)
k→∞
→
2 2 ξ k
考察幂级数exp[ξ2}的展开式的收敛性 考察幂级数exp[ξ
势垒贯穿与应用解读

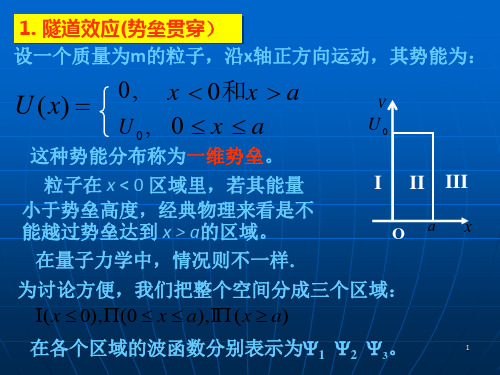
势垒贯穿与应用 势垒贯穿设一个质量为m 的粒子,沿x 轴正方向运动,其势能为: U(x)=0 x<0 和x>a U(x)=U 0 0≤x ≤a这种势能分布称为一维势垒。
粒子在 x < 0 区域里,若其能量小于势垒高度,经典物理来看是不能越过势垒达到 x > a 的区域。
在量子力学中,情况又如果呢?为讨论方便,我们把整个空间分成三个区域: 在各个区域的波函数分别表示为ψ1 ψ2 ψ3三个区间的薛定谔方程简化为:求出解的形式是)(),0(),0(a x a x x ≥I ∏≤≤∏≤I ),()(212122x E dx x d m ϕϕ=- 0≤x ),()()(22202222x E x U dxx d m ϕϕϕ=+- ax ≤≤0),()(232322x E dxx d m ϕϕ=- a x ≥222 mEk =2021)(2 E U m k -=,0)()(12212≤=+x x k dxx d ϕϕa x x k dxx d ≤≤=-0,0)()(221222ϕϕa x x k dxx d ≥=+,0)()(32232ϕϕikxikx e A Ae -'+=ψ1x ik Be 12+=ψikx Ce =ψ3O(1)E>U 0按照经典力学观点,在E>U 0情况下,粒子应畅通无阻地全部通过势垒,而不会在势垒壁上发生反射而在微观粒子的情形,却会发生反射。
(2)E<U 0从解薛定谔方程的结果来看,在势垒内部存在波函数ψ。
即在势垒内部找出粒子的概率不为零,同时,在x>a 区域也存在波函数,所以粒子还可能穿过势垒进入x>a 区域粒子在总能量E 小于势垒高度时仍能贯穿势垒的现象称为隧道效应定义粒子穿过势垒的贯穿系数是:透射波的概率密度与入射波概率密度的比值。
势垒高度U 0越低、势垒宽a 度越小,则粒子穿过势垒的概率就越大。
隧道效应是经典力学所无法解释的由于电子的隧道效应,金属中的电子并不完全局限于表面边界之内,电子密度并不在表面边界处突变为零,而是在表面以外呈指数形式衰减,衰减长度约为1nm只要将原子线度的极细探针以及被研究物质的表面作为两个电极,当样品与针尖的距离非常接近时,它们的表面电子云就可能重叠若在样品与针尖之间加一微小电压U b 电子就会穿过电极间的势垒形成隧道电流。
隧道效应及其应用
8
1981年宾尼希和罗雷尔利用电子扫描隧道显微镜 (STM)给出了晶体表面的三维图象。
钻石中的原子已被看到
利用光学中的受抑全反射理论,研制成功光子 扫描隧道显微镜(PSTM)。1989年提出成象技术。 它可用于不导电样品的观察。
9
Hale Waihona Puke 2a 2 m (U 0 E )
隧道效应是经典力学所无法解释的,因为按经典 力学计算结果,在势垒区,粒子的动能小于零,动 量是虚数。 隧道效应来源于微观粒子的波粒二象性。
由于微观粒子的波动性,微观粒子遵守“不确定关系”, 粒子的坐标x和动量P不可能同时具有确定的值,自然作为坐 标函数的势能和作为动量函数的动能当然也不能同时具有确 定的值。因此,对微观粒子而言,“总能量等于势能和动能 6 之和”这一概念不再具有明确的意义。
2.隧道显微镜STM
Scanning tunneling microscopy 由于电子的隧道效应,金属中的电子并不完全局限于 表面边界之内,电子密度并不在表面边界处突变为零, 而是在表面以外呈指数形式衰减,衰减长度越为1nm。 只要将原子线度的极细探针 以及被研究物质的表面作为 两个电极,当样品与针尖的 距离非常接近时,它们的表 面电子云就可能重叠。 若在样品与针尖之间 加一微小电压U,电子 就会穿过电极间的势 垒形成隧道电流。
2a 2 m (U 0 E )
| 3 (a) |2 | 2 (a) |2 T exp(2k1a) T 2 2 | 1 (0) | | 2 (0) | T exp(2k1 0)
e
2 k1a
e
5
结果表明:势垒高度U0越低、势垒宽a T e 度越小,则粒子穿过势垒的概率就越大。 如果a或m为宏观大小时,T 0 ,粒子实际上将不 能穿过势垒。 隧道效应是一种微观效应。 U 0 E 5eV 时,势垒的宽度约50nm 以上时,贯穿 当 系数会小六个数量级以上。隧道效应在实际上已经 没有意义了。量子概念过渡到经典了。
势垒贯穿效应的应用

势垒贯穿效应的应用
势垒贯穿效应是一种特殊的物理效应,可以广泛应用于电子学、
半导体工业、光电子学等领域。
它是指当两块不同的半导体接触时,
会形成一层势垒,阻碍电子的流动。
但当外加电压达到某一特定值时,这层势垒会被贯穿,电子开始自由流动。
这种效应可以用于制造二极管、晶体管等电子元件,也可以应用于光电探测器、太阳能电池等领域。
在半导体制造中,势垒贯穿效应可以被用来制造pn结。
pn结是
一种半导体器件,由两块接触的不同半导体组成,其中一块为p型半
导体,另一块为n型半导体。
在接触处形成的势垒使得器件只允许有
一个方向的电流通过,这种器件被广泛应用于电力电子、电子通信等
领域。
势垒贯穿效应也可以被用来制造场效应晶体管(FET),这是一
种非常重要的电子元件,被广泛应用于微电子学、电脑制造等领域。
在光电子学中,势垒贯穿效应可以被用来制造光电探测器。
这种
探测器利用势垒贯穿效应来提高光电子的感受性能,能够将光信号转
换为电信号,被广泛应用于通信、医疗、安全等领域。
最后,势垒贯穿效应也可以被用来制造太阳能电池。
太阳能电池
的工作原理就是利用势垒贯穿效应将光能转换为电能。
当光照射到太
阳能电池上时,会激发电子从势垒中跃出,形成电流。
这种技术已经
被广泛应用于环保、节能等领域,成为未来能源发展的重要方向。
势垒贯穿的量子力学解释和应用

如果是经典力学问题,由于E >0ν,粒子不能越过势垒,将在0=x 处被势垒反弹回去。
作为量子力学问题,由于粒子的波动性,结论就不一样,可以证明,粒子将有一定概率透过势垒进入a x >区域而继续前进。
由于粒子的能量是给定的,而且粒子是从-∞=x 处射来,这是属于游离态的定态,波函数可以表示成()() /,iEt ex t x -=ψψ (2)空间波函数()x ψ满足定态薛定谔方程: ()ψψψνψmk x m 22222 =E =+''- (3) 亦即⎩⎨⎧≤≤=-''><=+''a x a x x k 0,0,0,022ψβψψψ (3a)(3b) 其中,2 mE k =)(20E m -=νβ (4) (3a )式的解为ikx e ±~ψ,考虑到“粒子由左方入射”这个边界条件,应取()⎩⎨⎧><+=-)5(,)5(0,Re b a x De a x Ae x ikx ikx ikx ψA 项为入射波,R 项为反射波,D 项为透射波。
由于并无粒子从右方入射,所以a x > 区域没有ikx e -项。
(3b )式的解为())5(0,c a x Ce Be x x x <<+=-ββψ透射概率相当大,由此可见在微观领域势垒贯穿现象是容易发生的。
隧道扫描显微镜就是用原子尺度的探针针尖在不到一个纳米的高度上扫描样品时,外加一电压(2mV~2V),针尖与样品之间产生隧道效应而有电子逸出,形成隧道电流.电流强度随针尖与样品间的距离的减少而呈指数上升,当探针沿物质表面按给定高度扫描时,因样品表面原子凹凸不平,使探针与物质表面间的距离不断发生改变,从而引起隧道电流不断发生改变.将电流的这种改变图象化就显示出原子水平的凹凸形态。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3. 求解线性方程组
求解方程组得:
A B B A ik2a Be ik2a Ce ik1a 0 Be k1 A k 2 B k 2 B k1 A k Be ik2a k Be ik2a k Ce ik1a 0 2 1 2
2 2i ( k 12 k2 ) sin k2a
C
4k1k2e A 2 ik2a 2 ik2 a ( k1 k2 ) e ( k1 k2 ) e
ik1a
A
( k1 k2 ) e
2
ik2a
( k1 k2 ) e
2
ik2 a
A
4. 透射系数和反射系数
I 透射系数: 透射波几率流密度与入射波 几率流密度之比称为透射系数 D = JD/JI
ik2 Be ik2a ik2 Be ik2a ik1Ce ik1a
A B B A ik2a ik2 a ik1a Be B e Ce 0 k1 A k 2 B k 2 B k1 A k Be ik2a k Be ik2a k Ce ik1a 0 2 1 2
因为 E > 0, E > V0, 所以 k1 > 0, k2 > 0. 上面的方程可改写为:
k 2 0 1 1 1 2 2 k2 2 0 2 3 k1 3 0
解得:
x0 0 xa xa I 区 II 区 III 区
为了定量描述入射粒子透射势垒的几率和被 势垒反射的几率,定义透射系数和反射系数。
II 反射系数: 反射波几率流密度与入射波 几率流密度之比称为反射系数 R = JR/JI
下面求
其物理意义是:描述贯穿到 x > a 的 III区中的粒子在单位时间内流过垂 直 x方向的单位面积的数目与入射粒子(在 x < 0 的 I 区)在 单位时间内流过垂直于x方向单位面积的数目之比。
同理得反射系数:
2 2 2 J R | A |2 ( k1 k2 ) si n2 k2a R 2 2 2 2 2 2 JI | A| ( k1 k2 ) si n2 k2a 4k1 k2
由以上二式显然有 D+R=1,说明入射粒子一部分贯穿势 垒到 x > a 的III区,另一部分则被势垒反射回来。
(二)方程求解
上述三个区域的 Schrodinger 方程可写为:
(1)E > V0 情况
2 令:k1 2 k2 2 E 2 2 ( E V0 ) 2
2 E 0 x0 1 2 1 2 0 xa 2 2 [ E V0 ] 2 0 3 22E 3 0 xa
1 Ae ik1 x A e ik1 x ik x ik x 2 Be 2 Be 2 ik1 x Ce 3 1. 波函数连续利用波函数标准条件来定系数。来自首先, 解单值、有限条件满足。
2. 波函数导数连续
x 0:
1 (0) 2 (0) A A B B
§9 势垒贯穿
(一)引言 (二)方程求解 (三)讨论
(四)应用实例
(一)引言
势垒穿透是粒子入射被势垒散射的 一维运动问题。典型势垒是方势垒, 其定义如下:
V0 V ( x) 0
0 xa x 0, xa
E
I 0 V(x) V0 II a III
现在的问题是已知粒子以 能量 E 沿 x 正向入射。
反射波ψ= A’exp[-ik1x], 所以反射波几率流密度: 对透射波ψ= Cexp[ik1x], 所以透射波几率流密度:
JR
其中负号表示与入 射波方向相反。
J
i [ d 2 dx
k1
| A'|2
JD
k1
| C |2
d ] dx
4k1k 2e ik1a C A 2 ik2 a 2 ik2 a (k1 k 2 ) e (k1 k 2 ) e
D 和 R
几率流密度矢量:
对一维定态问题,J 与 时间无关,所以入射波 Ψ = Aexp[ik1x] ψ* = A* exp[-ik1x]
J J
i 2
[ ]
i 2
[
d dx
d dx
]
则入射波几率流密度
i k1 ik1 x d ik1 x ik1 x ik1 x d JI [ Ae Ae Ae Ae | A |2 2 dx dx
x a: 2 (a ) 3 (a ) Be ik2a Be ik2a Ce ik1a
综合 整理 记之
x 0: 1 ' (0) 2 ' (0) ik1 A ik1 A ik2 B ik2 B
x a:
2 ' (a ) 3 ' (a )
1 Ae ik1 x A e ik1 x ik x ik x 2 Be 2 Be 2 ik1 x ik1 x Ce C e 3
波函数意义
定态波函数ψ1,ψ2,ψ3 分别乘以含时因子 exp[-iEt/] 即可看出:
式中第一项是沿x正向传播的平面波,第二项是沿x负向传播的平面波。由于在 x > a 的III 区没有 反射波,所以 C'=0,于是解为:
A
2i (k 12 k 22 ) sin k 2 a (k1 k 2 ) e
2 ik2 a
(k1 k 2 ) e
2 ik2 a
A
于是透射系数为:
2 J D | C |2 4k12 k2 D 2 2 2 2 2 JI | A| ( k1 k2 ) sin2 k2a 4k12 k2
