整式乘法与乘法公式
整式的乘法和乘法公式
学之导教育中心教案 学生: 陈林茵 授课时间： 月 日 课时： 2 年级： 八年级 教师： 陆老师课 题 整式的乘法和乘法公式教案构架 ：一、 知识回顾二、 知识检验三、 知识新授四、 知识小结教案内容：一、知识回顾二、知识检验三、知识新授22222()(,,)()()()():()()()2m n m n m n mn n n n a a a a a m n a b ab a b m a b ma mb m n a b ma mb na nb a b a b a b a b a ab b +⎧⎫⋅⎪⎪=⎨⎬⎪⎪=⋅⎩⎭⨯⎧⎪⨯+=+⨯++=+++⎨⎧+-=-⎪−−−→⎨±=±+⎪⎩特殊的=幂的运算法则为正整数，可为一个单项式或一个式项式单项式单项式单项式多项式:多项式多项式：整式的乘法平方差公式 乘法公式完全平方公式：⎧⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎩本次内容掌握情况总结 教 务 老 师 签 字 学 生 签 字整式的乘法1、同底数幂的乘法例：计算。
()()432a a a -∙-∙- ()()()x y x y y x -∙-∙-32 ()()122--∙-m m x y y x例：已知568122222⨯⨯=-x ，1211101010=∙+-y y ，求y x +的值。
练一练：已知1112x x x n n m =∙+-，且541y y y n m =∙--，求2mn 的值。
例：已知510=a ，610=b ，求b a 3210+的值。
2、幂的乘方例：计算。
()()31212+-∙n n a a ()()3223x x -∙- 归纳： 1、当a ＞0，m 为奇数时，()m m a a -=-，当m 为偶数时，()m m a a =-； 2、对于()m b a -，当m 为奇数时，()()m m a b b a --=-，当m 为偶数时，()()m m a b b a -=-。
初中数学知识归纳整式的乘法公式
初中数学知识归纳整式的乘法公式在初中数学中，我们学习了很多关于整式的知识，其中包括整式的乘法公式。
整式的乘法公式是指两个整式相乘时所遵循的一些规则和方法。
本文将对初中数学中整式的乘法公式进行归纳总结。
一、单项式和单项式相乘当两个单项式相乘时，我们需要将它们的系数相乘，指数相加。
例如，当我们计算2x和3x的乘积时，可以用如下的方法：2x * 3x = 2 * 3 * x * x = 6x^2在这个例子中，乘积6x^2的系数为2和3的乘积，即6；指数为x 的指数1加x的指数1，即2。
二、单项式和多项式相乘当单项式和多项式相乘时，我们需要将单项式的每一项与多项式的每一项相乘，然后将结果进行合并。
例如，当计算2x与3x^2 + 4x的乘积时，可以按照如下的步骤来进行：2x * (3x^2 + 4x) = 2x * 3x^2 + 2x * 4x = 6x^3 + 8x^2在这个例子中，首先将2x与3x^2相乘得到6x^3，然后将2x与4x 相乘得到8x^2，最后将结果合并得到6x^3 + 8x^2。
三、多项式和多项式相乘当两个多项式相乘时，我们需要将第一个多项式的每一项与第二个多项式的每一项相乘，然后将结果进行合并。
例如，当计算(2x + 3) * (3x - 4)时，可以按照如下的步骤来进行：(2x + 3) * (3x - 4) = 2x * 3x + 2x * (-4) + 3 * 3x + 3 * (-4) = 6x^2 - 8x + 9x - 12在这个例子中，首先将2x与3x相乘得到6x^2，然后将2x与-4相乘得到-8x，接着将3与3x相乘得到9x，最后将3与-4相乘得到-12，将结果合并得到6x^2 - 8x + 9x - 12。
总结：整式的乘法公式可以归纳为以下几个规则：1. 单项式和单项式相乘时，系数相乘，指数相加。
2. 单项式和多项式相乘时，将单项式的每一项与多项式的每一项相乘，然后将结果进行合并。
复杂整式的乘法和除法运算
整式除法运算技巧
确定商的符号：与被除式相同
确定商的系数：被除式的系数 除以除式的系数
确定商的字母及指数：被除式 中某字母的指数-除式中该字母 的指数
约分：简化运算过程
复杂整式的乘法和除法运算
复杂整式的乘法运算
乘法分配律的应用
幂的乘法法则
整式的乘法运算顺序
乘法运算的简化技巧
复杂整式的除法运算
定义：复杂整式的除法运算是指将一个复杂整式除以一个单项式或多项式， 得到商和余数的过程。
复杂整式的乘法和除法运算
汇报人：XX
整式乘法运算 整式除法运算
复杂整式的乘法和除法运算
整式乘法运算
整式乘法法则
乘法分配律：a(b+c)=ab+ac 乘法结合律：(ab)c=a(bc) 乘法交换律：ab=ba 幂的乘法法则：a^m*a^n=a^(m+n)
整式乘法运算步骤
确定系数相乘：将两个整式的 系数相乘，得到结果的系数。
复杂整式的混合运算
乘法和除法运算的顺序：先乘除后加减 乘法分配律的应用：a(b+c) = ab+ac 除法分配律的应用：a/(b+c) = a/b + a/c 乘法和除法的结合律：a(bc) = (ab)c
THANK YOU
汇报人：XX
确定字母因式相乘：将两个整 式中的相同字母因式进行相乘， 得到结果的相应字母因式。
确定单项式乘多项式：将单项 式与多项式的每一项分别相乘， 得到结果的相应项。
确定多项式乘多项式：将两个 多项式的相应项分别相乘，得 到结果的相应项。
整式乘法运算技巧
分配律的应用：将乘法分配到各个 项上，简化运算。
平方差公式和完全平方公式：利用 公式化简复杂整式。
七年级数学下册第2章整式的乘法2.2乘法公式教学课件新版湘教版
3.计算： （1）202×198；
（2）49.8×50.2.
答案：（1）39996；（2）2499.96.
我思 我进步
通过本节课，你有什么收获？ 你还存在哪些疑问，和同伴 交流。
2.2.2 完全平方公式
思考
计算下列各式，你能发现什么规律： ( a+1 )2=( a+1 )( a+1 )=a2+a+a+12=a2+2·a·1+12， ( a+2 )2=( a+2 )( a+2 )=a2+2a+2a+22=a2+2·a·2+22， ( a+3 )2=( a+3 )( a+3 )=a2+3a+3a+32=a2+2·a·3+32， ( a+4 )2=( a+4 )( a+4 )=a2+4a+4a+42=a2+2·a·4+42. 我们用多项式乘法来推导一般情况： ( a+b )2=( a+b )=a2+ab+ab+b2=a2+2ab+b2.
（2）1982.
解：（1）1042=( 100+4 )2 （2）1982=( 200-2 )2
= 1002+2×100×4+42
= 2002-2×200×2+22
= 10000+800+16
= 40000-800+16
= 10816.
= 39204.
练习
1.运用完全平方公式计算： （1）( -2a+3 )2； （3）( -x2-4y )2；
整式的乘法和乘法公式
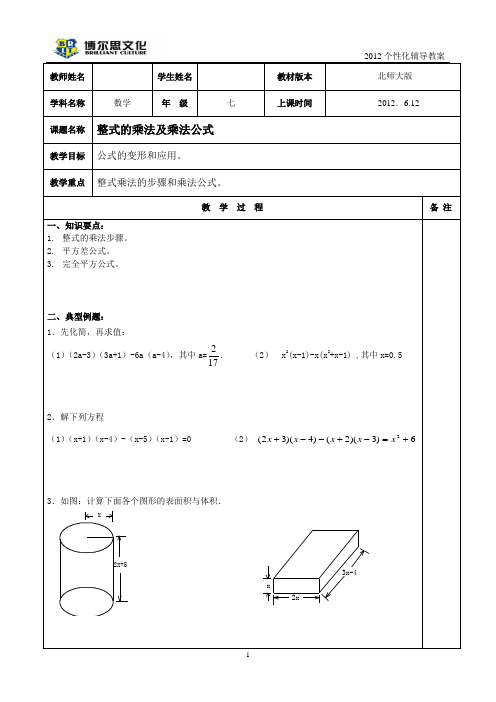
教师姓名 学生姓名 教材版本 北师大版学科名称 数学年 级七上课时间2012．6.12课题名称 整式的乘法及乘法公式教学目标 公式的变形和应用。
教学重点整式乘法的步骤和乘法公式。
教 学 过 程备 注一、 知识要点：1. 整式的乘法步骤。
2. 平方差公式。
3. 完全平方公式。
二、 典型例题： 1．先化简，再求值：（1）（2a-3）（3a+1）-6a （a-4），其中a=217． （2） x 2(x-1)-x(x 2+x-1) ,其中x=0.52．解下列方程（1）（x+1）（x-4）-（x-5）（x-1）=0 （2） ()()()()2342362x x x x x +--+-=+3．如图：计算下面各个图形的表面积与体积．3x-42xxx2x+54．若（x 2+mx+8）（x 2-3x+n ）的展开式中不含x 3和x 2项，求m 和n 的值．5.(2-1)(2+1) (22+1) (24+1)…(216+1)+16．用完全平方公式计算：（1）4992（2）9982（3）5992×60127．已知22124,10n m mn n m +==+），求（ 2))(2(n m -三、 课堂练习: 整式的乘法练习： 一．填空1．x x x ⋅⋅=32；-⋅-=a a 22() ；y y m m ⋅=+1；---=()()a a 3 。
2．()y 35= ；()-=2324xy z ；()-⨯=31033；()()x x 2322⋅= 。
3．()()--=5323a b a ；()()-=1222222x y xy 。
4．52342x x x ()-+= ；()()422ab b bc --= 。
5．()()x x +-=32 ；()()y y +-=1213。
6．()()32x y x y +-= ；()x y +=2。
7．（1）2x 5•5x 2=_________； （2）（2xy 2）•（13x 2y ）=_________； （3）（-5a 3bc ）•（3ac 2）=________． （4）3x 2y •（-4xy 2）•（x 3）2=_________．（5）（a+2b ）（a-b ）=___________； （6）（3a-2）（2a+5）=__________； （7）（x-3）（3x-4）=___________； （8）（3x-y ）（x+2y ）=__________． 8．已知（x+3）（x-2）=x 2+ax+b ，则a= ,b= .9．已知（x+2）（x 2+ax+b ）的积不含x 的二次项和一次项，a= ，b= ． 10．8012519981997⨯=. ；()()-+-=2210099 ； 11．若am=3，a n =5，则a m n 2+= ；12．若()-+2215x y m 与()13152x y n -是同类项，则m = ，n = 。
整式乘法公式
整式乘法公式
1 什么是整式乘法
整式乘法是由欧拉在19世纪早期提出来的一种常见的数学运算方式，是数学分支学科中基本算法之一。
它是用来解决复合乘积问题，即把一个大问题分解为若干个小问题，并利用乘法运算把它们连接起来而解决整个问题，在数学加法、减法、乘法、除法四则运算中被称为第三则运算。
2 整式乘法公式
整式乘法把复杂的乘积运算简化为四个熟调的模式，其中的形式公式为： `(a+b)*(a-b)=a*a - b*b`，其中a，b分别表示算式中的平方数。
它简化了乘积运算，因此，当参与运算的数值变成更大时，整式乘法是十分有效的。
3 应用范围
整式乘法在众多数学问题中得到了很好的应用，例如：如果要求算术组合的乘积，整式乘法可以让我们简化乘积运算，降低难度。
它还可以应用于三角形的计算，例如：根据勾股定理，任意一个直角三角形的斜边的平方等于它的两个直角边的平方总和，这其中就涉及到整式乘法的应用，而且可以方便我们求出它们的相关参数。
4 总结
整式乘法是一种基本的数学运算，它把一个大问题分解为若干个
小问题，并利用乘法运算把它们连接起来，以便快速解决整个问题。
它可以极大的简化乘积的运算，在众多的数学问题中有着重要的应用。
整式的乘法和乘法公式最新版
择 (2) 如果4x2+12xy+k是一个关于x、y的完全
B 平方式，则k=( )
(A) 3y 2 (B) 9y 2 (C) y
(D) 36y 2
如果4x2+kxy +9y2是一个关于x、y的完全平 方式，则k=(+ 12)
A （3）如果a+
1
a
=3,则a2+
1
a2
=(
)
选 (A) 7 (B) 9 (C) 10 (D) 11
=(-1)2-(2xy)2 =1-4x2y2
口答练习一
(1) (x-2y)(x+2y) =x2-4y 2
(2)
(x-1y)(2源自x-1 2y
) =x2-xy +
1 4
y2
(3)
( 3x-
1 2
y
)
(
9x2+
23xy+
1
4
y
2
) =27x3-
y1 3
8
(4) (-x-2y)(-x+2y) =x2-4y2
整式的乘复法习和乘法公
式
a a a 同底数幂的乘法
m · n = m+n
幂的乘方
a a ( m )n = mn
整 式
积的乘方
( ab )n= an b n
的 乘
单项式的乘法
4a2x5 ·(-3a3bx2)
法
=[4 ( -3)](a2a3) (x5x2)b
=-12a5bx7
a a a 同底数幂的乘法
动手做
（1） 已知x=a+2b,y=a-2b，
求:x2+xy+y 2
整式的乘和乘法公式复习法
例1 利用完全平方公式计算： （1） 197 2
练习 利用整式乘法公式计算： （1）998 2
（2）( a b 3 )( a b 3 )
( x 2 )( x 2 ) ( x 1 )( x 3 ) （3 ）
ab 1 ) ( ab 1 ) （4）(
三乘法公式 四（一） 平方差公式 2 2 ( a b )( a b ) a b 五 （a、b可以 是数，也可以是整式） 六即：两数和与这两数差的积，等 于它们的平方差。
例2 利用平方差公式计算： 1 1 （1）( x y )( x y )
4
4
（2）
( m n )( m n ) 3 n
练习：计算 1 . (b5 ) 2
1 3 ( ) 2. 3
3 2
3 8
2
3 .(a
(p )
4
5 .(x ) 7 . 3
4 6
(x ) 6 .(2)
8. (2)
3 2
2 3
（三）积的乘方 n n n ( ab ) a b （n是正整数） 法则： 积的乘方等于各乘因数（或式）的 乘方的积。
例：计算： n 2 （1 ） (3 a ) （3 ） (2xy)
4
（2） (2 3)
2
（4 ） ( 2 b )
5
练习 ：计算 2 2 3 （1 ） (4a ) （2） (ab)
（3）( x
4
2
y )
2
3 3
（4） ( p q)
2
2
( 3 x ) ( 2 x ) （5 ） （6 ） 2 3 5
三） 多项式乘多项式 四法则 多项式与多项式相乘，先 用一个多项式的每一项乘另一多 项式的每一项，再把所得的积相 加。
整式的乘除知识点整理
一、知识点归纳： （一）幂的四种运算：1、同底数幂的乘法：⑴语言叙述：同底数幂相乘，底数不变，指数相加； ⑵字母表示：a m ·a n = a m+n ；(m ，n 都是整数) ；⑶逆运用：a m+n = a m ·a n2、幂的乘方：⑴语言叙述：幂的乘方，底数不变，指数相乘； ⑵字母表示：(a m ) n = a mn ；(m ，n 都是整数)； ⑶逆运用：a mn =(a m )n =(a n )m ；3、积的乘方：⑴语言叙述：积的乘方，等于每个因式乘方的积； ⑵字母表示：(ab)n = a n b n ；(n 是整数)； ⑶逆运用：a n b n = (a b)n ；4、同底数幂的除法：⑴语言叙述：同底数幂相除，底数不变，指数相减；⑵字母表示：a m ÷a n = a m-n ；(a≠0，m 、n 都是整数)； ⑶逆运用：a m-n = a m ÷a n .（二）整式的乘法：1、单项式乘以单项式：⑴语言叙述：单项式与单项式相乘，把它们的系数、相同字母的幂分别相乘，其余字母连同它的指数不变，作为积的因式。
⑵实质：分三类乘：⑴系数乘系数；⑵同底数幂相乘；⑶单独一类字母，则连同它的指数照抄； 2、单项式乘以多项式：⑴语言叙述：单项式与多项式相乘，就是根据分配律用单项式去乘多项式中的每一项，再把所得的积相加。
⑵字母表示：c)＝ma ＋mb ＋mc ；（注意各项之间的符号！） 3、多项式乘以多项式：(1)语言叙述：多项式与多项式相乘，先用一个多项式的每一项去乘另一个多项式的每一项，再把所得的积相加；(2)字母表示：＝mn ＋mb ＋an ＋ab ；（注意各项之间的符号！） 注意点：⑴在未合并同类项之前，积的项数等于两个多项式项数的积。
⑵多项式的每一项都包含它前面的符号，确定乘积中每一项的符号时应用“同号得正，异号得负”。
⑶运算结果中如果有同类项，则要 合并同类项（三）乘法公式： 1、平方差公式：(1)语言叙述：两数和与这两数差的积，等于这两个数的平方差。
整式乘法运算法则公式
整式乘法运算法则公式在代数中，整式乘法是一种常见的运算，它可以帮助我们简化复杂的代数表达式。
整式乘法运算法则公式是指在乘法运算中使用的规则和公式，通过这些规则和公式，我们可以将复杂的代数表达式化简为简单的形式。
本文将介绍整式乘法运算法则公式的基本概念和具体应用。
一、整式乘法的基本概念在代数中，整式是由数字、变量和运算符（如加法、减法、乘法、除法）组成的表达式。
整式乘法是指两个或多个整式相乘的运算。
例如，给定两个整式x+2和3x-4，它们的乘积可以通过整式乘法运算法则公式进行计算。
二、整式乘法运算法则公式整式乘法运算法则公式包括以下几个基本规则：1. 分配律：对于任意的整式a、b和c，有a*(b+c) = a*b + a*c。
2. 乘法交换律：对于任意的整式a和b，有a*b = b*a。
3. 乘法结合律：对于任意的整式a、b和c，有(a*b)*c =a*(b*c)。
这些基本规则可以帮助我们在整式乘法中进行化简和计算，从而得到最终的乘积结果。
三、整式乘法的具体应用整式乘法运算法则公式在代数中有着广泛的应用，特别是在多项式的乘法中。
多项式是由多个整式相加或相减而成的代数表达式，它们在代数中有着重要的地位。
通过整式乘法运算法则公式，我们可以将复杂的多项式乘法化简为简单的形式，从而更方便地进行计算和分析。
例如，考虑两个多项式(x+2)(3x-4)，我们可以利用整式乘法运算法则公式来计算它们的乘积。
首先，我们可以使用分配律将乘法展开：(x+2)(3x-4) = x*(3x-4) + 2*(3x-4)。
然后，我们再利用分配律将每一项再次展开：x*(3x-4) = 3x^2 - 4x，2*(3x-4) = 6x - 8。
最后，将这些展开后的结果相加，得到最终的乘积：(x+2)(3x-4)= 3x^2 - 4x + 6x - 8 = 3x^2 + 2x - 8。
通过以上的计算过程，我们可以看到整式乘法运算法则公式的应用非常简单直观，它可以帮助我们快速地计算多项式的乘积，从而简化代数表达式的计算。
整式的乘法公式
整式的乘法公式整式的乘法公式是数学中的重要概念，它可以帮助我们快速、准确地进行整式的乘法运算。
在本文中，我将详细介绍整式的乘法公式及其应用。
一、整式的乘法公式整式是由常数和变量的乘积以及它们之间的加减运算所构成的代数式。
在乘法运算中，可以利用整式的乘法公式来简化计算。
整式的乘法公式包括以下几条：1. 乘法分配律：对于任意的整式a、b和c，有如下公式：a(b+c) = ab + ac(b+c)a = ba + ca这条乘法分配律的应用非常广泛，它可以用于加法和乘法的结合。
例如，对于整式3(x+2)，根据乘法分配律，我们可以得到：3(x+2) = 3x + 62. 平方差公式：对于任意的整式a和b，有如下公式：(a+b)(a-b) = a^2 - b^2这条平方差公式在整式乘法中十分常用，可以用来求平方差的计算。
例如，对于整式(x+3)(x-4)，根据平方差公式，我们可以得到：(x+3)(x-4) = x^2 - 4x + 3x - 12 = x^2 - x - 123. 三角形式乘法公式：对于任意的整式a、b和c，有如下公式：(a+b)(b+c)(c+a) = (ab+bc+ca)(a+b+c) - abc这条三角形式乘法公式常用于多项式的乘法运算。
例如，对于整式(x+1)(x+2)(x+3)，根据三角形式乘法公式，我们可以得到：(x+1)(x+2)(x+3) = (x^2+3x+x+2)(x+3) - (x+1)(x+2)(x+3) =(x^2+4x+2)(x+3) - (x^2+3x)(x+3) = x^3 + 6x^2 +11x + 6二、整式的乘法公式的应用整式的乘法公式在代数学中有着广泛的应用。
下面我将通过实际例子来说明整式的乘法公式的应用。
例题1：计算(2x+3)(x+1)。
根据乘法分配律，我们可以按照以下步骤进行计算：(2x+3)(x+1) = 2x(x+1) + 3(x+1) = 2x^2 + 2x + 3x + 3 = 2x^2 + 5x + 3例题2：计算(3x+2)(3x-2)。
整式的乘法乘法公式
先算乘方，再算乘除，最后算 加减；
运用分配律
将括号内的代数式展开，并运用 分配律进行计算；
合并同类项
将同类项进行合并，得到最简结果 。
整式乘法公式的计算技巧
熟记公式
熟练掌握整式乘法公式，如平 方差公式、完全平方公式等；
化简代数式
在计算过程中，尽量化简代数 式，减少计算量；
灵活运用运算法则
整式乘法公式是一种简化的运算方法，适用于任何两个整式 的乘法运算。
整式乘法公式的特点
1
整式乘法公式具有普遍适用性，适用于任何两 个整式的乘法运算。
2
整式乘法公式可以简化复杂的计算过程，提高 运算效率。
3
整式乘法公式有助于培养学生的数学思维能力 和符号意识。
整式乘法公式的历史与发展
01
整式乘法公式是数学运算中的基本工具，有着悠久的历史和广 泛的应用。
2023
《整式的乘法乘法公式》
contents
目录
• 整式乘法公式概述 • 整式乘法公式的形式与证明 • 整式乘法公式的计算方法与技巧 • 整式乘法公式的应用实例
01
整式乘法公式概述
整式乘法公式的定义
整式乘法公式定义：整式乘法公式是单项式与单项式相乘， 把他们的系数，相同字母的幂分别相乘，其余字母连同他的 指数不变，作为积的因式的运算。
交换律公式
$(a+b)(c+d)=(a+b)(c+d)$
整式乘法公式的证明方法
分配律公式的证明
根据乘法分配律，可以得出$(a+b)(c+d)=ac+ad+bc+bd$。
结合律公式的证明
根据乘法结合律，可以得出$(a+b)(a+b)=a^2+2ab+b^2$。
整式的乘法运算法则
整式的乘法运算法则乘法运算法则1. 相同数乘以相同数等于它们的乘积：a*a=a²；2. 指数乘积性质：xⁿ*xᵐ=xⁿ⁺ᵐ；3. 幂乘积性质：(x*y)ᵐ=xᵐ*yᵐ；4. 相反数乘积：(-a)*(-b)=a*b；5. 乘积与商乘积性质：a¹／b¹=a*b；6. 乘积与商除积性质：a¹／b⁰=a/b；7. 乘积与和差乘积性质：(a+b)*(a-b)=a²-b²；8. 乘积的特点：乘积不受其中的任意一个因子的变化而受影响。
9. 乘方：x*x*x=x³；10. 平方根：x*x=√x；11. 积与分母乘积：(x*x)*(1/x)=x，(x*y/a)*(a/z)= x*y/z。
12. 求倒数乘积：（1/a）*（1/b）=1/(ab)；13. 指定数乘积：x*a=a*x=a，x*0=0*x=0；14. 除数与商的乘积性质：a/b*b=a；15. 乘法减法：x/(x-a)=1+a／x；16. 四、三、二乘方：a⁴*b³*c²=(abc)⁶；17. 乘积减法：a*b*c-a*b=a*b*(c-1)；18. 乘积的和减去乘积的差：a*b-c*d=(a-c)*(b-d)。
乘法运算在日常生活中很常见，由小孩子到成年人，都会用到乘法，小学是孩子学习数学中最基础的概念，乘法运算是学习过程中重要的一步。
乘法运算分为乘法公式和乘法运算法则两部分。
乘法公式主要是指某些具体的情形，根据这些具体情形来估算和求解数学问题；乘法运算法则则是一些更宽泛的知识，用来解决不同概念之间的关系。
以下是乘法运算法则的18条规则：1、相同数乘以相同数等于它们的乘积：a*a=a²；2、指数乘积性质：xⁿ*xᵐ=xⁿ⁺ᵐ；3、幂乘积性质：(x*y)ᵐ=xᵐ*yᵐ；4、相反数乘积：(-a)*(-b)=a*b；5、乘积与商乘积性质：a¹／b¹=a*b；6、乘积与商除积性质：a¹／b⁰=a/b；7、乘积与和差乘积性质：(a+b)*(a-b)=a²-b²；8、乘积的特点：乘积不受其中的任意一个因子的变化而受影响；9、乘方：x*x*x=x³；10、平方根：x*x=√x；11、积与分母乘积：(x*x)*(1/x)=x，(x*y/a)*(a/z)= x*y/z；12、求倒数乘积：（1/a）*（1/b）=1/(ab)；13、指定数乘积：x*a=a*x=a，x*0=0*x=0；14、除数与商的乘积性质：a/b*b=a；15、乘法减法：x/(x-a)=1+a／x；16、四、三、二乘方：a⁴*b³*c²=(abc)⁶；17、乘积减法：a*b*c-a*b=a*b*(c-1)；18、乘积的和减去乘积的差：a*b-c*d=(a-c)*(b-d)。
整式的乘除—乘法公式
整式的乘除—乘法公式【复习】(a+b)(a-b)=a 2-b 2 (a+b)2=a 2+2ab+b 2 (a-b)2=a 2-2ab+b 2(a+b)(a 2-ab+b 2)=a 3+b 3 (a-b)(a 2+ab+b 2)=a 3－b 3归纳小结公式的变式，准确灵活运用公式：① 位置变化，(x +y )(-y +x )=x 2-y 2② 符号变化，(-x +y )(-x -y )=(-x )2-y 2= x 2-y 2③ 指数变化，(x 2+y 2)(x 2-y 2)=x 4-y 4④ 系数变化，(2a +b )(2a -b )=4a 2-b 2⑤ 换式变化，[xy +(z +m )][xy -(z +m )]=(xy )2-(z +m )2=x 2y 2-(z +m )(z +m )=x 2y 2-(z 2+zm +zm +m 2)=x 2y 2-z 2-2zm -m 2⑥ 增项变化，(x -y +z )(x -y -z )=(x -y )2-z 2=(x -y )(x -y )-z 2=x 2-xy -xy +y 2-z 2=x 2-2xy +y 2-z 2⑦ 连用公式变化，(x +y )(x -y )(x 2+y 2)=(x 2-y 2)(x 2+y 2)=x 4-y 4⑧ 逆用公式变化，(x -y +z )2-(x +y -z )2=[(x -y +z )+(x +y -z )][(x -y +z )-(x +y -z )]=2x (-2y +2z )=-4xy +4xz【典例分析】例1．已知2=+b a ，1=ab ，求22b a +的值。
例2．已知8=+b a ，2=ab ，求2)(b a -的值。
例3：计算19992-2000×1998例4：已知a+b=2，ab=1，求a 2+b 2和(a-b)2的值。
例5：已知x-y=2，y-z=2，x+z=14。
求x 2-z 2的值。
整式的乘法与乘法公式考点归纳
人教版八年级上第十四章14.1整式的乘法、14.2乘法公式必背重点公式考点归纳黎平县地坪附中80（2）班、80（4）班 姓名14.1整式的乘法1、同底数幂的乘法：p n m p n ma a a a ++=∙∙ 例如：621323x x x x x ==∙∙++2、幂的乘方：()mnnm aa = 例如：()()[]24342342126262;x xxm mm ====⨯⨯⨯3、积的乘方：()m m mb a ab =例如：()()()242222223333422;y x y x y xc b a abc ===4、单项式⨯单项式（单单）：①有乘方先算乘方；②系数乘系数；③同底数幂相乘；④单独的字母连同它的指数作为积的一个因式。
例如：()()()255322432222232212343232z y x xy z y x xy zy x xy yz x =⨯=⨯-=⨯-5、单项式⨯多项式（单多）：()cx bx ax c b a x ++=++（类似乘法分配律）例如：6、多项式⨯多项式（多多）：bn bm an am n m b a +++=++))((例如：4)3(5)3(4252)45)(32(∙-+∙-+∙+∙=+-y x y x y x1215810)12()15(810--+=-+-++=y x xy y x xy7、同底数幂的除法：),(n m n m aa anm nm＞都是正整数，-=÷)0(10≠=a a 重点公式： 例如：()12020114.3;1)2019(;052727-=-=-=-==÷-；πx xx x8、单项式÷单项式：①有乘方先算乘方；②系数除系数；③同底数幂相除；④对于被除式里单独的字母连同它的指数作为商的一个因式。
（也可以变成分数的约分来理解）5)3(4)3(23)542)(3(2222⨯--⨯-+⨯-=-+-ab ab ab a ab ab a ab abb a b a ab b a b a 15126)15()12(6323323+--=---+-=例如：333364332343234686)()2(6)2(b a a b a a b a a b a -=÷-=÷-=÷-9多项式÷单项式：m c m b m a m c b a ÷+÷+÷=÷++)(（类似乘法分配律）例如：124333)6(3123)3612(22323+-=÷+÷-+÷=÷+-a a a a a a a a a a a a 14.2乘法公式10、平方差公式：22))((b a b a b a -=-+11、完全平方公式：①完全平方和公式：2222)(bab a b a ++=+②完全平方差公式：2222)(bab a b a +-=-12、整式的加减乘除混合运算：①有乘方先算乘方；②再算乘除；③最后算加减说明：整式的加减乘除混合运算必须要以以上11个公式为运算工具，所以必须掌握上面11个公式。
整式乘法及乘法公式(复习)
D
x y z ) (- x y ) = x y
2 2
4 7 3 5 3 2 2 3
(-10 ) · (B) (-2 10 ) · ( 3 10 ) = -6 10
(C) (1 2
10
ab )= - a b
2 3 3 1 6 8
27
(b ) = (ab) (D) (a ) ·
3n 2
2 3n
6n
- 新世纪教育网版 权所有
- 新世纪教育网版 权所有
同底数幂的乘法
幂的乘方
整 积的乘方 式 的 单项式的乘法 乘 法
a ·a = a ( am )n = amn n ( ab ) = an b n 3 2 2 5 (-3 · 4a x a bx ) 2 3 5 2 =[4 ( -3)](a a ) (x x )b 5 7 =-12a bx
=[a-(2b-3)][a+(2b-3)] =a -(2b-3) =a -(4b -12b+9)
2
2 2 2
= a -4b +12b-9
- 新世纪教育网版 权所有
2
- 新世纪教育网版 权所有
2
平方差公式
(a+b)(a-b) =
2
a -b
2
2
乘 完全平方公式 2 法 (a+b) = 公 式
二次三项型乘法公式
a + 2ab +b
2
2
(x+a)(x+b)=
x +(a+b)x+ab
- 新世纪教育网版 权所有
3
(5) 5a · 2a =10a (6) (8)
7 4
10a
整式乘法公式
整式乘法公式
整式乘法公式是指将一个整式乘以另一个整式，并得出最终结果的一种公式。
整式乘法公式可以用来解决各种数学问题，例如求解多项式的乘积、积分运算等。
整式乘法公式的基本结构是：(a+b)(c+d)=ac+ad+bc+bd，其中a,b,c,d分别是整式中的四个单项，ac表示a乘以c的积，ad表示a 乘以d的积，bc表示b乘以c的积，bd表示b乘以d的积，最后结果是ac+ad+bc+bd。
整式乘法公式可以用来解决多项式的乘积问题。
首先，需要将多项式分解成单项，并用整式乘法公式进行运算。
例如，求解(x-2)(x+3) 的积，首先将其分解为(x-2)(x) + (x-2)(3)，然后根据整式乘法公式，最终结果为x^2-2x+3x-6，即 x^2+x-6。
另外，整式乘法公式也可以用来解决积分运算问题。
积分运算是求解一个函数在一定区间上的积分，例如求解 f(x) = x^2+3x+2 在区间[0,1] 上的积分。
首先，将函数f(x) 进行分解，即f(x) = (x+2)(x+1)，然后根据整式乘法公式，最终结果为x^2+3x+2，即积分的结果为x^3/3+3x^2/2+2x。
总之，整式乘法公式是一种非常有用的公式，它可以用来解决多项式的乘积以及积分运算等多项数学问题。
在解决这些数学问题时，
要特别注意把握整式乘法公式，才能得到正确的答案。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
整式乘法与乘法公式2017一．选择题（共12小题）1．若（a n b•ab m）5=a10b15，则3m（n+1）=（）A．15 B．8 C．12 D．102．如果（x2﹣a）x+x的展开式中只含有x3这一项，那么a的值为（）A．1 B．﹣1 C．O D．不能确定3．若2m2n2•B=14m4n3﹣8m3n3，那么B=（）A．7mn2﹣4mn B．28m2n﹣16n C．7m2n﹣4mn D．7m2﹣4n4．计算（a4+b4）（a2+b2）（b﹣a）（a+b）的结果是（）A．a8﹣b8B．a6﹣b6C．b8﹣a8D．b6﹣a65．若（﹣a+b）•M=a2﹣b2，则M等于（）A．﹣a﹣b B．﹣a+b C．a﹣b D．a+b6．已知x﹣y=9，xy=8，则x2+y2等于（）A．100 B．97 C．94 D．917．若|x+y﹣5|+（xy﹣3）2=0，则x2+y2的值为（）A．19 B．31 C．27 D．238．（a+b）3=﹣1，（a﹣b）2=1，则a2009+b2009的值是（）A．2 B．1 C．0 D．﹣19．一个正方形的边长增加1cm，它的面积就增加7cm2，这个正方形的边长是（）A．3cm B．4cm C．5cm D．6cm10．图中，阴影部分面积等于（）A．a2+b2B．a2﹣b2C．ab D．2ab11．4x2+（）+25y2可写成一个完全平方式，则括号中可填入（）A．10xy B．±10xy C．20xy D．±20xy12．当x=2时，代数式2x4（x2+2x+2）﹣x2（4+4x3+2x4）的值是（）A．﹣48 B．0 C．24 D．48二．填空题（共6小题）13．若2|a+b﹣1|与互为相反数，则﹣3a2（ab2+2a）+4a（﹣ab）2的值是．14．已知x2﹣2x﹣10=0，则（x﹣1）2+（x+3）（x﹣3）+（x﹣5）（x+1）=．15．计算：（2000+2001+2002+2003）（2000﹣2001﹣2002）﹣（2000+2001+2002）（2000﹣2001﹣2002﹣2003）的结果是．16．如图是用4个全等的长方形拼成的一个“回形”正方形，将图中阴影部分面积用2种方法表示可得一个等式，这个等式为．17．若n为正整数，且a2n=3，则（3a3n）2÷（27a4n）的值为．18．用简便方法计算：99×101×10 001=三．解答题（共10小题）19．计算下列各题．（1）（x﹣y）•2（x﹣y）2•3（x﹣y）3；（2）．20．计算：（1）（a2+3）（a﹣2）﹣a（a2﹣2a﹣2）；（2）（2m+n）（2m﹣n）+（m+n）2﹣2（2m2﹣mn）．21．计算：（1﹣）（1﹣）…（1﹣）（1﹣）=．22．计算．（1）（2x2+3y）（2x2﹣3y）；（2）（2x﹣y）（﹣2x﹣y）；（3）（x+y）（x﹣y）+（2x+y）（2x﹣y）；（4）（a﹣3）（a+3）（a2+9）．23．计算：（1）（x+3y）（x﹣3y）；（2）（x3+2）（x3﹣2）：（3）（2m﹣n）（﹣2m﹣n）．24．计算：12﹣22+32﹣42+52﹣62+…+20012﹣20022+20032﹣20042．25．已知x2﹣4x+1=0，求x4+的值．．26．（1）计算：（﹣1）0﹣|﹣3|+﹣（﹣1）2012（2）化简：a•a5+（﹣a）3•a3﹣（2a2）2•a2（3）化简：（2x﹣y）2﹣4（x+2y）（x﹣y）（4）．27．计算（1）30﹣（）﹣2+（﹣3）2（2）（﹣a2）3+a•a5﹣a3÷a（3）x2•x4+（x3）2（4）（x2•x m）3÷x2m+1（5）5x2y（4xy2z﹣6xz）（6）（3x+4y）（2x﹣8y）（7）（﹣4x﹣y）（4x﹣y）（8）4x2﹣（﹣2x+3）（﹣2x﹣3）28．图1是一个长为2x、宽为2y的长方形，沿图中虚线用剪刀剪成四个完全相同的小长方形，然后按图2所示拼成一个正方形．（1）你认为图2中的阴影部分的正方形的边长等于．（2）试用两种不同的方法求图2中阴影部分的面积．方法1：；方法2：．（3）根据图2你能写出下列三个代数式之间的等量关系吗？代数式：（x+y）2，（x﹣y）2，4xy．（4）根据（3）题中的等量关系，解决如下问题：若x+y=4，xy=3，则（x﹣y）2=．整式乘法与乘法公式2017参考答案与试题解析一．选择题（共12小题）1．若（a n b•ab m）5=a10b15，则3m（n+1）=（）A．15 B．8 C．12 D．10【分析】根据已知条件可以求得m、n的值，然后将其代入所求的代数式进行求值．【解答】解：∵（a n b•ab m）5=a5（n+1）b5（m+1）=a10b15，∴5（n+1）=10，5（m+1）=15，解得，n=1，m=2，∴3m（n+1）=3×2×2=12．故选：C．【点评】本题考查了单项式乘单项式，幂的乘方与积的乘方．熟练掌握运算法则是解题的关键．2．如果（x2﹣a）x+x的展开式中只含有x3这一项，那么a的值为（）A．1 B．﹣1 C．O D．不能确定【分析】首先利用单项式乘以多项式整理得出x3+（1﹣a）x进而根据展开式中只含有x3这一项得出1﹣a=0，求出即可．【解答】解：∵（x2﹣a）x+x的展开式中只含有x3这一项，∴x3﹣ax+x=x3+（1﹣a）x中1﹣a=0，∴a=1，故选：A．【点评】此题主要考查了单项式乘以多项式以及解一元一次方程，能正确进行去括号合并同类项是解题关键．3．若2m2n2•B=14m4n3﹣8m3n3，那么B=（）A．7mn2﹣4mn B．28m2n﹣16n C．7m2n﹣4mn D．7m2﹣4n【分析】直接利用多项式除以单项式运算法则求出即可．【解答】解：∵2m2n2•B=14m4n3﹣8m3n3，∴B=（14m4n3﹣8m3n3）÷2m2n2=7m2n﹣4mn．故选：C．【点评】此题主要考查了多项式除以单项式运算，熟练将原式变形求出是解题关键．4．计算（a4+b4）（a2+b2）（b﹣a）（a+b）的结果是（）A．a8﹣b8B．a6﹣b6C．b8﹣a8D．b6﹣a6【分析】多次运用平方差公式计算即可．【解答】解：（a4+b4）（a2+b2）（b﹣a）（a+b），=（a4+b4）（a2+b2）（b2﹣a2），=（a4+b4）（b4﹣a4），=b8﹣a8．故选C．【点评】本题主要考查了平方差公式的应用．解题时要正确应用公式．5．若（﹣a+b）•M=a2﹣b2，则M等于（）A．﹣a﹣b B．﹣a+b C．a﹣b D．a+b【分析】利用平方差公式化简即可得到结果．【解答】解：（﹣a+b）（﹣a﹣b）=a2﹣b2，则M=﹣a﹣b．故选A【点评】此题考查了平方差公式，熟练掌握公式是解本题的关键．6．已知x﹣y=9，xy=8，则x2+y2等于（）A．100 B．97 C．94 D．91【分析】根据完全平方公式第二个公式，把（x﹣y）平方再加上2xy，就可以得到x2+y2，代入数据求解即可．【解答】解：∵x﹣y=9，xy=8，∴x2+y2=（x﹣y）2+2xy，=92+2×8，=81+16，=97．故选B．【点评】本题考查了完全平方公式，熟练掌握公式结构是求解的关键．7．若|x+y﹣5|+（xy﹣3）2=0，则x2+y2的值为（）A．19 B．31 C．27 D．23【分析】根据非负数的性质可得x+y﹣5=0，xy﹣3=0，整理后再利用完全平方公式展开并整理即可得解．【解答】解：根据题意得，x+y﹣5=0，xy﹣3=0，∴x+y=5，xy=3，∵（x+y）2=x2+2xy+y2=25，∴x2+y2=25﹣2×3=25﹣6=19．故选A．【点评】本题考查了完全平方公式，非负数的性质，熟记公式的几个变形公式对解题大有帮助．8．（a+b）3=﹣1，（a﹣b）2=1，则a2009+b2009的值是（）A．2 B．1 C．0 D．﹣1【分析】先求出a+b，a﹣b的值，然后列出方程组，求出a、b的值即可，代入计算即可．【解答】解：∵（a+b）3=﹣1，（a﹣b）2=1，∴a+b=﹣1，a﹣b=±1，∴或，解得或，所以a2009+b2009=﹣1．故选D．【点评】本题主要考查完全平方公式，先求出a、b的值是解题关键，注意不要根据公式展开．9．一个正方形的边长增加1cm，它的面积就增加7cm2，这个正方形的边长是（）A．3cm B．4cm C．5cm D．6cm【分析】设原来正方形的边长为xcm，根据题意列出方程，求出方程的解即可得到结果．【解答】解：设原来正方形的边长为xcm，增加后边长为（x+1）cm，根据题意得：（x+1）2﹣x2=7，解得：x=3．则这个正方形原来的边长为3cm．故选：A．【点评】此题考查了完全平方公式，平方差公式以及一元一次方程的应用，弄清题意是解本题的关键．10．图中，阴影部分面积等于（）A．a2+b2B．a2﹣b2C．ab D．2ab【分析】观察图形得到阴影部分面积等于以a+b为边长的正方形的面积减去4个直角三角形的面积，然后根据正方形的面积公式和三角形面积公式进行计算．【解答】解：阴影部分面积=（a+b）2﹣2•a•a﹣2•b•b=a2+2ab+b2﹣a2﹣b2=2ab．故选D．【点评】本题考查了完全平方公式的几何背景：运用几何直观理解、解决完全平方公式的推导过程，通过几何图形之间的数量关系对完全平方公式做出几何解释．11．4x2+（）+25y2可写成一个完全平方式，则括号中可填入（）A．10xy B．±10xy C．20xy D．±20xy【分析】根据完全平方公式的公式结构解答．【解答】解：∵4x2±2•2x•5y+25y2=（2x±5y）2，∴要填入的数是±2•2x•5y=±20xy．故选D．【点评】本题是完全平方公式的应用，两数的平方和，再加上或减去它们积的2倍，就构成了一个完全平方式．此题解题的关键是利用乘积项来确定这两个数．12．当x=2时，代数式2x4（x2+2x+2）﹣x2（4+4x3+2x4）的值是（）A．﹣48 B．0 C．24 D．48【分析】首先利用单项式于多项式的乘法法则计算，然后合并同类项即可求解．【解答】解：原式=2x6+4x5+4x4﹣4x2﹣4x5﹣2x6=4x4﹣4x2．当x=2时，原式=4×24﹣4×22=48．故选D．【点评】本题考查了整式的化简求值，注意正确进行合并同类项是关键．二．填空题（共6小题）13．若2|a+b﹣1|与互为相反数，则﹣3a2（ab2+2a）+4a（﹣ab）2的值是﹣40．【分析】根据绝对值以及完全平方的性质得出，再利用单项式乘以多项式去括号，再合并同类项，最后把a，b的值代入计算即可．【解答】解：∵2|a+b﹣1|与互为相反数，∴，解得：，﹣3a2（ab2+2a）+4a（﹣ab）2=﹣3a3b2﹣6a3+4a3b2=﹣6a3+a3b2将a=2，b=﹣1代入得出：原式=﹣6a3+a3b2=﹣6×23+23×（﹣1）2=﹣40．故答案为：﹣40．【点评】本题考查了整式的化简求值，解题的关键是正确利用单项式乘去括号、合并同类项．14．已知x2﹣2x﹣10=0，则（x﹣1）2+（x+3）（x﹣3）+（x﹣5）（x+1）=17．【分析】先利用乘法公式展开得到原式=x2﹣2x+1+x2﹣9+x2﹣4x﹣5，再合并同类项得原式=3x2﹣6x﹣13，由于x2﹣2x﹣10=0，则x2﹣2x=10，然后变形原式得到3（x2﹣2x）﹣13，接着利用整体代入的方法计算即可．【解答】解：原式=x2﹣2x+1+x2﹣9+x2﹣4x﹣5=3x2﹣6x﹣13，∵x2﹣2x﹣10=0，∴x2﹣2x=10，∴原式=3（x2﹣2x）﹣13=3×10﹣13=17．故答案为17．【点评】本题考查了整式的混合运算﹣化简求值：先按运算顺序把整式化简，再把对应字母的值代入求整式的值．15．计算：（2000+2001+2002+2003）（2000﹣2001﹣2002）﹣（2000+2001+2002）（2000﹣2001﹣2002﹣2003）的结果是8012000．【分析】设2000+2001+2002=a，2000﹣2001﹣20002=b，求出a+b=4000，原式=（a+2003）b﹣a（b﹣2003），化简后代入即可．【解答】解：设2000+2001+2002=a，2000﹣2001﹣20002=b，a+b=4000原式=（a+2003）b﹣a（b﹣2003）=ab+2003b﹣ab+2003a=2003（a+b）=2003×4000=8012000．故答案为：8012000．【点评】本题考查了整式的混合运算的应用，主要考查学生能否选择适当的方法进行计算，题目比较好，难度适中．16．如图是用4个全等的长方形拼成的一个“回形”正方形，将图中阴影部分面积用2种方法表示可得一个等式，这个等式为（a+b）2﹣（b﹣a）2=4ab．【分析】利用矩形的面积公式以及正方形的面积公式即可表示．【解答】解：第一种表示是4ab，第二种表示是（a+b）2﹣（b﹣a）2，则等式是（a+b）2﹣（b﹣a）2=4ab．【点评】本题考查了完全平方公式，正确表示出阴影部分的面积是关键．17．若n为正整数，且a2n=3，则（3a3n）2÷（27a4n）的值为1．【分析】先利用积的乘方，等于把积的每一个因式分别乘方，再把所得的幂相乘计算，再利用单项式的除法化简，然后代入数据计算即可．【解答】解：（3a3n）2÷（27a4n），=9a6n÷（27a4n），=a2n，当a2n=3时，原式=×3=1．【点评】本题主要考查幂的乘方的性质，单项式除单项式，熟练掌握运算性质和法则是解题的关键．18．用简便方法计算：99×101×10 001=99999999【分析】先把前两个数写成100与1的和与差的积，利用平方差公式计算后再与10 001写成10 000与1的和与差的积，继续利用平方差公式计算即可．【解答】解：99×101×10 001，=（100﹣1）（100+1）×10 001，=9 999×10001，=（10 000﹣1）（10 000+1），=99 999 999．【点评】本题考查了平方差公式的应用，关键在于把99×101×10 001转化为平方差的形式，然后进行计算．三．解答题（共10小题）19．计算下列各题．（1）（x﹣y）•2（x﹣y）2•3（x﹣y）3；（2）．【分析】（1）根据同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加，即可得出答案．（2）根据（y﹣x）2=（x﹣y）2，再根据同底数幂相乘，底数不变，指数相加和单项式乘单项式的法法则进行计算即可．【解答】解：（1）（x﹣y）•2（x﹣y）2•3（x﹣y）3=6（x﹣y）6；（2）=﹣6a2b（x﹣y）3•ab2（x﹣y）2=﹣2a3b3（x ﹣y）5．【点评】本题考查了同底数幂的乘法和单项式乘单项式，要求熟练记忆同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加是解题的关键．20．计算：（1）（a2+3）（a﹣2）﹣a（a2﹣2a﹣2）；（2）（2m+n）（2m﹣n）+（m+n）2﹣2（2m2﹣mn）．【分析】（1）原式第一项利用多项式乘多项式法则计算，第二项利用单项式乘多项式法则计算，去括号合并即可得到结果；（2）原式第一项利用平方差公式化简，第二项利用完全平方公式展开，去括号合并即可得到结果．【解答】解：（1）原式=a3﹣2a2+3a﹣6﹣a3+2a2+2a=5a﹣6；（2）原式=4m2﹣n2+m2+2mn+n2﹣4m2+2mn=m2+4mn．【点评】此题考查了多项式乘多项式，平方差公式，以及完全平方公式，熟练掌握运算法则是解本题的关键．21．计算：（1﹣）（1﹣）…（1﹣）（1﹣）=．【分析】利用平方差公式对各项分解因式，前一项与后一项出现倒数，然后再根据有理数的乘法计算即可．【解答】解：（1﹣）（1﹣）…（1﹣）（1﹣），=（1﹣）（1+）（1﹣）（1+）•…•（1﹣）（1+）（1﹣）（1+），=××××××…××××，=×，=．【点评】本题考查了平方差公式的逆运用，利用公式分解成两数的积，并且出现倒数相乘是解题的关键，求解方法灵活巧妙．22．计算．（1）（2x2+3y）（2x2﹣3y）；（2）（2x﹣y）（﹣2x﹣y）；（3）（x+y）（x﹣y）+（2x+y）（2x﹣y）；（4）（a﹣3）（a+3）（a2+9）．【分析】原式各项利用平方差公式化简，即可得到结果．【解答】解：（1）（2x2+3y）（2x2﹣3y）=4x4﹣9y2；（2）（2x﹣y）（﹣2x﹣y）=（﹣y）2﹣（2x）2=y2﹣4x2；（3）（x+y）（x﹣y）+（2x+y）（2x﹣y）=x2﹣y2+4x2﹣y2=5x2﹣2y2；（4）（a﹣3）（a+3）（a2+9）=（a2﹣9）（a2+9）=a4﹣81．【点评】此题考查了平方差公式，熟练掌握平方差公式是解本题的关键．23．计算：（1）（x+3y）（x﹣3y）；（2）（x3+2）（x3﹣2）：（3）（2m﹣n）（﹣2m﹣n）．【分析】（1）直接运用平方差公式展开；（2）先根据平方差公式展开得到原式=（x3）2﹣22，然后根据幂的乘方法则运算；（3）先提负号得到原式=﹣（2m﹣n）（2m+n），然后根据平方差公式计算．【解答】解：（1）原式=x2﹣9y2；（2）原式=（x3）2﹣22=x6﹣4；（3）原式=﹣（2m﹣n）（2m+n）=﹣（4m2﹣n2）=﹣4m2+n2．【点评】本题考查了平方差公式：a2﹣b2=（a+b）（a﹣b）．24．计算：12﹣22+32﹣42+52﹣62+…+20012﹣20022+20032﹣20042．﹣2009010【分析】本题是平方差公式的应用．【解答】解：12﹣22+32﹣42+52﹣62+…+20012﹣20022+20032﹣20042=﹣[（22﹣12）+（42﹣32）+（62﹣52）+…+（20022﹣20012）+（20042﹣20032）]，利用平方差公式12﹣22+32﹣42+52﹣62+…+20012﹣20022+20032﹣20042=﹣[（22﹣12）+（42﹣32）+（62﹣52）+…+（20022﹣20012）+（20042﹣20032）]=﹣[（2﹣1）（2+1）+（4﹣3）（4+3）+（6﹣5）（6+5）+…+（2002﹣2001）（2002+2001）+（2004﹣2003）（2004+2003）]=﹣（1+2+3+4+…+2002+2003+2004）==﹣2 009 010．【点评】运用平方差公式计算时，关键要找相同项和相反项，其结果是相同项的平方减去相反项的平方．要把多项式转化为平方差公式的形式．25．已知x2﹣4x+1=0，求x4+的值．194．【分析】完全平方公式：（a±b）2=a2±2ab+b2，先把x2﹣4x+1=0两边同除x（由题意可知x≠0），得到x+=4，然后把该式子两边平方，整理后再次平方即可得到x4+的值．【解答】解：∵x2﹣4x+1=0，∴x﹣4+=0，即x+=4，∴x2+=（x+）2﹣2，=42﹣2，=14，∴x4+=（x2+）2﹣2，=142﹣2，=194．故答案为：194．【点评】本题考查了完全平方公式，解题关键是利用隐含条件x≠0，x2﹣4x+1=0两边同除x得到x+=4，利用x和互为倒数乘积是1与完全平方公式来进行解题．26．（1）计算：（﹣1）0﹣|﹣3|+﹣（﹣1）2012（2）化简：a•a5+（﹣a）3•a3﹣（2a2）2•a2（3）化简：（2x﹣y）2﹣4（x+2y）（x﹣y）（4）．【分析】（1）求出每一部分的值，代入求出即可；（2）先算乘方、再算乘法，最后合并同类项即可；（3）先算乘方和乘法，再合并同类项即可；（4）先算乘方，再算乘除即可．【解答】解：（1）原式=1﹣3+4﹣1=1；（2）原式=a6﹣a6﹣4a6=﹣4a6；（3）原式=4x2﹣4xy+y2﹣4x2+4xy﹣8xy+8y2=﹣8xy+9y2；（4）原式=a6b3•（﹣9ab3）÷（﹣a5b3）=[×（﹣9）×（﹣2）]a6+1﹣5b3+3﹣3=a2b3．【点评】本题考查了整式和有理数的混合运算的应用，主要考查学生的计算能力和化简能力．27．计算（1）30﹣（）﹣2+（﹣3）2（2）（﹣a2）3+a•a5﹣a3÷a（3）x2•x4+（x3）2（4）（x2•x m）3÷x2m+1（5）5x2y（4xy2z﹣6xz）（6）（3x+4y）（2x﹣8y）（7）（﹣4x﹣y）（4x﹣y）（8）4x2﹣（﹣2x+3）（﹣2x﹣3）【分析】（1）先求出每一部分的值，再代入求出即可；（2）先算乘方，再算乘除，最后合并即可；（3）先算乘方，再算乘法，最后合并即可；（4）先算乘方，再算除法即可；（5）根据多项式乘以单项式法则进行计算即可；（6）根据多项式乘以多项式法则进行计算即可；（7）根据平方差公式进行计算即可；（8）先根据平方差公式进行计算，再合并即可．【解答】解：（1）30﹣（）﹣2+（﹣3）2=1﹣9+9=1；（2）（﹣a2）3+a•a5﹣a3÷a=﹣a6+a6﹣a2=a2；（3）x2•x4+（x3）2=x6+x6=2x6；（4）（x2•x m）3÷x2m+1=x6+3m÷x2m+1=x5+m；（5）5x2y（4xy2z﹣6xz）=20x3y3z﹣30x3yz；（6）（3x+4y）（2x﹣8y）=6x2﹣24xy+8xy﹣32y2=6x2﹣16xy﹣32y2；（7）（﹣4x﹣y）（4x﹣y）=（﹣y）2﹣（4x）2=y2﹣16x2；（8）4x2﹣（﹣2x+3）（﹣2x﹣3）=4x2﹣4x2+9=9．【点评】本题考查了零指数幂，负整数指数幂，有理数的混合运算和整式的混合运算的应用，能综合运用知识点进行计算和化简是解此题的关键，注意：运算顺序．28．（2017春•雁塔区校级月考）图1是一个长为2x、宽为2y的长方形，沿图中虚线用剪刀剪成四个完全相同的小长方形，然后按图2所示拼成一个正方形．（1）你认为图2中的阴影部分的正方形的边长等于x﹣y．（2）试用两种不同的方法求图2中阴影部分的面积．方法1：（x﹣y）2 ；方法2：（x+y）2﹣4xy．（3）根据图2你能写出下列三个代数式之间的等量关系吗？代数式：（x+y）2，（x﹣y）2，4xy．（x+y）2=（x﹣y）2+4xy（4）根据（3）题中的等量关系，解决如下问题：若x+y=4，xy=3，则（x﹣y）2=4．【分析】（1）图①分成了4个长为x，宽为y的长方形，图②中的阴影部分的小正方形的边长等于x﹣y，大正方形的边长等于x+y；（2）直接利用正方形的面积公式得到②中阴影部分的面积为（x﹣y）2；也可以用大正方形的面积减去4个长方形的面积即②（x+y）2﹣4xy；（3）利用面积之间的关系易得（x+y）2=（x﹣y）2+4xy．【解答】解：（1）图②中的阴影部分的小正方形的边长=x﹣y；故答案为：（x﹣y）；（2）方法①（x﹣y）2；方法②（x+y）2﹣4xy；故答案为：（x﹣y）2 ，（x+y）2﹣4xy；（3）（x+y）2=（x﹣y）2+4xy；故答案为：（x+y）2=（x﹣y）2+4xy；（4）（x﹣y）2=（x+y）2﹣4xy=42﹣12=4故答案为：4．【点评】本题考查了列代数式：根据题中的已知数量利用代数式表示其他相关的量．。