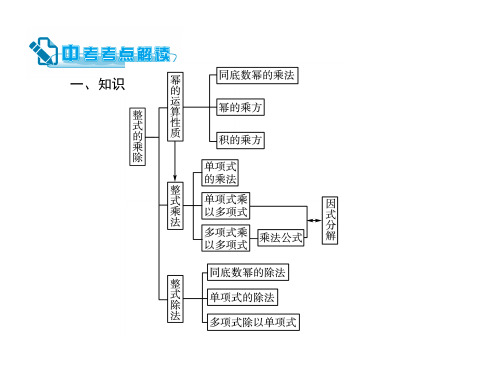
整式的乘除及乘法公式
初中数学.整式的乘除与乘法公式

)
2 2 4
B. x 2 y 2 y x x 2 y
7
C. x 2 y 2 y x x 2 y x 2 y 【例 1】 1000 100 10 的结果是 【巩固】计算: 10 104 105 103 107
幂的运算
模块一
1.
同底数幂的乘法法则
同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加.
即 a m a n a m n ( m 、 n 都是正整数) 【巩固】如果把 x 2 y 看作一个整体,下列计算正确的是( A. x 2 y 2 y x x 2 y
3 6 ⑵ ( a8b 2 a 3b 4 1.8a 2 b3 ) 0.6ab 2 5 5
【巩固】计算:⑴ (4 x 2 y )2 8 y 2 ;
1 3 ⑶ ( a 3b 2 )3 ( ab 2 ) 2 ; 3 4
⑵ 9a m n b 2 m n c3n 2 m 3a 2 b3 . ⑷ (0.8 x 2 y n )3 (4 x 2 y n )2
2 3 2
计算下列各式:⑴ 2 x y
3 2 2 1 xy 4 z ;⑵ 3a 2 a 2 2a 2 5a 3 2
4
初中数学.整式的乘除.第 01 讲.学生版
Page 2 of 14
⑶ a a 3 a 4 a 2 2a 4 ;⑷ 2 x 2 x3 3x3 5 x x 7
计算 ( x3 2 x 2 5)(2 x 2 3x 1)
【巩固】计算: (3x 2 2)(5 x 4 2 x 2 3) (5 x 4 x 2 3)(3x 2 3)
2023年中考数学《整式的运算与因式分解》专题知识回顾及练习题(含答案解析)

2023年中考数学《整式的运算与因式分解》专题知识回顾及练习题(含答案解析)1. 合并同类型:法则:“一相加,两不变”,即系数相加,字母与字母的指数不变照写。
2. 整式的加减的实质:合并同类项。
3. 整式的乘除运算:①单项式×单项式:系数相乘,同底数幂相乘,其中一个因式单独存在的字母连同它的指数作为积的一个因式。
②单项式×多项式:单项式乘以多项式的每一项,变成单项式乘以单项式。
③多项式×多项式:用其中一个多项式的每一项乘以另一个多项式的每一项,变成单项式乘以单项式。
④单项式÷单项式:系数相除,同底数幂相除,被除数中单独存在的字母连同它的指数作为商的一个因式。
4. 乘法公式:①平方差公式:()()22b a b a b a −=−+。
②完全平方公式:()2222b ab a b a +±=±。
5. 因式分解的方法:①提公因式法:()c b a m cm bm am ++=++;②公式法:平方差公式:()()b a b a b a −+=−22完全平方公式:()2222b a b ab a ±=+±。
③十字相乘法:在c bx x ++2中,若()均为整数,且n m b n m mn c =+=,则: ()()n x m x c bx x ++=++2。
31.(2022•湖北)先化简,再求值:4xy﹣2xy﹣(﹣3xy),其中x=2,y=﹣1.【分析】先去括号,再合并同类项,然后把x,y的值代入化简后的式子进行计算即可解答.【解答】解:4xy﹣2xy﹣(﹣3xy)=4xy﹣2xy+3xy=5xy,当x=2,y=﹣1时,原式=5×2×(﹣1)=﹣10.32.(2022•盐城)先化简,再求值:(x+4)(x﹣4)+(x﹣3)2,其中x2﹣3x+1=0.【分析】根据平方差公式、完全平方公式、合并同类项法则把原式化简,整体代入即可.【解答】解:原式=x2﹣16+x2﹣6x+9=2x2﹣6x﹣7,∵x2﹣3x+1=0,∴x2﹣3x=﹣1,∴2x2﹣6x=﹣2,∴原式=﹣2﹣7=﹣9.33.(2022•长春)先化简,再求值:2+a)(2﹣a)+a(a+1),其中a=2﹣4.【分析】先去括号,再合并同类项,然后把a的值代入化简后的式子进行计算即可解答.【解答】解:(2+a)(2﹣a)+a(a+1)=4﹣a2+a2+a=4+a,当a=﹣4时,原式=4+﹣4=.34.(2022•北京)已知x2+2x﹣2=0,求代数式x(x+2)+(x+1)2的值.【分析】先去括号,再合并同类项,然后把x2+2x=2代入化简后的式子进行计算即可解答.【解答】解:x(x+2)+(x+1)2=x2+2x+x2+2x+1=2x2+4x+1,∵x 2+2x ﹣2=0,∴x 2+2x =2,∴当x 2+2x =2时,原式=2(x 2+2x )+1=2×2+1=4+1=5.35.(2022•广西)先化简,再求值:(x +y )(x ﹣y )+(xy 2﹣2xy )÷x ,其中x =1,y =21. 【分析】根据平方差公式和多项式除以单项式,可以将题目中的式子化简,然后将x 、y 的值代入化简后的式子计算即可.【解答】解:(x +y )(x ﹣y )+(xy 2﹣2xy )÷x=x 2﹣y 2+y 2﹣2y=x 2﹣2y ,当x =1,y =时,原式=12﹣2×=0.36.(2022•衡阳)先化简,再求值.(a +b )(a ﹣b )+b (2a +b ),其中a =1,b =﹣2.【分析】根据平方差公式以及单项式乘多项式的运算法则化简后,再把a =1,b =﹣2代入计算即可.【解答】解:(a +b )(a ﹣b )+2a +b )=a 2﹣b 2+2ab +b 2=a 2+2ab ,将a =1,b =﹣2代入上式得:原式=12+2×1×(﹣2)=1﹣4=﹣3.37.(2022•丽水)先化简,再求值:(1+x )(1﹣x )+x (x +2),其中x =21. 【分析】先根据平方差公式和单项式乘多项式的运算法则化简,再把x =代入计算即可.【解答】解:(1+x )(1﹣x )+x (x +2)=1﹣x 2+x 2+2x=1+2x ,当x =时,原式=1+=1+1=2.38.(2022•南充)先化简,再求值:(x +2)(3x ﹣2)﹣2x (x +2),其中x =3﹣1.【分析】提取公因式x +2,再利用平方差公式计算,再代入计算.【解答】解:原式=(x +2)(3x ﹣2﹣2x )=(x +2)(x ﹣2)=x 2﹣4,当x =﹣1时, 原式=(﹣1)2﹣4=﹣2.39.(2022•安顺)(1)计算:(﹣1)2+(π﹣3.14)0+2sin60°+|1﹣3|﹣12.(2)先化简,再求值:(x +3)2+(x +3)(x ﹣3)﹣2x (x +1),其中x =21. 【分析】(1)先化简各式,然后再进行计算即可解答;(2)先去括号,再合并同类项,然后把x 的值代入化简后的式子,进行计算即可解答.【解答】解:(1)(﹣1)2+(π﹣3.14)0+2sin60°+|1﹣|﹣ =1+1+2×+﹣1﹣2 =2++﹣1﹣2=1;(2)(x +3)2+(x +3)(x ﹣3)﹣2x (x +1)=x 2+6x +9+x 2﹣9﹣2x 2﹣2x=4x ,当x =时,原式=4×=2.40.(2022•岳阳)已知a 2﹣2a +1=0,求代数式a (a ﹣4)+(a +1)(a ﹣1)+1的值.【分析】先化简所求的式子,再结合已知求解即可.【解答】解:a (a ﹣4)+(a +1)(a ﹣1)+1=a 2﹣4a +a 2﹣1+1=2a 2﹣4a=2(a 2﹣2a ),∵a 2﹣2a +1=0,∴a 2﹣2a =﹣1,∴原式=2×(﹣1)=﹣2.41.(2022•苏州)已知3x 2﹣2x ﹣3=0,求(x ﹣1)2+x (x +32)的值. 【分析】直接利用整式的混合运算法则化简,进而合并同类项,再结合已知代入得出答案.【解答】解:原式=x 2﹣2x +1+x 2+x=2x 2﹣x +1,∵3x 2﹣2x ﹣3=0,∴x 2﹣x =1,∴原式=2(x 2﹣x )+1=2×1+1=3.42.(2022•荆门)已知x +x1=3,求下列各式的值: (1)(x ﹣x 1)2; (2)x 4+41x. 【分析】(1)利用完全平方公式的特征得到:(a ﹣b )2=(a +b )2﹣4ab ,用上述关系式解答即可;(2)将式子用完全平方公式的特征变形后,利用整体代入的方法解答即可.【解答】解:(1)∵=, ∴= = =﹣4x • =32﹣4=5;(2)∵=,∴=+2 =5+2=7,∵=,∴=﹣2=49﹣2=47.43.(2022•无锡)计算:(1)|﹣21|×(﹣3)2﹣cos60°; (2)a (a +2)﹣(a +b )(a ﹣b )﹣b (b ﹣3).【分析】(1(2)根据单项式乘多项式,平方差公式化简,去括号,合并同类项即可.【解答】解:(1)原式=×3﹣=﹣=1;(2)原式=a 2+2a ﹣(a 2﹣b 2)﹣b 2+3b=a 2+2a ﹣a 2+b 2﹣b 2+3b=2a +3b .44.(2022•安徽)观察以下等式:第1个等式:(2×1+1)2=(2×2+1)2﹣(2×2)2,第2个等式:(2×2+1)2=(3×4+1)2﹣(3×4)2,第3个等式:(2×3+1)2=(4×6+1)2﹣(4×6)2,第4个等式:(2×4+1)2=(5×8+1)2﹣(5×8)2,……按照以上规律,解决下列问题:(1)写出第5个等式:;(2)写出你猜想的第n个等式(用含n的式子表示),并证明.【分析】(1)根据题目中等式的特点,可以写出第5个等式;(2)根据题目中等式的特点,可以写出猜想,然后将等式左边和右边展开,看是否相等,即可证明猜想.【解答】解:(1)因为第1个等式:(2×1+1)2=(2×2+1)2﹣(2×2)2,第2个等式:(2×2+1)2=(3×4+1)2﹣(3×4)2,第3个等式:(2×3+1)2=(4×6+1)2﹣(4×6)2,第4个等式:(2×4+1)2=(5×8+1)2﹣(5×8)2,第5个等式:(2×5+1)2=(6×10+1)2﹣(6×10)2,故答案为:(2×5+1)2=(6×10+1)2﹣(6×10)2;(2)第n个等式:(2n+1)2=[(n+1)×2n+1]2﹣[(n+1)×2n]2,证明:左边=4n2+4n+1,右边=[(n+1)×2n]2+2×(n+1)×2n+12﹣[(n+1)×2n]2=4n2+4n+1,∴左边=右边.∴等式成立.45.(2022•西宁)八年级课外兴趣小组活动时,老师提出了如下问题:将2a﹣3ab﹣4+6b因式分解.【观察】经过小组合作交流,小明得到了如下的解决方法:解法一:原式=(2a﹣3ab)﹣(4﹣6b)=a(2﹣3b)﹣2(2﹣3b)=(2﹣3b)(a﹣2)解法二:原式=(2a﹣4)﹣(3ab﹣6b)=2(a﹣2)﹣3b(a﹣2)=(a﹣2)(2﹣3b)【感悟】对项数较多的多项式无法直接进行因式分解时,我们可以将多项式分为若干组,再利用提公因式法、公式法达到因式分解的目的,这就是因式分解的分组分解法.分组分解法在代数式的化简、求值及方程、函数等学习中起着重要的作用.(温馨提示:因式分解一定要分解到不能再分解为止)【类比】(1)请用分组分解法将x2﹣a2+x+a因式分解;【挑战】(2)请用分组分解法将ax+a2﹣2ab﹣bx+b2因式分解;【应用】(3)“赵爽弦图”是我国古代数学的骄傲,我们利用它验证了勾股定理.如图,“赵爽弦图”是由四个全等的直角三角形围成的一个大正方形,中间是一个小正方形.若直角三角形的两条直角边长分别是a和b(a>b),斜边长是3,小正方形的面积是1.根据以上信息,先将a4﹣2a3b+2a2b2﹣2ab3+b4因式分解,再求值.【分析】(1)用分组分解法将x2﹣a2+x+a因式分解即可;(2)用分组分解法将ax+a2﹣2ab﹣bx+b2因式分解即可;(3)先将a4﹣2a3b+2a2b2﹣2ab3+b4因式分解,再求值即可.【解答】解:(1)原式=(x2﹣a2)+(x+a)=(x+a)(x﹣a)+(x+a)=(x+a)(x﹣a+1);(2)原式=(ax﹣bx)+(a2﹣2ab+b2)=x(a﹣b)+(a﹣b)2=(a﹣b)(x+a﹣b);(3)原式=(a4+2a2b2+b4)﹣(2ab3+2a3b)=(a2+b2)2﹣2ab(a2+b2)=(a2+b2)(a2+b2﹣2ab)=(a2+b2)(a﹣b)2,∵直角三角形的两条直角边长分别是a和b(a>b),斜边长是3,小正方形的面积是1,∴a2+b2=32=9,(a﹣b)2=1,∴原式=9.。
3整式的乘除法、乘法公式复习
多项式除以单项式, 先把这个多项式的每一项分别除以单项式, 再把所得的商相加。
1 1 ( 1)(3x y xy xy ) ( xy ) 2 2
2 2
(1)原式=
1 3x y ( xy) 2
2
1 1 1 xy ( xy ) xy ( xy) 2 2 2
(1) (-a+b)2 = (b-a)2
(2) (-2m-1)2 = -(2m+1)
2
= (2m+1)2
(3) (2x+5)(-2x-5) = -(2x+5)(2x+5) = -(2x+5)2 (4) (x+y-1)2 = (x+y)-1
2
先变形再运用乘法公式计算:
(1)( x +2y-3) (x- 2y +3) ;
练习
考点训练
2、 9
1. 已知2m=a,32n=b,求:23m+10n. 3 2
n 2
3 ,求n的值
16
ab
4
2
- 2 3、
2009
2
2010
2009 ______
1、单项式的乘法
让我们一起来回顾:
1)、系数相乘 2)、同底数幂相乘 3)、只在一个单项式出现的 字母,连同它的指数作为积得 一个因式
2
a 1 1, 则a的取值范围____ 3)、 a 1
0
2 10 4)、 4 10 2 10 ___
9 3
6
考点训练
平方差公式
(a+b)(a-b) =
整式的乘除知识点整理

一、知识点归纳: (一)幂的四种运算:1、同底数幂的乘法:⑴语言叙述:同底数幂相乘,底数不变,指数相加; ⑵字母表示:a m ·a n = a m+n ;(m ,n 都是整数) ;⑶逆运用:a m+n = a m ·a n2、幂的乘方:⑴语言叙述:幂的乘方,底数不变,指数相乘; ⑵字母表示:(a m ) n = a mn ;(m ,n 都是整数); ⑶逆运用:a mn =(a m )n =(a n )m ;3、积的乘方:⑴语言叙述:积的乘方,等于每个因式乘方的积; ⑵字母表示:(ab)n = a n b n ;(n 是整数); ⑶逆运用:a n b n = (a b)n ;4、同底数幂的除法:⑴语言叙述:同底数幂相除,底数不变,指数相减;⑵字母表示:a m ÷a n = a m-n ;(a≠0,m 、n 都是整数); ⑶逆运用:a m-n = a m ÷a n .(二)整式的乘法:1、单项式乘以单项式:⑴语言叙述:单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式。
⑵实质:分三类乘:⑴系数乘系数;⑵同底数幂相乘;⑶单独一类字母,则连同它的指数照抄; 2、单项式乘以多项式:⑴语言叙述:单项式与多项式相乘,就是根据分配律用单项式去乘多项式中的每一项,再把所得的积相加。
⑵字母表示:c)=ma +mb +mc ;(注意各项之间的符号!) 3、多项式乘以多项式:(1)语言叙述:多项式与多项式相乘,先用一个多项式的每一项去乘另一个多项式的每一项,再把所得的积相加;(2)字母表示:=mn +mb +an +ab ;(注意各项之间的符号!) 注意点:⑴在未合并同类项之前,积的项数等于两个多项式项数的积。
⑵多项式的每一项都包含它前面的符号,确定乘积中每一项的符号时应用“同号得正,异号得负”。
⑶运算结果中如果有同类项,则要 合并同类项(三)乘法公式: 1、平方差公式:(1)语言叙述:两数和与这两数差的积,等于这两个数的平方差。
《乘法公式》整式的乘除与因式分解

把系数,同底数幂分别相除后,作为商的因式;对于只在被 除式里含有的字母,则连同他的指数一起作为商的一个因式 。
多项式除以单项式
定义
把一个多项式除以另一个单项式的商叫做多项式除以单项式。
运算法则
把这个多项式的每一项分别除以单项式,再把所得的商相加。
多项式除以多项式
定义
把一个多项式除以另一个多项式的商叫 做多项式除以多项式。
《乘法公式》整式的乘除与 因式分解
2023-11-09
目录
• 乘法公式 • 整式的乘法 • 整式的除法 • 因式分解 • 乘法公式、整式的乘除与因式分解的关系 • 经典例题解析
01
乘法公式
乘法公式的定义
乘法公式的定义
乘法公式是指将两个或多个数相 乘的结果用一个简单的符号表示
。例如,$(a+b)^2$ 表示 $a^2+2ab+b^2$。
因式分解的例题
3. 双十字相乘法
$x^2 + 5xy + 6y^2 = (x+2y)(x+3y)$。
2. 公式法
$a^2 - 8a + 16 = (a-4)^2$。
总结词
因式分解的方法多种多样,通过经典例题 解析可以更好地理解各种方法的适用条件 和操作技巧。
详细描述
因式分解是将一个多项式分解为若干个因 式之积的过程,下面通过一些例题及解析 来探讨因式分解的方法
乘法公式与因式分解的关系
乘法公式在因式分解中的应用
在因式分解中,乘法公式被广泛应用,例如利用乘法公 式进行多项式的展开、分组、约分等,这些方法都是基 于乘法公式进行推导和复杂的乘法公式问题时,通过因式分解可以 将问题转化为更简单的形式,例如利用因式分解解决一 些分式的约分问题。
数与代数复习 第一章 数与式 第2课 整式及其运算

课前准备:调音量、草稿本、笔等
请计算: 6 6 6 6 6 =3
解:设 : x 6 6 6 6 6
两边都平方得:x2 6 6 6 6 6
x2 6 x
即x2 x 6 0
解得:x 3, x 2(舍去)
1
2
字母的引入帮我们解决了一些复杂的问题. 代数式是传统数上的一种质的飞跃,你还知道 它的其他作用么?
并的结果是 2a 2b3 .
海宁名师云课堂
知识点二:整式的运算
2.整式的乘除运算
(1)幂的运算法则(m,n均为常数,a,b不为零)
①am an amn 请计算:4m 2n 请计算:2x2 (3xy2 )
②(am )n amn
22m 2n
6x3 y2
③(ab)m ambm
22mn 请计算:2x2 (3xy2 1)
了如图所示的三种方案:
ab
ab
b a
ab a
a
b
b
方案一
方案二
方案三
小明发现这三种方案都能验证公式: a2+2ab+b2=(a+b)2 , 对于方案一,小明是这样验证的: a2+ab+ab+b2=a2+2ab+b2=(a+b)2 请你根据方案二,方案三,写出公式的验证过程。
海宁名师云课堂
整式及其运算中考热点四:乘法公式的几何背景
a 2a3 2 x2 y 6 3
海宁名师云课堂
知识点二:整式的运算
1.整式的加减运算 整式的加减实质上就是合并同类项,遇到括号要先去括号
a 2a 3a
a2 (2a2 b2 ) a2 2a2 b2 3a2 b2 (x2 3x 4) (2x 4) x2 3x 4 2x 4 x2 5x
整式的乘除--乘法公式教案

乘法公式例:(1)计算:(22+1)(42+1)(82+1)(162+1). (2)计算:(2+1)(22+1)(42+1)(82+1)…(10242+1)变式练习:(1+12)(1+212)(1+412)(1+812)(1+1612)+(1+3112)例2 计算:(1)(2x+3y)²(2x-3y)²;(2)(a-2b+3c)(a-3c-2b). 例3 已知a+b+c=0,a²+b²+c²=4,那么4a+4b+4c的值等于 .小结:在运用完全平方公式时,常常借助下面的变形:2ab=(a+b)2-(a2+b2), 4ab=(a+b)2-(a-b)2,a2+b2=(a-b)2+2ab=(a+b)2-2ab.例4 阅读材料:把形如ax²+bx+c的二次三项式(或其中的一部分)配成完全平方式的方法叫做配方法,配方法的基本形式是完全平方公式的逆写,即a²±2ab+b²=(a±b)².例如:(x-1)²+3,(x-2)²+2x, (12x-2)²+34x²是x²-2x+4的三种不同形式的配方(“余项”分别是常数项、一次项、二次项——见横线上的部分).请根据阅读材料解决下列问题:(1)参考上面的例子,写出x²-4x+2的三种不同形式的配方;(2)将a²+ab+b²配方(至少两种形式);(3)已知a²+b²+c²-ab-3b-2c+4=0,求a+b+c的值.例5 已知9a²-12ab+8b²-4bc+2c²-4c+4=0,求a+b+c的值.课堂作业:1.计算a2(a+b)(a-b)+a2b2等于()A.a4B.a6C.a2b2D.a2-b22.将代数式x2+6x+2化成(x+p)2+q的形式为()A.(x-3)2+11B. (x+3)2-7C.(x+3)2-11D. (x+2)2+43. 如图,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为().A. (a-b)²=a²-2ab+b²B. (a+b) ²=a²+2ab+b²C. a²-b²=(a+b)(a-b)D. a²+ab=a(a+b)4、已知(m-n)2=8,(m+n)2=2,则m2+n2=()A.10B.6C.5D.35、先化简,再求值:(x+3)2+(2+x)(2-x),其中x=-2.6.多项式9x 2+1加上一个单项式后,使它能成为一个整式的完全平方,那么加上的单项式可以是多少?(给出一个你认为正确的答案即可)7.已知a,b,c 满足a ²+b ²+c ²-ab-bc-ac=0(a,b,c 为正数),则a,b,c 之间有怎样的大小关系?1.化简()42a a ⋅-的结果是 ( )2.化简()2423a a a ⋅+ 的结果正确的是( )3.()()()2x 2x 2x 4+-+的计算结果是( )4.若a +b =6,a b =3,则3a 2b +3ab 2的值是( )5.若x x a 2,b 3==,则()3xab = .6.已知:()35m 11a a a ⋅=,则m 的值为 .7.计算()2242a a 9a 39⎛⎫--⋅- ⎪⎝⎭的结果是 . 8.若a -b =1,a b =-2,则()()a 1b-1+= .9.已知:()()2222x y 1,x y 17,y =+=-=+则x ,x y = .10.若9x 2+m x y +16y 2是一个完全平方式,则m 的值是 .11.在边长为a 的正方形中挖去一个边长为b 的小正方形(a >b )(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,第20题图图乙图甲a a 可以验证 (填写序号).①()2a+b =a 2+2ab +b 2 ②()2a -b =a 2-2ab +b 2③a 2-b 2=()()a b a b +- ④()()a 2b a b +-=a 2+a b -2b 212.探究题:观察下列式子:(x 2-1)÷(x -1)=x +1;(x 3-1)÷(x -1)=x 2+x +1;(x 4-1)÷(x -1)=x 3+x 2+x +1(x 5-1)÷(x -1)=x 4+x 3+x 2+x +1⑴.你能得到一般情况下(x n -1)+(x -1)的结果吗?(n 为正整数)⑵.根据⑴的结果计算:1+2+22+23+24+…+262+263.数学人教版八年级上第十四章 整式的乘法与因式分解单元检测一、选择题1.下列计算中正确的是( ).A .a 2+b 3=2a 5B .a 4÷a =a 4C .a 2·a 4=a 8D .(-a 2)3=-a 62.(x -a )(x 2+ax +a 2)的计算结果是( ).A .x 3+2ax 2-a 3B .x 3-a 3C .x 3+2a 2x -a 3D .x 3+2ax 2+2a 2-a 33.下面是某同学在一次测验中的计算摘录,其中正确的个数有( ).①3x 3·(-2x 2)=-6x 5;②4a 3b ÷(-2a 2b )=-2a ;③(a 3)2=a 5;④(-a )3÷(-a )=-a 2.A .1个B .2个C .3个D .4个4.已知被除式是x 3+2x 2-1,商式是x ,余式是-1,则除式是( ).A .x 2+3x -1B .x 2+2xC .x 2-1D .x 2-3x +15.下列各式是完全平方式的是( ).A .x 2-x +14B .1+x 2C .x +xy +1D .x 2+2x -16.把多项式ax 2-ax -2a 分解因式,下列结果正确的是( ).A .a (x -2)(x +1)B .a (x +2)(x -1)C .a (x -1)2D .(ax -2)(ax +1)7.如(x +m )与(x +3)的乘积中不含x 的一次项,则m 的值为( ).A .-3B .3C .0D .18.若3x =15,3y =5,则3x -y 等于( ).A .5B .3C .15D .109、下列多项式中能用平方差公式分解因式的是( )(A )22)(b a -+ (B )mn m 2052- (C )22y x -- (D )92+-x10、 下列各式能用完全平方公式分解因式的是( )A 、4x 2+1B 、4x 2-4x -1C 、x 2+xy +y 2D 、x 2-4x +411、△ABC 的三边长分别a 、b 、c ,且a+2ab =c+2bc ,△ABC 是( )A.等边三角形B.等腰三角形C.直角三角形D.等腰直角三角形12、 把(-2)2009+(-2)2010分解因式的结果是( ).A. 22008B. -2 2008C. -2 2009D. 2200913、一个正方形的边长增加了2cm ,面积相增加了32cm 2,则这个正方形的边长为( )A 、6cmB 、5cmC 、8cmD 、7cm二、填空题14.计算(-3x 2y )·(213xy )=__________. 15.计算:22()()33m n m n -+--=__________. 16.计算:223()32x y --=__________. 17.计算:(-a 2)3+(-a 3)2-a 2·a 4+2a 9÷a 3=__________.18.当x __________时,(x -4)0=1.19.若多项式x 2+ax +b 分解因式的结果为(x +1)(x -2),则a +b 的值为__________.20.若|a -2|+b 2-2b +1=0,则a =__________,b =__________.21.已知a +1a =3,则a 2+21a的值是__________. 22、已知a b ab +=-=31,,求 a b 22+ =23、观察下列各式,探索发现规律:22-1=3=1×3;42-1=15=3×5;62-1=35=5×7;82-1=63=7×9;102-1=99=9×11;……用含正整数n 的等式表示你所发现的规律为 .24、在日常生活中如取款、上网等都需要密码.有一种用“因式分解”法产生密码,方便记忆.原理是:如对于多项式44y x -,因式分解的结果是))()((22y x y x y x ++-,若取x=9,y=9时,则各个因式的值是:(x -y)=0,(x+y)=18,(x 2+y 2)=162,于是就可以把“018162”作为一个六位数的密码.对于多项式234xy x -,取x=10,y=10时,用上述方法产生的密码是: __________ (写出一个即可).三、解答题1、计算:(1)32a 3b 2c ÷21a 2b (2)3223)()(x x -⋅- (3)(-4x -3y )2(4))32)(32(+--+y x y x (5) (a +2b -c )2. (6(ab 2)2·(-a 3b )3÷(-5ab );(7)x 2-(x +2)(x -2)-(x +1x)2; (8)[(x +y )2-(x -y )2]÷(2xy ).26.把下列各式因式分解:(1)3x -12x 3; (2)-2a 3+12a 2-18a ; (3)9a 2(x -y )+4b 2(y -x );(4)(x +y )2+2(x +y )+1. (5))(3)(2x y b y x a --- (6)1222-+-b ab a(7)(x -1)(x +4)-36 (8)(m 2+n 2)2-4m 2n227、用简便方法计算:⑴20042-2005×2003 ⑵22 293⎛⎫ ⎪⎝⎭28.先化简,再求值.2(x-3)(x+2)-(3+a)(3-a),其中,a=-2,x=1.,其中.5、若a2+2a+b2-6b+10=0,求a2-b2的值.29.已知:a,b,c为△ABC的三边长,且2a2+2b2+2c2=2ab+2ac+2bc,试判断△ABC 的形状,并证明你的结论.6、若△ABC三边a、b、c满足a2+b2+c2=ab+bc+ca.判断△ABC的形状30.在日常生活中,如取款、上网等都需要密码.有一种用“因式分解”法产生的密码,方便记忆.原理是:如对于多项式x4-y4,因式分解的结果是(x-y)(x+y)·(x2+y2),若取x=9,y=9时,则各个因式的值是:(x-y)=0,(x+y)=18,x2+y2=162,于是就可以把“018162”作为一个六位数的密码.对于多项式4x3-xy2,取x=10,y=10时,请你写出用上述方法产生的密码.整式的乘除与因式分解习题练习一、选择题(每题3分,共30分)1、44221625)(______)45(b a b a -=+-括号内应填( )A 、2245b a +B 、2245b a +C 、2245b a +-D 、2245b a --2、下列计算正确的是( )A 、22))((y x x y y x -=-+B 、22244)2(y xy x y x +-=+-C 、222414)212(y xy x y x +-=- D 、2224129)23(y xy x y x +-=--3、在2222222)())(3(,)()2(),5)(5()5()1(b a b a y x y x x x x +=--+=+-+=-+(4)ab ab ab a b b a =-=--23)2)(3(中错误的有( )A 、1个B 、2个C 、3个D 、4个4、下列各式中,能用平方差公式计算的是( )A 、))((b a b a +--B 、))((b a b a ---C 、))((c b a c b a +---+-D 、))((b a b a -+-5、如果:=-==+-222)32,5,0168y x x y xy x 则(且( )A 、425B 、16625C 、163025D 、162256、计算:1.992-1.98×1.99+0.992得( )A 、0B 、1C 、8.8804D 、3.96017、如果k x x ++82可运用完全平方公式进行因式分解,则k 的值是( )A 、8B 、16C 、32D 、648、(x 2+px+8)(x 2-3x+q)乘积中不含x 2项和x 3项,则p,q 的值 ( )A 、p=0,q=0B 、p=3,q=1C 、p=–3,–9D 、p=–3,q=19、对于任何整数m ,多项式9)54(2-+m 都能( )A 、被8整除B 、被m 整除C 、被m -1整除D 、被(2m -1)整除10.已知多项式2222z y x A -+=,222234z y x B ++-=且A+B+C=0,则C 为() A 、2225z y x -- B 、22253z y x -- C 、22233z y x -- D 、22253z y x +-二、填空题(每题3分,共30分)11、++xy x 1292 =(3x + )212、2012= , 48×52= 。
七年级下册整式的乘除

【练习1】计算:
① (a+b-c)4·(a+b-c)5 ② (a-b)2·(b-a)3
【练习2】判断(正确的 错误的打“×”)
打“√”,
(1) x3·x5=x15 (×) (2) x·x3=x3 (×)
(3) x3+x5=x8 (×) (3)x2·x2=2x4 (×)
1.计算:
(1)s7 s3
(3)(t)11 (t)2
(5)(3)6 (3)2
(2)x10 x8
(4)(ab)5 (ab)
(6)a100 a100
2.填空:
x x (1) 7 ( )= 8
a a (2)(
)
3
=
8
c c b (3)b4 b3 ( ) = 21 (4) 8 ( )= 5
3. 与整式加法之间的关系。如2a与a2的区别。
【法则推导】 33·32=?(-3)3·(-3)2=?
am ·an等于什么(m,n都是正整数)? 为什么?
am ·an =(a·a·… ·a)(a·a·… ·a)
m个a
=a·a·… ·a
m+n个a
=am+n
n个a
同底数幂相乘 底数 不变 , 指数 相加 .
(3) (an)3 = an×3 =a3n ;
(4) -(x2)m = -x2×m = -x2m ;
(5) (y2)3 ·y= y2×3 ·y = y6 ·y = y7;
(6) 2(a2)6 – (a3)4 =2a2×6 - a3×4 =2a12-a12 =a12.
【练习1】计算
⑴( [ a)3 ]2 ⑵( [ x 2 y)3 ]2n
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
整式的乘除和因式分解
【考点知识】
1、整式的乘法法则
2、整式的乘法公式
3、同底数幂的除法
4、整式的除法法则
5、因式分解
【基础过关】
1.(2014•邵阳,第2题3分)下列计算正确的是( ) A . )
2x ﹣x =x
B . a 3•a 2=a 6
C . (a ﹣b )2=a 2﹣b 2
D . (a +b )(a ﹣b )=a 2+b 2
2、下列运算正确的是 ( )
A 、 9
3
3
842x x x ÷= B 、 23
23
440a b a b ÷= C 、22m m a
a a ÷= D 、221
2()42
ab c ab c ÷-=-
3、下列多项式乘法中可以用平方差公式计算的是( )
^
A 、))((b a b a -+-
B 、)2)(2(x x ++
C 、)3
1
)(31(x y y x -
+ D 、)1)(2(+-x x 4、若多项式x 2
+kx+25是一个完全平方式,则值是( ) B.±10 D.±5
5、在边长为a 的正方形中挖去一个边长为b 的小正方形(a >b ),再沿
虚线剪开,如图①,然后拼成一个梯形,如图②,根据这两个图形的面积关系,表明下列式子成立的是( )。
A 、a 2+b 2=(a +b )(a -b )
B 、(a +b )2=a 2+2ab +b 2
C 、(a -b )2=a 2-2ab +b 2
D 、a 2-b 2=(a -b )2
6.如图,你能根据面积关系得到的数学公式是( )
A .a 2-b 2=(a+b )(a -b )
B .(a+b )2=a 2+2ab+b 2
C .(a -b )2=a 2-2ab+b 2
D .a (a+b )=a 2
+ab 7、下列分解因式正确的是( )
A .3x 2
- 6x =x(x -6) B .-a 2
+b 2
=(b+a)(b -a)
C .4x 2 - y 2=(4x -y)(4x+y)
D .4x 2-2xy+y 2=(2x -y)2
a
b
b b a
a
图①
!
(第05题
:
8.如果m -n=-5,mn=6,则m 2
n -mn 2
的值是( ) A .30 B .-30 C .11 D .-11
【专题讲解】
知识专题一:同底数幂的乘除及应用
1.若43=x ,79=y ,则y
x 23-的值为( )
A .74
B .47
C .3-
D .72
2、若a 为正整数,且x 2a =5,则(2x 3a )2÷4x 4a 的值为( )
(A )5 (B )2
5
(C )25 (D )10
3、已知a m =5,a n =4, 求a 3m-2n
的值.4、已知3a -2b =2,求27a ÷9b
的值.
[
5、已知83x
÷162x
=4,求x 的值 6、已知2x ÷16y
=8,求2x -8y 的值.
专题知识二:整式乘法公式综合应用
1.若25x 2
+30xy +k 是一个完全平方式,则k 是( )
A .36y 2
B .9y 2
C .6y 2
D .y 2
2.(-a +1)(a +1)(a 2+1)等于……………( ) ,
(A )a 4-1 (B )a 4+1 (C )a 4+2a 2+1 (D )1-a 4
3、计算
(1)(a+b+c )(a+b-c ) (2)(a-2b+c )(a+2b-c )
(3)(a+b-c )2 (4)(m-n+3)2
^
专题知识三:整式乘法公式变形逆用
1.已知a +b =10,ab =24,则a 2
+b 2
的值是 ( )
(A )148 (B )76 (C )58 (D )52
2.若a -b =8,a 2+b 2
=82,则3ab 的值为( )
A .9
B .-9
C .27
D .-27
3.已知(m ﹣n )2=8,(m+n )2=2,则m 2+n 2
=( ) A .10 B .6 C .5 D .3
4、已知a+b=10,ab=24,则a 2
+b 2等于( )
5、若x 2
-y 2
=20,且x +y =-5,则x -y 的值是( ) A .5 B .4 C .-4 D .以上都不对 "
6、如果a+b=2006,a -b=2,那么a 2
-b 2
=________. 7、已知x 2
-y 2
=6,x+y=3,则x-y=__________.
8.已知1,5==+xy y x ,求 ①22y x +;②2
)(y x -.
9、已知x+y=3,xy=40,求下列各式的值 (1)x 2
+y 2
(2)(x-y)
2
10、已知:x+y=4,x 2+y 2 =10,求(x -y )2
的值。
|
11、已知:x 2+y 2=26,4xy=12,求(x+y )2和(x-y )2
的值。
12、若(a+b )2
=13(a-b )2
=7求a 2
+b 2
和ab 的值。
知识专题四:化简与求值
>
1.计算:求当75,15
a b = =时,22
(1)(1)21ab ab a b ⎡⎤+--+⎣⎦÷ab 的值.
2、先化简,再求值.(2x+3)(2x ﹣3)﹣4x (x ﹣1)+(x ﹣2)2
,其中x=﹣
.
)
3.[(3x+2y)(3x-2y)-(x+2y)(5x-2y)]÷4x ,其中x=-2,y=-3。
%
4.先化简,后求值.x y x y x y x 2)])(()[(2
÷--+-,其中5.1,3==y x
5.[(x +21y )2+(x -21y )2](2x 2-2
1
y 2),其中x =-3,y =4.
[
知识专题五:不含几次项,求其他字母的值。
1、如(x+m)与(x+3)的乘积中不含x 的一次项,则m 的值为( ) A. –3 B. 3 C. 0 D. 1
2、若(x +m )(x -8)中不含x 的一次项,则m 的值为( )
(A )8 (B )-8 (C )0 (D )8或-8
3、试说明:代数式(2x +3)(6x +2)-6x (2x +13)+8(7x +2)的值与x 的取值无关.
^
4、若(x 2+px +q )(x 2-2x -3)展开后不含x 2,x 3项,求p 、q 的值。
5、若(x 2
+nx+3)(x 2
-3x+m)的展开式中不含x 2
和x 3
项,求m 、n 的值.
.
知识专题五:因式分解综合应用 类型一:较复杂的因式分解
(1) 16x 4-y 4
(2)abx 2
-2abx+ab
(3)x 2-y 2-6x+9 (4)a 2+b 2-c 2-2ab
(5)3mx 2+12mxy+12my 2 (6)(x+2)(x -3)+4
~
类型二:因式分解应用求值
1、已知x 2+x -1=0,求x 3+2x 2
+3的值.
2、已知;,012=-+a a 求199922
3++a a 的值
—
3、已知:a -b=3,ab=4,求3a 2
b -3ab 2
的值.
4、已知,8=+n m ,15=mn 求2
2n mn m +-的值
、
5、已知1=-y x ,2=xy ,求3
2
2
3
2xy y x y x +-的值.
6、已知a b ab +==53,,求代数式a b a b ab 32232++的值。
#
7.已知x +x 1=2,求x 2+21x ,x 4
+41x
的值.
8、已知则,51=+a a 2
241
a a a ++的值.。
9、若a 与b 都是有理数,且满足a 2
+b 2
+5=4a-2b,则(a+b)2009
的值.
10、已知:x 2
+y 2
+z 2
-2x-4y-6z+14=0,求(xz )y
的值。
类型二:因式分解与图形判定
1.若a 、b 、c 、为三角形的三边,且a 2
+b 2
+c 2
-ab-bc-ac=0,试确定三角形的形状。
2.已知c b a 、、是△ABC 的三边的长,且满足0)(222
2
2
=+-++c a b c b a ,试判断 此三角形的形状.
3、已知a、b、c是△ABC的三边,且满足关系式a2+c2=2ab+2bc-2b2,试说明△ABC是等边三角形.。
