Origin的非线性拟合功能
用origin拟合流变曲线

用origin拟合流变曲线流变学是研究物质在外力作用下变形和流动规律的学科。
在实际应用中,流变学被广泛应用于材料科学、化学工程、食品工业、医药等领域。
流变曲线是流变学中最基本的曲线,它描述了物质在外力作用下的变形规律。
在流变学中,常用的流变曲线包括剪切应力-剪切速率曲线、应力-应变曲线等。
本文将介绍如何使用Origin软件拟合流变曲线。
一、数据处理首先,我们需要将实验得到的流变数据导入Origin软件中。
在导入数据时,需要注意数据的格式和单位。
通常,流变数据的单位为Pa或Pa·s,而剪切速率的单位为s^-1。
在导入数据后,我们需要对数据进行处理,以便进行拟合。
具体来说,我们需要对数据进行平滑处理和去噪处理。
平滑处理可以使用Origin软件中的平滑函数进行,去噪处理可以使用滤波函数进行。
二、拟合流变曲线在数据处理完成后,我们可以开始拟合流变曲线。
在Origin软件中,拟合流变曲线可以使用非线性拟合功能进行。
具体来说,我们需要选择合适的拟合函数,并设置拟合参数的初值和范围。
常用的拟合函数包括Maxwell模型、Kelvin模型、Bingham模型等。
在选择拟合函数时,需要根据实验数据的特点进行选择。
例如,对于粘弹性流体,可以选择Maxwell模型进行拟合。
在设置拟合参数的初值和范围时,需要根据实验数据的范围进行选择。
通常,初值可以选择实验数据的平均值,范围可以选择实验数据的最大值和最小值。
在设置好拟合参数后,我们可以使用非线性拟合功能进行拟合。
拟合完成后,我们可以得到拟合曲线和拟合参数。
三、结果分析在得到拟合曲线和拟合参数后,我们可以进行结果分析。
具体来说,我们可以计算拟合曲线和实验数据之间的误差,并评估拟合结果的可靠性。
常用的误差计算方法包括均方根误差、平均绝对误差等。
在评估拟合结果的可靠性时,需要考虑拟合曲线的拟合度和拟合参数的误差范围。
四、结论在本文中,我们介绍了如何使用Origin软件拟合流变曲线。
oringe多未知数拟合曲线

oringe多未知数拟合曲线在Origin软件中,进行多未知数拟合曲线通常指的是使用非线性拟合(Nonlinear Fitting)功能。
非线性拟合可以用来分析和确定数据点与某个非线性方程之间的最佳拟合关系。
在Origin中,可以使用内置的拟合工具箱(Fit Tools)来进行非线性拟合。
以下是使用Origin进行多未知数非线性拟合的基本步骤:1. 打开Origin软件,并导入或创建你的数据文件。
2. 在数据表格中,确保你有足够的列来表示你的X数据和Y数据。
如果你的数据集包含多个Y变量,你可能需要对每个变量分别进行拟合。
3. 选择你的数据列,然后点击菜单栏中的“分析”(Analysis)。
4. 在下拉菜单中选择“拟合”(Fitting),然后选择“非线性拟合”(Nonlinear Fitting)。
5. 在弹出的对话框中,你可以选择不同的拟合类型,如“自定义方程”(Custom Equations)或“内置函数”(Built-in Functions)。
如果你知道你想要拟合的方程形式,可以选择“自定义方程”并输入你的方程。
如果你想要从一系列内置函数中选择,可以选择“内置函数”并从列表中选择一个。
6. 设置拟合参数。
在“拟合设置”(Fit Settings)区域,你可以设置初始参数值、拟合范围、拟合精度等。
7. 点击“开始拟合”(Start Fit)按钮,Origin将开始拟合过程,并在对话框下方显示拟合结果。
8. 查看拟合结果。
拟合结果包括最佳拟合参数、拟合曲线图、残差图等。
9. 根据需要,你可以导出拟合结果或使用拟合曲线进行进一步的分析。
请注意,非线性拟合可能需要较长的计算时间,尤其是对于复杂的数据集或方程。
此外,拟合结果的质量很大程度上取决于数据的质量和初始参数的选择。
在使用非线性拟合时,可能需要多次尝试和调整以达到满意的拟合效果。
关于origin的自定义非线性拟合操作
关于origin的自定义非线性拟合操作
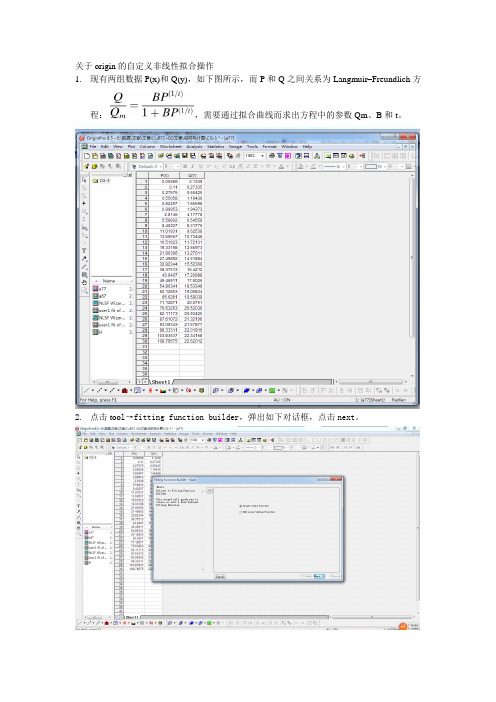
1.现有两组数据P(x)和Q(y),如下图所示,而P和Q之间关系为Langmuir–Freundlich方
程:,需要通过拟合曲线而求出方程中的参数Qm、B和t。
2.点击too l→fitting function builder,弹出如下对话框,点击next。
3.输入方程名称Langmuir–Freundlich,并选择origin C,如图所示,点击next。
4.输入自变量P、因变量Q和参数(Qm, B, t),如图所示,点击next。
5.将方程表达式转化为:Q=Qm*B*P^(1/t)/(1+(B*P^(1/t)))输入后,点击途中红圈所示编译
按钮。
后返回上图。
7.一直点击next,直到finish。
选中P(x)和Q(y)两列数值后点击annlysis→fitting→nonliner
curve fit→open dialog,出现下图对话框,通过category和function两个下拉菜单选择
我们刚才编辑好的方程:Langmuir–Freundlich。
由于参数的初始值系统默认均为1,这并不符合方程的收敛要求,所以需要点击红圈所示的粗拟合以便得到符合要求的参数初
始值,然后点击fit即可得到通过最小二乘法拟合出的自定义非线性曲线的各项参数值。
8.拟合后的参数值以及曲线数据等均会在同一个worbook的新sheet中展示,如下图所示。
origin 拟合曲线 x数据类型

origin 拟合曲线x数据类型Origin 是一款常用的科学数据处理和绘图软件。
对于数据拟合,Origin 支持多种方法,例如线性回归、非线性回归等。
关于x 数据类型的问题,具体的要求会取决于你要进行哪种拟合。
一般来说,Origin 支持的数据类型包括:
1. 数值型:这是最基本的数据类型,用于表示连续的数值。
例如,温度、压力、时间等。
2. 字符串型:用于表示文本数据,例如人的名字、标签等。
3. 逻辑型:用于表示真或假的数据,例如开/关、是/否等。
如果你想要对一组数据点进行拟合,通常x 轴应该是数值型数据,例如时间、距离、电压等。
如果你的x 数据是字符串型数据,例如日期,你可能需要先将它们转换为数值型数据再进行拟合。
如果你需要进行非线性拟合,你可以使用Origin 的非线性最小二乘法拟合功能。
在拟合之前,确保你的x 和y 数据都正确地输入到了Origin 中。
然后,你可以选择适合的函数形式,并调整其参数,使它们适应你的数据。
你可以查看Origin 的帮助文档或者在线教程,以了解更多关于拟合和非线性拟合的详细信息。
使用Origin进行非线性高斯拟合

使用Origin进行非线性高斯拟合在数据科学和机器学习中,非线性高斯拟合是一种常见的技术,用于拟合非线性函数到实际观测数据。
它是通过最小化误差函数来确定拟合参数的过程。
在本文中,我们将介绍如何使用Origin进行非线性高斯拟合。
首先,我们需要准备数据。
在Origin中,我们可以将数据导入为一个数据集。
选择"File"菜单中的"Import"选项,然后选择要导入的数据文件。
一旦数据被导入,我们可以在Origin的工作表中看到它。
接下来,我们需要选择适当的拟合函数。
对于非线性高斯拟合,我们可以选择高斯函数作为拟合函数。
在Origin中,我们可以通过选择"Analysis"菜单中的"Peak Analysis"选项来找到高斯函数。
在"Peak Analysis"对话框中,我们可以看到各种各样的拟合函数。
选择高斯函数,并点击"OK"按钮。
接下来,我们需要在工作表中选择我们要拟合的数据。
在Origin的工作表中,我们可以使用鼠标选择数据。
选择我们要拟合的数据之后,我们可以点击工具栏上的"Peak Analysis"按钮。
这将打开"Peak Analysis"对话框。
在"Peak Analysis"对话框中,我们可以设置拟合参数的初值。
我们可以手动输入初值,或者使用"Auto Search"按钮自动初值。
一旦我们设置好初值,我们可以点击"Fit"按钮开始拟合过程。
在拟合过程完成后,我们可以在Origin的工作表中看到拟合结果。
拟合结果包括拟合参数的值、标准误差、相关系数等。
我们还可以在工作表中绘制拟合曲线和残差图。
在拟合过程完成后,我们可以对拟合结果进行分析。
我们可以计算拟合曲线上的极值点,并计算其位置和幅值。
Origin的非线性拟合功能

拟合函数仔细分析,以及用户的经验
6、进行拟合
误差 拟合的结果 取值范围是 [0, 1],越接 近 1,则越表明该参数有 取消选中的话,则这个参 数在迭代过程中保持不变, 可能过参数化了。这个时 候,用户就要考虑拟合的 当函数中某个参数被确定 模型是否正确了,是否可 的话,就可以在这里设置 以简化模型,除去一些参 数。 大多数情况下,过参数化的模型都应该认真审视,但并不是所有的过参数化的模型 都是坏的模型。比如说,绝大多数的指数方程都是这样的模型
执行一次LM iteration
7、生成结果
创建一个matrix,将 Var-Cov Matrix写入 其中
创建一个worksheet, 将拟合结果写入其中
要Find X,在这里填入y的值,y 必须在数据集之内
要Find Y,在这里填入x的值,x 在数据集内、外都可以
自定义拟合函数
1.添加一个新的函数类别,将自定义的函数都放置 在这个类别里,以便以后重复使用
点击这里进行编译
用户自定义函数存放在Origin\FitFunc 文件夹,文 件名为\FunctionName.FDF
自定义函数NLSF拟合上机练习1
完成Origin软件自带的使用自定义函数进 行NLSF拟合的例题文件:
C:\Program Files\OriginLab\OriginPro75 \Samples\Analysis\Curve Fitting\NLSF User Def Func.OPJ
1、选择拟合 函数
若自定义函数就 选择New
2、设置函数参数的 一些约束条件(没 有的话就跳过)
这里可以写一些参数的线性约束条件, 设参数为a, b, c, d,条件可以是: a>b; a+2*b>=c*2-d; 4<b<c<6; a/3<9 支持5种关系: =, <, <=, >, >=. 约束之间用分号分分隔,换行按 CTRL+ENTER.
Origin的非线性拟合功能

Origin的非线性拟合功能Origin是一种科学绘图和数据分析软件,其中的非线性拟合功能是其最强大和最重要的功能之一、非线性拟合是一种数学技术,用于通过数据点来拟合非线性函数。
在科学和工程领域中,很多实际现象都对应着非线性关系,因此非线性拟合在数据分析中具有广泛的应用。
Origin的非线性拟合功能可以帮助用户通过对试验数据进行拟合,找到最佳的曲线拟合来描述数据之间的关系。
此功能通过多种拟合方法,包括非线性最小二乘法、加权非线性最小二乘法、全局拟合和多曲线拟合,提供了丰富的拟合选择。
1. 多种拟合方法:Origin提供了多种非线性拟合方法,包括Levenberg-Marquardt算法、Trust-Region算法和递归拟合等。
用户可以根据实际数据和需要选择最适合的拟合方法。
2. 自定义模型:Origin允许用户自定义拟合模型。
用户可以通过添加自定义公式和参数,构建适合自己研究的非线性模型。
这使得Origin的非线性拟合功能灵活而且可扩展。
3. 拟合统计分析:Origin的非线性拟合功能提供了丰富的统计分析工具,包括拟合参数的置信区间估计、拟合曲线的置信带计算、拟合误差分析等。
这些统计分析工具可以帮助用户评估拟合结果的可靠性。
4. 多变量拟合:Origin允许用户进行多变量非线性拟合,即同时拟合多个数据集、多个模型或多个曲线。
这种功能在研究多因素影响、复杂数据处理和模型比较等方面非常有用。
5. 拟合优化:Origin的非线性拟合功能提供了拟合优化选项,用户可以通过设置拟合参数的初始值、约束条件和拟合目标的权重等来改善拟合结果。
这些优化选项能够帮助用户更好地处理复杂数据和噪声。
6. 数据可视化:Origin的非线性拟合功能可以将拟合结果与原始数据一起绘制在图表中,方便用户直观地比较和分析拟合效果。
用户还可以使用Origin的丰富绘图工具,对拟合结果进行进一步的可视化和优化。
7. 输出和导出:Origin的非线性拟合功能可以输出拟合参数、统计分析结果和拟合曲线等信息,方便用户进行后续数据处理和报告撰写。
用Origin软件的线性拟合和非线性曲线拟合功能处理实验数据

用Origin软件的线性拟合和非线性曲线拟合功能处理实验数据用Origin软件的线性拟合和非线性曲线拟合功能处理实验数据在科学研究和实验中,数据处理是一个至关重要的环节。
通过对实验数据进行分析和拟合,可以得到对现象的更深入和准确的理解。
Origin软件是一种功能齐全且易于使用的数据分析软件,它提供了各种分析和拟合功能,包括线性拟合和非线性曲线拟合。
本文将探讨如何使用Origin软件的这两个功能来处理实验数据。
首先,我们需要明确线性拟合的概念。
线性拟合是通过一条直线来近似表示实验数据的趋势。
它通常用于分析变量之间的线性关系,并确定其相关性。
在Origin软件中,我们可以通过选择线性拟合的功能来进行这一分析。
以某个实验数据为例,我们首先打开Origin软件并加载实验数据。
然后,在图表中选择需要进行线性拟合的数据集,并点击工具栏上的“线性拟合”按钮。
Origin软件会自动计算最佳拟合直线,并在图表中显示出来。
此外,Origin软件还提供了拟合曲线的各种统计信息,如拟合趋势线的斜率、截距、相关系数和拟合误差等。
线性拟合的结果可以帮助我们推断实验数据中的相关性和趋势。
如果拟合直线的斜率为正值,并且有较高的相关系数,那么我们可以得出结论,实验数据之间存在正相关关系。
反之,如果斜率为负值,则表示实验数据之间存在负相关关系。
此外,线性拟合还可以用于预测未知数据的数值。
值得注意的是,线性拟合适用于处理线性关系较为明显的数据。
如果实验数据的分布较为复杂,并且存在非线性关系,就需要使用非线性曲线拟合功能来分析数据。
非线性曲线拟合是通过曲线来近似表示实验数据的趋势。
与线性拟合类似,非线性曲线拟合也能提供各种统计信息,如拟合曲线的拟合度、参数值、相关系数等。
使用Origin软件的非线性曲线拟合功能,可以进行多种拟合模型的选择和分析。
例如,常见的非线性模型有指数、对数、幂函数等。
我们可以根据实验数据的特点和分布选择合适的非线性模型,并进行参数估计和曲线拟合。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C:\Program Files\OriginLab\OriginPro75 \Samples\Analysis\Curve Fitting\Exp Decay.OPJ
Fit Exponential Growth 一阶指数增长拟合
Fit Sigmoidal S拟合
2、定义新函数
参数的数目 默认的参数名为P1,P2等, 若要使用自定义的符号,选中 这里 ,参数之间用英文逗号 分隔开,与C语言相同
使用Origin C 编写函数
定义参数和变量时,以下 定义参数和变量时, 符号不可以使用(Origin内 部要用):
x1,x2,…,xn , , , y1,y2,…,yn , , , z1,z2,…,zn , , , i,t,j ,e ,,
• Simplex Method(单纯形算法):当L-M算法不 能得出最佳的拟合结果时,可尝试使用该算法。
非线性拟合的结果如何评价?
确定系数R 2: ≤ R 2 ≤ 1 , 对同一组数据,越大越好 0 ˆ 残差平方和:χ 2 = ∑ Yi − Yi , 对同一组数据,越小越好
i =1 n
(
)
2
reduced χ =
自定义函数NLSF拟合上机练习2
时间 (小时) 0.25 0.5 0.75 1 1.5 2 2.5 3 3.5 4 4.5 5 6 7 8 9 10 11 12 13 14 15 酒精含量 (毫克/百毫升) 30 68 75 82 82 77 68 68 58 51 50 41 38 35 28 25 18 15 12 10 7 7
1、选变量
2、选数据 3、确认将数 据赋予变量
设X变量的时候 也是点左边的按 钮,不要点这个 按钮!!
5、模拟曲线
存放模拟曲线的数据 点的数据集名称 根据这里的参数绘制曲线, 选择 Action:Fit, 则最后一 次选中的参数被传递给Fit程 序
使用Origin进行非线性拟合,必须指定各参数 的初始值,使用内置拟合函数时,Origin会自 动设置好比较合适的初始值。 使用自定义函数拟合时,用户必须自己指定 初始值,初始值选的不好,拟合就有可能不 成功。好的初始值的选择需要对拟合数据、
执行一次LM iteration
2
7、生成结果 、
创建一个matrix,将 Var-Cov Matrix写入 其中
创建一个worksheet, 将拟合结果写入其中
要Find X,在这里填入y的值,y 必须在数据集之内
要Find Y,在这里填入x的值,x 在数据集内、外都可以
自定义拟合函数
1.添加一个新的函数类别,将自定义的函数都放置 添加一个新的函数类别, 添加一个新的函数类别 在这个类别里, 在这个类别里,以便以后重复使用
2
χ2
n− p
=
χ2
dof
,
其中n为参与拟合的数据点的数目,p为参数的数目 n − p称为自由度 ( degrees of freedom ) 置信区间:越窄越好 预期区间:越窄越好
Origin中进行非线性拟合的步骤
1、将数据输入worksheet 2、做数据的散点图 3、进行非线性拟合:
A、若有相应的菜单命令,点击相应的菜单命令即可 B、使用Origin内置拟合函数,可以使用拟合向导,按向 导指示操作即可 C、若自定义函数,使用高级非线性拟合工具进行拟合, 所有的拟合过程都可以控制
Fit Multi-peaks 多峰拟合
按照峰值分段拟合, 每一段采用Gaussion或Lorentzian方法
150
100
50
0
上机练习
完成Origin软件自带的 多峰拟合 例题文件:
C:\Program Files\OriginLab\OriginPro75 \Samples\Analysis\Curve Fitting\Multi Peak Fit.OPJ
y
373 336 303 277 258 242 239 246 266 293 339 373
左表中的(x,y)为某次 实验测得的数据,理论上 满足方程:
( x − x0 ) + ( y − y0 )
2
2
=R
2
试确定
x0 , y0 , R
本数据用simplex算法拟合 能得到最佳结果。
点击这里进行编译
用户自定义函数存放在Origin\FitFunc 文件夹,文 件名为\FunctionName.FDF
自定义函数NLSF拟合上机练习1
完成Origin软件自带的使用自定义函数进 行NLSF拟合的例题文件:
C:\Program Files\OriginLab\OriginPro75 \Samples\Analysis\Curve Fitting\NLSF User Def Func.OPJ
)
b1 = ? , b2 = ?
C、The NLSF Advanced Fitting Tool
Nonlinear Least Squares Fitting
NLSF高级拟合工具
NLSF的两种模式
这是Basic Mode,点击More Basic Mode, More 按钮,即可切换到Advanced Mode
χ2
参数 设置
显示各测量 点的残差图
显示置信 区间曲线
显示预期 区间曲线
第5步:输出结果
是否绘制这些曲线?
是否输出这些参数?
选中的话,会提示把本次拟合的过程保存为一个工 具栏上的图标,为以后进行同样的拟合提供方便
在此区域右击鼠标,可弹出图示的快捷菜单,可对拟合向导进行一些设置
Origin内置函数NLSF拟合
B、Fitting Wizard 非线性拟合向导
第1步:选择要拟合的数据
在这里控制参与拟合的数据点自 变量(独立变量的)范围,
数据点在图形中的显示设置
第2步;选择合适的拟合函数
函数的类别 函数公式 函数图形
函数名称
第3步:选择权重数据
没有权重就选 择None
第4步:拟合控制
置信区间 预期区间
Origin的非线性拟合功能
非线性模型
有n组观测数据: i = 1, 2,3,L , n 拟合 设因变量Y 和自变量X 满足: Y = f ( X ,θ ) + ε
(Yi , X i )
求出最佳的 参数θ
例如 : y = a+e
bx − bx
y = a (1 + e
)
c y = a + sin ( bx1 ) + ln x2
3、拟合过程 、 中一些参数的 设置( 设置(一般用 默认设置即可) 默认设置即可)
一般不 要选中
Delta一定程度上会 影响拟合的结果
设置权重方法, 没有就选None
在迭代过程中, 若χ t2 − χ t2−1 < Tolerance 则迭代(拟合结束)
设置最大的迭 代次数 设置参数的有效数字
4、选择要 、 拟合的数据
用这两个按钮可以浏览拟合 过程中每次迭代得到的参数 迭代过程的输出结果显示 在这里 执行n次LM迭代,迭代过程中 要终止的话,按ESC键即可 当LM迭代方法无法进行时,可 以尝试进行Simplex迭代方法 (一般情况下,此方法不如LM 方法好)(downhill simplex method)
计算并显示 χ
完成Origin软件自带的使用内置函数进行 NLSF拟合的例题文件:
C:\Program Files\OriginLab\OriginPro75 \Samples\Analysis\Curve Fitting\NLSF Built In Func.OPJ
拟合向导上机练习
y = b1 (1 − e
− b2 x
A、使用菜单进行非线性拟合
Fit Exponential Decay - first order 一阶指数衰减拟合
Fit Exponential Decay - second order
二阶指数衰减拟合
Fit Exponential Decay - third order 三阶指数衰减拟合
上机练习
当x轴为线性坐标时, 采用Boltzmann函数拟合 当x轴为对数坐标时, Logistic函数拟合 采用Logistic Logistic
S拟合工具
使用菜单命令进行线性拟合,很 多参数都是选用缺省值,用户无 法对整个过程进行干预。选用 【tool】菜单中的【Sigmoidal Fit】可以对S拟合过程中的相关 参数进行选择,使拟合过程按要 求进行,适合高级用户使用。
上机练习
完成Origin软件自带的 S拟合 例题文件:
C:\Program Files\OriginLab\OriginPro75 \Samples\Analysis\Curve Fitting\Sigmoidal Fit.OPJ
F Lorentzian 洛仑兹拟合
体重约70kg的某人在短时 间内喝下2瓶啤酒后,隔一定 时间测量他的血液中酒精含量 (毫克/百毫升),得到数据 如左表。设饮酒后血液中酒精 含量的数学模型为:
y = a (e
试确定
− bt
−e
− ct
)
a, b, c
16
4
自定义函数NLSF拟合上机练习3
x
245 249 264 285 308 348 375 416 454 483 504 508
拟合函数仔细分析,以及用户的经验
6、进行拟合 、
误差 拟合的结果 取值范围是 [0, 1] 1],越接 近 1,则越表明该参数有 取消选中的话,则这个参 数在迭代过程中保持不变, 可能过参数化了。这个时 候,用户就要考虑拟合的 当函数中某个参数被确定 的话,就可以在这里设置 模型是否正确了,是否可 以简化模型,除去一些参 数。 大多数情况下,过参数化的模型都应该认真审视,但并不是所有的过参数化的模型 都是坏的模型。比如说,绝大多数的指数方程都是这样的模型
