Origin8.0 非线性拟合法
Origin简明教程五章:非线性拟合

Origin 简明教程五章:非线性拟合Origin 简明教程五章:非线性拟合拟合曲线的目的为要根据已知数据照出响应函数的系数。
5-1 使用菜单命令拟合首先激活绘图窗口,选择菜单命令Analysis ,则可以看到名称 含义 拟合模型函数Fit Linear 线性拟合 y=A+B*xFit Polynomial 多项式拟合 y=A+B1*x+B2*x^2Fit Exponential Decay指数衰减拟合Fit Exponential Growth 指数增长拟合Fit Sigmoidal S 拟合 ,Boltzmann Fit Gaussion Gaussion 拟合Fit Lorentzian Lorentzian 拟合Fit Multipeaks 多峰值拟合 按照峰值分段拟和,每一段采用Gaussion 或者Lorentzian 方法Nonlinear Curve Fit 非线性曲线拟合 内部提供了相当丰富的拟合函数,还支持用户定制5-2 使用拟合工具拟合为了给用户提供更大的拟合控制空间,Origin 提供了三种拟合工具,即线性拟合工具、多项式拟合工具、S 拟和工具。
具体自己去体会。
5-3 非线性最小平方拟合NLSF这是Origin 提供的功能最强大、使用也最复杂的拟合工具。
方法是Analysis-》Non-Linear Curve Fit -》Advanced Fitting Tools 或者Fitting Wizad具体的请自己体会。
高级模式 利用Function-》new 可以自定义拟合函数 基本模式,利用new 可以自定义拟合函数Wizad 模式,高级模式中利用Action -》Dataset 设置,在基本模式中用Select Dataset 设置。
origin非线性拟合示例
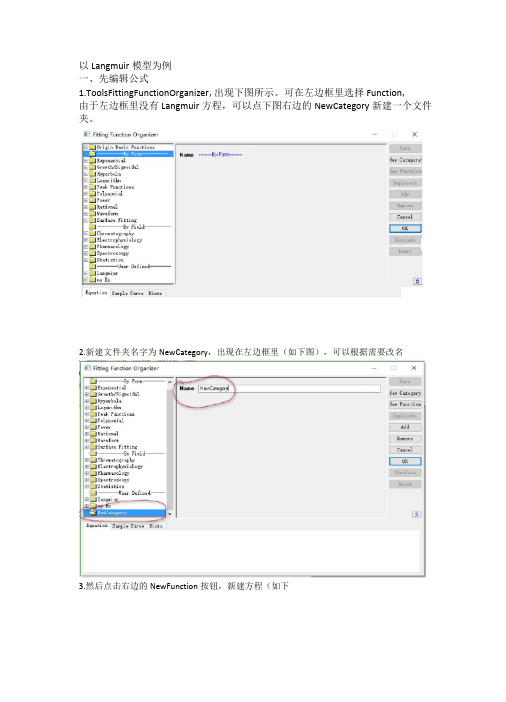
以Langmuir模型为例一、先编辑公式1.ToolsFittingFunctionOrganizer,出现下图所示。
可在左边框里选择Function,由于左边框里没有Langmuir方程,可以点下图右边的NewCategory新建一个文件夹。
2.新建文件夹名字为NewCategory,出现在左边框里(如下图),可以根据需要改名字。
3.然后点击右边的NewFunction按钮,新建方程(如下图)。
Equb.ti.an.Sun pie C UTE^ESpft4ify30rM l ti■皿口54inthisaditbox.ffote LnatsjacesaridEpecialchar aster5arenotslicedandM21bestripped out T&E>JDC ti OIL EileonilisJ:ivilLhiretLa白XLIITIC vithgMtenEion.IBFE?zanpLe:町上工疝“咐4.将Functionname改为Langmuir,IndependentVariables为x,DependentVariables为y, ParameterNames为A,B;再对公式进行编辑,如下图。
这样就编辑好了Langmuir公式,点击OK。
5.公式的模拟应用:首先根据吸附数据绘制出下图所示曲线和DriaiPr D £l-SQDjtilGraph'qurBph2目Jafihm 典&1印H 典日即h 15用T J H B I+°*+』七。
TA 4口 6.选中上图绘制的曲线,点击Analysis-NonlinearCurveFit ,出现下面的界面,在Category 项选择前面编辑方程时新建的NewCategory ,Function 选择编辑的Langmuir 。
如下图。
7.再点击Parameters 。
]i:=JogTKem <L:iEtused> I回圃Sat11ngECedePai--am£hers|FuTLctionSelectionDataSelect!oriCategory NewCategoriiFittedCui-i ieEAd\r:±riced Function Langmiur(User)」DescriptionFileNameLFDF)C:\Users\Acer\DocumentsVOriginUserFiles<>由旧I旦]史]立]曳电r^nf^^n告8.在输入参数A,B的初始值(这可以根据原始数据大概得出)这也是关键的步骤,初始值如果给得不合适,会直接影响模拟结果。
Origin8.0实验数据处理与曲线拟合详解

1.1 Origin的一些变化
1、新增了“X-Functions”技术 自1991年Origin问世以来,版本从4.0、5.0、
6.0、7.0、7.5到2007年推出的8.0版,软件不断完 善。与7.5版相比,Origin8.0在菜单设计、具体操 作等很多方面都有显著改进,特别是采用了X- Functions技术,更是把“模块化”和“对象化” 发挥到了淋漓尽致的程度。
6、非线性曲线拟合
(1) 导入Gaussian.dat数据文件,选中C(Y)列数据,将 其坐标属性改为C(yEr?)栏,选中B(Y)和C(yEr?)栏,选择 菜单命令[Plot]→[Symbol]→[Scatter],绘制散点图如下:
6、非线性曲线拟合
选择菜单命令[Analysis]→[Fitting]→[Nonlinear Curve Fit],打开[NLFit]对话框如下图
•设定级数为3
3、多项式拟合
点击“OK”后画出的拟合曲线事下图,从图中可以看 出,拟合曲线与数 据点吻合的非常好, 而且它的相关系数 也很好,达到了 0.99767。
3、多项式拟合
因此,这组数据的变化规律可以用一元三次多项式来描述:
3、多项式拟合
如果把拟合多项式的级数进一步增大,比如增大到6, 拟合结果又会是怎样的呢?请同学们自己立刻拟合一次!
5、指数拟合
可以看出,拟 合曲线与散点 变化规律非常 吻合
5、指数拟合
6、非线性曲线拟合
非线性曲线拟合(Nonlinear Curve Fit , NLFit)是Origin 所提供的功能最强大、使用也最复杂的数据拟合工具。有 多达200多个数据表达式,用于曲线拟合函数,这些数学表 达式选自不同的学科领域的数据模型,能满足绝大多数科 技工程中的曲线拟合需求。Origin的非线性曲线拟合是通 过[NLFit]对话框实现的。下面以Samples\Curve Fitting\Gaussian.dat数据进行非线性曲线拟合演示。
origin8 非线性拟合及切线斜率

第4步, 查看拟合曲线(做点图)及拟合后切线斜率(需要下载angent插件)
第5步,查看切线信息
如有侵权请联系告知删除,感谢你们的配合!
analysisfittingnonlinearcurvefitopendialog选择拟合方程可以点击选项卡右下角的下三角预览拟合曲线注意拟合后数据在新的数据表里查看拟合曲线做点图及拟合后切线斜率需要下载angent插件
散点数据非线性拟合以及查看拟合后切线(变化速率)
第1步,ห้องสมุดไป่ตู้入数据,做散点图
第2步,非线性拟合:analysis→fitting→nonlinear curve fit →open dialog
用Origin软件的线性拟合和非线性曲线拟合功能处理实验数据

用Origin软件的线性拟合和非线性曲线拟合功能处理实验数据用Origin软件的线性拟合和非线性曲线拟合功能处理实验数据在科学研究和实验中,数据处理是一个至关重要的环节。
通过对实验数据进行分析和拟合,可以得到对现象的更深入和准确的理解。
Origin软件是一种功能齐全且易于使用的数据分析软件,它提供了各种分析和拟合功能,包括线性拟合和非线性曲线拟合。
本文将探讨如何使用Origin软件的这两个功能来处理实验数据。
首先,我们需要明确线性拟合的概念。
线性拟合是通过一条直线来近似表示实验数据的趋势。
它通常用于分析变量之间的线性关系,并确定其相关性。
在Origin软件中,我们可以通过选择线性拟合的功能来进行这一分析。
以某个实验数据为例,我们首先打开Origin软件并加载实验数据。
然后,在图表中选择需要进行线性拟合的数据集,并点击工具栏上的“线性拟合”按钮。
Origin软件会自动计算最佳拟合直线,并在图表中显示出来。
此外,Origin软件还提供了拟合曲线的各种统计信息,如拟合趋势线的斜率、截距、相关系数和拟合误差等。
线性拟合的结果可以帮助我们推断实验数据中的相关性和趋势。
如果拟合直线的斜率为正值,并且有较高的相关系数,那么我们可以得出结论,实验数据之间存在正相关关系。
反之,如果斜率为负值,则表示实验数据之间存在负相关关系。
此外,线性拟合还可以用于预测未知数据的数值。
值得注意的是,线性拟合适用于处理线性关系较为明显的数据。
如果实验数据的分布较为复杂,并且存在非线性关系,就需要使用非线性曲线拟合功能来分析数据。
非线性曲线拟合是通过曲线来近似表示实验数据的趋势。
与线性拟合类似,非线性曲线拟合也能提供各种统计信息,如拟合曲线的拟合度、参数值、相关系数等。
使用Origin软件的非线性曲线拟合功能,可以进行多种拟合模型的选择和分析。
例如,常见的非线性模型有指数、对数、幂函数等。
我们可以根据实验数据的特点和分布选择合适的非线性模型,并进行参数估计和曲线拟合。
origin非线性拟合示例

origin非线性拟合示例以Langmuir模型为例一、先编辑公式1. Tools——Fitting Function Organizer,出现下图所示。
可在左边框里选择Function,由于左边框里没有Langmuir方程,可以点下图右边的New Category 新建一个文件夹。
2. 新建文件夹名字为NewCategory,出现在左边框里(如下图),可以根据需要改名字。
3. 然后点击右边的New Function按钮,新建方程(如下图)。
4. 将Function name改为Langmuir,Independent Variables为x,Dependent Variables 为y, Parameter Names 为A,B;再对公式进行编辑,如下图。
这样就编辑好了Langmuir公式,点击OK。
5. 公式的模拟应用:首先根据吸附数据绘制出下图所示曲线6. 选中上图绘制的曲线,点击Analysis-Nonlinear Curve Fit,出现下面的界面,在Category项选择前面编辑方程时新建的NewCategory,Function选择编辑的Langmuir。
如下图。
7.再点击Parameters。
8.在输入参数A,B的初始值(这可以根据原始数据大概得出)这也是关键的步骤,初始值如果给得不合适,会直接影响模拟结果。
在例子给出的数据中,A值对应Langmiure平衡常数,B值对应吸附剂的平衡吸附量,从原始数据得出,B值约为350,A值根据方程小于0.1,假设为0.05。
输入为下图:9.再点击下图所示的1次迭代按钮,参数A,B会变化,然后点击Fit进行拟合即可得到拟合图形和拟合结果。
用Origin软件的线性拟合和非线性曲线拟合功能处理实验数据

&$0.111+0.008 73t,
t∈[1,10],R=0.996 95;
$
$
$
T2=
$$ # $ $
1+exp[-
2.256 1.05(4 t-
12.20)]
,
t∈[11,19],CDhoif2 =0.002 48;
$
$
%$$2.46- 0.088 38t,
t∈[20,28],R=- 0.992 36。
Origin提供了多种非线性曲线拟合方式:①在Analysis菜单中提供了如下拟合函数:多项式拟合、指数 衰减拟合、指数增长拟合、S形拟合、Gaussian拟合、Lorentzian 合和多峰拟合;在Tools菜单中提供了多项式 拟合和S形拟合。②在Analysis菜单中的Non2linear Curve Fit选项提供了许多拟合函数的公式和图形。③ Analysis菜单中的Non2linear Curve Fit选项可让用户自定义函数。
第 12 卷第 6 期 2006 年 12 月
江苏技术师范学院学报 JOURNAL OF JIANGSU TEACHERS UNIVERSITY OF TECHNOLOGY
Vol.12,No.6 Dec ., 2006
用O rigin软件的线性拟合和非线性 曲线拟合功能处理实验数据
陈旭红
( 江苏技术师范学院 化学化工学院,江苏 常州 213001)
图1所示的曲线由于试验装置的绝热性能良好,热漏很小,而搅拌器功率较大,不断引进的能量使得 曲线不出现极高温度点;图2所示的曲线由于热量计向环境的热漏造成了温度的降低。可把A、B间的距离 作为校正后的ΔT。
为减小处理方法给所处理的数据带来的误差,可以采用曲线拟合的方法,求出曲线的函数表达式,通 过计算函数值得到需要的结果。
Origin拟合操作

a) 图 9 非线性拟合 Code 项 a) Function b) Parameter Init
-5-
b)
在 Parameters 页和 Bounds 页中可以对参数作系统的全面地修改和约束, 如图 10~11 所示。
图 10 非线性拟合 Parameters 项
图 11 非线性拟合 Bounds 项
-7-
a)
b)
图 8-
二、 多项式拟合
与线性拟合相比,多项式拟合仅多了一项功能,即选择拟合多项式的次数。如图 3 所示 的“Polynomial Order”选项。
三、 拟合报表
拟合报表是拟合操作完成后,Origin 会默认给出两个表单。可以根据需要在图 1 所示的 扩展选项中勾选相关功能,一般情况下,不需要输出报表的所有拟合相关结果,这样只会增 加寻找目标参数的时间。拟合报表是 Origin 拟合操作中的核心功能。我们不仅可以从中读取 到拟合曲线(曲面)的具体信息,还可以从概率论与数理统计的基础上获得大量拟合结果参 数,用于对各类模型或者试验离散点的拟合效果的对比。 图 4 和图 5 分别是拟合报表 1 和 2。表单名称为“Fit Linear 1”和“Fit Linear Curves 1” 。
a) 图 8 非线性拟合 Setting 项 a) Data Selection b) Function Selection
b)
“Code” , “Parameters”和“bounds”三页都是对已选拟合函数类型具体表达式和参数的 查看与修改。如图 9 所示,函数项(Function)在这里是不可编译的。而参数赋值和参数约束 项可以修改,注意使用 C 语言的格式。
一、 线性拟合
线性拟合(Linear Fitting)是最简单的一种拟合方式。线性回归拟合将选中的数据点拟合 为直线,选择 Analysis-Fit linear,那么 Origin 将曲线拟合为直线,以 X 为自变量,Y 为因变 量,回归拟合的函数形式为: y Ax b ,其中 A,b 为参数,由最小二乘法确定。对话框如 下图 1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Origin8.0 非线性拟合法
1.打开Origin 8.0软件。
2.在A(X)列输入自变量,在B(Y)列输入因变量。
不能把二
者位置搞错。
3.点击analysis下拉菜单→点击Fitting→Nonlinear Curve Fit
→Open Dialog…
4.在打开的新窗口中选择Function Selection,点击Gauss下
拉菜单→点击<New…>,这时会出现新的页面。
然后在新页面进行如下操作:
5.在Independent Variables中选定自变量,在Dependent
Variables中选定因变量,在Parameters name 中给出所有待拟合参数的符号如p1,p2,p3……
6.在Function中建立待拟合的非线性函数关系。
7.就建立了待拟合的非线性函数关系后,依次点击右上角的
Save和右边靠近下方的Ok,这时会出现新的页面。
8.从新页面的Function栏可查看欲用的函数名(即刚建立的
非线性拟合函数);点击新页面的Code,可查看新建的非线性拟合函数;点击Parameters,然后在Value下分别给待拟合参数输入初始值。
9.接下来,可一次次点击下方从左到右第五个按钮,一次一
次进行拟合;也可以击下方从左到右第六个按钮,此时系统会反复进行多次拟合直到收敛为止。
收敛后,第五和第六个按钮就都改变颜色变成不能再点击了。
这时,点击Ok按钮。
结果就出来了。
10.可从中读取待拟合参数的拟合值。
11.双击其中的拟合曲线(Fitted Curves Plot),即可把图放大,
并可按下法进行适当编辑。
12.右键单击横坐标轴或纵坐标轴,点击下拉菜单钟的
Properties…,然后可以选择性调整坐标轴的刻度、刻度线的朝向(朝里或朝外)
13.在Origin中把坐标刻度、刻度线的朝向、数据点的符号、
线条的粗细等编辑好以后,选取整个拟合线图,点击左上角工具栏的Edit,在下拉菜单中点击Copy page,然后在Word文档中,即可用Ctrl+V键将此图粘贴上去。
14.在Word文档中,右键单击该图,在下拉菜单中点击“编
辑图片(E)”,这时便可以对该图片进行适当的编辑,如添加图名、添加纵横坐标所代表的物理量及其单位等。
15.如欲删除自定义的函数关系,可在打开的Origin 8.0页面
单击工具栏中的tool下拉菜单→点击Fitting Function Organizer…,这是从出现的新页面左侧选择与删除的函数名,点击新页面右侧的Remove,这样自定义的函数关系就被删除了。
