一元非线性回归
第九章 一元非线性回归分析

一、Logistic曲线方程及性质
.
.
.
Y
K
.
K
.
2
.
K
.
1a
0 ln a
∞
x
b
.
.
Yˆ K
(a、b、K 均大于0)
.
1 aebX
(一)Logistic曲线方程
.
. .
Yˆ K 1 aebX
(a、b、K 均大于0)
.
式中:X—生长发育时间;
.
Y—累积生长量;
.
.
K—极限生长量,或叫终极量,表
63.7
. 35 75.2
-1.1093
79.3
.
40 90.2
-202196
89.4
45 95.4
-3.0320
94.8
50 97.5
-3.6636
97.6
本章小结:
.
. 1.用线性转换法配置曲线方程的基本步骤。
.
2.指数曲线方程与Logistic生长曲线方程在进 行线性转换时有什么区别?
.
. 3.Logistic生长曲线方程的信息分析:起始量、 . 极限量和拐点日期的计算及生物学意义。
.
6
.
7
.
8
9
10
.
11
.
12
13
.
14
15
16
0.29 0.52 0.79 1.25 1.81 2.61 4.25 7.38 11.30 18.82 28.12
-0.538 -0.284 -0.102 0.097 0.258 0.417 0.628 0.868 1.053 1.275 1.449
一元非线性回归分析

模型,并预测第14年的销售额预测值。
年序号 t
1 2 3 4 5 6 7
年销售额 Y
年序号t
3
8
8
9
12
10
10
11
25
12
14
13
18
年销售额 Y
36 32 57 70 115 150
预测结果:
年销售额的指数拟合结果
年销售额Y
年销售额估计值
160
140
120
100
80
60
40
20
0
年
0
2
4
6
8
10
X
3
二.指数函数
指数函数 Y aebX 设 V ln Y 则 V ln a (b ln e)X
Y
Y
a
O
X
(b> 0)
a
O
X
(b< 0)
4
三.对数函数
对数函数 Y a bln X 设 U ln X 则 Y a bU
Y
Y
O
X
(b> 0)
O (b< 0)
X
5
四.双曲线函数
双曲线函数
一元非线性回归分析
• 非线性回归分析方法就是用一条曲线来拟合因变 量对于自变量的依赖关系。根据问题的性质,拟 合曲线可以是指数曲线、对数曲线、平方根曲线 以及多项式曲线等。具体采用何种曲线主要由两 方面的因素决定。一方面就是自变量与因变量之 间本来就存在着一种内在函数依赖关系,而这种 依赖关系是分析者根据自己的知识背景和经验已 经了解的。另一方面,根据由自变量和因变量观 测值作出的散点图,可以看出它们之间的依赖关 系。
一元非线性回归

ˆ i 间的平 s为诸观测点yi与由曲线给出的拟合值 y 均偏离程度的度量,s越小,方程越好。
第八章 方差分析与回归分析
第29页
在观测数据给定后,不同的曲线选择不会影
响 ( yi y )2 的取值,但会影响到残差平方
第八章 方差分析与回归分析
第24页
b = 1.0e+002 *
1.06301275014382
0.01194728720517
R2 = 0.78514164407253
第八章 方差分析与回归分析
第25页
112 散点图 回归函数 111
110
109
108
107
106
2
4
6
8
10
12
14
110
109
108
107
106
2
4
6
8
10
12
14
16
18
20
第八章 方差分析与回归分析
第17页
第一种方法的程序
format long x=[2 3 4 5 7 8 10 11 14 15 16 18 19]; y=[106.42 108.20 109.58 109.5 110 109.93 110.49 110.59 110.60 110.9 110.76 111
110.9 110.76 111 111.20]; x1=log(x); y1=y; x2=[ones(13,1) x1']; [b,bint,rint,stats]=regress(y1',x2); b z=b(1)+b(2)*x1; yc=z; n=length(x); lyy=sum(y.^2)-n*(mean(y))^2; R2=1-sum((y-yc).^2)/lyy; plot(x,y,'k+',x,yc,‘c'); legend('散点图','回归函数')
交通数据处理与分析-一元非线性回归分析剖析.
未知参数的选取时一个难点,从散点图上看,随着
年龄的增长,人的头围也在增长,但不会一直增长, 到了一定的年龄之后,头围就稳定在50~55之间。 注意到
,
2
lim
x
1e x
3
1
可以选取β1的初值为50~55之间的一个数,不妨 选取为53.
再注意到,初生婴儿的头围在35左右,可得
2
53e 3 35
还返回残差值向量r,雅克比矩阵J,未知参数的协 方差矩阵COVB,误差方差σ2的估计mse(均方误差 平方和)。这里的输出可作为其他后续函数的输入, 用来计算参数估计值的置信区间,也可用来计算给 定x处的预测值及预测值的置信区间。
[…] = nlinfit(X, y, fun, beta0, options) nlinfit函数利用麦夸特(Levenberg-Marquardt)算
yhat modelfun b, X
modelfun为函数名,b为未知参数向量。nlinfit函 数的输入参数beta0为用户设定的未知参数的初值,
不同的初值可能会有不同的估计结果,故设定初值 时最好能够根据实际问题有个提前的预判
[beta, r, J, COVB, mse] = nlinfit(X, y, fun, beta0)
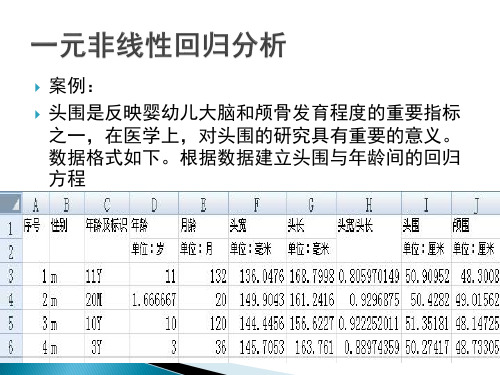
案例:
头围是反映婴幼儿大脑和颅骨发育程度的重要指标 之一,在医学上,对头围的研究具有重要的意义。 数据格式如下。根据数据建立头围与年龄间的回归 方程
令x表示年龄,y表示头围。x和y均为一维变量,同 样可以从x和y的散点图上直观地观察它们之间的关 系,然后再作进一步的分析
从图中可以看出,年龄和头围服从非线性关系,可 以考虑做非线性回归分析。根据散点图的走势,可 以选取以下函数作为理论回归方程
数学软件与建模4.2 一元非线性回归

实验4.2 一元非线性回归模型实验目的熟练掌握参数初始值的数值计算以及非线性拟合的Matlab 命令,并能根据输出结果计算均方误差及可决系数,并能据此进行拟合效果分析。
实验内容解决一元非线性回归模型有以下几个步骤: (1)首先作出散点图,确定函数)(x f 的类别。
对非线性拟合,下面的图形给出了常见曲线与方程的对应关系: 幂函数:bax y =指数函数:bxae y =双曲线函数:bax xy +=对数函数:x b a y ln +=指数函数:xb ae y =S 形曲线:xbea y -+=1具有S 形曲线的常见方程有: 罗杰斯蒂(logistic )模型:xey γβα-+=1 龚帕兹(Gomperty )模型:)ex p(xk e y --=βα理查德(Richards )模型:δγβα/1)]ex p(1/[x y -+=威布尔(Weibull)模型:)ex p(δγβαt y --=(2)①根据已知数据确定待定参数的初始值。
②正确输入函数。
③利用非线性拟合命令计算最佳参数。
(3)根据可决系数,比较拟合效果。
在Matlab 中进行非线性拟合的命令如下:[b,r,J] = nlinfit(x,y,fun,b0)其中,x,y 为原始数据,fun 是在M 文件中定义的函数,b0是函数中参数的初始值;b 为参数的最优值,r 是各点处的拟合残差,J 为雅克比矩阵的数值.注意:在6.1版本中输入x 是列向量,y 是行向量,而在7.0以上版本要求x ,y 要一致. 【例题4.2】炼钢厂出钢时所用盛钢水的钢包,由于钢水对耐火材料的侵蚀,容积不断增大,我们希望找出使用次数与增大容积之间的函数关系.实验数据如表4.2:表4.2 钢包使用次数与增大容积(1)分别选择函数bax x y +=、)1(cx be a y +=、c bx ax y 2++=、x bae y =拟合钢包容积与使用次数的关系,在同一坐标系内作出函数图形;(2)计算四种拟合曲线的均方差,并以此作为判别标准确定最佳拟合曲线 (3)二次多项式拟合的效果如何?分析内在原因 解:x1=[2:16];y1=[6.42,8.2,9.58,9.5,9.7,10,9.93,9.99,10.49,10.59,10.6,10.8,10.6,10.9,10.76]; b01=[0.1435,0.084]; %初始参数值 fun1=inline('x ./(b(1)+b(2)*x)','b','x'); [b1,r1,j1]=nlinfit(x1',y1,fun1,b01); y=x1./(0.1152+0.0845*x1); subplot(221)plot(x1,y1,'*',x1,y,'-or'); legend('原始数据','y=x/(ax+b)') b02=[112,0.4,0.2]; %初始参数值fun2=inline('b(1)*(1-b(2)*exp(-b(3)*x))','b','x'); [b2,r2,j2]=nlinfit(x1',y1,fun2,b02); f=10.5975*(1-0.9287*exp(-0.4531*x1)); subplot(222)plot(x1,y1,'*',x1,f,'-or');legend('原始数据','y=a(1+bexp(cx)') p=polyfit(x1,y1,2);g= -0.0290*x1.^2+0.7408*x1+6.0927; subplot(223)plot(x1,y1,'*',x1,g,'-or'); legend('原始数据','二次函数') b04=[112,-0.11]; %初始参数值 fun4=inline('b(1)*exp(b(2)./x)','b','x'); [b4,r4,j4]=nlinfit(x1',y1,fun4,b04); h=11.6037*exp(-1.0641./x1); subplot(224)plot(x1,y1,'*',x1,h,'-or'); legend('原始数据','y=aexp(b/x)')51015206810125101520510152068101205101520图4.3 原始数据与四种拟合曲线图为了比较上述四条曲线拟合的效果,我们首先确定如下的评价准则:均方残差)/()ˆ(1512p n y y MSE i i i --=∑=越小越好 其中i y 是原始数据,i yˆ是拟合曲线在i x 处的函数值,n 是原始数据的个数,p 是拟合曲线中参数个数.我们计算均方残差程序如下:[sum(r1.^2)/(15-2),sum(r2.^2)/(15-3),sum((y1-g).^2)/(15-3),sum(r4.^2)/(15-2)]ans = 0.0921 0.0875 0.2306 0.0664由此可知选择函数xbae y 进行拟合效果最好,而多项式的拟合效果最差.其原因在于多项式没有任何渐近线,而从实际问题可知钢包使用的年龄是有限的,因此选择函数应该考虑到其右上方有一条水平渐近线.结果说明:(1)在Matlab6.1版本中输入x 是列向量,y 是行向量,而在7.0以上版本要求x ,y 应同为行向量(或同为列向量).(2)如果确定初始参数值时遇到复杂的方程组,我们可以根据第三章中介绍的计算方程零点的方法,利用Matlab 计算初始值.【例4.3】表4.3给出了淮南市从1978年到20001年国民生产总值、第一产业、第二产业以及第三产业的数据,根据数据分析解决以下问题:(1)将各指标进行标准化,即减去各自的均值再比上标准差,计算各指标之间的相关系数矩阵;哪两个指标之间具有高度线性关系?(2)利用原始数据建立第一产业与第二产业之间的函数关系,在同一坐标系内作出原始数据与拟合曲线的散点图,计算均方误差、决定系数并预测2002年的第二产业生产总值.(3)利用标准化后的数据解决(2)中的问题,结果是否比用原始数据要好?为什么?表4.3淮南市部分经济指标题目分析:本题的第一问是解决大样本数据的处理问题,利用zscore命令即可解决,而计算指标之间的相关系数矩阵以后,可以获知那些指标之间有较强的线性相关性,若有两个非平稳的经济指标,随着时间的推移各自变化比较复杂,但是两者之间存在长期的均衡关系则可以利用回归分析建立两者之间的函数关系.从相关系数矩阵(表 4.4)和散点图(图4.4)可以看出国民生产总值与各产业都具有较强的线性关系,第一产业与第二产业以及第三产业之间也具有较大的线性相关.计算程序:首先将原始数据输入a=[78258 9230 51827 1720181785 10007 52274 1950487645 10751 55502 2139299072 17263 58182 23627105386 17282 62020 26084118832 20961 66988 30883148277 25755 86215 36307166410 30103 93586 42721189776 35906 101085 52785208477 43335 104604 60538258354 45125 146327 66902284792 52227 164217 68348306605 57351 169721 79533275928 27740 173600 74588351233 55847 200975 94411532686 80047 324491 128148683059 124984 392063 166012834994 135121 472819 2270541063871 154935 603812 3051241187782 169629 644155 3739981203396 178378 603230 4217881238310 187165 595097 4560481259965 174217 586677 4990711348558 170622 638398 539538];z=zscore(a); % 将原始数据标准化corrcoef(a); % 计算各指标的相关系数,得到如下结果表4.4 国民生产总值与各产业的相关系数[b,bint,r,rint,s]=regress(a(1:24,3),[ones(24,1),a(1:24,2)]);作图程序subplot(221),plot(a(1:24,2),a(1:24,3),'x'),legend('一产与二产')subplot(222),plot(a(1:24,1),'-*'),legend('第一产业')subplot(223),plot(a(1:24,3),'-o'),legend('第二产业')t=1:24;y= a(1:24,3);x=a(1:24,2);subplot(224),plot(t,y, '-*',t,3.5*x+2819.4,'-or'),legend('原始','拟合')均方差与可决系数计算程序sum(r.^2)/22,1- sum(r.^2)/sum((y-mean(y)).^2)利用2002年第一产业的产值187438,代入拟合曲线计算出2002年淮南市第二产业生产总值为658850实际数值为740059,相对误差为0.1097图4.4 国民生产总值与第二产业关系结果说明:(1)建立一次函数可以利用多项式回归的命令,本题我们利用了多元线性回归的命令;(2)我们用第一产业的一次函数近似计算第二产业生产总值,得到的绝对误差较大,其中的原因可以从第一产业与第二产业的图形中看出,第一产业在1991年处有一个异常点这是由于该年淮河洪灾造成淮南地区严重减产,而第二产业从1997年开始逐年下降直到2001年才出现上升,因此如果我们选取虚拟变量纠正异常点,或者分段拟合就可以进一步缩小误差。
一元非线性回归

⼀元⾮线性回归⼀元⾮线性回归有时,回归函数并⾮是⾃变量的线性函数,但通过变换可以将之化为线性函数,从⽽利⽤⼀元线性回归对其分析,这样的问题是⾮线性回归问题。
为了检验X射线得到杀菌作⽤。
⽤200kv的X射线照射杀菌,每次照射6分钟,照射次数为x,照射后所剩的细菌数为y,下表是⼀组试验结果x y x y x y1 783 815415282 621 912916203 433 1010317164 431 117218125 287 12501996 251 13432077 175 1431根据经验知道y关于x的曲线回归⽅程如bxyae试给出具体的回归⽅程,并对其对应的决定系数R^2和剩余标准差s。
⼀、⾸先描出数据的散点图,如下图散点图呈现出⼀个明显的向下且下凸的趋势,可能选择的函数关系很多,⽐如我们可以给出如下三个曲线函数:1.1bay x=+(1)2.baxy=(2)3.bxy ae=(3)⼆、参数估计1.为了能采⽤⼀元线性回归分析⽅法,我们做如下变换yv ln=u=x则(1)式的曲线图就化为如下的散点图u i∑= 3655 i v ∑=87.22497u =182.75 v =4.3612482ui∑=1611149 u i i v ∑=21281.692nu =667951.3 nuv =15940.36uu l = 943197.8 uv l =5341.3291B =uuuvl l =130.9375 0B=v - B1=-388.301得出⽅程v=-388.301+130.9375x四、结束语对于可化为线性模型的回归问题,⼀般先将其化为线性模型,然后再⽤最⼩⼆乘法求出参数的估计值,最后再经过适当的变换,得到所求回归曲线。
在熟练掌握最⼩⼆乘法的情况下,解决上述问题的关键是确定曲线类型和怎样将其转化为线性模型。
确定曲线类型⼀般从两个⽅⾯考虑:⼀是根据专业知识,从理论上推导或凭经验推测、⼆是在专业知识⽆能为⼒的情况下,通过绘制和观测散点图确定曲线⼤体类型。
第 2 讲(1) 一元线性、非线性回归分析

2
14
• 因此,点估计:
ˆ y ( x0 ) = a + bx0
• 区间估计:
ˆ y1 ( x0 ) = a + bx0 − δ ( x0 )
ˆ y 2 ( x0 ) = a + bx0 + δ ( x0 )
15
进似地, 很大( 进似地,当n很大(即 n → ∞ )时,t α 很大
α = 0.05
② 单侧控制
y < y,或 y < y 2
' 1 '
19
• 回归分析注意事项
(1)自变量、因变量的选择 )自变量、 (2)样本回归方程 ) (3)必须进行显著性检验 ) (4)任何回归方程都具有使用范围 )
20
二、一元非线性回归分析
1. 可化为线性回归的非线性回归
某石灰土强度与龄期关系 强度(Mpa Mpa) 2.5 2 1.5 1 0.5 0 0 50 100 150 200 龄期(d)
y1 < y < y2
' '
为此我们要合理控制x的取值,参照式(1)有下式:
P{
y1 < y < y2
' '
}≥ 1 − α
17
• 一般情况下可参照图求解:
′ y1 = a + bx −
t α ( n − 2 ) σˆ
2
1 (x − x )2 1 + + n L xx
′ y 2 = a + bx + t α
ˆ δ ( x0 ) ≈ 1.96σ
x0 又在 x 的平均值附近,取
= 1.96
2
ˆ ˆ y1 ( x0 ) ≈ a + bx0 − 1.96σ
一元非线性回归分析

Non-linear Regression Analysis
1.常用旳目旳函数及其线性化旳措施 2.回归方程旳评价措施 3.应用范例与MATLAB实现
1. 常用旳目旳函数及其线性化措施
在某些实际问题中,变量间旳关系并不都是线性旳, 那时就应该用曲线去进行拟合.用曲线去拟合数据首先要 处理旳问题是回归方程中旳参数怎样估计?
处理问题旳基本思绪
对于曲线回归建模旳非线性目旳函数 y f (x), 经过
某种数学变换
v u
v( u(
y) x)
使之“线性化”化为一元线性
函数 v a bu 旳形式,继而利用线性最小二乘估计旳
措施估计出参数a和b ,用一元线性回归方程 vˆ aˆ bˆu
来描述 v 与 u 间旳统计规律性,然后再用逆变换
SSR SST SSE.
3. 应用范例与MATLAB实现
商店销售额与流通率旳非线性回归分析
流通率是反应商业活动旳一种质量指标,指每元 商品流转额所分摊旳流通费用.
搜集了九个商店旳有关数据 。
2. 回归方程旳评价措施
对于可选用回归方程形式,需要加以比 较以选出较 好旳方程,常用旳准则有:
⑴ 决定系数 R2
定义
R2 1 SSE , SST
称为决定系数.显然 R2 1 . R2 大表达观察值 yi 与拟 合值 yˆi比较接近,也就意味着从整体上看,n个点旳散
布离曲线较近.所以选 R2 大旳方程为好.
b>0
b<0
线性化措施
令 v ln y , u 1/ x, 则 v ln a bu. ⑹ 对数函数 y a bln x
函数图象
b>0
b<0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 656.824 1 846.988 1 616.684 1 730.563 11 303.970 14 019.790 9 277.172 13 684.750 1 949.164 4 846.016 521 457.400 564 370.800
298.473 179.866 172.808 172.143 881.042 638.176 862.088 712.787 228.403 324.481 7 393.938 12 212.410
求解
① 根据有关研究,景观斑块面积与周长关系可 用双对数关系拟合:LnA = t1*lnP + t2 y = ln A x = ln P ② 作变量替换,令 ,将表中原始数 据进行对数变换,变换后得到的各新变量对 应的观测数据如表。
序号 1 2 3 4 5 6 7 y=lnA 9.254 106 9.678 763 10.340 99 9.153 019 9.292 742 9.977 338 8.838 07 x=LnP 6.438 379 6.417 2 6.653 782 6.273 258 7.552 816 7.168 551 6.033 226 序号 42 43 44 45 46 47 48 y=lnA 12.358 13 8.307 622 10.336 37 7.508 433 10.176 19 9.515 909 11.091 18 x=LnP 8.362 186 5.667 487 6.797 918 5.323 65 6.875 294 6.951 841 7.718 879
0.8
(a>0 and b>0)
0.6
20
y
y
0.4 0.2 0 0 5 10 15 20 25
0
-20
-40
x
0
5
10
15
20
25
(2)
幂函数
(3)指数函数1
(4)指数函数2
(5)对数函数
(6)Logistic生长曲线
内线性模型应用的特征
关键:确定变量与x间的曲线关系的类型。
9 首先需利用有关专业知识 9 若没有已知的理论规律和经验可资利用,则可用 描点法将实测点在直角坐标纸上描出,观察实测 点的分布趋势与哪些已知的函数曲线最接近。 9 多项式拟和,最后不得以的选择。
1 946.184 77.305 7 977.719 19 271.820 8 263.480 14 697.130 4 519.867 13 157.660 6 617.270 4 064.137 5 645.820 6 993.355 4 304.281 6 336.383 2 651.414
198.661 56.902 715.752 1 011.127 680.710 1 234.114 326.317 1 172.916 609.801 437.355 432.355 503.784 267.951 347.136 292.235
数据-续 1 597.993 58
30 31 32 33 34 35 36 37 38 39 40 41
3 638.766 58 5425.100 35 220.640 10 067.820 27 422.570 43 071.550 57 585.940 28 254.130 497 261.000 24 255.030 1 837.699 1 608.625
F Significance F 11.7 0.0188
预测:7月均温28度时的棉铃虫历期(天)
1 b = a + y x ⇒ ⇒ ⇒ ⇒ ⇒ y = y = y = y = x ax + b 0 . 0688 0 . 0688 x x − 1 . 0947 x x − 1 . 0947 28 × 28 − 1 . 0947
y = 1.505 x − 0.505 7
x与y的相关系数R=0.9665。 ⑥ 将上式还原成双对数曲线,即:
ln A = 1 . 505 ln P − 0 . 5057
700000 600000 面积(m ) 500000 400000 300000 200000 100000 0 0 2000
一元非线性回归
1. 非线性问题 2. 回归模型分类 3. 常用内线性模型及其线性化方法 4. 内线性模型求解 5. 内线性模型评价
1. 非线性问题 小动物喂养试验:小动物重量增量 y 与小动物每日喂食量 x 之间建立模型。
a) 响应变量y可能被限制下界,而下界是不喂食动物 的生长增量; b) 响应变量也可能由喂食引起的某些生物的最大生长 增量而被限制上界; c) 喂食量刚开始增加时,重量增加可能增加较快,以 后减慢。
内线性模型应用需注意的几个方面
① 优先考虑线性模型。 ② 关键-选择合适内线性模型:选择恰 当,就相当于成功了一半。 ③ 内线性模型,通过某种数学转换转换成 线性模型(线性化),其数学转换方法 针对不同的模型形式而不尽相同。 ④ 内线性模型线性化求解,其结果如决定 系数、残差平方和等一般是相对线性化 后的模型。
4. 内线性模型求解
43 42 41 40 历期(天) 历期 (天) 拟和历期(天) 39 39 37 37
实例:棉铃虫实例-双曲线方程 1 b = a + y x
38
36 35
35
34 33
33
31 32 31 25
32 25
26
34 26
27
7月均温(度)
36 27
28
38 28
40 29
29
③
以x为横坐标、y为纵坐标,在平面直角坐标系中 作出散点图。很明显,y与x呈线性关系。
14 13 12 11 10 ln A 9 8 7 6 5 4 4 5 6 7
Ln P
8
9
10
④ 景观斑块面积(A)与周长(P)间-双对数关系。
⑤ 根据新表数据,运用建立线性回归模型的方 法,建立y与x之间的线性回归模型,得到
14 12 10 8 6 4 4
y = 1.505x - 0.5057 R2 = 0.9342
5
6
7 x=lnP
8
9
10
景观斑块面积与周长
5. 内线性模型评价
① 线性化后方程求解的评价
9 显著性 9 回归系数 9 拟合度
② 线性化后方程求解,代入原方程再评价
9 残差平方和 9 预测值与拟合值的相关系数 9 预测值与拟合值的散点图
3) (狭义)非线性回归模型
回归模型参数是非线性的,且不能通过变 换转化为线性形式。
3. 常用内线性模型及其线性化方法
(1) 双曲线
z
对于双曲线
1
1 b = a+ y x
,令 y ′ =
40
1 1 , x′ = y x
,转化为直线
y ′ = a + bx ′ . 形式:
(a>0 and b<0)
11 474.770 72 2 数据-续 1 877.476 497.394 1 934.596 1 171.413 2 275.389 1 322.795 9 581.298 994.906 229.401 225.842 73 74 75 76 77 78 79 80 81 82
399.725
71
∂Q =0 ∂a
z
∂Q =0 ∂b
非线性形式方程的偏导数一般比较复杂,通常 很难求解。
2. 回归模型类型
1) 线性回归模型:参数线性,变量线性。
y = b 0 + b1 x
y=β0+β1x1+β2x2+…+βkxk
2) 内线性回归模型
参数虽不是线性,但经变换可使参数化 为线性形式,然后可按线性回归模型求解。
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
527 620.200 179 686.200 14 196.460 22 809.180 71 195.940 3 064.242 46 9416.700 5 738.953 8 359.465 6 205.016 6 0619.020 1 4517.740 31 020.100 26 447.160 7 985.926
0 . 0688 y = 33 . 666
例:某地区各林地景观斑块面积(m2)与周长(m)
序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 面积A 10 447.370 15 974.730 30 976.770 9 442.902 10 858.920 21 532.910 6 891.680 3 695.195 2 260.180 334.332 11 749.080 2 372.105 8 390.633 6 003.719 周长P 625.392 612.286 775.712 530.202 1 906.103 1 297.962 417.058 243.907 197.239 99.729 558.921 199.667 592.893 459.467 序号 42 43 44 45 46 47 48 49 50 51 52 53 54 55 面积A 232 844.300 4 054.660 30 833.840 1 823.355 26 270.300 13 573.960 65 590.080 157 270.400 2 086.426 3 109.070 2 038.617 3 432.137 1 600.391 3 867.586 周长P 4 282.043 289.307 895.980 205.131 968.060 1 045.072 2 250.435 2 407.549 266.541 261.818 320.396 253.335 230.030 419.406
